Derivative-Free Conformable Iterative Methods for Solving Nonlinear Equations
Abstract
1. Introduction
2. Deduction of the Methods
3. Convergence Analysis
4. Numerical Results
Qualitative Performance
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, W.; Liang, Y.; Cai, W. Hausdorff Calculus: Applications to Fractal Systems, 1st ed.; de Gruyter: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- Miller, K.S. An Introduction to Fractional Calculus and Fractional Differential Equations, 1st ed.; J. Wiley and Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, 1st ed.; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Fractional and Multivariable Calculus, Model Building and Optimization Problems, 1st ed.; Springer Optimization and Its Applications: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Akgül, A.; Grow, D. Fractal Newton Methods. Mathematics 2023, 11, 2277. [Google Scholar] [CrossRef]
- Akgül, A.; Cordero, A.; Torregrosa, J.R. A fractional Newton method with 2αth-order of convergence and its stability. Appl. Math. Lett. 2019, 98, 344–351. [Google Scholar] [CrossRef]
- Candelario, G.; Cordero, A.; Torregrosa, J.R. Multipoint Fractional Iterative Methods with (2α + 1)th-Order of Convergence for Solving Nonlinear Problems. Mathematics 2020, 452, 452. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Newton’s method with fractional derivatives and various iteration processes via visual analysis. Numer. Algorithms 2021, 86, 953–1010. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A.; Ozbilge, E. On Fractional Newton-Type Method for Nonlinear Problems. J. Math. 2022, 2022, 7070253. [Google Scholar] [CrossRef]
- Nayak, S.K.; Parida, P.K. The dynamical analysis of a low computational cost family of higher-order fractional iterative method. Int. J. Comput. Math. 2023, 100, 1395–1417. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal Order of One-Pont and Multipoint Iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2014, 279, 57–66. [Google Scholar] [CrossRef]
- Candelario, G.; Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. An optimal and low computational cost fractional Newton-type method for solving nonlinear equations. Appl. Math. Lett. 2022, 124, 107650. [Google Scholar] [CrossRef]
- Candelario, G.; Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Generalized conformable fractional Newton-type method for solving nonlinear systems. Numer. Algorithms 2023, 93, 1171–1208. [Google Scholar] [CrossRef]
- Candelario, G.; Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Solving Nonlinear Transcendental Equations by Iterative Methods with Conformable Derivatives: A General Approach. Mathematics 2023, 11, 2568. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J. Conformable fractional Traub’s method for solving nonlinear systems. Numer. Algorithms 2023. [Google Scholar] [CrossRef]
- Candelario, G. Métodos Iterativos Fraccionarios para la Resolución de Ecuaciones y Sistemas no Lineales: Diseño, Análisis y Estabilidad. Doctoral Thesis, Universitat Politècnica de València, Valencia, Spain, 2023. Available online: http://hdl.handle.net/10251/194270 (accessed on 16 May 2023).
- Singh, H.; Sharma, J.R. A fractional Traub-Steffensen-type method for solving nonlinear equations. Numer. Algorithms 2023. [Google Scholar] [CrossRef]
- Toprakseven, S. Numerical Solutions of Conformable Fractional Differential Equations by Taylor and Finite Difference Methods. J. Nat. Appl. Sci. 2019, 23, 850–863. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables, 1st ed.; Academic Press: Boston, MA, USA, 1970. [Google Scholar]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint Methods for Solving Nonlinear Equations, 1st ed.; Elsevier: St. Francisco, CO, USA, 2013. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations, 1st ed.; Prentice-Hall: Des Moines, IA, USA, 1964. [Google Scholar]
- Steffensen, J.F. Remarks on iteration. Scand. Actuar. J. 1933, 1, 64–72. [Google Scholar] [CrossRef]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics, 1st ed.; Addison-Wesley Longman Publishing: Boston, MA, USA, 1994. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 1st ed.; Dover Publications: Mineola, NY, USA, 1970. [Google Scholar]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Magreñan, A.Á. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]
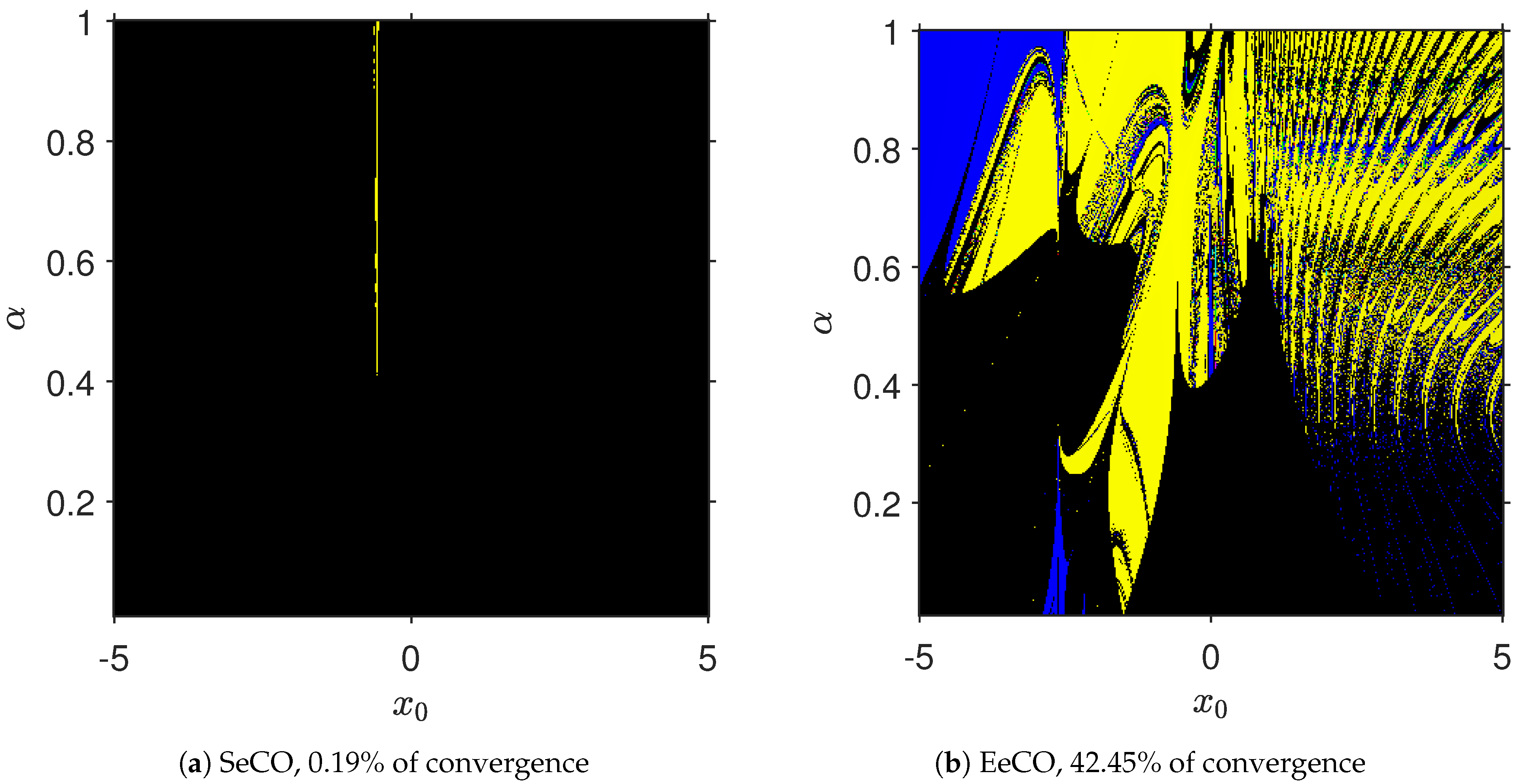
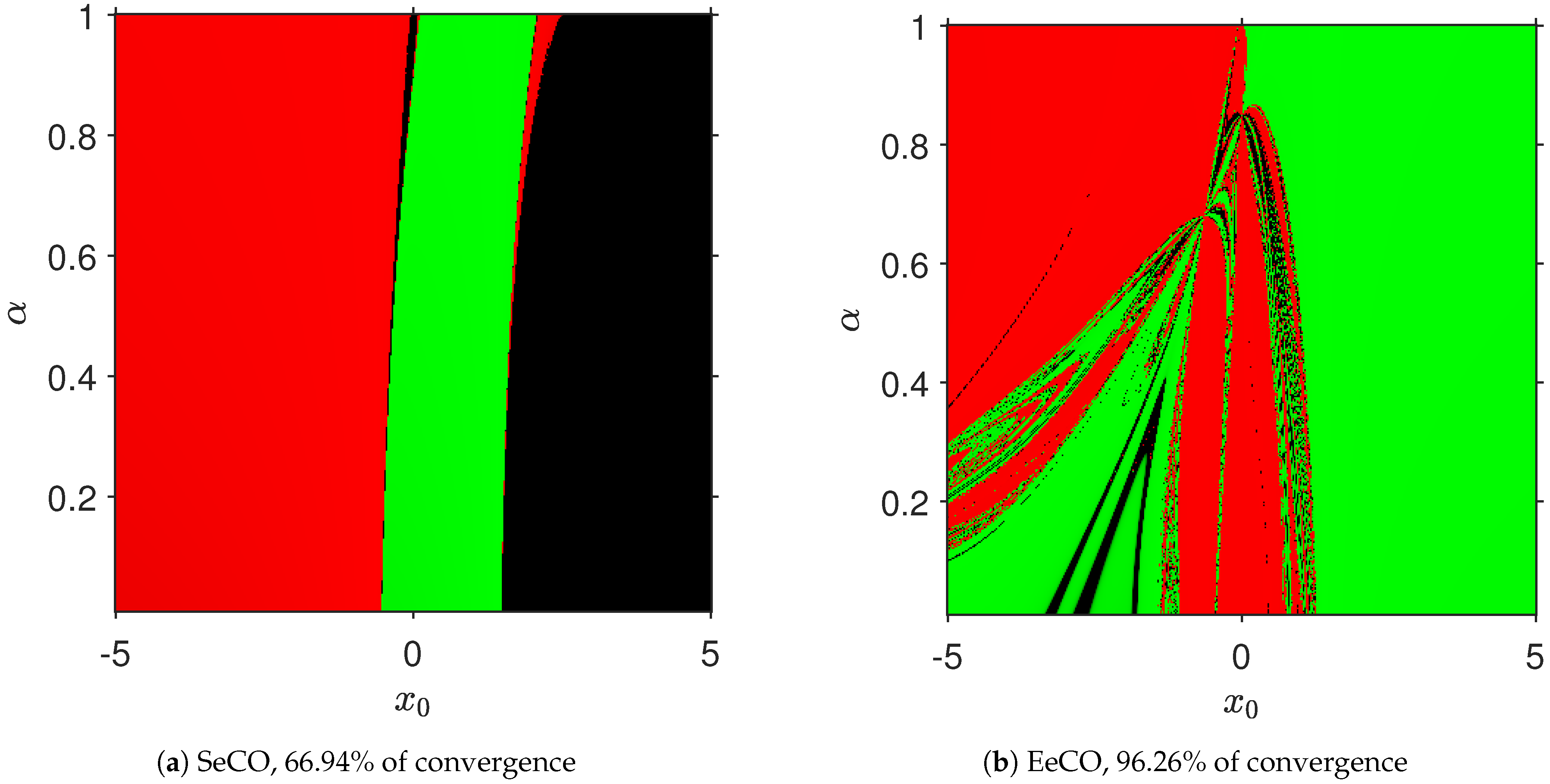
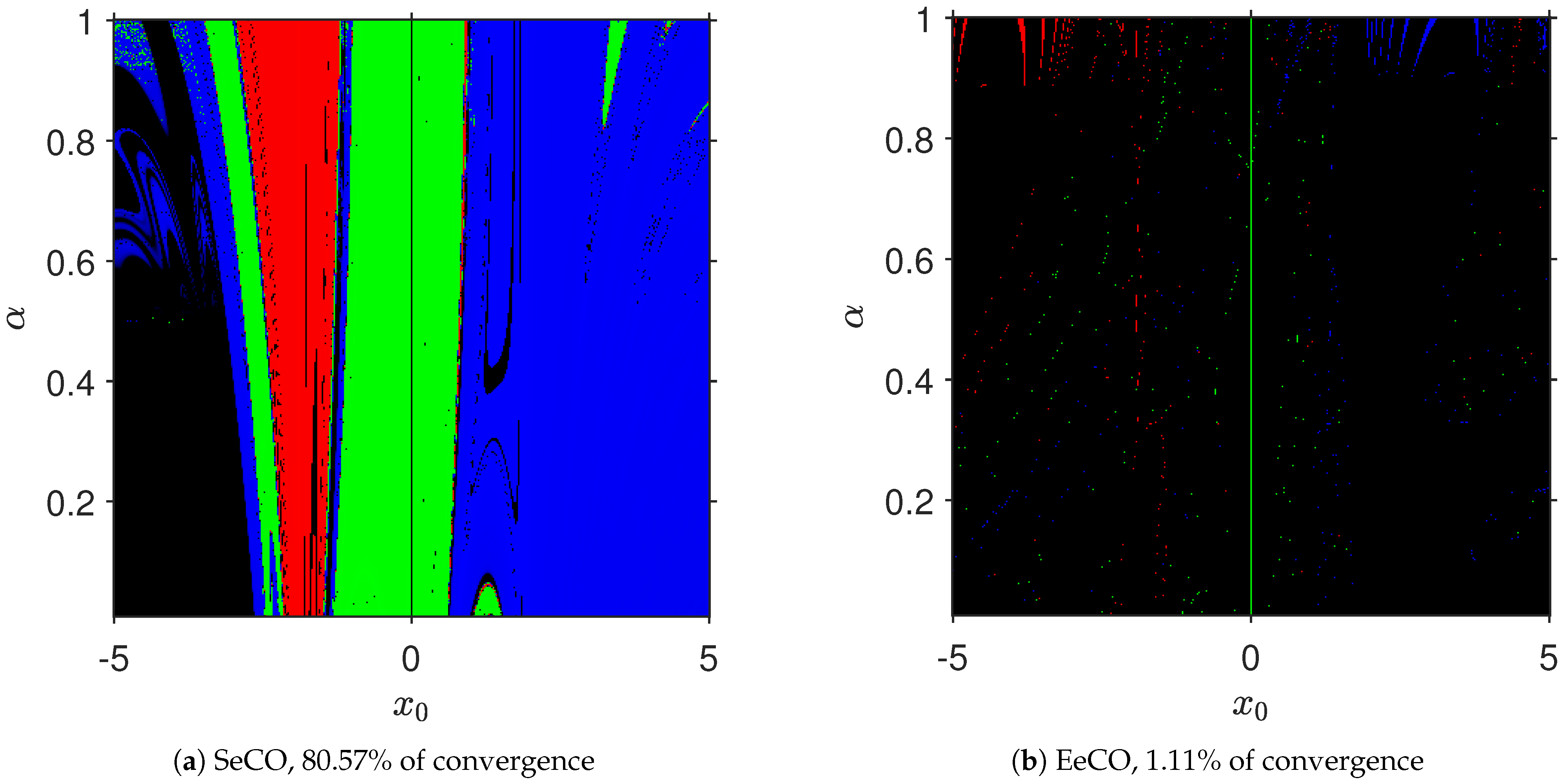
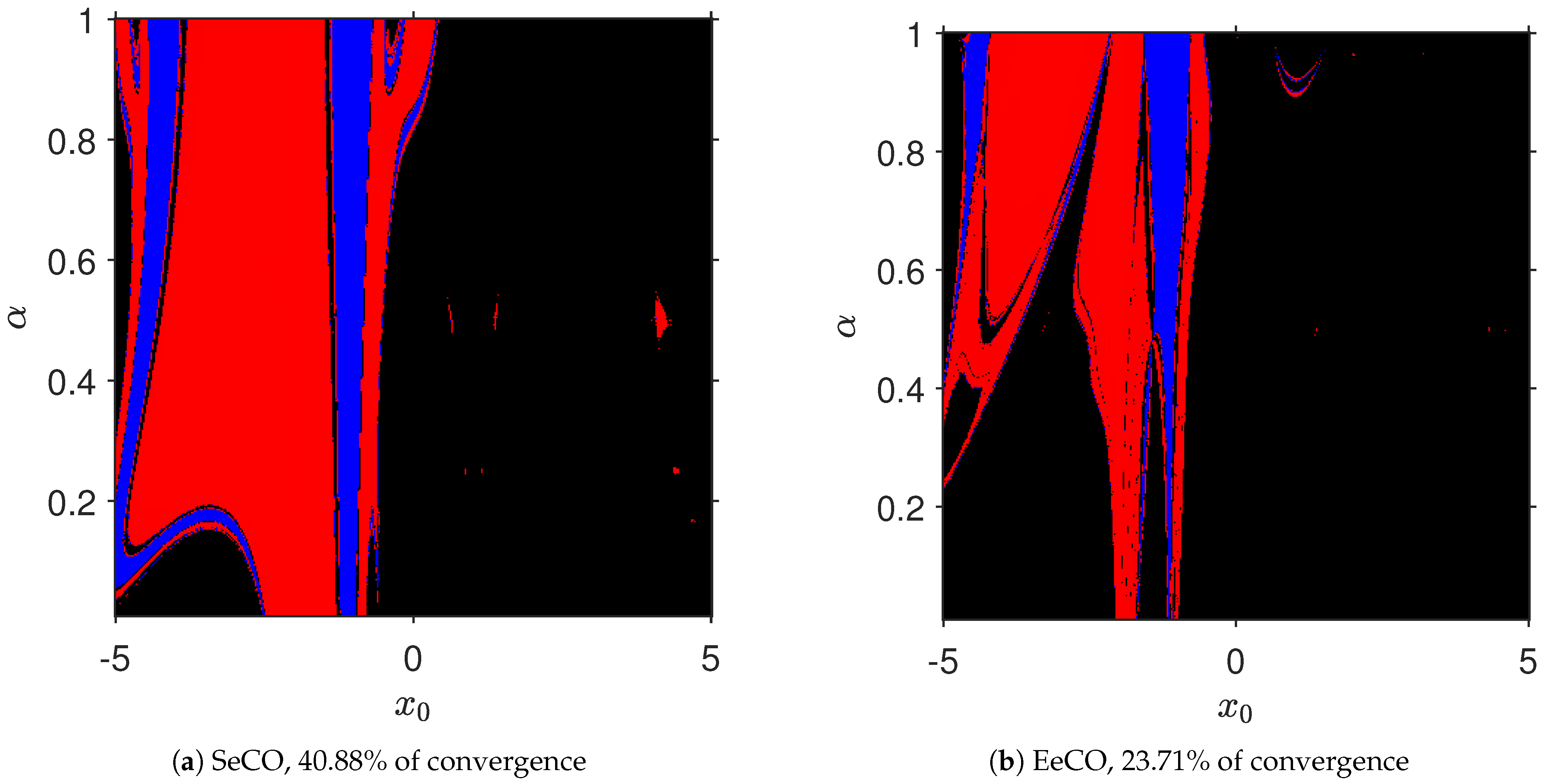
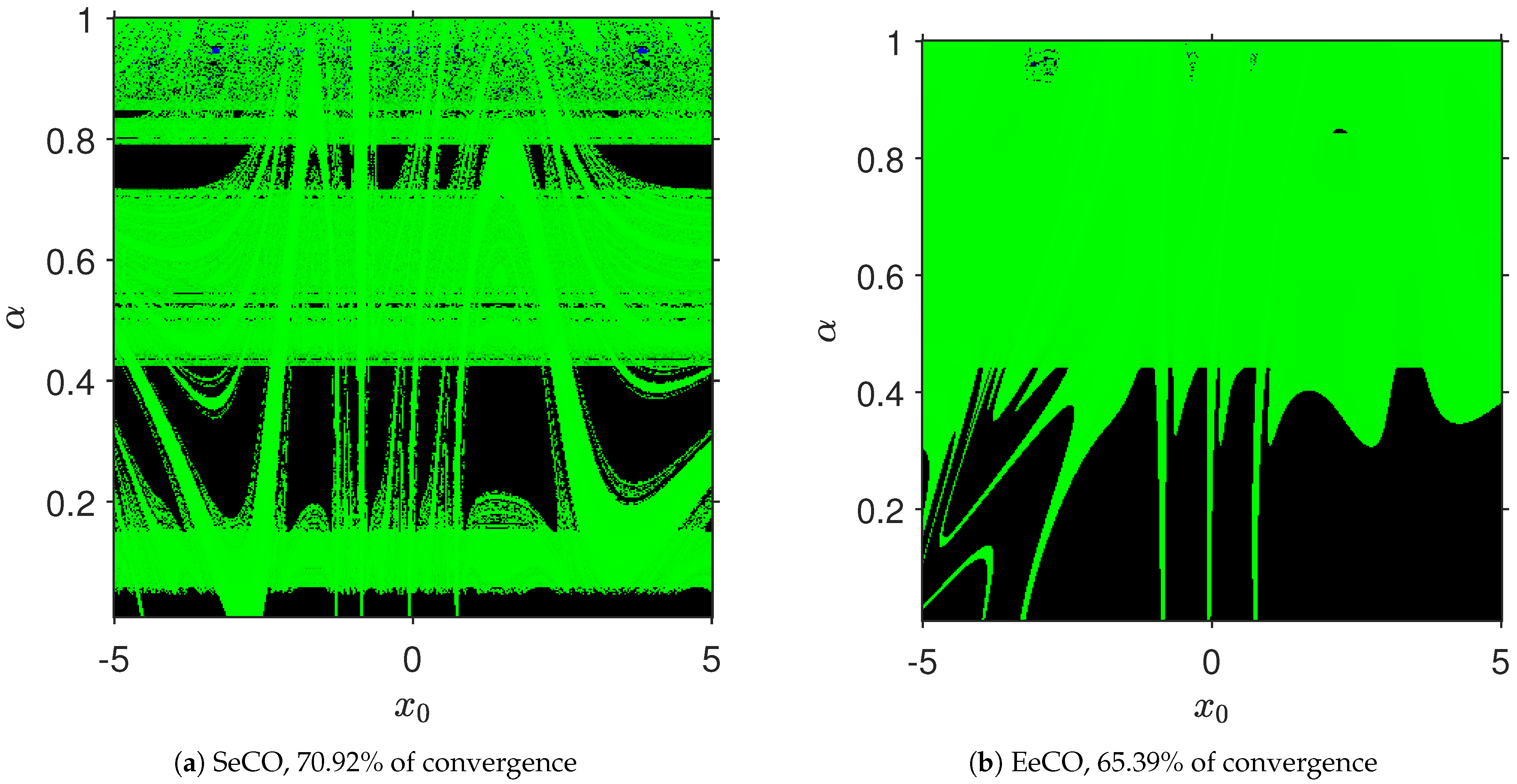
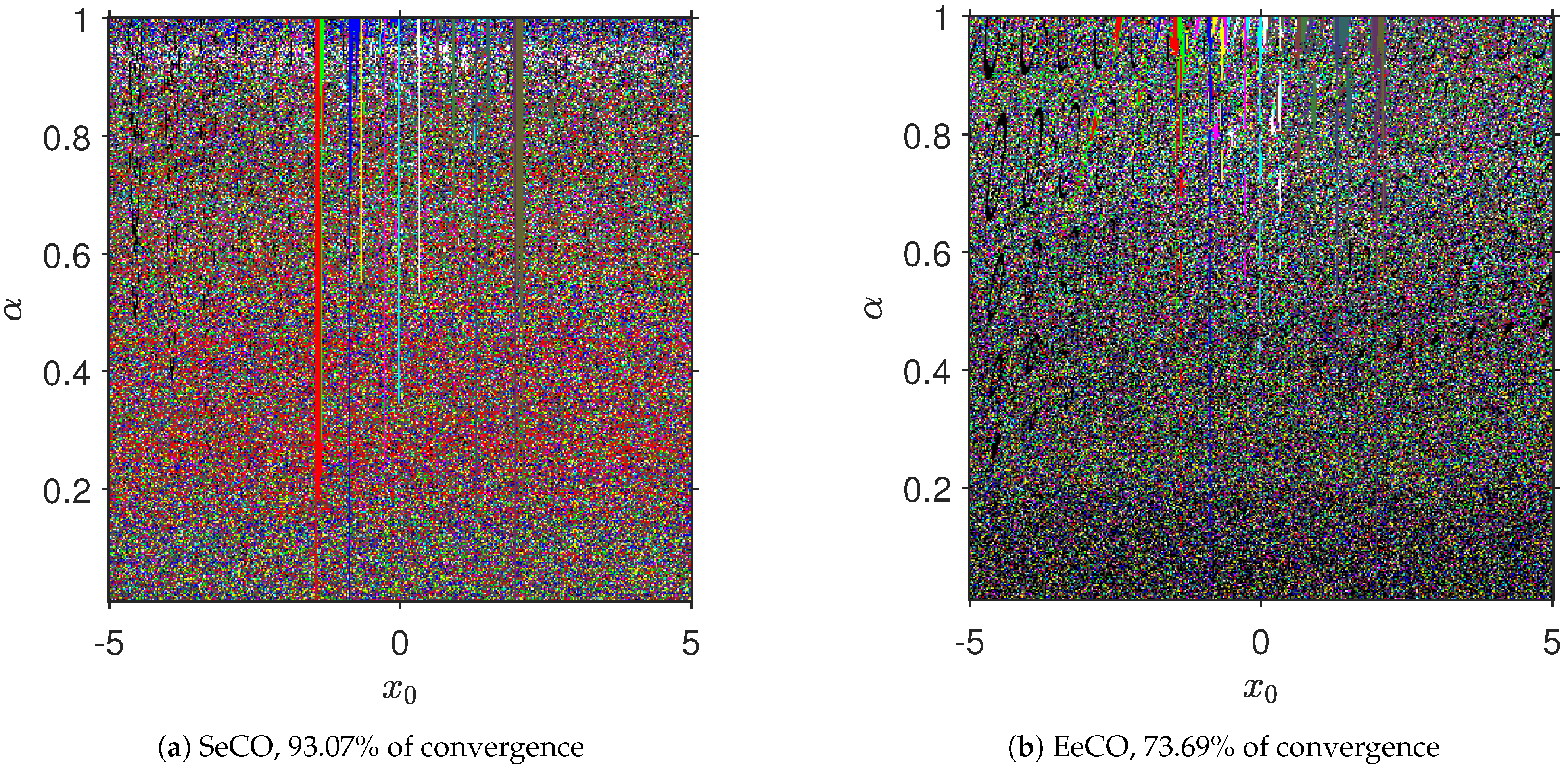
| SeCO Method | EeCO Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Iter | Iter | |||||||||
| 1 | 5 | 2.00 | 5 | 2.38 | ||||||
| 0.9 | 5 | 2.01 | 5 | 2.47 | ||||||
| 0.8 | 5 | 2.03 | 5 | 2.23 | ||||||
| 0.7 | 5 | 2.07 | 4 | 1.48 | ||||||
| 0.6 | 6 | 2.02 | 4 | 0.90 | ||||||
| 0.5 | 6 | 2.07 | 4 | 0.80 | ||||||
| 0.4 | 7 | 2.04 | 4 | 0.74 | ||||||
| 0.3 | 8 | 2.02 | 4 | 0.70 | ||||||
| 0.2 | 9 | 2.02 | 5 | 2.53 | ||||||
| 0.1 | 9 | 2.03 | 5 | 2.63 | ||||||
| SeCO Method | EeCO Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Iter | Iter | |||||||||
| 1 | 6 | 2.01 | 6 | 1.62 | ||||||
| 0.9 | 5 | 2.00 | 6 | 1.62 | ||||||
| 0.8 | - | - | - | - | - | 7 | 1.63 | |||
| 0.7 | - | - | - | >500 | - | 7 | 1.63 | |||
| 0.6 | - | - | - | >500 | - | 7 | 1.64 | |||
| 0.5 | - | - | - | >500 | - | 7 | 1.65 | |||
| 0.4 | - | - | - | >500 | - | 8 | 1.61 | |||
| 0.3 | - | - | - | >500 | - | 8 | 1.60 | |||
| 0.2 | - | - | - | >500 | - | 9 | 1.64 | |||
| 0.1 | - | - | - | >500 | - | 9 | 1.65 | |||
| SeCO Method | EeCO Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Iter | Iter | |||||||||
| 1 | 18 | 1.00 | 19 | 1.00 | ||||||
| 0.9 | 20 | 1.00 | 24 | 1.00 | ||||||
| 0.8 | 19 | 1.00 | - | - | - | - | - | |||
| 0.7 | 19 | 1.00 | 23 | 1.00 | ||||||
| 0.6 | 12 | 1.00 | 26 | 1.00 | ||||||
| 0.5 | 18 | 1.00 | 53 | 1.00 | ||||||
| 0.4 | 14 | 1.00 | - | - | - | - | - | |||
| 0.3 | 9 | 1.00 | 57 | 1.00 | ||||||
| 0.2 | 9 | 1.00 | 29 | 1.00 | ||||||
| 0.1 | 16 | 1.00 | 55 | 1.01 | ||||||
| SeCO Method | EeCO Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Iter | Iter | |||||||||
| 1 | 4 | 2.04 | - | - | - | - | - | |||
| 0.9 | 4 | 2.04 | 4 | 1.18 | ||||||
| 0.8 | 4 | 2.03 | 5 | 2.75 | ||||||
| 0.7 | 3 | 1.56 | 9 | 1.49 | ||||||
| 0.6 | 3 | 1.72 | - | - | - | - | - | |||
| 0.5 | 0.0335 | 2 | - | - | - | - | - | - | ||
| 0.4 | 3 | 1.78 | - | - | - | - | - | |||
| 0.3 | 4 | 2.01 | - | - | - | - | - | |||
| 0.2 | 5 | 2.00 | - | - | - | - | - | |||
| 0.1 | - | - | - | - | - | - | - | - | - | - |
| SeCO Method | EeCO Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Iter | Iter | |||||||||
| 1 | 11 | 2.09 | 11 | 2.51 | ||||||
| 0.9 | 131 | 2.00 | 9 | 1.06 | ||||||
| 0.8 | 15 | 3.01 | 11 | 1.36 | ||||||
| 0.7 | 33 | 2.67 | 8 | 1.49 | ||||||
| 0.6 | 17 | 1.97 | 7 | 1.89 | ||||||
| 0.5 | 7 | 2.04 | 6 | 3.60 | ||||||
| 0.4 | 9 | 1.76 | - | - | - | >500 | - | |||
| 0.3 | - | - | - | >500 | - | - | - | - | >500 | - |
| 0.2 | - | - | - | >500 | - | - | - | - | >500 | - |
| 0.1 | 7 | 2.04 | - | - | - | >500 | - | |||
| SeCO Method | EeCO Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Iter | Iter | |||||||||
| 1 | 20 | 2.00 | 17 | 1.20 | ||||||
| 0.9 | 16 | 2.01 | 10 | 0.74 | ||||||
| 0.8 | 18 | 1.99 | 11 | 1.31 | ||||||
| 0.7 | 28 | 2.02 | 24 | 1.38 | ||||||
| 0.6 | 23 | 2.01 | 23 | 1.14 | ||||||
| 0.5 | 21 | 1.95 | 20 | 1.81 | ||||||
| 0.4 | 95 | 2.05 | 14 | 1.98 | ||||||
| 0.3 | - | - | - | - | - | 104 | 1.37 | |||
| 0.2 | 66 | 1.47 | 175 | 1.67 | ||||||
| 0.1 | 58 | 2.00 | - | - | - | >500 | - | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Candelario, G.; Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Derivative-Free Conformable Iterative Methods for Solving Nonlinear Equations. Fractal Fract. 2023, 7, 578. https://doi.org/10.3390/fractalfract7080578
Candelario G, Cordero A, Torregrosa JR, Vassileva MP. Derivative-Free Conformable Iterative Methods for Solving Nonlinear Equations. Fractal and Fractional. 2023; 7(8):578. https://doi.org/10.3390/fractalfract7080578
Chicago/Turabian StyleCandelario, Giro, Alicia Cordero, Juan R. Torregrosa, and María P. Vassileva. 2023. "Derivative-Free Conformable Iterative Methods for Solving Nonlinear Equations" Fractal and Fractional 7, no. 8: 578. https://doi.org/10.3390/fractalfract7080578
APA StyleCandelario, G., Cordero, A., Torregrosa, J. R., & Vassileva, M. P. (2023). Derivative-Free Conformable Iterative Methods for Solving Nonlinear Equations. Fractal and Fractional, 7(8), 578. https://doi.org/10.3390/fractalfract7080578







