Abstract
Biological and financial models are examples of dynamical systems where both stochastic and historical behavior are important to be considered. The fractional Brownian motion (fBM) is commonly used, sometimes with fractional-order derivatives, to model the combined stochastic and fractional effects. Recently, spectral techniques are used to analyze models with fBM using, e.g., iterated Itô fractional integrals such as the fractional Wiener-Hermite (FWHE). In the current work, FWHE is generalized and adapted to be consistent with the Malliavin calculus approach. The conditions for existence and uniqueness are outlined in addition to the proof of convergence. The solution algorithm is described in detail. Using FWHE, the stochastic fractional model is replaced by a deterministic fractional-order system that can be handled using well-known mathematical tools to evaluate the solution statistics. Analytical solutions can be obtained for many important models such as the fractional stochastic Black–Scholes model. The convergence is studied and compared with the exact solution and high convergence is noticed compared with other techniques. A general numerical algorithm is described to analyze the resultant deterministic system in the case of no feasible analytical solutions. The algorithm is applied to study and simulate the population model with nonlinear losses for different values of the Hurst parameter. The results show the efficiency of FWHE in analyzing practical linear and nonlinear models.
1. Introduction
Many real-life applications require mathematical models with random and/or stochastic terms to account for the uncertainties originating from different internal and external sources. The classical Brownian motion (BM) is commonly used in modeling and analysis of such models. However, stochastic processes with history-dependency or long-distance correlations cannot be modeled with the classical BM and hence the fBM is developed to model processes with heavy tails such as internet traffic, biological systems, financial markets, and hydrology [1,2].
Modeling with fBM is characterized by the Hurst parameter which represents the decay rate power. In the case of , we return to the classical BM at which the model uncertainties are independent. In many applications, positively correlated behavior is noticed as the decay rate is slower than the exponential rate, and the Hurst parameter will be . Such models are called to be self-similar processes. In the case of models with negative correlations, violent fluctuations are noticed and the Hurst parameter in this case will be [3,4].
Real systems are more accurate than the classical ones when enabled to include the fractional effects. The memory or fractional effects can also be considered by the fractional derivatives and/or integrals. Fractional calculus is then developed as a natural extension of the classical one. Models driven by fractional derivatives and/or integrals should be analyzed and compared to the well-established integer-order models [5]. Another important rule of fractional derivatives is to describe some behaviors that could not be modeled with the integer-order derivatives. The anomalous diffusion, observed in biological and other models, is an important example where using the integer-order derivatives could not describe the model while using the fractional derivatives enables to describe the sub-/super-diffusion behavior [6,7].
There is much research work conducted for studying the stochastic and random effects in the case of models with integer-order and/or fractional-order derivatives. For techniques based on solving the Fokker–Planck equation, analytical solutions, numerical approaches, and transformations, see [2,8] and references therein.
In the literature, there are some developed methods to study the stochastic models excited by fBM. One example is the Euler–Maruyama (EM) technique that requires generating samples of the fBM [9]. The drawbacks of using sampling-based techniques are the slow convergence rate, which is only 0.5 order for the classical EM and () for the fractional EM with the Hurst parameter [10]. Additionally, some difficulties arise in generating fractionally correlated samples. Recent research works have tried to enhance the performance of EM, for example, using the sum-of-exponential technique [9,11]. Spectral techniques are good alternatives with higher efficiency than EM-based techniques. Examples include using Haar wavelets [12] and the recently developed FWHE that uses Hermite functionals of the fractional noise [2]. The spectral techniques have many advantages such as obtaining analytical exact or approximate statistics for many models with high convergence rates, sometimes exponential, without generating the time-consuming samples.
In the current work, we generalize the development of FWHE and outline the solution strategy along with the required mathematical background for the solution’s existence and uniqueness. The FWHE is then used to analyze some common models that appear in biology and finance such as the fractional stochastic Black–Scholes and population models. Both analytical and numerical techniques using FWHE are outlined, verified, and compared.
The paper is organized into five sections. Section 2 introduces the required background and definitions. Development of FWHE is reviewed and extended in Section 3 along with the solution methodology and the required conditions. Section 4 discusses the application of FWHE to some models. Conclusions are listed in Section 5.
2. Mathematical Background
Many definitions for fractional integration and differentiation exist in the literature. Examples are Riemann–Liouville (RL), Grunwald–Letnikov (GL), Caputo, Hilfer, Hadamard, and many others that are still under investigation [13]. For the advantages and disadvantages of each definition, we can refer to [14]. In the current work, we shall consider using the RL definition in the analysis as it appears naturally in our derivations and due to other advantages as outlined below.
Consider the locally integrable function , the RL integral of order is:
where is the Gamma function of . The operator is a continuous, bounded, and linear operator from to itself and satisfies [15]:
The GL fractional integral of order can be given as:
where and .
For the fractional differentiation, the RL differential operator of order is defined as:
This is an mth-order derivative of the order fractional integral of . The Caputo definition, slightly different from RL, is also commonly used and is defined as:
This is an order fractional integral to the mth-order derivative of . The definition of the GL fractional derivative of order can be simply obtained by replacing with − in (3). If , both GL and RL definitions are equivalent. This provides a numerical technique for analyzing models with fractional RL integrals and/or derivatives.
It is straightforward to show that for the RL definitions [16]:
But:
And hence, it requires m initial conditions of different fractional orders . For m = 1 (i.e., ), we obtain [17]:
The RL and Caputo fractional definitions are related as:
Relation (9) is helpful to transform the fractional-order initial conditions (7), (8) required when using the RL definition to integer-order conditions. This eliminates one of the common RL drawbacks in the analysis. Moreover, the Caputo definition is not consistent with the classical integer-order derivative when the derivative order as we have:
Another drawback of the RL definition is the singular kernel that causes difficulties in handling the fractional derivatives. These drawbacks lead the researchers to suggest other stable definitions of the fractional operators [18,19,20,21].
The fBM process appears in many real applications to model oscillations that depend on the memory or history. The process starts from zero and is Gaussian with:
It has continuous trajectories and satisfies that the increments are homogeneous with the same law for all . The covariance function of fBM is defined as:
The paths of fBM are almost Hölder continuous everywhere in order , i.e., there exists and such that:
Moreover, the fBM process is not a semi-martingale for . Additionally, the process is nowhere differentiable in the classical sense. But, as will be shown below, we shall consider the Malliavin calculus at which the sense of differentiation is wider and the derivatives of can be defined. The derivative of the classical BM process is known as the white noise , i.e., . Similarly, the derivative of , also known as the fractional noise is used in some analysis approaches instead of fBM. It is straightforward to show that can be written as the order derivative of the noise , i.e., .
The Malliavin calculus and the white noise approach as outlined in [22,23] will be considered in the current work. In this approach, the space of smooth functions on that are rapidly decreasing is considered. This space is also known as the Schwartz space . For persistent processes, in the case of Hurst parameter , the function is defined as:
It will be used as a kernel function and it satisfies:
The inner-product function will be equipped with the space and is defined as:
The function should satisfy:
Stochastic integrals with respect to BM are also known as Skorohod integrals or divergence-type integrals. In case of adapted processes , the Skorohod integral will be equivalent to the Itô integral. The Skorohod integral is defined as the adjoint operator of the Malliavin derivative where the definition of differentiability of processes is extended to a wider sense. This enables to define the differentiation of the stochastic processes that are not differentiable in the classical sense.
The stochastic models can be analyzed in different senses such as Itô and Stratonovich. In the current work, the Itô sense is considered. Conversion to Stratonovich or any other sense is straightforward.
The classical Itô integral can be extended to the fBM case after considering the Malliavin calculus and the dual Schwartz space of all tempered distributions; we can write the derivative which is the fractional white noise process.
The stochastic integral of a square integrable function is well defined and is Gaussian with zero mean and variance as defined in (17). In the white noise analysis, the integral is defined in terms of the fractional white noise as:
where the operator is the Wick product [24]. The product of two fractional stochastic integrals for two square-integrable functions and has an average value computed as:
We define the iterated Itô integral for the square integrable function in the domain as:
Then, it is straightforward to obtain:
Which means . It is common to assume that the variables are symmetric and hence integral (20) will be evaluated in the domain and multiplied by .
Theorem 1
([22,25]). Consider the complete filtered probability space with all mean-square integrable processes , i.e., , then there exists a sequence of kernels with such that:
The mean and .
The proof of Theorem 1 can be constructed using the white noise analysis as follows. Consider the function , such that , and let the Hermite polynomials be . From this, we define the following functions: and the set which construct an orthonormal basis for . Consider the pairing between and ; then, we can write and can be expanded as . According to Bochner–Minlos theorem [26], we can obtain the Fourier transform given as:
where is a measure on . We define the exponential functional , and we can write:
If we consider the sequences of finite indices with such that , and the Hermite functionals , then we can write:
Which means that is a dense linear span in . We use the fundamental Itô theorem to write in iterated Itô integrals as:
So, the function can be expanded as iterated Itô fractional integrals as:
where . By assuming the symmetry of variables , the proof is now complete. The mean and variance are computed as declared above.
The theorem does not provide the technique to obtain the deterministic kernels . To make use of the FWHE and to obtain the solution statistics, we should have a practical technique to evaluate the expectations . This will be described in the following sections.
In the current work, persistent processes, at which , are considered due to their wide applications compared with anti-persistent processes. In the analysis using fBM or the fractional noise, terms such as and are common. So, we can define the parameter such that . This means that for the persistent processes and for the anti-persistent processes. The case of will be for the classical BM analysis.
3. Construction of FWHE Basis
We shall follow [2] and extend the development of FWHE basis functionals and use their properties to derive the solution statistics. The Hermite functions will be selected to represent the basis of FWHE due to their properties that are suitable for the Gaussian processes such as fBM. We shall consider Hermite functionals of the fractional noise processes with representing the time or any of the auxiliary variables . The auxiliary variables are used as pseudo-time variables in the case of higher-order approximations being included. We can design the basis of Hermite functionals to be orthogonal as follows. As is common in the Hermite polynomials, the zero and first-order functionals should be and . The second-order Hermite functional that is zero-mean and is orthogonal to both and can be deduced as:
Following the same idea with all Hermite functionals, we can deduce the following recurrence relation:
The set of Hermite functionals will construct a complete orthogonal set in the Hilbert space that is associated with the inner product defined in (16). This orthogonal set will be used as a basis to represent the stochastic process of the fractional Brownian motion. Using , the nth-order iterated Itô integrals appearing in the FWHE can be expressed as:
The FWHE of any stochastic process with can be expressed as:
For brevity, we can write and eliminate the parameters to write:
where and are the deterministic and Hermite functionals, respectively. Practically, we need only the first-degree approximation for the Gaussian processes that appear usually as linear stochastic differential equations (SDEs) with additive noise. For the non-linear SDEs, additional higher-order terms should be included for higher accuracy. The FWHE has the mean-square convergence property, i.e.,:
It has been shown that [27] Wiener-Hermite expansion (WHE) and, similarly, its fractional extension FWHE have a high convergence rate when approximating Gaussian and near-Gaussian processes. Only a few terms will be sufficient for the analysis, as shall be shown below.
3.1. Existence and Uniqueness
Consider the following SDE excited with fBM:
where with is a Euclidean space of dimension d. The functions should satisfy Lipschitz continuity in both and in addition to the bounded linear growth criteria. The process is, in general, a d-dimensional independent Brownian vector with Hurst indices , i.e., . The initial condition process is assumed to be independent of and satisfies . The model fractional SDE (30) with the associated conditions should have a unique mild solution in the form [28]:
3.2. Methodology to Analyze SDEs Using FWHE
To analyze (30) using FWHE, we replace and its initial value with their FWHE expansions:
To obtain:
where are the kernels of the initial condition . The deterministic kernels can be obtained by multiplying (32) with and then applying the mean operator. For the mean , we obtain:
And for the other kernels :
We solve (33) and (34) to obtain the kernels . The mean is computed as . The variance is evaluated as:
One of the main issues in using FWHE is to obtain . Using the definition (14), we can show that [2]:
The first approximation of variance is evaluated as:
We can notice the symmetry of the integral (37) with respect to parameters u and v and also with respect to the region of integration, see Figure 1.
Figure 1.
Symmetry of the integration domain.
So, we can integrate only on the half region and write:
The integral with respect to is an order fractional integral to , i.e., we can write:
where is the RL integral of order to .
The first-order (Gaussian contribution) variance has a fractional-order integral of order followed by an integer-order integral. A close relation to fractional calculus is noticed in computing the solution moments using FWHE. For , the variance will be:
And in general, we can write the following variance formula:
We can note that each term of the variance requires fractional integrals with respect to the disposable variables followed by integer-order integrals with respect to same variables. For simple expressions, analytical formulae can be obtained, otherwise numerical techniques will be required as described in the next section.
For , we return to variance formula of WHE [27]:
4. Examples
Two practical examples are analyzed in this section, one analytically and the other numerically, to show the efficiency and validity of FWHE. We start with the well-known Black–Scholes model as it has an exact solution to compare with in addition to its importance in biology and finance. The population model with nonlinearities will be also considered. In this case, there is no practical exact solution and there will be a need for an approximate and/or numerical solution. The two models discussed in this section have multiplicative fractional noise and hence require some additional efforts compared with the additive noise models that are usually Gaussian and straightforward to be analyzed using FWHE as shown in [2].
4.1. Model 1: Black–Scholes SDE
The Black–Scholes SDE motivated with fBM Brownian motion and a deterministic initial condition is considered in this section. The model with positive correlation is common in finance and biology.
where and are deterministic parameters. We should note here that Equation (43) can be written in the Wick sense as:
Then, we can directly show that the exact solution is:
where is the exponential function in Wick sense. In financial applications, using Wick calculus with dual Schwartz space enables researchers to make use of the Black–Scholes model to obtain a solution with no arbitrage. Financial markets with arbitrage appear when following the classical pathwise approach instead of the white noise approach [24].
To obtain the solution in the classical calculus, we use the relation:
where is the ordinary/classical exponential function. This means that the solution is:
The following relations are helpful to obtain the statistical properties:
The exact mean is then obtained as follows:
The variance is computed similarly as:
We apply FWHE in (43) after dividing by to obtain:
To obtain the initial conditions of kernels , we multiply (51) by and apply the statistical mean at t = 0 to obtain:
where the functional is defined as:
and it commonly appears in the FWHE analysis. We multiply (51) by and apply the expectation to obtain:
This is the exact mean as in (49). We multiply (51) by and apply the mean to obtain:
We solving for to obtain:
Using the variance formula (41), the first variance approximation is:
which is an approximation of the variance (50). At , the first variance approximation is , which is consistent with the WHE solution [25]. To obtain , we multiply (51) by and apply the mean to obtain:
The right side RHS in (59) can be expressed as:
We solve for the kernel to obtain:
The second approximation of the variance is now obtained as:
This is an approximation of the exact variance (50). Extra approximations are straightforward to deduce the nth-order kernel as:
which means that the kernels are decaying exponentially. An variance approximation will be:
which converges to the exact variance (50) as . We can notice the exponential convergence in this example when using FWHE. The high convergence rate of FWHE makes it an attractive technique in analyzing models with fBM.
Models with additive noise can also be handled analytically. For example, the well-known Ornstein–Uhlenbeck process is as follows:
It is straightforward to show that and exact variance is . In the case of constant coefficients and , the mean will equal and variance will be [2].
4.2. Model 2: Population Growth SDE
Another important model that commonly appears in many biological and financial applications is the stochastic population model. This model is like the Black–Scholes model but with an additional term, usually nonlinear quadratic, that represents some losses in the system. The nonlinear losses make the analytical analysis not easy to obtain. The equivalent deterministic system, after using FWHE, will be coupled and nonlinear. Numerical analysis will be a good choice in this case. There are many well-known numerical techniques to analyze nonlinear systems, see, e.g., Ref. [29], but extension for the fractional nonlinear systems is still required. In the current example, we suggest an algorithm to numerically analyze the resulting nonlinear fractional system that appears when applying the FWHE. The numerical technique is described for a first-order approximation but extension to a higher accuracy is straightforward.
Consider the population model with quadratic losses motivated by a multiplicative fBM:
where , , and are deterministic coefficients. The term represents nonlinear quadratic losses in the system due to some internal or external effects.
In the case of a deterministic system (), we have:
This is a Bernoulli differential equation with the solution:
For , the mean solution approaches a finite carrying capacity as . For , the solution decays to zero. In the case of > 0, model (66), there is a unique positive solution [30]:
in the Wick calculus. In the classical calculus, the equivalent solution will be:
The solution (70) is convergent to a stationary Gamma distribution in the case of . And for , the solution converges almost surely to zero. If , the solution will be oscillatory as it is primarily driven by the fBM [31].
It is not easy to use the exact solution (70) to obtain the moments of such as the mean and variance. In the current work, FWHE along with numerical techniques are used to approximate the kernels and statistics as follows.
We re-write (66) after dividing by dt, write , and then apply FWHE to obtain:
Then:
We take average of (72) to obtain:
where is the variance of as given in (41). To obtain and hence the variance, we multiply (72) by and apply the average to obtain:
But:
where the dots mean higher-order neglected terms. Then, the first-order approximation will result in the system:
and
With the initial conditions and .
The time axis t can be discretized into equidistant subintervals with constant width . The auxiliary axes () can also be subdivided similarly with, for simplicity, . Using the Euler first-order technique for the derivative and the trapezoidal second-order rule for the integration, the discrete form will be as follows:
where and . We solve (78) to obtain as:
where the weights when using the trapezoidal rule. A good approximation is to assume only, and hence we can analytically obtain:
The fractional integral can be now approximated for each using, e.g., the GL technique:
where are the GL coefficients (3). Then, the integral is approximated using the trapezoidal rule to obtain:
Finally, we can solve for by discretizing (76) to obtain:
We can summarize the proposed numerical algorithm as follows: from (78), we solve for ; then, from (79 or 80), we solve for ; and finally, from (83), we solve for .
For , , = 0.05, = 0.5, = 0.01, = 0.02, and the solution mean and variance are shown in Figure 2. We can notice that increasing the Hurst parameter will smooth the solution (less oscillations) but at the same time increase the variance. In the case of being relatively small, as in the current case, the mean is not sensitive to the Hurst parameter and hence the stochastic (diffusion) term is small compared to the mean solution.
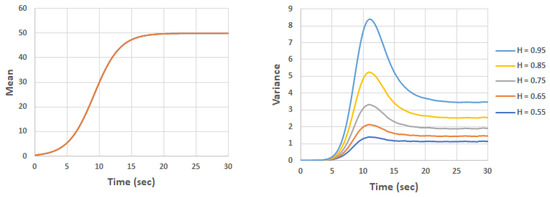
Figure 2.
Mean and variance for the population model at .
The numerical solution accuracy is dominated with the lowest approximation order which is the GL approximation in our case. Higher-order approximations for the fractional integrations can be used instead, see, for example, [32]. The numerical time integration can be enhanced as well using higher-order time integration such as the modified Euler technique.
Adding more kernels to the FWHE will enhance the numerical solution as well. As outlined in example 1, the FWHE kernels are decaying exponentially. For the population example, the first term of variance is of order 1 while an additional kernel will affect the variance only with order 10−5. The details will be similar as above but are deleted here for brevity.
The above results assure the efficiency of the FWHE by obtaining an accurate solution with only a few terms. Only one additional kernel will be sufficient to accurately quantify the non-Gaussian contribution. This is clear from the design of FWHE with basis functionals of fBM. The drawback in using FWHE is the appearance of multiple integrals of integer and/or fractional orders that may complicate the analysis in some cases.
Extension to the case of the presence of fractional-order derivatives in the model analyzed by FWHE is straightforward. The resulting deterministic system will include mixed integer-order and fractional-order derivatives in addition to the fractional-order integrals naturally appearing from using FWHE. In this case, the above numerical algorithm should be modified to account for approximating the mixed derivatives and integrals.
5. Conclusions
In this paper, the FWHE is generalized to analyze real-life models commonly appearing in financial and biological applications. The models are excited with fractional Brownian motion in addition to integer- and/or fractional-order derivatives. The theoretical background and the existence conditions for analyzing fractional SDEs with FWHE are outlined. The FWHE when used with the statistical properties of the fractional Brownian motion will simplify the stochastic model to a set of deterministic equations that are analyzed to obtain the solution statistics. The FWHE basis functionals depend on the fractional noise and hence are efficient in approximating fractional stochastic models with high accuracy. The accuracy of the approximations is shown to be of exponential order when analyzing the fractional Black–Sholes model which is linear with multiplicative fractional noise. In case of nonlinearities, a numerical technique is described to obtain the solution statistics. The fractional stochastic population model with quadratic nonlinear losses is analyzed numerically for different Hurst parameters . The variance is found to increase with the Hurst parameter. The developed numerical algorithm is general for linear and nonlinear models and its accuracy can be enhanced using higher-order integrations and differentiation techniques.
The current research study is planned to be further extended in the future to enhance the accuracy of the numerical treatment and to account for the case at which the initial conditions and/or the model parameters are correlated with the Brownian motion. Also adding fractional-order derivatives to the model should enable us to analyze more complicated models. Using recent definitions of the fractional-order derivatives, other than RL, is worthwhile to be considered as well.
Author Contributions
Methodology and conceptualization, A.N. and M.B.; software, A.N. and M.E.-B.; validation, M.B. and M.E.-B.; formal analysis, M.B.; investigation, A.N. and M.E.-B.; resources, A.N. and M.E.-B.; data curation, M.B. and M.E.-B.; writing—original draft preparation, M.B.; writing—review and editing, A.N. and M.E.-B.; visualization, A.N. and M.B.; supervision, A.N.; project administration, M.B.; funding acquisition, A.N. and M.E.-B. All authors have read and agreed to the published version of the manuscript.
Funding
Authors appreciate the funding from the Deputyship for Research Innovation, Ministry of Education in Saudi Arabia through project number IFPHI-005-611-2020. Appreciation is also given to King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- El-Beltagy, M.; Etman, A.; Maged, S. Development of a fractional Wiener-Hermite expansion for analyzing the fractional stochastic models. Chaos Solitons Fractals 2022, 156, 111847. [Google Scholar] [CrossRef]
- Schennach, S. Long memory via networking. Econometrica 2018, 86, 2221–2248. [Google Scholar] [CrossRef]
- Witt, A.; Malamud, B. Quantification of long-range persistence in geophysical time series: Conventional and benchmark-based improvement techniques. Surv. Geophys. 2013, 34, 541–651. [Google Scholar] [CrossRef]
- Paweł, Ł.; Rafał, P. On the equivalence between fractional and classical oscillators. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106871. [Google Scholar] [CrossRef]
- Saporta-Katz, O.; Efrati, E. Self-driven fractional rotational diffusion of the harmonic three-mass system. Phys. Rev. Lett. 2019, 122, 024102. [Google Scholar] [CrossRef] [PubMed]
- Sabri, A.; Xu, X.; Krapf, D.; Weiss, M. Elucidating the origin of heterogeneous anomalous diffusion in the cytoplasm of mammalian cells. Phys. Rev. Lett. 2020, 12, 058101. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Aifantis, E. Stochastically forced dislocation density distribution in plastic deformation. Phys. Rev. E 2016, 94, 022139. [Google Scholar] [CrossRef]
- Huang, J.; Huo, Z.; Zhang, J.; Tang, Y. An Euler–Maruyama method and its fast implementation for multiterm fractional stochastic differential equations. Math. Methods Appl. Sci. 2023, 46, 1556–1573. [Google Scholar] [CrossRef]
- Yaozhong, H.; Liu, Y.; Nualart, D. Modified Euler approximation scheme for stochastic differential equations driven by fractional Brownian motions. arXiv 2013, arXiv:1306.1458. [Google Scholar]
- Zhang, J.; Tang, Y.; Huang, J. A fast Euler-Maruyama method for fractional stochastic differential equations. J. Appl. Math. Comput. 2023, 69, 273–291. [Google Scholar] [CrossRef]
- Wen, X.; Huang, J. A Haar wavelet method for linear and nonlinear stochastic Itô-Volterra integral equation driven by a fractional Brownian motion. Stoch. Anal. Appl. 2021, 39, 926–943. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order; Springer: Berlin/Heidelberg, Germany, 1997; pp. 223–276. [Google Scholar]
- Atangana, A.; Secer, A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef]
- Atangana, A. Fractional Operators with Constant and Variable Order with Application to Geo-Hydrology, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Weilbeer, M. Efficient Numerical Methods for Fractional Differential Equations and Their Analytical Background. PhD Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2006. [Google Scholar]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Kilicman, A.; Ahmood, W. On some applications of the multi-dimensional new fractional calculus for the Riemann-Liouville with Atangana-Balenau. Int. J. Pure Appl. Math. 2016, 111, 373–381. [Google Scholar] [CrossRef][Green Version]
- Shah, N.; El-Zahar, E.; Chung, J. Fractional analysis of coupled Burgers equations within Yang Caputo-Fabrizio operator. J. Funct. Spaces 2022, 2022, 6231921. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Lopes, A. Spectral solutions for fractional Black–Scholes equations. Math. Probl. Eng. 2022, 2022, 9365292. [Google Scholar] [CrossRef]
- Kesue, L.; Jigen, P. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar] [CrossRef]
- Biagini, F.; Hu, Y.; Øksendal, B.; Zhang, T. Stochastic Calculus for Fractional Brownian Motion and Applications; Springer: London, UK, 2008. [Google Scholar] [CrossRef]
- Zaugg, N. Stochastic Calculus for Fractional Brownian Motion. Master’s Thesis, Universiteit Utrecht, Utrecht, The Netherland, 2022. [Google Scholar]
- Holden, H.; Øksendal, B.; Ubøe, J.; Zhang, T. Stochastic Partial Differential Equations A Modeling, White Noise Functional Approach, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- El-Beltagy, M. A practical comparison between the spectral techniques in solving the SDEs. Eng. Comput. 2019, 36, 2369–2402. [Google Scholar] [CrossRef]
- Tlas, T. Nonstandard proofs of Herglotz, Bochner and Bochner–Minlos theorems. J. Fourier Anal. Appl. 2015, 21, 1–10. [Google Scholar] [CrossRef]
- El-Beltagy, M.; El-Tawil, M. Toward a solution of a class of non-linear stochastic perturbed PDEs using automated WHEP algorithm. Appl. Math. Model. 2013, 37, 7147–7192. [Google Scholar] [CrossRef]
- Ahmadova, A.; Mahmudov, N. Existence and uniqueness results for a class of fractional stochastic neutral differential equations. Chaos Solitons Fractals 2020, 139, 110253. [Google Scholar] [CrossRef]
- Kelley, C. Solving Nonlinear Equations with Newton’s Method; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar] [CrossRef]
- Noor, A.; Barnawi, A.; Nour, R.; Assiri, A.; El-Beltagy, M. Analysis of the Stochastic Population Model with Random Parameters. Entropy 2020, 22, 562. [Google Scholar] [CrossRef] [PubMed]
- Giet, J.; Vallois, P.; Wantz-Mezieres, S. The logistic S.D.E. Theory Stoch. Process. 2015, 20, 28–62. [Google Scholar]
- Cai, M.; Li, C. Numerical approaches to fractional integrals and derivatives: A Review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).