Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review
Abstract
1. Introduction
- A systematic review procedure that describes the relationship between the MHA and FOCs optimization is presented;
- The searching keywords are introduced;
- The searching resources included four popular databases such as Scopus, Web of Science, Science Direct and Google Scholar;
- The FOCs include PI, PID, Type-1 and Type-2 fuzzy controllers;
- The search domain is focused on the recent work published only during the last decade (2014:2023);
- The popular objective functions, used in the optimization process, are presented.
2. Classical Integer-Order Control Systems
2.1. Classical PID Controller
2.2. Classical Fuzzy Controller
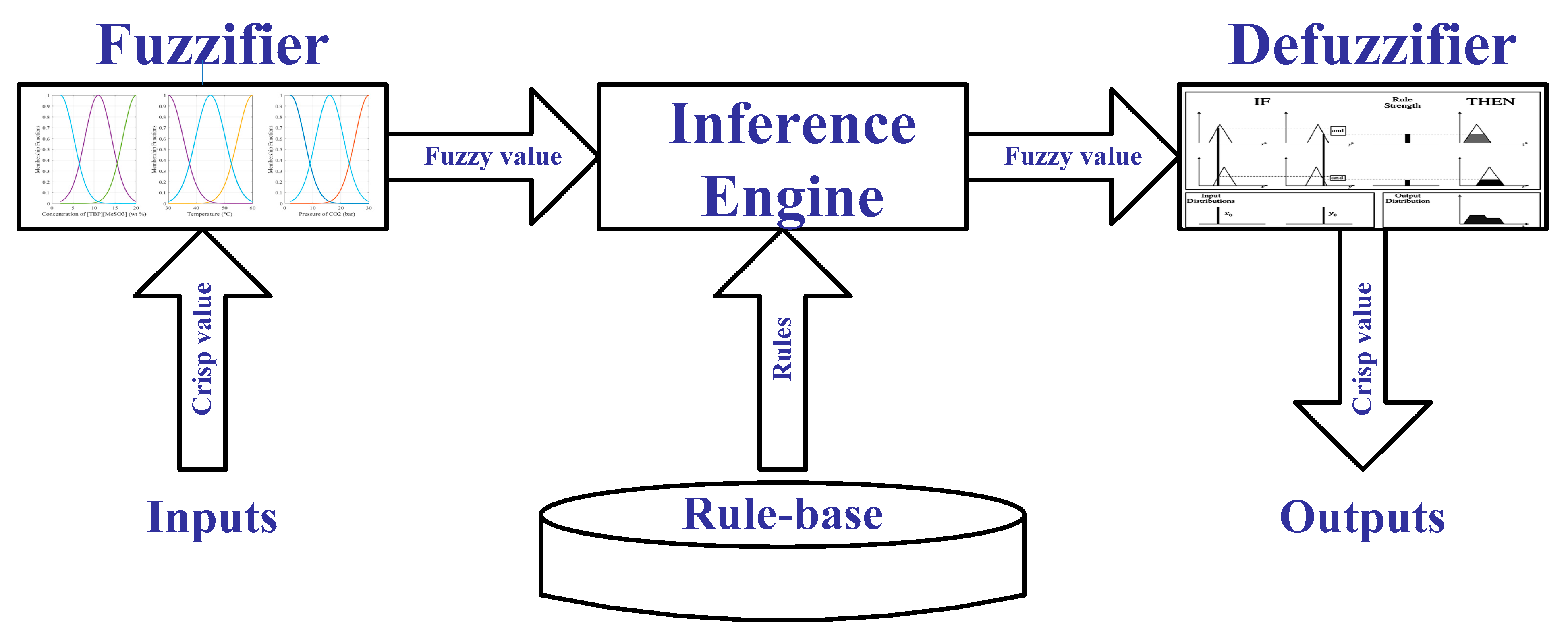
2.2.1. Type-1 Fuzzy Logic Controller (T1FLC)
Structure of Type-1 Fuzzy Logic Controller
Fuzzifier
Rule-Base
- IF a is α and b is β THEN c is γ, (Mamdani-type)
- IF a is α and b is β THEN c = f(a, b), (Sugeno-type)
Inference Engine
Defuzzifier
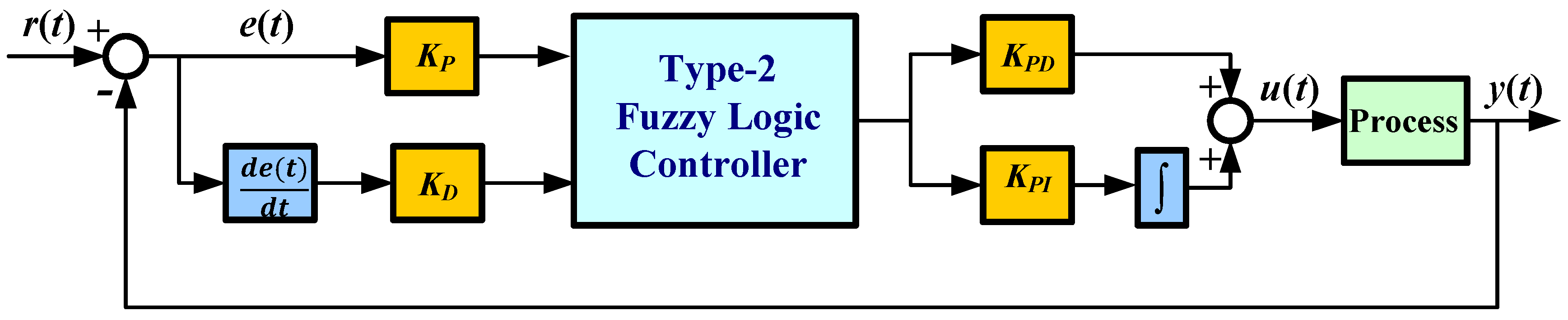
2.2.2. Type-2 Fuzzy Logic Controller (T2FLC)
3. Fractional-Order Systems
3.1. Fractional-Order PID Controller
3.2. Fractional-Order Fuzzy Controller
3.2.1. Fractional-Order Type-1 Fuzzy Controller
3.2.2. Fractional-Order Type-2 Fuzzy Controller
4. Metaheuristic Algorithms (MHA)
4.1. History of MHA
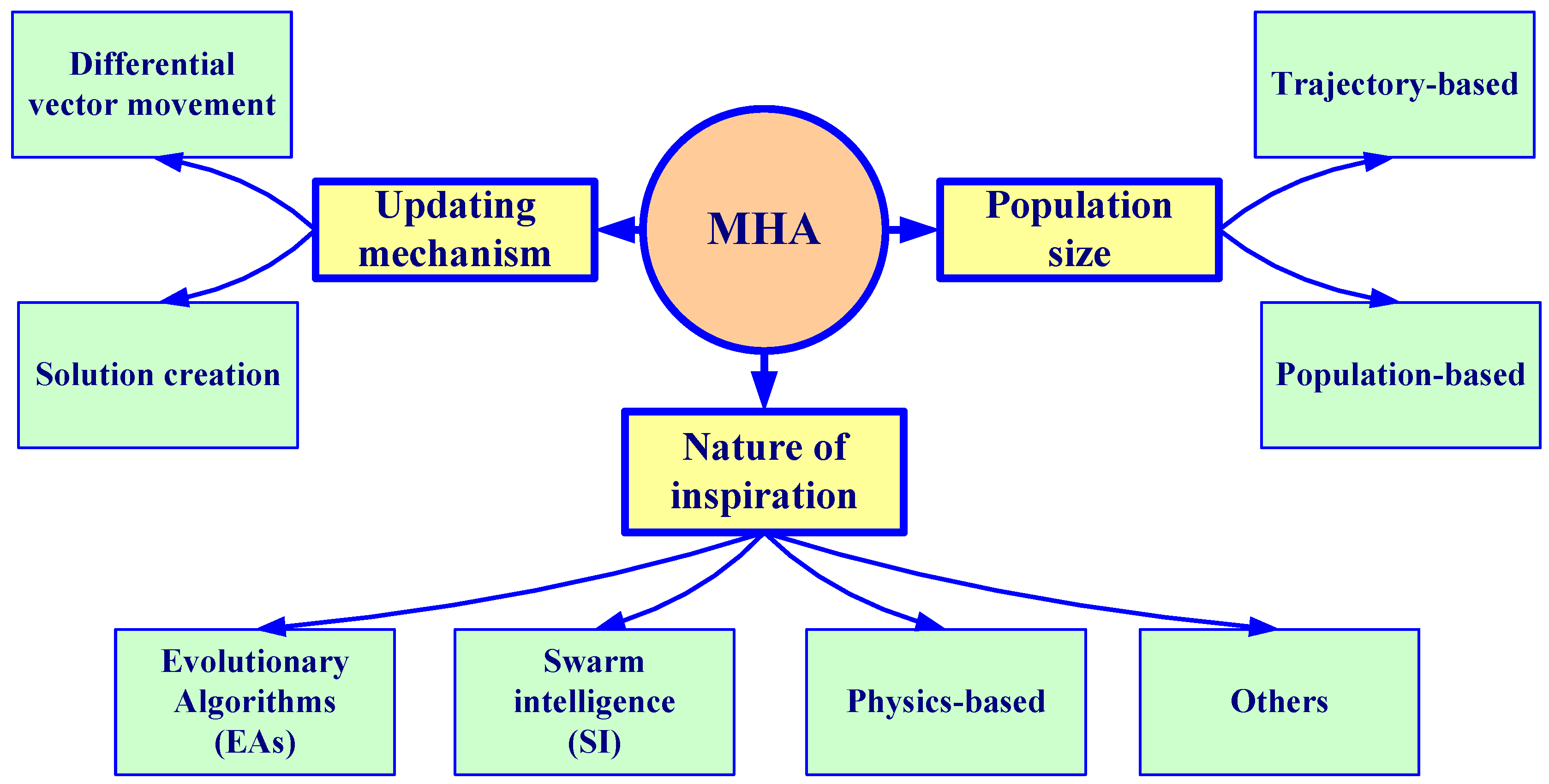
4.2. Classifications of MHA
4.2.1. Swarm-Based Algorithms
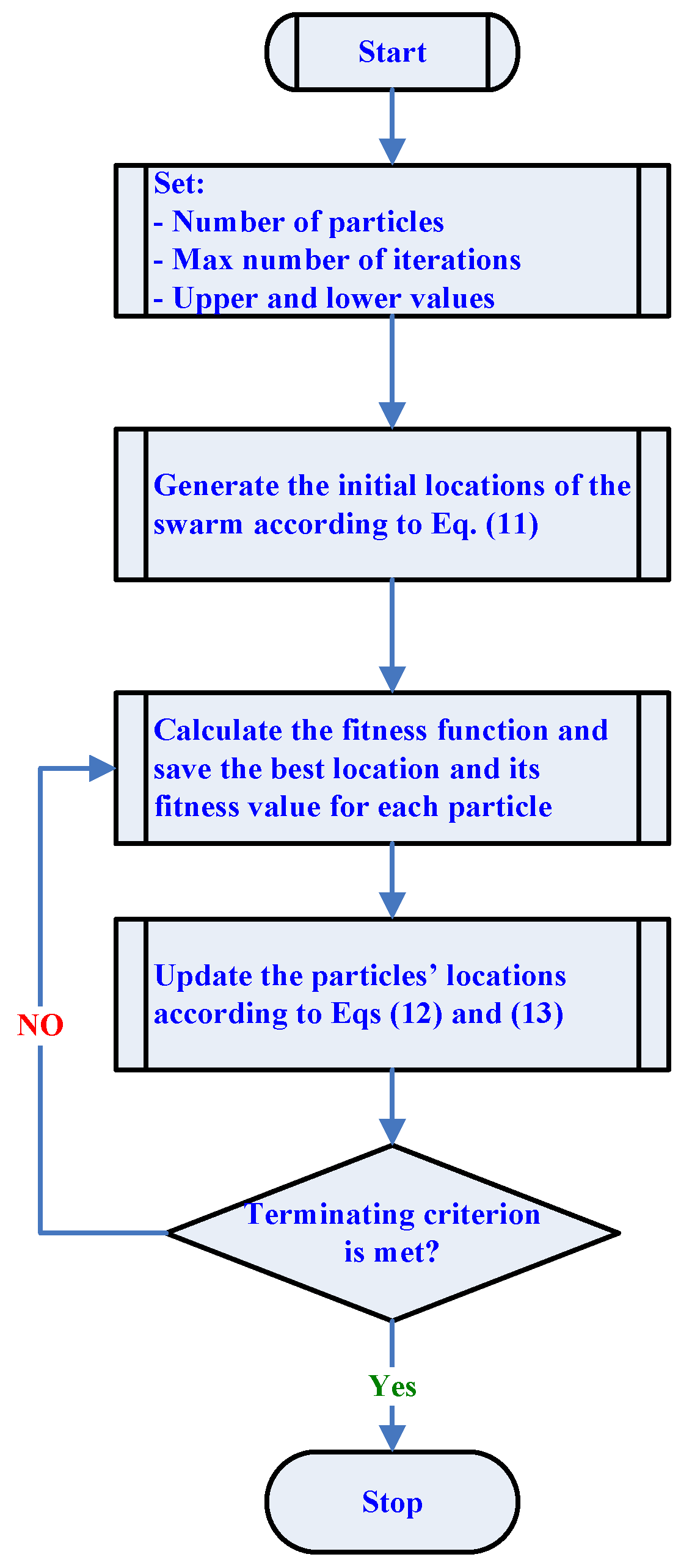
Particle Swarm Optimization
4.3. Objective Function
4.4. Simulation Toolboxes
4.4.1. FOMCON Toolbox
4.4.2. FOTF
4.4.3. Ninteger Toolbox
4.4.4. CRONE
5. Methodology
5.1. Scopus
“TITLE (((PI OR PID OR fuzzy) AND controller) AND (“factional order” OR “fractional-order”) AND (optimization OR optimal OR swarm OR tuning OR metaheuristic)) AND (LIMIT-TO (PUBYEAR, 2023) OR LIMIT-TO (PUBYEAR, 2022) OR LIMIT-TO (PUB/YEAR, 2021) OR LIMIT-TO (PUBYEAR, 2020) OR LIMIT-TO (PUBYEAR, 2019) OR LIMIT-TO (PUBYEAR, 2018) OR LIMIT-TO (PUBYEAR, 2017) OR LIMIT-TO (PUBYEAR, 2014))”.
5.2. Web of Science (WOS)
5.3. Science Direct
“(PI OR PID OR fuzzy) AND controller AND (“factional order” OR “fractional-order”) AND (optimization OR optimal OR swarm OR tuning OR metaheuristic)”.
5.4. Google Scholar
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DesRoches, C.T. The Concept of Sustainability. In Environmental Ethics for Canadians, 3rd ed.; Williston, B., Ed.; Oxford University Press: Oxford, UK, 2023; pp. 385–390. [Google Scholar]
- Dli, M.; Puchkov, A.; Vasiliev, A.; Kirillova, E.; Selyavskiy, Y.; Kulyasov, N. Intelligent Control System Architecture for Phosphorus Production from Apatite-Nepheline Ore Waste. Energies 2021, 14, 6469. [Google Scholar] [CrossRef]
- Kelektsoglou, K.; Karali, D.; Stavridis, A.; Loupa, G. Efficiency of the Air-Pollution Control System of a Lead-Acid-Battery Recycling Industry. Energies 2018, 11, 3465. [Google Scholar] [CrossRef]
- Rezk, H.; Nassef, A.M.; Abdelkareem, M.A.; Alami, A.H.; Fathy, A. Comparison among various energy management strategies for reducing hydrogen consumption in a hybrid fuel cell/supercapacitor/battery system. Int. J. Hydrogen Energy 2021, 46, 6110–6126. [Google Scholar] [CrossRef]
- Saber, E.M.; Chaer, I.; Gillich, A.; Ekpeti, B.G. Review of Intelligent Control Systems for Natural Ventilation as Passive Cooling Strategy for UK Buildings and Similar Climatic Conditions. Energies 2021, 14, 4388. [Google Scholar] [CrossRef]
- Nassef, A.M.; Houssein, E.H.; Rezk, H.; Fathy, A. Optimal Allocation of Biomass Distributed Generators Using Modified Hunger Games Search to Reduce CO2 Emissions. J. Mar. Sci. Eng. 2023, 11, 308. [Google Scholar] [CrossRef]
- Yayla, A.; Świerczewska, K.S.; Kaya, M.; Karaca, B.; Arayici, Y.; Ayözen, Y.E.; Tokdemir, O.B. Artificial Intelligence (AI)-Based Occupant-Centric Heating Ventilation and Air Conditioning (HVAC) Control System for Multi-Zone Commercial Buildings. Sustainability 2022, 14, 16107. [Google Scholar] [CrossRef]
- Ding, X.; Yu, J. The Design of Intelligent Building Lighting Control System Based on CNN in Embedded Microprocessor. Electronics 2023, 12, 1671. [Google Scholar] [CrossRef]
- Rezk, H.; Inayat, A.; Abdelkareem, M.A.; Olabi, A.G.; Nassef, A.M. Optimal operating parameter determination based on fuzzy logic modeling and marine predators algorithm approaches to improve the methane production via biomass gasification. Energy 2022, 239, 122072. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Ilyushin, Y.V.; Afanaseva, O.V. Development of a Distributed Mathematical Model and Control System for Reducing Pollution Risk in Mineral Water Aquifer Systems. Water 2022, 14, 151. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Cacciacarne, S.; Invernizzi, M.; Lanzarotto, D.; Palmieri, A.; Procopio, R. A Sliding Mode Control Approach for Gas Turbine Power Generators. IEEE Trans. Energy Convers. 2019, 34, 921–932. [Google Scholar] [CrossRef]
- Daou, R.A.Z.; Moreau, X. Comparison between integer order and fractional order controllers. In Proceedings of the MELECON 2014-2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 292–297. [Google Scholar]
- Caponetto, R.; Machado, J.T.; Murgano, E.; Xibilia, M.G. Model Order Reduction: A Comparison between Integer and Non-Integer Order Systems Approaches. Entropy 2019, 21, 876. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M.; Nassef, A.M.; Rezk, H.; Nisar, K.S. Optimal parameter design of fractional order control based INC-MPPT for PV system. Sol. Energy 2018, 159, 650–664. [Google Scholar] [CrossRef]
- Nassef, A.M.; Rezk, H. Optimal Tuning of FOPID-Like Fuzzy Controller for High-Performance Fractional-Order Systems. CMC-Comput. Mater. Contin. 2022, 70, 171–180. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y.V. Fractional Order Controller and its Applications: A Review. In Proceedings of the IASTED Asian Conference Modelling, Identification and Control/770: Advances in Computer Science and Engineering, Phuket, Thailand, 2–4 April 2012. [Google Scholar]
- Chaib, L.; Choucha, A.; Arif, S. Optimal design and tuning of novel fractional order PID power system stabilizer using a new metaheuristic Bat algorithm. Ain Shams Eng. J. 2017, 8, 113–125. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Mavridou, T.D. Simulated Annealing. In Encyclopedia of Optimization; Floudas, C.A., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2009; pp. 3591–3593. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Yadav, A.; Deep, K.; Kim, J.H.; Nagar, A.K. Gravitational swarm optimizer for global optimization. Swarm Evol. Comput. 2016, 31, 64–89. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.; Ionescu, C.; Dulf, E.H.; De Keyser, R. A Review of Recent Developments in Autotuning Methods for Fractional-Order Controllers. Fractal Fract. 2022, 6, 37. [Google Scholar] [CrossRef]
- Kumarasamy, V.; KarumanchettyThottam Ramasamy, V.; Chandrasekaran, G.; Chinnaraj, G.; Sivalingam, P.; Kumar, N.S. A review of integer order PID and fractional order PID controllers using optimization techniques for speed control of brushless DC motor drive. Int. J. Syst. Assur. Eng. Manag. 2023. [Google Scholar] [CrossRef]
- Jamil, A.A.; Tu, W.F.; Ali, S.W.; Terriche, Y.; Guerrero, J.M. Fractional-Order PID Controllers for Temperature Control: A Review. Energies 2022, 15, 3800. [Google Scholar] [CrossRef]
- Joseph, S.B.; Dada, E.G.; Abidemi, A.; Oyewola, D.O.; Khammas, B.M. Metaheuristic algorithms for PID controller parameters tuning: Review, approaches and open problems. Heliyon 2022, 8, e09399. [Google Scholar] [CrossRef] [PubMed]
- Alilou, M.; Azami, H.; Oshnoei, A.; Mohammadi-Ivatloo, B.; Teodorescu, R. Fractional-Order Control Techniques for Renewable Energy and Energy-Storage-Integrated Power Systems: A Review. Fractal Fract. 2023, 7, 391. [Google Scholar] [CrossRef]
- Reddy, K.; Saha, A.K. A review of swarm-based metaheuristic optimization techniques and their application to doubly fed induction generator. Heliyon 2022, 8, e10956. [Google Scholar] [CrossRef] [PubMed]
- Ogata, K. Modern Control Engineering; Prentice Hall PTR: Hoboken, NJ, USA, 2001. [Google Scholar]
- Golnaraghi, F.; Kuo, B.C. Automatic Control Systems; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Maddi, A.; Guessoum, A.; Berkani, D. Design of nonlinear PID-smith predictor controllers with large time delays. In Proceedings of the 2015 Third World Conference on Complex Systems (WCCS), Marrakech, Morocco, 23–25 November 2015; pp. 1–4. [Google Scholar]
- Mashor, M.Y.; Mahdi, M.C. Performance of Manual and Auto-Tuning PID Controller for Unstable Plant-Nano Satellite Attitude Control System. In Proceedings of the 2018 6th International Conference on Cyber and IT Service Management (CITSM), Parapat, Indonesia, 7–9 August 2018; pp. 1–5. [Google Scholar]
- Elhosseini, M.A.; El Sehiemy, R.A.; Salah, A.H.; Abido, M.A. Modeling and control of an interconnected combined cycle gas turbine using fuzzy and ANFIS controllers. Electr. Eng. 2018, 100, 763–785. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Passino, K.M.; Yurkovich, S. Fuzzy Control; Addison Wesley Longman: Menlo Park, CA, USA, 1998. [Google Scholar]
- Yan, J.; Ryan, M.; Power, J. Using Fuzzy Logic: Towards Intelligent Systems; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Rahman, S.M.A.; Rezk, H.; Shaikh, B.; Abdelkareem, M.A.; Olabi, A.G.; Nassef, A.M. Prediction of mass transfer during osmotically treated zucchini fruit product using advanced fuzzy inference system. Neural Comput. Appl. 2023, 35, 3125–3141. [Google Scholar] [CrossRef]
- Nassef, A.M.; Rezk, H.; Alahmer, A.; Abdelkareem, M.A. Maximization of CO2 Capture Capacity Using Recent RUNge Kutta Optimizer and Fuzzy Model. Atmosphere 2023, 14, 295. [Google Scholar] [CrossRef]
- Reznik, L. Fuzzy Controllers Handbook; Biddles Ltd.: Norfolk, VA, USA, 1997. [Google Scholar]
- Gilda, K.; Satarkar, S. Analytical overview of defuzzification methods. Int. J. Adv. Res. Ideas Innov. Technol. 2020, 6, 359–365. [Google Scholar]
- Shvedov, A.S. On Type-2 Fuzzy Sets and Type-2 Fuzzy Systems. J. Math. Sci. 2021, 259, 376–384. [Google Scholar] [CrossRef]
- De, A.K.; Chakraborty, D.; Biswas, A. Literature review on type-2 fuzzy set theory. Soft Comput. 2022, 26, 9049–9068. [Google Scholar] [CrossRef]
- Mendel, J.M.; Hagras, H.; Tan, W.-W.; Melek, W.W.; Ying, H. Introduction to Type-2 Fuzzy Logic Control; Wiley-IEEE Press: Piscataway, NJ, USA, 2014. [Google Scholar]
- Linda, O.; Manic, M. Uncertainty-Robust Design of Interval Type-2 Fuzzy Logic Controller for Delta Parallel Robot. IEEE Trans. Ind. Inform. 2011, 7, 661–670. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Petráš, I. Chapter Three-Fractional-order control: New control techniques. In Fractional Order Systems; Radwan, A.G., Khanday, F.A., Said, L.A., Eds.; Academic Press: Cambridge, MA, USA, 2022; Volume 1, pp. 71–106. [Google Scholar]
- Sun, Z.-Z.; Gao, G.-h. Fractional Differential Equations; De Gruyter: Berlin, Germany, 2020. [Google Scholar]
- Oustaloup, A.; Cois, O.; Lanusse, P.; Melchior, P.; Moreau, X.; Sabatier, J. The crone aproach: Theoretical developments and major applications. IFAC Proc. Vol. 2006, 39, 324–354. [Google Scholar] [CrossRef]
- Axtell, M.; Bise, M.E. Fractional calculus application in control systems. IEEE Conf. Aerosp. Electron. 1990, 562, 563–566. [Google Scholar]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelasticallydamped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Makroglou, A.; Miller, R.K.; Skaar, S.B. Computational results for a feedback control for a rotating viscoelastic beam. J. Guid. Control Dyn. 1994, 17, 84–90. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and fractional-order controllers. Inst. Exp. Phys. Slovak Acad. Sci. Kosice 1994, 12, 1–18. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Matignon, D. Some Results on Controllability and Observability of Finite-dimensional Fractional Differential Systems. Comput. Eng. Syst. Appl. 1996, 2, 952–956. [Google Scholar]
- Shalaby, R.; El-Hossainy, M.; Abo-Zalam, B.; Mahmoud, T.A. Optimal fractional-order PID controller based on fractional-order actor-critic algorithm. Neural Comput. Appl. 2023, 35, 2347–2380. [Google Scholar] [CrossRef]
- He, J.; Xiao, M.; Lu, Y.; Wang, Z.; Zheng, W.X. Fractional-order PID control of tipping in network congestion. Int. J. Syst. Sci. 2023, 54, 1873–1891. [Google Scholar] [CrossRef]
- Chipipop, B.; Puangdownreong, D. Designing of Fractional Order PID Controller for Stable Fractional Order System. In Proceedings of the 2019 Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT-NCON), Nan, Thailand, 30 January–2 February 2019; pp. 77–80. [Google Scholar]
- Pradhan, R.; Majhi, S.K.; Pradhan, J.K.; Pati, B.B. Optimal fractional order PID controller design using Ant Lion Optimizer. Ain Shams Eng. J. 2020, 11, 281–291. [Google Scholar] [CrossRef]
- El-Khazali, R. Fractional-order PIλDμ controller design. Comput. Math. Appl. 2013, 66, 639–646. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M. Fuzzy fractional-order PID control for heat exchanger. Alex. Eng. J. 2023, 63, 11–16. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Kumbasar, T. A new fractional-order general type-2 fuzzy predictive control system and its application for glucose level regulation. Appl. Soft Comput. 2020, 91, 106241. [Google Scholar] [CrossRef]
- Rao, S.S. Classical Optimization Techniques. In Engineering Optimization Theory and Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 57–108. [Google Scholar]
- Sörensen, K.; Sevaux, M.; Glover, F. A History of Metaheuristics. In Handbook of Heuristics; Springer: Cham, Switzerland, 2018; pp. 791–808. [Google Scholar]
- Sörensen, K.; Glover, F.W. Metaheuristics. In Encyclopedia of Operations Research and Management Science; Kluwer Academic: New York, NY, USA, 2013; pp. 960–970. [Google Scholar]
- Ho, Y.C.; Pepyne, D.L. Simple Explanation of the No-Free-Lunch Theorem and Its Implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Almufti, S.M. Historical survey on metaheuristics algorithms. Int. J. Sci. World 2019, 7, 1–12. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023. [Google Scholar] [CrossRef]
- Rajabi Moshtaghi, H.; Toloie Eshlaghy, A.; Motadel, M.R. A comprehensive review on meta-heuristic algorithms and their classification with novel approach. J. Appl. Res. Ind. Eng. 2021, 8, 63–89. [Google Scholar] [CrossRef]
- Stegherr, H.; Heider, M.; Hähner, J. Classifying Metaheuristics: Towards a unified multi-level classification system. Nat. Comput. 2020, 21, 155–171. [Google Scholar] [CrossRef]
- Tilahun, S.L.; Tawhid, M.A. Swarm hyperheuristic framework. J. Heurist. 2018, 25, 809–836. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Simulation of global MPPT based on teaching–learning-based optimization technique for partially shaded PV system. Electr. Eng. 2017, 99, 847–859. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Rezk, H. Global MPPT based on flower pollination and differential evolution algorithms to mitigate partial shading in building integrated PV system. Sol. Energy 2017, 157, 171–186. [Google Scholar] [CrossRef]
- Yousef, B.A.A.; Rezk, H.; Abdelkareem, M.A.; Olabi, A.G.; Nassef, A.M. Fuzzy modeling and particle swarm optimization for determining the optimal operating parameters to enhance the bio-methanol production from sugar cane bagasse. Int. J. Energy Res. 2020, 44, 8964–8973. [Google Scholar] [CrossRef]
- Tepljakov, A.; Vunder, V.; Petlenkov, E.; Nakshatharan, S.S.; Punning, A.; Kaparin, V.; Belikov, J.; Aabloo, A. Fractional-order modeling and control of ionic polymer-metal composite actuator. Smart Mater. Struct. 2019, 28, 084008. [Google Scholar] [CrossRef]
- Tepljakov, A. FOMCON Toolbox for MATLAB. Available online: https://github.com/extall/fomcon-matlab/releases/tag/v1.50.4 (accessed on 1 June 2023).
- Xue, D.Y.; Bai, L. Fractional Calculus: Numerical Algorithms and Implementations; Tsinghua University Press: Beijing, China, 2022. [Google Scholar]
- Xue, D. FOTF Toolbox. Available online: https://www.mathworks.com/matlabcentral/fileexchange/60874-fotf-toolbox (accessed on 1 June 2023).
- Valério, D.; Costa, J.S.d. Ninteger: A non-integer control toolbox for matlab. In Proceedings of Fractional Differentiation and Its Applications; Springer: Bordeaux, France, 2004. [Google Scholar]
- Valério, D. Ninteger. Available online: https://www.mathworks.com/matlabcentral/fileexchange/8312-ninteger (accessed on 1 June 2023).
- Agence de Protection de Programmes (APP). CRONE Toolbox; Agence de Protection de Programmes (APP): Paris, France, 2000. [Google Scholar]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Teodorović, D. Bee Colony Optimization (BCO). In Innovations in Swarm Intelligence; Lim, C.P., Jain, L.C., Dehuri, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 39–60. [Google Scholar]
- Talatahari, S.; Azizi, M. Chaos Game Optimization: A novel metaheuristic algorithm. Artif. Intell. Rev. 2020, 54, 917–1004. [Google Scholar] [CrossRef]
- Hekimoğlu, B. Optimal Tuning of Fractional Order PID Controller for DC Motor Speed Control via Chaotic Atom Search Optimization Algorithm. IEEE Access 2019, 7, 38100–38114. [Google Scholar] [CrossRef]
- Ibrahim, A.; Ali, H.A.; Eid, M.M.; El-kenawy, E.S.M. Chaotic Harris Hawks Optimization for Unconstrained Function Optimization. In Proceedings of the 2020 16th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 29–30 December 2020; pp. 153–158. [Google Scholar]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2011, 29, 17–35. [Google Scholar] [CrossRef]
- Abedinpourshotorban, H.; Mariyam Shamsuddin, S.; Beheshti, Z.; Jawawi, D.N.A. Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm. Swarm Evol. Comput. 2016, 26, 8–22. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Yang, X.-S. Flower Pollination Algorithm for Global Optimization. In Proceedings of the Unconventional Computation and Natural Computation, Orléan, France, 3–7 September 2012; pp. 240–249. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Zong Woo, G.; Joong Hoon, K.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2016, 76, 60–68. [Google Scholar] [CrossRef]
- Madadi, M.R.; Akbarifard, S.; Qaderi, K. Improved Moth-Swarm Algorithm to predict transient storage model parameters in natural streams. Environ. Pollut. 2020, 262, 114258. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Saber, S.; Askar, S.; Abouhawwash, M. Modified Flower Pollination Algorithm for Global Optimization. Mathematics 2021, 9, 1661. [Google Scholar] [CrossRef]
- Ouaar, F.; Boudjemaa, R. Modified salp swarm algorithm for global optimisation. Neural Comput. Appl. 2021, 33, 8709–8734. [Google Scholar] [CrossRef]
- Sulaiman, M.; Salhi, A.; Fraga, E.S.; Mashwani, W.K.; Rashidi, M.M. A Novel Plant Propagation Algorithm: Modifications and Implementation. Sci. Int. 2016, 28, 201–209. [Google Scholar]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Gomes, G.F.; da Cunha, S.S.; Ancelotti, A.C. A sunflower optimization (SFO) algorithm applied to damage identification on laminated composite plates. Eng. Comput. 2018, 35, 619–626. [Google Scholar] [CrossRef]
- Satapathy, S.; Naik, A. Social group optimization (SGO): A new population evolutionary optimization technique. Complex Intell. Syst. 2016, 2, 173–203. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Li, V.O.K. A social spider algorithm for global optimization. Appl. Soft Comput. 2015, 30, 614–627. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Maamir, F.; Guiatni, M.; El Hachemi, H.M.S.M.; Ali, D. Auto-tuning of fractional-order PI controller using particle swarm optimization for thermal device. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–6. [Google Scholar]
- Guha, D.; Roy, P.K.; Banerjee, S. Grasshopper optimization algorithm scaled fractional order PI-D controller applied to reduced order model of load frequency control system. Int. J. Model. Simul. 2019, 40, 217–242. [Google Scholar] [CrossRef]
- Barakat, M. Novel chaos game optimization tuned-fractional-order PID fractional-order PI controller for load–frequency control of interconnected power systems. Prot. Control Mod. Power Syst. 2022, 7, 16. [Google Scholar] [CrossRef]
- Ramadan, H.S.; Padmanaban, S.; Mosaad, M.I. Metaheuristic-based Near-Optimal Fractional Order PI Controller for On-grid Fuel Cell Dynamic Performance Enhancement. Electr. Power Syst. Res. 2022, 208, 107897. [Google Scholar] [CrossRef]
- Kakkar, S.; Maity, T.; Ahuja, R.K.; Walde, P.; Saket, R.K.; Khan, B.; Padmanaban, S. Design and control of grid-connected PWM rectifiers by optimizing fractional order PI controller using water cycle algorithm. IEEE Access 2021, 9, 125941–125954. [Google Scholar] [CrossRef]
- Leena, J.G.; Sundaravadivu, K.; Monisha, R.; Rajinikanth, V. Design of Fractional-Order PI/PID Controller for SISO System Using Social-Group-Optimization. In Proceedings of the 2018 IEEE International Conference on System, Computation, Automation and Networking (ICSCA), Pondicherry, India, 6–7 July 2018; pp. 1–5. [Google Scholar]
- Agarwal, S.; Mathur, S.; Mishra, P.; Kumar, V.; Rana, K.P.S. Online tuning of fractional order PI controller using particle swarm optimization. In Proceedings of the International Conference on Computing, Communication & Automation, Greater Noida, India, 15–16 May 2015; pp. 1026–1031. [Google Scholar]
- Bouderres, N.; Kerdoun, D.; Djellad, A.; Chiheb, S.; Dekhane, A. Optimization of Fractional Order PI Controller by PSO Algorithm Applied to a Grid-Connected Photovoltaic System. J. Eur. Des Systèmes Autom. 2022, 55, 427–438. [Google Scholar] [CrossRef]
- Zamee, W. A Novel Plant Propagation-Based Cascaded Fractional Order PI Controller for Optimal Operation of Grid-Connected Single-Stage Three-Phase Solar Photovoltaic System. Appl. Sci. 2019, 9, 4269. [Google Scholar] [CrossRef]
- Sahul Hameed, J.B.; Ramasubramanian, J. Optimal Fractional Order PI Controller for Frequency Ancillary Services in Restructured Power System. Energy Syst. 2020, 13, 79–109. [Google Scholar] [CrossRef]
- Özyetkin, M.M.; Birdane, H. The processes with fractional order delay and PI controller design using particle swarm optimization. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2023, 13, 81–91. [Google Scholar] [CrossRef]
- Altawil, I.; Momani, M.A.; Al-Tahat, M.A.; Al Athamneh, R.; Al-Saadi, M.A.; Albataineh, Z. Optimization of fractional order PI controller to regulate grid voltage connected photovoltaic system based on slap swarm algorithm. Int. J. Power Electron. Drive Syst. (IJPEDS) 2023, 14, 1184–1200. [Google Scholar] [CrossRef]
- Labed, N.; Attoui, I.; Makhloufi, S.; Bouraiou, A.; Bouakkaz, M.S. PSO Based Fractional Order PI Controller and ANFIS Algorithm for Wind Turbine System Control and Diagnosis. J. Electr. Eng. Technol. 2022, 18, 2457–2468. [Google Scholar] [CrossRef]
- ÇElebİ, M.; BaŞÇİ, A. Parameter Optimization of Bidirectional Three-Phase DC-AC Power Inverter by an Improved Particle Swarm Optimization based Fractional Order PI Controller for the Grid Forming Operation. Int. J. Eng. Technol. IJET 2022, 8, 25–30. [Google Scholar] [CrossRef]
- Dwivedi, R.; Singh, S.; Singh, B. Design and development of three-phase EV charger based on the integration of voltage-oriented pulse width modulation control and water cycle algorithm fractional-order PI controller. Int. J. Ambient Energy 2022, 44, 157–170. [Google Scholar] [CrossRef]
- Aghababa, M.P. Optimal design of fractional-order PID controller for five bar linkage robot using a new particle swarm optimization algorithm. Soft Comput. 2015, 20, 4055–4067. [Google Scholar] [CrossRef]
- Vanchinathan, K.; Valluvan, K.R. A Metaheuristic Optimization Approach for Tuning of Fractional-Order PID Controller for Speed Control of Sensorless BLDC Motor. J. Circuits Syst. Comput. 2017, 27, 1850123. [Google Scholar] [CrossRef]
- Khan, I.A.; Alghamdi, A.S.; Jumani, T.A.; Alamgir, A.; Awan, A.B.; Khidrani, A. Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System. Electronics 2019, 8, 1472. [Google Scholar] [CrossRef]
- Babu, A.G.S.; Chiranjeevi, B.T. Implementation of Fractional Order PID Controller for an AVR System Using GA and ACO Optimization Techniques. IFAC-Pap. 2016, 49, 456–461. [Google Scholar] [CrossRef]
- Vanchinathan, K.; Selvaganesan, N. Adaptive fractional order PID controller tuning for brushless DC motor using Artificial Bee Colony algorithm. Results Control Optim. 2021, 4, 100032. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Equilibrium optimizer-tuned cascade fractional-order 3DOF-PID controller in load frequency control of power system having renewable energy resource integrated. Int. Trans. Electr. Energy Syst. 2020, 31, e12702. [Google Scholar] [CrossRef]
- Bouakkaz, M.S.; Boukadoum, A.; Boudebbouz, O.; Fergani, N.; Boutasseta, N.; Attoui, I.; Bouraiou, A.; Necaibia, A. Dynamic performance evaluation and improvement of PV energy generation systems using Moth Flame Optimization with combined fractional order PID and sliding mode controller. Sol. Energy 2020, 199, 411–424. [Google Scholar] [CrossRef]
- Ghamari, S.M.; Narm, H.G.; Mollaee, H. Fractional-order fuzzy PID controller design on buck converter with antlion optimization algorithm. IET Control Theory Appl. 2021, 16, 340–352. [Google Scholar] [CrossRef]
- Jaiswal, S.; Suresh Kumar, C.; Seepana, M.M.; Babu, G.U.B. Design of fractional order PID controller using genetic algorithm optimization technique for nonlinear system. Chem. Prod. Process Model. 2020, 15, 20190072. [Google Scholar] [CrossRef]
- Karahan, O. Design of optimal fractional order fuzzy PID controller based on cuckoo search algorithm for core power control in molten salt reactors. Prog. Nucl. Energy 2021, 139, 103868. [Google Scholar] [CrossRef]
- Mohanty, D.; Panda, S. Modified Salp Swarm Algorithm-Optimized Fractional-Order Adaptive Fuzzy PID Controller for Frequency Regulation of Hybrid Power System with Electric Vehicle. J. Control Autom. Electr. Syst. 2021, 32, 416–438. [Google Scholar] [CrossRef]
- Nayak, P.C.; Nayak, B.P.; Prusty, R.C.; Panda, S. Sunflower optimization based fractional order fuzzy PID controller for frequency regulation of solar-wind integrated power system with hydrogen aqua equalizer-fuel cell unit. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–19. [Google Scholar] [CrossRef]
- Prusty, U.C.; Nayak, P.C.; Prusty, R.C.; Panda, S. An improved moth swarm algorithm based fractional order type-2 fuzzy PID controller for frequency regulation of microgrid system. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 1–23. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. A metaheuristic approach for interval type-2 fuzzy fractional order fault-tolerant controller for a class of uncertain nonlinear system*. Automatika 2022, 63, 656–675. [Google Scholar] [CrossRef]
- Bennaoui, A.; Saadi, S.; Ameur, A. Performance Comparison of MFO and PSO for Optimal Tuning the fractional order fuzzy PID Controller for A DC-DC Boost Converter. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 3–5 July 2020; pp. 1–5. [Google Scholar]
- Naga Sai Kalyan, C.H.; Goud, B.S.; Reddy, C.R.; Udumula, R.R.; Bajaj, M.; Sharma, N.K.; Elgamli, E.; Shouran, M.; Kamel, S. Seagull Optimization Algorithm–Based Fractional-Order Fuzzy Controller for LFC of Multi-Area Diverse Source System with Realistic Constraints. Front. Energy Res. 2022, 10, 921426. [Google Scholar] [CrossRef]
- Sahoo, D.K.; Sahu, R.K.; Panda, S. Chaotic Harris Hawks Optimization based type-2 Fractional Order Fuzzy PID controller for frequency regulation of power systems. Int. J. Ambient Energy 2020, 43, 3832–3844. [Google Scholar] [CrossRef]
- Ghaleb, A.F.; Oglah, A.A.; Humaidi, A.J.; Al-Obaidi, A.S.M.; Ibraheem, I.K. Optimum of fractional order fuzzy logic controller with several evolutionary optimization algorithms for inverted pendulum. Int. Rev. Appl. Sci. Eng. 2023, 14, 1–12. [Google Scholar] [CrossRef]










| Timeline | Description |
|---|---|
| 1953s | George Dantzig and others develop the simplex algorithm, one of the first optimization algorithms for linear programming. |
| 1950s–1960s | Researchers begin developing stochastic optimization algorithms, such as Monte Carlo methods and simulated annealing, that use probabilistic techniques to find good solutions. |
| 1960s–1970s | Evolutionary algorithms, inspired by the principles of natural selection, are developed by researchers such as John Holland and Ingo Rechenberg. |
| 1980s | Genetic algorithms, a type of evolutionary algorithm, gain popularity as a means of solving optimization problems. |
| 1990s | Swarm intelligence approaches, such as particle swarm optimization and ant colony optimization, emerge as a new class of metaheuristics that are based on the collective behaviour of simple agents. |
| 1990s–2000s | Local search-based metaheuristics, such as tabu search and variable neighbourhood search, become popular for solving combinatorial optimization problems. |
| 2000s–present | Hybrid and multi-objective metaheuristics gain popularity, as researchers seek to combine different classes of metaheuristics or combine metaheuristics with other optimization techniques to improve their performance on a wide range of problems. |
| Item | Description |
|---|---|
| Main searching keywords | Factional order; PID; Fuzzy; Controller; Optimization |
| Date Range | 2014–2023 |
| Databases | Scopus (SC); Web of Science (WOS); Science Direct (SD); Google Scholar (GS) |
| Keyword | Synonyms |
|---|---|
| Factional order | FO OR fractional-order |
| Optimization | optimal OR swarm OR tuning OR metaheuristic |
| Database Source | |||||
|---|---|---|---|---|---|
| Controller Type | Scopus | Web of Science | Google Scholar | Science Direct | Total |
| FO-PI | 32 | 44 | 35 | 12 | 123 |
| FO-PID | 158 | 165 | 181 | 42 | 546 |
| FO-Fuzzy | 83 | 38 | 46 | 22 | 189 |
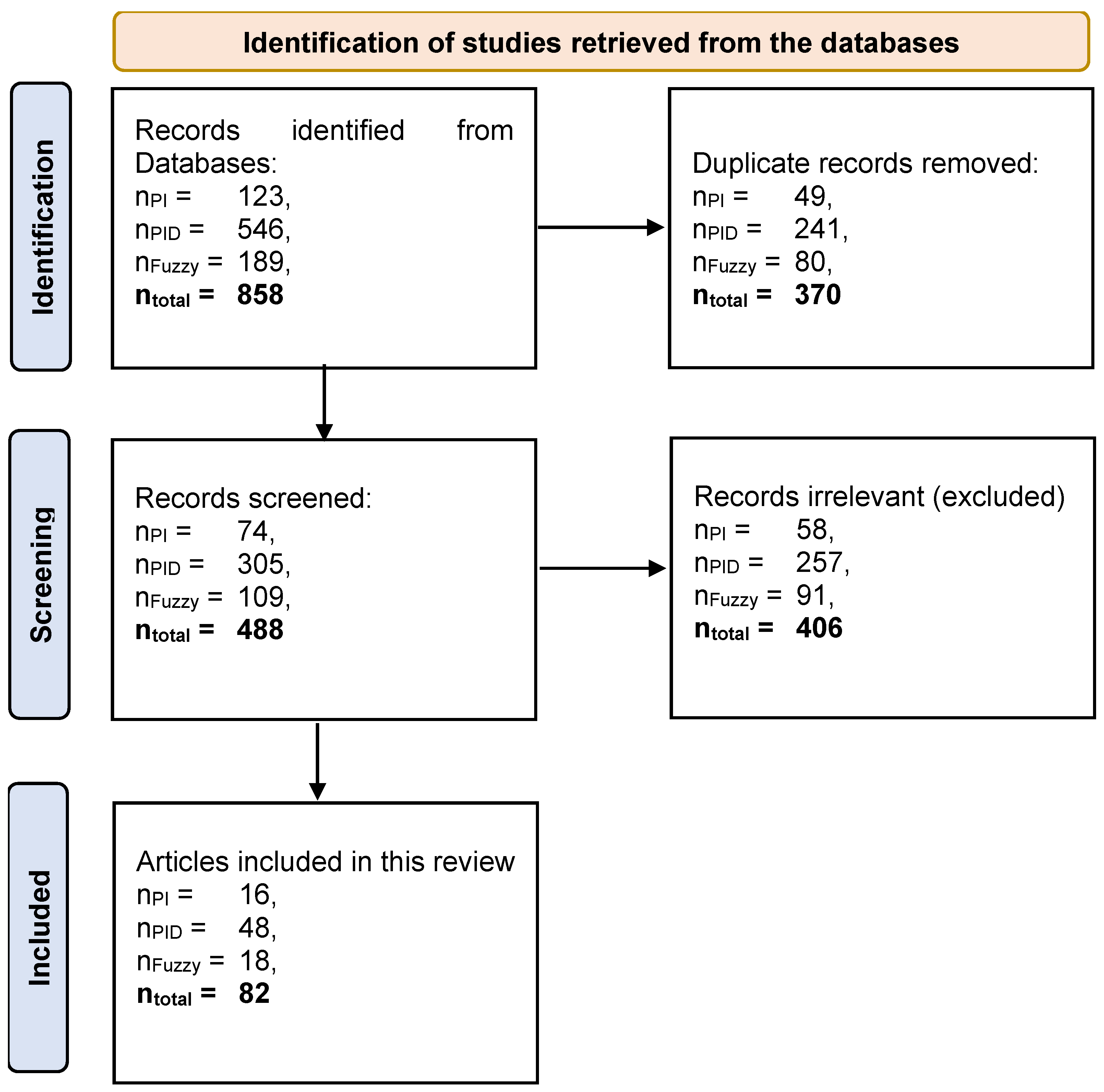
| Total | 273 | 247 | 262 | 76 | 858 |
| Controller Type | Initial | Duplicates | Remaining |
|---|---|---|---|
| FO-PI | 123 | 49 | 74 |
| FO-PID | 546 | 241 | 305 |
| FO-Fuzzy | 189 | 80 | 109 |
| Total | 858 | 370 | 488 |
| Controller Type | Initial | Irrelevant Excluded | Included |
|---|---|---|---|
| FO-PI | 74 | 58 | 16 |
| FO-PID | 305 | 257 | 48 |
| FO-Fuzzy | 109 | 91 | 18 |
| Total | 488 | 406 | 82 |
| No. | Author | Optimizer | Abbreviation | Year | Inspiration | DOI |
|---|---|---|---|---|---|---|
| 1 | Dorigo et al. [20] | Ant Colony Optimization | ACO | 2006 | Ant foraging behaviour | https://doi.org/10.1109/MCI.2006.329691 |
| 2 | Mirjalili [83] | Ant Lion Optimization | ALO | 1992 | Ant lion hunting mechanism | https://doi.org/10.1016/j.advengsoft.2015.01.010 |
| 3 | Yang and Gandomi [84] | Bat Algorithm | BA | 2012 | Echolocation behaviour of bats | https://doi.org/10.1108/02644401211235834 |
| 4 | Teodorović [85] | Bee Colony Algorithm | BCA | 2009 | The behaviour of bees in nature | https://doi.org/10.1007/978-3-642-04225-6_3 |
| 5 | Talatahari and Azizi [86] | Chaos Game Optimization | CGO | 2020 | Configuration of fractals by chaos game | https://doi.org/10.1007/s10462-020-09867-w |
| 6 | Baran Hekimoğlu [87] | Chaotic Atom Search Optimization | ChASO | 2019 | Atomic motion in nature | https://doi.org/10.1109/ACCESS.2019.2905961 |
| 7 | Ibrahim et al. [88] | Chaotic Harris Hawks Optimization | CHHO | 2020 | Hunting strategy of Harris’s hawks | https://doi.org/10.1109/ICENCO49778.2020.9357403 |
| 8 | Gandomi et al. [89] | Cuckoo Search Algorithm | CS | 2013 | Breed behaviour of cuckoo species | https://doi.org/10.1007/s00366-011-0241-y |
| 9 | Abedinpourshotorban et al. [90] | Electromagnetic Field Optimization | EFO | 2016 | Behaviour of electromagnets with different polarities | https://doi.org/10.1016/j.swevo.2015.07.002 |
| 10 | Faramarzi et al. [91] | Equilibrium Optimizer | EO | 2020 | Mass balance models | https://doi.org/10.1016/j.knosys.2019.105190 |
| 11 | Yang [92] | Flower Pollination Algorithm | FPA | 2012 | Pollination process of flowers | https://doi.org/10.1007/978-3-642-32894-7_27 |
| 12 | Genetic Algorithm [18] | Genetic Algorithm | GA | 1975 | Evolution and natural selection theory | https://www.jstor.org/stable/24939139 |
| 13 | Saremi et al. [93] | Grasshopper Optimization Algorithm | GOA | 2017 | Food source seeking by grasshopper swarms | https://doi.org/10.1016/j.advengsoft.2017.01.004 |
| 14 | Mirjalili et al. [94] | Grey Wolf Optimizer | GWO | 2014 | Hunting behaviour of grey wolf packs | https://doi.org/10.1016/j.advengsoft.2013.12.007 |
| 15 | Heidari e. al. [95] | Harris Hawks Optimization | HHO | 2019 | Cooperative behaviour and chasing style of Harris’s hawks | https://doi.org/10.1016/j.future.2019.02.028 |
| 16 | Geem and Kim [96] | Harmony Search | HS | 2001 | Artificial phenomenon in musical performance | https://doi.org/10.1177/003754970107600201 |
| 17 | Madadi et al. [97] | Improved Moth Swarm Algorithm | IMSA | 2020 | Behaviour of moths in nature | https://doi.org/10.1016/j.envpol.2020.114258 |
| 18 | Mirjalili [98] | Moth Flame Optimization | MFO | 2015 | Navigation method of moths in nature | https://doi.org/10.1016/j.knosys.2015.07.006 |
| 19 | Abdel-Basset et al. [99] | Modified Flower Pollination Algorithm | MFPA | 2021 | Pollination process of flowers | https://doi.org/10.3390/math9141661 |
| 20 | Ouaar and Boudjemaa [100] | Modified Salp Swarm Algorithm | MSSA | 2021 | Swimming and foraging behaviour of salps in oceans | https://doi.org/10.1007/s00521-020-05621-z |
| 21 | Sulaiman et al. [101] | Plant Propagation Algorithm | PPA | 2016 | Propagation of strawberry plant | Sci. Int. (Lahore), 28(1), 201–209, 2016 |
| 22 | Eberhart and Kennedy [21] | Particle Swarm Optimization | PSO | 1995 | Social movement of flock of birds | https://doi.org/10.1109/ICNN.1995.488968 |
| 23 | Mirjalili [102] | Sine Cosine Algorithm | SCA | 2016 | Periodical oscillations of the sine/cosine functions | https://doi.org/10.1016/j.knosys.2015.12.022 |
| 24 | Gomes et al. [103] | Sunflower Optimization | SFO | 2019 | Motion of sunflowers in capturing solar radiation | https://doi.org/10.1007/s00366-018-0620-8 |
| 25 | Satapathy and Naik [104] | Social Group Optimization | SGO | 2016 | Behaviour of humans in solving complex problems | https://doi.org/10.1007/s40747-016-0022-8 |
| 26 | Dhiman and Kumar [105] | Seagull Optimization Algorithm | SOA | 2018 | Migration and attacking behaviours of a seagull | https://doi.org/10.1016/j.knosys.2018.11.024 |
| 27 | Seyedali Mirjalili [106] | Salp Swarm Algorithm | SSA | 2017 | Swarming behaviour of salps (salp chain) | https://doi.org/10.1016/j.advengsoft.2017.07.002 |
| 28 | Yu and Li [107] | Social Spider Algorithm | SSA | 2015 | Foraging strategy of the social spider | https://doi.org/10.1016/j.asoc.2015.02.014 |
| 29 | Eskandar et al. [108] | Water Cycle Algorithm | WCA | 2012 | Movements of rivers and streams | https://doi.org/10.1016/j.compstruc.2012.07.010 |
| No. | Ref | * Cited by | Year | Optimizer | # of Optimal Variables | Objective Function | Value | System | Controlled Variable |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Maroufi et al. [109] | 64 | 2019 | BA | - | IAE | 6.89 | MPPT-Pitch control of a Wind Turbine | Pitch angle |
| 2 | Guha et al. [110] | 63 | 2020 | GOA | 6 | ITAE | - | Load frequency control | Frequency |
| 3 | Barakat [111] | 13 | 2022 | CGO | 3 | ITAE | - | Interconnected power systems | Frequency |
| 4 | Ramadan et al. [112] | 12 | 2022 | MFPA | 3 | Absolute of steady-state error | 0.015 | On-grid Fuel Cell | Overshoot Settling time Execution time |
| 5 | Kakkar et al. [113] | 10 | 2021 | WCA | 3 | ITAE, absolute steady-state error, and settling time. A multiobjective external optimization (MOEO) technique (FOMCON toolbox for MATLAB) | - | Grid-connected PWM Rectifiers | - |
| 6 | Leena et al. [114] | 6 | 2018 | SGO | 3 | ISE | - | SISO process | Response |
| 7 | Maamir et al. [109] | 4 | 2015 | PSO | - | - | - | Control thermal device (heat pump) | Temperature |
| 8 | Agarwal et al. [115] | 3 | 2015 | PSO | 3 | ITAE | 0.982009 | Speed control of DC motor | Speed |
| 9 | Bouderres et al. [116] | 2 | 2022 | PSO | - | - | - | Grid-connected photovoltaic system | Voltage |
| 10 | Zamee and Won [117] | 2 | 2019 | PPA | 6 | ITAE | 0.2918 | Grid-connected single-stage three-phase solar photovoltaic system | Dc link voltage |
| 11 | Hameed and Ramasubramanian [118] | 1 | 2020 | (ALO), (MFO), (WOA) (SCA) | Case 1: 6 Case 2: 12 Case 3: 12 Case 4: 12 | ITAE | - | Multi-area thermal power system | Deviation in frequency |
| 12 | Özyetkin and Birdane [119] | 0 | 2023 | PSO | - | - | - | Numerical example | Response |
| 13 | Altawil et al. [120] | 0 | 2023 | SSO | - | ITAE | - | Photovoltaic system | Voltage |
| 14 | Labed et al. [121] | 0 | 2022 | PSO | - | - | - | Wind turbine system | Output |
| 15 | Mehmed and Abdullah [122] | 0 | 2022 | PSO | - | Total harmonic distortion | 1.65% | Bidirectional three-phase dc-ac power inverter | Output |
| 16 | Dwivedi et al. [123] | 0 | 2022 | WCA | - | (MATLAB–Simulink) | - | Three-phase EV charger | Voltage |
| No. | Ref | * Cited by | Year | Optimizer | # of Optimal Variables | Objective Function | Value | Plant | Controlled Variable |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Hekimoğlu [87] | 196 | 2019 | ChASO | - | ITSE | 5.4978 × 10−5 | Dc motor | Speed |
| 2 | Aghababa [124] | 91 | 2015 | Modified PSO | - | IAE ISE ITSE | - | Five-bar linkage robot | Dynamic response |
| 3 | Vanchinathan and Valluvan [125] | 75 | 2018 | BA | - | - | - | Sensor-less BLDC Motor | Speed |
| 4 | Khan et al. [126] | 70 | 2019 | SSO | - | ITAE | 0.004195 | Automatic voltage regulator system | Voltage |
| 5 | Suri babu and Chiranjeevi [127] | 68 | 2016 | GA ACO | 5 | ITAE | - | Automatic voltage regulator (AVR) system | Voltage |
| 6 | Vanchinathan and Selvaganesan [128] | 65 | 2021 | ABC | - | IAE ITAE ISE | 0.008 0.002 0.008 | Brushless DC motor | Speed |
| 7 | Guhaet al. [129] | 49 | 2020 | EO | - | ISE | 0.70112 × 10−4 | Load frequency control of power system | Frequency |
| 8 | Bouakkaz et al. [130] | 46 | 2020 | PSO | 5 | ISE | - | PV energy generation systems | Cell’s output power |
| 9 | Ghamar et al. [131] | 26 | 2021 | ALO | 5 | - | - | Buck converter | Voltage |
| 10 | Jaiswal et al. [132] | 13 | 2020 | GA | 5 | IAE | 0.098 | Conical tank (nonlinear) system | Magnitude |
| No. | Ref | * Cited by | Fuzzy Type | Year | Optimizer | # of Optimal Variables | Objective Function | Value | Plant | Controlled Variable |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Karahan [133] | 23 | Type-1 | 2021 | CS | - | ITSE | 0.000052 | Molten salt reactors | Power control |
| 2 | Debidasi and Panda [134] | 21 | Type-1 | 2021 | MSSA | - | Frequency variation plus control signal output | 4.0846 | Hybrid Power System with Electric Vehicle | Frequency |
| 3 | Nayak et al. [135] | 14 | Type-1 | 2021 | SFO | 8 | ITSE | 0.0091 | Solar-wind integrated power system with hydrogen aqua equalizer-fuel cell unit | Frequency |
| 4 | Prusty et al. [136] | 8 | Type-2 | 2022 | IMSA | 8 | ISE | 0.0224 | Microgrid | Frequency |
| 5 | Patel and Shah [137] | 7 | Type-2 | 2022 | FPA | 6 | close loop error | 6.723 × 10−1 | Nonlinear uncertain level control systems | Response |
| 6 | Bennaoui et al. [138] | 7 | Type-1 | 2020 | MFO | 5 | IAE | 0.1691 | Dc-dc boost converter | Voltage |
| 7 | Kalyan [139] | 5 | Type-1 | 2022 | SOA | 5 | ISE | 5.2 × 10–3 | Multi-Area Diverse Source System with Realistic Constraints | Load frequency control |
| 8 | Sahoo et al. [140] | 5 | Type-2 | 2020 | CHHO | 8 | ITAE | 2.33 × 10−2 | Power system | Frequency deviation and Deviance in tie-line power |
| 9 | Ghaleb et al. [141] | 0 | Type-1 | 2023 | SSA (Social Spider) | 5 | Rise Time, Settling Time, Peak Time, Peak value | - | Inverted pendulum | Angle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review. Fractal Fract. 2023, 7, 553. https://doi.org/10.3390/fractalfract7070553
Nassef AM, Abdelkareem MA, Maghrabie HM, Baroutaji A. Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review. Fractal and Fractional. 2023; 7(7):553. https://doi.org/10.3390/fractalfract7070553
Chicago/Turabian StyleNassef, Ahmed M., Mohammad Ali Abdelkareem, Hussein M. Maghrabie, and Ahmad Baroutaji. 2023. "Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review" Fractal and Fractional 7, no. 7: 553. https://doi.org/10.3390/fractalfract7070553
APA StyleNassef, A. M., Abdelkareem, M. A., Maghrabie, H. M., & Baroutaji, A. (2023). Metaheuristic-Based Algorithms for Optimizing Fractional-Order Controllers—A Recent, Systematic, and Comprehensive Review. Fractal and Fractional, 7(7), 553. https://doi.org/10.3390/fractalfract7070553












