Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order
Abstract
:1. Introduction
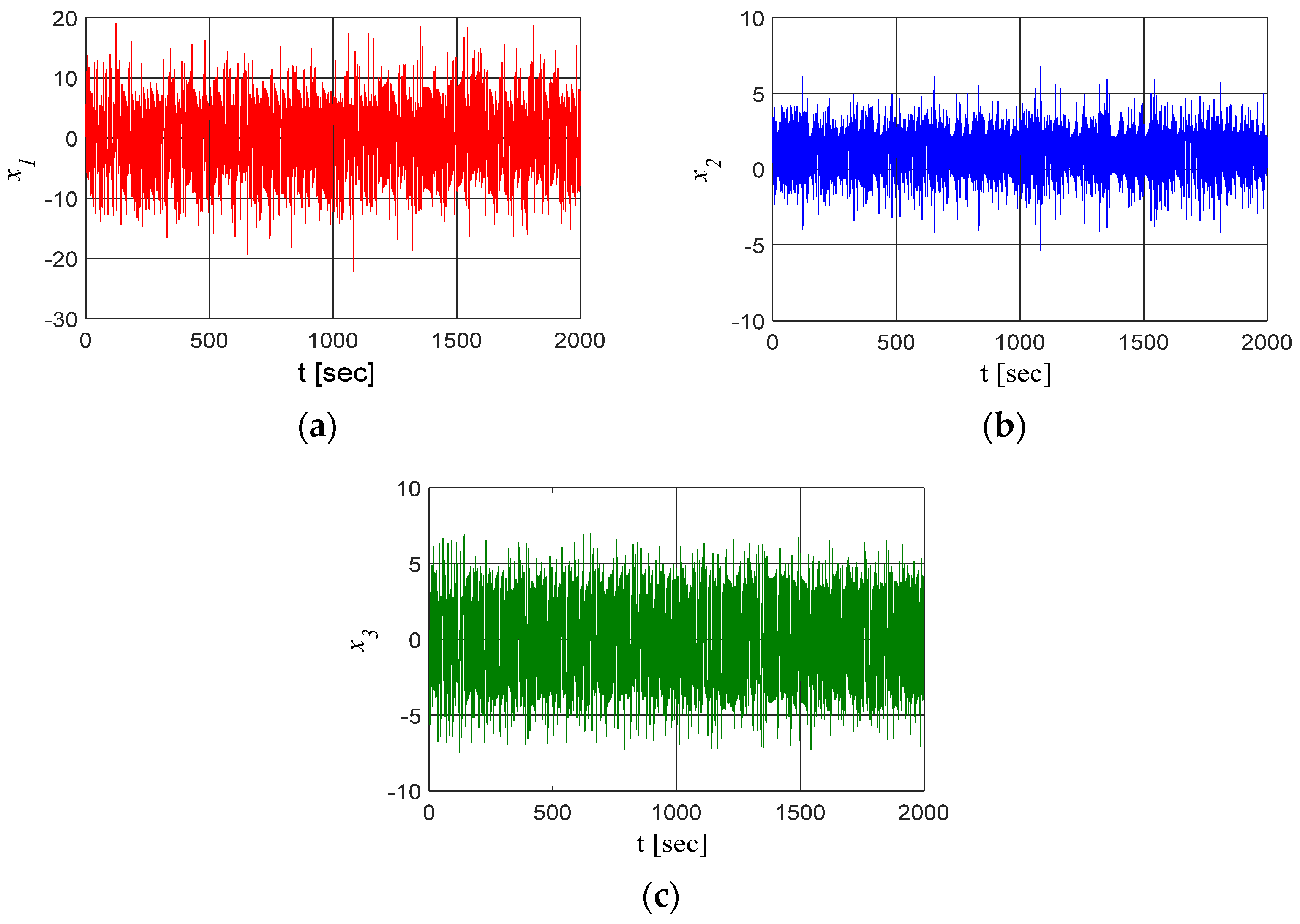
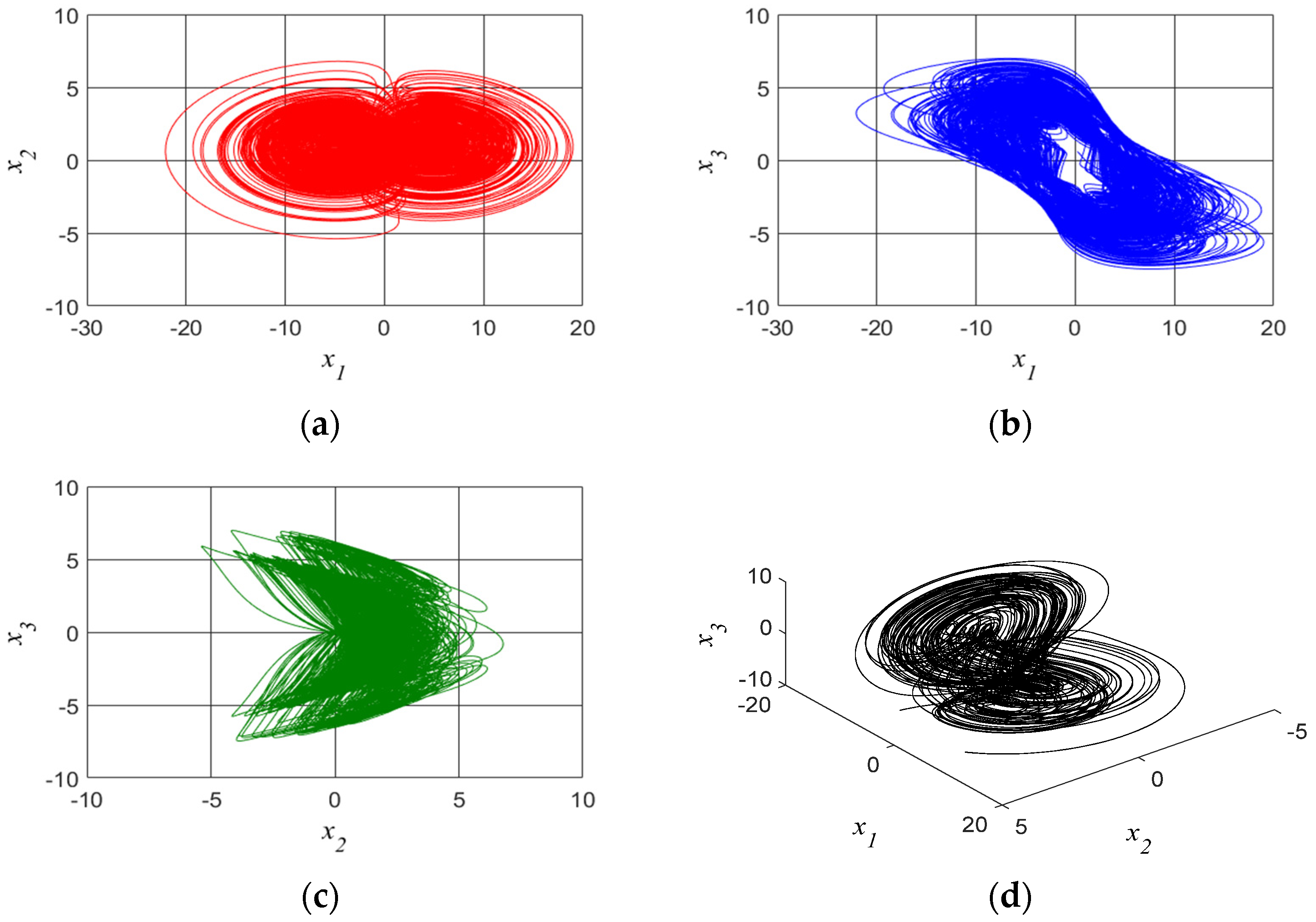
2. Dynamic Analysis
2.1. Mathematical Model
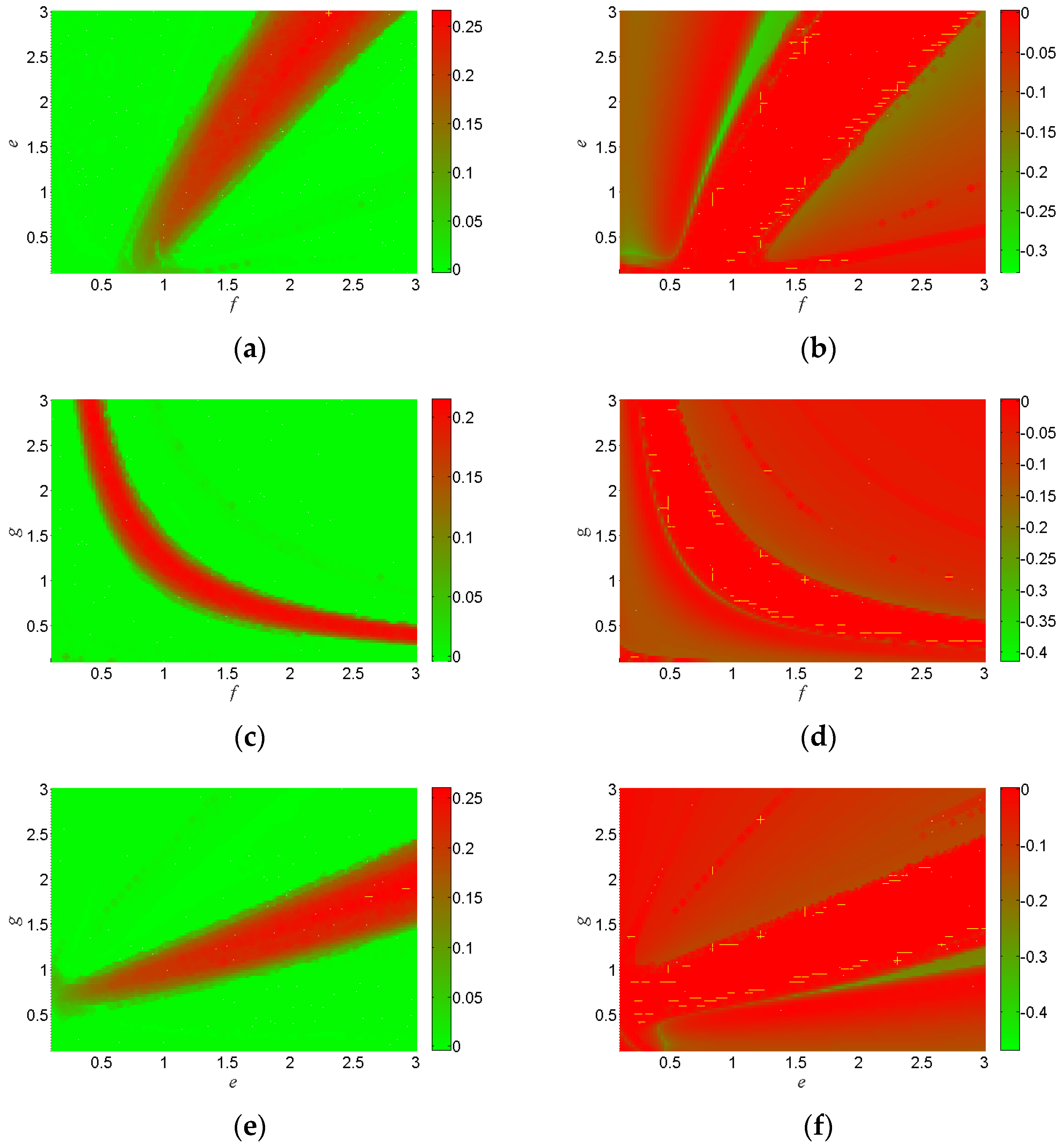
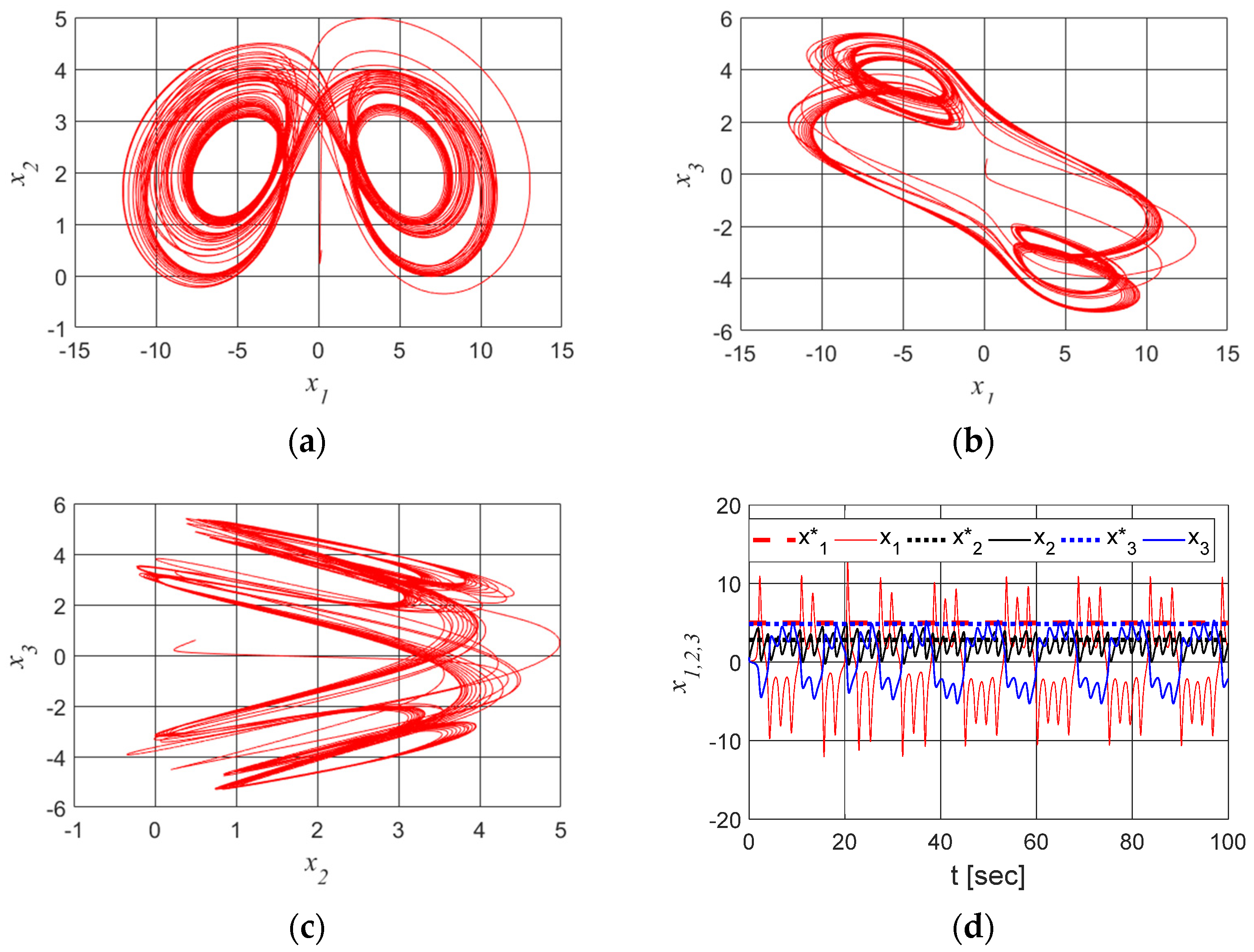
2.2. Dynamic Analysis for Parametric Variations
2.3. Dynamic Analysis for Fractional Order
Application of 0-1 Test
3. Proposed Control by SDRE Control and Feedforward Control
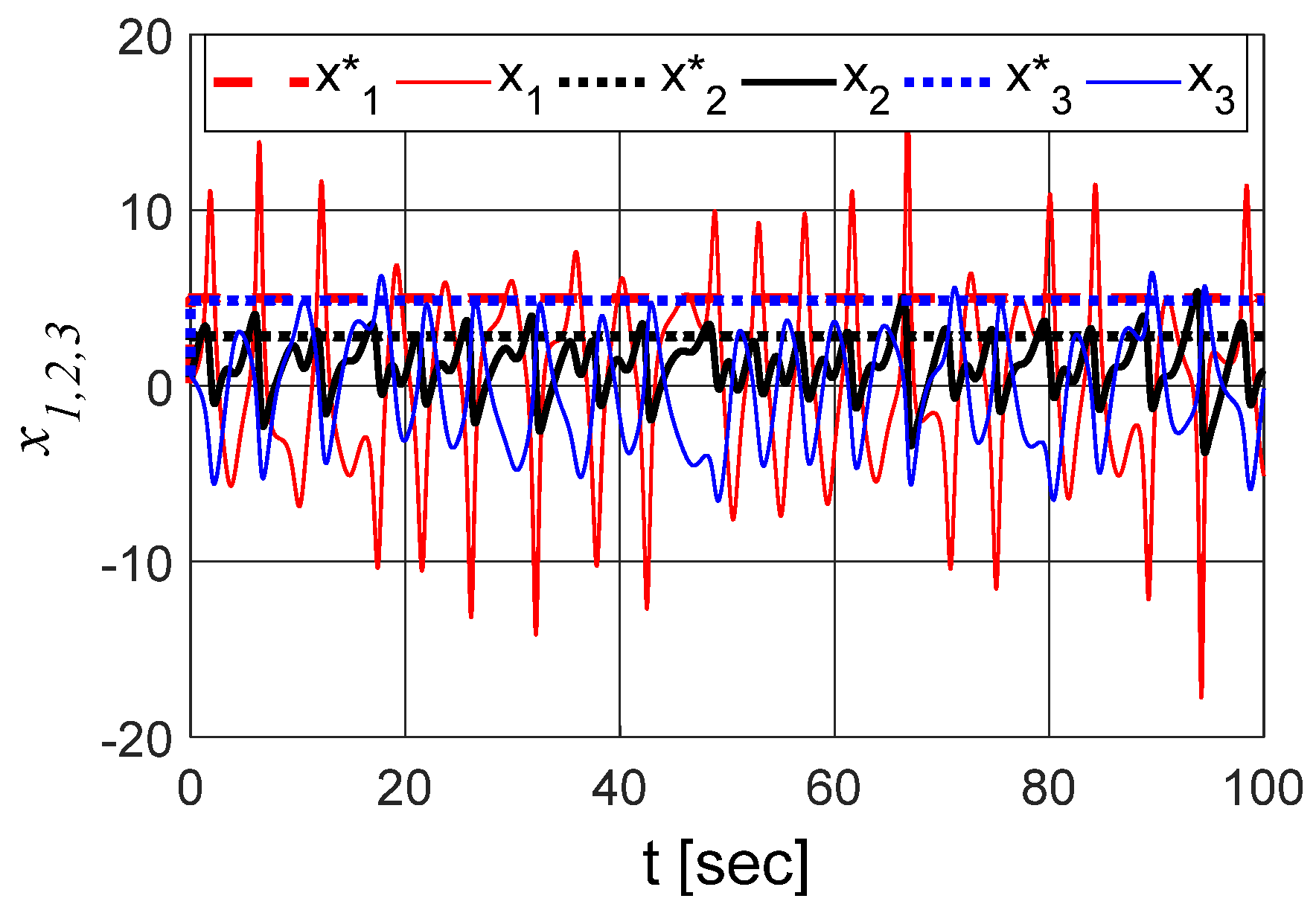
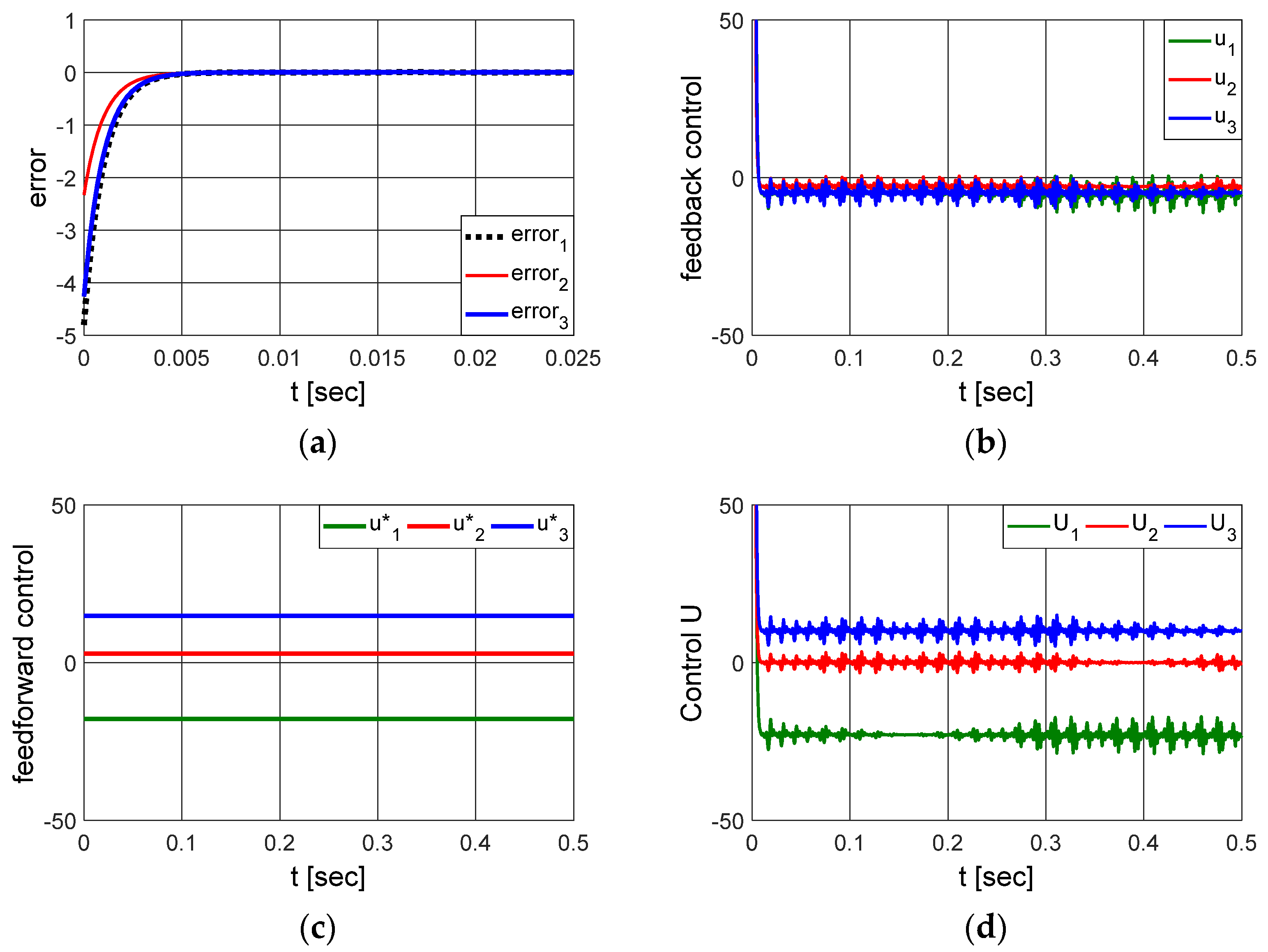
3.1. Integer Order System
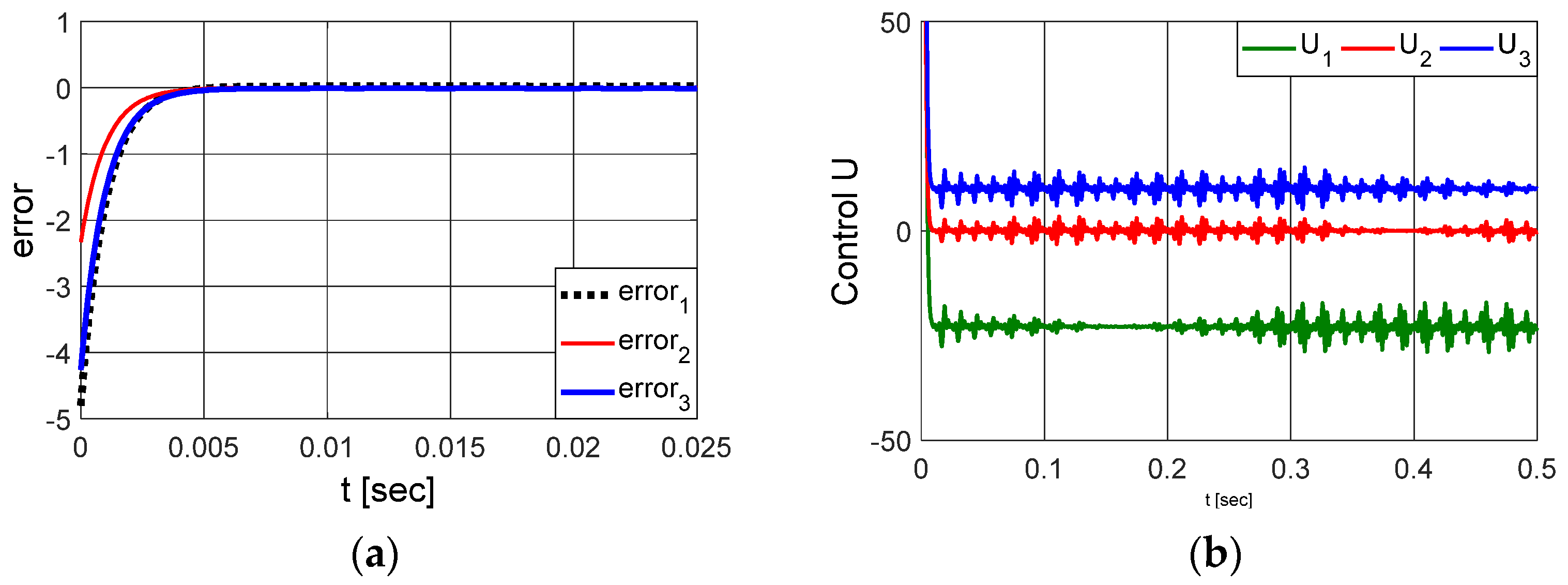
Parametric Sensitivity Analysis
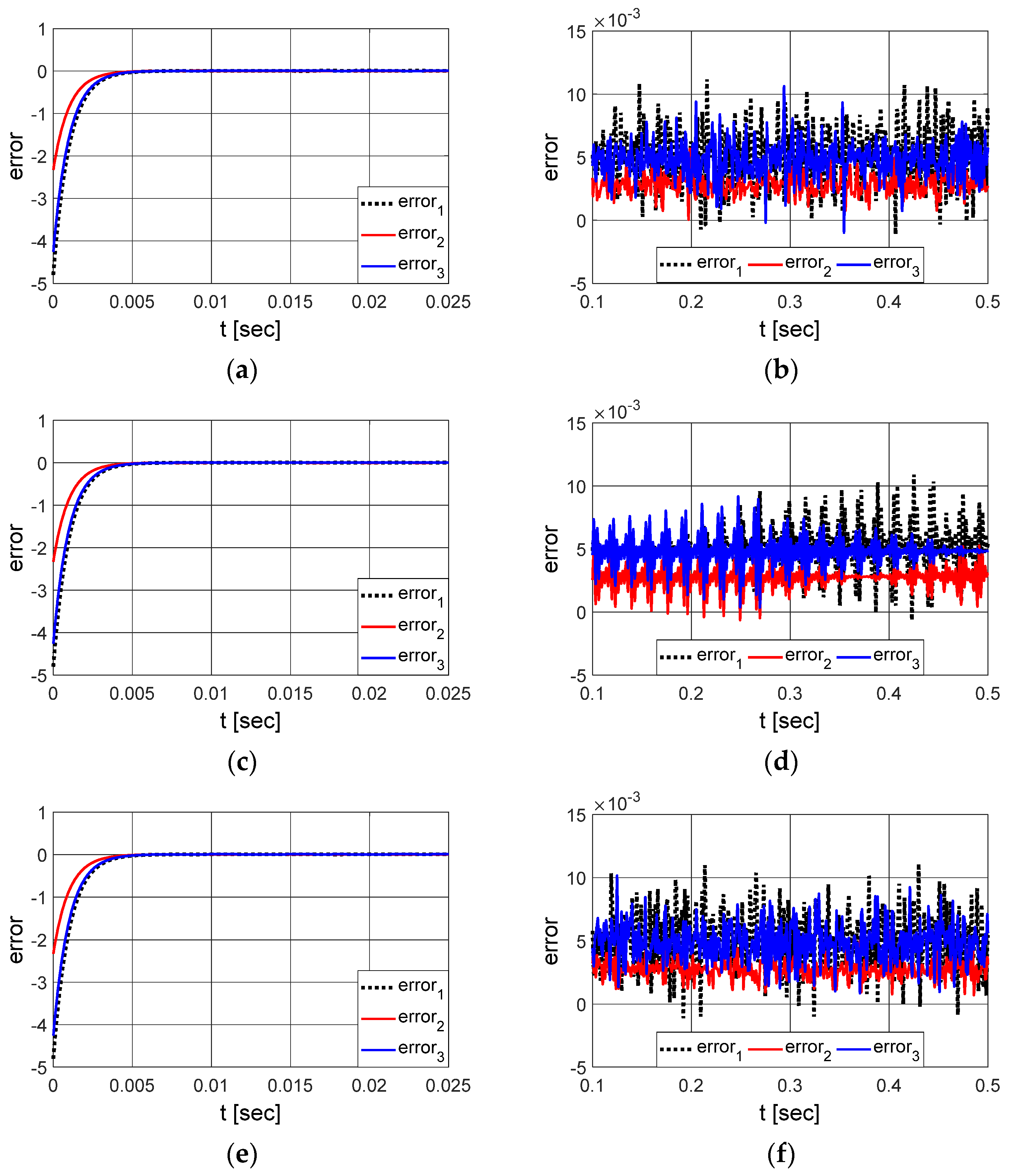
3.2. Fractional Order System
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tacha, O.I.; Munoz-Pacheco, J.M.; Zambrano-Serrano, E.; Stouboulos, I.N.; Pham, V.-T. Determining the chaotic behavior in a fractional-order finance system with negative parameters. Nonlinear Dyn. 2018, 94, 1303–1317. [Google Scholar] [CrossRef]
- Stutzer, M.J. Chaotic Dynamics and bifurcation in a macro model. J. Econ. Dyn. Control 1980, 3, 353–376. [Google Scholar] [CrossRef] [Green Version]
- Meyers, R.A. Complex Systems in Finance and Econometrics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Xu, C.; Aouiti, C.; Liao, M.; Li, P.; Liu, Z. Chaos control strategy for a fractional-order financial model. Adv. Differ. Equ. 2020, 2020, 573. [Google Scholar] [CrossRef]
- Liao, Y.; Zhou, Y.; Xu, F.; Shu, X.-B. A Study on the Complexity of a New Chaotic Financial System. Complexity 2020, 2020, 8821156. [Google Scholar] [CrossRef]
- Matrosov, V.V.; Shalfeev, V. Simulation of the Business-Cycle Synchronization Processes in an Ensemble of Coupled Economic Oscillators. Radiophys. Quantum. Electron. 2022, 64, 750–759. [Google Scholar] [CrossRef]
- Dousseh, Y.P.; Monwanou, A.V.; Koukpémèdji, A.A.; Miwadinou, C.H.; Orou, J.B.C. Dynamics analysis, adaptive control, synchronization and anti-synchronization of a novel modified chaotic financial system. Int. J. Dynam. Control 2023, 11, 862–876. [Google Scholar] [CrossRef]
- Fanti, L.; Manfredi, P. Chaotic business cycles and fiscal policy: An IS-LM model with distributed tax collection lags. Chaos Solitons Fractals 2007, 32, 736–744. [Google Scholar] [CrossRef]
- Chian, A.L.; Rempel, E.L.; Rogers, C. Complex economic dynamics: Chaotic saddle, crisis and intermittency. Chaos Solitons Fractals 2006, 29, 1194–1218. [Google Scholar] [CrossRef]
- Albulescu, C.T.; Tiwari, A.K.; Kyophilavong, P. Nonlinearities and Chaos: A New Analysis of CEE Stock Markets. Mathematics 2021, 9, 707. [Google Scholar] [CrossRef]
- Inglada-Perez, L. A Comprehensive Framework for Uncovering Non-Linearity and Chaos in Financial Markets: Empirical Evidence for Four Major Stock Market Indices. Entropy 2020, 22, 1435. [Google Scholar] [CrossRef]
- Cheng, H.; Huang, J.-B.; Guo, Y.-Q.; Zhu, X.-H. Long memory of price-volume correlation in metal futures market based on fractal features. Trans. Nonferrous Metals Soc. China 2013, 23, 3145–3152. [Google Scholar] [CrossRef]
- David, S.A.; Machado, J.A.T.; Quintino, D.D.; Balthazar, J.M. Partial chaos suppression in a fractional order macroeconomic model. Math. Comput. Simul. 2016, 122, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Baskonus, H.M.; Mekkaoui, T.; Hammouch, Z.; Bulut, H. Active control of a chaotic fractional order economic system. Entropy 2015, 17, 5771–5783. [Google Scholar] [CrossRef] [Green Version]
- Tacha, O.I.; Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N.; Vaidyanathan, S.; Pham, V.T. Analysis, adaptive control and circuit simulation of a novel nonlinear finance system. Appl. Math. Comput. 2016, 276, 200–217. [Google Scholar] [CrossRef]
- Xu, C.; Cui, X.; Li, P.; Yan, J.; Yao, L. Exploration on dynamics in a discrete predator–prey competitive model involving feedback controls. J. Biol. Dyn. 2023, 17, 2220349. [Google Scholar] [CrossRef]
- Ou, W.; Xu, C.; Cui, Q.; Liu, Z.; Pang, Y.; Farman, M.; Ahmad, S.; Zeb, A. Mathematical study on bifurcation dynamics and control mechanism of tri-neuron bidirectional associative memory neural networks including delay. Math. Meth. Appl. Sci. 2023, 1, 1–25. [Google Scholar] [CrossRef]
- Huang, C.; Liu, H.; Shi, X.; Chen, X.; Xiao, M.; Wang, Z.; Cao, J. Bifurcations in a fractional-order neural network with multiple leakage delays. Neural Netw. 2020, 131, 115–126. [Google Scholar] [CrossRef]
- Huang, C.; Liu, H.; Chen, X.; Cao, J.; Alsaedi, A. Extended feedback and simulation strategies for a delayed fractional-order control system. Phys. A Stat. Mech. Its Appl. 2020, 545, 123127. [Google Scholar] [CrossRef]
- Johansyah, M.D.; Sambas, A.; Mobayen, S.; Vaseghi, B.; Al-Azzawi, S.F.; Sukono; Sulaiman, I.M. Dynamical Analysis and Adaptive Finite-Time Sliding Mode Control Approach of the Financial Fractional-Order Chaotic System. Mathematics 2023, 11, 100. [Google Scholar] [CrossRef]
- He, Y.; Peng, J.; Zheng, S. Fractional-Order Financial System and Fixed-Time Synchronization. Fractal Fract. 2022, 6, 507. [Google Scholar] [CrossRef]
- Rao, R. Global Stability of a Markovian Jumping Chaotic Financial System with Partially Unknown Transition Rates under Impulsive Control Involved in the Positive Interest Rate. Mathematics 2019, 7, 579. [Google Scholar] [CrossRef] [Green Version]
- Xin, B.; Li, Y. 0-1 Test for Chaos in a Fractional Order Financial System with Investment Incentive. Abstr. Appl. Anal. 2013, 2013, 876298. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.B.; Jahanshahi, H.; Abba, O.A.; Solís-Pérez, J.E.; Bekiros, S.; Gómez-Aguilar, J.F.; Yousefpour, A.; Chu, Y.M. The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization. Chaos Solitons Fractals 2020, 140, 110223. [Google Scholar] [CrossRef]
- Yu, H.; Cai, G.; Li, Y. Dynamic analysis and control of a new hyperchaotic finance system. Chaos Solitons Fractals 2012, 45, 1048–1057. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Cao, Y. Chaotic synchronization based on fractional order calculus financial system. Chaos Solitons Fractals 2020, 130, 109410. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Tusset, A.M.; Ribeiro, M.A.; Lenz, W.B.; Rocha, R.T.; Balthazar, J.M. Time Delayed Feedback Control Applied in an Atomic Force Microscopy (AFM) Model in Fractional-Order. J. Vib. Eng. Technol. 2020, 8, 327–335. [Google Scholar] [CrossRef]
- Tusset, A.M.; Balthazar, J.M.; Ribeiro, M.A.; Lenz, W.B.; Rocha, R.T. Chaos control of an atomic force microscopy model in fractional-order. Eur. Phys. J.-Spec. Top. 2021, 230, 3643–3654. [Google Scholar] [CrossRef]
- Ribeiro, M.A.; Balthazar, J.M.; Lenz, W.B.; Rocha, R.T.; Tusset, A.M. Numerical Exploratory Analysis of Dynamics and Control of an Atomic Force Microscopy in Tapping Mode with Fractional Order. Shock. Vib. 2020, 2020, 4048307. [Google Scholar] [CrossRef]
- Bassinello, D.G.; Tusset, A.M.; Rocha, R.T.; Balthazar, J.M. Dynamical Analysis and Control of a Chaotic Microelectromechanical Resonator Model. Shock. Vib. 2018, 2018, 4641629. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.D. Approximation methods in optimal control. J. Electron. Control 1962, 13, 453–469. [Google Scholar] [CrossRef]
- Tusset, A.M.; Balthazar, J.M.; Rocha, R.T.; Ribeiro, M.R.; Lenz, W.B. On suppression of chaotic motion of a nonlinear MEMS oscillator. Nonlinear Dyn. 2020, 99, 537–557. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Daũm, H.H.; Rocha, R.T.; Balthazar, J.M.; Tusset, A.M. Dynamic Analysis and Synchronization for a System with Hyperchaotic Behavior. Braz. J. Phys. 2021, 51, 1333–1345. [Google Scholar] [CrossRef]
- Gao, Q.; Ma, J. Chaos and Hopf bifurcation of a finance system. Nonlinear Dyn. 2009, 58, 209–216. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Günerhan, H.; Kaabar, M.K.A.; Çelik, E. Novel analytical and approximate-analytical methods for solving the nonlinear fractional smoking mathematical model. Sigma J. Eng. Nat. Sci. 2023, 41, 331–343. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. Testing for chaos in deterministic systems with noise. Phys. D Nonlinear Phenom. 2005, 212, 100–110. [Google Scholar] [CrossRef] [Green Version]
- Bernardini, D.; Litak, G. An overview of 0-1 test for chaos. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1433–1450. [Google Scholar] [CrossRef]
- Yuan, L.; Yang, Q.; Zeng, C. Chaos detection and parameter identification in fractional-order chaotic systems with delay. Nonlinear Dyn. 2013, 73, 439–448. [Google Scholar] [CrossRef]
- Peruzzi, N.; Chavarette, F.; Balthazar, J.M.; Tusset, A.M.; Perticarrari, A.; Brasil, R. The dynamic behavior of a parametrically excited time-periodic MEMS taking into account parametric errors. J. Vib. Control 2016, 22, 4101–4110. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tusset, A.M.; Fuziki, M.E.K.; Balthazar, J.M.; Andrade, D.I.; Lenzi, G.G. Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order. Fractal Fract. 2023, 7, 535. https://doi.org/10.3390/fractalfract7070535
Tusset AM, Fuziki MEK, Balthazar JM, Andrade DI, Lenzi GG. Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order. Fractal and Fractional. 2023; 7(7):535. https://doi.org/10.3390/fractalfract7070535
Chicago/Turabian StyleTusset, Angelo M., Maria E. K. Fuziki, Jose M. Balthazar, Dana I. Andrade, and Giane G. Lenzi. 2023. "Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order" Fractal and Fractional 7, no. 7: 535. https://doi.org/10.3390/fractalfract7070535
APA StyleTusset, A. M., Fuziki, M. E. K., Balthazar, J. M., Andrade, D. I., & Lenzi, G. G. (2023). Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order. Fractal and Fractional, 7(7), 535. https://doi.org/10.3390/fractalfract7070535









