Dynamic Behavior of a Class of Six-Neuron Fractional BAM Neural Networks
Abstract
1. Introduction
2. Preliminaries
3. Stability and Hopf Bifurcation
| (H2) Each of the following expressions holds: |
| (H3) . |
- (1)
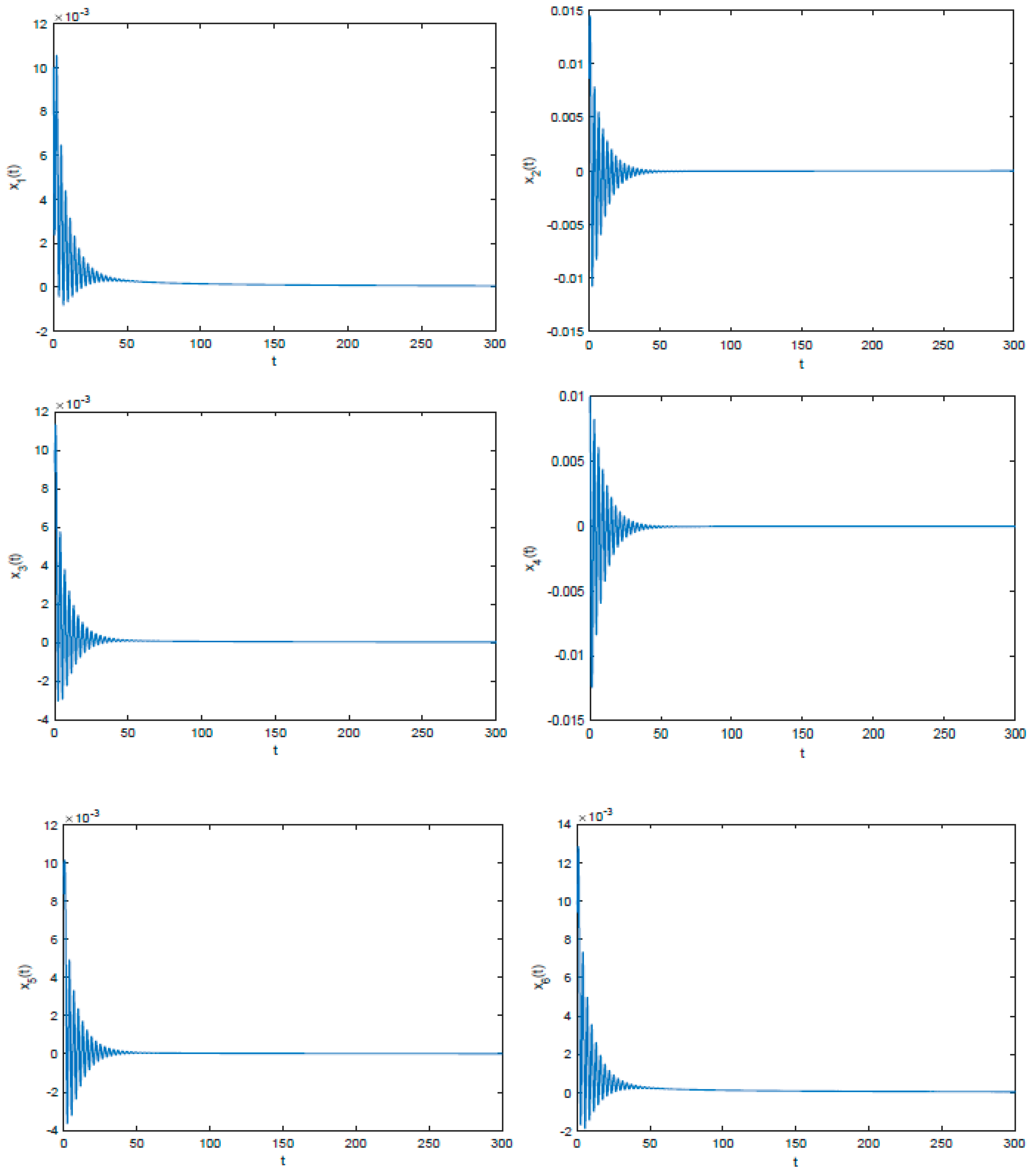
- When , the zero equilibrium point of system (5) has global asymptotic stability, while when , the zero solution of fractional order system (5) is unstable.
- (2)
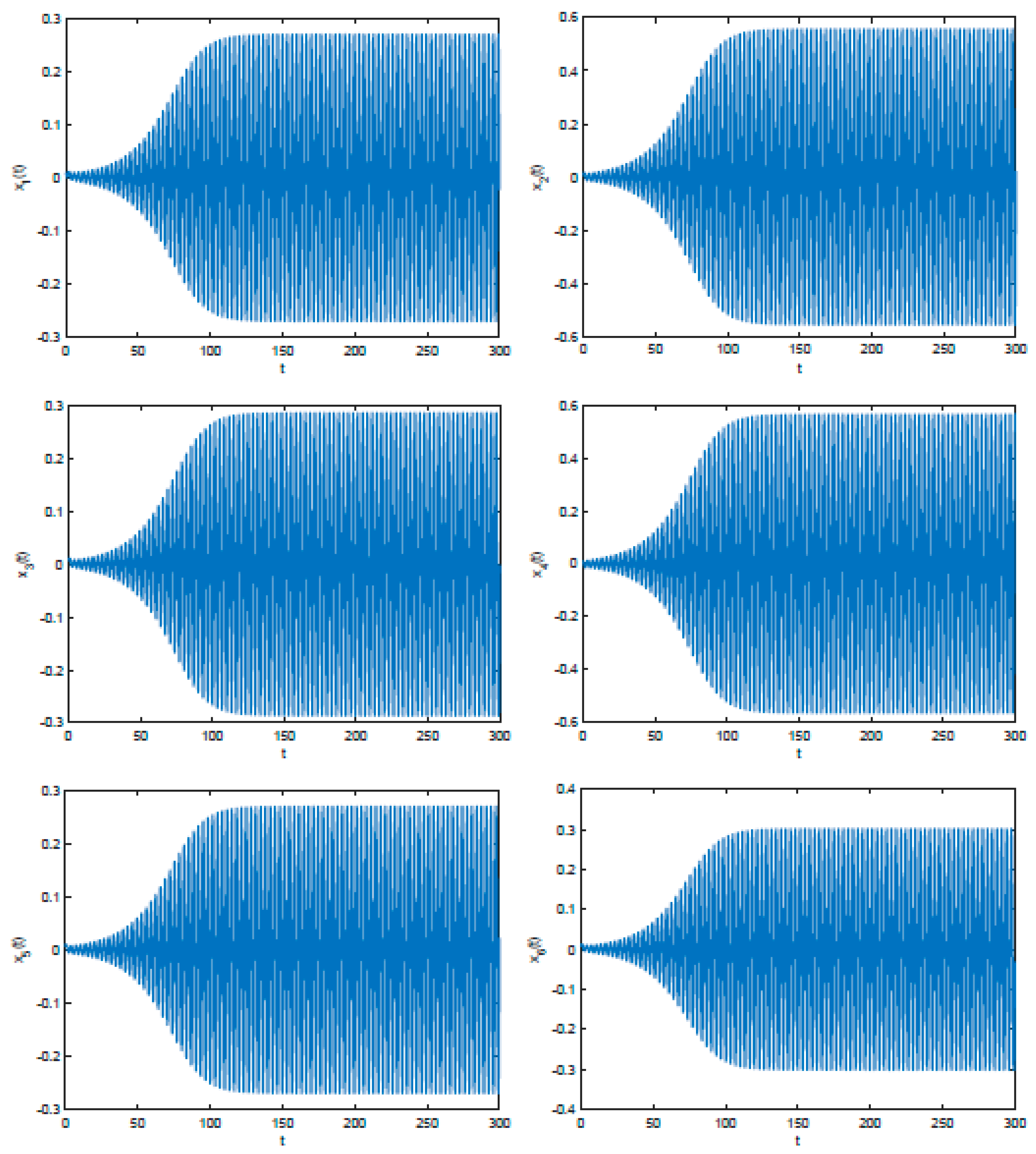
- When , System (5) loses stability at the zero equilibrium point and Hopf bifurcation occurs.
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mao, X.; Wang, Z. Stability, bifurcation, and synchronization of delay-coupled ring neural networks. Nonlinear Dyn. 2016, 84, 1063–1078. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Wang, Z.; Li, Y. Nonlinear dynamics and chaos in a simplified memristor-based fractional-order neural network with discontinuous memductance function. Nonlinear Dyn. 2018, 93, 611–627. [Google Scholar] [CrossRef]
- Xu, C. Local and global Hopf bifurcation analysis on simplified bidirectional associative memory neural networks with multiple delays. Math. Comput. Simul. 2018, 149, 69–90. [Google Scholar] [CrossRef]
- Ge, J.; Xu, J. Stability and Hopf bifurcation on four-neuron neural networks with inertia and multiple delays. Neurocomputing 2018, 287, 34–44. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Liao, M.; Li, P.; Xiao, Q.; Yuan, S. Fractional-order bidirectional associate memory (BAM) neural networks with multiple delays: The case of Hopf bifurcation. Math. Comput. Simul. 2021, 182, 471–494. [Google Scholar] [CrossRef]
- Dong, T.; Xu, W.; Liao, X. Hopf bifurcation analysis of reaction diffusion neural oscillator system with excitatory-to-inhibitory connection and time delay. Nonlinear Dyn. 2017, 89, 2329–2345. [Google Scholar] [CrossRef]
- Cao, Y.; Ramajayam, S.; Sriraman, R.; Samidurai, R. Leakage delay on stabilization of finite-time complex-valued BAM neural network: Decomposition approach. Neurocomputing 2021, 463, 505–513. [Google Scholar] [CrossRef]
- Sriraman, R.; Vignesh, P.; Amritha, V.; Rachakit, G.; Balaji, P. Direct quaternion method-based stability criteria for quaternion-valued Takagi-Sugeno fuzzy BAM delayed neural networks using quaternion-valued Wirtinger-based integral inequality. AIMS Math. 2023, 8, 10486–10512. [Google Scholar] [CrossRef]
- Sriraman, R.; Rajchakit, G.; Kwon, O.; Lee, S. Stability analysis for delayed Cohen-Grossberg Clifford-valued neutral-type neural networks. Math. Methods Appl. Sci. 2022, 45, 10925–10945. [Google Scholar] [CrossRef]
- Cheng, Z.; Xie, K.; Wang, T.; Cao, J. Stability and Hopf bifurcation of three-triangle neural networks with delays. Neurocomputing 2018, 322, 206–215. [Google Scholar] [CrossRef]
- Lin, J.; Xu, R.; Li, L. Turing-Hopf bifurcation of reaction-diffusion neural networks with leakage delay. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105241. [Google Scholar] [CrossRef]
- Mao, X.; Wang, Z. Stability switches and bifurcation in a system of four coupled neural networks with multiple time delays. Nonlinear Dyn. 2015, 82, 1551–1567. [Google Scholar] [CrossRef]
- Li, H.; Jiang, H.; Hu, C. Existence and global exponential stability of periodic solution of memristor-based BAM neural networks with time-varying delays. Neural Netw. 2016, 75, 97–109. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Huang, T.; Tan, J. Exponential stability of inertial BAM neural networks with time-varying delay via periodically intermittent control. Neural Comput. Appl. 2015, 26, 1781–1787. [Google Scholar] [CrossRef]
- Arik, S. New criteria for stability of neutral-type neural networks with multiple time delays. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1504–1513. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, L. Global stability analysis for delayed complex-valued BAM neural networks. Neurocomputing 2016, 173, 2083–2089. [Google Scholar] [CrossRef]
- Zhou, L. Novel global exponential stability criteria for hybrid BAM neural networks with proportional delays. Neurocomputing 2015, 161, 99–106. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P.; Guo, Y.; Liu, Z. Bifurcation properties for fractional order delayed BAM neural networks. Cogn. Comput. 2021, 13, 322–356. [Google Scholar] [CrossRef]
- Li, B.; Liao, M.; Xu, C.; Chen, H.; Li, W. Stability and Hopf bifurcation of a class of six-Neuron fractional BAM neural networks with multiple delays. Fractal Fract. 2023, 7, 142. [Google Scholar] [CrossRef]
- Li, B.; Liao, M.; Xu, C.; Li, W. Hopf Bifurcation Analysis of a Delayed Fractional BAM Neural Network Model with Incommensurate Orders. Neural Process. Lett. 2022; in press. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Li, P.; Yao, L.; Qin, Q. Comparative exploration on bifurcation behavior for integer-order and fractional-order delayed BAM neural networks. Nonlinear Anal. Model. Control 2022, 27, 1–24. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Aouiti, C. New insight into bifurcation of fractional-order 4D neural networks incorporating two different time delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107043. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Zhang, S. New criteria on the finite-time stability of fractional-order BAM neural networks with time delay. Neural Comput. Appl. 2022, 34, 4501–4517. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Aouiti, C.; Liu, Z.; Liao, M.; Li, P. Further investigation on bifurcation and their control offractional-order bidirectional associative memory neuralnetworks involving four neurons and multiple delays. Math. Meth. Appl. Sci. 2023, 46, 3091–3114. [Google Scholar] [CrossRef]
- Xu, C.; Aouiti, C.; Liu, Z. A further study on bifurcation for fractional order BAM neural networks with multiple delays. Neurocomputing 2020, 417, 501–515. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J. Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw. 2018, 98, 223–235. [Google Scholar] [CrossRef]
- Wang, B.; Jian, J. Stability and Hopf bifurcation analysis on a four-neuron BAM neural network with distributed delays. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 189–204. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.; Chen, X.; Cao, J. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 2021, 141, 344–354. [Google Scholar] [CrossRef]
- Huang, C.; Mo, S.; Cao, J. Detections of bifurcation in a fractional-order Cohen-Grossberg neural network with multiple delays. Cogn. Neurodyn. 2023; in press. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Li, P.; Yan, J.; Yao, L. Bifurcation Mechanism for Fractional-Order Three-Triangle Multi-delayed Neural Networks. Neural Process. Lett. 2022, 1–27. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Liu, Z.; Wang, R. High codimensional bifurcation analysis to a six-neuron BAM neural network. Cogn. Neurodyn. 2016, 10, 149–164. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Deng, W.; Li, C.; Lü, J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Liao, M.; Li, D.; Xu, C.; Li, B. Dynamic Behavior of a Class of Six-Neuron Fractional BAM Neural Networks. Fractal Fract. 2023, 7, 520. https://doi.org/10.3390/fractalfract7070520
Li W, Liao M, Li D, Xu C, Li B. Dynamic Behavior of a Class of Six-Neuron Fractional BAM Neural Networks. Fractal and Fractional. 2023; 7(7):520. https://doi.org/10.3390/fractalfract7070520
Chicago/Turabian StyleLi, Weinan, Maoxin Liao, Dongsheng Li, Changjin Xu, and Bingbing Li. 2023. "Dynamic Behavior of a Class of Six-Neuron Fractional BAM Neural Networks" Fractal and Fractional 7, no. 7: 520. https://doi.org/10.3390/fractalfract7070520
APA StyleLi, W., Liao, M., Li, D., Xu, C., & Li, B. (2023). Dynamic Behavior of a Class of Six-Neuron Fractional BAM Neural Networks. Fractal and Fractional, 7(7), 520. https://doi.org/10.3390/fractalfract7070520




