A Unified Description of the Electrical Properties with Complex Dynamical Patterns in Metal Halide Perovskite Photovoltaics
Abstract
:1. Introduction
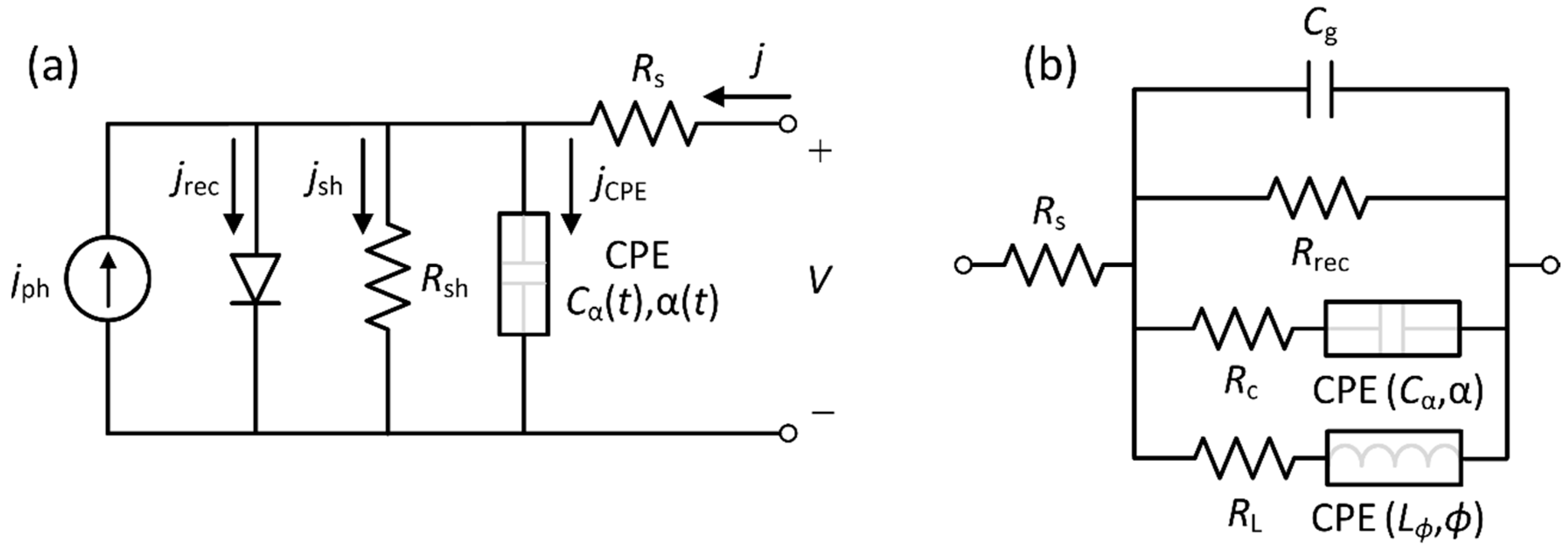
2. Device Modeling
2.1. Advanced Surface Polarization Model
2.2. On the Impedance Spectroscopy Dynamics
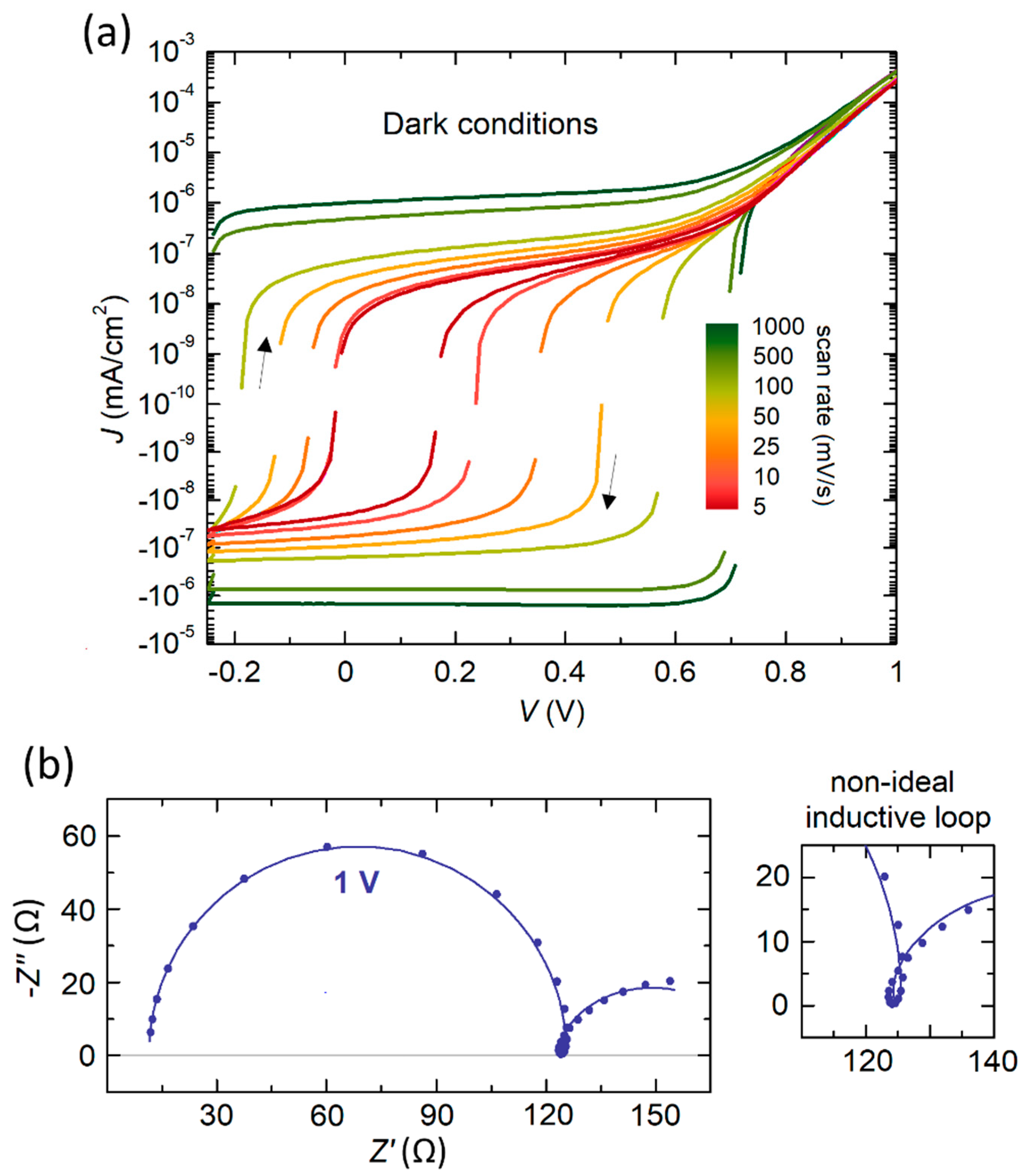
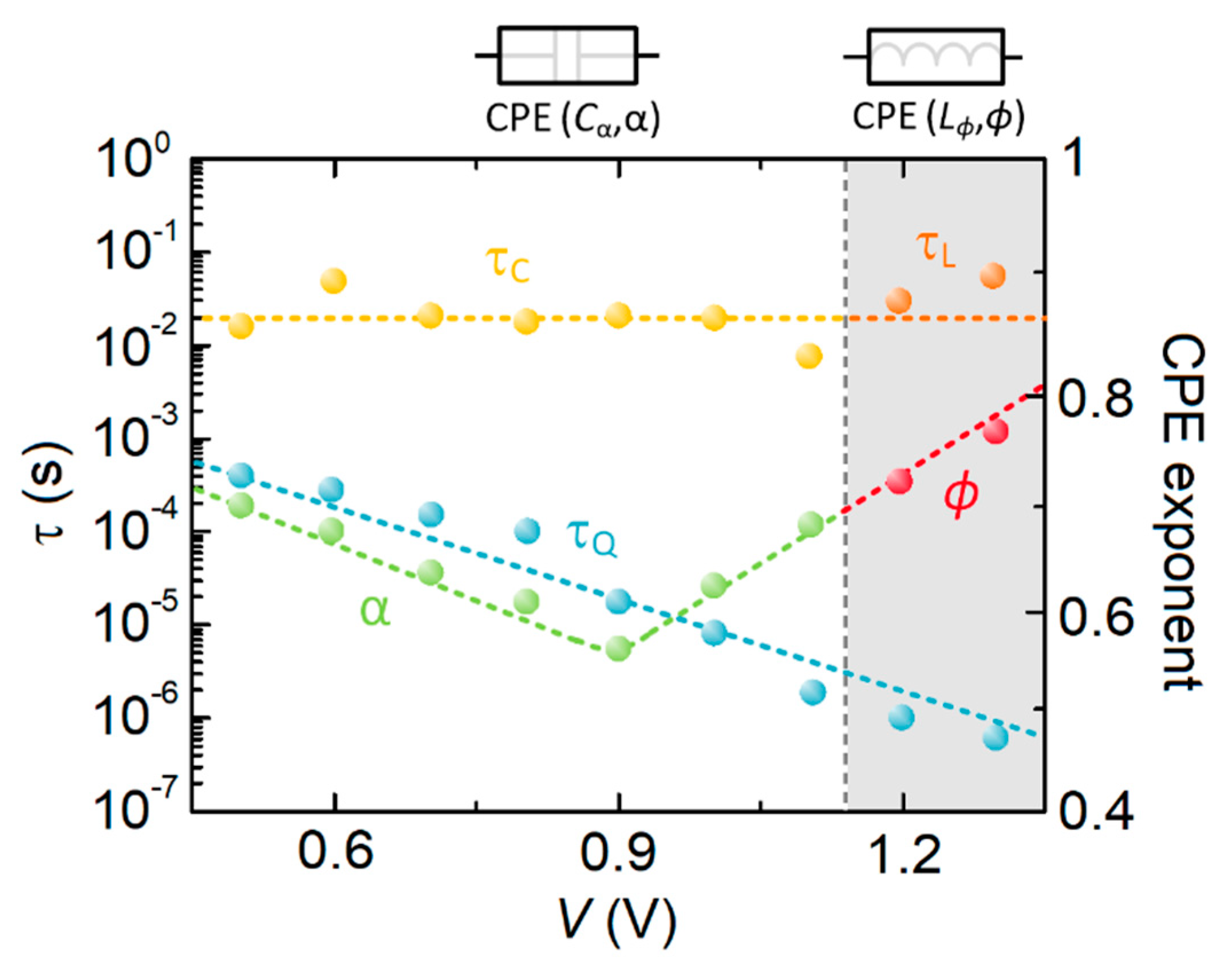
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Park, N.-G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Dou, L.; Yang, Y.; You, J.; Hong, Z.; Chang, W.-H.; Li, G.; Yang, Y. Solution-processed hybrid perovskite photodetectors with high detectivity. Nat. Commun. 2014, 5, 5404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, Z.; Huang, J. Energy-efficient hybrid perovskite memristors and synaptic devices. Adv. Electron. Mater. 2016, 2, 1600100. [Google Scholar] [CrossRef]
- Fakharuddin, A.; Gangishetty, M.K.; Abdi-Jalebi, M.; Chin, S.-H.; Mohd Yusoff, A.R.b.; Congreve, D.N.; Tress, W.; Deschler, F.; Vasilopoulou, M.; Bolink, H.J. Perovskite light-emitting diodes. Nat. Electron. 2022, 5, 203–216. [Google Scholar] [CrossRef]
- Sakhatskyi, K.; John, R.A.; Guerrero, A.; Tsarev, S.; Sabisch, S.; Das, T.; Matt, G.J.; Yakunin, S.; Cherniukh, I.; Kotyrba, M.; et al. Assessing the drawbacks and benefits of ion migration in lead halide perovskites. ACS Energy Lett. 2022, 7, 3401–3414. [Google Scholar] [CrossRef] [PubMed]
- Ravishankar, S.; Almora, O.; Echeverría-Arrondo, C.; Ghahremanirad, E.; Aranda, C.; Guerrero, A.; Fabregat-Santiago, F.; Zaban, A.; Garcia-Belmonte, G.; Bisquert, J. Surface polarization model for the dynamic hysteresis of perovskite solar cells. J. Phys. Chem. Lett. 2017, 8, 915–921. [Google Scholar] [CrossRef]
- Ghahremanirad, E.; Bou, A.; Olyaee, S.; Bisquert, J. Inductive loop in the impedance response of perovskite solar cells explained by surface polarization model. J. Phys. Chem. Lett. 2017, 8, 1402–1406. [Google Scholar] [CrossRef]
- Guerrero, A.; Bisquert, J.; Garcia-Belmonte, G. Impedance spectroscopy of metal halide perovskite solar cells from the perspective of equivalent circuits. Chem. Rev. 2021, 121, 14430–14484. [Google Scholar] [CrossRef]
- Bisquert, J.; Guerrero, A. Chemical Inductor. J. Am. Chem. Soc. 2022, 144, 5996–6009. [Google Scholar] [CrossRef]
- Ebadi, F.; Taghavinia, N.; Mohammadpour, R.; Hagfeldt, A.; Tress, W. Origin of apparent light-enhanced and negative capacitance in perovskite solar cells. Nat. Commun. 2019, 10, 1574. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, A.O.; Arcas, R.; Aranda, C.A.; Bethencourt, L.; Mas-Marzá, E.; Saliba, M.; Fabregat-Santiago, F. Negative capacitance and inverted hysteresis: Matching features in perovskite solar cells. J. Phys. Chem. Lett. 2020, 11, 8417–8423. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Balaguera, E.; Bisquert, J. Negative transient spikes in halide perovskites. ACS Energy Lett. 2022, 7, 2602–2610. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E.; Romero, B.; Najafi, M.; Galagan, Y. Analysis of light-enhanced capacitance dispersion in perovskite solar cells. Adv. Mater. Interfaces 2022, 9, 2102275. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E.; Arredondo, B.; Pereyra, C.; Lira-Cantú, M. Parameterization of the apparent chemical inductance of metal halide perovskite solar cells exhibiting constant-phase-element behavior. J. Power Sources 2023, 560, 232614. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E.; Romero, B.; Arredondo, B.; del Pozo, G.; Najafi, M.; Galagan, Y. The dominant role of memory-based capacitive hysteretic currents in operation of photovoltaic perovskites. Nano Energy 2020, 78, 105398. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E.; del Pozo, G.; Arredondo, B.; Romero, B.; Pereyra, C.; Xie, H.; Lira-Cantú, M. Unraveling the key relationship between perovskite capacitive memory, long timescale cooperative relaxation phenomena, and anomalous J–V hysteresis. Solar RRL 2021, 5, 2000707. [Google Scholar] [CrossRef]
- Bisquert, J. Electrical charge coupling dominates the hysteresis effect of halide perovskite devices. J. Phys. Chem. Lett. 2023, 14, 1014–1021. [Google Scholar] [CrossRef]
- Nemnes, G.A.; Besleaga, C.; Tomulescu, A.G.; Pintilie, I.; Pintilie, L.; Torfason, K.; Manolescu, A. Dynamic electrical behavior of halide perovskite based solar cells. Sol. Energy Mater. Sol. Cells 2017, 159, 197–203. [Google Scholar] [CrossRef] [Green Version]
- Nemnes, G.A.; Besleaga, C.; Stancu, V.; Dogaru, D.E.; Leonat, L.N.; Pintilie, L.; Torfason, K.; Ilkov, M.; Manolescu, A.; Pintilie, I. Normal and inverted hysteresis in perovskite solar cells. J. Phys. Chem. C 2017, 121, 11207–11214. [Google Scholar] [CrossRef] [Green Version]
- Fouda, M.E.; Allagui, A.; Elwakil, A.S.; Das, S.; Psychalinos, C.; Radwan, A.G. Nonlinear charge-voltage relationship in constant phase element. Int. J. Electron. Commun. 2020, 117, 153104. [Google Scholar] [CrossRef]
- Pandey, V. Origin of the Curie-von Schweidler law and the fractional capacitor from time-varying capacitance. J. Power Sources 2022, 532, 231309. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Martynyuk, V.; Kosenkov, V.; Guimarães Batista, A. A new look at the capacitor theory. Fractal Fract. 2023, 7, 86. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valério, D.; Machado, J.T. Variable order fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 231–243. [Google Scholar] [CrossRef]
- Valério, D.; da Costa, J.S. Variable-order fractional derivatives and their numerical approximations. Signal Process. 2011, 91, 470–483. [Google Scholar] [CrossRef]
- Juarez-Perez, E.J.; Sanchez, R.S.; Badia, L.; Garcia-Belmonte, G.; Kang, Y.S.; Mora-Seró, I.; Bisquert, J. Photoinduced giant dielectric constant in lead halide perovskite solar cells. J. Phys. Chem. Lett. 2014, 5, 2390–2394. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E.; Arredondo, B.; del Pozo, G.; Romero, B. Exploring the impact of fractional-order capacitive behavior on the hysteresis effects of perovskite solar cells. A theoretical perspective. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105371. [Google Scholar] [CrossRef]
- Filipoiu, N.; Preda, A.T.; Anghel, D.-V.; Patru, R.; Brophy, R.E.; Kateb, M.; Besleaga, C.; Tomulescu, A.G.; Pintilie, I.; Manolescu, A.; et al. Capacitive and inductive effects in perovskite solar cells: The different roles of ionic current and ionic charge accumulation. Phys. Rev. Appl. 2022, 18, 064087. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E. Fractional model of the chemical inductor. Chaos Solitons Fractals 2023, 172, 113470. [Google Scholar] [CrossRef]
- Zarazua, I.; Han, G.; Boix, P.P.; Mhaisalkar, S.; Fabregat-Santiago, F.; Mora-Seró, I.; Bisquert, J.; Garcia-Belmonte, G. Surface recombination and collection efficiency in perovskite solar cells from impedance analysis. J. Phys. Chem. Lett. 2016, 7, 5105–5113. [Google Scholar] [CrossRef] [Green Version]
- Almora, O.; Cho, K.T.; Aghazada, S.; Zimmermann, I.; Matt, G.J.; Brabec, C.J.; Nazeeruddin, M.K.; Garcia-Belmonte, G. Discerning recombination mechanisms and ideality factors through impedance analysis of high-efficiency perovskite solar cells. Nano Energy 2018, 48, 63–72. [Google Scholar] [CrossRef]
- Gonzales, C.; Guerrero, A.; Bisquert, J. Transition from capacitive to inductive hysteresis: A neuron-style model to correlate I-V curves to impedances of metal halide perovskites. J. Phys. Chem. C 2022, 126, 13560–13578. [Google Scholar] [CrossRef]
- Bisquert, J.; Guerrero, A.; Gonzales, C. Theory of hysteresis in halide perovskites by integration of the equivalent circuit. ACS Phys. Chem Au 2021, 1, 25–44. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Balaguera, E.; Muñoz-Díaz, L.; Pereyra, C.; Lira-Cantú, M.; Najafi, M.; Galagan, Y. Universal control strategy for anomalous ionic-electronic phenomenology in perovskite solar cells efficiency measurements. Mater. Today Energy 2022, 27, 101031. [Google Scholar] [CrossRef]
- Córdoba-Torres, P.; Mesquita, T.J.; Devos, O.; Tribollet, B.; Roche, V.; Nogueira, R.P. On the intrinsic coupling between constant-phase element parameters α and Q in electrochemical impedance spectroscopy. Electrochim. Acta 2012, 72, 172–178. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Balaguera, E.; Martin-Martin, D. A Unified Description of the Electrical Properties with Complex Dynamical Patterns in Metal Halide Perovskite Photovoltaics. Fractal Fract. 2023, 7, 516. https://doi.org/10.3390/fractalfract7070516
Hernández-Balaguera E, Martin-Martin D. A Unified Description of the Electrical Properties with Complex Dynamical Patterns in Metal Halide Perovskite Photovoltaics. Fractal and Fractional. 2023; 7(7):516. https://doi.org/10.3390/fractalfract7070516
Chicago/Turabian StyleHernández-Balaguera, Enrique, and Diego Martin-Martin. 2023. "A Unified Description of the Electrical Properties with Complex Dynamical Patterns in Metal Halide Perovskite Photovoltaics" Fractal and Fractional 7, no. 7: 516. https://doi.org/10.3390/fractalfract7070516





