The Evolution of COVID-19 Transmission with Superspreaders Class under Classical and Caputo Piecewise Operators: Real Data Perspective from India, France, and Italy
Abstract
:1. Introduction
2. Preliminaries
3. Existence and Uniqueness Results
- (C1)
- ∃, ∀, so that
- (C2)
- ∃& so that
4. Numerical Results
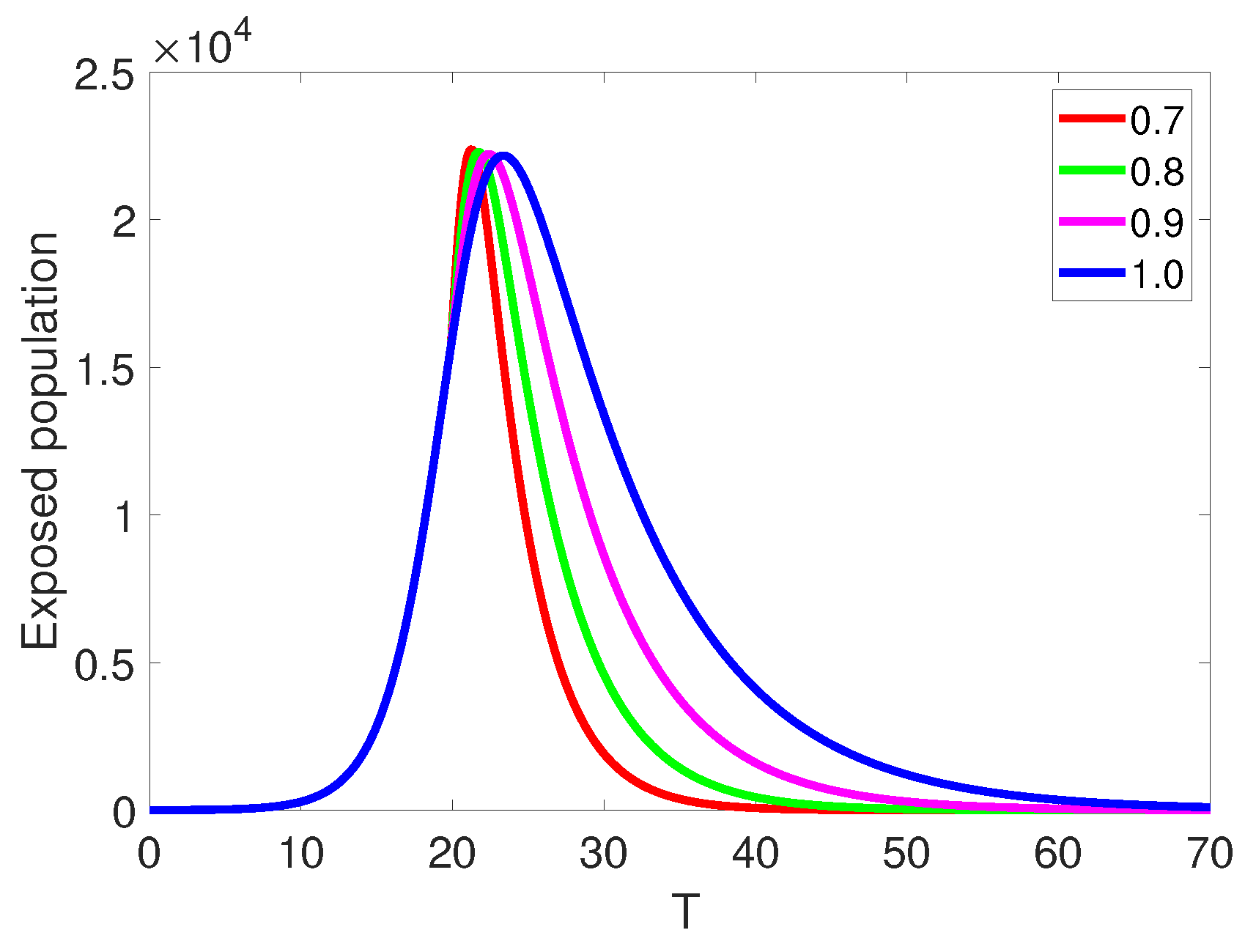
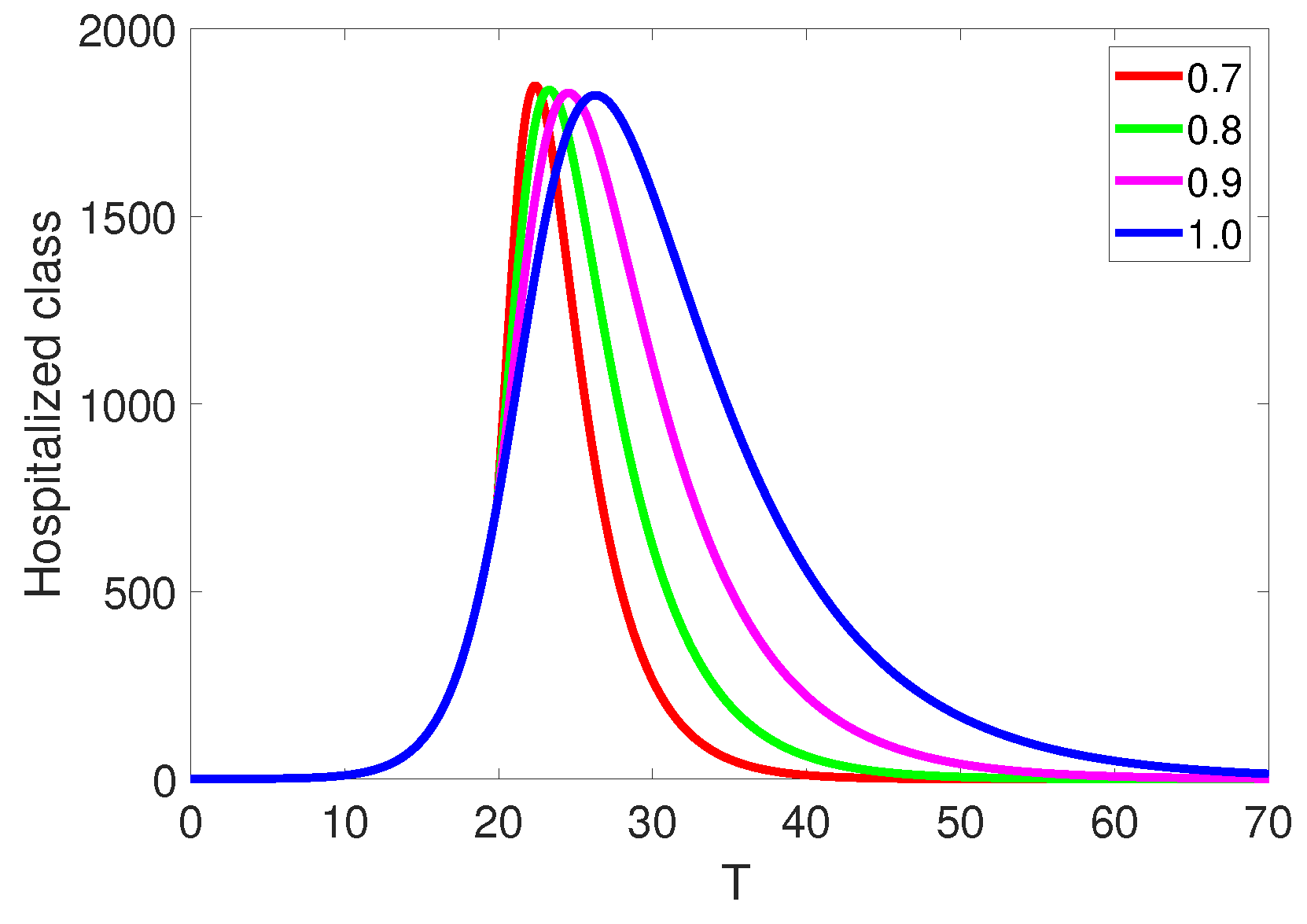
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, Y.; Zhao, K.; Shi, Z.-L.; Zhou, P. Bat Coronaviruses in China. Viruses 2019, 11, 210. [Google Scholar] [PubMed] [Green Version]
- Wang, C.; Horby, P.W.; Hayden, F.G.; Gao, G.F. A novel coronavirus outbreak of global health concern. Lancet 2020, 395, 470–473. [Google Scholar] [PubMed] [Green Version]
- Guo, Y.-R.; Cao, Q.-D.; Hong, Z.-S.; Tan, Y.-Y.; Chen, S.-D.; Jin, H.-J. The origin, transmission and clinical therapies on coronavirus disease 2019 (COVID-19) outbreak—An update on the status. Mil. Med. Res. 2020, 7, 11. [Google Scholar] [PubMed] [Green Version]
- Riou, J.; Althaus, C.L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance 2020, 25, 2000058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roser, M.; Ortiz-Ospina, E.; Ritchie, H.; Hasell, J. Coronavirus Pandemic (COVID-19). Our World in Data. 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 1 January 2023).
- World Health Organization (WHO). Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance2020 (accessed on 1 January 2023).
- Kizito, M.; Tumwiine, J. A mathematical model of treatment and vaccination interventions of pneumococcal pneumonia infection dynamics. J. Appl. Math. 2018, 2018, 2539465. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Machado, J.A.T.; Simón, C.B. Modified SIQR model for the COVID-19 outbreak in several countries. Math. Methods Appl. Sci. 2022. ahead of print. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, P553–P558. [Google Scholar] [CrossRef] [Green Version]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar]
- Ullah, S.; Khan, M.A. Modeling the impact of non-pharmaceutical interventions on the dynamics of novel coronavirus with optimal control analysis with a case study. Chaos Solitons Fractals 2020, 139, 110075. [Google Scholar]
- Alasmawi, H.; Aldarmaki, N.; Tridane, A. Modeling of a super-spreading event of the mers-corona virus during the hajj season using simulation of the existing data. Int. J. Statist. Med. Biolog. Res. 2017, 1, 24–30. [Google Scholar]
- Kojabad, E.A.; Rezapour, S. Approximate solutions of a sum-type fractional integro-differential equation by using Chebyshev and Legendre polynomials. Adv. Differ. Equ. 2017, 2017, 351. [Google Scholar]
- Hui, D.S.; Azhar, E.I.; Kim, Y.-J.; Memish, Z.A.; Oh, M.-D.; Zumla, A. Middle East respiratory syndrome coronavirus: Risk factors and determinants of primary, household, and nosocomial transmission. Lancet Infect. Dis. 2018, 18, 217–227. [Google Scholar]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCoV) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Thabet, S.T.M.; Abdo, M.S.; Shah, K.; Abdeljawad, T. Study of transmission dynamics of COVID-19 mathematical model under ABC fractional order derivative. Results Phys. 2020, 19, 103507. [Google Scholar]
- Shah, K.; Abdeljawad, T.; Mahariq, I.; Jarad, F. Qualitative analysis of a mathematical model in the time of COVID-19. Biomed Res. Int. 2020, 2020, 5098598. [Google Scholar]
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 1999, 198, 340. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Baleanu, D.; Jajarmi, A.; Bonyah, E.; Hajipour, M. New aspects of poor nutrition in the life cycle within the fractional calculus. Adv. Differ. Equ. 2018, 2018, 230. [Google Scholar]
- Ahmad, S.; Ullah, A.; Al-Mdallal, Q.M.; Khan, H.; Shah, K.; Khan, A. Fractional order mathematical modeling of COVID-19 transmission. Chaos Solitons Fractals 2020, 139, 110256. [Google Scholar]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Torres, D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 2020, 27, 109846. [Google Scholar]
- Atangana, A.; Araz, S.I. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar]
- Xu, C.; Alhejaili, W.; Saifullah, S.; Khan, A.; Khan, J.; El-Shorbagy, M.A. Analysis of Huanglongbing disease model with a novel fractional piecewise approach. Chaos Solitons Fractals 2022, 161, 112316. [Google Scholar]
- Ansari, K.J.; Asma; Ilyas, F.; Shah, K.; Khan, A.; Abdeljawad, T. On new updated concept for delay differential equations with piecewise Caputo fractional-order derivative. Waves Random Complex Media 2023, 1–20. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Jarad, F. Study on the dynamics of a piecewise tumor–immune interaction model. Fractals 2022, 30, 2240233. [Google Scholar]
- Naowarat, S.; Ahmad, S.; Saifullah, S.; la Sen, M.D.; Akgül, A. Crossover Dynamics of Rotavirus Disease under Fractional Piecewise Derivative with Vaccination Effects: Simulations with Real Data from Thailand, West Africa, and the US. Symmetry 2022, 14, 2641. [Google Scholar]
- Ahmad, S.; Yassen, M.F.; Alam, M.M.; Alkhati, S.; Jarad, F.; Riaz, M.B. A numerical study of dengue internal transmission model with fractional piecewise derivative. Results Phys. 2022, 39, 105798. [Google Scholar]
- Abdelmohsen, S.A.M.; Yassen, M.F.; Ahmad, S.; Abdelbacki, A.M.M.; Khan, J. Theoretical and numerical study of the rumours spreading model in the framework of piecewise derivative. Eur. Phys. J. Plus 2022, 137, 738. [Google Scholar]
- Chávez, J.P.; Wijaya, K.P.; Pinto, C.M.A.; Simón, C.B. A model for type I diabetes in an HIV-infected patient under highly active antiretroviral therapy. Chaos Solitons Fractals 2022, 155, 111716. [Google Scholar]
- Pinto, C.M.A.; Carvalho, A.R.M. Analysis of a Non-integer Order Model for the Coinfection of HIV and HSV-2. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 291–302. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Aouiti, C.; Liu, Z.; Yao, L. Bifurcation insight for a fractional-order stage-structured predator–prey system incorporating mixed time delays. Math. Methods Appl. Sci. 2023, 46, 9103–9118. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Aouiti, C. New insight into bifurcation of fractional-order 4D neural networks incorporating two different time delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107043. [Google Scholar]
- Ou, W.; Xu, C.; Cui, Q.; Liu, Z.; Pang, Y.; Farman, M.; Ahmad, S.; Zeb, A. Mathematical study on bifurcation dynamics and control mechanism of tri-neuron bidirectional associative memory neural networks including delay. Math. Methods Appl. Sci. 2023. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Pan, Y.; Aouiti, C.; Yao, L. Exploring Bifurcation in a Fractional-Order Predator-Prey System with Mixed Delays. J. Appl. Anal. Comput. 2023, 13, 1119–1136. [Google Scholar]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Li, P.; Yao, L.; Qin, Q. Comparative exploration on bifurcation behavior for integer-order and fractional-order delayed BAM neural networks. Nonlinear Anal. Model. Control. 2022, 27, 1030–1053. [Google Scholar] [CrossRef]
- Xu, C.J.; Mu, D.; Liu, Z.X.; Pang, Y.C.; Liao, M.X.; Li, P. Bifurcation dynamics and control mechanism of a fractional-order delayed Brusselator chemical reaction model. Match Commun. Math. Comput. Chem. 2023, 89, 73–106. [Google Scholar]








| Parameter | Definition | Value | Units |
|---|---|---|---|
| “spread from the diseased populace” | 2.54 | per day | |
| l | “Transmissibility (relative) of ” | 1.56 | dimensionless |
| “spread due to ” | 7.5 | per day | |
| “Rate of exposed becoming infectious” | 0.26 | per day | |
| “Rate of exposed individuals becoming infectious I” | 0.579 | dimensionless | |
| “Rate of the exposed becoming super-spreaders” | 0.099 | dimensionless | |
| “Rate at which individuals hospitalized” | 0.93 | per day | |
| “Rate recovery with no hospitalization” | 0.269 | per day | |
| “Recovered hospitalized patients’ rate” | 0.5 | per day | |
| “Rate of deaths due to infections” | 3.49 | per day | |
| “Disease influenced rate of deaths due to ” | 1.00001 | per day | |
| “Disease influenced rate of deaths due to hospitalized” | 0.30001 | per day |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.; Haque, S.; Khan, K.A.; Mlaiki, N. The Evolution of COVID-19 Transmission with Superspreaders Class under Classical and Caputo Piecewise Operators: Real Data Perspective from India, France, and Italy. Fractal Fract. 2023, 7, 501. https://doi.org/10.3390/fractalfract7070501
Ahmad S, Haque S, Khan KA, Mlaiki N. The Evolution of COVID-19 Transmission with Superspreaders Class under Classical and Caputo Piecewise Operators: Real Data Perspective from India, France, and Italy. Fractal and Fractional. 2023; 7(7):501. https://doi.org/10.3390/fractalfract7070501
Chicago/Turabian StyleAhmad, Shabir, Salma Haque, Khalid Ali Khan, and Nabil Mlaiki. 2023. "The Evolution of COVID-19 Transmission with Superspreaders Class under Classical and Caputo Piecewise Operators: Real Data Perspective from India, France, and Italy" Fractal and Fractional 7, no. 7: 501. https://doi.org/10.3390/fractalfract7070501
APA StyleAhmad, S., Haque, S., Khan, K. A., & Mlaiki, N. (2023). The Evolution of COVID-19 Transmission with Superspreaders Class under Classical and Caputo Piecewise Operators: Real Data Perspective from India, France, and Italy. Fractal and Fractional, 7(7), 501. https://doi.org/10.3390/fractalfract7070501









