Overlap Functions-Based Fuzzy Mathematical Morphological Operators and Their Applications in Image Edge Extraction

Abstract

As special aggregation functions, overlap functions have been widely used in the soft computing field. In this work, with the aid of overlap functions, two new groups of fuzzy mathematical morphology (FMM) operators were proposed and applied to image processing, and they obtained better results than existing algorithms. First, based on overlap functions and structuring elements, the first group of new FMM operators (called OSFMM operators) was proposed, and their properties were systematically analyzed. With the implementation of OSFMM operators and the fuzzy C-means (FCM) algorithm, a new image edge extraction algorithm (called the OS-FCM algorithm) was proposed. Then, the second group of new FMM operators (called ORFMM operators) was proposed based on overlap functions and fuzzy relations. Another new image edge extraction algorithm (called OR-FCM algorithm) was proposed by using ORFMM operators and FCM algorithm. Finally, through the edge segmentation experiments of multiple standard images, the actual segmentation effects of the above-mentioned two algorithms and relevant algorithms were compared. The acquired results demonstrate that the image edge extraction algorithms proposed in this work can extract the complete edge of foreground objects on the basis of introducing the least noise.

1. Introduction

Because of the application requirements in image processing and other soft computing fields, H. Bustine et al. created the overlap function theory [1,2,3]. As a kind of aggregation function, overlap functions not only have continuity and suitable boundary conditions, but also are closely related to fuzzy implications and t-norms. The dual concept of overlap functions and grouping functions and their applications have also received wide attention [4,5,6]. The relationship between overlap functions and grouping functions is similar to that between t-norms and t-conorms, which correspond to “logical AND” and “logical OR” operations, respectively. The overlap and grouping functions are widely used, including for information fusion, image processing, multi-attribute decision-making, uncertainty reasoning, rule-based data analysis [5,7,8], etc. With the in-depth study of the overlap functions, some generalized concepts [9,10,11,12] (such as quasi-overlap functions, general overlap functions, semi-overlap functions, pseudo overlap functions, etc.) have been proposed. The application scope of overlap functions was further expanded.

On the other hand, in the mid-1960s, mathematical morphology (MM) was created by Matheron and Serra G. Matherone and was published in his monograph [13], Random Sets and Integral Geometry, which discussed the technology of shape processing and analysis and laid the theoretical foundation of MM. In 1982, J. Sera published a monograph [14], Image Analysis and Mathematical Morphology, which truly linked MM with image processing and initially formed a theoretical system of MM. Next, Isabelle Bloch et al. published an extended review [15] in 2007 which systematically summarized the basic theory and development of MM.

MM is considered a discipline of image processing and spatial structure analysis based on integral geometry, set theory, topology, and lattice theory. Its basic idea and method are to use a “probe” called a structuring element to collect the information in images. It can examine the relationship between the various parts of the image to understand the structural characteristics of the image when the probe moves continuously in the image. There are four basic operators: erosion, dilation, closing, and opening in MM. They have their own characteristics in gray-scale images and binary images. Various MM practical algorithms can also be combined and derived based on these basic operators, which can be used to process and analyze image structure and shape, including image enhancement and restoration, edge detection, feature extraction, image filtering, image segmentation, etc. MM has become a major research direction of image processing. Its theory and method are powerful tools in the image analysis field. As a result, it has been successfully applied in computer character recognition, medical image processing, industrial inspection, geology, metallurgy, robot vision, video compression, etc. In recent years, MM has been combined with deep learning and has proposed a variety of deep morphological networks [16,17,18,19,20], showing the strong vitality of MM.

Initially, MM dealt with binary images. For dealing with gray-scale images, various forms of FMM [20,21,22,23,24,25,26,27,28,29,30,31,32] have been introduced with the help of fuzzy set theory (including lattice-valued fuzzy sets, classical Zadeh’s fuzzy sets, interval-valued fuzzy sets, etc.). It is natural to generalize from binary to gray-scale images. A simple generalization process is to replace the union and intersection operations in binary morphology with supremum and infimum operations, respectively. As further extensions of this concept, fuzzy mathematical morphology operators based on conjunction, t-norm, innorm, etc. [29,30,31,32,33] (in these works, concepts such as fuzzy implication and residual implication are often applied), and FMM based on fuzzy preference relations [34] and lattice-valued fuzzy relations [35] have been successively studied (see [36] for the role of the lattice structure in mathematical morphology).

Along these lines, the above-mentioned two aspects of the research were combined here. More specifically, the existing FMM was expanded by means of overlap function, fuzzy implication, and other concepts. At the same time, two groups of new morphological operators were proposed, and the FCM algorithm was combined to establish two new algorithms for image edge extraction. The main goal was to demonstrate the important role and the comparative advantages of overlap functions in image processing and MM. The contents of this work are organized as follows. In Section 2, some preliminary concepts related to this work are recalled, including classical morphological operators, overlap function, fuzzy implication, classical FCM algorithm, etc. In Section 3, FMM operators based on overlap functions and structuring elements (called OSFMM operators) are discussed and an image edge extraction OS-FCM algorithm is proposed. In Section 4, the FMM operators based on overlap functions and fuzzy relations (called ORFMM operators) are introduced and another image edge extraction algorithm is proposed, namely the OR-FCM algorithm. The contents of Section 5 include the execution of experiments and analysis with the developed algorithm. Through edge segmentation experiments on multiple standard images, the actual segmentation effects of the two algorithms proposed in this work (OS-FCM, OR-FCM) and the existing relevant typical algorithms are thoroughly compared and analyzed. From our analysis, it was revealed that the two groups of FMM operators based on overlap functions have obvious advantages in image edge extraction applications. The operators and algorithm proposed by us are shown in Figure 1. Section 6 summarizes the study, and the future research direction is also pointed out.

2. Preliminaries

Some preliminary concepts related to this work are introduced in this section, including classical morphological operators, overlap function, fuzzy implication, classical FCM algorithm, etc. In order not to cause confusion, R is used to represent the real numbers set, and R is used to denote fuzzy binary relations and binary relations.

Definition 1

([14]). Let A and B be subsets of Rⁿ, corresponding to binary image and structuring elements, respectively. In MM, the erosion E(A, B) and dilation D(A, B) of A by B are two sets (binary images) given by the following expressions:

$$\begin{array}{l}E(A,B)=\{\forall y\in {\mathbf{ℛ}}^n|T_y(B)\subseteq A\},\\ D(A,B)=\{\forall y\in {\mathbf{ℛ}}^n|T_y(B)\cap A\ne \varnothing \},\end{array}$$

where the definition of T_y(B) is T_y(B) = $\{\forall x\in {\mathbf{ℛ}}^n|x-y\in B\}.$

Definition 2

 ([23]). Let A and B be two fuzzy sets in Rⁿ, i.e., A: Rⁿ→[0, 1], B: Rⁿ→[0, 1]. In FMM, the fuzzy erosion E(A, B) and fuzzy dilation D(A, B) of gray-scale image A by structuring element B are given by the following expressions:

$$\begin{array}{l}E(A,B)(y)=\underset{x\in {ℛ}^n}{\inf }(\max (B(x),A(y+x))), \forall y\in {\mathbf{ℛ}}^n,\\ D(A,B)(y)=\underset{x\in {ℛ}^n}{\sup }(\min (B(x),A(y+x))), \forall y\in {\mathbf{ℛ}}^n.\end{array}$$

Definition 3

 ([29]). A function C: [0, 1]²→[0, 1] is called a conjunction if it meets the following conditions:

• (C1) C is increasing;
• (C2) C(0, 0) = C(1,0) = C(0, 1) = 0;
• (C3) C(1, 1) = 1.

Definition 4

([37]). A binary function I: [0, 1]²→[0, 1] is said to be a fuzzy implication if it satisfies the following conditions: ∀x, y, z ∈ [0, 1],

• (I1) If x ≤ y, then I(y, z) ≤ I(x, z);
• (I2) If x ≤ y, then I(z, x) ≤ I(z, y);
• (I3) I(1, 0) = 0;
• (I4) I(1, 1) = 1;
• (I5) I(0, 0) = 1.

A fuzzy implication I is said to satisfy the LOP condition if ∀x, y ∈ [0, 1], x ≤ y⇒I(x, y) = 1.

Theorem 1

([11,37]). Let binary function C be a conjunction. The definition of binary function I_C is the following:

I_C(x, y) = sup{t ∈ [0, 1]|C(x, t) ≤ y}, ∀x, y ∈ [0, 1].

If C satisfies C(1, x) > 0 (∀x ∈ (0, 1]), then I_C is a fuzzy implication. I_C is said to be the residual implication derived from conjunction C.

Definition 5

([37]). A binary function T: [0, 1]²→[0, 1] is called a t-norm if it meets the following conditions:

• (T1) T is increasing;
• (T2) T is commutative;
• (T3) T is associative;
• (T4) T(y, 1) = y, ∀y ∈ [0, 1].

Definition 6

([29]). Let A and B be two fuzzy sets in Rⁿ, I be a fuzzy implication, and C be a conjunction. Let d(B) = {x|B(x) ≠ 0} ⊆ R². The fuzzy erosion E_I(A, B) and fuzzy dilation D_C(A, B) of gray-scale image A by structuring element B are given by the following expressions: ∀y ∈ Rⁿ,

$$\begin{array}{l}{E}_I(A,B)(y)=\underset{x\in d(B)}{\inf }(I(B(x),A(y+x))), \\ D_C(A,B)(y)=\underset{x\in d(B)}{\sup }(C(B(x),A(y+x))).\end{array}$$

Definition 7

([1]). A binary function O: [0, 1]²→[0, 1] is called an overlap function if it meets the following conditions: ∀x, y ∈ [0, 1],

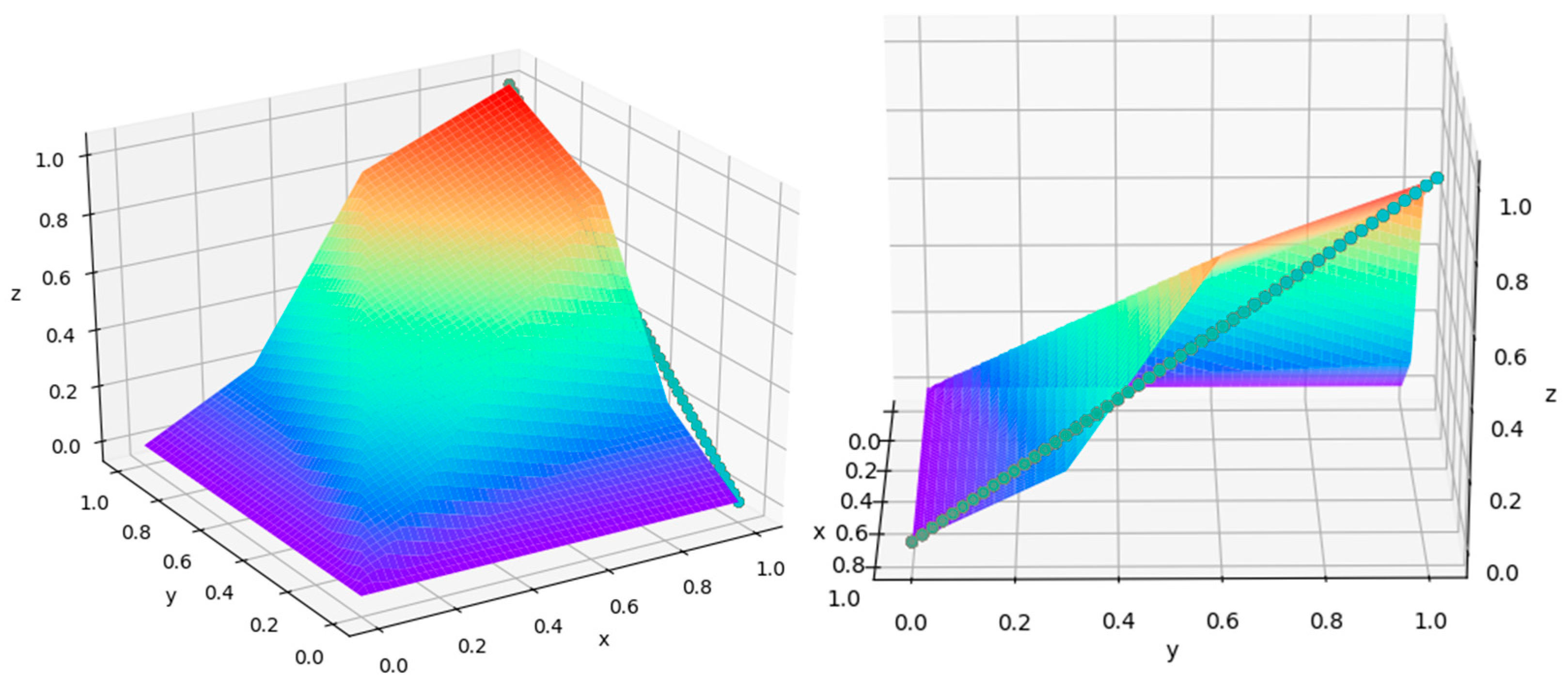
• (O1) O is increasing;
• (O2) O is continuous;
• (O3) O(y, x) = O(x, y);
• (O4) O(y, x) = 0 iff yx = 0;
• (O5) O(y, x) = 1 iff yx = 1.

Furthermore, an overlap function O is called 1-section inflation if O(1, y) ≥ y, ∀y ∈ [0, 1] and 1-section deflation if O(y, 1) ≤ y, ∀y ∈ [0, 1].

Example 1.

The functions O₁, O₂ given by: ∀x, y ∈ [0, 1],

$$\begin{array}{c}{O}_1=\sqrt{xy};\\ O_2(x,y)=\{\begin{array}{l}\frac{35+xy}{36}, \mathrm{if} 0.8\le x\le 1, 0.8\le y\le 1, (x,y)\ne (0.8,0.8),\hfill \\ \frac{99xy}{64}, \mathrm{if} 0\le x\le 0.8 \mathrm{and} 0\le y\le 0.8,\hfill \\ \frac{99x}{80}, \mathrm{if} 0\le x<0.8 \mathrm{and} 0.8<y\le 1, y\le \frac{-x}{4}+1,\hfill \\ \begin{array}{l}\frac{179x}{144}+\frac{y-1}{45}, \mathrm{if} 0\le x<0.8 \mathrm{and} 0.8<y\le 1, y>\frac{-x}{4}+1,\\ \begin{array}{l}\frac{99y}{80}, \mathrm{if} 0\le y<0.8 \mathrm{and} 0.8<x\le 1, y\le -4x+4,\hfill \\ \frac{179y}{144}+\frac{x-1}{45}, \mathrm{if} 0\le y<0.8 \mathrm{and} 0.8<x\le 1, y>-4x+4,\hfill \end{array}\end{array}\hfill \end{array}\end{array}$$

are two 1-section inflation overlap functions.

The functions O₃, O₄ given by: ∀x, y ∈ [0, 1],

$$O_3=x^2{y}^2, O_4=\mathrm{xy}\frac{x + y}{2}$$

are two 1-section deflation overlap functions.

The function O₅defined below is a special overlap function.

$$O_5(x,y)=\{\begin{array}{l}\frac{2}{3}y, \mathrm{if} y\le \frac{3}{10}x,\hfill \\ \frac{-2}{5}x+2y, \mathrm{if} \frac{3}{10}x<y\le \frac{3}{5}x,\hfill \\ \frac{x+y}{2}, \mathrm{if} \frac{3}{5}x<y\le \frac{5}{3}x,\hfill \\ \frac{-2}{5}y+2x, \mathrm{if} \frac{5}{3}x<y\le \frac{10}{3}x,\hfill \\ \frac{2}{3}x, \mathrm{if} \frac{10}{3}x<y,\hfill \end{array}\forall x,y\in [0,1]$$

Overlap function O₅ meets the following conditions:

O₅(1, y) ≤ y, ∀y ∈ [0, 0.4]

(1)

O₅(1, y) ≥ y, ∀y ∈ [0.4, 1]

(2)

Overlap function O₅ is depicted in Figure 2, where the analytic expression of line segment l in the right figure is: x = 1, z = y (0 ≤ y ≤ 1). As can be seen from the right figure of Figure 2, when y < 0.4, curve O₅(1, y) is on the lower side of l, and when y > 0.4, curve O₅(1, y) is on the upper side of l, which verifies that the overlap function O₅ satisfies inequality (1), (2).

Several aggregate functions closely related to the overlap function are introduced above. Next, we will continue to introduce a gray-scale edge extraction algorithm and an image preprocessing process algorithm.

Based on the FMM operators, image edge features can be extracted in detail [14]. The main idea of the edge extraction algorithm using FMM operators (Algorithm 1) is to first calculate the fuzzy erosion and fuzzy dilation of the gray-scale image. In general, fuzzy dilation will lighten the gray-scale image and fuzzy erosion will darken the gray-scale image, while the changes at the edge of the foreground object will be more obvious. Therefore, the edge of the gray-scale image can be obtained by calculating the difference between them.

Algorithm 1 ([29]). Edge detection algorithm using FMM operators.

Input: gray-scale structuring element B, gray-scale image A; Output: binary edge image; Step 1: Fuzzify the gray-scale image A; Step 2: Calculate the fuzzy erosion E(A) and fuzzy dilation D(A) of gray-scale image A; Step 3: Calculate the fuzzy edge image: D(A)$-$E(A); Step 4: Defuzzy and binarize the fuzzy edge image calculated in Step 3.

During the image processing process (including image segmentation, edge extraction, etc.), clustering is often used as a preprocessing process, while the FCM algorithm (Algorithm 2) is the clustering algorithm used more [38,39,40,41]. The FCM algorithm was first developed by Dunn in 1973 [38], and it later was improved by Bezdek [39] and widely used in pattern recognition [40,41]. Unlike K-means hard clustering (in the K-means algorithm, each element can only belong to one cluster), the FCM algorithm is a soft clustering idea, which believes that all objects in the cluster object set belong to a cluster with different membership degrees. Thus, each cluster is considered a fuzzy subset of the object set. The FCM algorithm calculates the membership matrix of the samples (the fuzzy matrix whose elements are taken from the unit interval) to maximize the similarity between objects divided into the same cluster and minimize the similarity between different clusters. The FCM algorithm divides N data samples x_j, {j = 1, 2, …, N} in the data set into c classes and updates the cluster centers and membership degrees through continuous iteration. After the objective function reaches the minimum value, the cluster is divided according to the membership degree of each point in different classes (clusters). The objective function [38] of the FCM algorithm is defined as follows:

$$J_{FCM}={\displaystyle \sum _{j=1}^N{\displaystyle \sum _{i=1}^c{u}_{ij}^{m}d(x_j,v_i)}}$$

where u_ij is the membership degree of point x_j in class i, v_i refers to the center of class i, d(x_j, v_i) represents the distance from point x_j to the cluster center v_i (usually Euclidean distance), and m denotes the weighted index (m usually takes 2). Generally speaking, it is quite difficult to find the optimal solution of objective function J, and the iterative algorithm is always used to find the approximate solution (Bezdek proved that the iterative algorithm is convergent). The iterative expressions [38] of membership degrees and cluster centers are as follows:

$$u_{ij}=\frac{1}{{\sum }_{k=1}^c{\left(\frac{d\left(x_j,v_i\right)}{d\left(x_j,v_k\right)}\right)}^{2/\left(m-1\right)}}$$

(3)

$$v_i=\frac{{\sum }_{j=1}^N{u}_{ij}^m{x}_j}{{\sum }_{j=1}^N{u}_{ij}^m}$$

(4)

The flow of the FCM algorithm is as follows.

Algorithm 2 ([38,39]). Fuzzy C-means algorithm.

Input: maximum iterations or stop iteration threshold, number of cluster categories c, data set (x1, x2,…, xN); Output: clustering centers (v1, v2,…, vc), membership degree uij (i = 1, 2,…, c, j = 1, 2,…, N); Step 1: Randomly initialize the clustering centers; Step 2: Update the membership degrees according to Formula (3); Step 3: Update the clustering centers according to Formula (4); Step 4: Judge whether the maximum iterations or stop iteration threshold is met. Return to Step 2, if the stop condition is not met; Step 5: Point xj is divided into class i, i satisfies uij = max{u1j, u2j,…, ucj}.

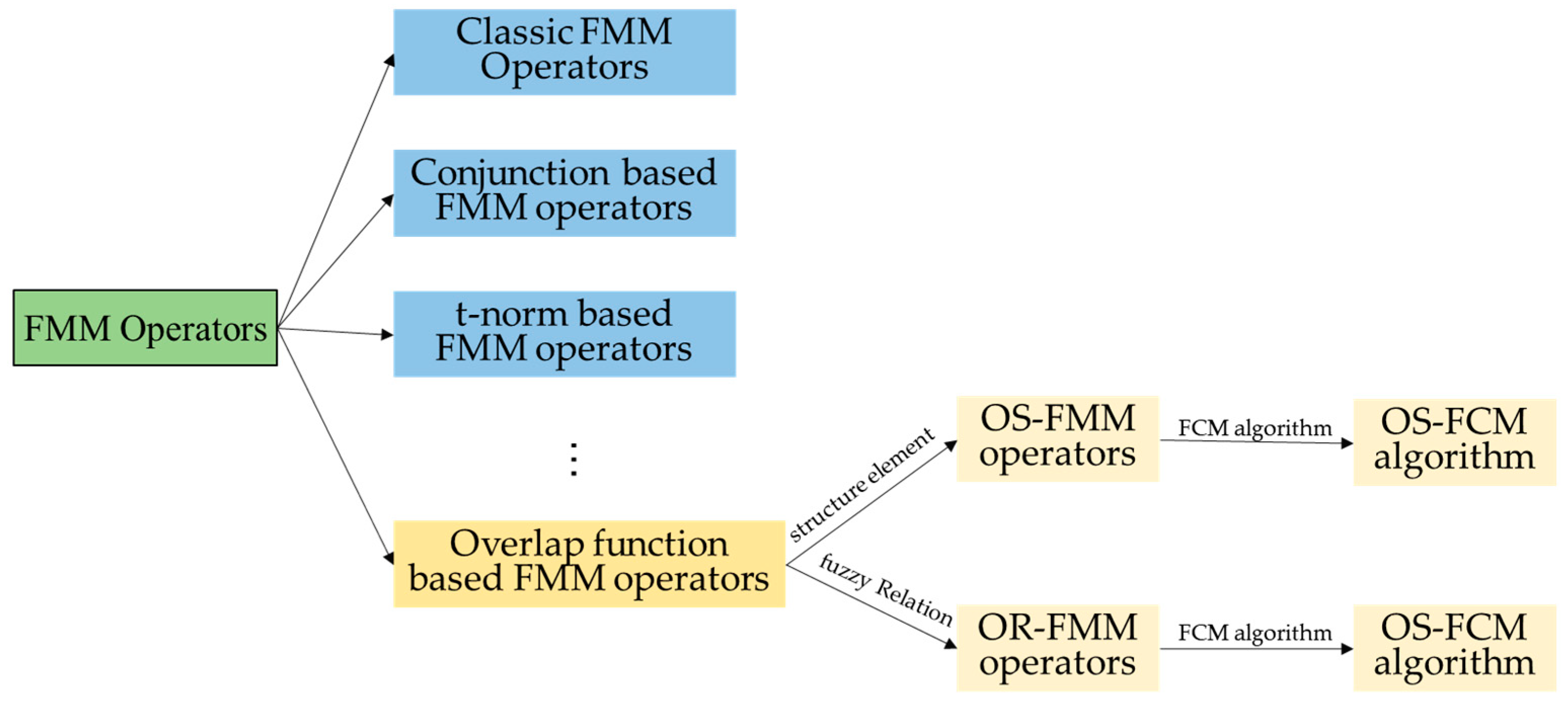
3. FMM Operators Based on Overlap Functions and Structuring Elements (OSFMM Operators) and OS-FCM Algorithm

As was mentioned earlier, in fuzzy mathematical morphology, t-norm, uninorm, etc., are used as special conjunctions to construct morphological operators [3,15,16,17,18]. As special conjunctions and special aggregation functions, do overlap functions have good performance and advantages when used to construct new morphological operators? At present, this issue has not been discussed in the literature.

After performing a preliminary comparative analysis, the following facts were found: (1) Although t-norm, uninorm, and other conjunctions meet the associativity, and the morphological operators constructed by them have good operational properties (such as associativity), the requirement of associativity is too strict. Moreover, the exclusion of the use of conjunctions or aggregation functions that do not meet the associativity also limits its flexibility and scope of application. In fact, associativity does not play a key role during image processing and other applications. At least in a large amount of the literature we have studied, there is no piece of evidence that indicates that associativity plays a significant role. At the same time, the t-norm requires that 1 is a unit element (conjunctions, such as uninorm also have unit elements), which leads to the fact that T(x, y) = min(x, y) is the largest t-norm. Thus, the fuzzy dilation operator constructed by the t-norm meets ∀x ∈ R², T(A(y), and B(x)) ≤ A(y), which also limits the effectiveness of morphological operators in applications. (2) The overlap function is not required to meet the associativity, nor does it require 1 to be the unit element (there are 1-section inflation and 1-section deflation overlap functions, and there are some overlap functions that simultaneously meet 1-section inflation and 1-section deflation in different intervals, see Example 1). Therefore, the morphological operators based on overlap functions have greater flexibility and can express relevance to a certain extent (the associative law usually reflects that the objects involved in the operation are independent, and if there is relevance between the objects involved in the operation, the associative law of the operation will not be established naturally). Through conducting preliminary experiments, it was found that the fuzzy dilation operator constructed by overlap functions enlarges the difference between the pixel values of the foreground and background points in the gray-scale image, which provides convenience for image segmentation and edge extraction. What is more, the overlap functions have continuity, which can deduce the continuity of fuzzy dilation with respect to the position and pixel value, which extends the applications of mathematical morphology operators to video processing.

Based on the above-mentioned considerations, OSFMM operators were proposed in this section based on structuring elements and overlap functions. Furthermore, their properties were analyzed, and OSFMM operators and FCM algorithms were applied to give a new algorithm for the image edge extraction OS-FCM algorithm.

3.1. OSFMM Operators

Definition 8.

Let A and B be two fuzzy sets in Rⁿ, I be a fuzzy implication, and O be an overlap function. Let d(B) = {x | B(x) ≠ 0} ⊆ R ². The fuzzy erosion E_I(A, B) and fuzzy dilation D_O(A, B) of gray-scale image A by gray-scale structuring element B are given by the following expressions:

$$\begin{array}{l}{E}_I(A,B)(y)=\underset{x\in d(B)}{\inf }I(B(x),A(y+x)), \forall y\in {\mathbf{ℛ}}^2,\\ D_O(A,B)(y)=\underset{x\in d(B)}{\sup }O(B(x),A(y+x)), \forall y\in {\mathbf{ℛ}}^2.\end{array}$$

The fuzzy sets Close(A, B) and Open(A, B) defined below are called fuzzy closing and fuzzy opening operators, respectively:

$$\begin{array}{l}Close(A,B)=E_I(D_O(A,B),B),\\ Open(A,B)=D_O(E_I(A,B),B).\end{array}$$

The above-defined group of morphological operators based on overlap functions and structuring elements are collectively referred to as OSFMM operators.

Note: The fuzzy opening and closing operators defined above can be expanded as follows: ∀y∈R²,

$$\begin{array}{l}Close(A,B)(y)=E_I(B,D_O(A,B))(y)\\ =\underset{z\in d(B)}{\inf }I(B(x),D_O(A,B)(y+z))\\ =\underset{z\in d(B)}{\inf }I(B(x),\underset{x\in d(B)}{\sup }O(B(x),A(y+x+z))),\\ Open(A,B)(y)=D_O(B,E_I(A,B))(y)\\ =\underset{z\in d(B)}{\sup }O(B(x),E_I(A,B)(y+x))\\ =\underset{z\in d(B)}{\sup }O(B(x),\underset{x\in d(B)}{\inf }I(B(x),A(y+x+z))).\end{array}$$

Because the overlap function is a special conjunction, it can be seen that the OSFMM operators have the following properties (only some properties are listed here. For more properties, see Properties 32–52 in [29]) by applying the conclusion of [29].

Theorem 2.

Let A, A_i be gray-scale images (i = 1, …, k), B, B_i be gray-scale structuring elements (i = 1, …, k), I be a fuzzy implication, and O be an overlap function. Then, the OSFMM operators satisfy the following properties:

(1)

The fuzzy dilation D_O is increasing in the first and the second arguments;

(2)

The fuzzy erosion E_I is decreasing in the second and increasing in the first argument;

(3)

$D_O\left({\displaystyle \underset{i=1}{\overset{k}{\cup }}{A}_i},B\right)={\displaystyle \underset{i=1}{\overset{k}{\cup }}{D}_O\left(A_i,B\right)},\hspace{0.17em}{D}_O\left(A,{\displaystyle \underset{i=1}{\overset{k}{\cup }}{B}_i}\right)={\displaystyle \underset{i=1}{\overset{k}{\cup }}{D}_O\left(A,B_i\right)}$;

(4)

$E_I\left(A,{\displaystyle \underset{i=1}{\overset{k}{\cup }}{B}_i}\right)={\displaystyle \underset{i=1}{\overset{k}{\cap }}{E}_I\left(A,B_i\right)},\hspace{0.17em}{E}_I\left({\displaystyle \underset{i=1}{\overset{k}{\cap }}{A}_i},B\right)={\displaystyle \underset{i=1}{\overset{k}{\cap }}{E}_I\left(A_i,B\right)}$.

Example 2.

This example shows the functions and roles of OSFMM operators. Figure 3 (left) depicts a gray-scale image A, where the pixel values of the whole foreground (duck) and noise are 120. Figure 3 (left) was processed by fuzzy erosion and fuzzy dilation of OSFMM operators (using 1-section inflation overlap function O₁ in Example 1, fuzzy implication I₁, and structuring element B as defined below). The results are shown in Figure 3 (right) and (center), respectively, where the pixel values of the foreground and noise of D_O(A) are 175. In the fuzzy dilation of OSFMM operators, the 1-section inflation overlap functions can make the pixel value of fuzzy dilation larger than the original image, while the 1-section deflation overlap functions can make the pixel value of fuzzy dilation smaller than the original image. If the FMM operators based on t-norm are used, the pixel values of fuzzy dilation D_T(A) of gray-scale image A in the image are less than or equal to 120.

$$I_1=\{\begin{array}{c}1,if \sqrt{x}\le y,\\ \frac{y^2}{x}, others.\end{array}B=\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right].$$

Theorem 3.

Let B be a gray-scale structuring element, A₁, A₂ be two gray-scale images, I be a fuzzy implication, O be an overlap function, and D_O(A, B), E_I(A, B) be fuzzy dilation and fuzzy erosion of OSFMM operators, respectively. Then: ∀y ∈ R ²,

• (1) D_O(A, B)(y) = 0 ⇔ (∀x ∈ d(B), A(y + x) = 0);
• (2) (∃x ∈ d(B), B(x) = 1 and A(y + x) = 1)⇒ D_O(A, B)(y) = 1;
• (3) (∃x ∈ d(B), B(x) = 1 and A(y + x) = 0) ⇒ E_I(A, B)(y) = 0.

Proof. 

(1) Assume ∀x ∈ d(B) satisfies A(y + x) = 0. By the condition (O2) in the definition of overlap function, we obtain ∀a ∈ [0, 1], O(0, a) = O(a, 0) = 0, hence:

$$\underset{x\in d(B)}{\sup }O(B(x),A(y+x))=0,$$

i.e., D_O(A, B)(y) = 0.

Assume D_O(A, B)(y) = 0. By the definition of D_O(A, B)(y), we have the following expression:

$$D_O(A,B)(y)=\underset{x\in d(B)}{\sup }O(B(x),A(y+x))=0.$$

This shows that ∀x ∈ d(B), O(B(x), A(y + x)) = 0. By condition (O2), we have B(x)·A(y + x) = 0. ∀x ∈ d(B), B(x) ≠ 0, hence A(y + x) = 0.

(2) Assume A(y + x) = 1and ∃x ∈ d(B), B(x) = 1. By the condition (O2),

O(B(x), A(y + x)) = 1.

Hence, D_O(A, B)(y) = $\underset{x\in d(B)}{\sup }O(B(x),A(y+x))=1$.

(3) Straightforward from the definition of fuzzy implication and fuzzy erosion.

Sufficient conditions for obtaining the maximum value in the definition of fuzzy dilation are given below. □

Theorem 4.

Let gray-scale image A and gray-scale structuring element B be two closed mappings, d(B) be a closed set, O be an overlap function, and D_O(A, B) be the fuzzy dilation in OSFMM operators. Then, ∀y∈ R²,

$$D_O(A,B)(y)=\underset{x\in d(B)}{\max }O(B(x),A(y+x)).$$

Proof. 

Since O is continuous and the domain of definition of O is closed set [0, 1]², O is uniformly continuous. Since d(B) is a closed set and B(x) and A(x) are closed mappings, we have Q = {t|t = B(x), ∀x ∈ d(B)} is a closed set, and

$$\forall z\in {\mathbf{ℛ}}^2,P=\left\{t\right|t=A(z+x),x\in d(B)\}$$

is closed set. Therefore, {(q, p)|q ∈ Q, p ∈ P} is a bounded closed set. Hence, by the uniform continuity of O, we have the following expression:

$$\forall z\in {\mathbf{ℛ}}^2,\exists a_z\in d(B),\underset{x\in d(B)}{\sup }(O(B(x),A(z+x)))=O(B(a_z),A(z+a_z)).$$

Thus, $\forall y\in {\mathbf{ℛ}}^2,$$D_O(A,B)(y)=\underset{x\in d(B)}{\max }O(B(x),A(y+x)).$□

Theorem 5.

Let B be a gray-scale structuring element, A₁, A₂ be two gray-scale images, O be an overlap function, and D_O(A, B) be the fuzzy dilation in OSFMM operators. Then ∀ε > 0, ∃δ, if$|A_1(z)-A_2(z)|\le \delta (\forall z\in {\mathbf{ℛ}}^2)$, we have the following expression:

$$|D_O(A_1,B)(y)-D_O(A_2,B)(y)|\le \epsilon (\forall y\in {\mathbf{ℛ}}^2).$$

Proof. 

Since O is continuous and the domain of definition of O [0, 1]² is a closed set, O is uniformly continuous. $\forall \epsilon >0$, for $\frac{1}{2}\epsilon$, by the uniform continuity of O, we have the following expression: $\exists \delta , \mathrm{if} \rho ((s_1,t_1),(s_2,t_2))\le \delta$, then $|O(s_1,t_1)-O(s_2,t_2)|<\frac{1}{2}\epsilon .$

Therefore, ∀ε > 0, select above δ, if $|A_1(z)-A_2(z)|\le \delta (\forall z\in {\mathbf{ℛ}}^2)$, we have

$$\forall y\in {\mathbf{ℛ}}^2,\forall x\in d(B), y+x\in {\mathbf{ℛ}}^2,|A_1(y+x)-A_2(y+x)|\le \delta ,$$

$$\rho ((B(x),A_1(y+x)),(B(x),A_2(y+x)))=|A_1(y+x)-A_2(y+x)|\le \delta ,$$

$$|O((B(x),A_1(y+x))-O(B(x),A_2(y+x))|\le \frac{1}{2}\epsilon .$$

Then,

$$\begin{array}{c}|\underset{x\in d(B)}{\sup }(O(B(x),A_1(y+x)))-\underset{x\in d(B)}{\sup }(O(B(x),A_2(y+x)))|\\ \le |\underset{x\in d(B)}{\sup }(O(B(x),A_1(y+x))-O(B(x),A_2(y+x)))|\\ \le \underset{x\in d(B)}{\sup }|O(B(x),A_1(y+x))-O(B(x),A_2(y+x))|\\ \le \frac{1}{2}\epsilon <\epsilon \end{array}$$

i.e., $|D_O(A_1,B)(y)-D_O(A_2,B)(y)|<\epsilon (\forall y\in {\mathbf{ℛ}}^2)$.□

According to Theorem 5, the fuzzy dilation operator has such continuity: if the gray-scale image changes from A₁ to A₂ where the difference of every pixel is small (∀z ∈ R²), then the difference of every pixel of D_O(A₁, B) and D_O(A₂, B) is small. This can be used for video processing. If the image of each frame in a video is continuously changing, then the video processed by the dilation operator is also continuous.

By considering Example 2 and Theorem 3, the OSFMM operators can extend the value range of the FMM operators to a certain extent, and the boundary conditions of the OSFMM operators are more suitable for image processing. However, Algorithm 1 cannot avoid introducing a large number of noises in the background when extracting the edges of foreground objects (details) whose brightness are close to the noise in the background. In order to solve this problem, the first new algorithm for image edge extraction will be proposed using the FCM algorithm and OSFMM operators in the next section.

3.2. OS-FCM Algorithm

In this section, the OS-FCM algorithm (Algorithm 3) for image edge extraction was provided. This algorithm can extract more edges of foreground objects on the one hand and avoid introducing a lot of noise in the background on the other hand. The main idea is as follows: First, the position information of the foreground object and background of the image was obtained according to the FCM algorithm. Second, using structuring elements B₁ and B₂, edge₁, the edge image with details’ edge and many noises, was calculated, and edge₂, the edge image without details’ edge or noise, was calculated, respectively. Finally, the edge of the original image was extracted according to edge₁ and edge₂, so that the result contains the edges of all foreground objects as much as possible without noise.

Algorithm 3. OS-FCM algorithm

Input: gray-scale image A, gray-scale structuring elements B1, B2; Output: binary edge image; Step 1: Fuzzify the gray-scale image A; Step 2: Cluster A with FCM algorithm, let Object and BG (background) be the sets of all foreground points and background points; Step 3: Calculate DO(A, B1), EI(A, B1), DO (A, B2), EI (A, B2); Step 4: Calculate DO(A, B1) − EI(A, B1), DO(A, B1) − EI(A, B1); Step 5: Defuzzy and binarize the two fuzzy edge images in Step 4 to get the binary edge edge(A, B1) and edge(A, B2); Step 6: Calculate the final binary edge image:$edge(A)(y)=\{\begin{array}{c}edge(A,B_1)(y), if y\in Object,\\ edge(A,B_2)(y), if y\in BG.\end{array}$

In this section, OSFMM operators were discussed and a new image edge extraction algorithm (OS-FCM algorithm) was proposed. After research, it was found that OSFMM operators have almost all the properties of other fuzzy morphological operators, and they have continuity which is not found in other fuzzy morphology operators.

4. ORFMM Operators and OR-FCM Algorithm

At present, MM based on fuzzy relations has been established in some literature. Although in these works fuzzy relations were used to define fuzzy dilation and erosion operators, fuzzy relations were equated with structuring elements. Moreover, the characteristics of fuzzy relations were not fully explored, and the role of fuzzy relations was not underlined. The relevant works in the literature either have no experimental cases or the experiment is not convincing: the experimental results of the FMM operators defined by the fuzzy relations are also not different from those of FMM operators based on the structuring elements.

From this perspective, in this work a group of new FMM operators, namely the ORFMM, were proposed by using overlap functions and fuzzy relations. In this section, the ORFMM operators are first introduced, and an example is provided to show that the FMM operators based on fuzzy relations are more flexible than the FMM operators based on structuring elements. Then, the ORFMM operators and the FCM algorithm are applied to give a new algorithm for the image edge extraction OR-FCM algorithm.

Definition 9.

Let A be a fuzzy set in R², R be a fuzzy binary relation on R², I be a fuzzy implication, and O be an overlap function. The fuzzy sets D_R(A), E_R(A) defined below are the fuzzy dilation operator and fuzzy erosion operator, respectively:∀y  ∈  R²,

$$\begin{array}{l}{D}_R(A)(y)=\underset{x\in R^2}{\sup }O(R(x,y),A(y)),\\ E_R(A)(y)=\underset{x\in R^2}{\inf }I(R(x,y),A(y)).\end{array}$$

The fuzzy sets Open(A, B) and Close(A, B) defined below are the fuzzy opening operator and fuzzy closing operator, respectively:

$$\begin{array}{l}Open(A,B)=D_R(E_R(A,B),B),\\ Close(A,B)=E_R(D_R(A,B),B).\end{array}$$

Note: In the FMM operators based on the structuring elements, structuring elements are defined in  R², which means that every point y in gray-scale image A corresponds to one structuring element with the same expression. In the FMM operators based on fuzzy relations, fuzzy relations R: R² × R²→[0, 1] are defined as  R² × R², where it can be considered that each point y in gray-scale image A corresponds to a group of structuring elements B(x) = R(x, y). Hence, the ORFMM operators have stronger expression ability and greater flexibility.

Example 3.

This example illustrates the functions and roles of the OSFMM operators. First, Figure 3 (left) is divided into three sets. A₁ represents the set of all points in the duck’s body, A₂ denotes the set of all points in the duck’s mouth and paws, and A₃ stands for the set of all background points (including noises). Second, the following fuzzy binary relationship R was defined (where B₁, B₂, and B₃ are three different structuring elements):∀x, y∈ R²,

$$B_1=\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right], B_2=\left[\begin{array}{ccc}0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\\ 0.5& 0.5& 0.5\end{array}\right], B_3=\left[\begin{array}{ccc}0.01& 0.01& 0.01\\ 0.01& 0.01& 0.01\\ 0.01& 0.01& 0.01\end{array}\right], R(x,y)=\{\begin{array}{c}{B}_1(x), if y\in A_1,\\ B_2(x), if y\in A_2,\\ B_3(x), if y\in A_3.\end{array}$$

Figure 3 (left) was processed by the fuzzy dilation (using the overlap function O₁) and fuzzy erosion (using the fuzzy implication I₁ in Example 2) of ORFMM operators, and the results are illustrated in Figure 4. After being processed by the ORFMM operators, different results can be obtained for the parts with the same pixel value. More specifically, the pixel value of the duck’s body is larger than the duck’s mouth and paws, and the pixel value of noises is almost zero. Compared with Figure 3 (center, right) and Figure 4, it can be seen that the introduction of fuzzy relations in FMM operators substantially increased the flexibility of the FMM operators.

OR-FCM Algorithm

In this section, ORFMM operators based on overlap functions were applied to give the OR-FCM algorithm for image edge extraction. The basic idea of the OR-FCM algorithm (Algorithm 4) is as follows: First, the FCM clustering algorithm was used to obtain the location information of foreground points and background points of a gray-scale image. Second, according to the results (knowledge) of the gray-scale image clustering analysis that was obtained from the previous step, the fuzzy relation R was designed (where the design principle of R is to make the ORFMM operators highlight the foreground points and annihilate the background points as much as possible), and the fuzzy dilation and erosion were calculated. Then, the fuzzy edge image was obtained by calculating the difference between the fuzzy dilation and fuzzy erosion, and the fuzzy edge image was defuzzed and binarized to get the binary edge image.

Algorithm 4. OR-FCM algorithm.

Input: gray-scale image A, fuzzy binary R; Output: binary edge image; Step 1: Fuzzify the gray-scale image A; Step 2: Cluster fuzzy image A with FCM algorithm, let Object and BG (background) be the sets of all foreground points and background points; Step 3: According to the clustering results of A (as existing knowledge), design the fuzzy relation R, setting the values corresponding to the points in Object and BG are different; Step 4: Calculate the fuzzy edge image DR(A) − ER(A); Step 5: Defuzzy and binarize fuzzy edge image in Step 4 to get final binary edge image.

In this section, we described the shortcomings of existing mathematical morphology based on fuzzy relations and proposed ORFMM operators to solve these problems. Then, another image edge extraction algorithm (OR-FCM algorithm) was proposed by ORFMM operators and FCM algorithm.

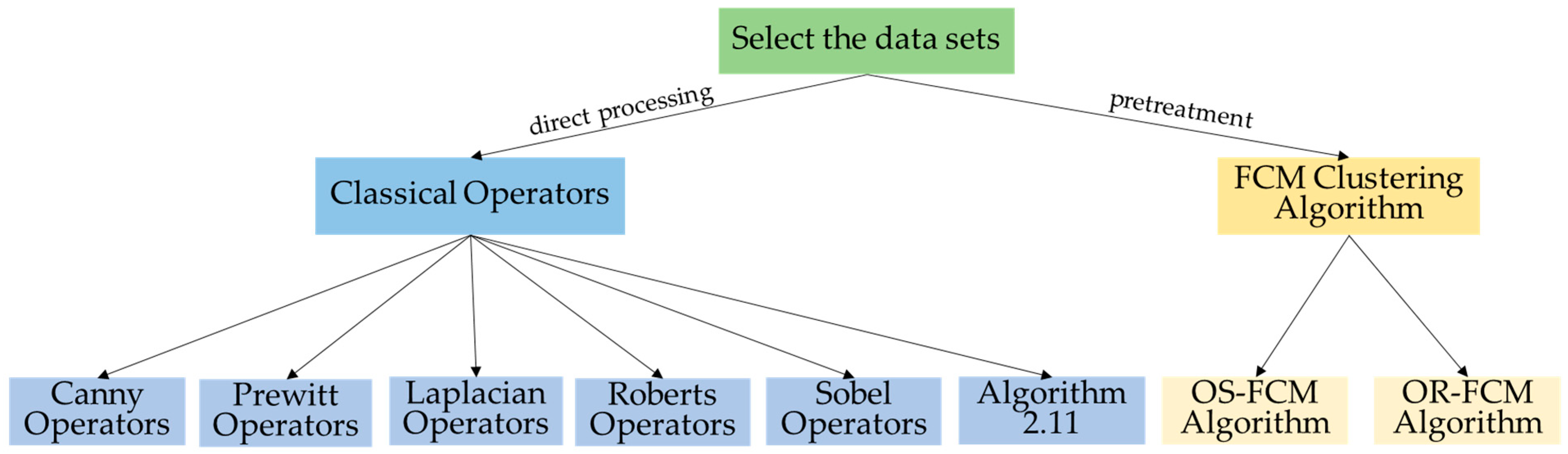
5. Edge Extraction Experiment

In this section, first the OS-FCM (Algorithm 3) algorithm and OR-FCM (Algorithm 4) algorithm are used to extract the edge of three standard images, and two fuzzy relations are used to implement the OR-FCM algorithm. Then, the existing relevant typical algorithm and operators are implemented (Algorithm 1, Prewitt operator, Laplacian operator, Canny operator, Roberts operator, Sobel operator [42]) to extract the edge of the same image. Finally, the experimental results of the three algorithms proposed by us and the existing classical algorithms are compared and analyzed.

5.1. Experimental Framework

The experimental processes in this section are shown in Figure 5, and the following will introduce each experimental step in detail.

Step 1. Select the data sets.

Three standard images, Cameraman, Lena, and Barbara, were chosen. The three gray-scale images are depicted in Figure 6 (left), (center), and (right), respectively.

The Cameraman’s image was used as an example to illustrate the processes of the three edge extraction algorithms.

Step 2. The FCM algorithm was used to cluster the Cameraman’s image.

Step 2.1: Every point x_j in the data set {x₁, x₂, …, x_M×N } was represented as a three-dimensional vector.

x_j = (m/M, n/N, A(m, n)/255), j = 1, 2, …, M × N.

where m, n indicate that point x_i is located in the m-th row and n-th column of the gray-scale image. M, N are the maximum of rows and columns of gray-scale image A, respectively, and A(m, n) represents the pixel value of gray-scale image A at point (m, n). In this step, each component of the vector x_j was mapped to [0, 1]. Hence, the weights of the three components were the same when calculating the vector distance.

Note: If only one component (pixel value) is used for clustering, the points with similar brightness will be classified into one class. However, this method has the following problems: if the brightness of noises in the image is similar to that of the foreground objects, then the noises and foreground objects cannot be distinguished, and different objects with similar brightness will be divided into one class. When the above three-dimensional vector is utilized for clustering, both the distance and brightness between each point are considered. The result is that points with similar brightness within a certain range are classified into one class, which is more consistent with the definition of the object in the image. This is an improvement of the FCM algorithm for clustering gray-scale images.

Step 2.2: Set the number of clustering categories to 20 and maximum iterations to 10;

Step 2.3: Randomly initialize clustering centers (v₁, v₂,…, v₂₀), where v_i ∈ [0, 1]³;

Step 2.4: Update the membership degrees according to Formula (3);

Step 2.5: Update the clustering centers according to Formula (4);

Step 2.6: Judge whether the maximum iterations are met. Return to Step 2.4, if the stop condition is not met;

Step 2.7: Point x_j is divided into class i, i satisfies u_ij = max{u_1j, u_2j,…, u_cj}.

Step 3. The OS-FCM algorithm calculates the image edge.

First, by using the structuring elements B₁_D and B₁_E, the fuzzy dilation D_O(A, B₁_D) and fuzzy erosion E_I(A, B₁_E) of the gray-scale image were calculated, respectively, to extract the edge of the buildings. In addition, by using the structuring element B₂, D_O(A, B₂) and E_I(A, B₂) were calculated to extract the edges of people and camera frames. The values of structuring elements are as follows:

$$B_1\_D=\left[\begin{array}{ccc}0.9& 0.9& 0.9\\ 0.9& 1.0& 0.9\\ 0.9& 0.9& 0.9\end{array}\right]B_1\_E=\left[\begin{array}{ccc}0.7& 0.7& 0.7\\ 0.7& 0.8& 0.7\\ 0.7& 0.7& 0.7\end{array}\right]B_2=\left[\begin{array}{ccc}0.6& 0.6& 0.6\\ 0.6& 0.7& 0.6\\ 0.6& 0.6& 0.6\end{array}\right]$$

Then, according to the fuzzy erosion and fuzzy dilation results calculated by two groups of the structuring elements, two kinds of the fuzzy edge images were calculated. The fuzzy edge images were defuzzed and binarized to get the binary edge images. Finally, according to the results of the FCM algorithm, the final binary edge image of the gray-scale image (Cameraman) was calculated.

Step 4. The OR-FCM algorithm calculates the image edge.

The edge extraction results of the gray-scale image (Cameraman) were calculated according to its compactness and existing gray-scale edge image (based on two fuzzy relations).

Step 4.1. The OR-FCM algorithm extracts the image edge according to compactness.

The fuzzy binary relation R₁(x, y) was defined as follows:

$$R_1(x,y)=\{\begin{array}{c}\frac{(r(y)-\rho (x,y))}{r(y)}, \mathrm{if} 0<\rho (x,y)<r\\ 0, \mathrm{others}\end{array}$$

where R₁(x, y) denotes the compactness of points x and y in radius r(y). When x = y, R₁(x, y) = 1 is derived, while when ρ(x, y) ≥ r(y), R₁(x, y) = 0 is obtained. In the experiment, r(y) = 4 when point y belongs to the foreground objects, and r(y) = 1.5 when point y belongs to the background.

First, the fuzzy erosion E_R(A) and fuzzy dilation D_R(A) were calculated by using the above-mentioned fuzzy relation R₁. Then, the fuzzy edge image was calculated according to D_R(A) and E_R(A), and the fuzzy edge images were defuzzed and binarized to obtain the final binary edge image.

Step 4.2. The OR-FCM algorithm extracts the image edge according to the existing gray edge image.

The fuzzy binary relation R₂(x, y) was defined as follows:

$$R_2(x,y)=\{\begin{array}{c}1, if \rho (x,y)=0\\ \max (edge(x),edge(y),0.75), if 0<\rho (x,y)\le 1 and y\in Object\\ \min (edge(x),edge(y),0.3), if 0<\rho (x,y)\le 1 and y\in BG\\ 0, if \rho (x,y)>1\end{array}$$

where the set Object and BG are the set of foreground points and background points of gray-scale image A classified by the FCM algorithm, respectively. As shown in Figure 7 (left), edge is the gray-scale edge image obtained by the existing algorithm. If one binarizes Figure 7 (left), the result is depicted in Figure 7 (right).

First, the fuzzy erosion E_R(A) and fuzzy dilation D_R(A) of gray-scale image A were calculated by using the above-mentioned fuzzy relation R₂. Then, the fuzzy edge image was calculated according to D_R(A) and E_R(A), and the fuzzy edge images were defuzzed and binarized to obtain the final binary edge image.

5.2. Experiment Result

The FCM algorithm was used to cluster gray-scale image A, and the result is shown in Figure 8 after defuzzying. As can be seen from Figure 8, the FCM algorithm can distinguish well the foreground points and the background spots of the gray-scale image. Among them, the points in classes 2, 3, and 18 belong to the set Object, and the points in classes 1, 19, and 20 belong to the set BG.

The results of the OS-FCM algorithm extracting gray-scale image edges in data sets are shown in Figure 9. The OR-FCM algorithm used the fuzzy relations R₁ and R₂ to extract the gray-scale image edges in the data sets, and the results are displayed in Figure 10 and Figure 11, respectively. Additionally, the results of Algorithm 1 extracting gray-scale image edges in data sets are displayed in Figure 12. The Canny, Laplacian, Prewitt, Roberts, and Sobel operators were used to extract gray-scale image edges in the data sets, and the results are shown in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, respectively.

5.3. Algorithm Evaluation

The most difficult problem in image edge extraction algorithms is to extract the edges of the foreground objects with similar brightness to noises without introducing noises. Therefore, the image edge extraction algorithms were comprehensively evaluated in relation to the following two aspects: whether more edges of the foreground objects can be extracted and the number of noises introduced while extracting the edges of the foreground objects.

By comparing the results of the OS-FCM algorithm, OR-FCM algorithm, and the other existing algorithms, it can be inferred that the results of the two proposed algorithms have complete edge information, such as the edges of the buildings in the Cameraman image and the edges of the scarf, pants, and tie stripes in the Barbara image. Although the Sobel operator can also extract complete edges of the image, it introduces a lot of noise. In the following, the concept of the noise introduction rate will be introduced to quantify the number of noises introduced by each algorithm when extracting image edges.

The black parts of the images shown in Figure 18 are set as the background of the images Cameraman, Lena, and Barbara. The intersection of the black areas in Figure 18 and the edge extraction results are called noise, and the ratio α defined below is called the noise introduction rate of the edge extraction:

$$\alpha =\frac{S_n}{S}$$

where S_n is total area of noises and S denotes total area of the image.

The overlap functions O₆ and O₇ and fuzzy implications I₁ and I₂ used in the OS-FCM and OR-FCM algorithms are defined as follows:

$$\begin{array}{l}{O}_6=\frac{2xy}{1+xy}, O_7=\min (\sqrt{x},\sqrt{y}),\\ I_1=\{\begin{array}{l}1, \mathrm{if} \sqrt{x}\le y,\hfill \\ \frac{y^2}{x}, others,\hfill \end{array}{I}_2=\{\begin{array}{l}\min (1,\frac{\sqrt{2y-1}}{2(2x-1)}+\frac{1}{2}), \mathrm{if} x\in (0.5,1],y\in [0.5,1],\hfill \\ \begin{array}{l}y, \mathrm{if} y\in [0, 0.5), x>y,\\ 1, \mathrm{if} x\in [0, 0.5], x\le y.\end{array}\hfill \end{array}\end{array}$$

In the OS-FCM algorithm, the (I, O) pairs used to extract the background objects of the Cameraman, Lena, and Barbara images are (I₁, O₁,), (I₁, O₂), and (I₁, O₂), respectively. In the OS-FCM algorithm, different (I, O) pairs were used to extract the foreground edge of the gray-scale images. The noise introduction rates of each (I, O) pair to extract the edge of Cameraman, Lena, and Barbara images are presented in

Table 1. Noise introduction rates of OS-FCM algorithm.

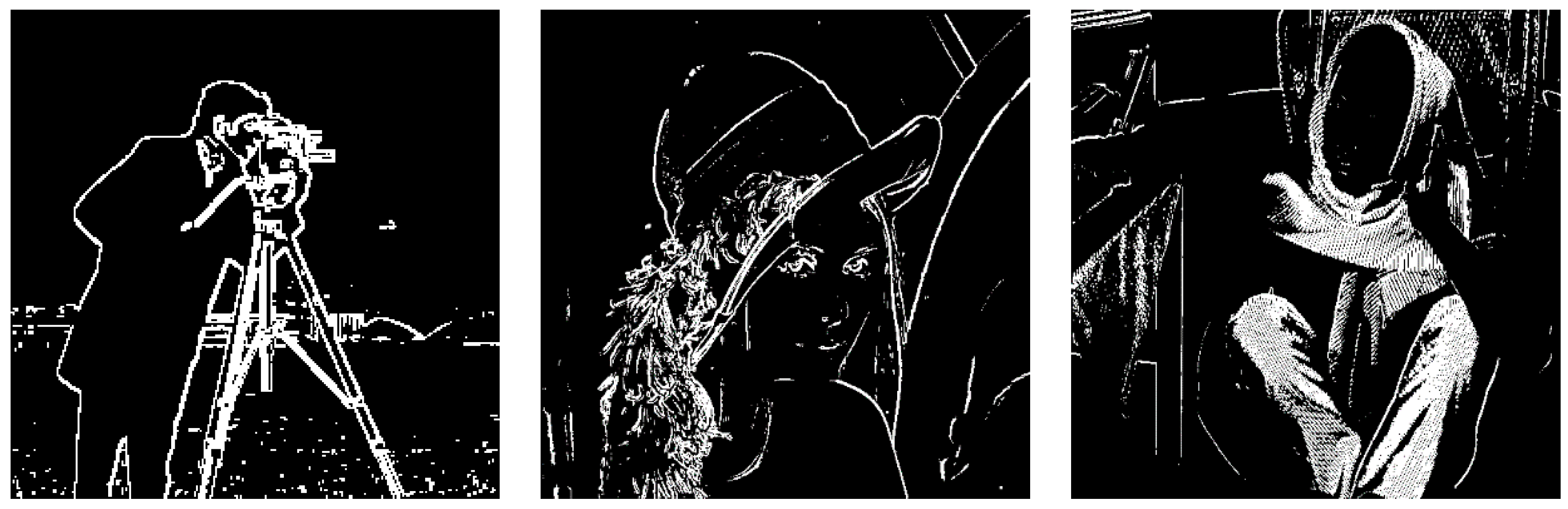
	Cameraman	Lena	Barbara
(I1, O2)	0.74%	3.02%	1.00%
(I1, O1,)	0.41%	2.27%	0.87%
(I1, O7)	0.41%	2.63%	0.82%
(I1, O5)	0.43%	1.69%	0.78%
(I1, O6)	0.39%	2.23%	0.91%
average introduction rate	0.48%	2.37%	0.88%

.

When the OR-FCM algorithm uses fuzzy relations R₁ and R₂, the noise introduction rate of each (I, O) pair to extract the edge of the Cameraman, Lena, and Barbara images are presented in

Table 2. Noise introduction rates of OR-FCM algorithm (R₁).

	Cameraman	Lena	Barbara
(I2, O2)	0.56%	4.84%	0.05%
(I2, O1)	0.65%	3.08%	1.02%
(I2, O7)	1.05%	3.20%	1.03%
(I2, O5)	0.55%	2.97%	0.58%
(I2, O6)	0.49%	2.34%	0.42%
average introduction rate	0.66%	3.29%	0.62%

and

Table 3. Noise introduction rates of OR-FCM algorithm (R₂).

	Cameraman	Lena	Barbara
(I1, O2)	0.07%	0.52%	1.00%
(I1, O1)	0.24%	2.60%	0.42%
(I1, O7)	0.52%	3.00%	0.94%
(I1, O5)	0.07%	0.74%	0.94%
(I1, O6)	0.14%	2.02%	0.79%
average introduction rate	0.21%	1.78%	0.82%

.

When Algorithm 1, the Canny operator, the Laplacian operator, the Prewitt operator, the Roberts operator, and the Sobel operator are used to extract the edges of Cameraman, Lena, and Barbara, the noise introduction rates of each operator (algorithm) are presented in

Table 4. Noise introduction rates of each algorithm (operator).

	Cameraman	Lena	Barbara
Algorithm 1	1.86%	4.00%	4.28%
Canny operator	7.65%	3.34%	3.07%
Laplacian operator	12.51%	4.87%	6.32%
Prewitt operator	5.76%	8.77%	10.23%
Roberts operator	3.11%	6.95%	6.15%
Sobel operator	9.67%	13.23%	8.84%
Average of OS-FCM algorithm	0.48%	2.37%	0.88%
Average of OR-FCM algorithm (two fuzzy relations)	0.66%	3.29%	0.62%
	0.21%	1.78%	0.82%

. There are some fluctuations in the noise introduction rate in Table 1, Table 2, Table 3 and Table 4. The reason is that the operators used in different algorithms are composed of different knowledge of grayscale images. By comparison, the average noise introduction rates of the OS-FCM and OR-FCM are lower than that of all other operators (algorithms). In addition, the OS-FCM and OR-FCM have a total of 45 groups of experiments, of which 44 groups of experimental results have lower noise introduction rates than the other six existing operators (algorithm). The experimental results demonstrate that the image edge extraction algorithms proposed in this work can extract more complete edges of the foreground objects and introduce less noise than classical algorithms and operators.

First, we introduced overlap functions, which are more suitable for image processing, into mathematical morphology operators, and proposed two groups of fuzzy mathematical morphology operators based on overlap functions (OSFMM and ORFMM). Secondly, the FCM algorithm was used to preprocess the gray image to obtain the position information of foreground objects and background objects. Different structure elements or binary relations were used for background points and foreground points, which further sharply expands the advantages of fuzzy morphological operators in edge extraction of gray images. The acquired results demonstrated that the image edge extraction algorithms proposed in this work can extract the complete edge of the foreground objects on the basis of introducing the least noise.

The operators used in the latest edge extraction algorithm [43] are very similar to the FMM operators. The addition and subtraction in these operators correspond to overlap functions and fuzzy implications, respectively. Overlap functions and fuzzy implications have the following advantages compared to addition and subtraction: better boundary conditions, nonlinearity, and most importantly, overlap functions can express the correlation between image and structure elements.

6. Conclusions and Future Work

In this paper, the FMM operators based on overlap functions and their application in image processing were systematically studied. First, the OSFMM operators were proposed based on the overlap functions and structuring elements. Compared with the FMM operators based on t-norm, the OSFMM operators have a wider value range and more suitable boundary conditions for image processing. On top of that, the continuity of the OSFMM operators is proved under certain conditions (this property can be applied to video image processing). By combining the OSFMM operators and the FCM algorithm, an OS-FCM algorithm for image edge extraction was proposed. Second, the ORFMM operators were proposed based on fuzzy relations and overlap functions. The shortcomings of the experiment, which use the existing FMM operators based on fuzzy relations, were pointed out. The flexibility of the ORFMM operator was fully exploited. The OR-FCM algorithm was proposed by combining the ORFMM operators and the FCM algorithm. Finally, by performing edge segmentation experiments of several standard images, it was found that OS-FCM and OR-FCM can not only extract the complete edge of the foreground objects, but also introduce the least noise compared with the existing relevant typical algorithms. It indicated that the two groups of FMM operators based on the overlap functions proposed in this work have obvious advantages in image edge extraction.

In future work, the mathematical characteristics and extensions of the two groups of fuzzy mathematical morphology operators proposed in this work will be discussed in depth (such as new morphological operators based on pseudo overlap functions and semi-overlap functions, related deep morphological networks, etc.). Moreover, some new results obtained from other papers (see [44,45,46,47]) will be applied to fuzzy mathematical morphology and medical images processing.