The Extended Direct Algebraic Method for Extracting Analytical Solitons Solutions to the Cubic Nonlinear Schrödinger Equation Involving Beta Derivatives in Space and Time
Abstract
1. Introduction
2. Definition of Beta Derivative and Its Properties
- i.
- .
- ii.
- here is a constant.
- iii.
- iv.
- v.
- .
- vi.
- .
- vii.
- .
3. Algorithm of the Extended Direct Algebraic Method
4. Mathematical Analysis
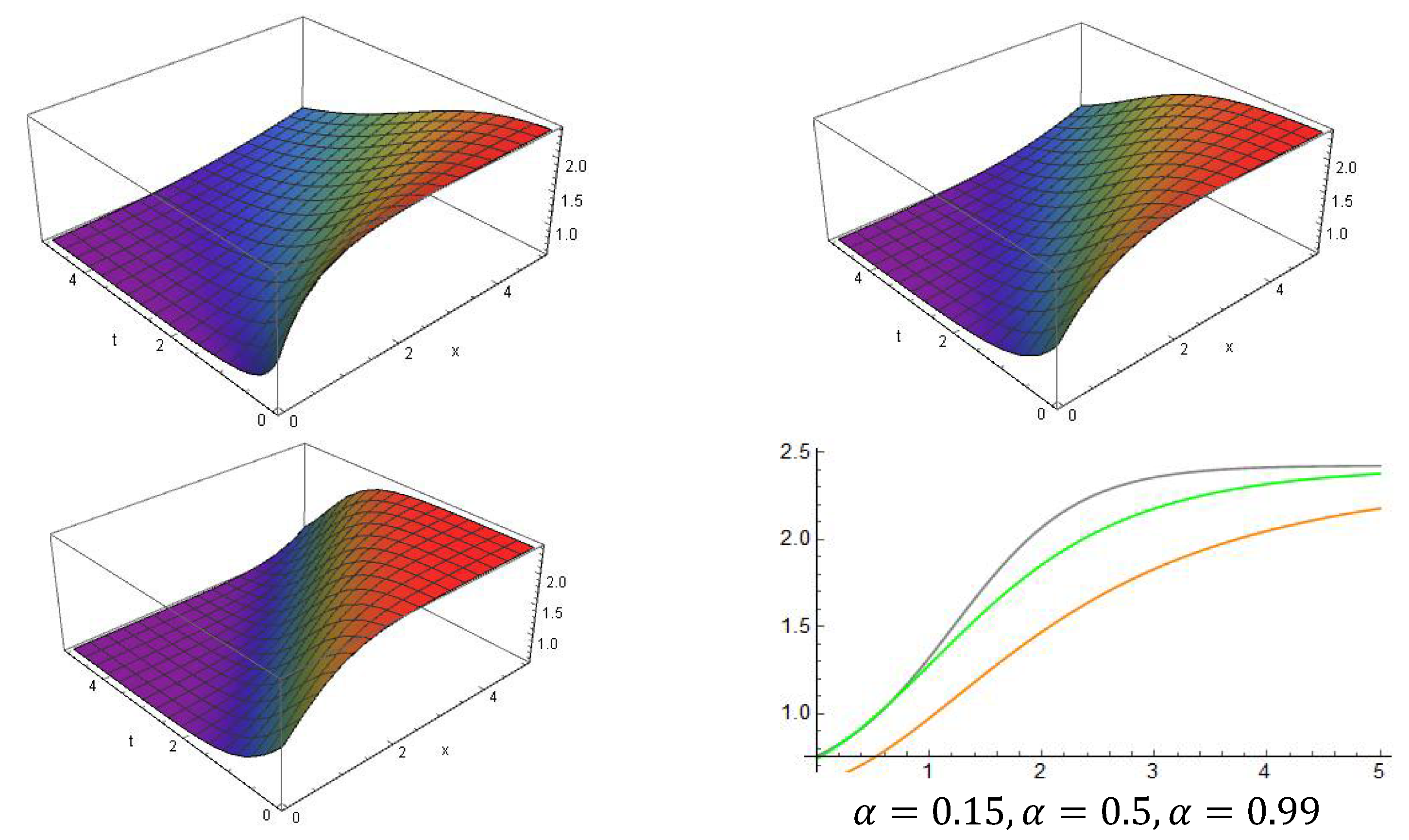
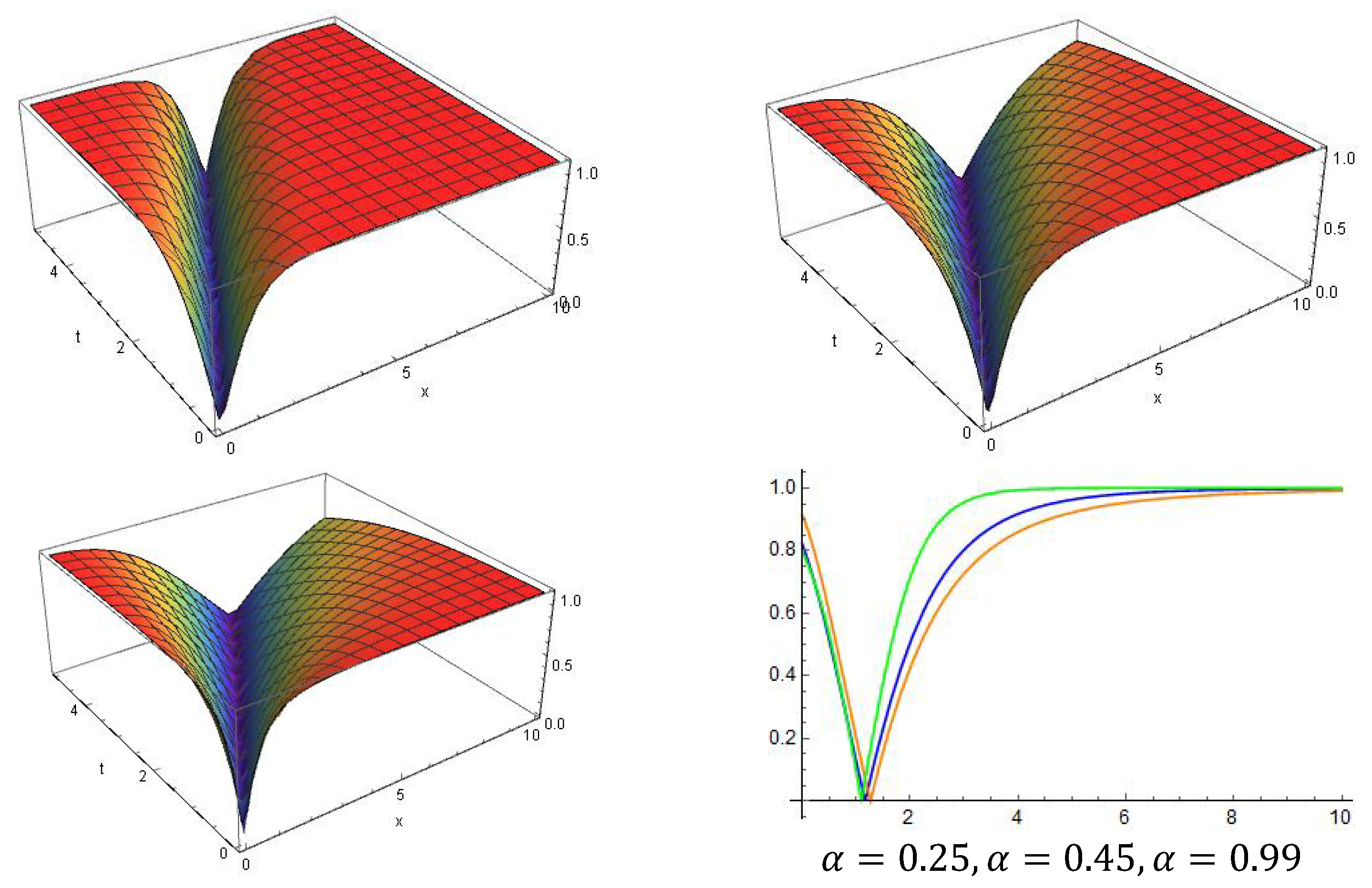
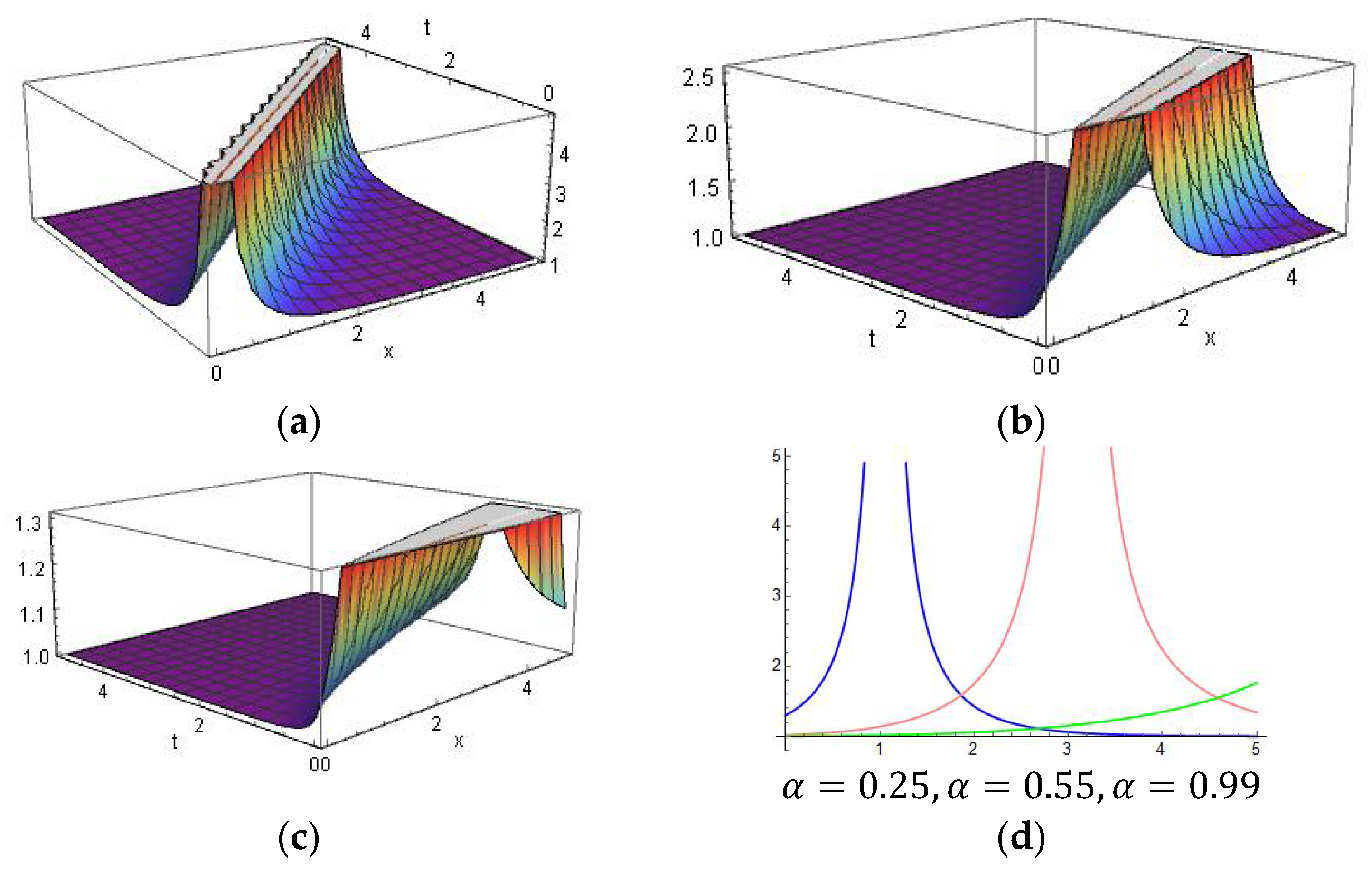
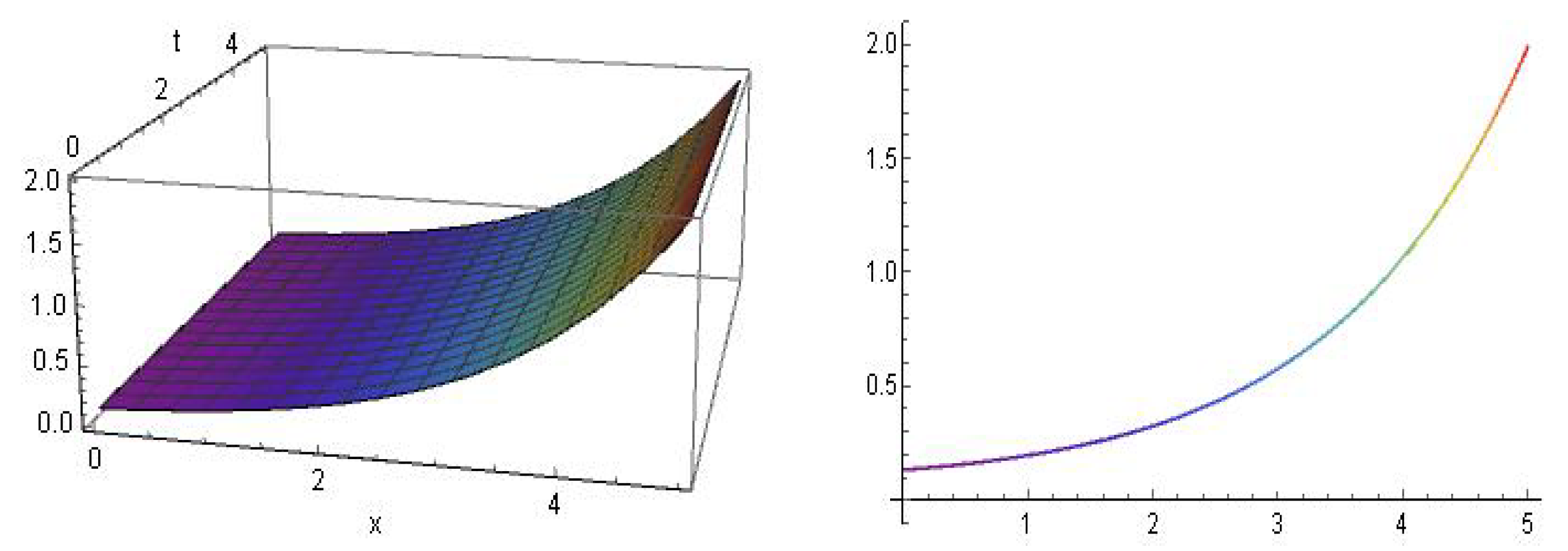
5. Physical Significance and Explanations
6. Comparison
| Solution Using the Simplest Equation Method | The Attained Solutions |
|---|---|
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Esen, H.; Ozisik, M.; Secer, A.; Bayram, M. Optical soliton perturbation with Fokas–Lenells equation via enhanced modified extended tanh-expansion approach. Optik 2022, 267, 169615. [Google Scholar] [CrossRef]
- Siddique, I.; Jaradat, M.M.; Zafar, A.; Mehdi, K.B.; Osman, M.S. Exact traveling wave solutions for two prolific conformable M-Fractional differential equations via three diverse approaches. Results Phys. 2021, 28, 104557. [Google Scholar] [CrossRef]
- Ahmed, H.M.; El-Sheikh, M.M.A.; Amous, A.H.; Rabie, W.B. Solitons and other solutions to (n + 1)-dimensional modified Zakharov-Kuznetsov equation by Exp-function method. SeMA J. 2021, 78, 1–13. [Google Scholar] [CrossRef]
- Shakeel, M.; Attaullah; Shah, N.A.; Chung, J.D. Modified Exp-Function Method to Find Exact Solutions of Microtubules Nonlinear Dynamics Models. Symmerty 2023, 15, 360. [Google Scholar] [CrossRef]
- Ali, M.R.; Khattab, M.A.; Mabrouk, S.M. Travelling wave solution for the Landau-Ginburg-Higgs model via the inverse scattering transformation method. Nonlinear Dyn. 2023, 111, 7687–7697. [Google Scholar] [CrossRef]
- Liu, N.; Xuan, Z.; Sun, J. Triple-pole soliton solutions of the derivative non linear Schrödinger equation via inverse scattering transform. Appl. Math. Lett. 2022, 125, 107741. [Google Scholar] [CrossRef]
- Dong, S.; Lan, Z.-Z.; Gao, B.; Shen, Y. Bäcklund transformation and multi-soliton solutions for the discrete Korteweg-de Vries equation. Appl. Math. Lett. 2022, 125, 107747. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Kou, W.; Wang, R.; Chen, X. Analytical solution of Balitsky-Kovchegov equation with homogeneous balance method. Phys. Rev. D 2021, 103, 056008. [Google Scholar] [CrossRef]
- Radha, B.; Duraisami, C. The homogeneous balance method and its applications for finding the exact solutions for nonlinear equations. J. Ambiant Intell. Humaniz. Comput. 2021, 12, 6591–6597. [Google Scholar] [CrossRef]
- Tarla, S.; Ali, K.K.; Yilmazer, R.; Osman, M. New optical solitons based on the perturbed Chen-Lee-Liu model through Jacobi elliptic function method. Opt. Quantum Electron. 2022, 54, 131. [Google Scholar] [CrossRef]
- Kilic, B.; Inc, M. Soliton solutions for the Kundu-Eckhaus equation with the aid of unified algebraic and auxiliary equation expansion methods. J. Electro-Magn. Waves Appl. 2016, 30, 871–879. [Google Scholar] [CrossRef]
- Sabi’u, J.; Rezazadeh, H.; Cimpoiasu, R.; Constantinescu, R. Traveling wave solutions of the generalized Rosenau-Kawahara RLW equation via the sine-cosine method and generalized auxiliary equation method. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 539–551. [Google Scholar] [CrossRef]
- Fendzi-Donfack, E.; William, G.; Temgoua, K.; Dioufack, Z.I. Exotical solitons for an intrinsic fractional circuit using the sine-cosine method. Chaos Solitons Fractals 2022, 160, 112253. [Google Scholar] [CrossRef]
- Naowarat, S.; Saifullah, S.; Ahmad, S.; De la Sen, M. Periodic, Singular and Dark Solitons of a Generalized Geophysical KdV Equation by Using the Tanh-Coth Method. Symmetry 2023, 15, 135. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.; Albalahi, A. The Impact of the Wiener Process on the Analytical Solutions of the Stochastic (2+1)-Dimensional Breaking Soliton Equation by using tanh-coth Method. Mathematics 2022, 10, 817. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Zaghrout, A.A.S.; Ahmed, H.M. Exploration new solitons in fiber Bragg gratings with cubic–quartic dispersive reflectivity using improved modified extended tanh-function method. Eur. Phys. J. Plus 2023, 138, 32. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Sulaiman, T.A.; Yusuf, A.; Bayram, M. Optical solitons of the (2 + 1)-dimensional Biswas-Milovic equation using modified extended tanh-function method. Optik 2021, 245, 167631. [Google Scholar] [CrossRef]
- Malik, S.; Almusawa, H.; Kumar, S.; Wazwaz, A.M.; Osman, M.S. A (2 + 1)-dimensional Kadomtsev–Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions. Results Phys. 2021, 23, 104043. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Kravchenko, O.V.; Deka, M.K.; Dev, A.N.; Churikov, D.V. The exact solutions of the (2 + 1)-dimensional Kadomtsev-Petviashvili equation with variable coefficients by extended generalized (G′/G)-expansion method. J. King Saud Univ.-Sci. 2023, 35, 102358. [Google Scholar] [CrossRef]
- Rasheed, N.; Al-Amr, M.O.; Az-Zo’bi, E.A.; Tashtoush, M.A. Akinyemi. Stable Optical Solitons for the Higher-Order Non-Kerr NLSE via the Modified Simple Equation Method. Mathematics 2021, 9, 1986. [Google Scholar] [CrossRef]
- Barman, H.K.; Akbar, M.A.; Osman, M.; Kottakkaran, S.; Zakarya, M.; Abdel-Aty, A.-H.; Eleuch, H. Solutions to the Konopelchenko-Dubrovsky equation and the Landau-Ginzburg-Higgs equation via the generalized Kudryashov technique. Results Phys. 2021, 24, 104092. [Google Scholar] [CrossRef]
- Barman, H.K.; Roy, R.; Mahmud, F.; Akbar, M.A.; Osman, M.S. Harmonizing wave solutions to the Fokas-Lenells model through the generalized Kudryashov method. Optik 2021, 229, 166294. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Fahim, R.A.; Kundu, P.R.; Islam, E.; Akbar, M.A.; Inc, M. Extension of the sine-Gordon expansion scheme and parametric effect analysis for higher-dimensional nonlinear evolution equations. J. King Saud Univ. Sci. 2021, 33, 101515. [Google Scholar] [CrossRef]
- Zahran, E.H.; Mirhosseini-Alizamini, S.M.; Shehata, M.S.M.; Rezazadeh, H.; Ahmad, H. Study on abundant explicit wave solutions of the thin-film Ferro-electric materials equation. Opt. Quantum Electron. 2022, 54, 48. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Ahamad, H.; Morshedy, M.E. Exact solutions of Hirota–Maccari system forced by multiplicative noise in the Itô sense. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 74–84. [Google Scholar] [CrossRef]
- Vahidi, J.; Zabih, A.; Rezazadeh, H.; Ansari, R. New extended direct algebraic method for the resonant nonlinear Schrödinger equation with Kerr law nonlinearity. Optik 2021, 227, 165936. [Google Scholar] [CrossRef]
- Ali, K.; Ali, T.; Orkun, T. Applying the New Extended Direct Algebraic Method to Solve the Equation of Obliquely Interacting Waves in Shallow Waters. J. Ocean. Univ. China 2020, 19, 772–780. [Google Scholar]
- Zhu, X.; Cheng, J.; Chen, Z.; Wu, G. New solitary-wave solutions of the Van der Waals normal form for granular materials via new auxiliary equation method. Mathematics 2022, 10, 2560. [Google Scholar] [CrossRef]
- Mahiuddin, M.; Khan, M.I.H.; Pham, N.D.; Karim, M.A. Development of fractional viscoelastic model for characterizing viscoelastic properties of food material during drying. Food Biosci. 2018, 23, 45–53. [Google Scholar] [CrossRef]
- Wu, G.-Z.; Yu, L.-J.; Wang, Y.-Y. Fractional optical solitons of the space-time fractional nonlinear Schrödinger equation. Optik 2020, 207, 164405. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Akgul, A. Solitary wave solutions of time-space nonlinear fractional Schordinger equation. J. Comput. Appl. Math. 2018, 339, 147–160. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.-B.; Yousif, E.A.; El-Aasser, M.A. Analytical Solution of the Space-Time Fractional Nonlinear Schrödinger Equation. Rep. Math. Phys. 2016, 77, 19–34. [Google Scholar] [CrossRef]
- Yousif, E.; Abdel-Salam, E.A.-B.; El-Aasser, M.A. On the solution of the space-time fractional cubic nonlinear Schrödinger equation. Result Phys. 2018, 8, 702–708. [Google Scholar] [CrossRef]
- Neirameh, A.; Eslami, M.; Mehdipoor, M. New types of soliton solutions for space-time fractional cubic nonlinear Schrodinger equation. Bol. Da Soc. Parana. De Mat. 2021, 39, 121–131. [Google Scholar] [CrossRef]
- Herzallah, M.A.E.; Gepreel, K.A. Approximate solution to the time–space fractional cubic nonlinear Schrodinger equation. Appl. Math. Model. 2012, 36, 5678–5685. [Google Scholar] [CrossRef]
- Djennadi, S.; Shawagfeh, N.; Inc, M.; Osman, M.S.; Gómez-Aguilar, J.F.; Arqub, O.A. The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique. Phys. Scr. 2021, 96, 094006. [Google Scholar] [CrossRef]
- Rahman, R.U.; Qousini, M.M.M.; Alshehri, A.; Eldin, S.M.; El-Rashidy, K.; Osman, M.S. Evaluation of the performance of fractional evolution equations based on fractional operators and sensitivity assessment. Results Phys. 2023, 49, 106537. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Modelling the Spread of River Blindness Disease via the Caputo Fractional Derivative and the Beta-Derivative. Entropy 2016, 18, 40. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H.; Baskonus, H.M.; Geo, W. Dynamical behaviors to the coupled Schrodinger-Boussinesq system with the beta derivative. AIMS Math. 2021, 6, 7909–7928. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Atangana, A. On the complex and hyperbolic structures of the longitudinal wave equation in a magneto-electro-elastic circular rod. Smart Mater. Struct. 2016, 25, 035022. [Google Scholar] [CrossRef]
- Akbar, M.A.; Abdullah, F.A.; Khatun, M.M. Divere geometric shape solutions of the time-fractional nonlinear model used in communication engineering. Alexandra Eng. J. 2023, 68, 281–290. [Google Scholar] [CrossRef]
- Abro, K.A.; Abro, I.A.; Yildirim, A. A comparative analysis of sulfate SO4−2 ion concentration via modern fractional derivatives: An industrial application to cooling system of power plant. Phys. A 2020, 541, 123306. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Escobar-Jimenez, R.F.; Lopez-Lopez, M.G.; Alvarado-Martinez, V.M. Atangana-Baleanu fractional derivative applied to electromagnetic waves in dielectric media. J. Electromagn. Waves Appl. 2016, 30, 1937–1952. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana-Baleanu-Caputo fractional derivative. Adv. Differ. Equ. 2020, 1, 1–21. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Akgul, A.; Shah, R.; Mahariq, I.; Kafle, J. A Comparative Analysis of the fractional-order coupled Korteweg-De Vries Equations with the Mittag-Leffter Law. J. Math. 2022, 2022, 8876149. [Google Scholar] [CrossRef]
- Qiang, X.; Mahboob, A.; Chu, Y.-M. Numerical approximation of fractional-order Volterra integrodifferential equation. J. Funct. Spaces 2020, 2020, 1–12. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tasnim, F.; Akbar, M.A.; Osman, M.S. The Extended Direct Algebraic Method for Extracting Analytical Solitons Solutions to the Cubic Nonlinear Schrödinger Equation Involving Beta Derivatives in Space and Time. Fractal Fract. 2023, 7, 426. https://doi.org/10.3390/fractalfract7060426
Tasnim F, Akbar MA, Osman MS. The Extended Direct Algebraic Method for Extracting Analytical Solitons Solutions to the Cubic Nonlinear Schrödinger Equation Involving Beta Derivatives in Space and Time. Fractal and Fractional. 2023; 7(6):426. https://doi.org/10.3390/fractalfract7060426
Chicago/Turabian StyleTasnim, Farhana, Md Ali Akbar, and Mohamed S. Osman. 2023. "The Extended Direct Algebraic Method for Extracting Analytical Solitons Solutions to the Cubic Nonlinear Schrödinger Equation Involving Beta Derivatives in Space and Time" Fractal and Fractional 7, no. 6: 426. https://doi.org/10.3390/fractalfract7060426
APA StyleTasnim, F., Akbar, M. A., & Osman, M. S. (2023). The Extended Direct Algebraic Method for Extracting Analytical Solitons Solutions to the Cubic Nonlinear Schrödinger Equation Involving Beta Derivatives in Space and Time. Fractal and Fractional, 7(6), 426. https://doi.org/10.3390/fractalfract7060426






