Experimental Investigation of the Non-Darcy Equivalent Permeability of Fractured Coal Bodies: The Role of Particle Size Distribution
Abstract
1. Introduction
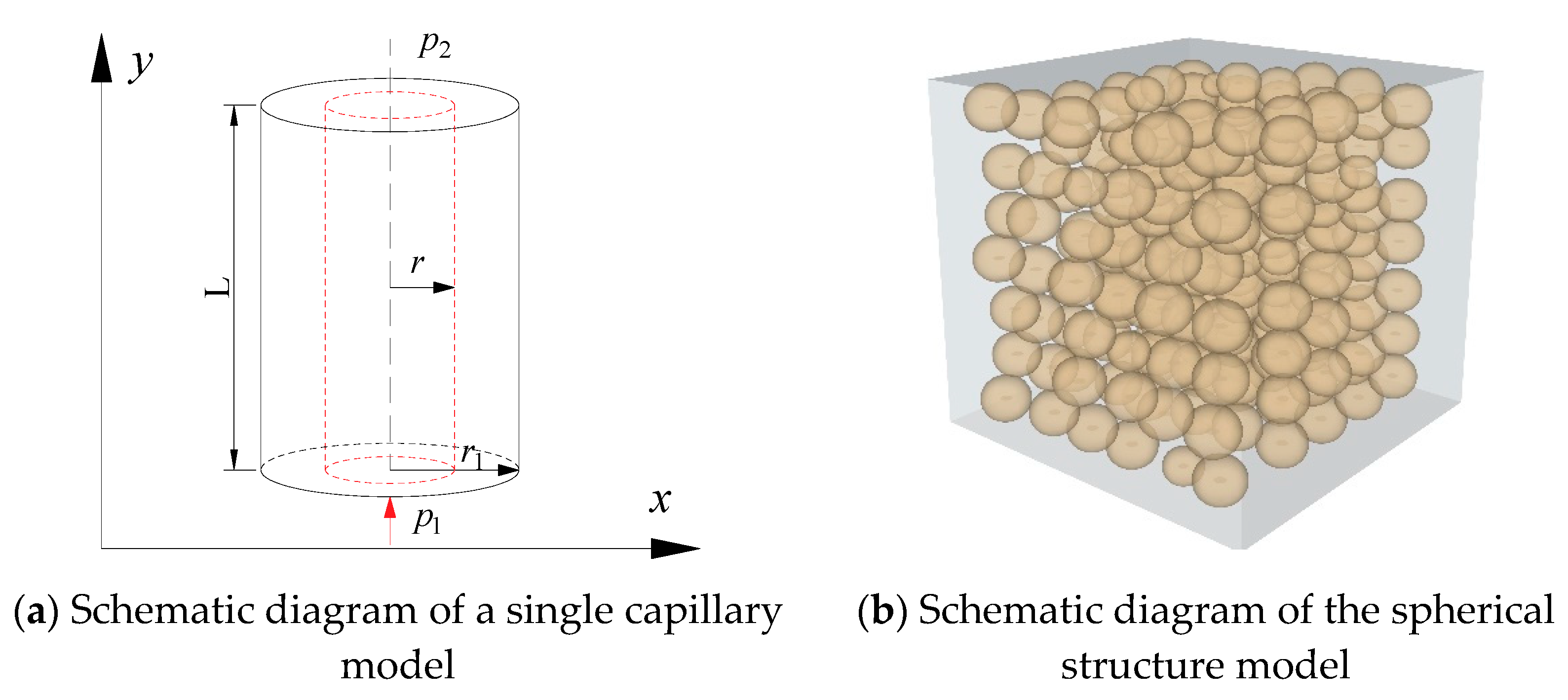
2. Theory
- (1)
- Principle of the particle size distribution of crushed coal bodies
- (2)
- Non-Darcy percolation principle in crushed coal bodies
3. Experiments
3.1. Materials
- (1)
- Research background
- (2)
- Material preparation
- (3)
- Experimental procedure
- ①
- The prepared specimen is loaded into a cylinder that is lined with a permeable sheet and felt to prevent the loss of small coal grains.
- ②
- A piston with a seal is fitted into the cylinder, a penetrometer is placed on the operating table of the press and the press is adjusted until it meets the piston; to ensure adequate contact, the actual stress on the specimen at this point is approximately 0.01 MPa. Then, the initial height of the specimen is measured.
- ③
- An axial load is applied to the specimen by a computer-controlled system and a high-pressure pump is switched on when the load reaches the set stress level. Then, the percolation test is completed and the flow rate is recorded at five successively increasing levels of osmotic pressure.
- ④
- The specimens are removed from the cylinder, dried, sifted and weighed, and the fractal dimension is calculated.
- ⑤
- At the end of the test, the same steps are carried out with the next set of specimens until all tests are completed.
3.2. Methodologies
- (1)
- Experiment design
- (2)
- Experimental equipment
4. Results and Discussion
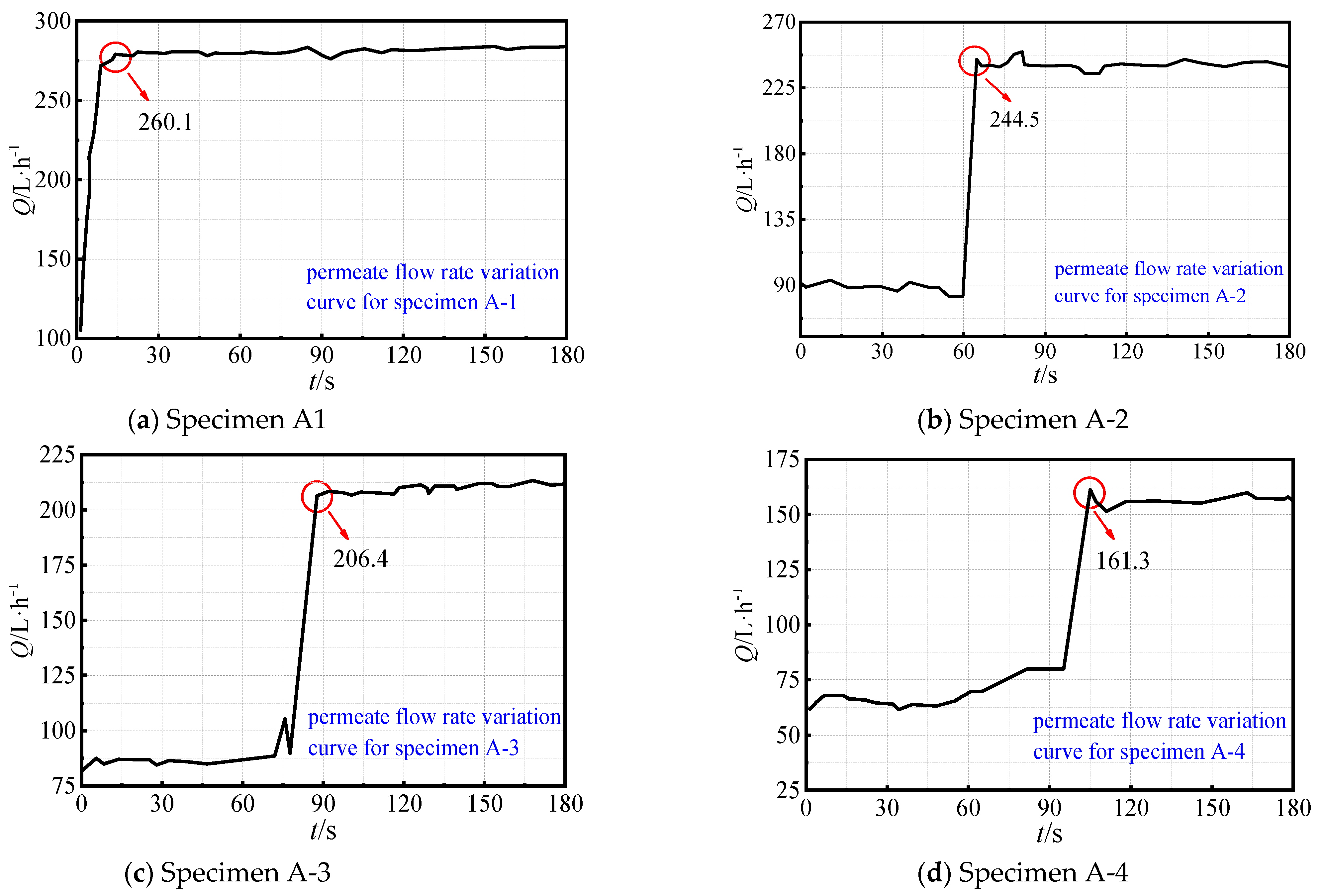
4.1. Basic Characteristics of Infiltration Flow Variations in Seepage Systems
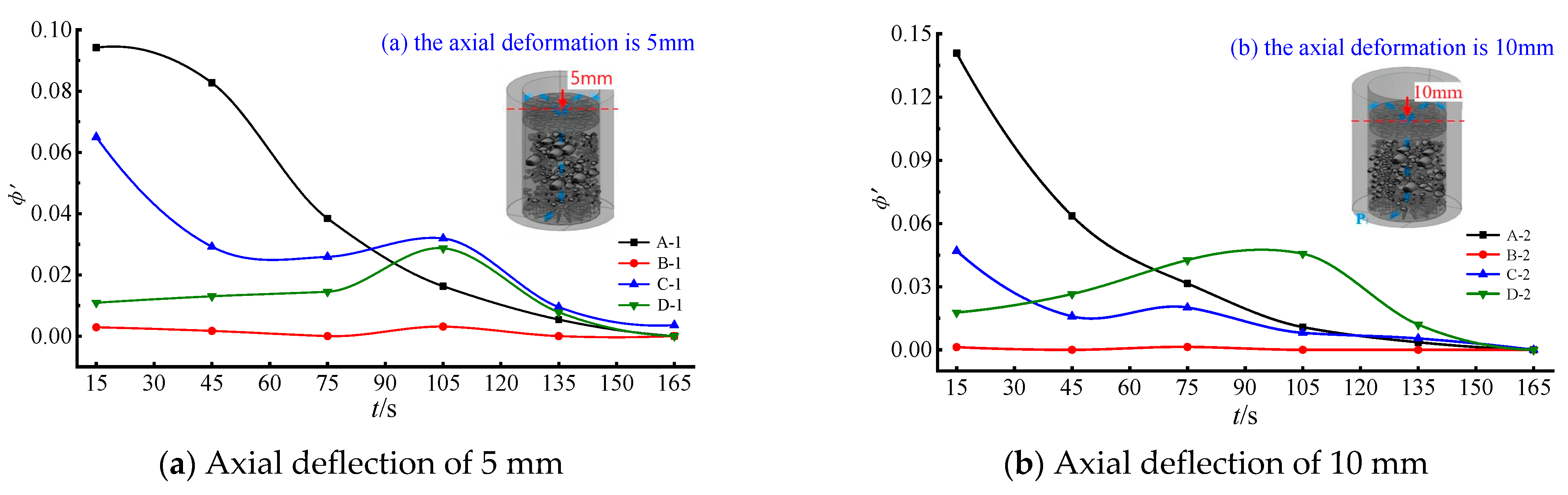
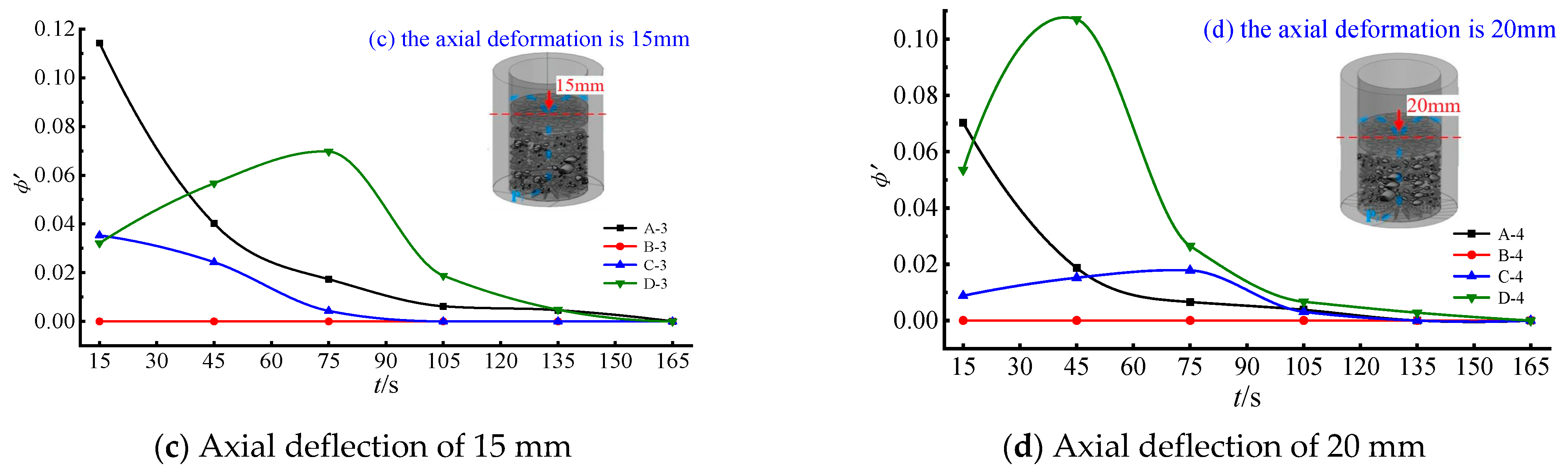
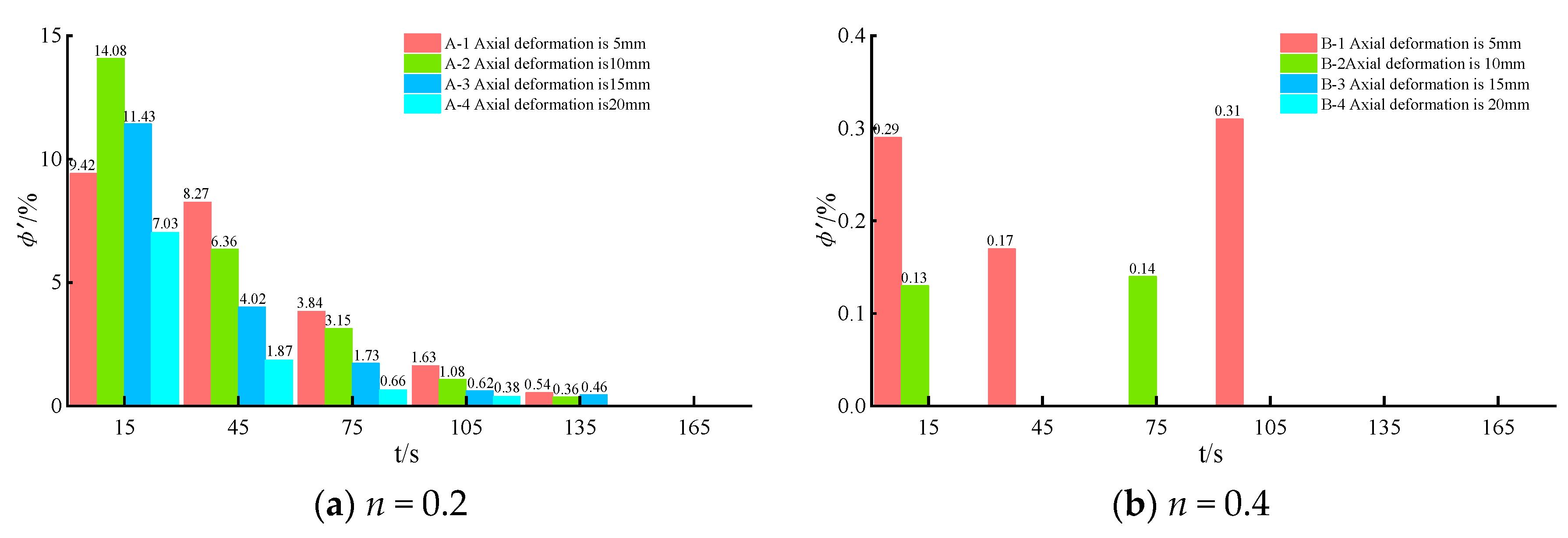
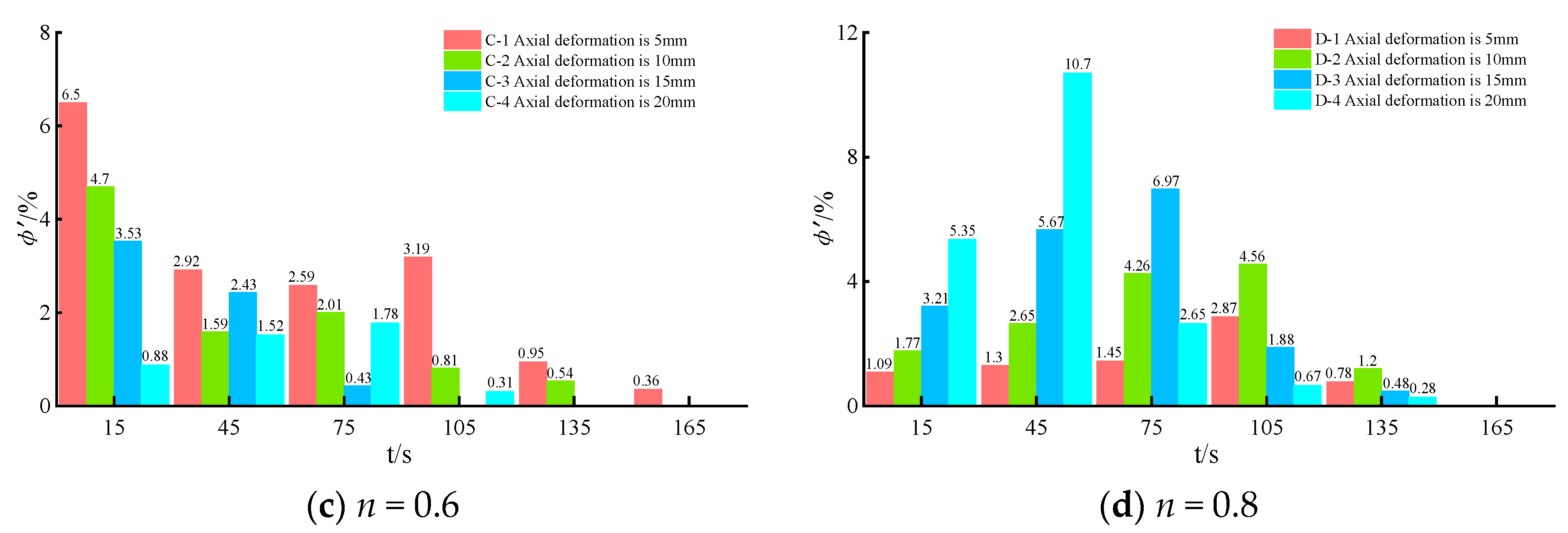
4.2. Time-Varying Characteristics of the Porosity for Structures with Different Initial Gradations
- (1)
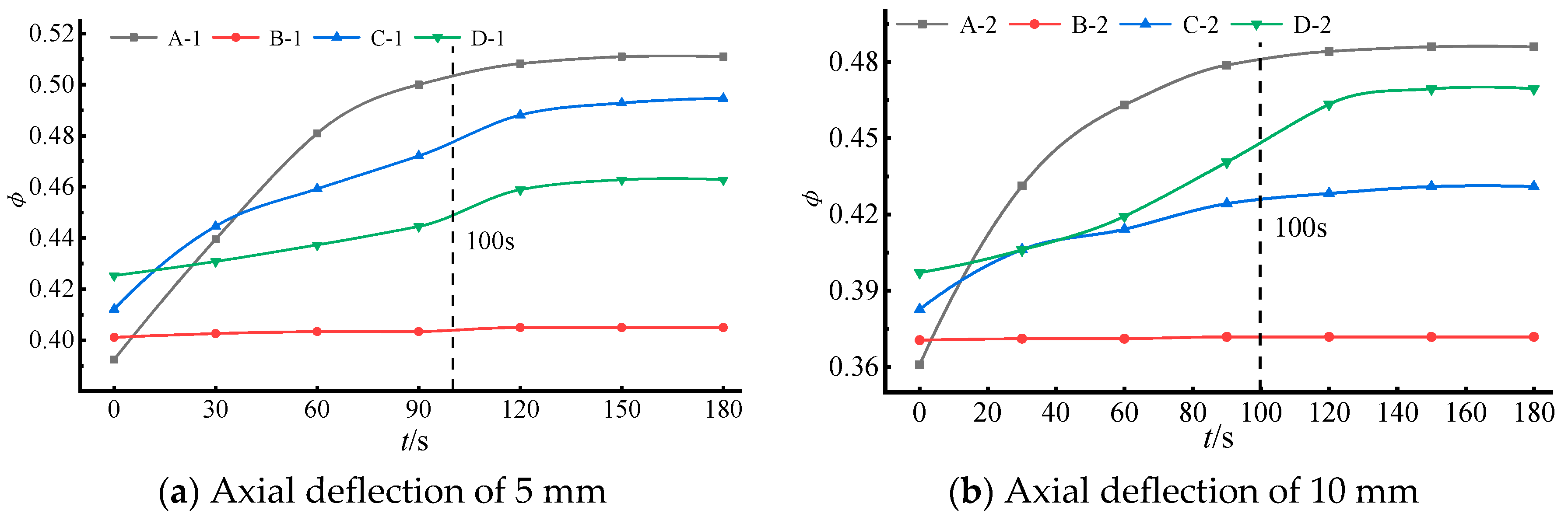
- Time-varying characteristics of the porosity
- (2)
- Basic variation characteristics of the rate of change in the porosity
- (3)
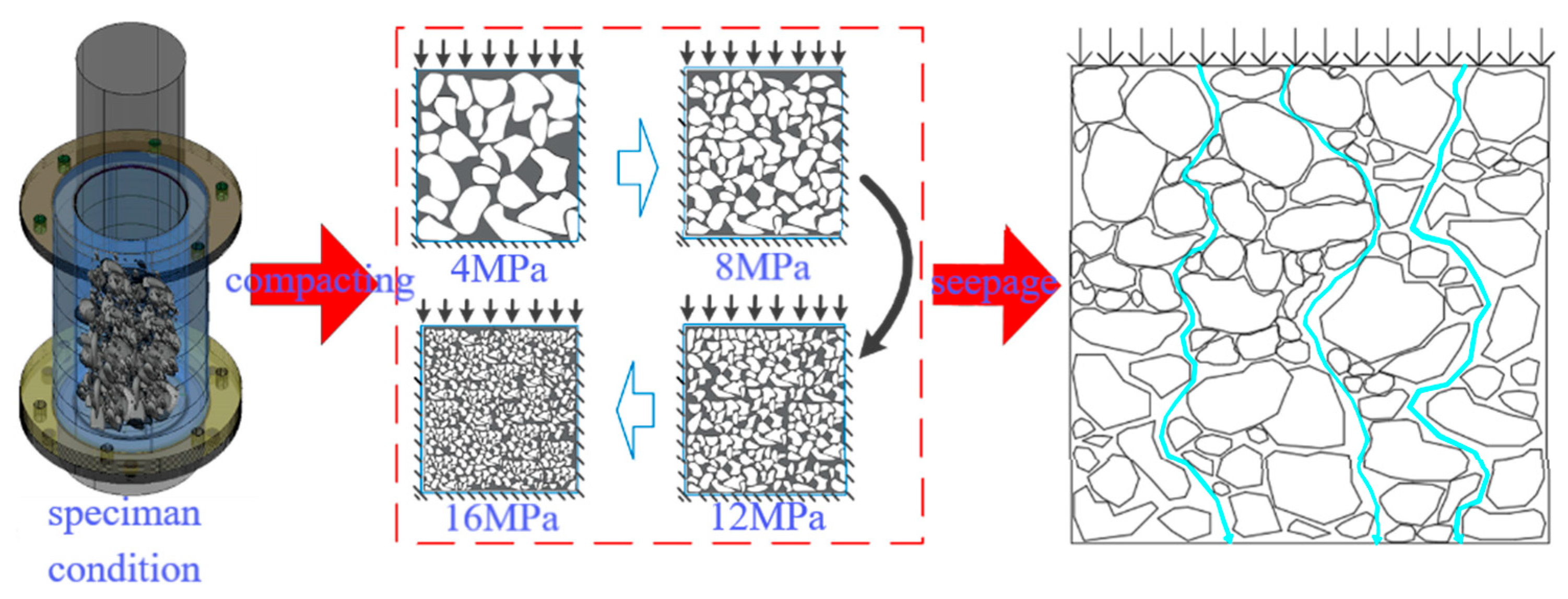
- Pore structure changes with different initial gradations
4.3. The Decisive Influence of the Porosity on the Specimen Permeability
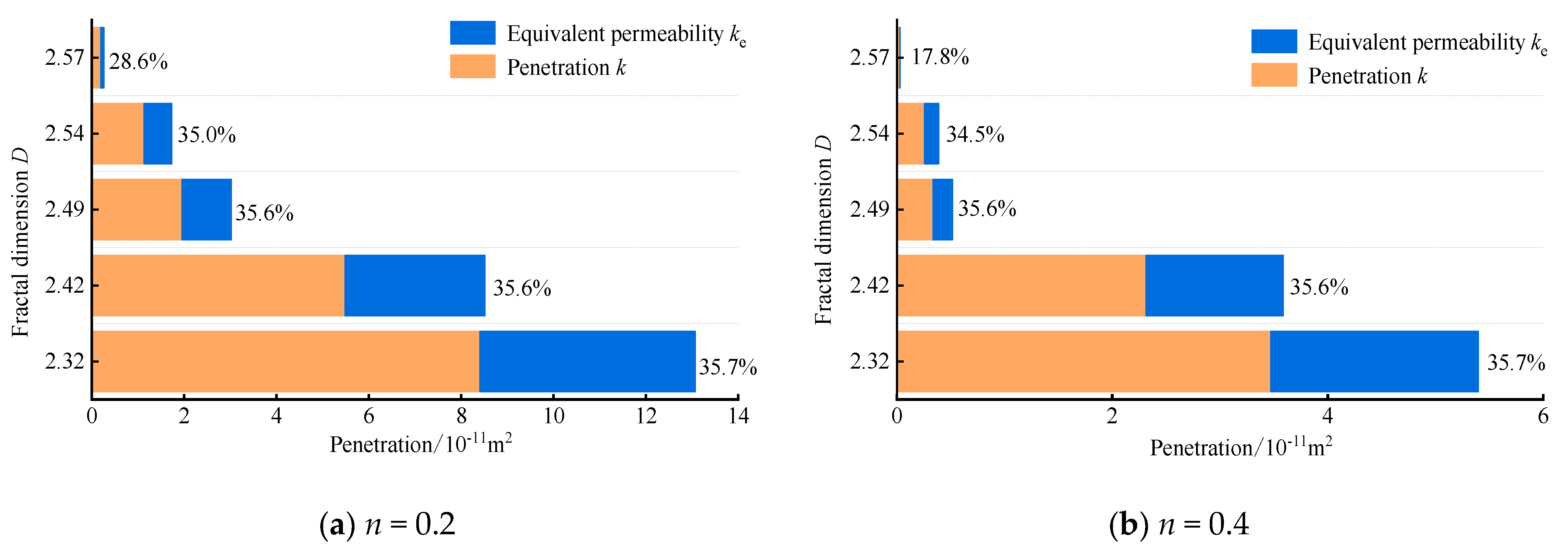
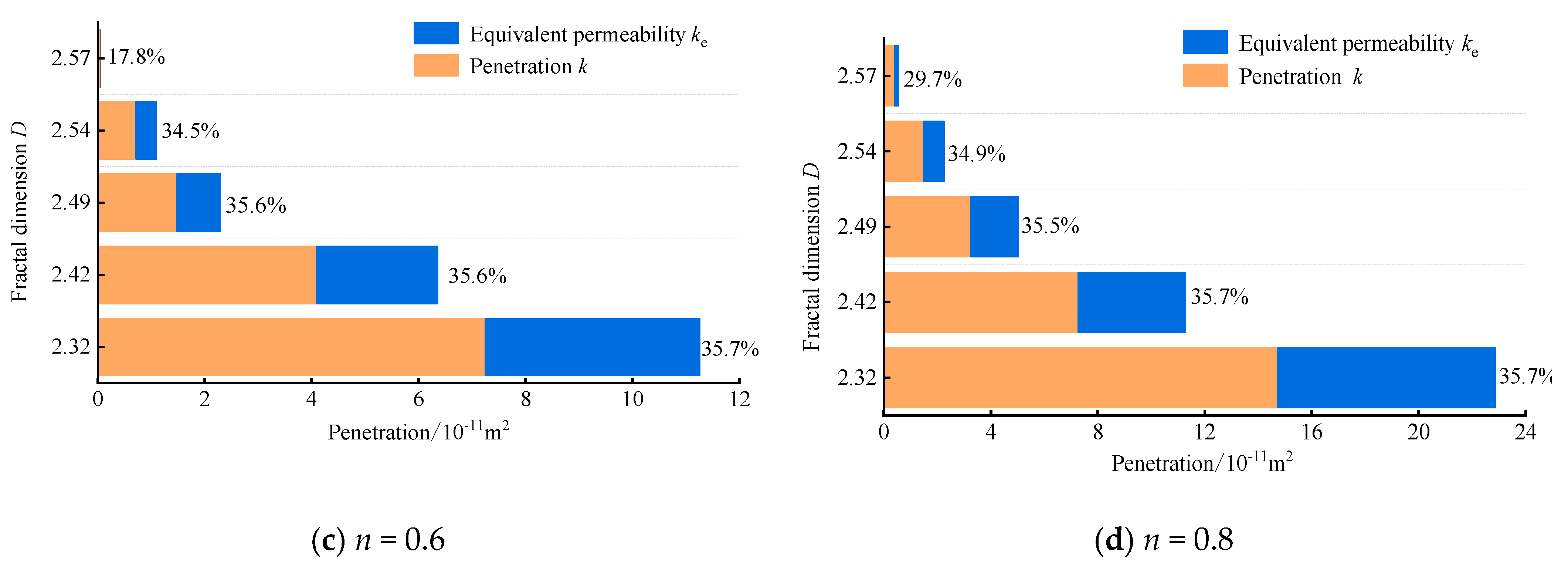
4.4. Equivalent Permeability Mathematical Model for the Crushed Coal Seepage System
4.5. Equivalent Permeability Model Test for the Crushed Coal Seepage System
5. Conclusions
- (1)
- According to the magnitude of the slope of the time-varying curve of the porosity change rate of the specimen, the change process can be divided into two stages: the rapid change stage and the slow change stage. At an axial compression of 5 mm, the porosity of a specimen with grade n = 0.2 increases from an initial value of 0.3924% to 0.5109%, an increase of 11.8%. With the extension of the permeation time, it is found that the permeation system gradually loses all fine particles that can migrate freely, which is of great significance for the study of the stability of the collapse column.
- (2)
- As the axial displacement increases, the axial deformation gradually increases and the porosity and permeability of the crushed specimens decrease, with the minimum porosity reaching 0.298. When the porosity decreases to approximately 0.375, crushed specimens with different initial grades have similar permeability values.
- (3)
- Before the sudden change in percolation, the solid particles in the crushed specimens are lost and the pore structure and permeability change; however, after the sudden change in percolation, with increasing percolation time, the skeleton and filler particles eventually stabilise and the permeability remains constant. The different specific surface area, pore distribution, pore size and the formation of an effective seepage channel of the sample under different particle size ratio also have certain influence on the seepage characteristic parameters of the collapse column structure.
- (4)
- At low porosity, the non-Darcy equivalent permeability ke is slightly smaller than the permeability k. However, the non-Darcy equivalent permeability that was calculated by applying the particle size fractal–percolation model is similar to the permeability obtained from the tests and has the same trend as the porosity, verifying the applicability and accuracy of this mathematical model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Donovan, J.J.; Perry, E.F. Mine Flooding History of a Regional Below-Drainage Coalfield Dominated by Barrier Leakage (1970–2014). Geofluids 2019, 2019, 5703108. [Google Scholar] [CrossRef]
- Li, H.; Bai, H.; Wu, J.; Ma, Z.; Ma, K.; Wu, G.; Du, Y.; He, S. A Cascade Disaster Caused by Geological and Coupled Hydro-Mechanical Factors—Water Inrush Mechanism from Karst Collapse Column under Confining Pressure. Energies 2017, 10, 1938. [Google Scholar] [CrossRef]
- Ma, D.; Cai, X.; Zhou, Z.; Li, X. Experimental Investigation on Hydraulic Properties of Granular Sandstone and Mudstone Mixtures. Geofluids 2018, 2018, 9216578. [Google Scholar] [CrossRef]
- Nomura, S.; Yamamoto, Y.; Sakaguchi, H. Modified expression of Kozeny–Carman equation based on semilog–sigmoid function—ScienceDirect. Soils Found. 2018, 58, 1350–1357. [Google Scholar] [CrossRef]
- Pang, M.; Pan, H.; Ji, B.; Zhang, H.; Zhang, T. Experimental investigation of flow regime transition characteristics of fractured coal bodies around gas extraction boreholes. Energy 2023, 270, 126758. [Google Scholar] [CrossRef]
- Feng, M.; Wu, J.; Ma, D.; Ni, X.; Yu, B.; Chen, Z. Experimental investigation on seepage property of saturated broken red sandstone of continuous gradation. Bull. Eng. Geol. Environ. 2018, 77, 1167–1178. [Google Scholar] [CrossRef]
- Karacan, C.O. Prediction of Porosity and Permeability of Caved Zone in Longwall Gobs. Transp. Porous Media 2010, 82, 413–439. [Google Scholar] [CrossRef]
- Mckee, C.R.; Bumb, A.C.; Koenig, R.A. Stress-dependent permeability and porosity of coal. Spe Form. Eval. 1988, 3, 81–91. [Google Scholar] [CrossRef]
- Li, S.C.; Miao, X.X.; Chen, Z.Q.; Mao, X.B. Experimental study on seepage propagerties of non-Darcy flow in confined broken rocks. Eng. Mech. 2008, 25, 85–92. [Google Scholar]
- El-Zehairy, A.A.; Nezhad, M.M.; Joekar-Niasar, V.; Guymer, I.; Kourra, N.; Williams, M.A. Pore-network modelling of non-Darcy flow through heterogeneous porous media. Adv. Water Resour. 2019, 131, 103378.1–103378.15. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N.; Papaspyros, I.; Tsihrintzis, V.A. Experimental investigation of inertial flow processes in porous media. J. Hydrol. 2009, 374, 242–254. [Google Scholar] [CrossRef]
- Yao, B.H. Research on Variable Mass Fluid-Solid Coupling Dynamic Theory of Broken Rock Mass and Application; China University of Mining and Technology: Xuzhou, China, 2012. [Google Scholar]
- Ma, D.; Duan, H.; Liu, W.; Ma, X.; Tao, M. Water-Sediment Two-Phase flow inrush hazard in rock fractures of overburden strata during coal mining. Mine Water Environ. 2020, 39, 308–319. [Google Scholar] [CrossRef]
- Shi, W.; Yang, T.; Yu, S. Experimental Investigation on Non-Darcy Flow Behavior of Granular Limestone with Different Porosity. J. Hydrol. Eng. 2020, 25, 06020004. [Google Scholar] [CrossRef]
- Sterpi, D. Effects of the Erosion and Transport of Fine Particles due to Seepage Flow. Int. J. Geomech. 2003, 3, 111–122. [Google Scholar] [CrossRef]
- Cividini, A.; Bonomi, S.; Vignati, G.C.; Gioda, G. Seepage-Induced Erosion in Granular Soil and Consequent Settlements. Int. J. Geomech. 2009, 9, 187–194. [Google Scholar] [CrossRef]
- Pang, M.; Zhang, T.; Ji, X.; Wu, J.; Song, S. Measurement of the coefficient of seepage characteristics in pore-crushed coal bodies around gas extraction boreholes. Energy 2022, 254, 124276. [Google Scholar] [CrossRef]
- Kong, H.; Wang, L. Seepage problems on fractured rock accompanying with mass loss during excavation in coal mines with karst collapse columns. Arab. J. Geosci. 2018, 11, 1–13. [Google Scholar] [CrossRef]
- Wu, J.; Han, G.; Feng, M.; Kong, H.; Yu, B.; Wang, L.; Gao, Y. Mass-loss effects on the flow behavior in broken argillaceous red sandstone with different particle-size distributions. Comptes Rendus Mécanique 2019, 347, 504–523. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraef, S.W. Fractal scaling of soil particle size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Lacey, M.; Hollis, C.; Oostrom, M.; Shokri, N. Effects of Pore and Grain Size on Water and Polymer Flooding in Micromodels. Energy & Fuels 2017, 31, 9026–9034. [Google Scholar]
- Yu, B.; Chen, Z.; Ding, Q.; Wang, L. Non-Darcy flow seepage characteristics of saturated broken rocks under compression with lateral constraint. J. Min. Sci. Technol. 2016, 26, 1145–1151. [Google Scholar] [CrossRef]
- Wang, C.X.; Shen, B.T.; Chen, J.T.; Tong, W.X.; Jiang, Z.; Liu, Y.; Li, Y.Y. Compression characteristics of filling gangue and simulation of mining with gangue backfilling: An experimental investigation. Geomech. Eng. 2020, 20, 485–495. [Google Scholar]
- Ostwal, M.; Lau, J.M.; Orme, C.J.; Stewart, F.F.; Way, J.D. The influence of temperature on the sorption and permeability of CO2 in poly(fluoroalkoxyphosphazene) membranes. J. Membr. Sci. 2009, 344, 199–203. [Google Scholar] [CrossRef]
- Cho, S.H.; Colin, F.; Sardin, M.; Prost, C. Settling velocity model of activated sludge. Water Res. 1993, 27, 1237–1242. [Google Scholar] [CrossRef]
- Kozeny, J. Uber kapillare leitung des wassersim Boden Stizurgsberichte. R. Acad. Sci. Vienna Procceedings Cl. I 1927, 136, 271–306. [Google Scholar]
- Quinton, W.L.; Hayashi, M.; Carey, S.K. Peat hydraulic conductivity in cold regions and its relation to pore size and geometry. Hydrol. Process. 2010, 22, 2829–2837. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases through Porous Media; Butterworths Scientific Publications: London, UK, 1956. [Google Scholar]
- Liu, C.H.; Wang, Y.J.; Gao, K.S.; Yuan, Z.G.; Ren, Z.Y. Determination of Particle Size Median Value and Well sand Control. In Proceedings of the National Academic Conference on Particle Testing, Zhangjiajie, China, 17–22 June 2008. (In Chinese). [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publications: New York, NY, USA, 1972. [Google Scholar]
- Barree RD Conway, M.W. Reply to Discussion of “Beyond Beta Factors: A Complete Model for Darcy, Forchheimer, and Trans-Forchheimer Flow in Porous Media. JPT 2005, 48, 73–74. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Kuntjoro Bayuaji, R.; Tatas Khoiri, M. Case study project notes on the hydrodynamic and morphologic effects on hydraulic structure. Eng. Fail. Anal. 2021, 119, 104995. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J. Solid grain migration on hydraulic properties of fault rocks in underground mining tunnel: Radial seepage experiments and verification of permeability prediction. Tunn. Undergr. Space Technol. 2022, 126, 104525. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Jain, A.; Singh, J. Numerical Study of a Non-Linear Porous Sublimation Problem With Temperature- Dependent Thermal Conductivity and Concentration-Dependent Mass Diffusivity. J. Heat Mass Transfer 2023, 145, 072701. [Google Scholar] [CrossRef]

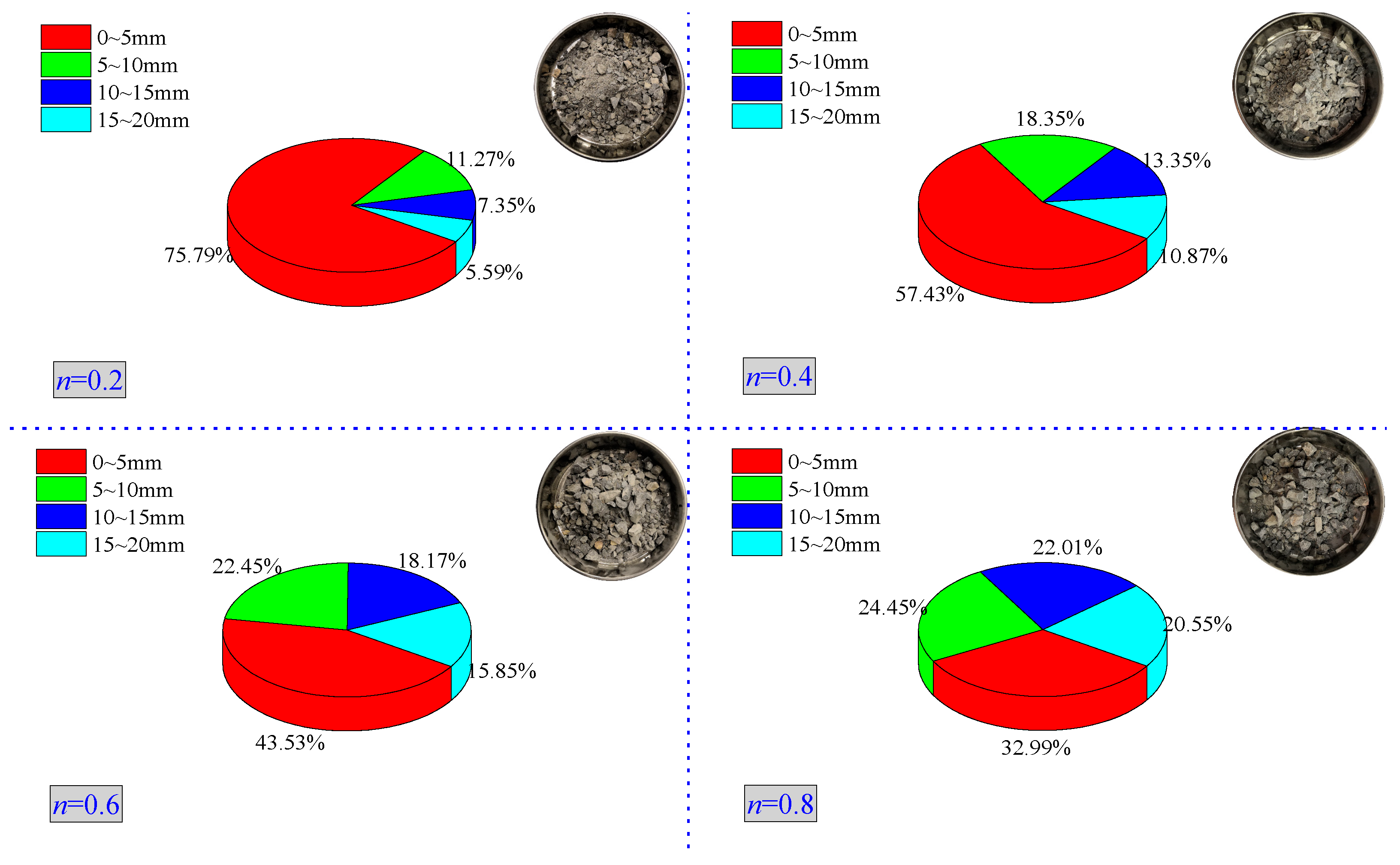




| Grain Size/mm | 0~5 | 5~10 | 10~15 | 15~20 | 20~25 |
| Mass/g | 220.76 | 163.60 | 147.27 | 137.58 | 130.79 |
| Talbot Power Index n | Fractal Dimension D | Permeability k/m2 | Equivalent Permeability ke/m2 |
| n = 0.2 | 2.32 | 8.40 × 10−11 | 4.67 × 10−11 |
| 2.42 | 5.48 × 10−11 | 3.04 × 10−11 | |
| 2.49 | 1.95 × 10−11 | 1.08 × 10−11 | |
| 2.54 | 1.13 × 10−11 | 6.09 × 10−12 | |
| 2.57 | 1.91 × 10−12 | 7.66 × 10−13 | |
| n = 0.4 | 2.22 | 3.47 × 10−11 | 1.93 × 10−11 |
| 2.34 | 2.31 × 10−11 | 1.28 × 10−11 | |
| 2.43 | 3.34 × 10−12 | 1.85 × 10−12 | |
| 2.51 | 2.56 × 10−12 | 1.35 × 10−12 | |
| 2.53 | 2.57 × 10−13 | 5.57 × 10−14 | |
| n = 0.6 | 2.14 | 7.24 × 10−11 | 4.02 × 10−11 |
| 2.34 | 4.09 × 10−11 | 2.27 × 10−11 | |
| 2.44 | 1.48 × 10−11 | 8.17 × 10−12 | |
| 2.50 | 7.14 × 10−12 | 3.82 × 10−12 | |
| 2.52 | 4.59 × 10−13 | 9.93 × 10−15 | |
| n = 0.8 | 2.06 | 1.47 × 10−10 | 8.17 × 10−11 |
| 2.27 | 7.25 × 10−11 | 4.03 × 10−11 | |
| 2.40 | 3.25 × 10−11 | 1.79 × 10−11 | |
| 2.48 | 1.47 × 10−11 | 7.91 × 10−12 | |
| 2.51 | 3.91 × 10−12 | 1.68 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Pang, M.; Guo, Y.; Zhang, L.; Zhang, T.; Pan, H. Experimental Investigation of the Non-Darcy Equivalent Permeability of Fractured Coal Bodies: The Role of Particle Size Distribution. Fractal Fract. 2023, 7, 423. https://doi.org/10.3390/fractalfract7060423
Song S, Pang M, Guo Y, Zhang L, Zhang T, Pan H. Experimental Investigation of the Non-Darcy Equivalent Permeability of Fractured Coal Bodies: The Role of Particle Size Distribution. Fractal and Fractional. 2023; 7(6):423. https://doi.org/10.3390/fractalfract7060423
Chicago/Turabian StyleSong, Shuang, Mingkun Pang, Yi Guo, Lei Zhang, Tianjun Zhang, and Hongyu Pan. 2023. "Experimental Investigation of the Non-Darcy Equivalent Permeability of Fractured Coal Bodies: The Role of Particle Size Distribution" Fractal and Fractional 7, no. 6: 423. https://doi.org/10.3390/fractalfract7060423
APA StyleSong, S., Pang, M., Guo, Y., Zhang, L., Zhang, T., & Pan, H. (2023). Experimental Investigation of the Non-Darcy Equivalent Permeability of Fractured Coal Bodies: The Role of Particle Size Distribution. Fractal and Fractional, 7(6), 423. https://doi.org/10.3390/fractalfract7060423






