A Novel Grey Seasonal Model for Natural Gas Production Forecasting
Abstract
1. Introduction
1.1. Background
1.2. Research Progress in Natural Gas Forecasting
1.3. Application of Grey Season Model in Natural Gas
1.4. Aim, Contribution, and Organization
2. Methodology
2.1. The Traditional FHGM (1,1) Model [33]
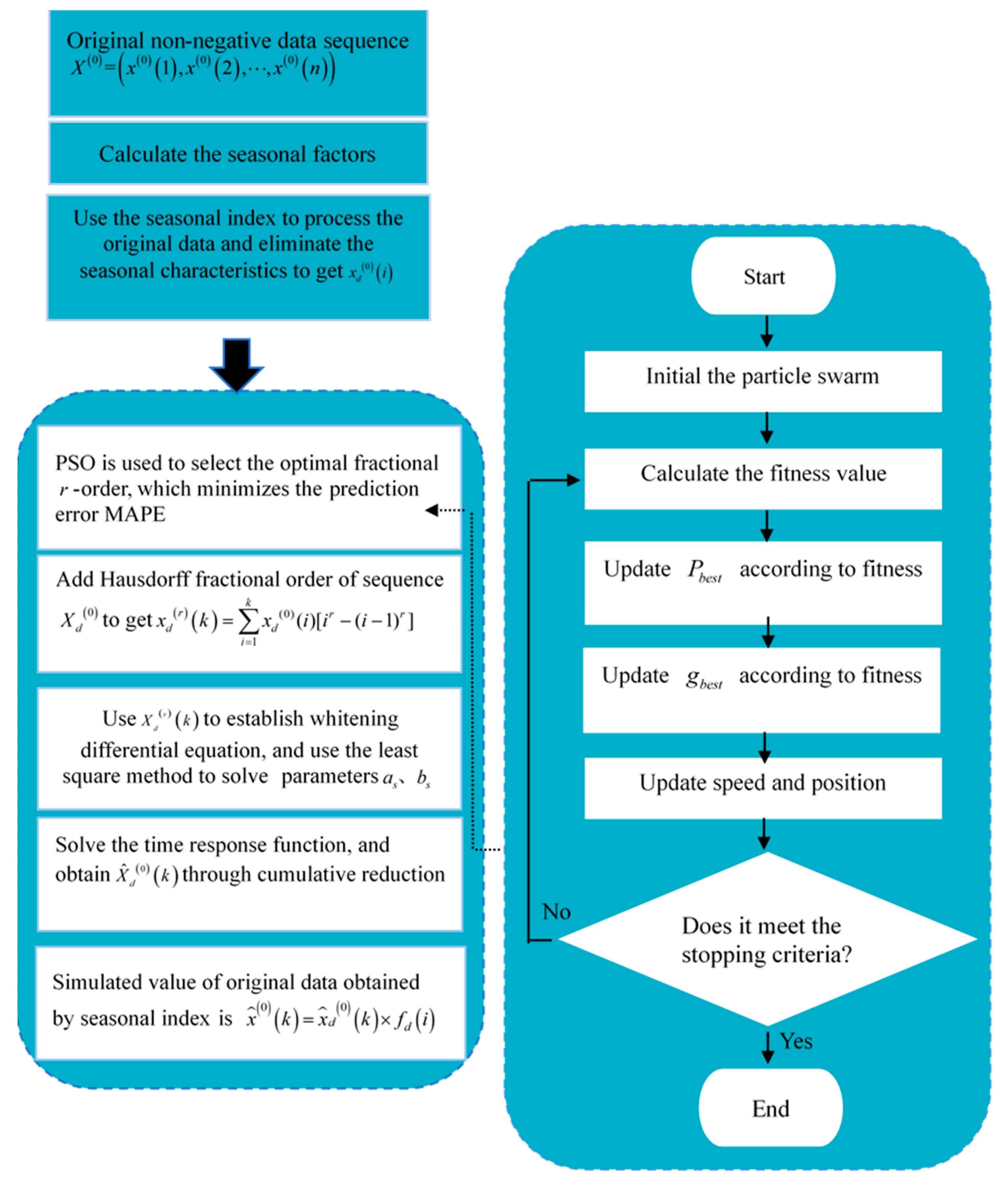
2.2. The SFHGM (1,1) Model
2.3. Model Error Test Criteria
3. Validation of the SFHGM (1,1) Model
3.1. Case 1. Forecasting Quarterly Hydropower Production in China
3.2. Case 2 Forecasting Quarterly Wind Power Production in China
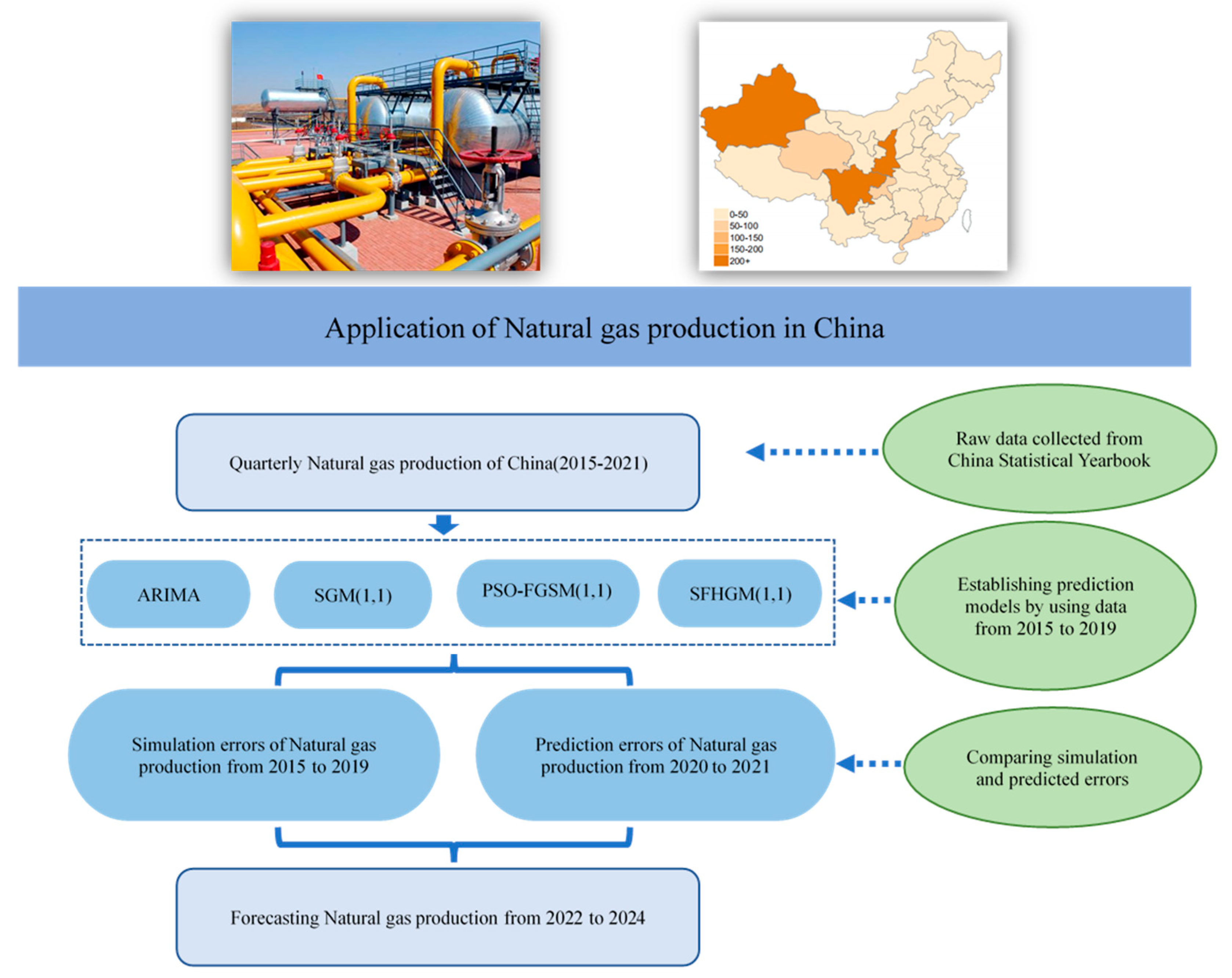
4. Application
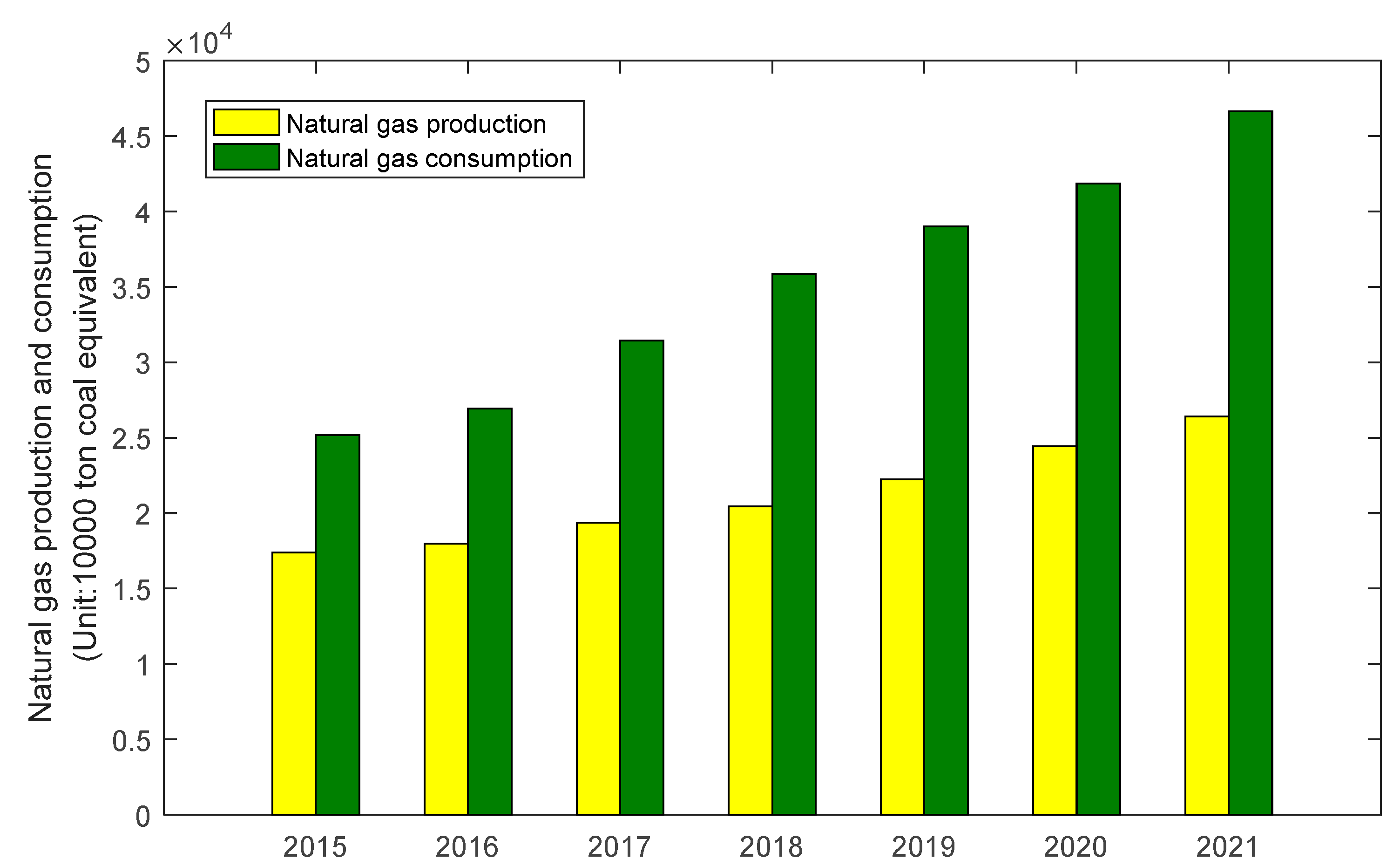
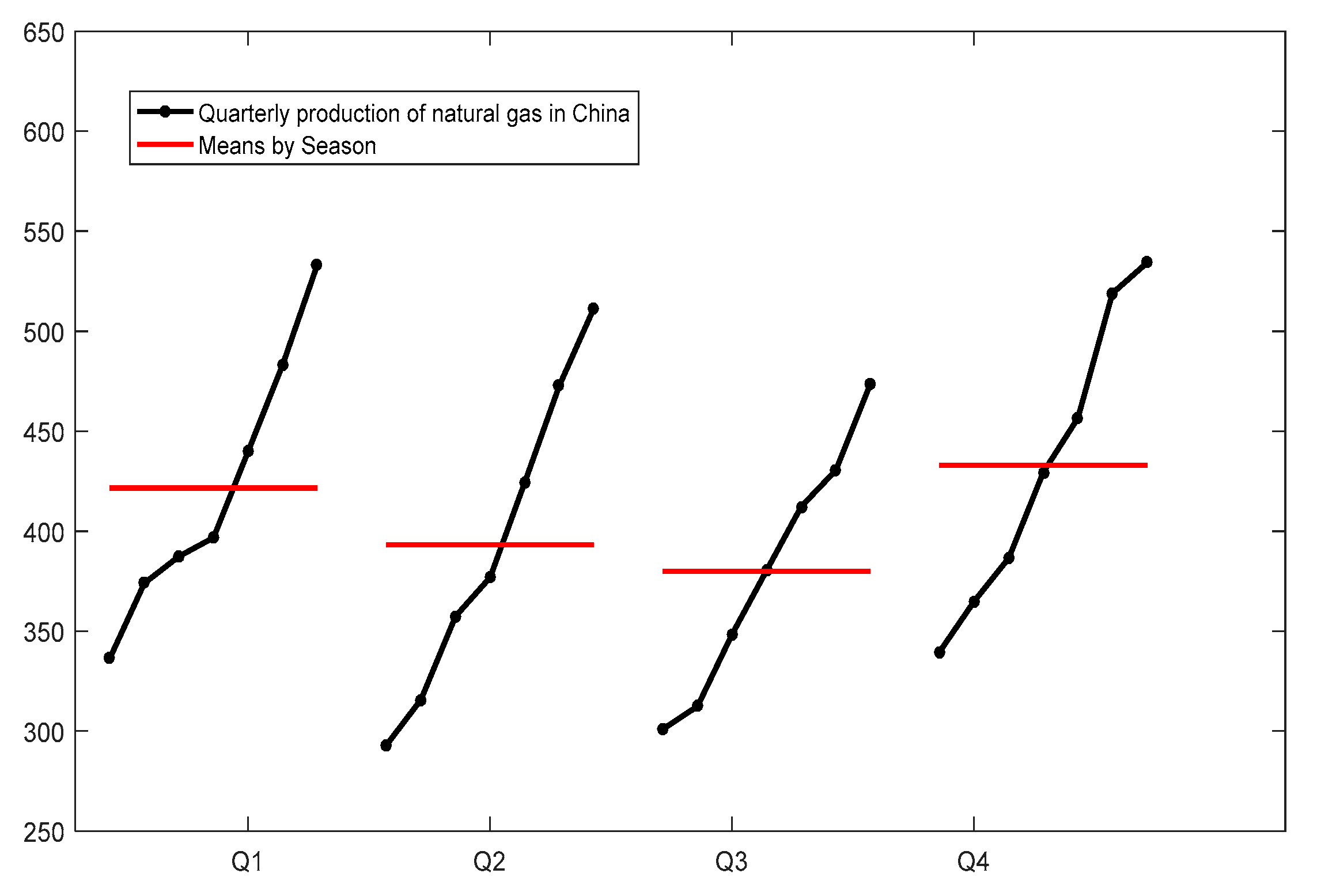
4.1. Data Description
4.2. Model Establishment
4.3. The Solution of SFHGM (1,1) Model
4.4. Model Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bianco, V.; Scarpa, F.; Tagliafico, L.A. Scenario analysis of nonresidential natural gas consumption in Italy. Appl. Energy 2014, 113, 392–403. [Google Scholar] [CrossRef]
- Dilaver, Ö.; Dilaver, Z.; Hunt, L.C. What drives natural gas consumption in Europe. Analysis and projections. J. Nat. Gas Sci. Eng. 2014, 19, 125–136. [Google Scholar] [CrossRef]
- Liu, C.; Lao, T.; Wu, W.Z.; Xie, W.; Zhu, H. An optimized nonlinear grey Bernoulli prediction model and its application in natural gas production. Expert Syst. Appl. 2022, 194, 116448. [Google Scholar] [CrossRef]
- Xiong, P.P.; Li, K.L.; Shu, H.; Wang, J. Forecast of Natural Gas Consumption in the Asia-Pacific Region Using a Fractional-Order Incomplete Gamma Grey Model. Energy 2021, 237, 121533. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, J.M. Trend prediction of natural gas consumption in different regions of China. Nat. Gas Ind. 2016, 36, 135–140. [Google Scholar]
- Zeng, B.; Duan, H.M.; Bai, Y.; Meng, W. Forecasting the output of shale gas in China using an unbiased grey model and weakening buffer operator. Energy 2018, 151, 238–249. [Google Scholar] [CrossRef]
- Li, H.X.; Wang, H.J. China’s Natural Gas Demand Forecast Based on the Improved Gray Model. Henan Sci. 2014, 32, 872–876. [Google Scholar]
- Ma, X.; Liu, Z.B. Application of a novel time-delayed polynomial grey model to predict the natural gas consumption in China. J. Comput. Appl. Math. 2017, 324, 17–24. [Google Scholar] [CrossRef]
- Zheng, C.L.; Wu, W.Z.; Xie, W.; Li, Q. A MFO-based conformable fractional nonhomogeneous grey Bernoulli model for natural gas production and consumption forecasting. Appl. Soft Comput. 2021, 99, 106891. [Google Scholar] [CrossRef]
- Ye, Z.H.; Chen, E.L. Study on the Prediction of Natural Gas Consumption Based on Residual Grey Model. J. Chongqing Univ. Technol. 2018, 32, 99–102. [Google Scholar]
- Liu, X.L.; Moreno, B.; García, A.S. A grey neural network and input-output combined forecasting model. Primary energy consumption forecasts in Spanish economic sectors. Energy 2016, 115, 1042–1054. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q.; Shaikh, P.H.; Mirjat, N.H.; Uqaili, M.A. Forecasting China’s natural gas demand based on optimized nonlinear grey models. Energy 2017, 140, 941–951. [Google Scholar] [CrossRef]
- Wu, Y.H.; Shen, H. Grey-related least squares support vector machine optimization model and its application in predicting natural gas consumption demand. J. Comput. Appl. Math. 2018, 338, 212–220. [Google Scholar] [CrossRef]
- Ding, S. A novel self-adapting intelligent grey model for forecasting China’s natural-gas demand. Energy 2018, 162, 393–407. [Google Scholar] [CrossRef]
- Ark, O.A. Artificial bee colony algorithm to forecast natural gas consumption of Turkey. SN Appl. Sci. 2019, 1, 1138. [Google Scholar] [CrossRef]
- Qiao, W.B.; Yang, Z.; Kang, Z.Y.; Pan, Z. Short-term natural gas consumption prediction based on Volterra adaptive filter and improved whale optimization algorithm. Eng. Appl. Artif. Intell. 2020, 87, 103323. [Google Scholar] [CrossRef]
- Wu, L.F.; Li, N.; Zhao, T. Using the seasonal FGM(1,1) model to predict the air quality indicators in Xingtai and Handan. Environ. Sci. Pollut. Res. 2019, 26, 14683–14688. [Google Scholar] [CrossRef]
- Yang, F. Extended Research and Application of Discrete Grey Prediction Model. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2014. [Google Scholar]
- Wang, Z.X.; Li, Q.; Pei, L.L. Grey forecasting method of quarterly hydropower production in China based on a data grouping approach. Appl. Math. Model. 2017, 51, 302–316. [Google Scholar] [CrossRef]
- Wei, Y.; Kong, X.H. Constructing methods of several kinds of strengthening and weakening buffer operators and their inner link. Control Decis. 2010, 25, 196–202. [Google Scholar]
- Sun, Y.J.; Li, G.; Cheng, C.T.; Cai, H.Q.; Tu, Q.Y. Combined with a two-stage Markov chain with weight and Grey forecasting model of small hydropower generation capacity forecasting methods. Sci. China 2015, 45, 1279–1288. [Google Scholar]
- Wang, J.Z.; Ma, X.L.; Wu, J.; Dong, Y. Optimization models based on GM (1, 1) and seasonal fluctuation for electricity demand forecasting. Electr. Power Energy Syst. 2012, 43, 109–117. [Google Scholar] [CrossRef]
- Zeng, B.; Meng, W. Interval prediction modeling method of small sample oscillation sequence based on Grey Theory. Control Decis. 2016, 31, 1311–1316. [Google Scholar]
- Zhang, W.Z.; Li, Y.Y. Application of the Improved Grey Model in the Monthly Electricity Consumption Forecasting. Sci. Discov. 2016, 4, 1–5. [Google Scholar]
- Wang, Z.X. Oscillating GM(1,1) power model and its application. Control Decis. 2013, 28, 1459–1464. [Google Scholar]
- Wang, Z.X. Grey prediction method of small sample oscillation sequence based on Fourier series. Control Decis. 2014, 29, 270–274. [Google Scholar]
- Zeng, L. Grey GM(1,1|sin) power model based on oscillation sequences and its application. J. Zhejiang Univ. 2019, 6, 697–704. [Google Scholar]
- Wu, Y.; Wang, J. Integrated Optimum Gray Support Vector Machine Model for the Seasonal Power Load Forecasting. East China Electr. Power 2012, 40, 0018–0021. [Google Scholar]
- Li, S.; Liu, B. Application of grey seasonal variation index model GSVI (1,1) in rural power consumption prediction. China Power 2006, 6, 15–18. [Google Scholar]
- Zhang, K.; Wu, L.F. Using Fractional Order Grey Seasonal Model to Predict the Power Generation in China. Environ. Process. 2020, 8, 413–427. [Google Scholar] [CrossRef]
- Dong, W.; Zhao, C. Stock price forecasting based on Hausdorff fractional grey model with convolution and neural network. Math. Biosci. Eng. 2021, 18, 3323–3347. [Google Scholar] [CrossRef]
- Shi, K.H.; Wu, L.F. Modelling the relationship between population density and air quality using fractional Hausdorff grey multivariate model. Kybernetes Int. J. Syst. Cybern. 2021, 50, 3129–3150. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, L.F.; Liu, L.Y.; Zhang, K. Fractional Hausdorff grey model and its properties. Chaos Solitons Fractals 2020, 138, 109915. [Google Scholar] [CrossRef]
- Xi, J.G. Research on step size relationship of two moving average in quadratic moving average method. J. Quant. Tech. Econ. 2019, 36, 152–168. [Google Scholar]
- Wang, Z.X.; Li, Q.; Pei, L.L. A seasonal GM(1,1) model for forecasting the electricity consumption of the primary economic sectors. Energy 2018, 154, 522–534. [Google Scholar] [CrossRef]
- Zhou, W.; Ding, S. A novel discrete grey seasonal model and its applications. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105493. [Google Scholar] [CrossRef]





| MAPE (%) | Forecasting Ability | MAPE (%) | Forecasting Ability |
|---|---|---|---|
| <10 | Excellent | 20–50 | Reasonable |
| 10–20 | Good | >50 | Inaccurate |
| Time | Actual Value | SARIMA | DGGM (1,1) [19] | SGM (1,1) [35] | SFHGM (1,1) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | ||
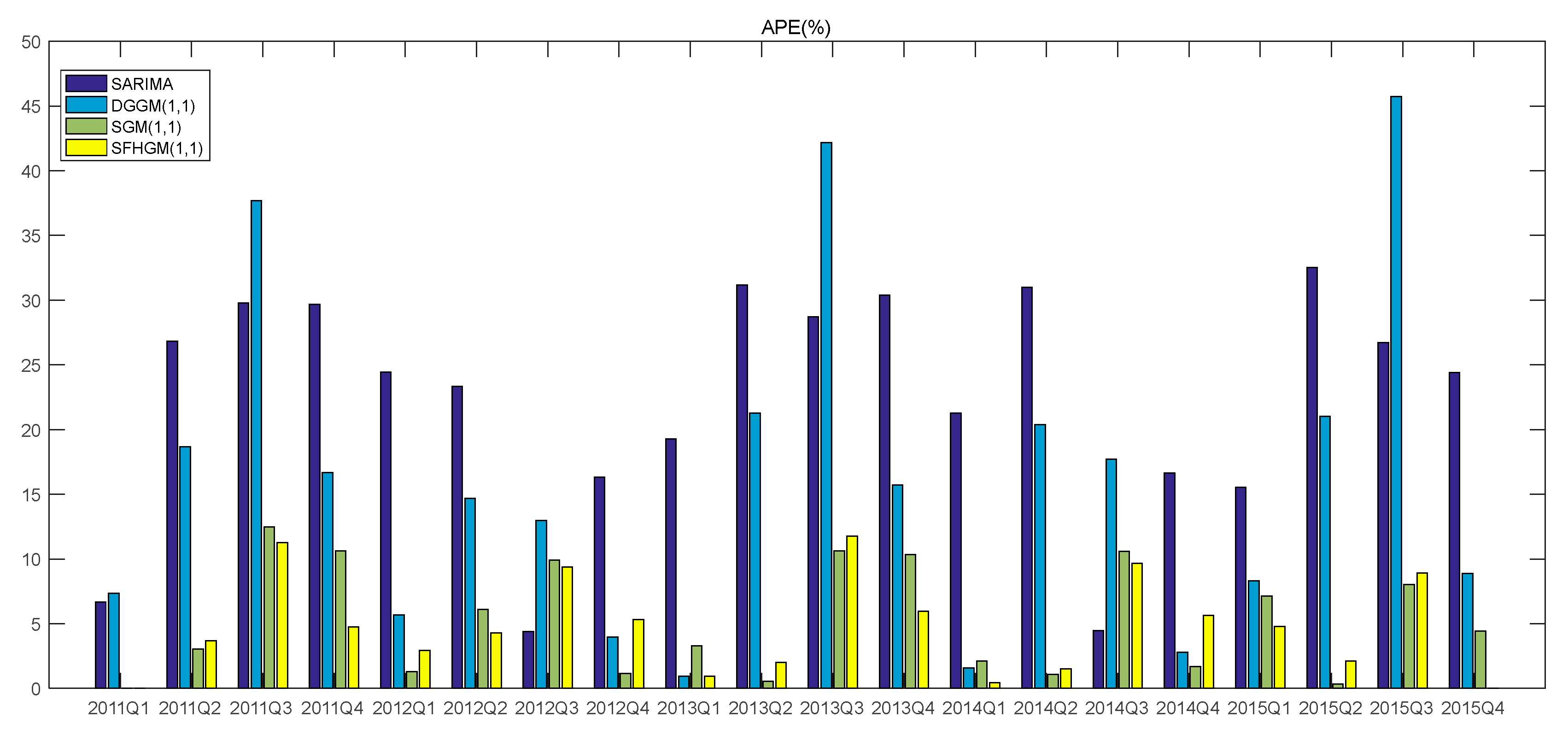
| 2011Q1 | 113.54 | 121.10 | 6.66 | 105.19 | 7.35 | 113.54 | 0.00 | 113.54 | 0.00 |
| 2011Q2 | 159.65 | 202.48 | 26.83 | 189.49 | 18.69 | 154.79 | 3.04 | 153.78 | 3.68 |
| 2011Q3 | 192.29 | 249.57 | 29.79 | 264.75 | 37.68 | 216.28 | 12.48 | 213.97 | 11.27 |
| 2011Q4 | 143.68 | 186.31 | 29.67 | 167.65 | 16.68 | 158.97 | 10.64 | 150.50 | 4.75 |
| 2012Q1 | 110.03 | 136.93 | 24.45 | 116.28 | 5.68 | 111.45 | 1.29 | 113.24 | 2.92 |
| 2012Q2 | 185.66 | 228.95 | 23.32 | 212.96 | 14.70 | 174.34 | 6.10 | 177.70 | 4.29 |
| 2012Q3 | 270.35 | 282.19 | 4.38 | 305.45 | 12.98 | 243.55 | 9.91 | 244.98 | 9.38 |
| 2012Q4 | 181.09 | 210.66 | 16.33 | 188.26 | 3.96 | 179.01 | 1.15 | 171.44 | 5.33 |
| 2013Q1 | 129.79 | 154.83 | 19.29 | 128.55 | 0.96 | 125.50 | 3.31 | 128.57 | 0.94 |
| 2013Q2 | 197.35 | 258.88 | 31.18 | 239.33 | 21.27 | 196.28 | 0.54 | 201.29 | 2.00 |
| 2013Q3 | 247.88 | 319.08 | 28.72 | 352.40 | 42.17 | 274.25 | 10.64 | 277.02 | 11.76 |
| 2013Q4 | 182.68 | 238.19 | 30.39 | 211.40 | 15.72 | 201.59 | 10.35 | 193.60 | 5.98 |
| 2014Q1 | 144.37 | 175.07 | 21.26 | 142.11 | 1.57 | 141.33 | 2.11 | 145.03 | 0.46 |
| 2014Q2 | 223.43 | 292.72 | 31.01 | 268.97 | 20.38 | 221.03 | 1.07 | 226.85 | 1.53 |
| 2014Q3 | 345.40 | 360.78 | 4.45 | 406.57 | 17.71 | 308.84 | 10.58 | 311.97 | 9.68 |
| 2014Q4 | 230.92 | 269.33 | 16.63 | 237.38 | 2.80 | 227.01 | 1.69 | 217.89 | 5.64 |
| 2015Q1 | 171.34 | 197.95 | 15.53 | 157.1 | 8.31 | 159.14 | 7.12 | 163.14 | 4.79 |
| 2015Q2 | 249.75 | 330.98 | 32.52 | 302.29 | 21.04 | 248.90 | 0.34 | 255.06 | 2.13 |
| 2015Q3 | 321.90 | 407.94 | 26.73 | 469.07 | 45.72 | 347.77 | 8.04 | 350.61 | 8.92 |
| 2015Q4 | 244.79 | 304.53 | 24.40 | 266.57 | 8.90 | 255.64 | 4.43 | 244.79 | 0.00 |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| SARIMA | 44.13 | 50.70 | 22.2 |
| DGGM (1,1) | 36.90 | 52.94 | 16.2 |
| SGM (1,1) | 11.60 | 16.32 | 5.2 |
| SFHGM (1,1) | 10.93 | 15.51 | 4.8 |
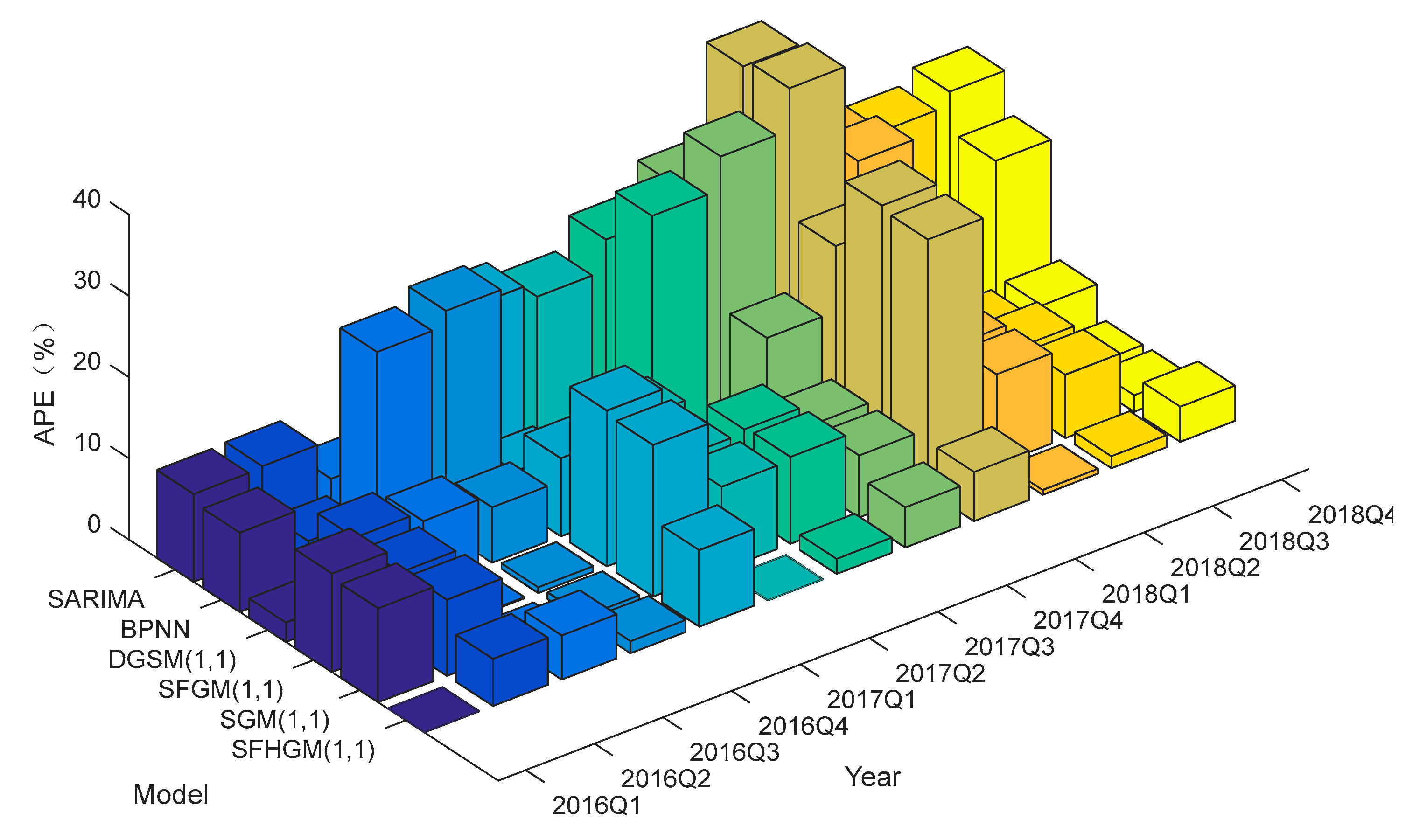
| Time | Actual Value | SARIMA | BPNN | DGSM (1,1) | SFGM (1,1) | SGM (1,1) | SFHGM (1,1) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | ||
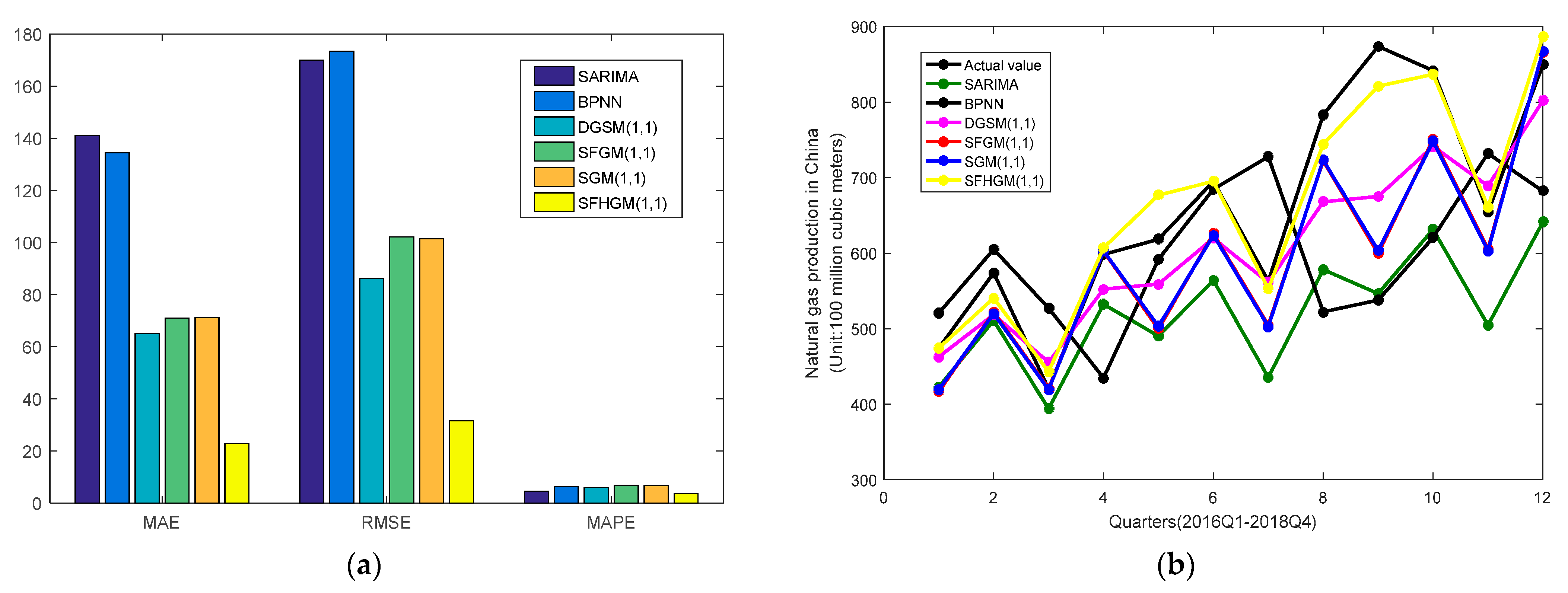
| 2016Q1 | 474.20 | 422.98 | 10.80 | 520.49 | 9.76 | 462.76 | 2.41 | 416.62 | 12.14 | 419.39 | 11.56 | 474.20 | 0.00 |
| 2016Q2 | 573.80 | 510.82 | 10.98 | 605.19 | 5.47 | 518.69 | 9.60 | 521.85 | 9.05 | 520.02 | 9.37 | 540.56 | 5.79 |
| 2016Q3 | 420.20 | 394.23 | 6.18 | 527.31 | 25.49 | 455.46 | 8.39 | 420.73 | 0.13 | 419.22 | 0.23 | 443.04 | 5.44 |
| 2016Q4 | 598.10 | 532.45 | 10.98 | 434.82 | 27.30 | 552.30 | 6.83 | 602.27 | 0.70 | 602.98 | 0.82 | 606.96 | 1.48 |
| 2017Q1 | 618.40 | 490.27 | 20.72 | 591.89 | 4.29 | 558.97 | 9.61 | 499.71 | 19.19 | 503.02 | 18.66 | 676.74 | 9.43 |
| 2017Q2 | 695.00 | 564.01 | 18.85 | 684.76 | 1.47 | 619.54 | 10.86 | 625.92 | 9.94 | 623.73 | 10.26 | 695.00 | 0.00 |
| 2017Q3 | 563.00 | 435.63 | 22.62 | 727.56 | 29.23 | 561.17 | 0.32 | 504.63 | 10.37 | 502.83 | 10.69 | 552.53 | 1.86 |
| 2017Q4 | 783.00 | 578.33 | 26.14 | 522.23 | 33.30 | 668.04 | 14.68 | 722.38 | 7.74 | 723.23 | 7.63 | 744.36 | 4.94 |
| 2018Q1 | 873.80 | 546.54 | 37.45 | 537.86 | 38.45 | 675.13 | 22.74 | 599.36 | 31.41 | 603.34 | 30.95 | 820.97 | 6.05 |
| 2018Q2 | 841.60 | 631.45 | 24.97 | 620.73 | 26.24 | 741.31 | 11.92 | 750.74 | 10.80 | 748.12 | 11.11 | 836.67 | 0.59 |
| 2018Q3 | 654.3 | 504.50 | 22.90 | 731.90 | 11.86 | 688.81 | 5.27 | 605.27 | 7.49 | 603.11 | 7.82 | 661.35 | 1.48 |
| 2018Q4 | 850.10 | 641.30 | 24.56 | 682.10 | 19.76 | 801.84 | 5.68 | 866.44 | 1.92 | 867.47 | 2.04 | 886.97 | 4.34 |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| SARIMA | 141.08 | 170.01 | 4.56 |
| BPNN | 134.38 | 173.44 | 6.42 |
| DGSM (1,1) | 65.09 | 86.27 | 6.02 |
| SFGM (1,1) | 70.97 | 102.20 | 6.83 |
| SGM (1,1) | 71.13 | 101.49 | 6.76 |
| SFHGM (1,1) | 22.84 | 31.53 | 3.73 |
| Quarter | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| Seasonal index | 1.113464 | 1.002941 | 0.969268 | 1.073026 |
| The Correlation Coefficient | The Development Coefficient | Grey Action | The Initial Value |
|---|---|---|---|
| Value | −0.0165 | 274.8715 | 302.12 |
| Time | Actual Value | ARIMA | SGM (1,1) | PSO-FGSM (1,1) | SFHGM (1,1) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | Forecasted Value | APE | ||
| Training stage | |||||||||
| 2015Q1 | 336.4 | 304.3 | 9.54 | 336.4 | 0.00 | 336.4 | 0.00 | 336.4 | 0.00 |
| 2015Q2 | 293.0 | 311.7 | 6.38 | 297.4 | 1.50 | 292.0 | 0.34 | 294.6 | 0.55 |
| 2015Q3 | 301.0 | 290.8 | 3.39 | 301.0 | 0.00 | 293.1 | 2.62 | 293.8 | 2.39 |
| 2015Q4 | 339.7 | 340.7 | 0.29 | 345.9 | 1.83 | 338.4 | 0.38 | 333.8 | 1.74 |
| 2016Q1 | 374.0 | 347.6 | 7.06 | 345.0 | 7.75 | 340.7 | 8.90 | 354.7 | 5.16 |
| 2016Q2 | 315.7 | 328.5 | 4.05 | 321.3 | 1.77 | 320.2 | 1.43 | 326.7 | 3.48 |
| 2016Q3 | 312.4 | 311.1 | 0.42 | 325.2 | 4.10 | 326.8 | 4.61 | 322.5 | 3.23 |
| 2016Q4 | 364.9 | 373.2 | 2.27 | 373.7 | 2.41 | 377.9 | 3.56 | 364.5 | 0.11 |
| 2017Q1 | 387.4 | 390.1 | 0.70 | 372.6 | 3.82 | 378.7 | 2.25 | 385.9 | 0.39 |
| 2017Q2 | 357.4 | 359.0 | 0.45 | 347.1 | 2.88 | 353.9 | 0.98 | 354.5 | 0.81 |
| 2017Q3 | 348.4 | 352.2 | 1.09 | 351.3 | 0.83 | 358.6 | 2.93 | 349.3 | 0.26 |
| 2017Q4 | 386.5 | 390.3 | 0.98 | 403.6 | 4.42 | 411.9 | 6.57 | 394.2 | 1.99 |
| 2018Q1 | 396.7 | 411.6 | 3.76 | 402.6 | 1.49 | 410.1 | 3.38 | 416.8 | 5.07 |
| 2018Q2 | 376.9 | 392.5 | 4.14 | 375.0 | 0.50 | 380.8 | 1.03 | 382.5 | 1.49 |
| 2018Q3 | 380.4 | 396.3 | 4.18 | 379.6 | 0.21 | 383.7 | 0.87 | 376.6 | 1.00 |
| 2018Q4 | 429.4 | 426.0 | 0.79 | 436.0 | 1.54 | 438.3 | 2.07 | 424.7 | 1.09 |
| 2019Q1 | 439.8 | 437.0 | 0.64 | 434.9 | 1.11 | 434.3 | 1.25 | 448.8 | 2.05 |
| 2019Q2 | 424.2 | 408.6 | 3.68 | 405.1 | 4.50 | 401.4 | 5.37 | 411.7 | 2.95 |
| 2019Q3 | 412.3 | 412.4 | 0.02 | 409.8 | 0.61 | 402.8 | 2.30 | 405.1 | 1.75 |
| 2019Q4 | 456.6 | 438.2 | 4.03 | 470.3 | 3.00 | 458.2 | 0.35 | 456.6 | 0.00 |
| Verification stage | |||||||||
| 2020Q1 | 483.2 | 462.1 | 4.37 | 469.9 | 2.75 | 452.4 | 6.37 | 482.4 | 0.17 |
| 2020Q2 | 472.7 | 437.6 | 7.43 | 437.6 | 7.43 | 416.7 | 11.85 | 442.3 | 6.43 |
| 2020Q3 | 430.4 | 445.3 | 3.46 | 443.0 | 2.93 | 416.8 | 3.16 | 435.2 | 1.12 |
| 2020Q4 | 518.9 | 479.1 | 7.67 | 508.9 | 1.93 | 472.9 | 8.86 | 490.4 | 5.49 |
| 2021Q1 | 533.1 | 486.2 | 8.80 | 507.7 | 4.76 | 465.6 | 12.66 | 517.9 | 2.85 |
| 2021Q2 | 511.5 | 470.6 | 8.00 | 472.8 | 7.57 | 427.9 | 16.34 | 474.8 | 7.17 |
| 2021Q3 | 473.7 | 477.2 | 0.74 | 478.6 | 1.03 | 426.9 | 9.88 | 467.0 | 1.41 |
| 2021Q4 | 534.3 | 503.4 | 5.78 | 549.8 | 2.90 | 483.5 | 9.51 | 526.2 | 1.52 |
| Year | 2022 | 2023 | 2024 | |
|---|---|---|---|---|
| Quarter | ||||
| Q1 | 555.7 | 595.8 | 638.6 | |
| Q2 | 509.3 | 546.1 | 585.2 | |
| Q3 | 500.9 | 537 | 575.4 | |
| Q4 | 564.3 | 604.8 | 648.1 | |
| Model | MAE | RMSE | MAPE (%) |
|---|---|---|---|
| ARIMA | 10.47 | 12.02 | 2.89 |
| SGM (1,1) | 8.37 | 11.39 | 0.07 |
| PSO-FGSM (1,1) | 9.61 | 13.25 | 0.12 |
| SFHGM (1,1) | 6.57 | 8.93 | 0.04 |
| Model | MAE | RMSE | MAPE(%) |
|---|---|---|---|
| ARIMA | 29.14 | 32.25 | 5.78 |
| SGM (1,1) | 19.44 | 23.60 | 3.91 |
| PSO-FGSM (1,1) | 49.39 | 55.75 | 9.83 |
| SFHGM (1,1) | 16.4 | 22.19 | 3.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, H.; Li, S.; Dong, R. A Novel Grey Seasonal Model for Natural Gas Production Forecasting. Fractal Fract. 2023, 7, 422. https://doi.org/10.3390/fractalfract7060422
Chen Y, Wang H, Li S, Dong R. A Novel Grey Seasonal Model for Natural Gas Production Forecasting. Fractal and Fractional. 2023; 7(6):422. https://doi.org/10.3390/fractalfract7060422
Chicago/Turabian StyleChen, Yuzhen, Hui Wang, Suzhen Li, and Rui Dong. 2023. "A Novel Grey Seasonal Model for Natural Gas Production Forecasting" Fractal and Fractional 7, no. 6: 422. https://doi.org/10.3390/fractalfract7060422
APA StyleChen, Y., Wang, H., Li, S., & Dong, R. (2023). A Novel Grey Seasonal Model for Natural Gas Production Forecasting. Fractal and Fractional, 7(6), 422. https://doi.org/10.3390/fractalfract7060422





