Qualitative and Quantitative Analysis of Fractional Dynamics of Infectious Diseases with Control Measures
Abstract
1. Introduction
2. Theory of Fractional Calculus
3. Evaluation of the Model
Model Analysis
4. Existence Theory
- (A1) Constants , and are considered such that(A2) Constants , and , are assumed in a way thatIn this case, we define a map T on X as follows:
- S1: We shall demonstrate the continuity of T in the first step. For this, we assume that is continuous for , which also means that is continuous. Here, take , in a way that . Further, take the following:
- This implies that the operator T is continuous, because is true as long as is continuous.
- S2: The boundedness of the operator T will be investigated in the second step. If we select any , then, we have
- S3: In the third stage, we select that to demonstrate the equi-continuity, and that , otherwise, the following:
- S4: In the final step of the theorem, we take the following:
5. Ulam–Hyers Stability
- (1) and ,
- (2)
- (a) , in which ,
- (b)
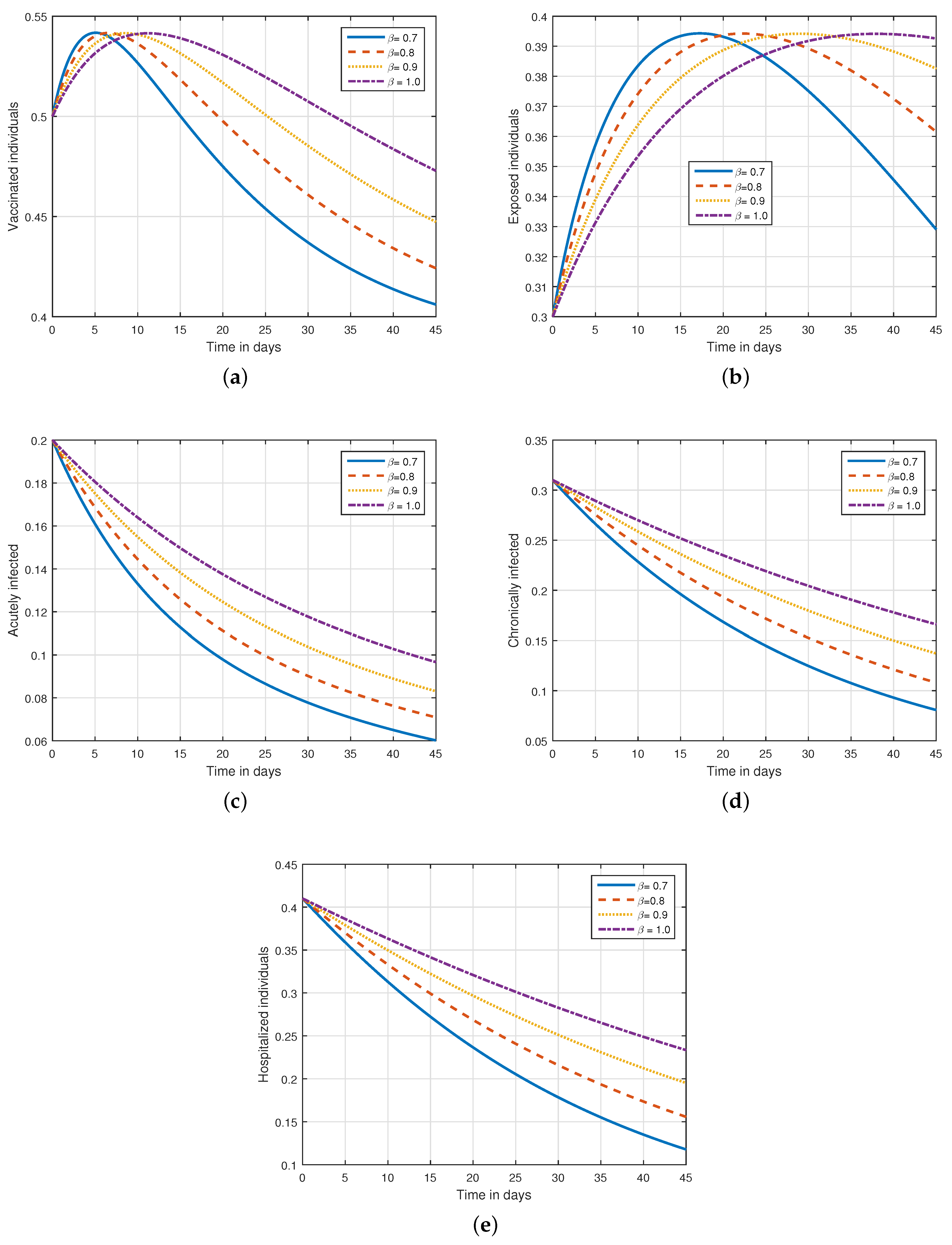
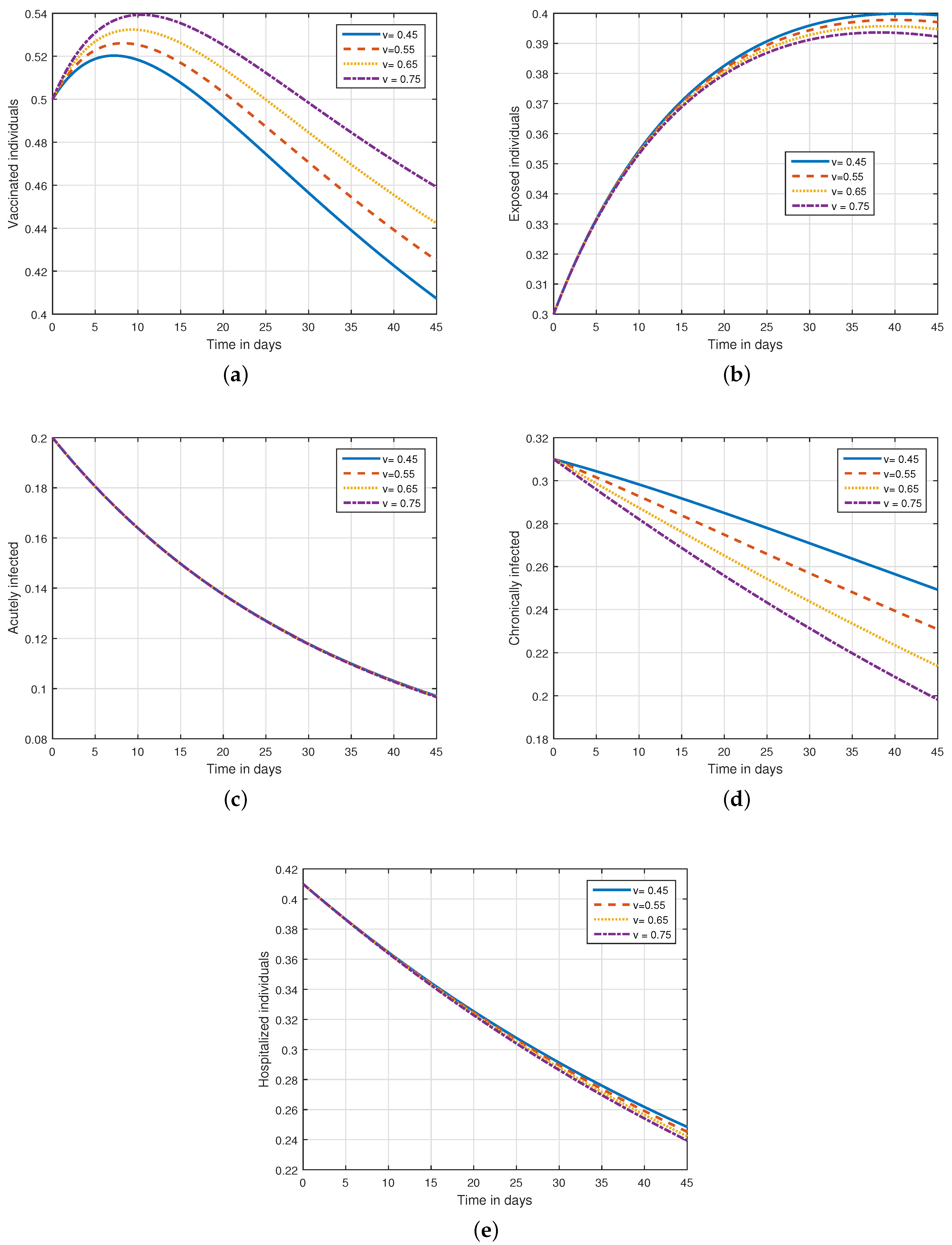
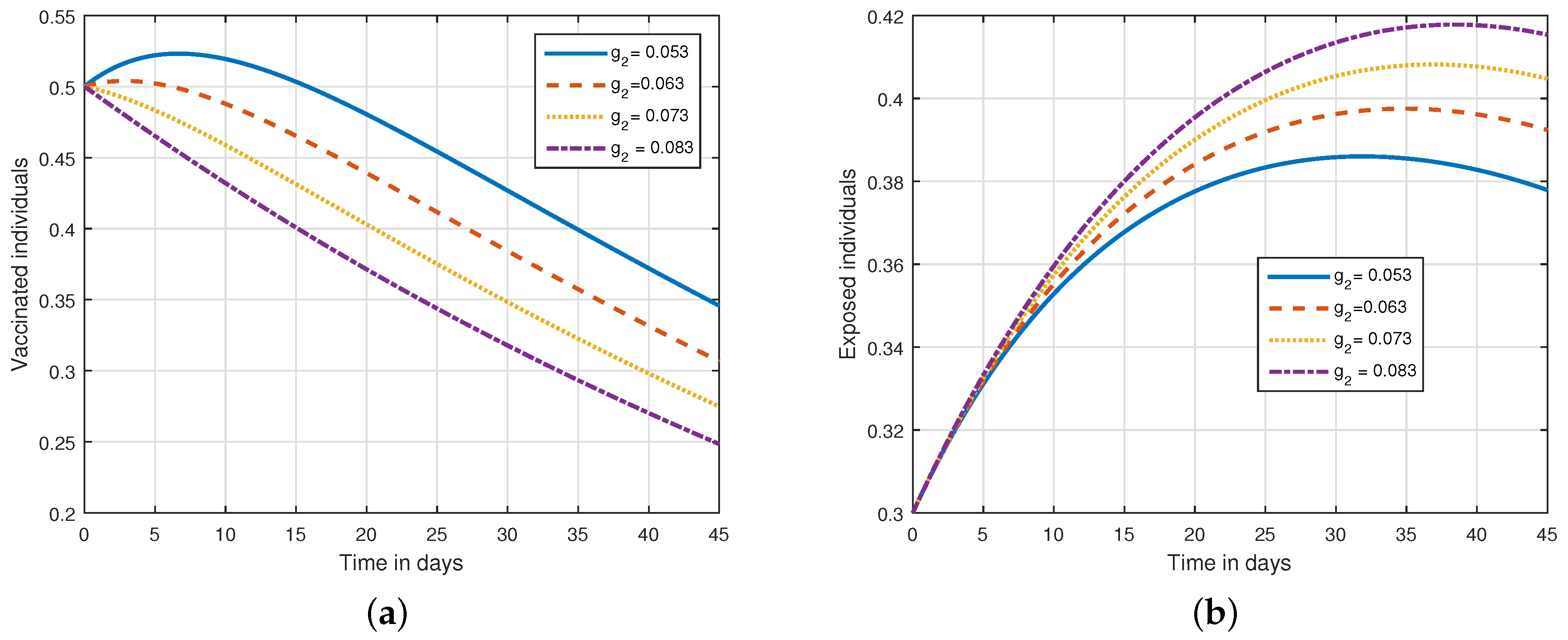
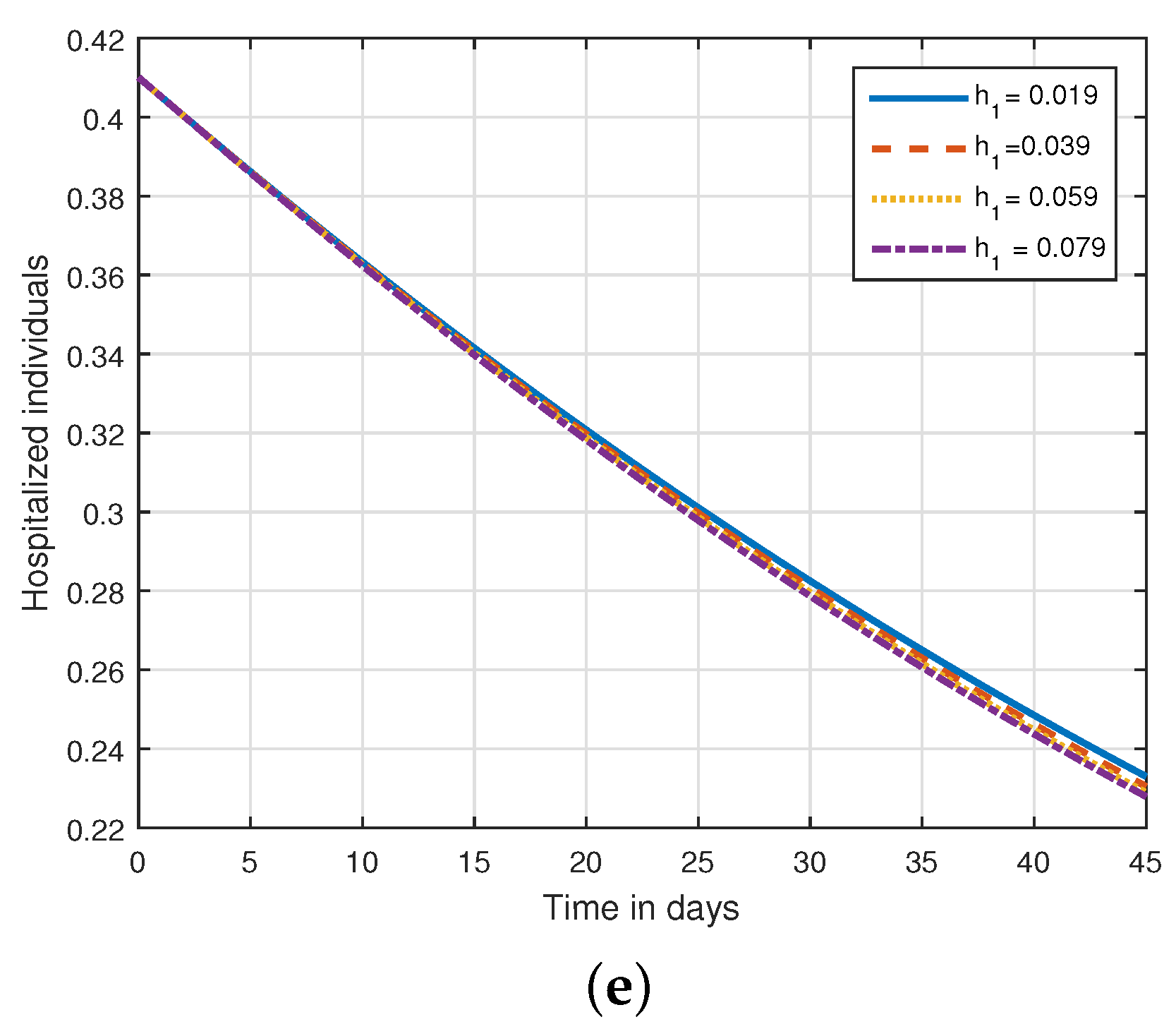
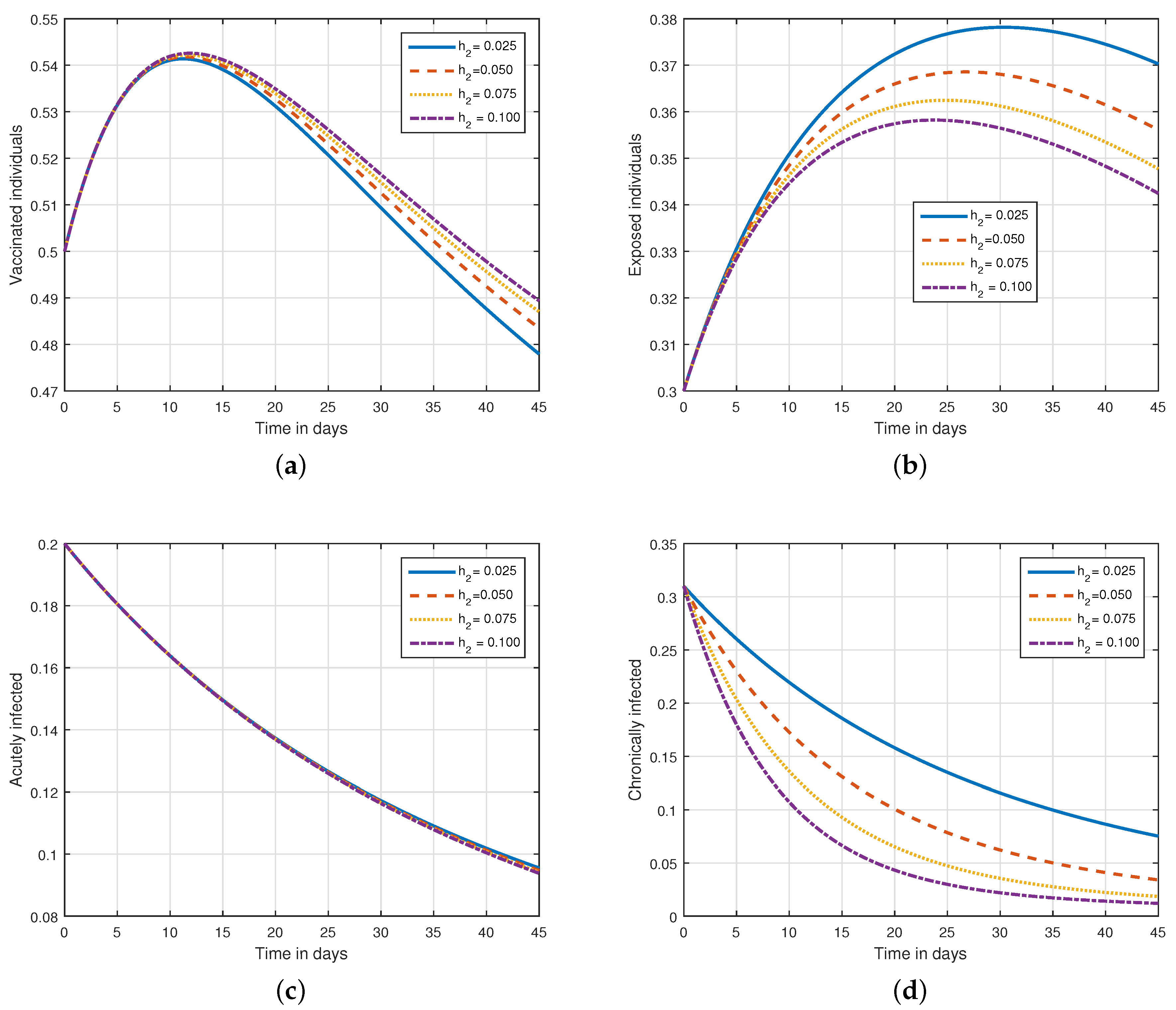
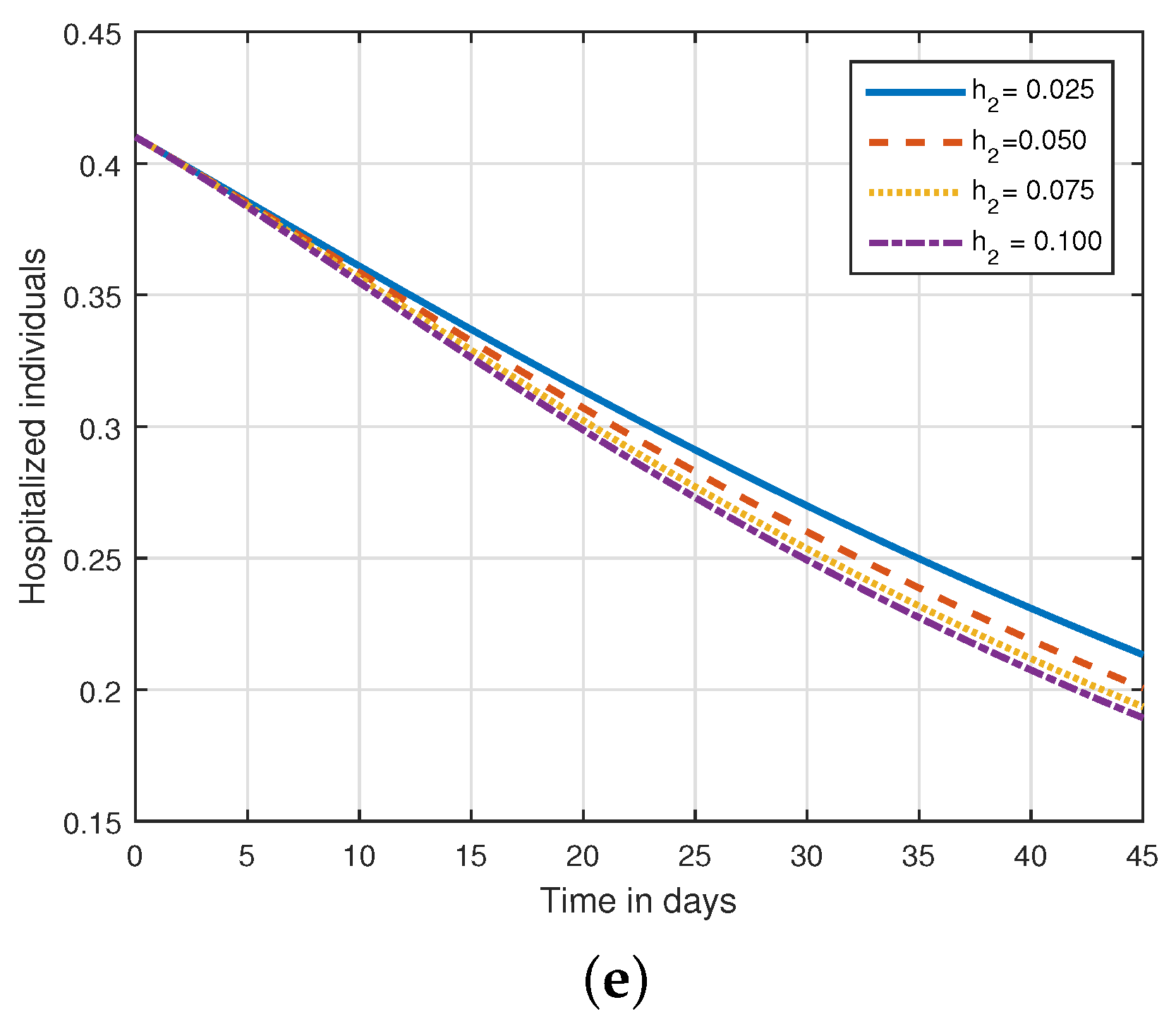
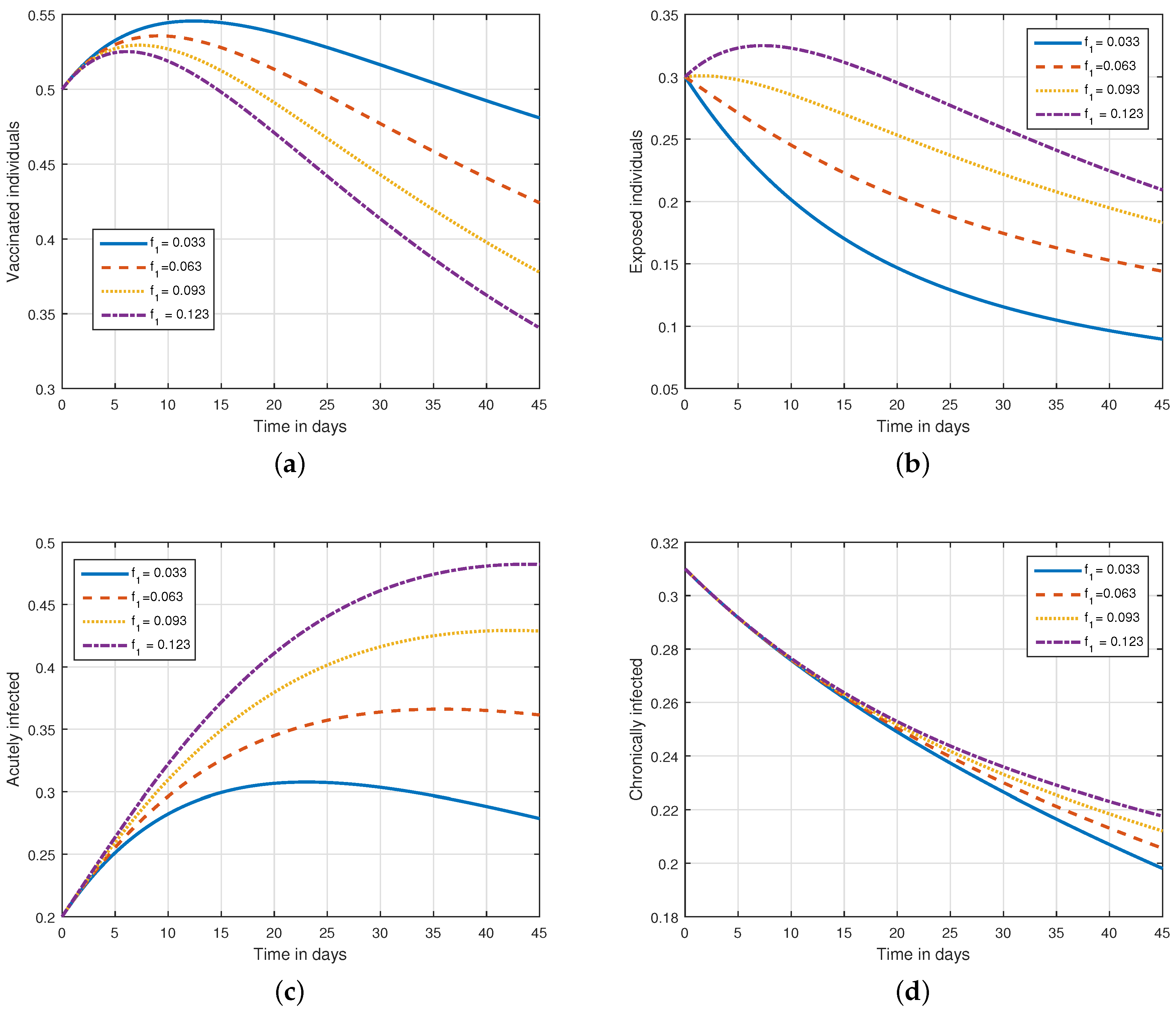
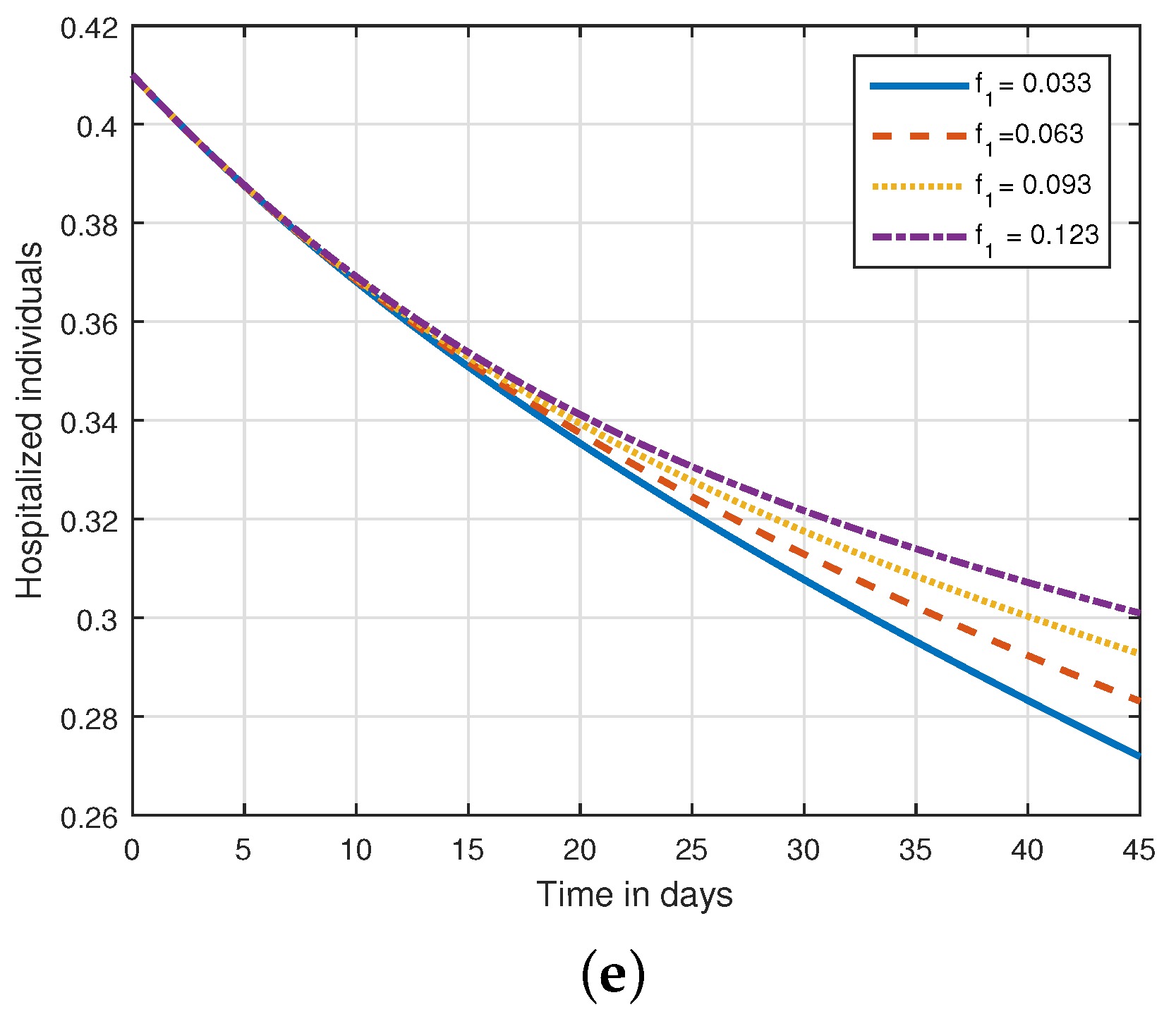
6. Numerical Results and Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pierce-Williams, R.A.; Sheffield, J.S. Hepatitis B in the Perinatal Period. In Neonatal Infections: Pathophysiology, Diagnosis, and Management; Springer: Cham, Switzerland, 2018; pp. 103–109. [Google Scholar]
- Zheng, Y.; Wu, J.; Ding, C.; Xu, K.; Yang, S.; Li, L. Disease burden of chronic hepatitis B and complications in China from 2006 to 2050: An individual-based modeling study. Virol. J. 2020, 17, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Cui, J.A.; Zhou, X. Dynamical behavior of a hepatitis B virus transmission model with vaccination. J. Theor. Biol. 2010, 265, 572–578. [Google Scholar] [CrossRef]
- Medley, G.F.; Lindop, N.A.; Edmunds, W.J.; Nokes, D.J. Hepatitis-B virus endemicity: Heterogeneity, catastrophic dynamics and control. Nat. Med. 2001, 7, 619–624. [Google Scholar] [CrossRef] [PubMed]
- Thornley, S.; Bullen, C.; Roberts, M. Hepatitis B in a high prevalence New Zealand population: A mathematical model applied to infection control policy. J. Theor. Biol. 2008, 254, 599–603. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Zhang, W.; Ruan, S. Modeling the transmission dynamics and control of hepatitis B virus in China. J. Theor. Biol. 2010, 262, 330–338. [Google Scholar] [CrossRef]
- Pang, J.; Cui, J.A.; Hui, J. The importance of immune responses in a model of hepatitis B virus. Nonlinear Dyn. 2012, 67, 723–734. [Google Scholar] [CrossRef]
- Wang, K.; Wang, W.; Song, S. Dynamics of an HBV model with diffusion and delay. J. Theor. Biol. 2008, 253, 36–44. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z. An HBV model with diffusion and time delay. J. Theor. Biol. 2009, 257, 499–509. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, Z.; Lu, Y. A mathematical model of hepatitis B virus transmission and its application for vaccination strategy in China. Int. J. Epidemiol. 2000, 29, 744–752. [Google Scholar] [CrossRef]
- Khan, M.A.; Islam, S.; Arif, M. Transmission model of hepatitis B virus with the migration effect. Biomed Res. Int. 2013, 2013. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, K.; Zhang, X. Modeling and analyzing the transmission dynamics of HBV epidemic in Xinjiang, China. PLoS ONE 2015, 10, e0138765. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Islam, S.; Zaman, G. Media coverage campaign in Hepatitis B transmission model. Appl. Math. Comput. 2018, 331, 378–393. [Google Scholar] [CrossRef]
- Alrabaiah, H.; Safi, M.A.; DarAssi, M.H.; Al-Hdaibat, B.; Ullah, S.; Khan, M.A.; Shah, S.A.A. Optimal control analysis of hepatitis B virus with treatment and vaccination. Results Phys. 2020, 19, 103599. [Google Scholar] [CrossRef]
- Sowndarrajan, P.T.; Shangerganesh, L.; Debbouche, A.; Torres, D.F. Optimal control of a heroin epidemic mathematical model. Optimization 2022, 71, 3107–3131. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Opoku, M.O.; Wiah, E.N.; Okyere, E.; Sackitey, A.L.; Essel, E.K.; Moore, S.E. Stability Analysis of Caputo Fractional Order Viral Dynamics of Hepatitis B Cellular Infection. Math. Comput. Appl. 2023, 28, 24. [Google Scholar] [CrossRef]
- Samraiz, M.; Perveen, Z.; Abdeljawad, T.; Iqbal, S.; Naheed, S. On certain fractional calculus operators and applications in mathematical physics. Phys. Scr. 2020, 95, 115210. [Google Scholar] [CrossRef]
- Jan, R.; Boulaaras, S. Analysis of fractional-order dynamics of dengue infection with non-linear incidence functions. Trans. Inst. Meas. Control 2022, 44, 2630–2641. [Google Scholar] [CrossRef]
- Tang, T.Q.; Shah, Z.; Jan, R.; Deebani, W.; Shutaywi, M. A robust study to conceptualize the interactions of CD4+ T-cells and human immunodeficiency virus via fractional-calculus. Phys. Scr. 2021, 96, 125231. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Granas, A.; Dugundji, J. Elementary fixed point theorems. In Fixed Point Theory; Springer: New York, NY, USA, 2003; pp. 9–84. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015; Volume 61, pp. 9–31. [Google Scholar]
- Ullam, S.M. Problems in Modern Mathematics (Chapter VI); Wiley: New York, NY, USA, 1940. [Google Scholar]
- Hyers, D.H. On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27, 222. [Google Scholar] [CrossRef]
- Rassias, T.M. On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Benkerrouche, A.; Souid, M.S.; Etemad, S.; Hakem, A.; Agarwal, P.; Rezapour, S.; Ntouyas, S.K.; Tariboon, J. Qualitative Study on Solutions of a Hadamard Variable Order Boundary Problem via the Ulam-Hyers-Rassias Stability. Fractal Fract. 2021, 5, 108. [Google Scholar] [CrossRef]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alyobi, S.; Jan, R. Qualitative and Quantitative Analysis of Fractional Dynamics of Infectious Diseases with Control Measures. Fractal Fract. 2023, 7, 400. https://doi.org/10.3390/fractalfract7050400
Alyobi S, Jan R. Qualitative and Quantitative Analysis of Fractional Dynamics of Infectious Diseases with Control Measures. Fractal and Fractional. 2023; 7(5):400. https://doi.org/10.3390/fractalfract7050400
Chicago/Turabian StyleAlyobi, Sultan, and Rashid Jan. 2023. "Qualitative and Quantitative Analysis of Fractional Dynamics of Infectious Diseases with Control Measures" Fractal and Fractional 7, no. 5: 400. https://doi.org/10.3390/fractalfract7050400
APA StyleAlyobi, S., & Jan, R. (2023). Qualitative and Quantitative Analysis of Fractional Dynamics of Infectious Diseases with Control Measures. Fractal and Fractional, 7(5), 400. https://doi.org/10.3390/fractalfract7050400







