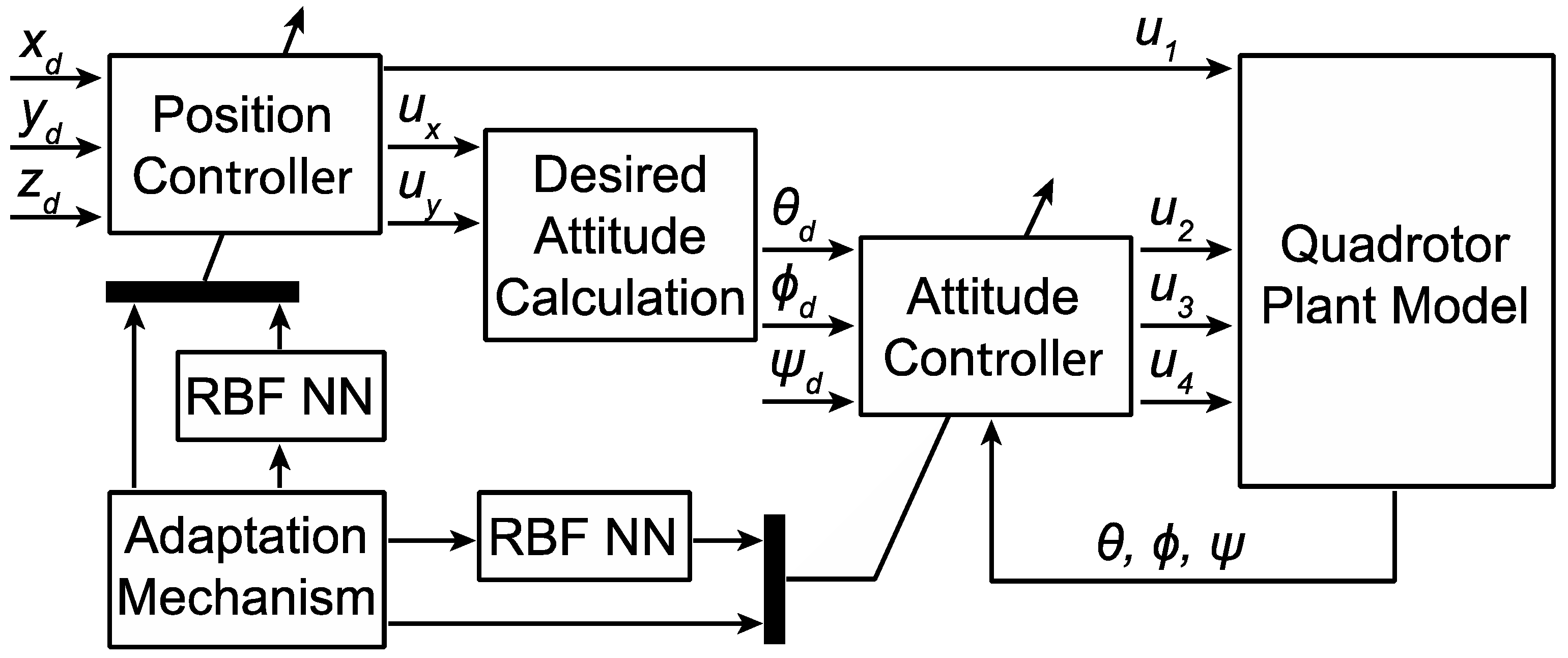
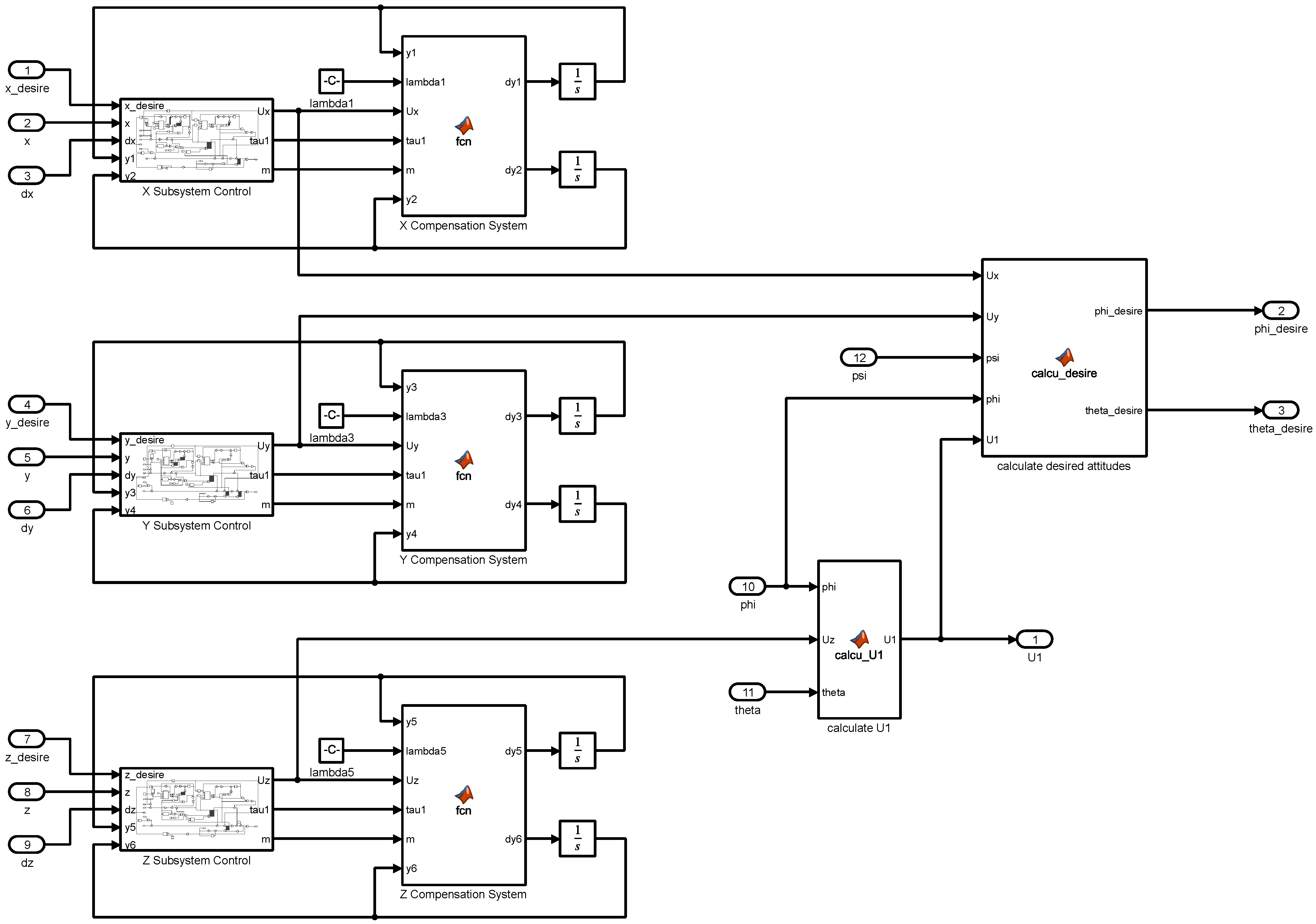
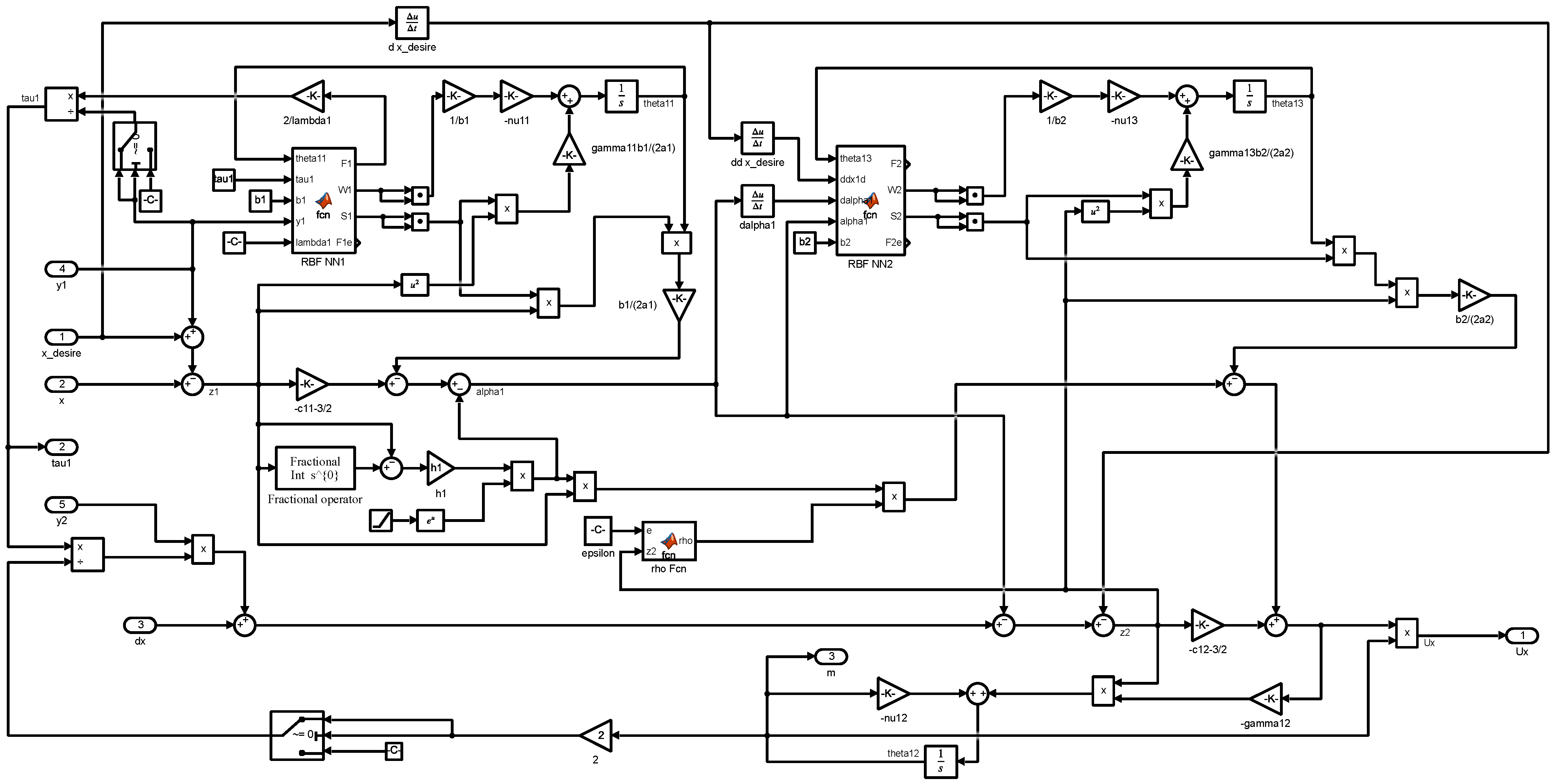
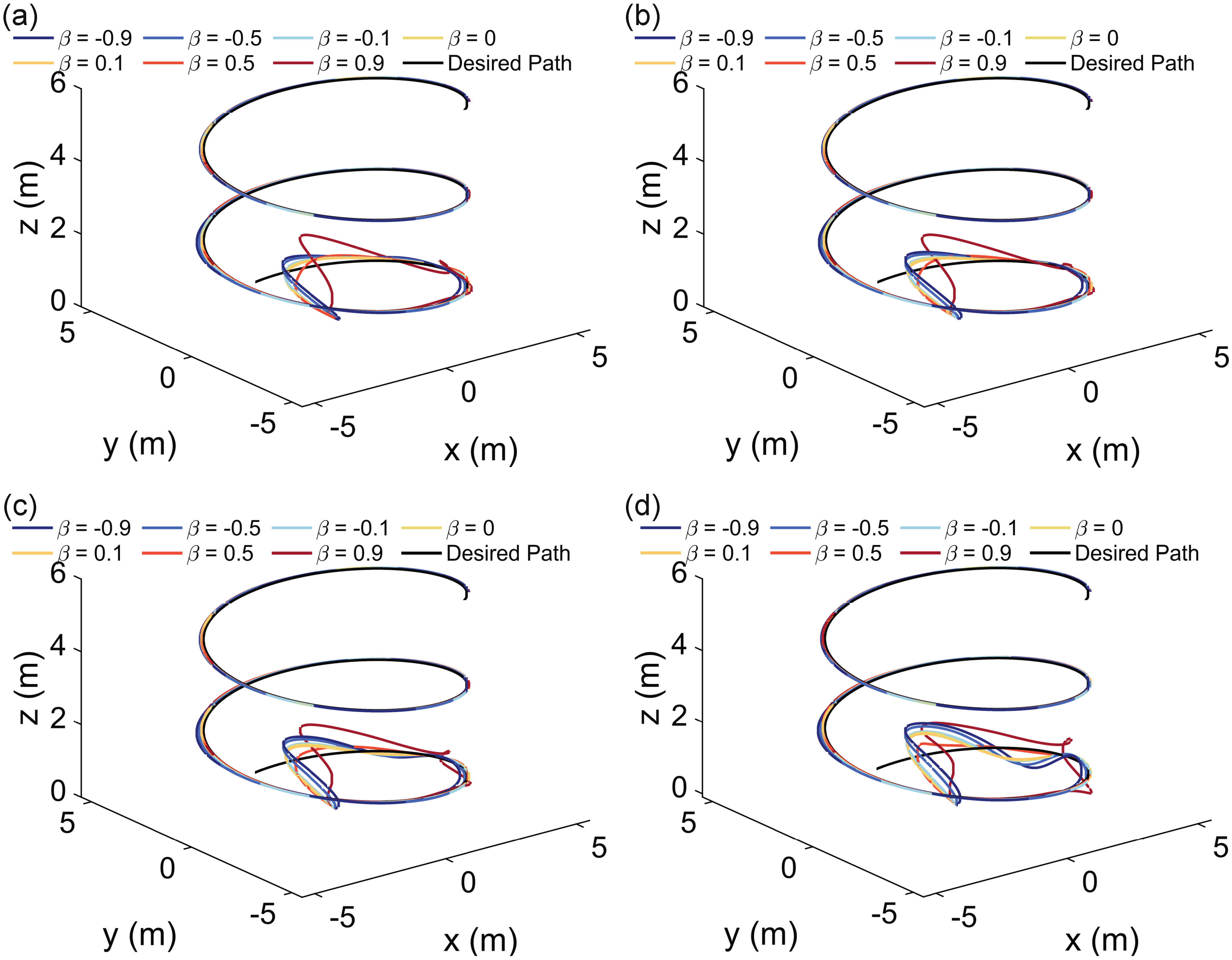
Figure 3.
Simulated results that demonstrate the robustness of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads: (a) m/s2, (b) m/s2, (c) m/s2, (d) m/s2. (Assume that and no input time delay.)
Figure 3.
Simulated results that demonstrate the robustness of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads: (a) m/s2, (b) m/s2, (c) m/s2, (d) m/s2. (Assume that and no input time delay.)
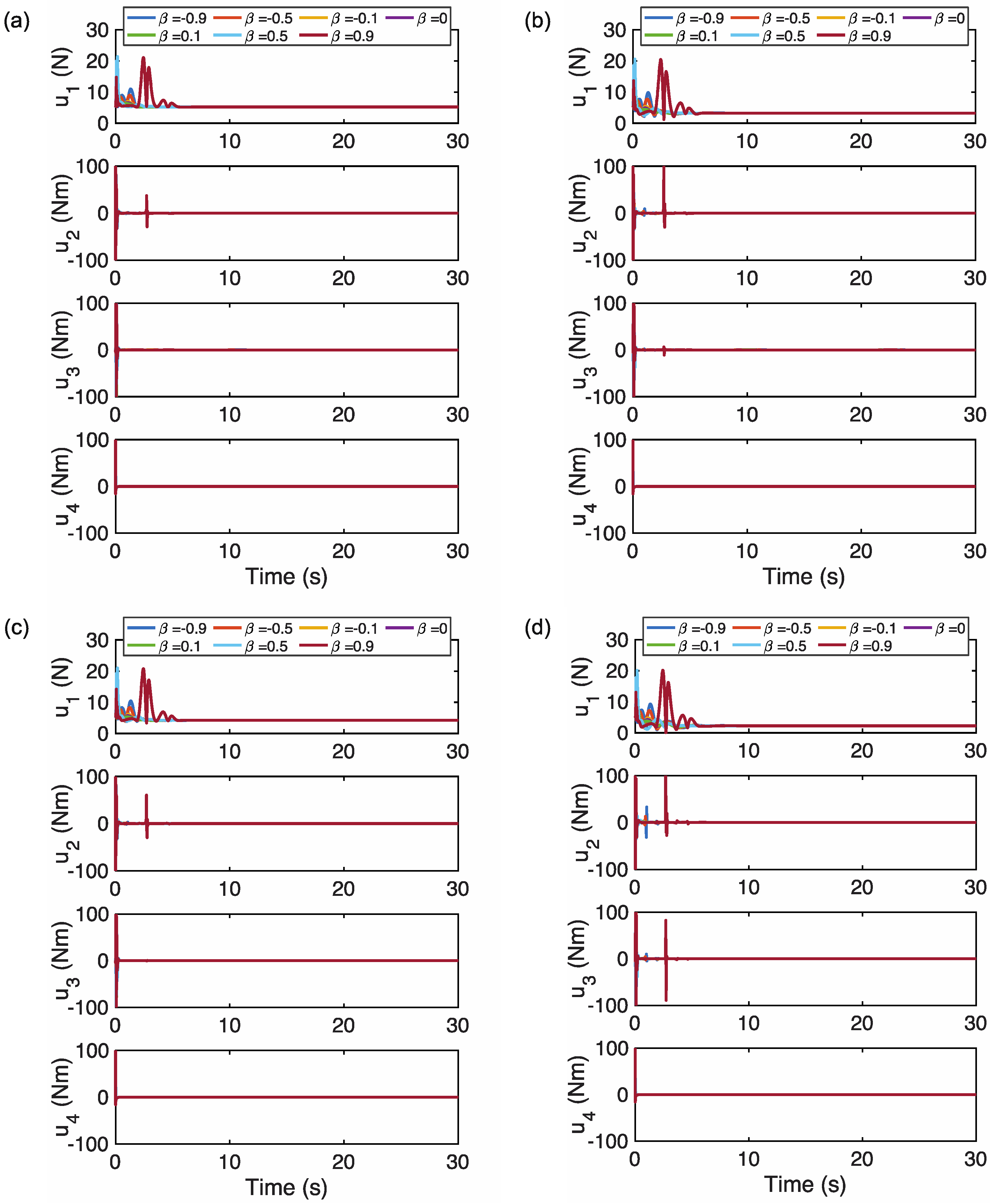
Figure 4.
Simulated control inputs of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads: (a) m/s2, (b) m/s2, (c) m/s2, (d) m/s2. (Assume that and no input time delay.)
Figure 4.
Simulated control inputs of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads: (a) m/s2, (b) m/s2, (c) m/s2, (d) m/s2. (Assume that and no input time delay.)
Figure 5.
Simulated results that demonstrate the robustness of the varying fractional orders in the proposed controller to various input delays: (a) s, (b) s. (Assume that and no payload is applied.)
Figure 5.
Simulated results that demonstrate the robustness of the varying fractional orders in the proposed controller to various input delays: (a) s, (b) s. (Assume that and no payload is applied.)
Figure 6.
Simulated control inputs of the varying fractional orders in the proposed controller to various input delays: (a) s, (b) s. (Assume that and no payload is applied.)
Figure 6.
Simulated control inputs of the varying fractional orders in the proposed controller to various input delays: (a) s, (b) s. (Assume that and no payload is applied.)
Figure 7.
Simulated results that demonstrate the robustness of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Figure 7.
Simulated results that demonstrate the robustness of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Figure 8.
Simulated control inputs of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Figure 8.
Simulated control inputs of the varying fractional orders in the proposed controller to uncertainty in the quadrotor dynamics with various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
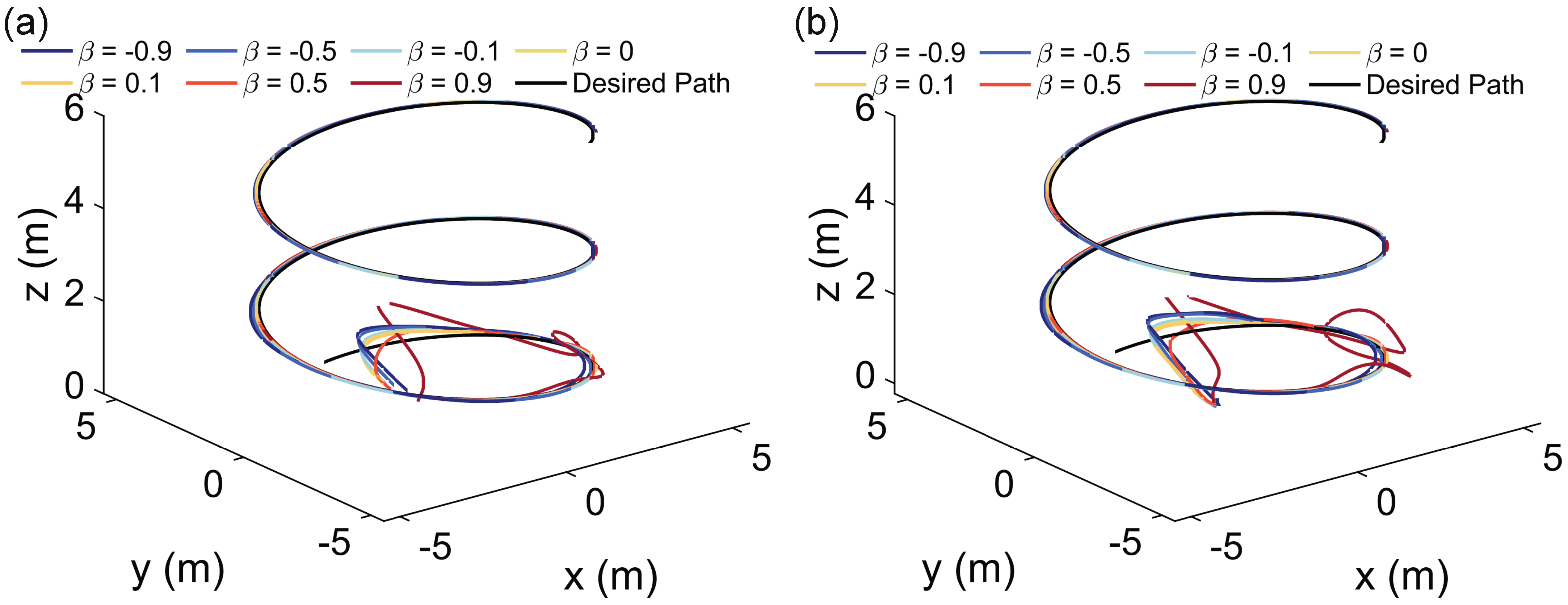
Figure 9.
Comparison of the simulated trajectories with three controllers ( in RBF-ADFOBC) in response to various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Figure 9.
Comparison of the simulated trajectories with three controllers ( in RBF-ADFOBC) in response to various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Figure 10.
Comparison of the simulated control signals with three controllers ( in RBF-ADFOBC) in response to various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Figure 10.
Comparison of the simulated control signals with three controllers ( in RBF-ADFOBC) in response to various payloads and uncertain input time delays: (a) m/s2 and s, (b) m/s2 and s, (c) m/s2 and s, (d) m/s2 and s. (Assume that and .)
Table 2.
Values for the selectable parameters in the proposed controllers.
Table 2.
Values for the selectable parameters in the proposed controllers.
| Param | Value | Param | Value | Param | Value | Param | Value | Param | Value |
|---|
| 5 | | 5 | | 1 | | 1 | | 5 |
| 5 | | 10 | | 10 | | 10 | | 10 |
| 10 | | 10 | | 2 | | 0.1 | | 2 |
| 5 | | 5 | | 1 | | 1 | | 5 |
| 5 | | 10 | | 10 | | 10 | | 10 |
| 10 | | 10 | | 2 | | 0.1 | | 2 |
| 5 | | 5 | | 1 | | 1 | | 5 |
| 5 | | 10 | | 10 | | 10 | | 10 |
| 10 | | 10 | | 2 | | 0.1 | | 2 |
| 5 | | 5 | | 1 | | 1 | | 5 |
| 5 | | 10 | | 10 | | 10 | | 10 |
| 10 | | 10 | | 2 | | 0.1 | | 2 |
| 5 | | 5 | | 1 | | 1 | | 5 |
| 5 | | 10 | | 10 | | 10 | | 10 |
| 10 | | 10 | | 2 | | 0.1 | | 2 |
| 5 | | 5 | | 1 | | 1 | | 5 |
| 5 | | 10 | | 10 | | 10 | | 10 |
| 10 | | 10 | | 2 | | 0.1 | | 2 |
Table 3.
Root mean squared error (RMSE) of the simulated tracks under different payloads and different fractional orders in the proposed controller.
Table 3.
Root mean squared error (RMSE) of the simulated tracks under different payloads and different fractional orders in the proposed controller.
| Payloads (m/s2) | | | | | | | |
|---|
| 0 | 0.6493 | 0.5963 | 0.5127 | 0.4953 | 0.4830 | 0.4786 | 0.7251 |
| 2 | 0.6459 | 0.5943 | 0.5132 | 0.4962 | 0.4841 | 0.4800 | 0.7241 |
| 4 | 0.6387 | 0.5900 | 0.5129 | 0.4964 | 0.4846 | 0.4806 | 0.7208 |
| 6 | 0.6295 | 0.5842 | 0.5119 | 0.4961 | 0.4847 | 0.4802 | 0.7139 |
Table 4.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
Table 4.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
| Payloads (m/s2) | | | | | | | |
|---|
| 0 | 5.4361 | 5.3713 | 5.3344 | 5.3429 | 5.3530 | 5.3857 | 5.9943 |
| 2 | 4.4824 | 4.4071 | 4.3638 | 4.3733 | 4.3848 | 4.4214 | 5.1261 |
| 4 | 3.5554 | 3.4652 | 3.4122 | 3.4234 | 3.4369 | 3.4796 | 4.3215 |
| 6 | 2.6900 | 2.5764 | 2.5065 | 2.5196 | 2.5354 | 2.5849 | 3.6169 |
Table 5.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
Table 5.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
| Payloads (m/s2) | | | | | | | |
|---|
| 0 | 2.0106 | 1.5832 | 1.9039 | 2.3651 | 2.4281 | 2.5267 | 5.6396 |
| 2 | 2.0257 | 1.6009 | 1.9399 | 2.3753 | 2.4359 | 2.5359 | 5.6718 |
| 4 | 2.0623 | 1.6288 | 1.9738 | 2.3862 | 2.4447 | 2.5460 | 5.7331 |
| 6 | 2.2329 | 1.7023 | 2.0095 | 2.3990 | 2.4547 | 2.5592 | 5.8290 |
Table 6.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
Table 6.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
| Payloads (m/s2) | | | | | | | |
|---|
| 0 | 4.5057 | 4.0187 | 4.7854 | 4.7979 | 4.8203 | 4.8216 | 6.1584 |
| 2 | 4.5158 | 4.0317 | 4.8005 | 4.8029 | 4.8229 | 4.8225 | 6.1636 |
| 4 | 4.5264 | 4.0436 | 4.8138 | 4.8068 | 4.8242 | 4.8224 | 6.1761 |
| 6 | 4.5476 | 4.0609 | 4.8264 | 4.8102 | 4.8249 | 4.8224 | 6.4069 |
Table 7.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
Table 7.
Root mean squared value of the control signal in the first 30 s under different payloads and different fractional orders in the proposed controller.
| Payloads (m/s2) | | | | | | | |
|---|
| 0 | 0.3847 | 0.3851 | 0.3871 | 0.3884 | 0.3903 | 0.4207 | 2.3505 |
| 2 | 0.3847 | 0.3851 | 0.3871 | 0.3884 | 0.3903 | 0.4207 | 2.3505 |
| 4 | 0.3847 | 0.3851 | 0.3871 | 0.3884 | 0.3903 | 0.4207 | 2.3505 |
| 6 | 0.3847 | 0.3851 | 0.3871 | 0.3884 | 0.3903 | 0.4207 | 2.3505 |
Table 8.
Root mean squared error (RMSE) of the simulated tracks under different input time delays and different fractional orders in the proposed controller.
Table 8.
Root mean squared error (RMSE) of the simulated tracks under different input time delays and different fractional orders in the proposed controller.
|
(s) | | | | | | | |
|---|
| 0.05 | 0.6484 | 0.5926 | 0.5187 | 0.5022 | 0.4898 | 0.4836 | 0.7429 |
| 0.10 | 0.6380 | 0.5855 | 0.5292 | 0.5150 | 0.5040 | 0.5075 | 0.7923 |
Table 9.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
Table 9.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
|
(s) | | | | | | | |
|---|
| 0.05 | 5.4411 | 5.3787 | 5.3541 | 5.3685 | 5.3829 | 5.4450 | 6.4784 |
| 0.10 | 5.4721 | 5.3984 | 5.3765 | 5.3830 | 5.3975 | 5.4649 | 7.4987 |
Table 10.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
Table 10.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
|
(s) | | | | | | | |
|---|
| 0.05 | 1.9331 | 1.5050 | 1.6891 | 2.3141 | 2.3788 | 2.5456 | 5.6385 |
| 0.10 | 1.9289 | 1.4889 | 1.6140 | 2.3026 | 2.3620 | 2.4665 | 13.3469 |
Table 11.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
Table 11.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
|
(s) | | | | | | | |
|---|
| 0.05 | 4.4377 | 3.9316 | 4.6976 | 4.7950 | 4.8502 | 4.9601 | 6.1635 |
| 0.10 | 4.4185 | 3.8899 | 4.6636 | 4.7569 | 4.8149 | 4.8853 | 15.0158 |
Table 12.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
Table 12.
Root mean squared value of the control signal in the first 30 s under different input time delays and different fractional orders in the proposed controller.
|
(s) | | | | | | | |
|---|
| 0.05 | 0.3842 | 0.3846 | 0.3866 | 0.3879 | 0.3885 | 0.4227 | 2.3533 |
| 0.10 | 0.3839 | 0.3841 | 0.3862 | 0.3873 | 0.3882 | 0.4223 | 2.3530 |
Table 13.
Root mean squared error (RMSE) of the simulated tracks under different payloads, different input time delays and different fractional orders in the proposed controller.
Table 13.
Root mean squared error (RMSE) of the simulated tracks under different payloads, different input time delays and different fractional orders in the proposed controller.
| Payloads (m/s2) |
(s) | | | | | | | |
|---|
| 2 | 0.05 | 0.6493 | 0.5944 | 0.5192 | 0.5027 | 0.4903 | 0.4843 | 0.7422 |
| 0.10 | 0.6436 | 0.5892 | 0.5298 | 0.5151 | 0.5040 | 0.5064 | 0.8158 |
| 4 | 0.05 | 0.6474 | 0.5942 | 0.5190 | 0.5025 | 0.4902 | 0.4844 | 0.7410 |
| 0.10 | 0.6447 | 0.5902 | 0.5296 | 0.5147 | 0.5037 | 0.5048 | 116.7240 |
Table 14.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
Table 14.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
| Payloads (m/s2) |
(s) | | | | | | | |
|---|
| 2 | 0.05 | 4.4959 | 4.4187 | 4.3881 | 4.4058 | 4.4231 | 4.4969 | 5.7538 |
| 0.10 | 4.5443 | 4.4461 | 4.4162 | 4.4248 | 4.4422 | 4.5285 | 17.8763 |
| 4 | 0.05 | 4.0347 | 3.9476 | 3.9126 | 3.9323 | 3.9515 | 4.0328 | 5.4364 |
| 0.10 | 4.0941 | 3.9813 | 3.9454 | 3.9547 | 3.9736 | 4.0731 | 9850.6 |
Table 15.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
Table 15.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
| Payloads (m/s2) |
(s) | | | | | | | |
|---|
| 2 | 0.05 | 1.9505 | 1.5200 | 1.7307 | 2.3233 | 2.3912 | 2.5839 | 5.6791 |
| 0.10 | 1.9681 | 1.5059 | 1.7089 | 2.3123 | 2.3691 | 2.5970 | 26.4734 |
| 4 | 0.05 | 1.9692 | 1.5315 | 1.7540 | 2.3293 | 2.4005 | 2.6100 | 5.7090 |
| 0.10 | 2.2984 | 1.5267 | 1.7438 | 2.3197 | 2.3781 | 2.6325 | 60.9009 |
Table 16.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
Table 16.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
| Payloads (m/s2) |
(s) | | | | | | | |
|---|
| 2 | 0.05 | 4.4485 | 3.9436 | 4.7216 | 4.8083 | 4.8637 | 4.9636 | 6.1716 |
| 0.10 | 4.4291 | 3.9022 | 4.6844 | 4.7717 | 4.8261 | 4.9236 | 27.0198 |
| 4 | 0.05 | 4.4540 | 3.9507 | 4.7341 | 4.8152 | 4.8723 | 4.9649 | 6.1762 |
| 0.10 | 4.4402 | 3.9089 | 4.6960 | 4.7793 | 4.8321 | 4.9332 | 67.0480 |
Table 17.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
Table 17.
Root mean squared value of the control signal in the first 30 s under different payloads, different input time delays and different fractional orders in the proposed controller.
| Payloads (m/s2) |
(s) | | | | | | | |
|---|
| 2 | 0.05 | 0.3835 | 0.3840 | 0.3855 | 0.3875 | 0.3892 | 0.4207 | 2.3505 |
| 0.10 | 0.3845 | 0.3849 | 0.3866 | 0.3883 | 0.3900 | 0.4211 | 2.3509 |
| 4 | 0.05 | 0.3850 | 0.3855 | 0.3875 | 0.3891 | 0.3905 | 0.4213 | 2.3515 |
| 0.10 | 0.3852 | 0.3866 | 0.3877 | 0.3899 | 0.3931 | 0.4222 | 2.3520 |
Table 18.
and matrices used in the LQR optimal gain calculation and the resulting optimal gains for each subsystem.
Table 18.
and matrices used in the LQR optimal gain calculation and the resulting optimal gains for each subsystem.
| Subsystem | | | |
|---|
| X Position () | diag(1000, 20, 100) | 3 | [19.8524, 5.2640, −5.7735] |
| Y Position () | diag(1000, 20, 100) | 3 | [19.8524, 5.2640, −5.7735] |
| Z Position () | diag(1000, 20, 100) | 3 | [19.8524, 5.2640, −5.7735] |
| Roll Angle () | diag(1000, 20, 100) | 3 | [19.0702, 2.6276, −5.7735] |
| Pitch Angle () | diag(1000, 20, 100) | 3 | [19.0702, 2.6276, −5.7735] |
| Yaw Angle () | diag(1000, 20, 100) | 3 | [19.0811, 2.6635, −5.7735] |
Table 19.
Root mean squared error (RMSE) of the simulated tracks under different payloads and different input time delays for the three different controllers.
Table 19.
Root mean squared error (RMSE) of the simulated tracks under different payloads and different input time delays for the three different controllers.
| Payloads (m/s2) |
(s) | FOPID | LQR | |
|---|
| 2 | 0.05 | 0.7580 | 0.5155 | 0.4843 |
| 0.10 | 0.7480 | 0.5988 | 0.5064 |
| 4 | 0.05 | 0.7623 | 0.5199 | 0.4844 |
| 0.10 | 0.7614 | 1.9011 | 0.5048 |
Table 20.
Comparison of the root mean squared value of the control signals in the three controllers under different payloads, different input time delays and different fractional orders.
Table 20.
Comparison of the root mean squared value of the control signals in the three controllers under different payloads, different input time delays and different fractional orders.
| Payloads (m/s2) |
(s) | FOPID | LQR | |
|---|
| | | | | | | | | | | |
|---|
| 2 | 0.05 | 4.4721 | 2.0972 | 0.6381 | 2.0977 | 34.9813 | 18.0742 | 17.0831 | 12.1074 | 4.4969 | 2.5839 | 4.9636 | 0.4207 |
| 0.10 | 4.4824 | 2.0707 | 0.8075 | 2.0977 | 55.8172 | 31.7920 | 23.8891 | 12.1074 | 4.5285 | 2.5970 | 4.9236 | 0.4211 |
| 4 | 0.05 | 3.9968 | 2.0992 | 0.6452 | 2.0977 | 29.2486 | 18.3960 | 17.1631 | 12.1074 | 4.0328 | 2.6100 | 4.9649 | 0.4213 |
| 0.10 | 4.0391 | 3.2332 | 1.2922 | 2.0977 | 1073.9 | 33.2098 | 32.3988 | 12.1074 | 4.0731 | 2.6325 | 4.9332 | 0.4222 |