Qualitatively Stable Schemes for the Black–Scholes Equation
Abstract
:1. Introduction
2. The Laplace Transform
3. The Laplace Transform Method for the BSM Equation
4. NSFD Strategy
- In the discretization of the derivatives in the equation using standard finite difference methods, instead of h in the denominator, a complex function such as of h is used which satisfies (26). Therefore, a complex analytic function can be presented that satisfies the following relation:
5. The New Scheme
6. Analysis of the New Scheme
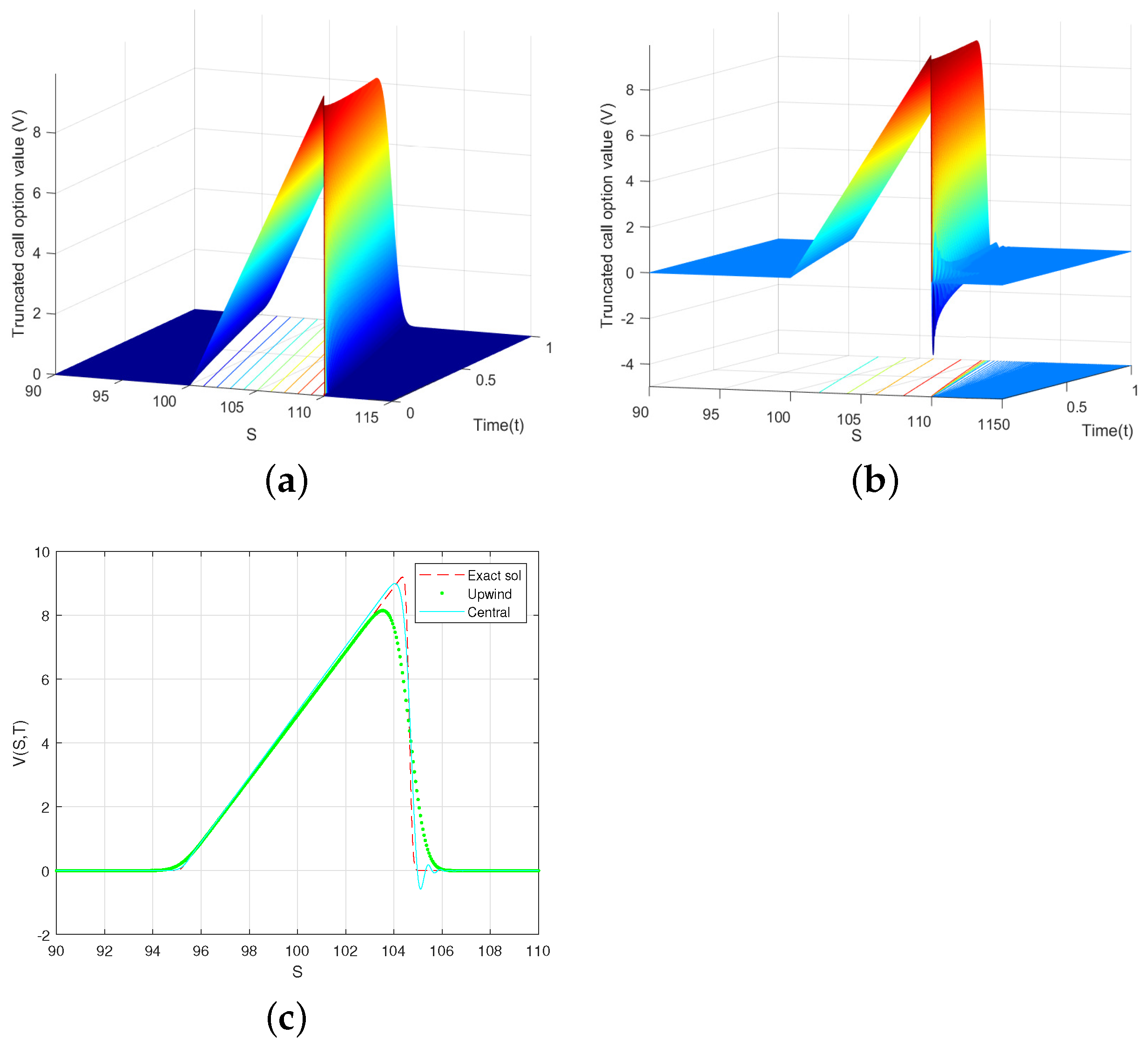
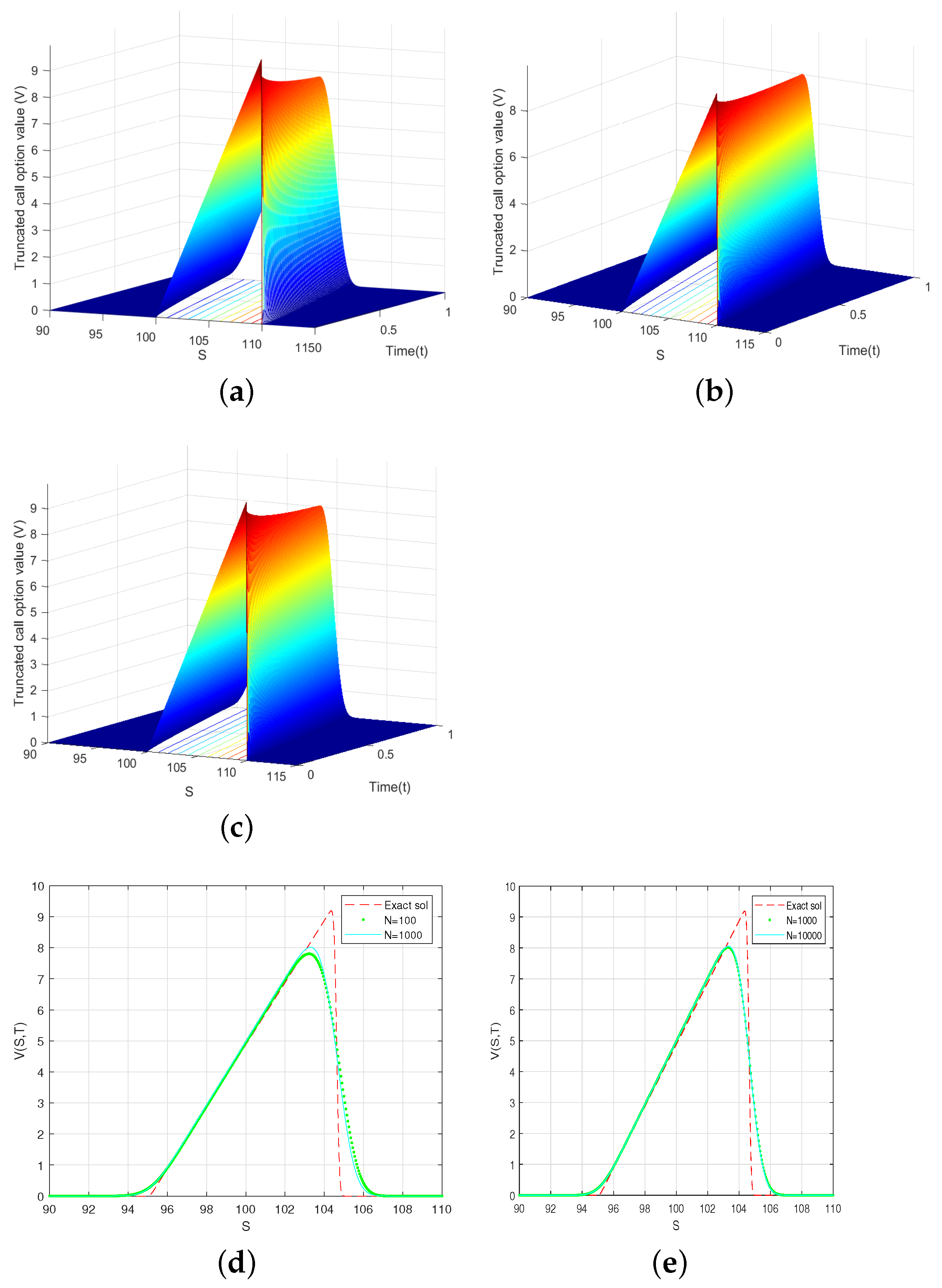
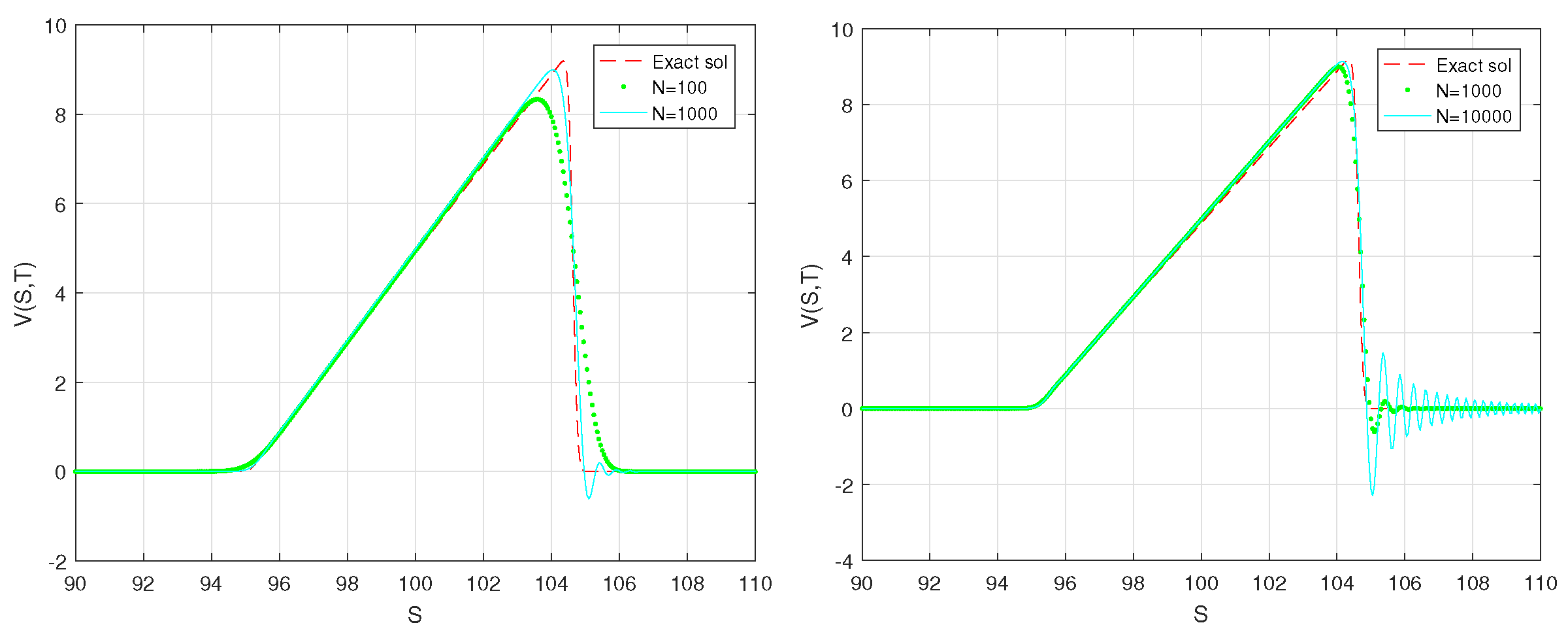
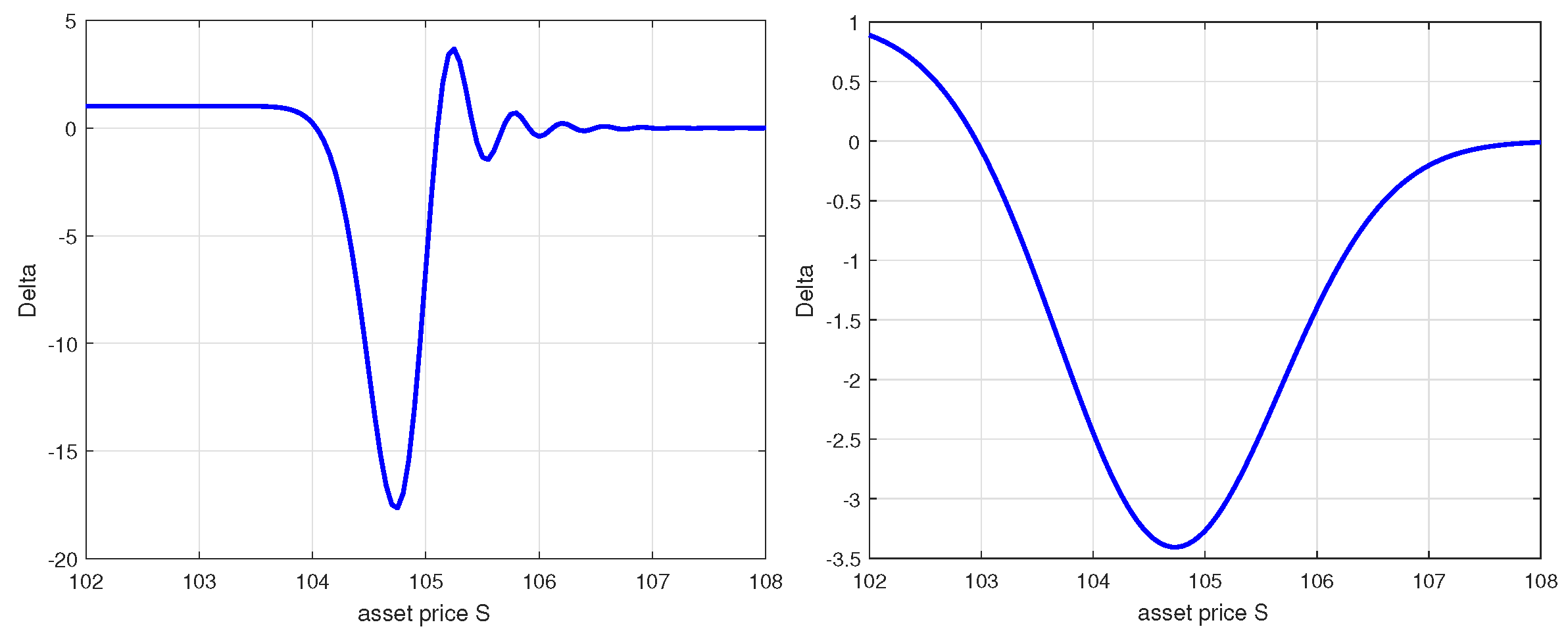
7. Numerical Experiments
8. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–659. [Google Scholar] [CrossRef]
- Hout, K.J.; Volders, K. Stability of central finite difference schemes on non-uniform grids for the Black–Scholes equation. Appl. Numer. Math. 2009, 59, 2593–2609. [Google Scholar] [CrossRef]
- Milev, M.; Tagliani, A. Numerical valuation of discrete double barrier options. J. Comput. Appl. Math. 2010, 233, 2468–2480. [Google Scholar] [CrossRef]
- Pealat, G.; Duffy, D.J. The alternating direction explicit (ADE) method for one-factor problems. Wilmott 2011, 2011, 54–60. [Google Scholar] [CrossRef]
- Golbabai, A.; Ballestra, L.V.; Ahmadian, D. Superconvergence of the finite element solutions of the Black–Scholes equation. Financ. Res. Lett. 2013, 10, 17–26. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. A modified explicit method for the Black–Scholes equation with positivity preserving property. J. Math. Comput. Sci. 2015, 15, 299–305. [Google Scholar] [CrossRef]
- Farnoosh, R.; Sobhani, A.; Beheshti, M.H. Efficient and fast numerical method for pricing discrete double barrier option by projection method. Comput. Math. Appl. 2017, 73, 1539–1545. [Google Scholar] [CrossRef]
- Jeong, D.; Yoo, M.; Kim, J. Finite difference method for the Black–Scholes equation without boundary conditions. Comput. Econ. 2018, 51, 961–972. [Google Scholar] [CrossRef]
- Heo, Y.; Han, H.; Jang, H.; Chot, Y.; Kim, J. Finite difference method for the two-dimensional Black–Scholes equation whit a hybrid boundary condition. J. Korean Soc. Ind. Appl. Math. 2019, 23, 19–30. [Google Scholar]
- Abdi-Mazraeh, S.; Khani, A.; Irandoust-Pakchin, S. Multiple shooting method for solving Black–Scholes equation. Comput. Econ. 2020, 56, 723–746. [Google Scholar] [CrossRef]
- Shokri, A.; Saadat, H. Trigonometrically fitted high-order predictor-corrector method with phase-lag of order infinity for the numerical solution of radial Schrödinger equation. J. Math. Chem. 2014, 52, 1870–1894. [Google Scholar] [CrossRef]
- Shokri, A. The symmetric two-step P-stable nonlinear predictor-corrector methods for the numerical solution of second order initial value problems. Bull. Iran. Math. Soci. 2015, 41, 201–215. [Google Scholar]
- Roul, P.; Goura, V.M.K. A sixth order numerical method and its convergence for generalized Black–Scholes PDE. J. Comput. Appl. Math. 2020, 377, 112881. [Google Scholar] [CrossRef]
- Milev, M.; Tagliani, A. Laplace transform and finite difference methods for the Black–Scholes equation. Appl. Math. Comput. 2013, 220, 649–658. [Google Scholar]
- Cohen, A.M. Numerical Methods for Laplace Transform Inversion; Springer: New York, NY, USA, 2007. [Google Scholar]
- Schiff, J.L. The Laplace Transform, Theory and Applications; Springer: New York, NY, USA, 1999. [Google Scholar]
- Duffy, D.G. Transform Methods for Solving Partial Differential Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri, A.; Ramos, H.; Heydari, S. A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease. Math. Comput. Simul. 2021, 182, 397–410. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Mickens, R.E.; Jordan, P.M. A positivity-preserving nonstandard finite difference scheme for the damped wave equation. Numer. Meth. Par. Differ. Equ. 2004, 20, 639–649. [Google Scholar] [CrossRef]
- Mickens, R.E.; Jordan, P.M. A new positivity-preserving nonstandard finite difference scheme for the DWE. Numer. Meth. Par. Differ. Equ. 2005, 21, 976–985. [Google Scholar] [CrossRef]
- Milev, M.; Tagliani, A. Efficient implicit scheme with positivity preserving and smoothing properties. J. Comput. Appl. Math. 2013, 243, 1–9. [Google Scholar] [CrossRef]
- Milev, M.; Tagliani, A. Low volatility options and numerical diffusion of finite difference schemes. Serd. Math. J. 2010, 36, 223–236. [Google Scholar]
- Windish, G. M-matrices in numerical analysis. In Teubner-Texte Zur Mathematik; Vieweg+Teubner Verlag: Leipzig, Germany, 1989; Volume 115. [Google Scholar]
- Smith, G.D. Numerical Solution of Partial Differential Equation: Finite Difference Method; Clarendon Press: Oxford, UK, 1985. [Google Scholar]
- Jha, N.; Wagley, M. Stability Analysis of Quasi-variable Grids Cubic Spline Fourth-Order Compact Implicit Algorithms for Burger’s Type Parabolic PDEs. Iran. J. Sci. Technol. Trans. A 2020, 44, 1875–1890. [Google Scholar] [CrossRef]



| 95 | 96 | 102 | 103 | 104 | 105 | ||
|---|---|---|---|---|---|---|---|
| For | |||||||
| Upwind | 3.9437 | 4.9433 | 5.9429 | ||||
| Central | 2.9581 | 3.9625 | 4.9668 | 5.9712 | |||
| Upwind | 3.9275 | 4.9266 | 5.9258 | 6.9249 | |||
| Central | 3.9659 | 4.9749 | 5.9838 | 6.9928 | |||
| Upwind | 4.9002 | 5.8989 | 6.8974 | 7.8717 | |||
| Central | 4.9730 | 5.9865 | 7.0001 | 8.0120 | |||
| For | |||||||
| Upwind | 2.0949 | 3.0948 | 4.0948 | 5.0948 | |||
| Central | 2.0958 | 3.0963 | 4.0967 | 5.0971 | |||
| Upwind | 2.1946 | 3.1946 | 4.1945 | 5.1944 | |||
| Central | 2.1967 | 3.1976 | 4.1985 | 5.1994 | |||
| Upwind | 2.2943 | 3.2942 | 4.2940 | 5.2939 | |||
| Central | 2.2976 | 3.2990 | 4.3003 | 5.3017 | |||
| For N = 10,000 | |||||||
| Upwind | 2.0095 | 3.0095 | 4.0095 | 5.0095 | |||
| Central | 2.010 | 3.010 | 4.010 | 5.010 | |||
| Upwind | 2.0195 | 3.0195 | 4.0195 | 5.0195 | |||
| Central | 2.0197 | 3.0198 | 4.0199 | 5.0199 | |||
| Upwind | 2.0295 | 3.0295 | 4.0294 | 5.0294 | |||
| Central | 2.0298 | 3.0299 | 4.0300 | 5.0302 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdizadeh Khalsaraei, M.; Shokri, A.; Wang, Y.; Bazm, S.; Navidifar, G.; Khakzad, P. Qualitatively Stable Schemes for the Black–Scholes Equation. Fractal Fract. 2023, 7, 154. https://doi.org/10.3390/fractalfract7020154
Mehdizadeh Khalsaraei M, Shokri A, Wang Y, Bazm S, Navidifar G, Khakzad P. Qualitatively Stable Schemes for the Black–Scholes Equation. Fractal and Fractional. 2023; 7(2):154. https://doi.org/10.3390/fractalfract7020154
Chicago/Turabian StyleMehdizadeh Khalsaraei, Mohammad, Ali Shokri, Yuanheng Wang, Sohrab Bazm, Giti Navidifar, and Pari Khakzad. 2023. "Qualitatively Stable Schemes for the Black–Scholes Equation" Fractal and Fractional 7, no. 2: 154. https://doi.org/10.3390/fractalfract7020154
APA StyleMehdizadeh Khalsaraei, M., Shokri, A., Wang, Y., Bazm, S., Navidifar, G., & Khakzad, P. (2023). Qualitatively Stable Schemes for the Black–Scholes Equation. Fractal and Fractional, 7(2), 154. https://doi.org/10.3390/fractalfract7020154







