New Fractional Integral Inequalities Pertaining to Center-Radius (cr)-Ordered Convex Functions

Abstract

In this work, we use the idea of interval-valued convex functions of Center-Radius ($\mathtt{cr}$)-order to give fractional versions of Hermite–Hadamard inequality. The results are supported by some numerical estimations and graphical representations considering some suitable examples. The results are novel in the context of $\mathtt{cr}$-convex interval-valued functions and deal with differintegrals of the $\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)$ type. We believe this will be an important contribution to spurring additional research.

1. Introduction

An exciting and dynamic area of study is the theory of convexity. A lot of researchers extend and generalize its various forms in different ways by utilizing creative concepts and successful methodologies. With the help of this theory, we can create and arrange highly effective numerical techniques to address and resolve a wide variety of problems that arise in both pure and applied sciences. The idea of convexity has undergone much development, generalization, and extension in recent years. The theory of convex functions and the theory of inequalities are closely related, according to a number of research. Convex analysis and inequalities have developed into an alluring, fascinating, and useful field for researchers due to numerous generalizations and extensions. The Hermite–Hadamard inequality is an analogous form of a convex function and it must satisfy generalized convexity to establish the said inequality. Interested readers are directed to Refs. [1,2,3,4,5,6,7,8,9,10,11], who discuss convex functions and the associated inequalities that have been researched in recent years.

However, interval analysis can be a helpful method when measuring uncertainty issues. Although it has a rich history that dates back to Archimedes’ measurement of $\pi$, it was not until Moore’s [12] first use of interval analysis for automated error analysis that it was given the attention it deserves. Numerous traditional integral inequalities have been extended to interval-valued functions and fuzzy-valued functions by Costa et al. [13], Flores-Franuli et al. [14], Chalco-cano et al. [15], and others. In particular, Zhao et al. [16] defined an interval h-convex function and using the interval-inclusion relation, demonstrated the related integral inequality. In 2021, Khan et al. [17], used the Kulisch–Miranker order to define an h-convex interval-valued function and certain inequalities for these types of convex functions were established. Because these two relations are in a partial order, any two intervals may not be comparable. As a result, finding a good order to investigate inequalities connected to interval-valued functions is an interesting task. Bhunia et al. [18] utilized the interval’s Center-Radius in 2014 to determine the cr-order, a new rank relationship. Given that this relationship is full-order, it allows the comparison of two intervals. For related works on interval valued inequalities, one can refer to Refs. [19,20,21,22,23,24].

The study of arbitrary order integrals and derivatives is known as fractional calculus. Despite the fact that fractional calculus was created not long after conventional calculus, numerous scientists and researchers are now looking into its origins and principles, particularly in light of the drawbacks of conventional calculus. For examples, see Refs. [25,26,27,28] and also a recent survey expository review article [29]. We draw attention to fractional integral inequalities that can be used to determine whether fractional ordinary and partial differential equations are unique. According to Refs. [30,31,32], there are linkages between integral inequalities and mathematical analysis, differential equations, discrete fractional calculus, difference equations, mathematical physics, and convexity theory.

It has been evident in recent years that mathematicians have a strong preference for presenting well-known inequalities using various novel conceptions of fractional integral operators. One may consult the works [33,34,35,36,37,38,39,40,41] included in this context.

Definition 1 

(see Ref. [42]). A function $\mathrm{H}:\mathrm{X}\subseteq \mathrm{R}\to \mathrm{R}$ is said to be convex for $\mathfrak{p},\mathfrak{s}\in \mathrm{X}$ if and only if

$$\mathrm{H}\left(\Phi \mathfrak{p}+\left(1-\Phi \right)\mathfrak{s}\right)\le \Phi \mathrm{H}\left(\mathfrak{p}\right)+\left(1-\Phi \right)\mathrm{H}\left(\mathfrak{s}\right),$$

(1)

holds true for all $\Phi \in [0,1].$

We first provide the traditional Hermite–Hadmard (H-H) inequality for further discussion, which claims that (see Ref. [43]):

If the function $\mathrm{H}:\mathrm{X}\subseteq \mathrm{R}\to \mathrm{R}$ be a convex function for $\mathfrak{p},\mathfrak{s}\in \mathrm{X}$, then

$$\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\le \frac{1}{\mathfrak{s}-\mathfrak{p}}{\int }_{\mathfrak{p}}^{\mathfrak{s}}\mathrm{H}\left(x\right)dx\le \frac{\mathrm{H}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)}{2},$$

(2)

where $\mathfrak{p}<\mathfrak{s}.$

2. Preliminaries

Here, we provide some fundamental mathematics related to interval analysis that will be extremely useful throughout the article.

$$\left[\mathtt{m}\right]=[\underline{\mathtt{m}},\overline{\mathtt{m}}](\underline{\mathtt{m}}\le x\le \overline{\mathtt{m}};x\in \mathrm{R});$$

$$\left[\mathtt{m}\right]+\left[\mathtt{n}\right]=[\underline{\mathtt{m}},\overline{\mathtt{m}}]+[\underline{\mathtt{n}},\overline{\mathtt{n}}]=[\underline{\mathtt{m}}+\underline{\mathtt{n}},\overline{\mathtt{m}}+\overline{\mathtt{n}}];$$

$$\sigma \mathtt{m}=\sigma [\underline{\mathtt{m}},\overline{\mathtt{m}}]=\left\{\begin{array}{cc}\left[\sigma \underline{\mathtt{m}},\sigma \overline{\mathtt{m}}\right]\hfill & (\sigma >0)\hfill \\ \\ \left\{0\right\}\hfill & (\sigma =0)\hfill \\ \\ \left[\sigma \overline{\mathtt{m}},\sigma \underline{\mathtt{m}}\right]\hfill & (\sigma <0),\hfill \end{array}\right.$$

where $\sigma \in \mathrm{R}$.

Let ${\mathrm{R}}_I,{\mathrm{R}}_I^{+}\mathrm{and}{\mathrm{R}}_I^{-}$ represent, in that order, the sets of all closed intervals of $\mathrm{R}$, all positive closed intervals of $\mathrm{R}$, and all negative closed intervals of $\mathrm{R}$.

Let $\mathtt{m}=[\underline{\mathtt{m}},\overline{\mathtt{m}}]\in {\mathrm{R}}_I$, then the center-radius form of interval $\mathtt{m}$ can be represented as:

$$\mathtt{m}=⟨{\mathtt{m}}_{\mathtt{c}},{\mathtt{m}}_{\mathtt{r}}⟩=⟨\frac{\overline{\mathtt{m}}+\underline{\mathtt{m}}}{2},\frac{\overline{\mathtt{m}}-\underline{\mathtt{m}}}{2}⟩.$$

Definition 2. 

For $\mathtt{m}=[\underline{\mathtt{m}},\overline{\mathtt{m}}]=⟨{\mathtt{m}}_{\mathtt{c}},{\mathtt{m}}_{\mathtt{r}}⟩$, $\mathtt{n}=[\underline{\mathtt{n}},\overline{\mathtt{n}}]=⟨{\mathtt{n}}_{\mathtt{c}},{\mathtt{n}}_{\mathtt{r}}⟩\in {\mathrm{R}}_I$, the center-radius order relation is defined as:

$$\mathtt{m}{⪯}_{\mathtt{cr}}\mathtt{n}⟺\left\{\begin{array}{cc}{\mathtt{m}}_{\mathtt{c}}<{\mathtt{n}}_{\mathtt{c}},\hfill & if{\mathtt{m}}_{\mathtt{c}}\ne {\mathtt{n}}_{\mathtt{c}},\hfill \\ {\mathtt{m}}_{\mathtt{r}}\le {\mathtt{n}}_{\mathtt{r}},\hfill & if{\mathtt{m}}_{\mathtt{r}}={\mathtt{n}}_{\mathtt{r}}.\hfill \end{array}\right.$$

Considering any two intervals $\mathtt{m},\mathtt{n}\in {\mathrm{R}}_I$, either $\mathtt{m}{⪯}_{\mathtt{cr}}\mathtt{n}$ or $\mathtt{n}{⪯}_{\mathtt{cr}}\mathtt{m}$.

Definition 3. 

Let $\mathrm{H}:[\mathfrak{p},\mathfrak{s}]$ be an interval-valued function given as $\mathrm{H}=[\underline{\mathrm{H}},\overline{\mathrm{H}}]$. Then, we say $\mathrm{H}$ is Interval Riemann integrable on $[\mathfrak{p},\mathfrak{s}]$ if $\underline{\mathrm{H}}and\overline{\mathrm{H}}$ are Riemann integrable on $[\mathfrak{p},\mathfrak{s}],$ i.e.,

$$\left(IR\right){\int }_{\mathfrak{p}}^{\mathfrak{s}}\mathrm{H}\left(\mathtt{w}\right)d\mathtt{w}=\left[\left(R\right){\int }_{\mathfrak{p}}^{\mathfrak{s}}\underline{\mathrm{H}}\left(\mathtt{w}\right)d\mathtt{w},\left(R\right){\int }_{\mathfrak{p}}^{\mathfrak{s}}\overline{\mathrm{H}}\left(\mathtt{w}\right)d\mathtt{w}\right].$$

According to the $\mathtt{cr}$-order relations, the integral is order-preserving, as demonstrated by Shi et al. [44].

Theorem 1. 

Suppose $\mathrm{H},\mathrm{Q}:[\mathfrak{p},\mathfrak{s}]\to \mathrm{R}$ given by $\mathrm{H}=[\underline{\mathrm{H}},\overline{\mathrm{H}}]$ and $\mathrm{Q}=[\underline{\mathrm{Q}},\overline{\mathrm{Q}}]$ are interval-valued functions. If $\mathrm{H}\left(\mathtt{w}\right){⪯}_{\mathtt{cr}}\mathrm{Q}\left(\mathtt{w}\right)$ for all $u\in [\mathfrak{p},\mathfrak{s}]$, then

$${\int }_{\mathfrak{p}}^{\mathfrak{s}}\mathrm{H}\left(\mathtt{w}\right)d\mathtt{w}{⪯}_{\mathtt{cr}}{\int }_{\mathfrak{p}}^{\mathfrak{s}}\mathrm{Q}\left(\mathtt{w}\right)d\mathtt{w}.$$

Definition 4 

(see Refs. [29,45]). Let $\mathrm{H}\in \mathrm{L}\left[\mathfrak{p},\mathfrak{s}\right]$ (the set of all Lebesgue measurable functions), where $\mathfrak{p}\le 0\le \mathfrak{s}$. Then the left $\left({\mathrm{J}}_{{\mathfrak{p}}^{+}}^{\alpha }\right)$ and right $\left({\mathrm{J}}_{{\mathfrak{s}}^{-}}^{\alpha }\right)$ Riemann–Liouville (R-L) fractional integrals of order $\alpha \in (0,1)$ are defined as follows:

$${\mathrm{J}}_{{\mathfrak{p}}^{+}}^{\alpha }\mathtt{F}\left(x\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{\mathfrak{p}}^x{\left(x-\Phi \right)}^{\alpha -1}\mathtt{F}\left(\Phi \right)d\Phi ,\left(x>\mathfrak{p}\right),$$

and

$${\mathrm{J}}_{{\mathfrak{s}}^{-}}^{\alpha }\mathtt{F}\left(x\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_x^{\mathfrak{s}}{\left(\Phi -x\right)}^{\alpha -1}\mathtt{F}\left(\Phi \right)d\Phi (x<\mathfrak{s}),$$

respectively, where $\Gamma \left(\alpha \right)={\int }_0^{\infty }{\Phi }^{\alpha -1}{e}^{-\Phi }d\Phi$ is the Euler gamma function.

The major objective of this article is to provide a link between the concepts of interval-valued analysis and fractional order integral inequalities using total order relations, specifically the Center-Radius order relation. We first introduce a novel midpoint type H-H inequality for $\mathtt{cr}$-convex interval-valued functions. Then, we propose integral inequalities for the product of two $\mathtt{cr}$-convex interval-valued functions using differintegrals of the $\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)$ type.

The paper is structured as follows: After reviewing the prerequisite information and pertinent details on inequalities and interval-valued analysis in Section 2, we address $\mathtt{cr}$-ordered interval-valued convex functions with numerical estimations and graphical representations in Section 3. The interval-valued H-H type inequalities for $\mathtt{cr}$ interval-valued convex functions are then derived in Section 4. Examples, numerical estimations and graphical behavior of the presented results are also taken into account to determine whether the predetermined results are advantageous. We conclude with Section 5, exploring a brief conclusion and possible areas for additional researches that are related to the findings in this paper.

3. Interval-Valued $\mathtt{cr}$-Convex Function

Definition 5. 

Let $\mathrm{H},\mathrm{Q}:[\mathfrak{p},\mathfrak{s}]\to \mathrm{R}$ be non negative functions defined by $\mathrm{H}=[\underline{\mathrm{H}},\overline{\mathrm{H}}]$. Then, we say the function $\mathrm{H}$ as a $\mathtt{cr}$-convex function if

$$\mathrm{H}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right){⪯}_{\mathtt{cr}}\Phi \mathrm{H}\left(\mathfrak{p}\right)+(1-\Phi )\mathrm{H}\left(\mathfrak{s}\right),(\forall \mathfrak{p},\mathfrak{s}\in \mathrm{X};\Phi \in \left[0,1\right]).$$

Proposition 1. 

Let $\mathrm{H}:[\mathfrak{p},\mathfrak{s}]\to {\mathrm{R}}_I$ defined by $\mathrm{H}=[\underline{\mathrm{H}},\overline{\mathrm{H}}]=⟨{\mathrm{H}}_{\mathtt{c}},{\mathrm{H}}_{\mathtt{r}}⟩$. Then, $\mathrm{H}$ is interval valued $\mathtt{cr}$-convex functions if and only if ${\mathrm{H}}_{\mathtt{c}}$ and ${\mathrm{H}}_{\mathtt{r}}$ are convex functions.

Proof. 

Since ${\mathrm{H}}_{\mathtt{c}}$ and ${\mathrm{H}}_{\mathtt{r}}$ are convex functions, then for each $\Phi \in [0,1]$, we have

$${\mathrm{H}}_{\mathtt{c}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right)\le \Phi {\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{s}\right),$$

and

$${\mathrm{H}}_{\mathtt{r}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right)\le \Phi {\mathrm{H}}_{\mathtt{r}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{r}}\left(\mathfrak{s}\right),$$

If ${\mathrm{H}}_{\mathtt{c}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right)\ne \Phi {\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{s}\right)$, then

$${\mathrm{H}}_{\mathtt{c}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right)<\Phi {\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{s}\right).$$

This implies,

$${\mathrm{H}}_{\mathtt{c}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right){⪯}_{\mathtt{cr}}\Phi {\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{c}}\left(\mathfrak{s}\right).$$

Otherwise, ${\mathrm{H}}_{\mathtt{r}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right)\le \Phi {\mathrm{H}}_{\mathtt{r}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{r}}\left(\mathfrak{s}\right)$.

This implies

$${\mathrm{H}}_{\mathtt{r}}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right){⪯}_{\mathtt{cr}}\Phi {\mathrm{H}}_{\mathtt{r}}\left(\mathfrak{p}\right)+(1-\Phi ){\mathrm{H}}_{\mathtt{r}}\left(\mathfrak{s}\right).$$

Now, from Definition 2, we can clearly see that,

$$\mathrm{H}\left(\Phi \mathfrak{p}+(1-\Phi )\mathfrak{s}\right){⪯}_{\mathtt{cr}}\Phi \mathrm{H}\left(\mathfrak{p}\right)+(1-\Phi )\mathrm{H}\left(\mathfrak{s}\right).$$

This concludes the proof. □

Example 1. 

Let $\mathrm{H}:[\mathfrak{p},\mathfrak{s}]\to {\mathrm{R}}_I^{+}$ be defined as

$$\mathrm{H}\left(\nu \right)=\left[-{\nu }^2+2,2{\nu }^2+3\right],\nu \in [0,1].$$

Then,

$${\mathrm{H}}_{\mathtt{c}}\left(\nu \right)=\frac{{\nu }^2+5}{2}and{\mathrm{H}}_{\mathtt{r}}\left(\nu \right)=\frac{3{\nu }^2+1}{2}.$$

Figure 1 is the graphical representation of the $\mathtt{cr}$ interval valued convex function i.e., $\mathrm{H}\left(\nu \right)$.

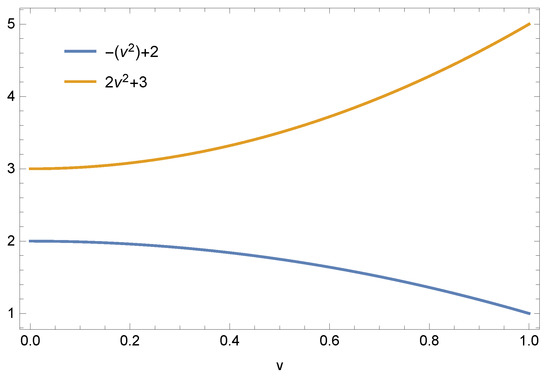
Figure 1. Graphical behaviour of the CR interval valued convex functions given in Example 1.

From Figure 2, it is clearly seen that both the ${\mathrm{H}}_{\mathtt{c}}\left(\nu \right)$ and ${\mathrm{H}}_{\mathtt{r}}\left(\nu \right)$ are convex in nature and hence Example 1 is $\mathtt{cr}$-convex function and Table 1 numerically proves this.

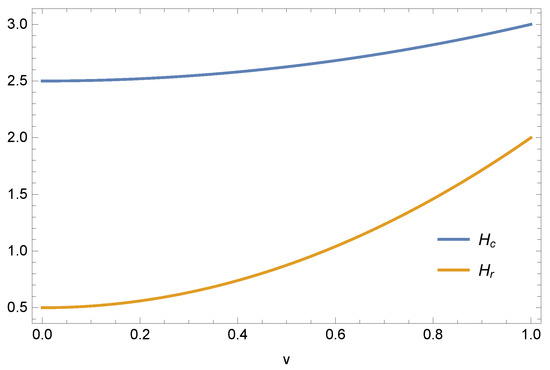
Figure 2. Graphical behaviour of ${\mathrm{H}}_{\mathtt{c}}\left(\nu \right)$ and ${\mathrm{H}}_{\mathtt{r}}\left(\nu \right)$ of Example 1.

Table 1. Numerical validation of Example 1 for $\mathfrak{p}=0$, $\mathfrak{s}=1$.

Value of $\mathit{\Phi }$	Center Value of $\mathbf{H}\left(\mathit{\Phi }\mathfrak{p}+(1-\mathit{\Phi })\mathfrak{s}\right)$	Center Value of $\mathit{\Phi }\mathbf{H}\left(\mathfrak{p}\right)+(1-\mathit{\Phi })\mathbf{H}\left(\mathfrak{s}\right)$
$0.1$	2.905	2.95
$0.2$	2.820	2.90
$0.3$	2.745	2.85
$0.4$	2.680	2.80
$0.5$	2.625	2.75
$0.6$	2.580	2.70
$0.7$	2.545	2.65
$0.8$	2.520	2.60
$0.9$	2.505	2.55

Example 2. 

Let $\mathrm{Q}:[\mathfrak{p},\mathfrak{s}]\to {\mathrm{R}}_I^{+}$ be defined as

$$\mathrm{Q}\left(\nu \right)=\left[-{\nu }^4+2,{\nu }^4+3\right],\nu \in [0,1].$$

Then,

$${\mathrm{Q}}_{\mathtt{c}}\left(\nu \right)=\frac{5}{2}and{\mathrm{Q}}_{\mathtt{r}}\left(\nu \right)=\frac{2{\nu }^2+1}{2}.$$

Again, by Proposition 1, $\mathrm{Q}$ is also $\mathtt{cr}$ convex function.

4. Integral Inequalities Pertaining to R-L Fractional Integrals

This section establishes interval-valued fractional integral inequalities of the Hermite–Hadamard type, which include the $\mathtt{cr}$-convex interval-valued function and are a product of two $\mathtt{cr}$-convex interval-valued functions.

Theorem 2. 

Let $\mathrm{H}:\left[\mathfrak{p},\mathfrak{s}\right]\to {\mathrm{R}}_I^{+}$ be an $\mathtt{cr}$-convex interval-valued function on $\left[\mathfrak{p},\mathfrak{s}\right],$ which is given by

$$\mathrm{H}\left(\omega \right)=\left[\underline{\mathrm{H}}\left(\omega \right),\overline{\mathrm{H}}\left(\omega \right)\right]$$

for all $\omega \in \left[\mathfrak{p},\mathfrak{s}\right]$, then

$$\begin{array}{cc}\hfill \mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)& {⪯}_{\mathtt{cr}}\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\frac{\mathrm{H}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)}{2}.\hfill \end{array}$$

Proof. 

Let $\mathrm{H}:\left[\mathfrak{p},\mathfrak{s}\right]\to {\mathrm{R}}_I^{+}$ be an $\mathtt{cr}$-convex interval-valued function. Then, choosing

$$\omega =\left(\frac{2-\Phi }{2}\right)\mathfrak{s}+\frac{\Phi }{2}\mathfrak{p}\mathrm{and}\nu =\left(\frac{2-\Phi }{2}\right)\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s},$$

we obtain

$$2\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right){⪯}_{\mathtt{cr}}\mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)+\mathrm{H}\left(\left(\frac{2-\Phi }{2}\right)\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right).$$

Multiplying both sides of the above equations by ${\Phi }^{\alpha -1}$ and integrating the obtained results with respect to $\Phi$ over $(0,1)$, we find that

$$\begin{array}{c}2{\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)d\Phi \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{⪯}_{\mathtt{cr}}{\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)d\Phi +{\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\left(\frac{2-\Phi }{2}\right)\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)d\Phi .\end{array}$$

This implies that

$$\begin{array}{cc}\hfill & \frac{2}{\alpha }\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)d\Phi \hfill \\ \hfill {⪯}_{\mathtt{cr}}& \left[{\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)d\Phi +{\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\left(\frac{2-\Phi }{2}\right)\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)d\Phi \right]\hfill \\ \hfill =& [{\int }_0^1{\Phi }^{\alpha -1}\left(\underline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)+\underline{\mathrm{H}}\left(\left(\frac{2-\Phi }{2}\right)\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\right)d\Phi ,\hfill \\ \hfill & {\int }_0^1{\Phi }^{\alpha -1}\left(\overline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)+\overline{\mathrm{H}}\left(\left(\frac{2-\Phi }{2}\right)\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\right)d\Phi ]\hfill \\ \hfill =& [\frac{2^{\alpha }}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\int }_{\mathfrak{p}}^{\frac{\mathfrak{p}+\mathfrak{s}}{2}}{\left(\nu -\mathfrak{p}\right)}^{\alpha -1}\underline{\mathrm{H}}\left(\nu \right)d\nu +{\int }_{\frac{\mathfrak{p}+\mathfrak{s}}{2}}^{\mathfrak{s}}{(\mathfrak{s}-\omega )}^{\alpha -1}\underline{\mathrm{H}}\left(\omega \right)d\omega \right),\hfill \\ \hfill & \frac{2^{\alpha }}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\int }_{\mathfrak{p}}^{\frac{\mathfrak{p}+\mathfrak{s}}{2}}{\left(\nu -\mathfrak{p}\right)}^{\alpha -1}\overline{\mathrm{H}}\left(\nu \right)d\nu +{\int }_{\frac{\mathfrak{p}+\mathfrak{s}}{2}}^{\mathfrak{s}}{(\mathfrak{s}-\omega )}^{\alpha -1}\overline{\mathrm{H}}\left(\omega \right)d\omega \right)]\hfill \\ \hfill =& \frac{2^{\alpha }\Gamma \left(\alpha \right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left[\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\underline{\mathrm{H}}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\underline{\mathrm{H}}\left(\mathfrak{p}\right)\right),\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\overline{\mathrm{H}}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\overline{\mathrm{H}}\left(\mathfrak{p}\right)\right)\right]\hfill \\ \hfill =& \frac{2^{\alpha }\Gamma \left(\alpha \right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left[{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\right].\hfill \end{array}$$

Upon further simplification, we have

$$\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right){⪯}_{\mathtt{cr}}\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\right).$$

(3)

Following a similar procedure as above, we also have

$$\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\right){⪯}_{\mathtt{cr}}\frac{\mathrm{H}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)}{2}.$$

(4)

From (3) and (4), we acquire

$$\begin{array}{cc}\hfill \mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)& {⪯}_{\mathtt{cr}}\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\right)\hfill \\ & {⪯}_{\mathtt{cr}}\frac{\mathrm{H}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)}{2}.\hfill \end{array}$$

This concudes the rest of the proof. □

Remark 1. 

Choosing $\alpha =1,$ in Theorem 2, we retrieve the following result presented in Ref. [44], Remark 4.2.

$$\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right){⪯}_{\mathtt{cr}}\frac{1}{\mathfrak{s}-\mathfrak{p}}{\int }_{\mathfrak{p}}^{\mathfrak{s}}\mathrm{H}\left(\omega \right)d\omega {⪯}_{\mathtt{cr}}\frac{\mathrm{H}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)}{2}.$$

Now, we show the validity of Theorem 2 through Figure 3.

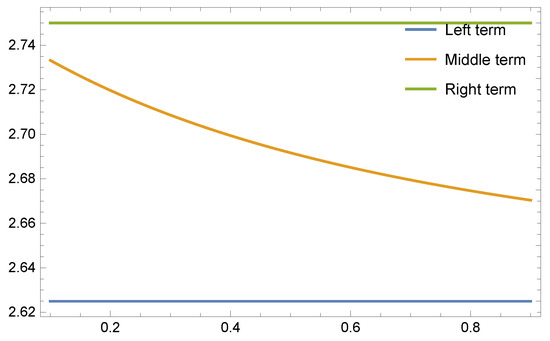
Figure 3. Graphical behaviour of Theorem 2 from the values of Table 2 for $0<\alpha <1$.

For further refinements, the next two theorems that follow are primarily concerned with proving interval fractional integral inequalities of the Pachpatte type.

Theorem 3. 

Let $\mathrm{H},\mathrm{Q}:\left[\mathfrak{p},\mathfrak{s}\right]\to {\mathrm{R}}_I^{+}$ be two $\mathtt{cr}$-convex interval-valued functions on $\left[\mathfrak{p},\mathfrak{s}\right]$ such that

$$\mathrm{H}\left(\omega \right)=\left[\underline{\mathrm{H}}\left(\omega \right),\overline{\mathrm{H}}\left(\omega \right)\right]\mathit{and}\mathrm{Q}\left(\omega \right)=\left[\underline{\mathrm{Q}}\left(\omega \right),\overline{\mathrm{Q}}\left(\omega \right)\right]$$

for all $\omega \in \left[\mathfrak{p},\mathfrak{s}\right]$, then

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\frac{\alpha }{4}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right){\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)+\frac{\alpha }{4}\left(\frac{2}{\alpha +1}-\frac{1}{\alpha +2}\right)\Delta \left(\mathfrak{p},\mathfrak{s}\right),\hfill \end{array}$$

where

$${\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)=\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right),$$

$$\Delta \left(\mathfrak{p},\mathfrak{s}\right)=\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{s}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{p}\right).$$

Proof. 

By the hypothesis of $\mathtt{cr}$-convex interval-valued functions, we can write

$$\mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right){⪯}_{\mathtt{cr}}\frac{\Phi }{2}\mathrm{H}\left(\mathfrak{p}\right)+\frac{(2-\Phi )}{2}\mathrm{H}\left(\mathfrak{s}\right),$$

and

$$\mathrm{Q}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right){⪯}_{\mathtt{cr}}\frac{\Phi }{2}\mathrm{Q}\left(\mathfrak{p}\right)+\frac{(2-\Phi )}{2}\mathrm{Q}\left(\mathfrak{s}\right).$$

So that

$$\begin{array}{cc}\hfill & \mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)\mathrm{Q}\left(\frac{\Phi }{2}\mathfrak{p}+\left(\frac{2-\Phi }{2}\right)\mathfrak{s}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\left(\frac{\Phi }{2}\mathrm{H}\left(\mathfrak{p}\right)+\frac{\left(2-\Phi \right)}{2}\mathrm{H}\left(\mathfrak{s}\right)\right)\left(\frac{\Phi }{2}\mathrm{Q}\left(\mathfrak{p}\right)+\frac{\left(2-\Phi \right)}{2}\mathrm{Q}\left(\mathfrak{s}\right)\right)\hfill \\ \hfill & =\frac{{\Phi }^2}{4}\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)+\frac{{\left(2-\Phi \right)}^2}{4}\underline{\mathrm{H}}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)+\frac{\Phi \left(2-\Phi \right)}{4}[\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{s}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{p}\right)].\hfill \end{array}$$

(5)

Analogously, we have

$$\begin{array}{cc}\hfill & \mathrm{H}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\mathrm{Q}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\left(\frac{2-\Phi }{2}\mathrm{H}\left(\mathfrak{p}\right)+\frac{\Phi }{2}\mathrm{H}\left(\mathfrak{s}\right)\right)\left(\frac{2-\Phi }{2}\mathrm{Q}\left(\mathfrak{p}\right)+\frac{\Phi }{2}\mathrm{Q}\left(\mathfrak{s}\right)\right)\hfill \\ \hfill & =\frac{{(2-\Phi )}^2}{4}\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)+\frac{{\Phi }^2}{4}\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)+\frac{\Phi \left(2-\Phi \right)}{4}[\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{s}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{p}\right)].\hfill \end{array}$$

(6)

Adding (5) and (6), we have

$$\begin{array}{cc}\hfill & \mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\mathrm{Q}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)+\mathrm{H}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\mathrm{Q}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\left(\frac{{{\Phi }^2+\left(2-\Phi \right)}^2}{4}\right)\left[\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)\right]+\frac{\Phi (2-\Phi )}{2}\left[\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{s}\right)\right].\hfill \end{array}$$

(7)

Upon multiplying ${\Phi }^{\alpha -1}$ to both sides of the above equation (7) and then integrating over (0, 1), we obtain

$$\begin{array}{cc}\hfill & {\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\mathrm{Q}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)d\Phi +{\int }_0^1{\Phi }^{\alpha -1}\mathrm{H}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\mathrm{Q}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)d\Phi \hfill \\ \hfill & {⪯}_{\mathtt{cr}}{\rm Y}\left(\mathfrak{p},\mathfrak{s}\right){\int }_0^1{\Phi }^{\alpha -1}\left(\frac{{{\Phi }^2+\left(2-\Phi \right)}^2}{4}\right)d\Phi +\Delta \left(\mathfrak{p},\mathfrak{s}\right){\int }_0^1{\Phi }^{\alpha -1}\frac{\Phi (2-\Phi )}{2}d\Phi .\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill & \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\frac{\alpha }{4}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right){\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)+\frac{\alpha }{4}\left(\frac{2}{\alpha +1}-\frac{1}{\alpha +2}\right)\Delta \left(\mathfrak{p},\mathfrak{s}\right).\hfill \end{array}$$

This concludes the proof of Theorem 3. □

Now, we show the validity of Theorem 3 through Figure 4.

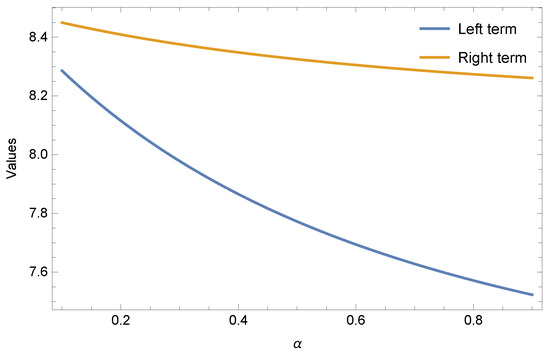
Figure 4. Graphical behavior of Theorem 3 from the values of Table 3 for $0<\alpha <1$.

Theorem 4. 

Let $\mathrm{H},\mathrm{Q}:\left[\mathfrak{p},\mathfrak{s}\right]\to {\mathrm{R}}_I^{+}$ be two $\mathtt{cr}$-convex interval-valued functions such that

$$\mathrm{H}\left(\omega \right)=\left[\underline{\mathrm{H}}\left(\omega \right),\overline{\mathrm{H}}\left(\omega \right)\right]\mathit{and}\mathrm{Q}\left(\omega \right)=\left[\underline{\mathrm{Q}}\left(\omega \right),\overline{\mathrm{Q}}\left(\omega \right)\right],$$

for all $\omega \in \left[\mathfrak{p},\mathfrak{s}\right],$ then, the following interval-valued fractional inequality holds true:

$$\begin{array}{cc}\hfill & 2\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\mathrm{Q}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\overline{\mathrm{Q}}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & +\frac{\alpha }{2}\left(\frac{1}{\alpha +1}-\frac{1}{2(\alpha +2)}\right){\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)+\frac{\alpha }{4}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right)\Delta \left(\mathfrak{p},\mathfrak{s}\right),\hfill \end{array}$$

where

$${\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)=\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{p}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right),$$

$$\Delta \left(\mathfrak{p},\mathfrak{s}\right)=\mathrm{H}\left(\mathfrak{p}\right)\mathrm{Q}\left(\mathfrak{s}\right)+\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{p}\right).$$

Proof. 

Suppose that $\mathrm{H},\mathrm{Q}:\left[\mathfrak{p},\mathfrak{s}\right]\to {\mathrm{R}}_I^{+}$ are $\mathtt{cr}$-convex interval-valued functions. Then, by the hypothesis, we have

$$\begin{array}{cc}\hfill & 4\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\mathrm{Q}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}[\underline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)+\underline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\hfill \\ \hfill & +\underline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)+\underline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right),\hfill \\ \hfill & \overline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)+\overline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\hfill \\ \hfill & +\overline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)+\overline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)]\hfill \\ \hfill & {⪯}_{\mathtt{cr}}[\underline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)+\underline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\hfill \\ \hfill & +\left(\frac{\Phi (2-\Phi )}{2}\right){\rm Y}(\mathfrak{p},\mathfrak{s})+\left(\frac{{\Phi }^2+2-2\Phi }{2}\right)\Delta (\mathfrak{p},\mathfrak{s}),\hfill \\ \hfill & \overline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)+\overline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\hfill \\ \hfill & +\left(\frac{\Phi (2-\Phi )}{2}\right){\rm Y}(\mathfrak{p},\mathfrak{s})+\left(\frac{{\Phi }^2+2-2\Phi }{2}\right)\Delta (\mathfrak{p},\mathfrak{s})].\hfill \end{array}$$

(8)

Multiplying the equations (8) by ${\Phi }^{\alpha -1}$ and then integrating over $(0,1),$ we get

$$\begin{array}{cc}\hfill & 4\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\mathrm{Q}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right){\int }_0^1{\Phi }^{\alpha -1}d\Phi \hfill \\ \hfill & {⪯}_{\mathtt{cr}}[{\int }_0^1{\Phi }^{\alpha -1}\underline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)d\Phi \hfill \\ \hfill & +{\int }_0^1{\Phi }^{\alpha -1}\underline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)d\Phi \hfill \\ \hfill & +{\rm Y}(\mathfrak{p},\mathfrak{s}){\int }_0^1{\Phi }^{\alpha -1}\frac{\Phi (2-\Phi )}{2}d\Phi +\Delta (\mathfrak{p},\mathfrak{s}){\int }_0^1{\Phi }^{\alpha -1}\frac{{\Phi }^2+2-2\Phi }{2}d\Phi ,\hfill \\ \hfill & {\int }_0^1{\Phi }^{\alpha -1}\overline{\mathrm{H}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{\Phi }{2}\mathfrak{p}+\frac{2-\Phi }{2}\mathfrak{s}\right)d\Phi \hfill \\ \hfill & +{\int }_0^1{\Phi }^{\alpha -1}\overline{\mathrm{H}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\frac{2-\Phi }{2}\mathfrak{p}+\frac{\Phi }{2}\mathfrak{s}\right)d\Phi \hfill \\ \hfill & +{\rm Y}(\mathfrak{p},\mathfrak{s}){\int }_0^1{\Phi }^{\alpha -1}\frac{\Phi (2-\Phi )}{2}d\Phi +\Delta (\mathfrak{p},\mathfrak{s}){\int }_0^1{\Phi }^{\alpha -1}\frac{{\Phi }^2+2-2\Phi }{2}d\Phi ].\hfill \end{array}$$

From the above developments, we find

$$\begin{array}{cc}\hfill & \frac{4}{\alpha }\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\mathrm{Q}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}[\frac{2^{\alpha }\Gamma \left(\alpha \right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\underline{\mathrm{H}}\left(\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\underline{\mathrm{H}}\left(\mathfrak{p}\right)\underline{\mathrm{Q}}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & +\left(\frac{1}{\alpha +1}-\frac{1}{2(\alpha +2)}\right){\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)+\frac{1}{2}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right)\Delta \left(\mathfrak{p},\mathfrak{s}\right),\hfill \\ \hfill & \frac{2^{\alpha }\Gamma \left(\alpha \right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\overline{\mathrm{H}}\left(\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\overline{\mathrm{H}}\left(\mathfrak{p}\right)\overline{\mathrm{Q}}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & +\left(\frac{1}{\alpha +1}-\frac{1}{2(\alpha +2)}\right){\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)+\frac{1}{2}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right)\Delta \left(\mathfrak{p},\mathfrak{s}\right)].\hfill \end{array}$$

Consequently, we have

$$\begin{array}{cc}\hfill & 2\left[\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\mathrm{Q}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\right]\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left[\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\underline{\mathrm{H}}\left(\mathfrak{s}\right)\underline{\mathrm{Q}}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\underline{\mathrm{H}}\left(\mathfrak{p}\right)\underline{\mathrm{Q}}\left(\mathfrak{p}\right)\right),\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\overline{\mathrm{H}}\left(\mathfrak{s}\right)\overline{\mathrm{Q}}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\overline{\mathrm{H}}\left(\mathfrak{p}\right)\overline{\mathrm{Q}}\left(\mathfrak{p}\right)\right)\right]\hfill \\ \hfill & +\frac{\alpha }{2}\left(\frac{1}{\alpha +1}-\frac{1}{2(\alpha +2)}\right)[{\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)]+\frac{\alpha }{4}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right)\left[\Delta \left(\mathfrak{p},\mathfrak{s}\right)\right],\hfill \end{array}$$

which readily yields

$$\begin{array}{cc}\hfill & 2\mathrm{H}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\mathrm{Q}\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)\hfill \\ \hfill & {⪯}_{\mathtt{cr}}\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(\mathfrak{s}-\mathfrak{p}\right)}^{\alpha }}\left({\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{+}}^{\alpha }\mathrm{H}\left(\mathfrak{s}\right)\mathrm{Q}\left(\mathfrak{s}\right)+{\mathrm{J}}_{{\left(\frac{\mathfrak{p}+\mathfrak{s}}{2}\right)}^{-}}^{\alpha }\mathrm{H}\left(\mathfrak{p}\right)\overline{\mathrm{Q}}\left(\mathfrak{p}\right)\right)\hfill \\ \hfill & +\frac{\alpha }{2}\left(\frac{1}{\alpha +1}-\frac{1}{2(\alpha +2)}\right){\rm Y}\left(\mathfrak{p},\mathfrak{s}\right)+\frac{\alpha }{4}\left(\frac{1}{\alpha +2}-\frac{2}{\alpha +1}+\frac{2}{\alpha }\right)\Delta \left(\mathfrak{p},\mathfrak{s}\right).\hfill \end{array}$$

This completes the proof of Theorem 4. □

5. Conclusions

This study examines an innovative approach of incorporating a Center-Radius order relation and the integral inequalities that go along with them. Hermite–Hadamard-type inequalities are generalized using the interval-valued Riemann–Liouville fractional operator. It will be very interesting to apply the idea of $\mathtt{cr}$-convex interval-valued functions and fuzzy interval-valued functions to the Hadamard–Mercer type and other related integral inequalities in future studies.

It is feasible to analyze varieties of convex inequalities using the methods and concepts presented in this study, with potential applicability to topics such as optimization and differential equations that have convex shapes.