A Generalization of Poiseuille’s Law for the Flow of a Self-Similar (Fractal) Fluid through a Tube Having a Fractal Rough Surface
Abstract
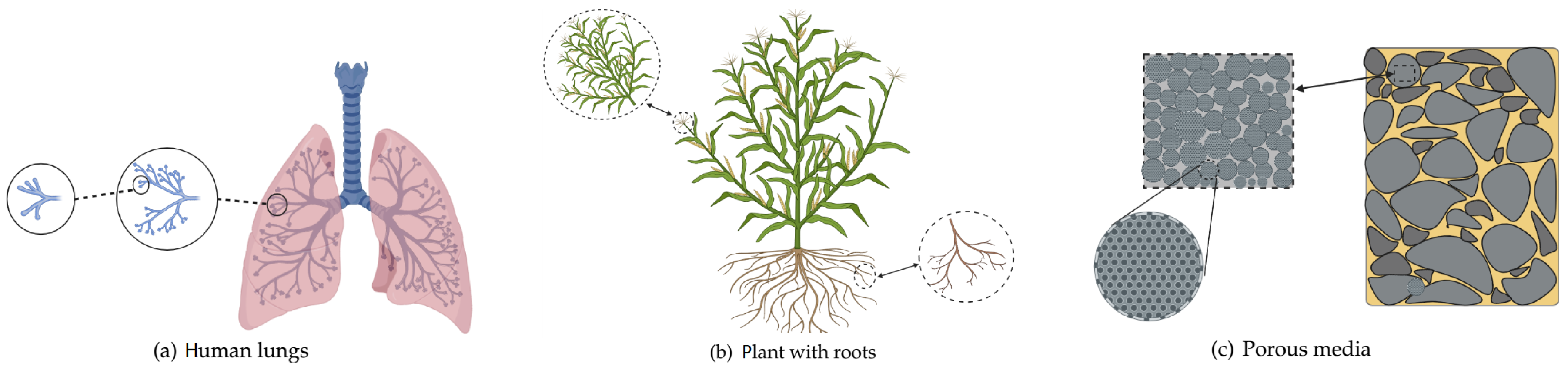
1. Introduction
2. Theoretical Models
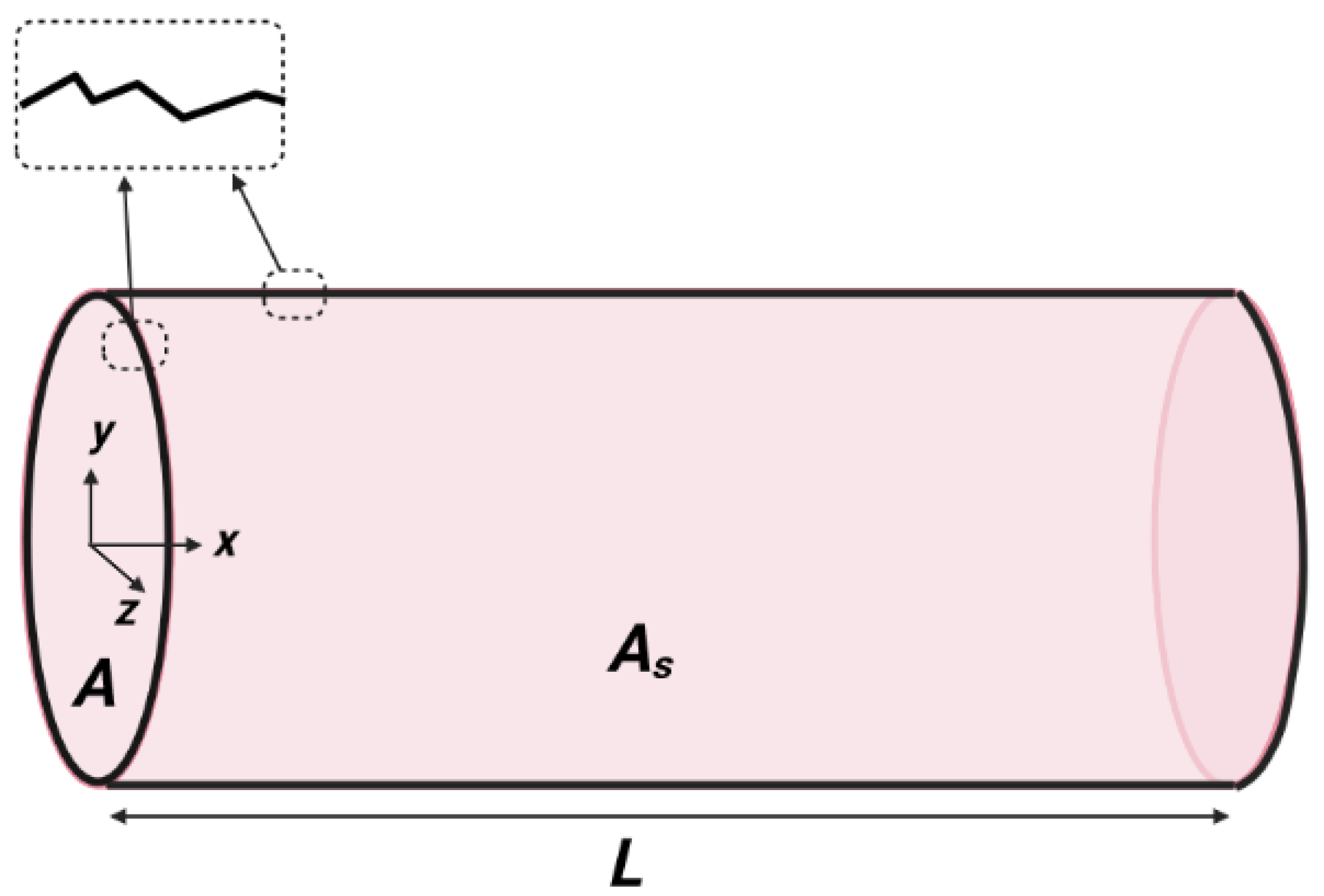
2.1. Poiseuille’s Law for Viscous Fluid Flow through a Cylindrical Pipe
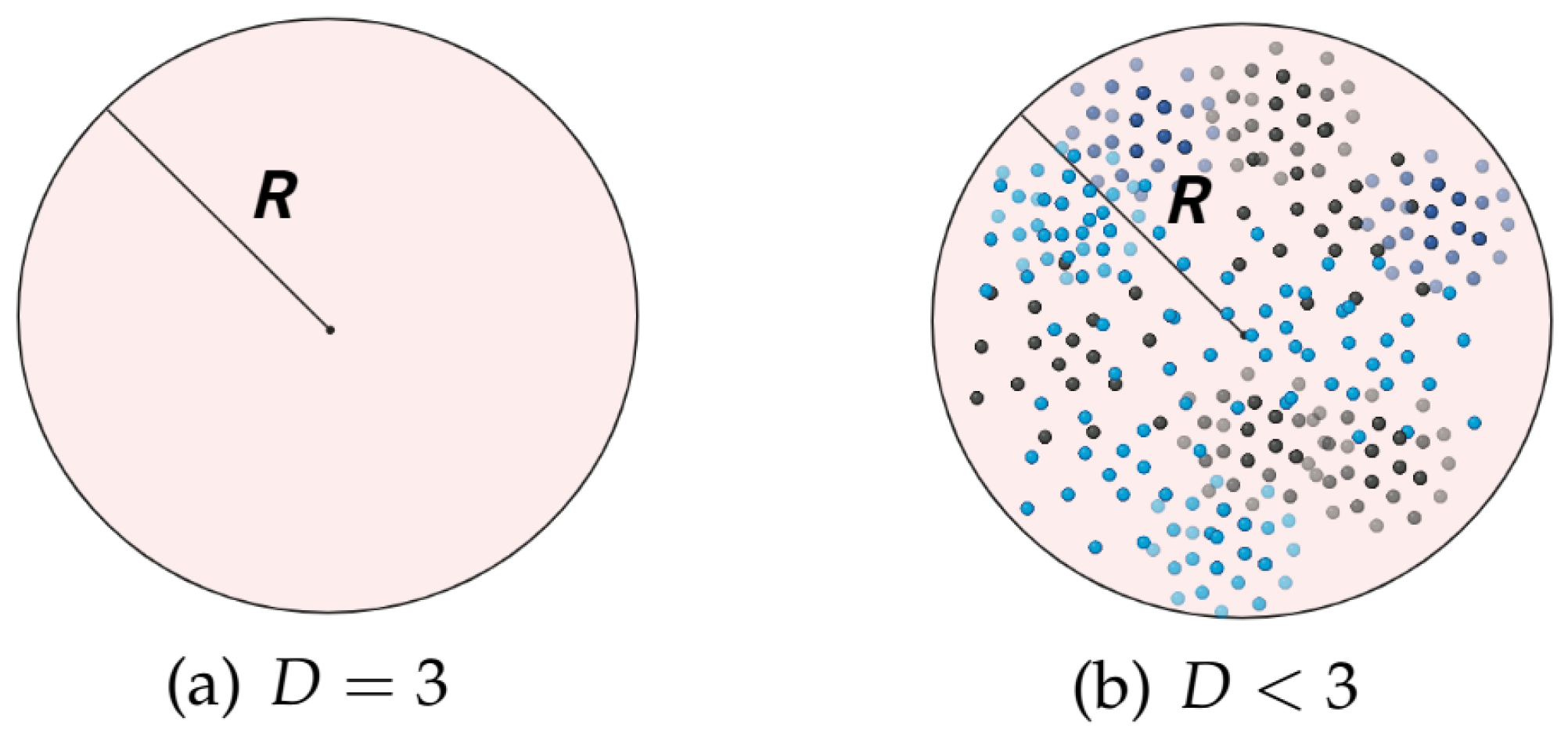
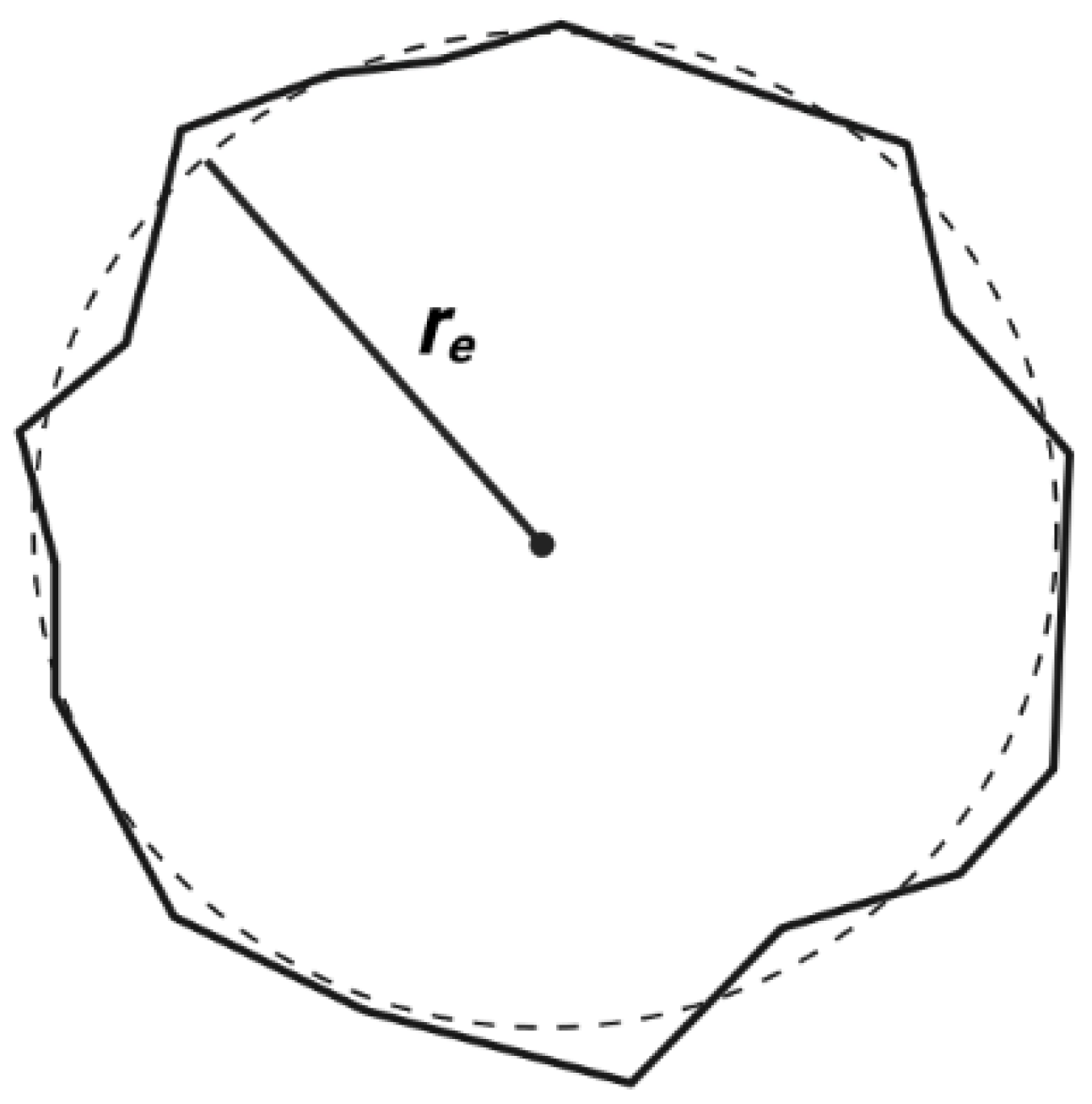
2.2. Modeling Surface Roughness Using Fractal Dimensions
The Length–Radius Relationship in a Tube
2.3. Vector Calculus in Noninteger Dimensional Space
3. Laminar Flow of a Self-Similar Fluid through a Tube with Rough Walls
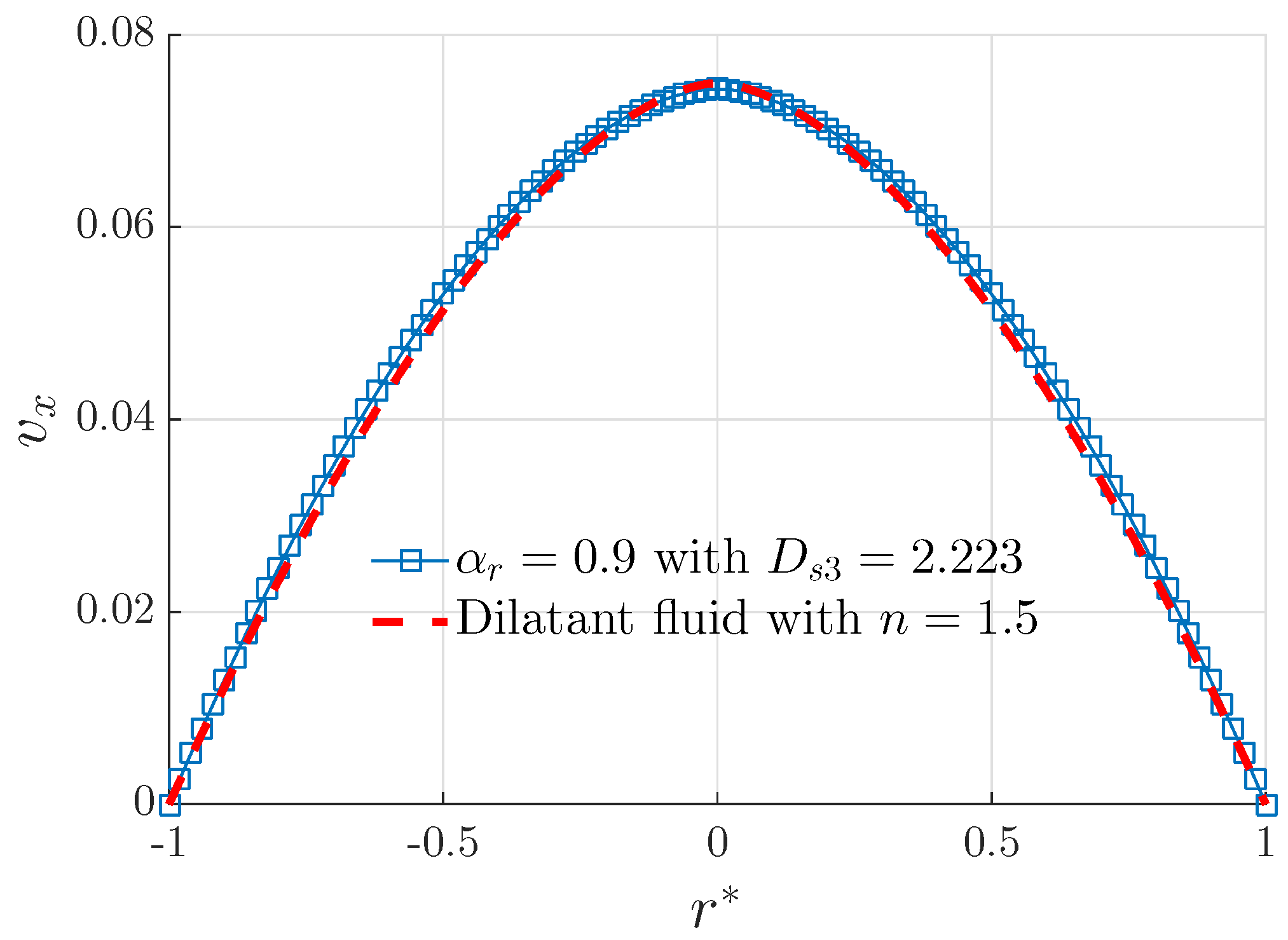
3.1. Velocity Profile of a Self-Similar Fluid
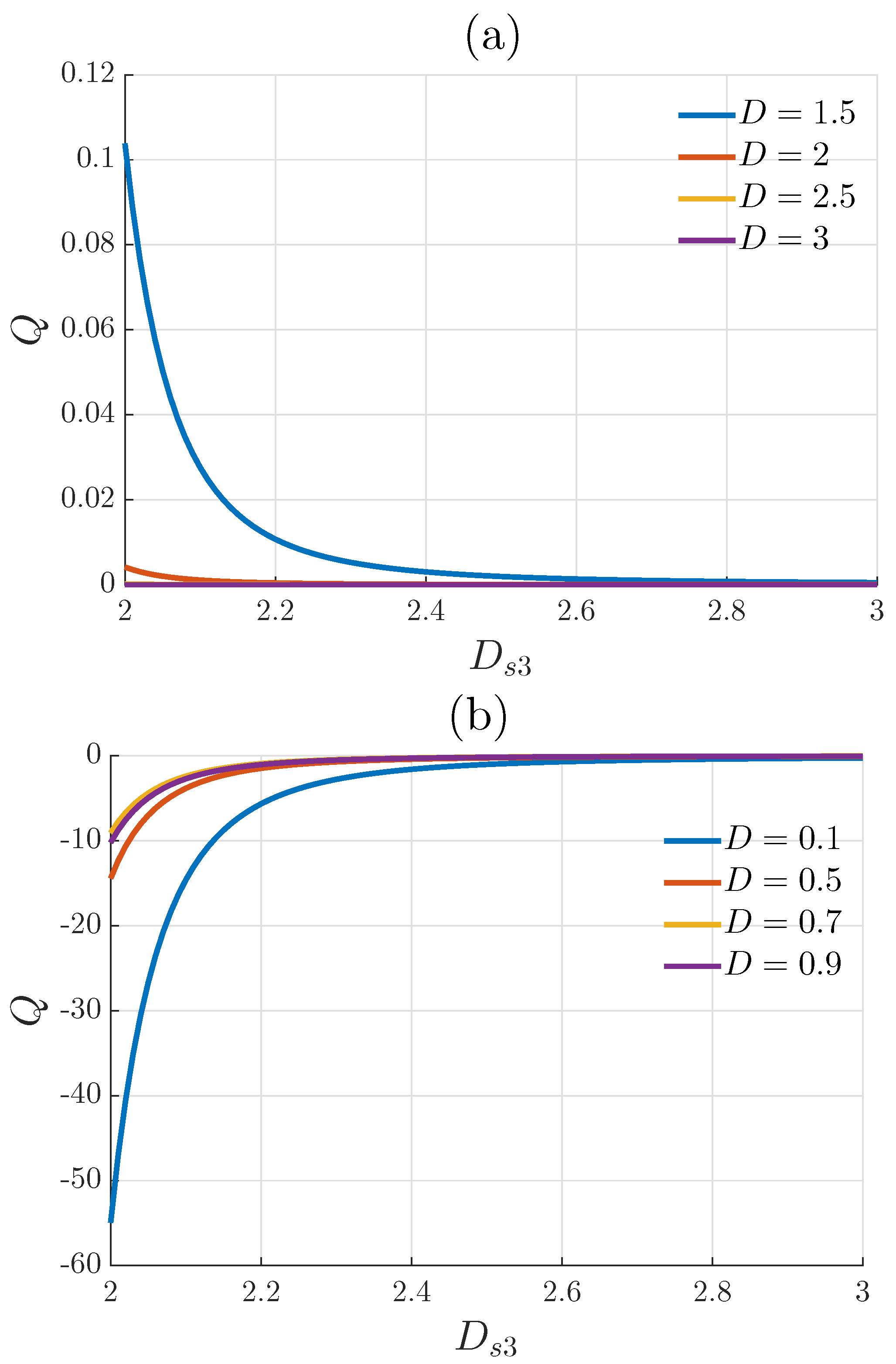
3.2. Fluid Discharge
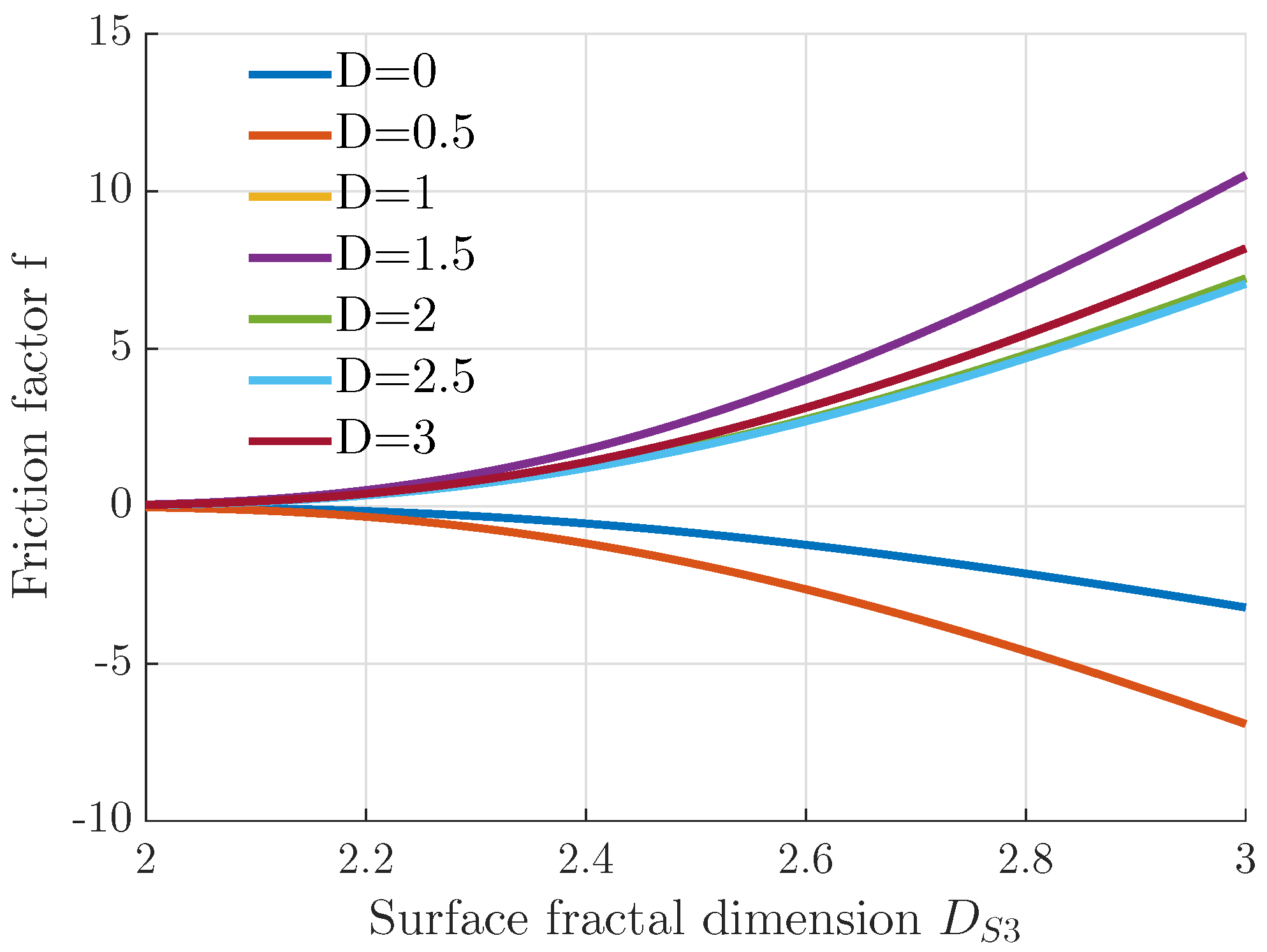
3.3. Darcy’s Friction Factor
4. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH freeman: New York, NY, USA, 1982. [Google Scholar]
- Mandelbrot, B.B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Bizzarri, M.; Giuliani, A.; Cucina, A.; Anselmi, F.D.; Soto, A.M.; Sonnenschein, C. Fractal analysis in a systems biology approach to cancer. Semin. Cancer Biol. 2011, 21, 175–182. [Google Scholar] [CrossRef] [PubMed]
- Mambetsariev, I.; Mirzapoiazova, T.; Lennon, F.; Jolly, M.K.; Li, H.; Nasser, M.H.; Vora, L.; Kulkarni, P.; Batra, S.K.; Salgia, R. Small cell lung cancer therapeutic responses through fractal measurements: From radiology to mitochondrial biology. J. Clin. Med. 2019, 8, 1038. [Google Scholar] [CrossRef] [PubMed]
- Avşar, E. Contribution of fractal dimension theory into the uniaxial compressive strength prediction of a volcanic welded bimrock. Bull. Eng. Geol. Environ. 2020, 79, 3605–3619. [Google Scholar] [CrossRef]
- Xie, H. Fractals in Rock Mechanics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Pierre, S.; Jean, F.R. On the validity of fractal dimension measurements in image analysis. J. Vis. Commun. Image Represent. 1996, 7, 217–229. [Google Scholar]
- Emanuel, G. Primality, fractality, and image analysis. Entropy 2019, 21, 304. [Google Scholar]
- Caicedo-Ortiz, H.E.; Santiago-Cortes, E.; Lopez-Bonilla, J.; Castaneda, H.O. Fractal dimension and turbulence in Giant HII Regions. J. Phys. Conf. Ser. 2015, 582, 012049. [Google Scholar] [CrossRef]
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 2019, 6587138. [Google Scholar] [CrossRef]
- Petros, M.; Alexandros, P. Fractal dimensions of speech sounds: Computation and application to automatic speech recognition. J. Acoust. Soc. Am. 1999, 105, 1925–1932. [Google Scholar]
- Berbiche, A.; Fellah, M.; Fellah, Z.E.A.; Ogam, E.; Mitri, F.G.; Depollier, C. Transient acoustic wave in self-similar porous material having rigid frame: Low frequency domain. Wave Motion 2017, 68, 12–21. [Google Scholar] [CrossRef]
- Fellah, M.; Fellah, Z.E.A.; Berbiche, A.; Ogam, E.; Mitri, F.G.; Depollier, C. Transient ultrasonic wave propagation in porous material of non-integer space dimension. Wave Motion 2017, 72, 276–286. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Ogam, E.; Berbiche, A.; Depollier, C. Reflection and transmission of transient ultrasonic wave in fractal porous material: Application of fractional calculus. Wave Motion 2021, 106, 102804. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Ongwen, N.O.; Ogam, O.; Depollier, C. Acoustics of Fractal Porous Material and Fractional Calculus. Mathematics 2021, 9, 1774. [Google Scholar] [CrossRef]
- Hills, B.P.; Manoj, P.; Destruel, C. NMR Q-space microscopy of concentrated oil-in-water emulsions. Magn. Reson. Imaging 2000, 18, 319–333. [Google Scholar] [CrossRef]
- Shui, H.; Zhou, H. Viscosity and fractal dimension of coal soluble constituents in solution. Fuel Process. Technol. 2004, 85, 1529–1538. [Google Scholar] [CrossRef]
- Shiyan, A.A. Viscosity for fractal suspensions: Dependence on fractal dimensionality. Phys. Lett. A 1996, 220, 117–119. [Google Scholar] [CrossRef]
- Demmie, P.N.; Ostoja-Starzewski, M. Waves in fractal media. J. Elast. 2011, 104, 187–204. [Google Scholar] [CrossRef]
- Joumaa, H.; Ostoja-Starzewski, M. Acoustic-elastoodynamic interaction in isotropic fractal media. Eur. Phys. J. Spec. Top. 2013, 222, 1951–1960. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Electromagnetism on anisotropic fractals. Z. Angew. Math. Phys. (J. Appl. Math. Mech.) 2013, 64, 381–390. [Google Scholar]
- Ostoja-Starzewski, M.; Li, J.; Joumaa, H.; Demmie, P.N. From fractal media to continuum mechanics. Z. Angew. Math. Phys. 2014, 94, 373–401. [Google Scholar] [CrossRef]
- Balankin, A.S. Steady laminar flow of fractal fluids. Phys. Lett. A 2017, 381, 623–628. [Google Scholar] [CrossRef]
- Balankin, A.S.; Bory-Reyes, J.; Shapiro, M. Towards a physics on fractals: Differential vector calculus in three-dimensional continuum with fractal metric. Physica A 2016, 444, 345–359. [Google Scholar] [CrossRef]
- Balankin, A.S. Fractional space approach to studies of physical phenomena on fractals and in confined low-dimensional systems. Chaos Solitons Fractals 2020, 132, 109572. [Google Scholar] [CrossRef]
- Tarasov, V.E. Vector calculus in non-integer dimensional space and its applications to fractal media. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 360–374. [Google Scholar] [CrossRef]
- Tarasov, V.E. Flow of fractal fluid in pipes: Non-integer dimensional space approach. Chaos Solitons Fractals 2014, 67, 26–37. [Google Scholar] [CrossRef]
- Hooft, G.; Veltman, M. Regularization and renormalization of gauge fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- Leibbrandt, G. Introduction to the technique of dimensional regularization. Rev. Modern Phys. 1975, 47, 849–876. [Google Scholar] [CrossRef]
- Wilson, K.G.; Fisher, M.E. Critical exponents in 3.99 dimensions. Phys. Rev. Lett. 1972, 28, 240–243. [Google Scholar] [CrossRef]
- Wilson, K.G. Kogut, J. The renormalization group and the ϵ expansion. Phys. Rep. 1974, 12, 75–199. [Google Scholar] [CrossRef]
- Tarasov, V.E. Poiseuille equation for steady flow of fractal fluid. Int. J. Mod. Phys. B 2016, 30, 1650128. [Google Scholar] [CrossRef]
- Tarasov, V.E. Anisotropic fractal media by vector calculus in non-integer dimensional space. J. Math. Phys. 2014, 55, 083510. [Google Scholar] [CrossRef]
- Brown, S.R. Fluid flow through rock joints: The effect of surface roughness. J. Geophys. Res. Solid Earth 1987, 92, 1337–1347. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Brown, S.R.; Stockman, H.W.; Reeves, S.J. Applicability of the Reynolds equation for modeling fluid flow between rough surfaces. Geophys. Res. Lett. 1995, 22, 2537–2540. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Shi, M.; Peterson, G.P. Role of surface roughness characterized by fractal geometry on laminar flow in microchannels. Phys. Rev. E 2009, 80, 026301. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Daigle, H. Fluid flow in porous media with rough pore-solid interface. Water Resour. Res. 2016, 52, 2045–2058. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M.; Revielle, J. Fractional calculus in hydrologic modeling: A numerical perspective. Adv. Water Resour. 2013, 51, 479–497. [Google Scholar] [CrossRef]
- Cowin, S.C.; Cardoso, L. Blood and Interstitial flow in the hierarchical pore space architecture of bone tissue. J. Biomech. 2015, 48, 842–854. [Google Scholar] [CrossRef]
- Gabrys, E.; Rybaczuk, M.; Kedzia, A. Blood flow simulation through fractal models of circulatory system. Chaos Solitons Fractals 2006, 27, 1–7. [Google Scholar] [CrossRef]
- Jayalalithaa, V.G.; Shanthoshini Devihab, V.; Uthayakumar, R. Fractal model for blood flow in cardiovascular system. Comput. Biol. Med. 2008, 38, 684–693. [Google Scholar] [CrossRef]
- Bouchendouka, A.; Fellah, Z.E.A.; Larbi, Z.; Ongwen, O.N.; Ogam, E.; Fellah, M.; Depollier, C. Flow of a self-similar non Newtonian fluid using fractal dimensions. Fractal Fract. 2022, 6, 582. [Google Scholar] [CrossRef]
- Bouchendouka, A.; Fellah, Z.E.A.; Larbi, Z.; Louna, Z.; Ogam, E.; Fellah, M.; Depollier, C. Fractal Analysis of a Non-Newtonian Fluid Flow in a Rough-Walled Pipe. Materials 2022, 15, 3700. [Google Scholar] [CrossRef] [PubMed]
- Carr, J.R. Statistical self-affinity, fractal dimension, and geologic interpretation. Eng. Geol. 1997, 48, 3–4. [Google Scholar] [CrossRef]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimensions. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Brown, G.O. Chapter: The history of the Darcy-Weisbach equation for pipe flow resistance. Proc. Environ. Water Resour. Hist. 2002, 38, 34–43. [Google Scholar]
- López, H.M.; Gachelin, J.; Douarche, C.; Auradou, H.; Clément, E. Turning Bacteria Suspensions into Superfluids. Phys. Rev. Lett. 2015, 115, 028301. [Google Scholar] [CrossRef]


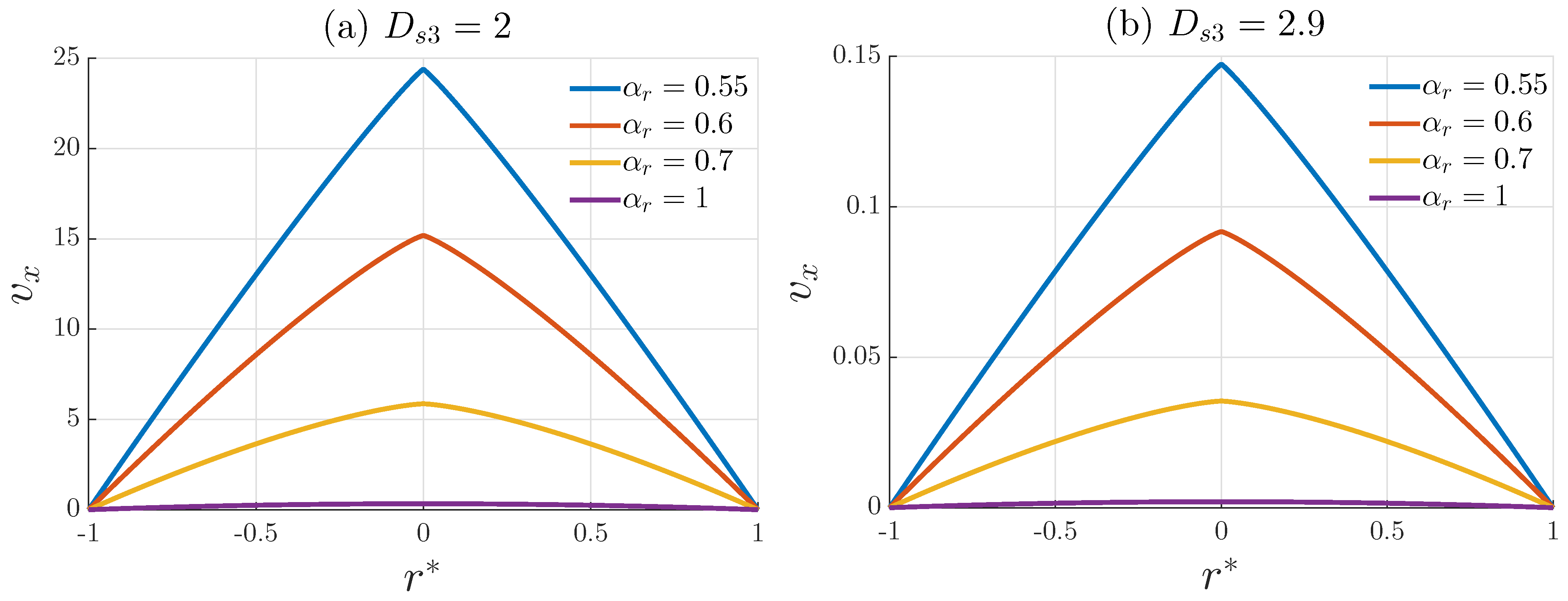

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouchendouka, A.; Fellah, Z.E.A.; Larbi, Z.; Ongwen, N.O.; Ogam, E.; Fellah, M.; Depollier, C. A Generalization of Poiseuille’s Law for the Flow of a Self-Similar (Fractal) Fluid through a Tube Having a Fractal Rough Surface. Fractal Fract. 2023, 7, 61. https://doi.org/10.3390/fractalfract7010061
Bouchendouka A, Fellah ZEA, Larbi Z, Ongwen NO, Ogam E, Fellah M, Depollier C. A Generalization of Poiseuille’s Law for the Flow of a Self-Similar (Fractal) Fluid through a Tube Having a Fractal Rough Surface. Fractal and Fractional. 2023; 7(1):61. https://doi.org/10.3390/fractalfract7010061
Chicago/Turabian StyleBouchendouka, Abdellah, Zine El Abiddine Fellah, Zakaria Larbi, Nicholas O. Ongwen, Erick Ogam, Mohamed Fellah, and Claude Depollier. 2023. "A Generalization of Poiseuille’s Law for the Flow of a Self-Similar (Fractal) Fluid through a Tube Having a Fractal Rough Surface" Fractal and Fractional 7, no. 1: 61. https://doi.org/10.3390/fractalfract7010061
APA StyleBouchendouka, A., Fellah, Z. E. A., Larbi, Z., Ongwen, N. O., Ogam, E., Fellah, M., & Depollier, C. (2023). A Generalization of Poiseuille’s Law for the Flow of a Self-Similar (Fractal) Fluid through a Tube Having a Fractal Rough Surface. Fractal and Fractional, 7(1), 61. https://doi.org/10.3390/fractalfract7010061








