Post Mortem Image Analysis of Astrocytes of the Human Principal Olivary Nucleus Using Geometrical and Fractal Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Histological Procedure and Images Preparation
2.2. Analyzed Parameters
2.3. Statistical Analysis and Tools
3. Results
3.1. PCA and the Selection of Parameters
(A) Size
(B) Shape
(C) Complexity
(D) Homogeneity

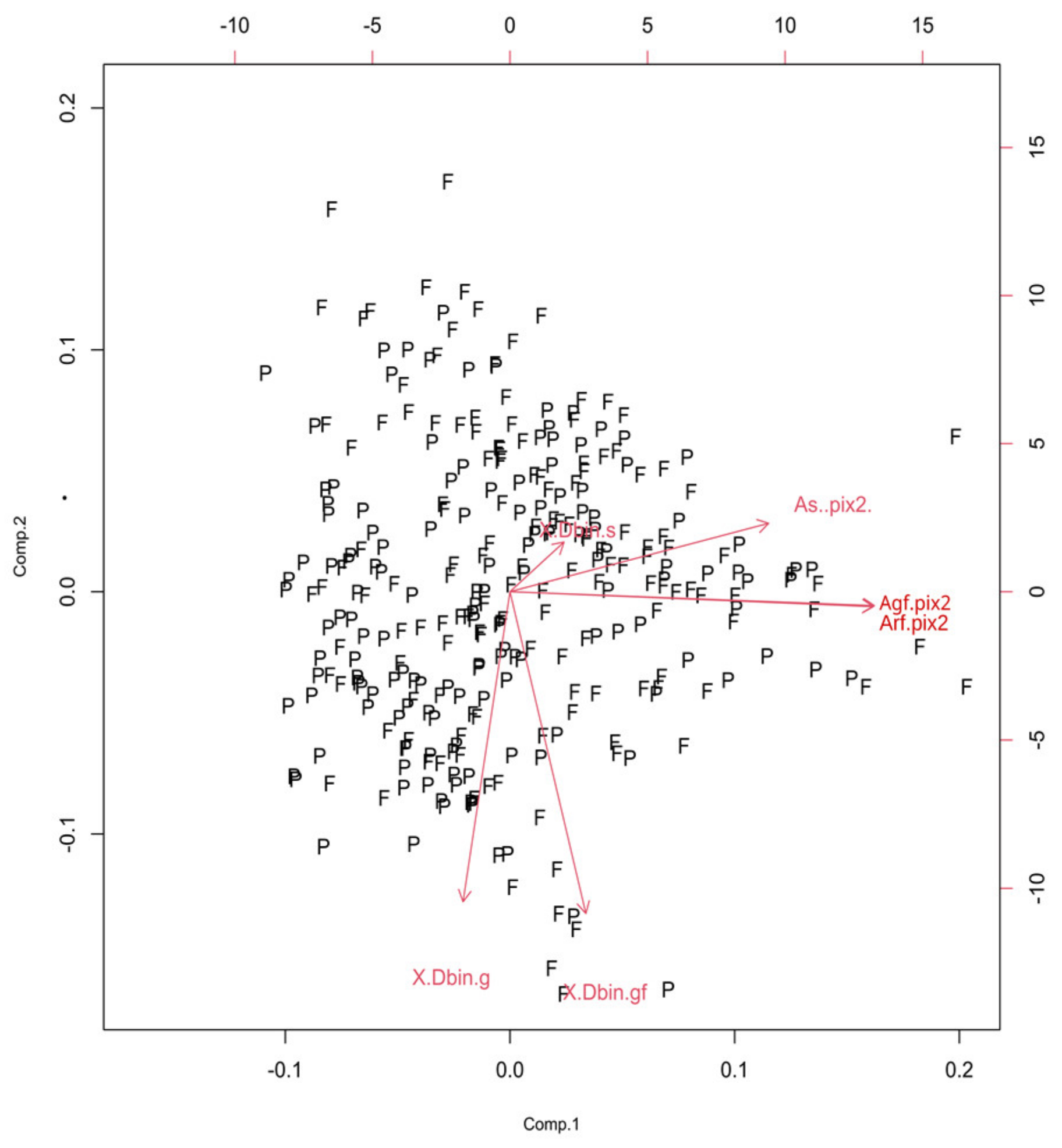
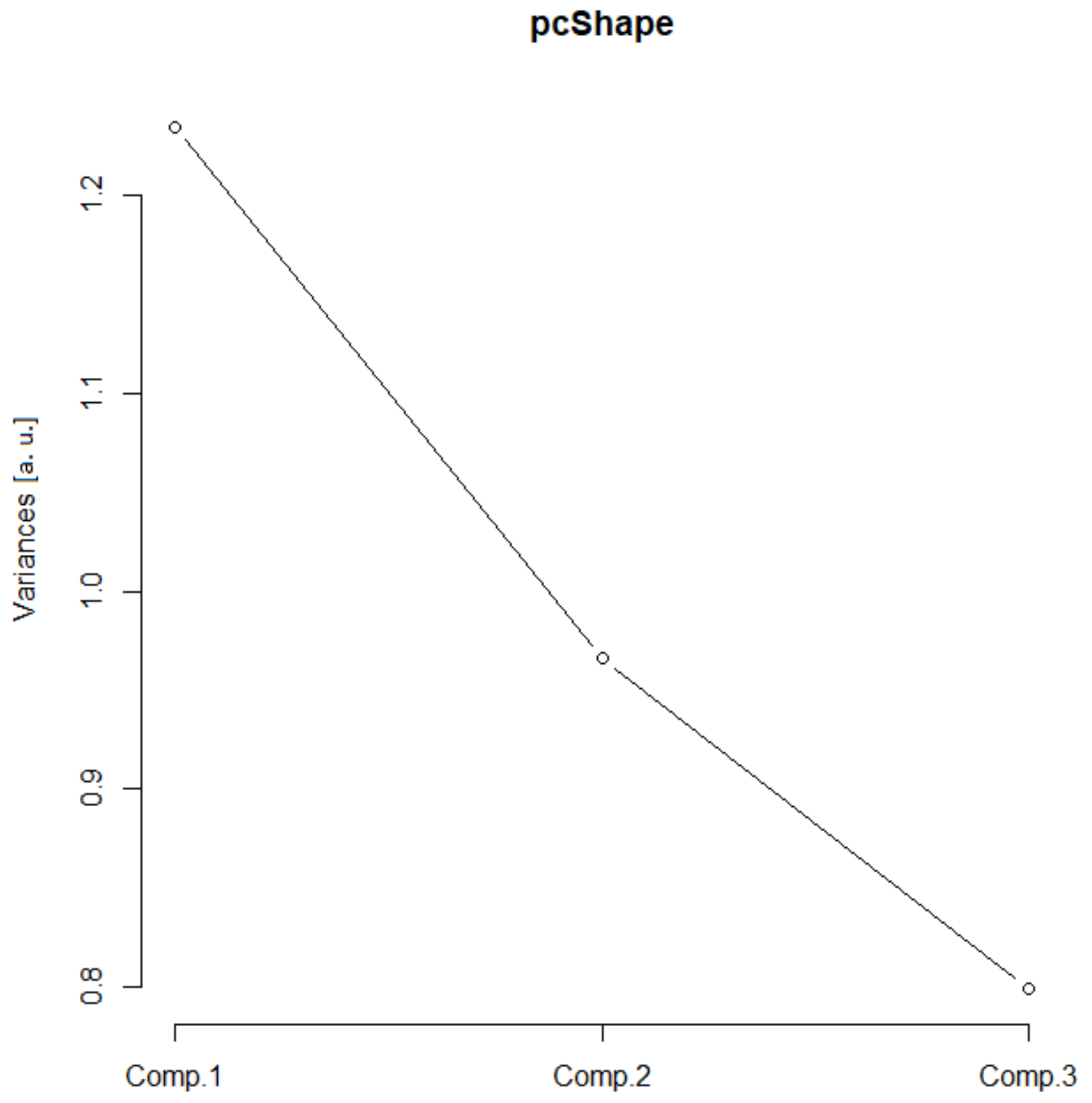

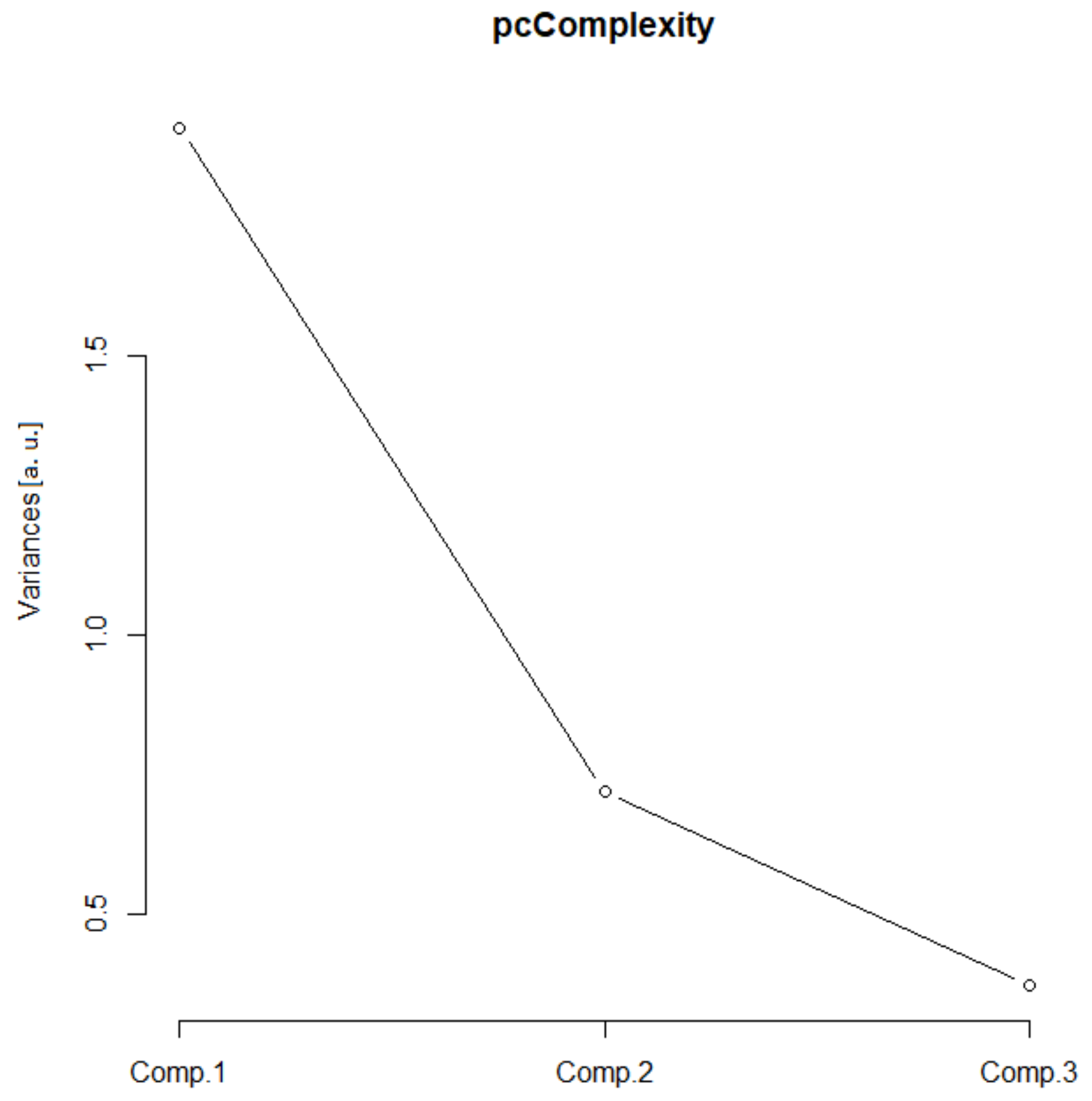
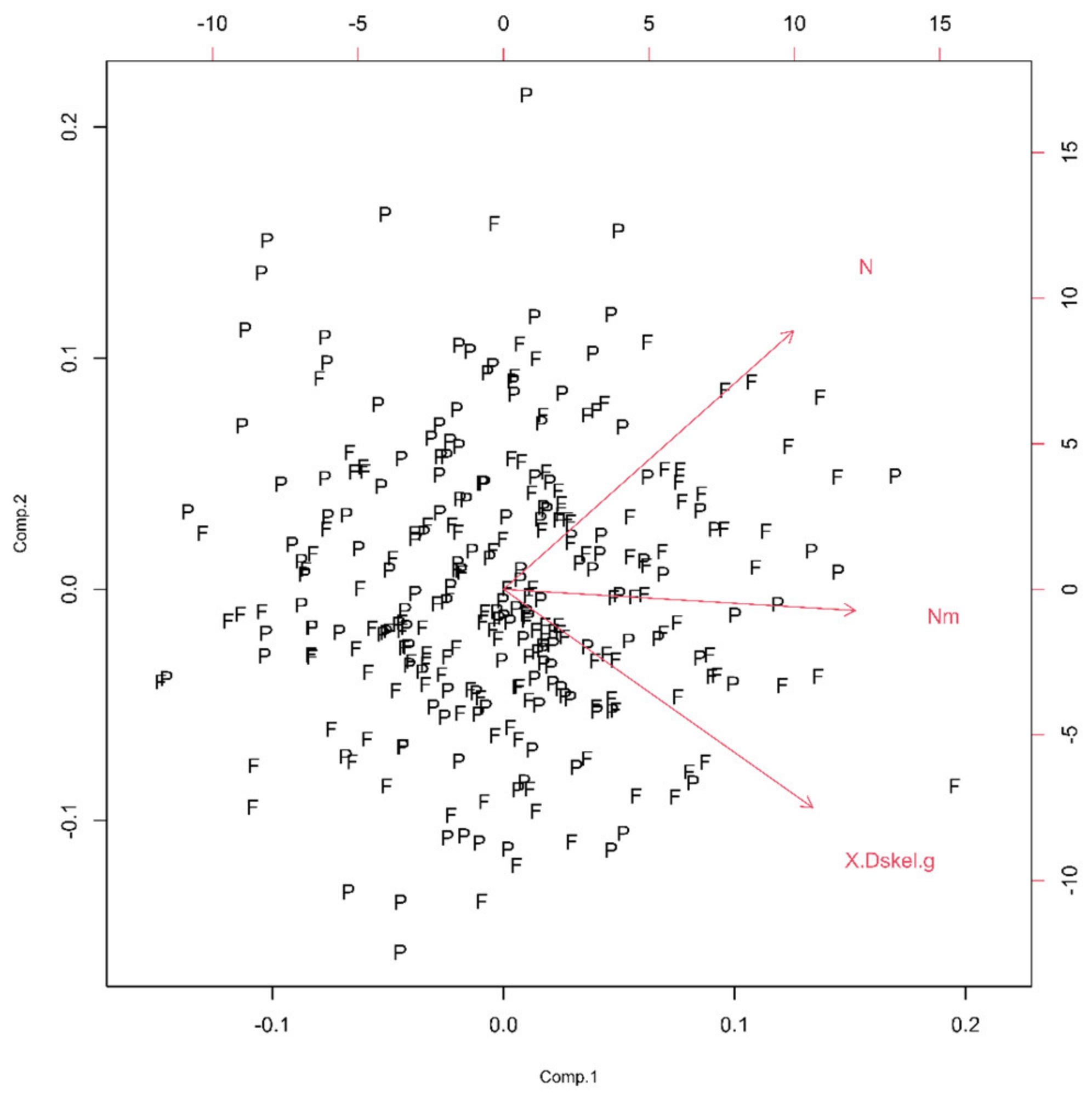
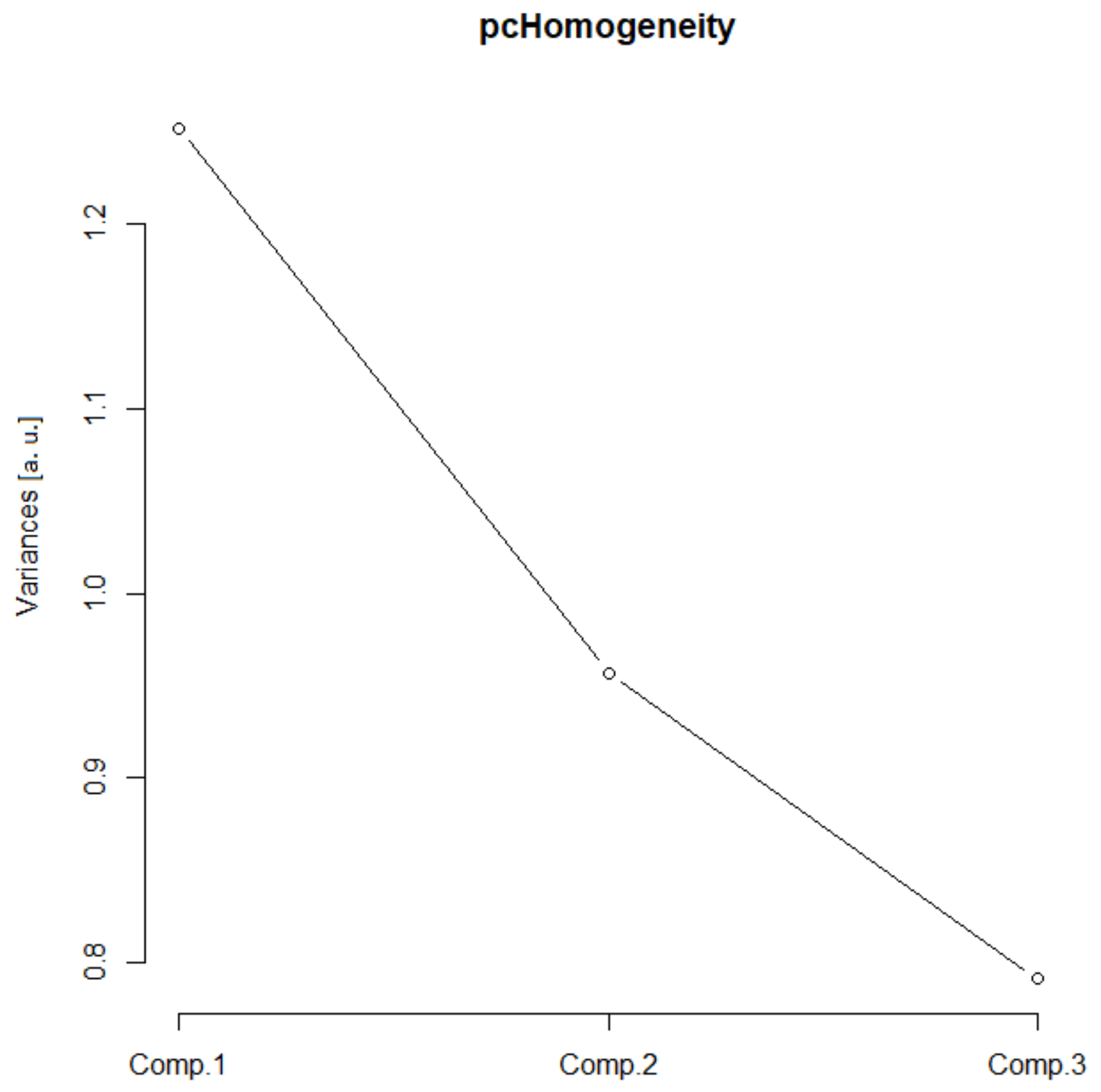
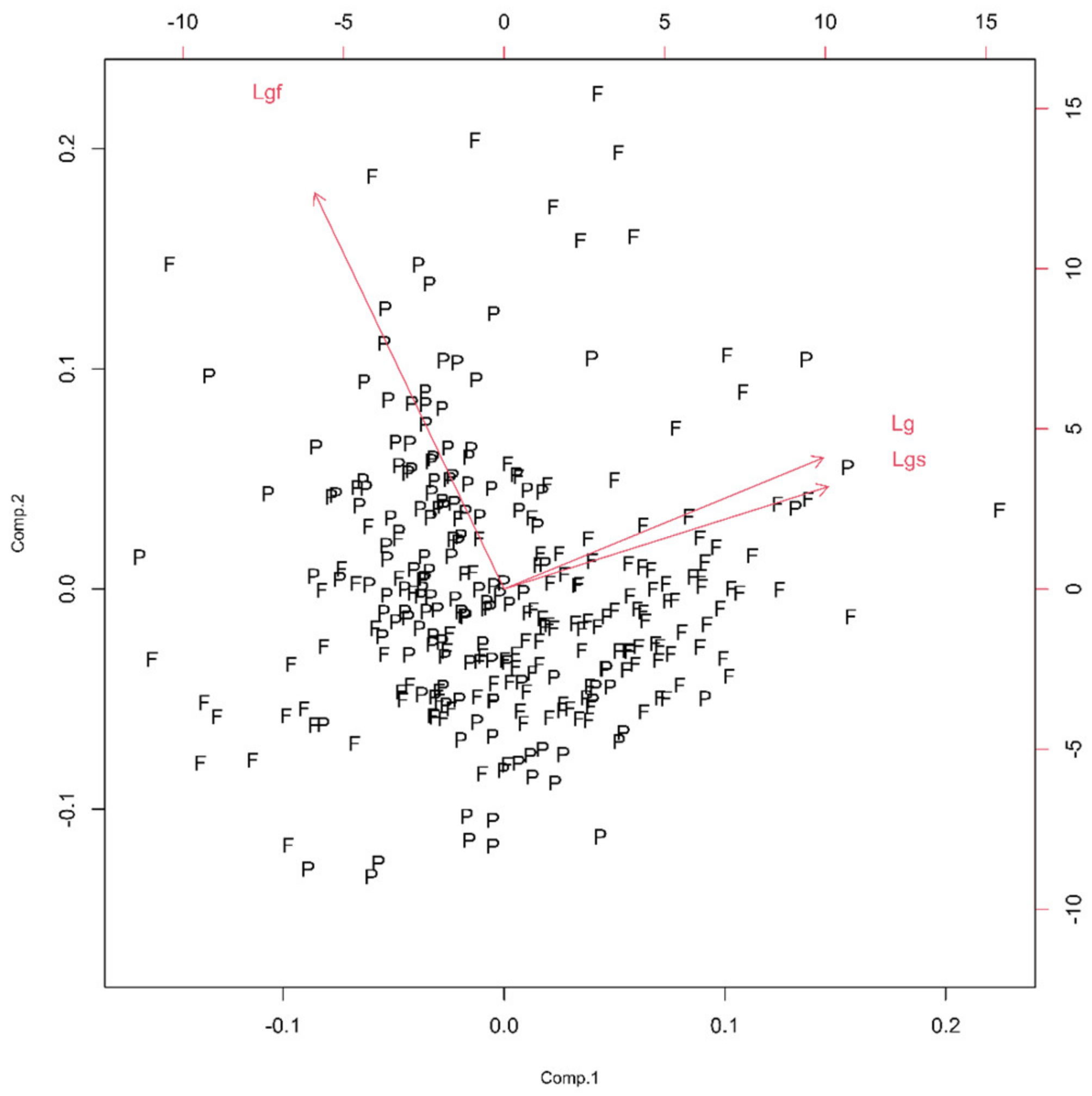
3.2. Quantitative Analysis of Types
3.3. Age Dependence of Parameters Describing the Morphology
| Parameter | Total PON Astrocytes | Fibrous | Protoplasmic |
|---|---|---|---|
| As | −0.53 *** | −0.61 ** | −0.29 |
| Pgf | −0.33 * | −0.56 ** | −0.07 |
| N | 0.03 | 0.13 | −0.09 |
| Lg | −0.53 *** | −0.60 ** | −0.25 |
| (Dskel)g | −0.41 ** | 0.1 | −0.75 *** |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- D’Angelo, E.; Galliano, E.; De Zeeuw, C.I. Editorial: The Olivo-Cerebellar System. Front. Neural Circuits 2016, 9, 66. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Walberg, F.; Ottersen, O.P. Demonstration of GABA immunoreactive cells in the inferior olive of baboons (Papio papio and Papio anubis). Neurosci. Lett. 1989, 101, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Bozhilova-Pastirova, A.; Ovtscharoff, W. The inferior oilvary complex. Adv. Anat. Embryol. Cell Biol. 2000, 155, III-84. [Google Scholar] [CrossRef] [PubMed]
- Verkhratsky, A.; Nedergaard, M. Physiology of Astroglia. Physiol. Rev. 2018, 98, 239–389. [Google Scholar] [CrossRef]
- Miller, S.J. Astrocyte Heterogeneity in the Adult Central Nervous System. Front. Cell Neurosci. 2018, 12, 401. [Google Scholar] [CrossRef]
- Radošević, D. A Morphological Analysis of the Neuronal and Glial Cells in the Human Principal Olivary Nucleus Dissertation. Ph.D. Thesis, School of Medicine, University of Novi Sad, Novi Sad, Serbia, 2019. [Google Scholar]
- Rowitch, D.H.; Kriegstein, A.R. Developmental genetics of vertebrate glial-cell specification. Nature 2010, 468, 214–222. [Google Scholar] [CrossRef]
- Koeppen, A.H. The pathogenesis of spinocerebellar ataxia. Cerebellum 2005, 4, 62–73. [Google Scholar] [CrossRef]
- Lasn, H.; Winblad, B.; Bogdanovic, N. Neuroglia in the inferior olivary nucleus during normal aging and Alzheimer’s disease. J. Cell Mol. Med. 2006, 10, 145–156. [Google Scholar] [CrossRef]
- Li, K.; Li, J.; Zheng, J.; Qin, S. Reactive Astrocytes in Neurodegenerative Diseases. Aging Dis. 2019, 10, 664–675. [Google Scholar] [CrossRef]
- Lalošević, D.; Somer, L.; Đolai, M.; Lalošević, V.; Mažibrada, J.; Krnojelac, D. Mikroskopska Laboratorijska Tehnika u Medicine; Medicinski Fakultet Novi Sad-WUS Austrija: Novi Sad, Serbia, 2005. [Google Scholar]
- Stojić, D.; Radošević, D.; Rajković, N.; Milošević, N.T. 2D Images of Astrocytes in the Human Principal Olivary Nucleus: Monofractal Analysis of the Morphology. J. Biosci. Med. 2021, 9, 38–48. [Google Scholar] [CrossRef]
- Krstonošić, B.; Milošević, N.T.; Marić, D.L.; Babović, S.S. Quantitative analysis of spiny neurons in the adult human caudate nucleus: Can it confirm the current qualitative cell classification? Acta Neurol. Belg. 2015, 115, 273–280. [Google Scholar] [CrossRef] [PubMed]
- Stojić, D.; Radošević, D.; Rajković, N.; Marić, D.L.; Milošević, N.T. Classification by morphology of multipolar neurons of the human principal olivary nucleus. Neurosci. Res. 2021, 170, 66–75. [Google Scholar] [CrossRef] [PubMed]
- Fernández, E.; Jelinek, H.F. Use of fractal theory in neuroscience: Methods, advantages, and potential problems. Methods 2001, 24, 309–321. [Google Scholar] [CrossRef] [PubMed]
- Ristanović, D.; Milosević, N.T.; Jelinek, H.F.; Stefanović, I.B. Mathematical modelling of neuronal dendritic branching patterns in two dimensions: Application to retinal ganglion cells in the cat and rat. Biol. Cybern. 2009, 100, 97–108. [Google Scholar] [CrossRef] [PubMed]
- Di Ieva, A.; Grizzi, F.; Jelinek, H.; Pellionisz, A.J.; Losa, G.A. Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. Neuroscientist 2014, 20, 403–417. [Google Scholar] [CrossRef]
- Milosevic, N.T. The Morphology of Brain Neurons: Box Counting Method in Quantitative Analysis of 2D Image; The Fractal Geometry of the Brain; Di Ieva, A., Ed.; Springer: New York, NY, USA, 2016; pp. 109–126. [Google Scholar]
- Karperien, A. FracLac for ImageJ. Version 2.0. 2007. Available online: https://imagej.nih.gov/ij/plugins/fraclac/fraclac-manual.pdf (accessed on 10 May 2022).
- Karl Pearson, F.R.S. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis. Google Research, Mountain View, CA. arXiv 2014, arXiv:1404.1100v1. [Google Scholar] [CrossRef]
- Grbatinić, I.; Milošević, N. Classification of Adult Human Dentate Nucleus Border Neurons: Artificial Neural Networks and Multidimensional Approach. J. Theor. Biol. 2016, 404, 273–284. [Google Scholar] [CrossRef]
- Rajković, N.; Krstonošić, B.; Milošević, N. Box-Counting Method of 2D Neuronal Image: Method Modification and Quantitative Analysis Demonstrated on Images from the Monkey and Human Brain. Comput. Math. Methods Med. 2017, 2017, 8967902. [Google Scholar] [CrossRef]
- Riffenburgh, R.H. Statistics in Medicine; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 14 September 2022).
- Lundgaard, I.; Osório, M.J.; Kress, B.T.; Sanggaard, S.; Nedergaard, M. White matter astrocytes in health and disease. Neuroscience 2014, 276, 161–173. [Google Scholar] [CrossRef]
- Oberheim, N.A.; Takano, T.; Han, X.; He, W.; Lin, J.H.C.; Wang, F.; Xu, Q.; Wyatt, J.D.; Pilcher, W.; Ojemann, J.G.; et al. Uniquely hominid features of adult human astrocytes. J. Neurosci. 2009, 29, 3276–3287. [Google Scholar] [CrossRef] [PubMed]
- Köhler, S.; Winkler, U.; Hirrlinger, J. Heterogeneity of Astrocytes in Grey and White Matter. Neurochem. Res. 2021, 46, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Azevedo, F.A.; Carvalho, L.R.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.L.; Leite, R.E.P.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Lasn, H.; Winblad, B.; Bogdanovic, N. The number of neurons in the inferior olivary nucleus in Alzheimer’s disease and normal aging: A stereological study using the optical fractionator. J. Alzheimer’s Dis. 2001, 3, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Lasn, H.M.D. The Principal Inferior Olivary Nucleus in Aging and Alzheimer’s Disease Dissertation. Ph.D. Thesis, Karolinska Institutet, Stockholm, Sweden, 2006. [Google Scholar]
- Zhou, B.; Zuo, Y.X.; Jiang, R.T. Astrocyte morphology: Diversity, plasticity, and role in neurological diseases. CNS Neurosci. Ther. 2019, 25, 665–673. [Google Scholar] [CrossRef] [PubMed]
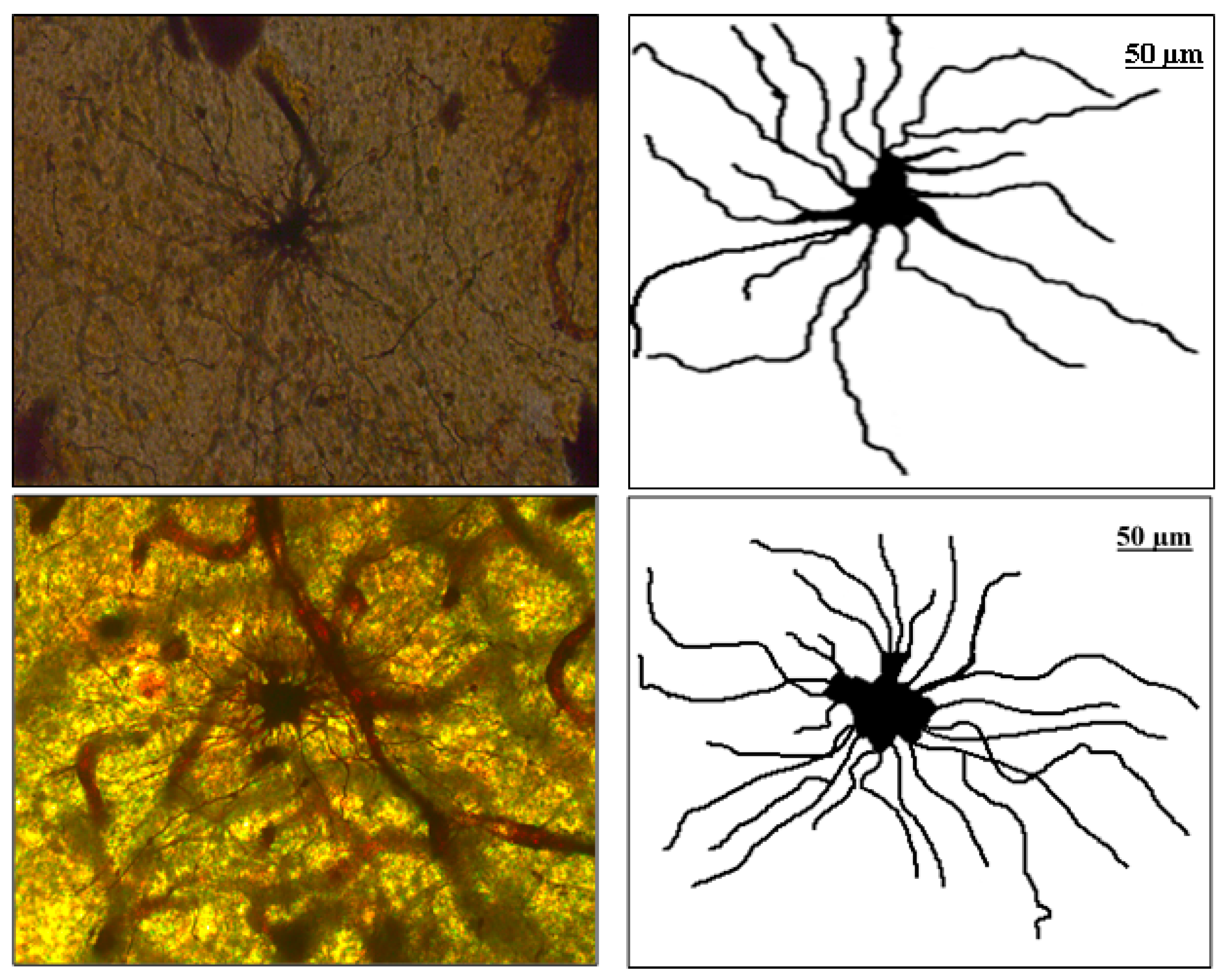
| Property | Parameters | Component | ν | SD |
|---|---|---|---|---|
| Size | As, Agf, Arf, (Dbin)s, (Dbin)g and (Dbin)gf | First | 2.4 | 1.6 |
| Second | 1.3 | 1.1 | ||
| Third | 1 | 1 | ||
| Fourth | 0.8 | 0.9 | ||
| Fifth | 0.6 | 0.7 | ||
| Sixth | 0 | 0 | ||
| Shape | Pgf, Mgf and (Dout)gf | First | 1.2 | 1.1 |
| Second | 1 | 1 | ||
| Third | 0.8 | 0.9 | ||
| Complexity | N, Nm and (Dskel)g | First | 1.9 | 1.4 |
| Second | 0.7 | 0.9 | ||
| Third | 0.4 | 0.6 | ||
| Homogeneity | Ls, Lg and Lgf | First | 1.3 | 1.1 |
| Second | 1 | 1 | ||
| Third | 0.8 | 0.9 |
| Property | Parameter | Fibrous | Protoplasmic | p |
|---|---|---|---|---|
| Size | As (×103 pix2) | 8.8 ± 0.3 | 6.6 ± 0.2 | <0.01 |
| Agf (×105 pix2) | 5.9 ± 0.2 | 4.9 ± 0.2 | 0.04 | |
| Arf (×105 pix2) | 5.8 ± 0.2 | 4.8 ±0.2 | 0.05 * | |
| (Dbin)s | 1.723 ± 0.006 | 1.745 ± 0.006 | 0.08 | |
| (Dbin)g | 1.425 ± 0.003 | 1.437 ± 0.003 | 0.1 | |
| (Dbin)gf | 1.816 ± 0.004 | 1.818 ± 0.003 | 0.73 | |
| Shape | Pgf (×103 pix) | 3.20 ± 0.06 | 2.83 ± 0.07 | <0.01 |
| Mgf (pix) | 0.703 ± 0.006 | 0.713 ± 0.005 | 0.24 | |
| (Dout)gf | 1.062 ± 0.002 | 1.064 ± 0.002 | 0.44 | |
| Complexity | N | 6.9 ± 0.1 | 7.0 ± 0.1 | 0.68 |
| Nm | 14.1 ± 0.3 | 14.4 ±0.2 | 0.38 | |
| (Dskel)g | 1.169 ± 0.003 | 1.150 ± 0.004 | <0.01 | |
| Homogeneity | Ls | 0.125 ± 0.003 | 0.119 ± 0.002 | <0.01 |
| Lg | 0.623 ± 0.008 | 0.588 ± 0.005 | <0.01 | |
| Lgf | 0.123#1 ± 0.001 | 0.123#4 ± 0.001 | <0.01 |
| Property | Parameter | Fibrous | p | Protoplasmic | p | ||
|---|---|---|---|---|---|---|---|
| Age Group 1 | Age Group 2 | Age Group 1 | Age Group 2 | ||||
| Size | As (×103 pix2) | 9.8 ± 0.7 | 7.5 ± 0.4 | < 0.01 | 8.0 ± 0.4 | 6.6 ± 0.3 | < 0.01 |
| Agf (×105 pix2) | 6.5 ± 0.3 | 5.2 ± 0.3 | < 0.01 | 6.0 ± 0.4 | 5.3 ± 0.4 | 0.2 | |
| Arf (×105 pix2) | 6.4 ± 0.3 | 5.2 ± 0.3 | < 0.01 | 6.0 ± 0.4 | 5.3 ± 0.4 | 0.207 | |
| (Dbin)s | 1.719 ± 0.009 | 1.747 ± 0.009 | 0.03 | 1.74 ± 0.01 | 1.753 ± 0.009 | 0.23 | |
| (Dbin)g | 1.427 ± 0.004 | 1.432 ± 0.006 | 0.473 | 1.427 ± 0.005 | 1.430 ± 0.005 | 0.627 | |
| (Dbin)gf | 1.816 ± 0.006 | 1.820 ± 0.007 | 0.696 | 1.825 ± 0.007 | 1.820 ± 0.006 | 0.589 | |
| Shape | Pgf (×103 pix) | 3.4 ± 0.1 | 3.0 ± 0.1 | < 0.01 | 2.5 ± 0.1 | 2.9 ± 0.1 | 0.086 |
| Mgf (pix) | 0.71 ± 0.01 | 0.70 ± 0.01 | 0.694 | 0.726 ± 0.008 | 0.717 ± 0.009 | 0.461 | |
| (Dout)gf | 1.061 ± 0.003 | 1.066 ± 0.007 | 0.202 | 1.063 ± 0.003 | 1.063 ± 0.003 | 0.957 | |
| Complexity | N | 6.9 ± 0.2 | 7.4 ± 0.2 | 0.107 | 7.1 ± 0.2 | 6.9 ± 0.2 | 0.296 |
| Nm | 14.2 ± 0.4 | 15.1 ± 0.5 | 0.146 | 14.6 ± 0.5 | 13.9 ± 0.4 | 0.24 | |
| (Dskel)g | 1.167 ± 0.004 | 1.176 ± 0.006 | 0.245 | 1.177 ± 0.004 | 1.097 ± 0.004 | < 0.001 | |
| Homogeneity | Ls | 0.134 ± 0.004 | 0.133 ± 0.005 | 0.799 | 0.121 ± 0.005 | 0.108 ± 0.003 | 0.027 |
| Lg | 0.67 ± 0.01 | 0.61 ± 0.01 | < 0.001 | 0.607 ± 0.007 | 0.589 ± 0.009 | 0.104 | |
| Lgf | 0.115 ± 0.005 | 0.108 ± 0.003 | 0.183 | 0.133 ± 0.005 | 0.136 ± 0.005 | 0.73 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stojić, D.; Radošević, D. Post Mortem Image Analysis of Astrocytes of the Human Principal Olivary Nucleus Using Geometrical and Fractal Parameters. Fractal Fract. 2023, 7, 6. https://doi.org/10.3390/fractalfract7010006
Stojić D, Radošević D. Post Mortem Image Analysis of Astrocytes of the Human Principal Olivary Nucleus Using Geometrical and Fractal Parameters. Fractal and Fractional. 2023; 7(1):6. https://doi.org/10.3390/fractalfract7010006
Chicago/Turabian StyleStojić, Damjan, and Dragana Radošević. 2023. "Post Mortem Image Analysis of Astrocytes of the Human Principal Olivary Nucleus Using Geometrical and Fractal Parameters" Fractal and Fractional 7, no. 1: 6. https://doi.org/10.3390/fractalfract7010006
APA StyleStojić, D., & Radošević, D. (2023). Post Mortem Image Analysis of Astrocytes of the Human Principal Olivary Nucleus Using Geometrical and Fractal Parameters. Fractal and Fractional, 7(1), 6. https://doi.org/10.3390/fractalfract7010006





