Dynamic Feedforward-Based Fractional Order Impedance Control for Robot Manipulator
Abstract
1. Introduction
2. Control Design
2.1. Fractional Calculus and Definitions
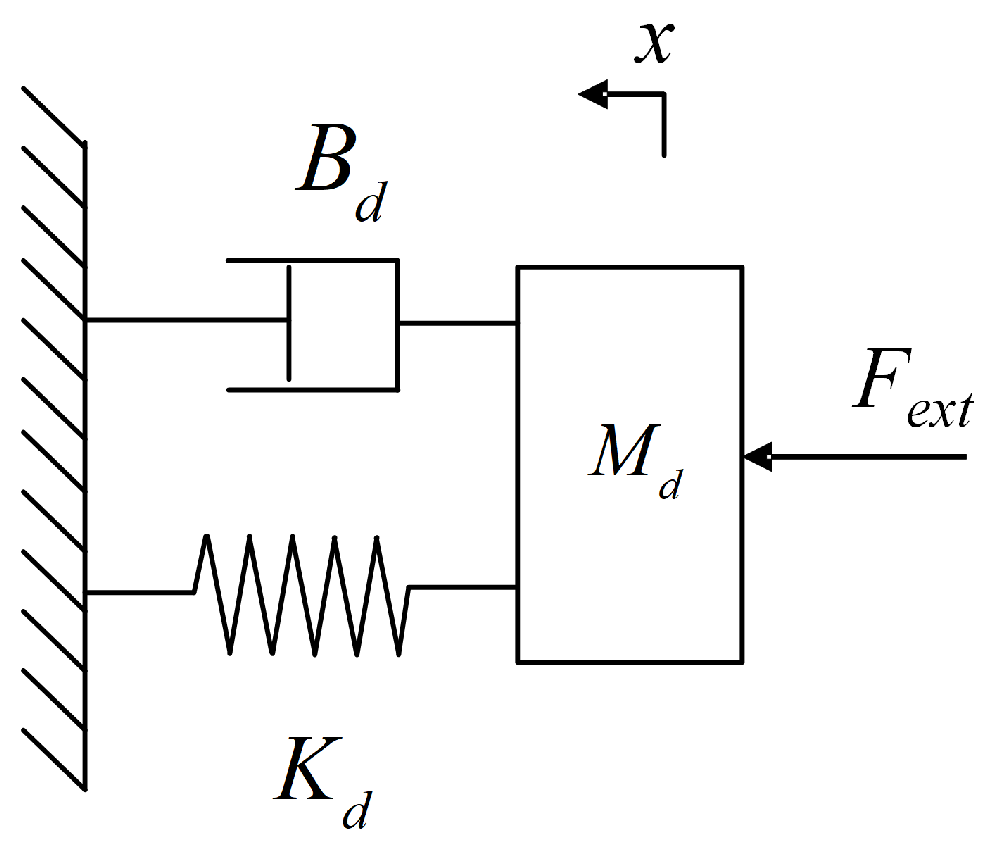
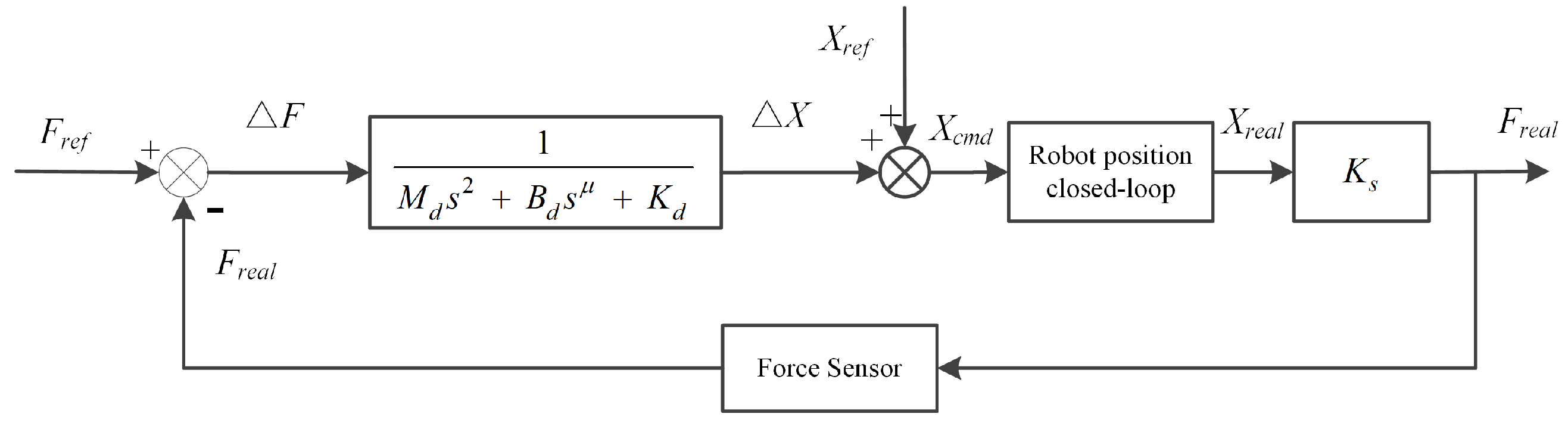
2.2. Design of FOIC
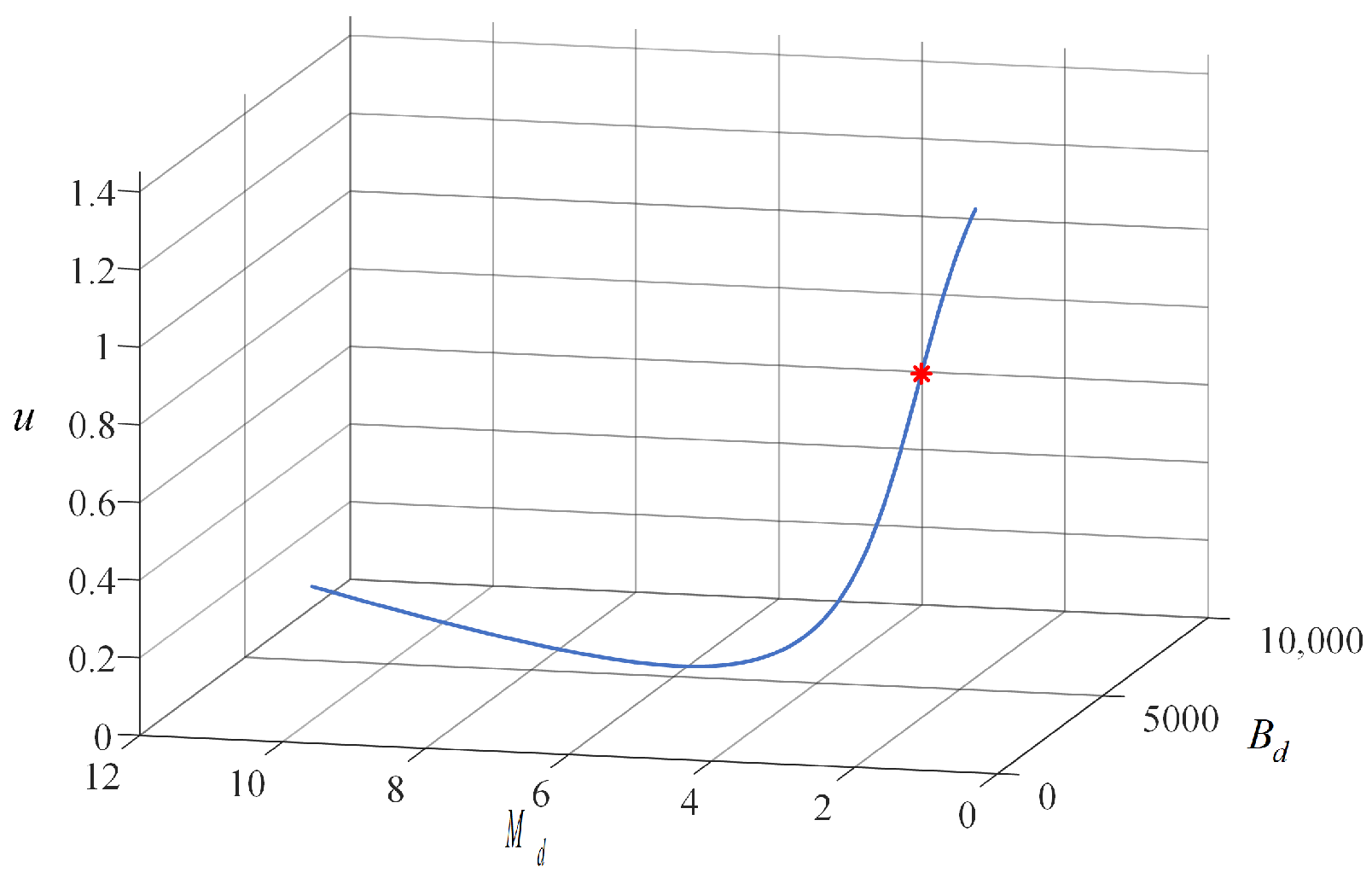
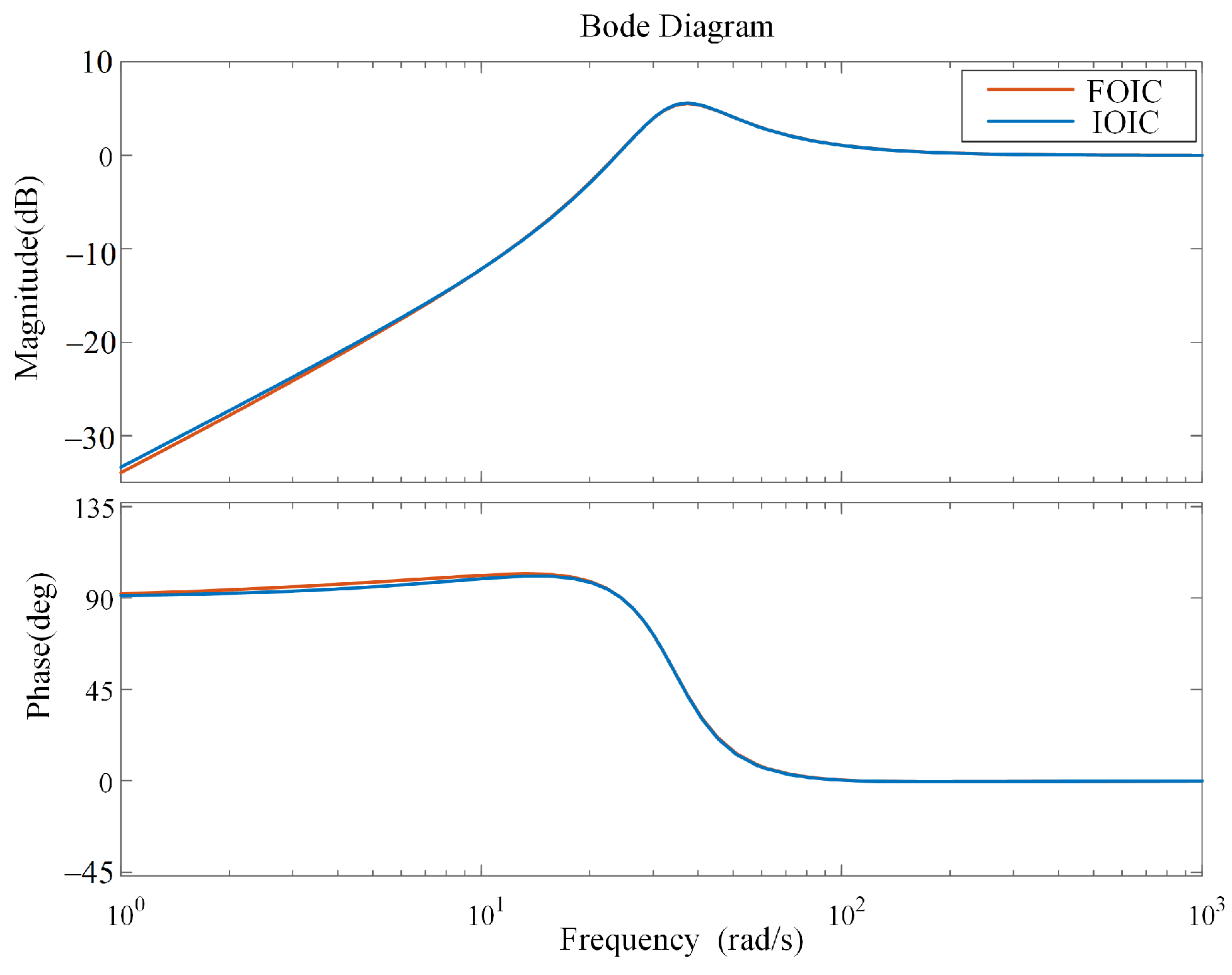
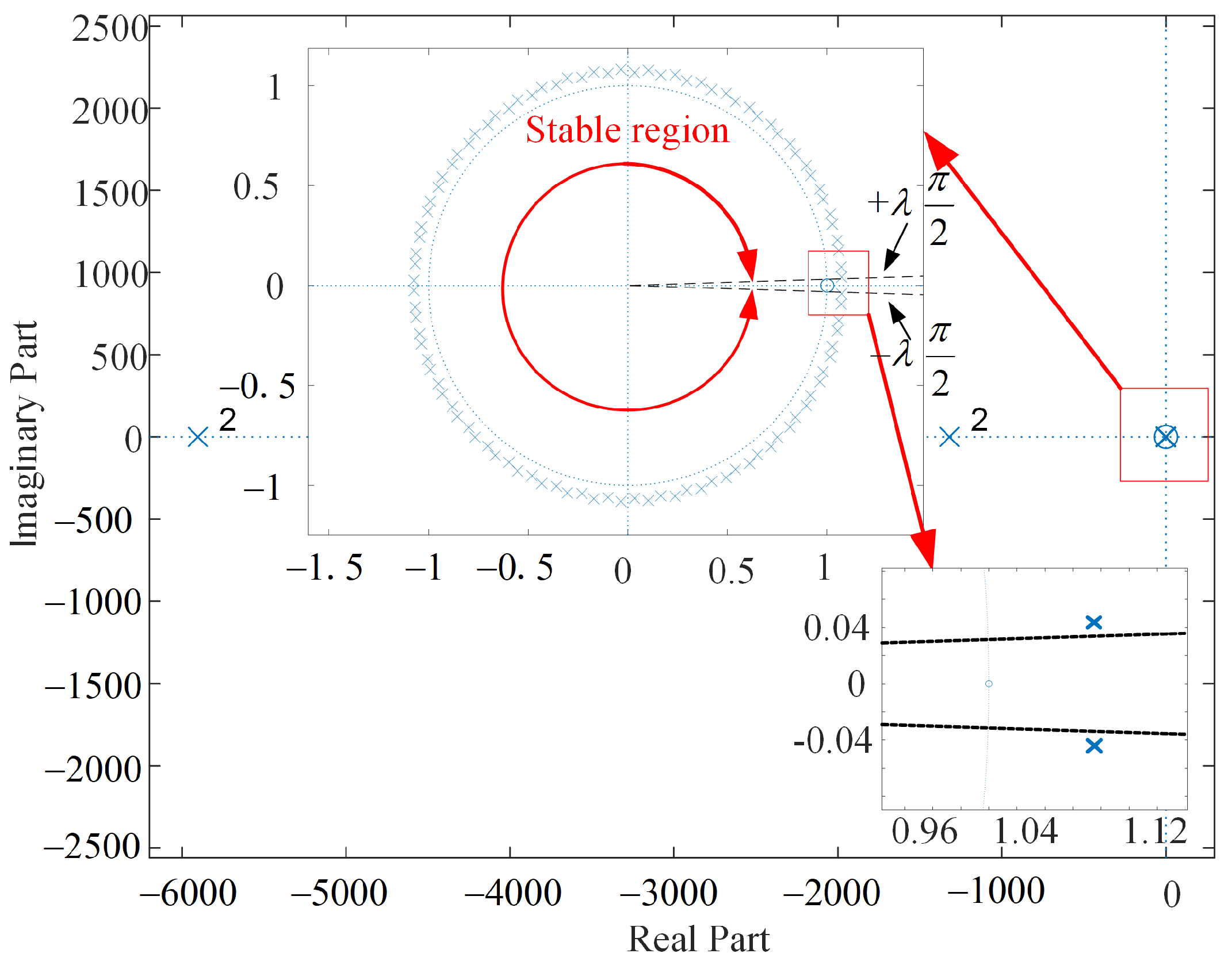
2.3. Stability Analysis
2.4. Dynamic Model for Robot Manipulator
3. Simulation and Experimental Results
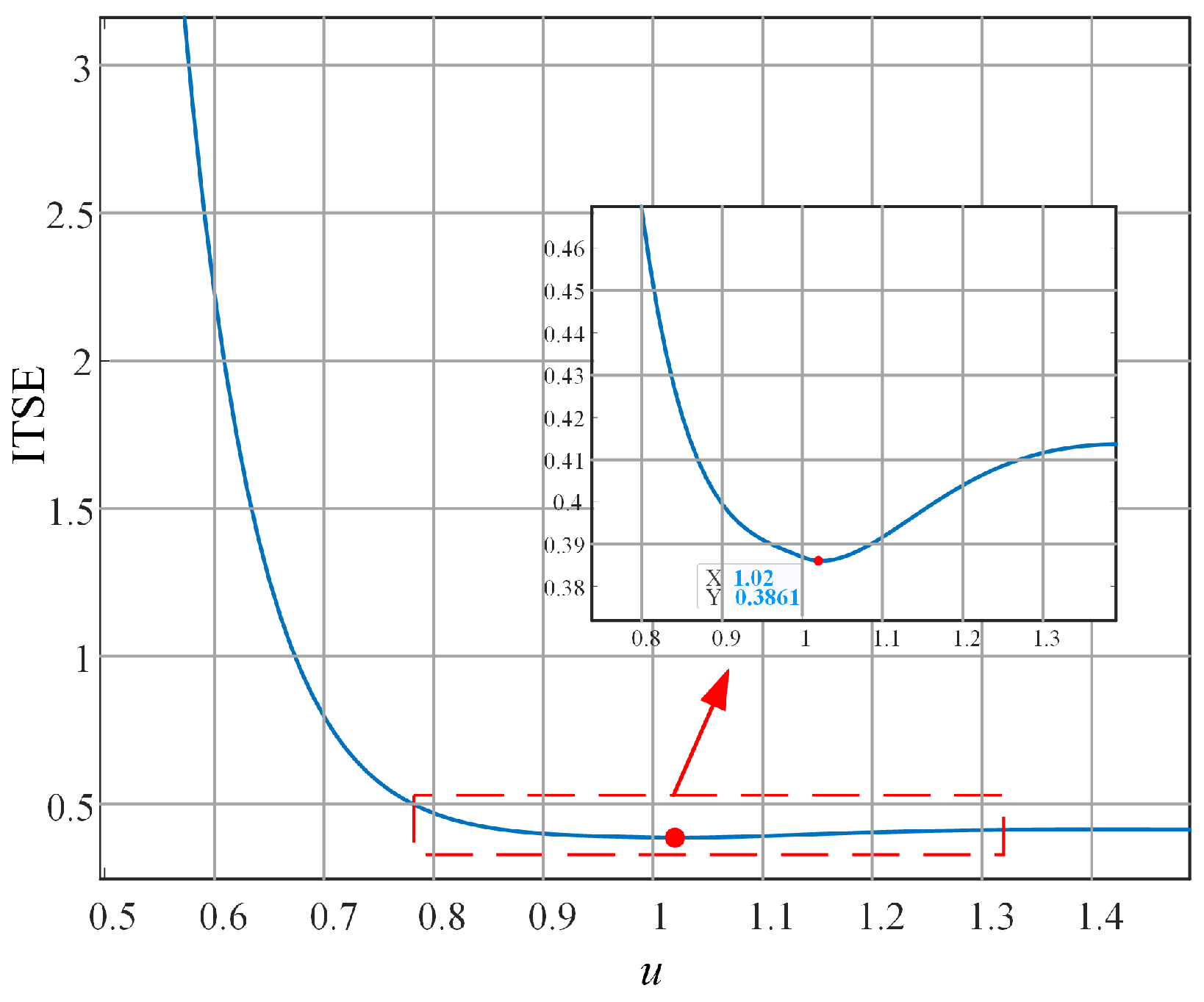
3.1. Simulation Illustration
3.1.1. Simulation System
3.1.2. Fractional Order Operator Implementation
3.1.3. Step Response Simulation
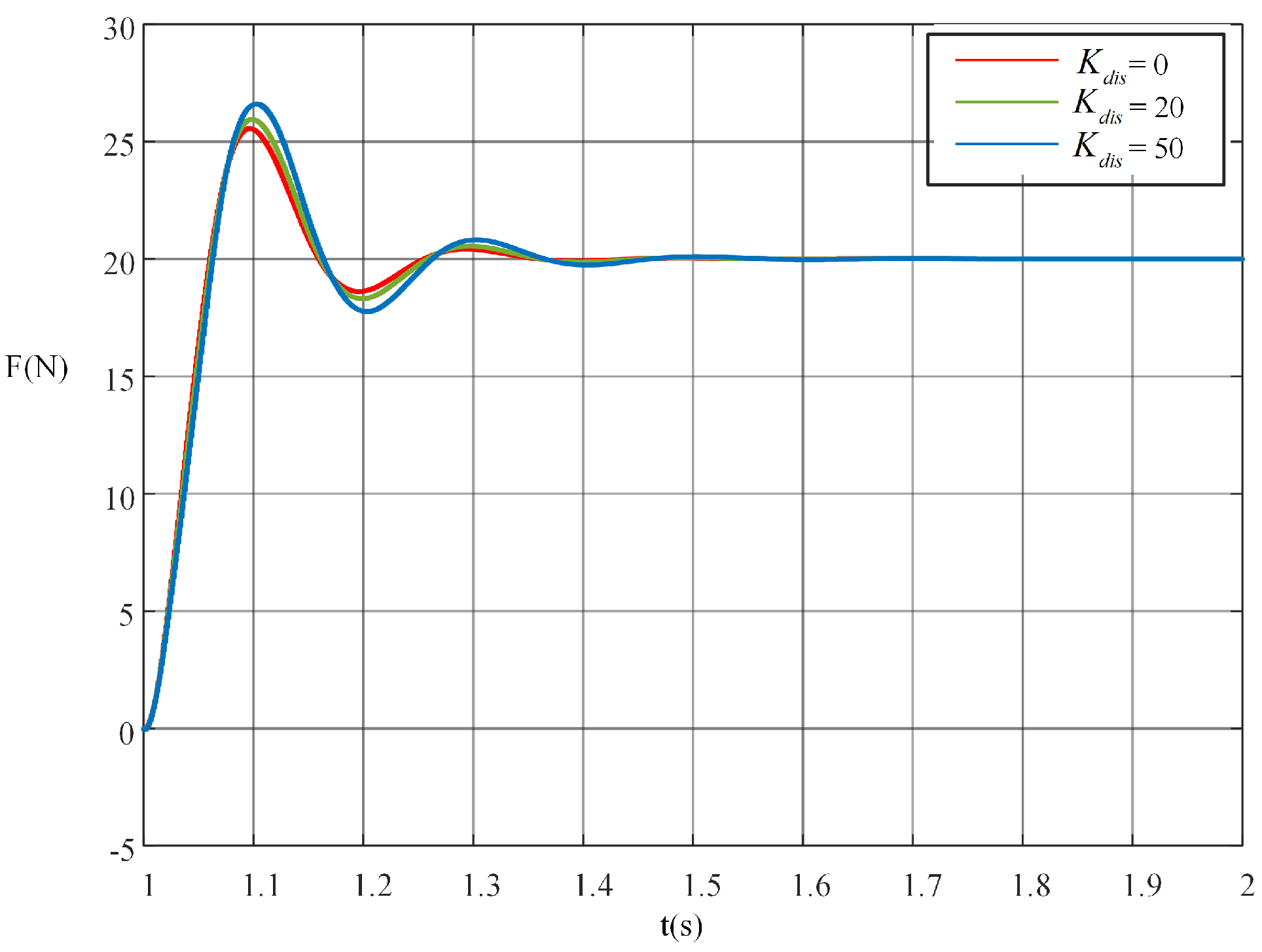
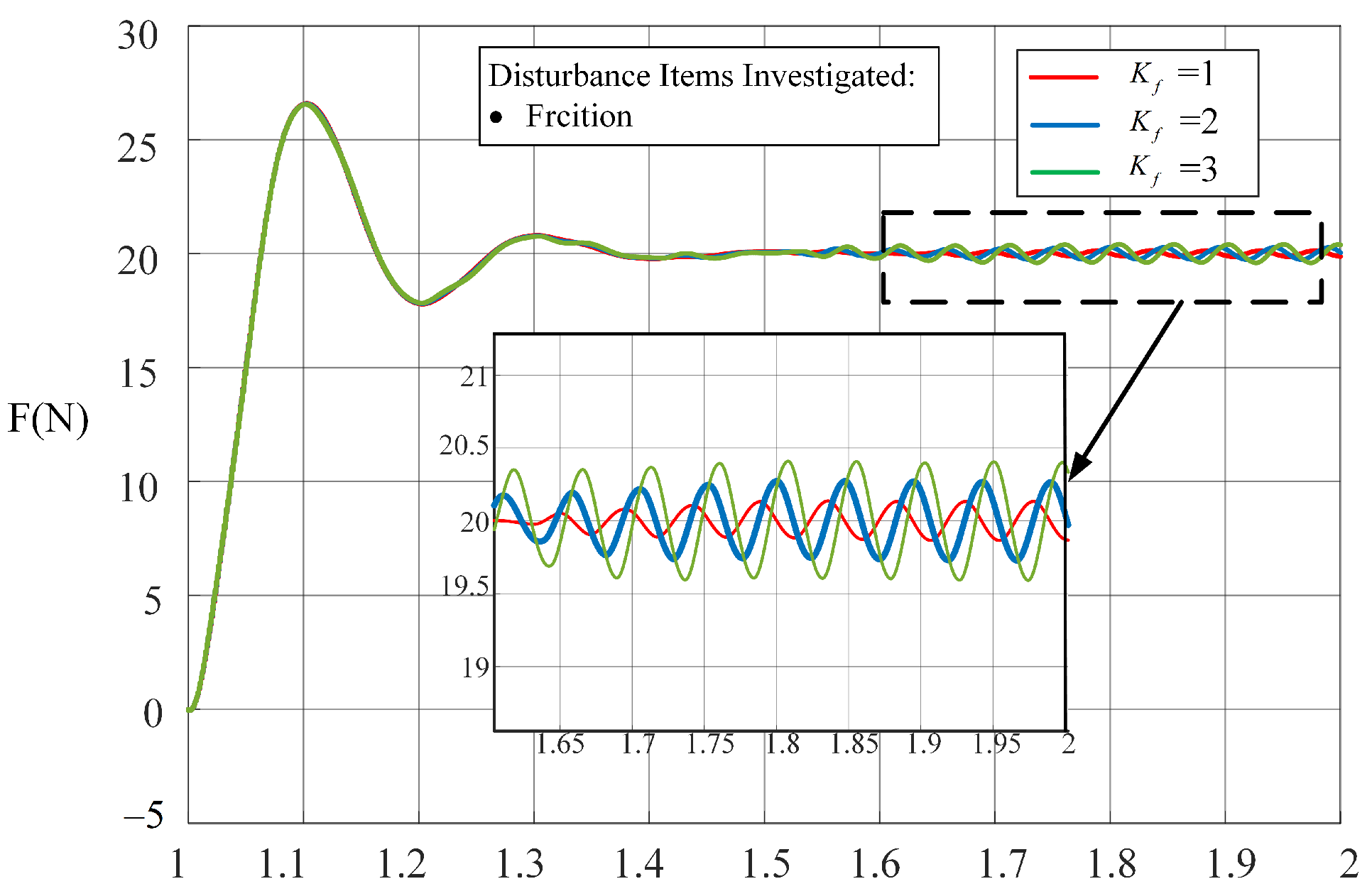
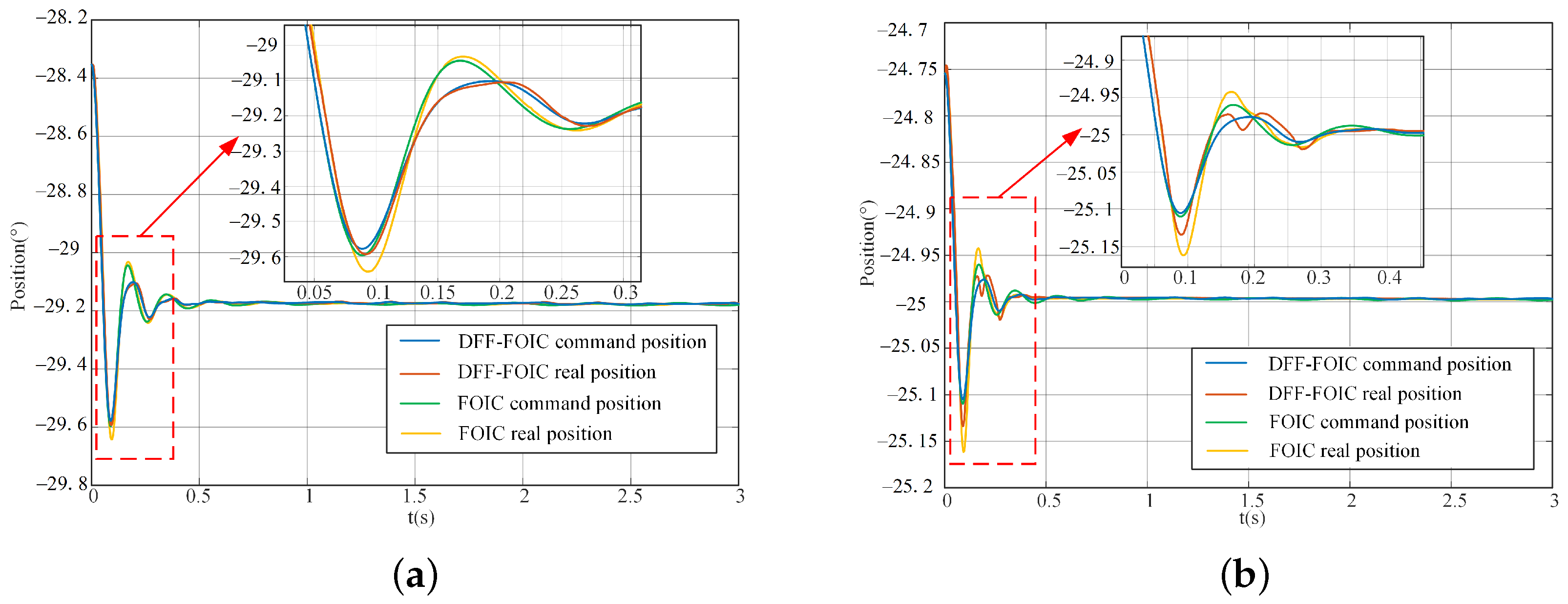
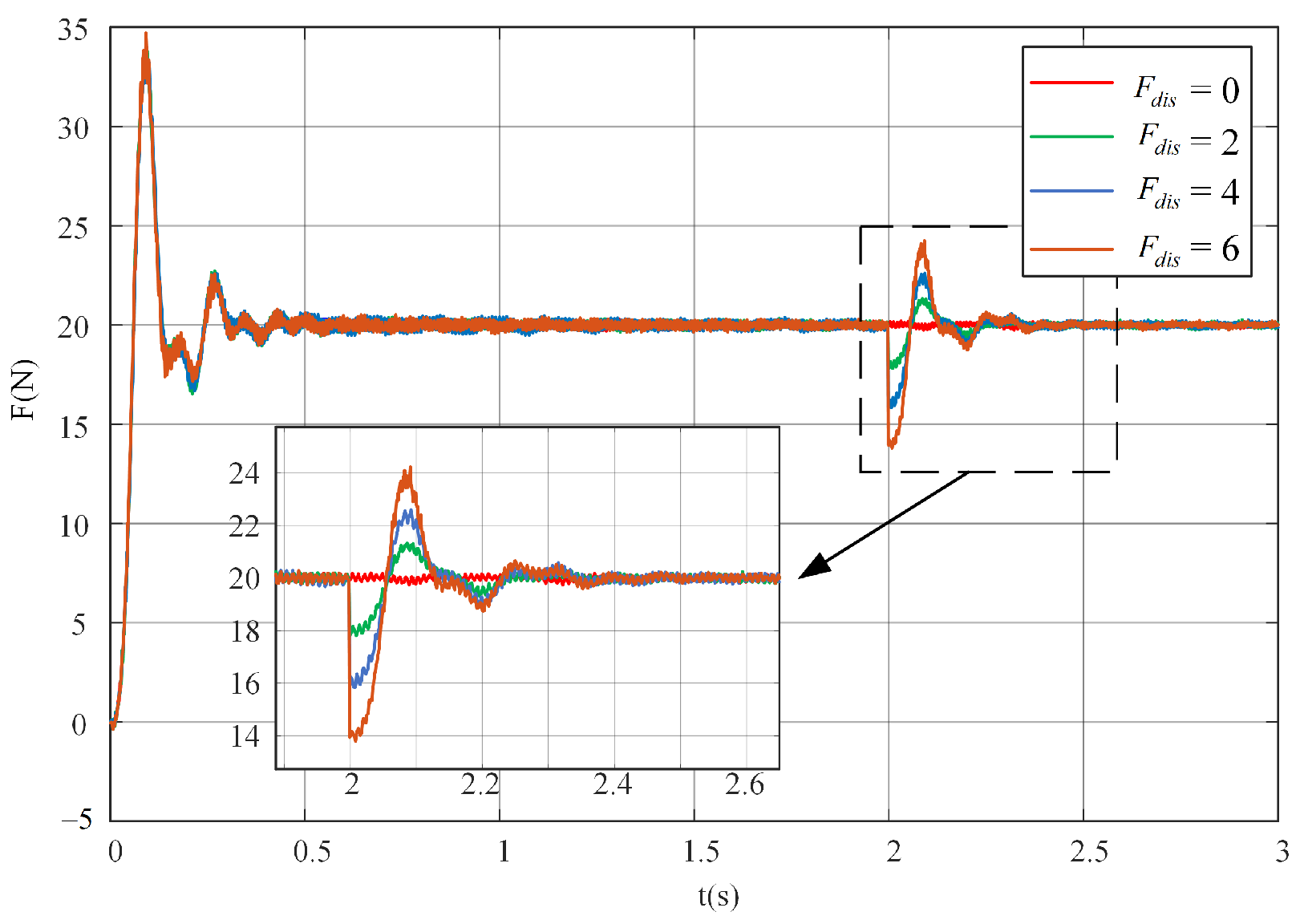
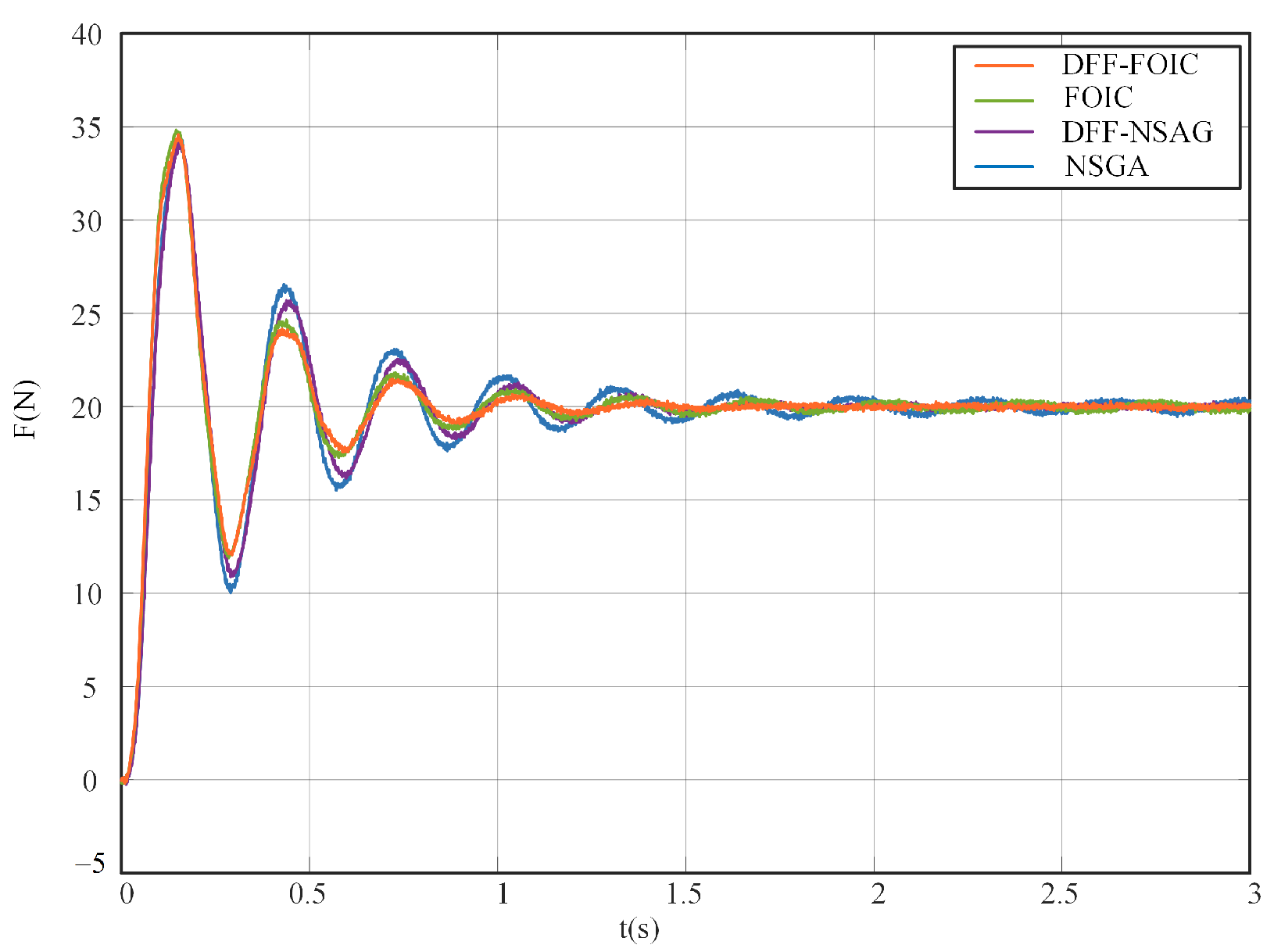
3.2. Experimental Verification
3.2.1. Experimental Setup
3.2.2. Experimental Tests
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
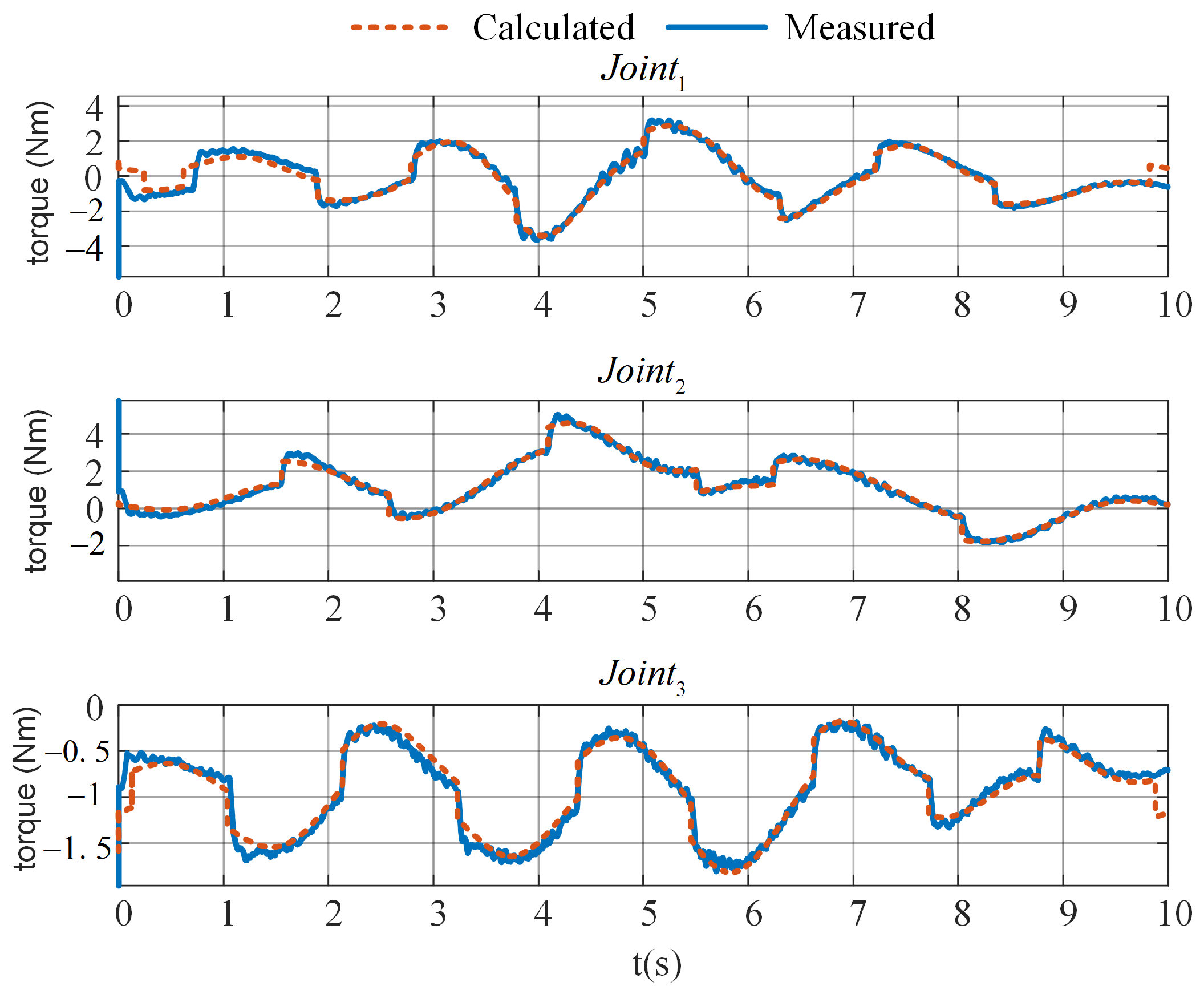
Appendix A. Identification of Robot Manipulator System
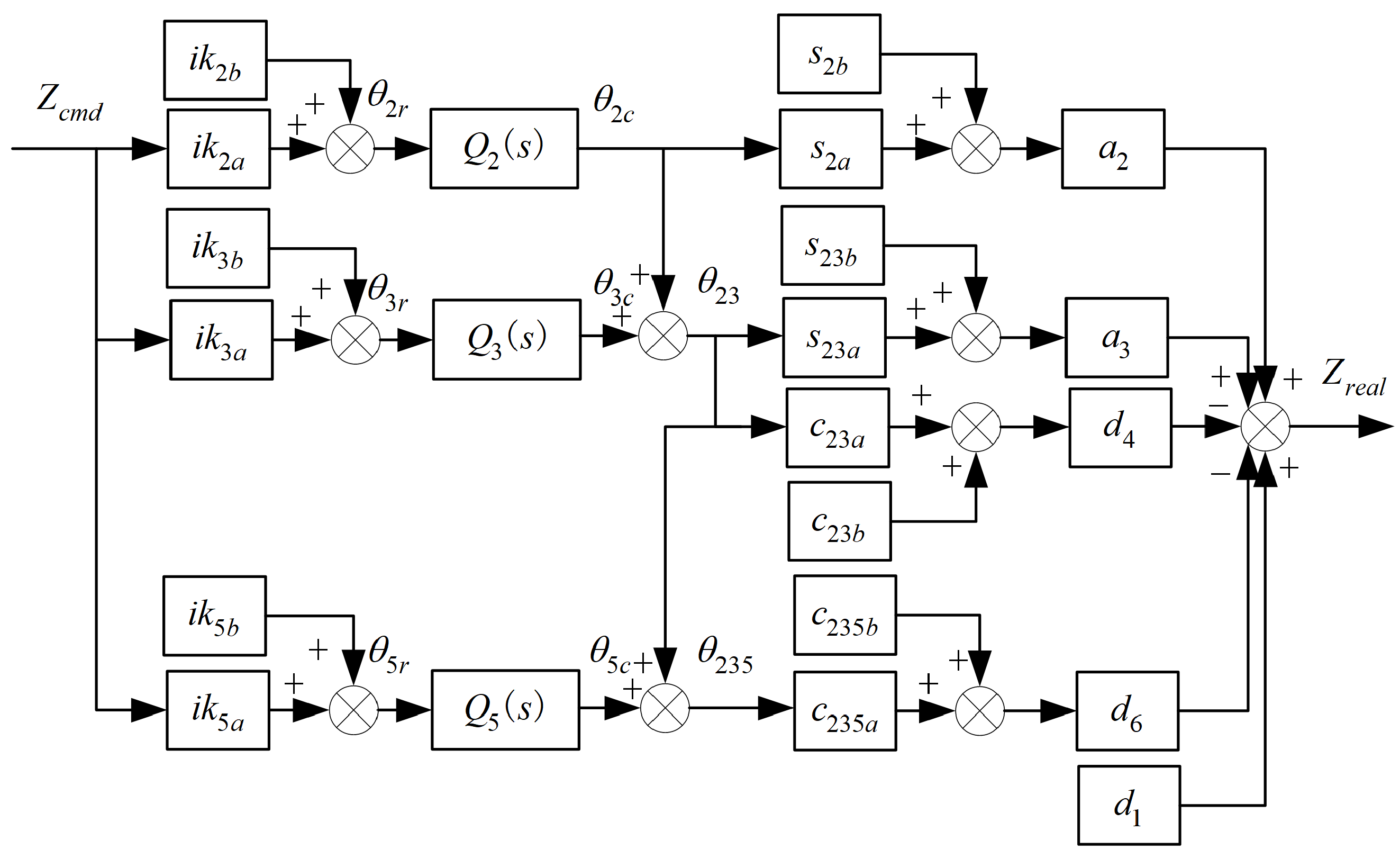
References
- Xu, J.; Zhang, C.; Liu, Z.; Pei, Y. A review on significant technologies related to the robot-guided intelligent bolt assembly under complex or uncertain working conditions. IEEE Access 2019, 7, 136752–136776. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.; Wang, L.; Yu, Z. Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot. Comput.-Integr. Manuf. 2020, 63, 101923. [Google Scholar] [CrossRef]
- He, Y.; Mei, J.; Fang, Z.; Zhang, F.; Zhao, Y. Minimum energy trajectory optimization for driving systems of palletizing robot joints. Math. Probl. Eng. 2018, 2018, 7247093. [Google Scholar] [CrossRef]
- Zhu, D.; Feng, X.; Xu, X.; Yang, Z.; Li, W.; Yan, S.; Ding, H. Robotic grinding of complex components: A step towards efficient and intelligent machining–challenges, solutions, and applications. Robot. Comput.-Integr. Manuf. 2020, 65, 101908. [Google Scholar] [CrossRef]
- Yang, C.; Xie, Y.; Liu, S.; Sun, D. Force modeling, identification, and feedback control of robot-assisted needle insertion: A survey of the literature. Sensors 2018, 18, 561. [Google Scholar] [CrossRef] [PubMed]
- Zeng, G.; Hemami, A. An overview of robot force control. Robotica 1997, 15, 473–482. [Google Scholar] [CrossRef]
- Hogan, N. Impedance Control: An Approach to Manipulation: Part II—Implementation. J. Dyn. Syst. Meas. Control 1985, 107, 8–16. [Google Scholar] [CrossRef]
- Al-Shuka, H.F.; Leonhardt, S.; Zhu, W.H.; Song, R.; Ding, C.; Li, Y. Active impedance control of bioinspired motion robotic manipulators: An overview. Appl. Bionics Biomech. 2018, 2018, 8203054. [Google Scholar] [CrossRef] [PubMed]
- Hogan, N. Impedance control: An approach to manipulation. In Proceedings of the 1984 American Control Conference, San Diego, CA, USA, 6–8 June 1984; pp. 304–313. [Google Scholar]
- Schmidt, A.; Gaul, L. On a critique of a numerical scheme for the calculation of fractionally damped dynamical systems. Mech. Res. Commun. 2006, 33, 99–107. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Onishi, A.; Hoshi, T.; Kawamura, K.; Hashizume, M.; Fujie, M.G. Validation of viscoelastic and nonlinear liver model for needle insertion from in vivo experiments. In Proceedings of the International Workshop on Medical Imaging and Virtual Reality, Tokyo, Japan, 1–2 August 2008; pp. 50–59. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Niu, H.; Chen, Y.; West, B.J. Why do big data and machine learning entail the fractional dynamics? Entropy 2021, 23, 297. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y. A Two-Degree-of-Freedom Controller Design Satisfying Separation Principle With Fractional-Order PD and Generalized ESO. IEEE/ASME Trans. Mechatronics 2021, 27, 137–148. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, T.; Lee, B.; Kang, C.; Chen, Y. Fractional-order proportional derivative controller synthesis and implementation for hard-disk-drive servo system. IEEE Trans. Control Syst. Technol. 2013, 22, 281–289. [Google Scholar] [CrossRef]
- Dadkhah Khiabani, E.; Ghaffarzadeh, H.; Shiri, B.; Katebi, J. Spline collocation methods for seismic analysis of multiple degree of freedom systems with visco-elastic dampers using fractional models. J. Vib. Control 2020, 26, 1445–1462. [Google Scholar] [CrossRef]
- Agila, A.; Baleanu, D.; Eid, R.; Irfanoglu, B. A freely damped oscillating fractional dynamic system modeled by fractional Euler–Lagrange equations. J. Vib. Control 2018, 24, 1228–1238. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; He, W.; Na, J.; Li, Z.; Xu, B. Adaptive parameter estimation and control design for robot manipulators with finite-time convergence. IEEE Trans. Ind. Electron. 2018, 65, 8112–8123. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.; Wang, L.; Yu, Z.; Fu, P. A method to realize accurate dynamic feedforward control of a spray-painting robot for airplane wings. IEEE/ASME Trans. Mechatronics 2018, 23, 1182–1192. [Google Scholar] [CrossRef]
- Hui, J.; Pan, M.; Zhao, R.; Luo, L.; Wu, L. The closed-form motion equation of redundant actuation parallel robot with joint friction: An application of the Udwadia–Kalaba approach. Nonlinear Dyn. 2018, 93, 689–703. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W.; Jiao, Z. Adaptive control of hydraulic actuators with LuGre model-based friction compensation. IEEE Trans. Ind. Electron. 2015, 62, 6469–6477. [Google Scholar] [CrossRef]
- Wu, J.; Li, W.; Xiong, Z. Identification of robot dynamic model and joint frictions using a baseplate force sensor. Sci. China Technol. Sci. 2022, 65, 30–40. [Google Scholar] [CrossRef]
- Xie, Z.; Xie, F.; Liu, X.J.; Wang, J.; Mei, B. Tracking error prediction informed motion control of a parallel machine tool for high-performance machining. Int. J. Mach. Tools Manuf. 2021, 164, 103714. [Google Scholar] [CrossRef]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y. Industrial feedforward control technology: A review. J. Intell. Manuf. 2019, 30, 2819–2833. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; You, Z. An overview of dynamic parameter identification of robots. Robot. Comput.-Integr. Manuf. 2010, 26, 414–419. [Google Scholar] [CrossRef]
- Huo, W. New formulas for complete determining base parameters of robots. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 3, pp. 3021–3026. [Google Scholar]
- Swevers, J.; Ganseman, C.; Tukel, D.B.; De Schutter, J.; Van Brussel, H. Optimal robot excitation and identification. IEEE Trans. Robot. Autom. 1997, 13, 730–740. [Google Scholar] [CrossRef]
- Swevers, J.; Ganseman, C.; De Schutter, J.; Van Brussel, H. Experimental robot identification using optimised periodic trajectories. Mech. Syst. Signal Process. 1996, 10, 561–577. [Google Scholar] [CrossRef]
- Caputo, M. Mean fractional-order-derivatives differential equations and filters. Ann. dell’Univ. Ferrara 1995, 41, 73–84. [Google Scholar] [CrossRef]
- Jung, S.; Hsia, T.C. Stability and convergence analysis of robust adaptive force tracking impedance control of robot manipulators. In Proceedings of the 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human and Environment Friendly Robots with High Intelligence and Emotional Quotients, Kyongju, Korea, 17–21 October 1999; Volume 2, pp. 635–640. [Google Scholar]
- Lee, K.; Buss, M. Force tracking impedance control with variable target stiffness. IFAC Proc. Vol. 2008, 41, 6751–6756. [Google Scholar] [CrossRef]
- Kim, T.; Kim, H.S.; Kim, J. Position-based impedance control for force tracking of a wall-cleaning unit. Int. J. Precis. Eng. Manuf. 2016, 17, 323–329. [Google Scholar] [CrossRef]
- Chen, G.; Guo, S.; Hou, B.; Wang, J.; Wang, X. Fractional order impedance control. In Nonlinear Dynamics and Control; Springer: Cham, Switzerland, 2020; pp. 167–175. [Google Scholar]
- Lahr, G.J.; Garcia, H.B.; Savazzi, J.O.; Moretti, C.B.; Aroca, R.V.; Pedro, L.M.; Barbosa, G.F.; Caurin, G.A. Adjustable interaction control using genetic algorithm for enhanced coupled dynamics in tool-part contact. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1630–1635. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Atkeson, C.G.; An, C.H.; Hollerbach, J.M. Estimation of inertial parameters of manipulator loads and links. Int. J. Robot. Res. 1986, 5, 101–119. [Google Scholar] [CrossRef]
- Impulse Response Invariant Discretization of Fractional Order Integrators/Dierentiators. Available online: http://www.mathworks.com/matlabcentral/fileexchange/21342-impulse-response-invariant-discretization-of-fractional-orderintegrators-dierentiators (accessed on 1 September 2020).








| i | |||||
| 1 | −0.0768 | −0.0675 | −0.0457 | 0.0521 | 0.1379 |
| 2 | −0.1505 | −0.0172 | −0.1307 | 0.2954 | 0.0030 |
| 3 | −0.0576 | 0.0177 | 0.0479 | −0.6920 | 0.6840 |
| i | |||||
| 1 | −0.0571 | 0.2280 | −0.0809 | 0.4996 | −0.4309 |
| 2 | −0.1795 | 0.2032 | −0.0809 | 0.2786 | 0.0938 |
| 3 | 0.0019 | 0.2032 | −0.0809 | 0.1852 | 0.1510 |
| Item | (Kgm) | (Kgm) | (Kgm) | (Kgm) | (Kgm) |
| Value | 27.88541 | 116.4740 | −11.9243 | 8.63456 | −13.4807 |
| Item | (Kgm) | (Kgm) | (Kgm) | (Kgm) | (Kgm) |
| Value | 70.4156 | −10.1249 | 48.6138 | 27.8231 | −2.0144 |
| Item | (Kgm) | (Kgm) | (Kgm) | (Kgm) | (Kgm) |
| Value | −7.4829 | 20.6031 | −3.6640 | 17.5760 | 4.0855 |
| Item | (m) | (Nm) | (Nm) | (Nms/rad) | (Nm) |
| Value | 12.9752 | 62.00688 | −93.8778 | 116.3661 | 176.8584 |
| Item | (Nm) | (Nms/rad) | (Nm) | (Nm) | (Nms/rad) |
| Value | −38.5557 | 119.6391 | 17.64926 | −47.8277 | 89.00266 |
| Component | Function | ||
|---|---|---|---|
| FOIC | Adjust the dynamic relation between the contact force error and robot end position | ||
| Robot System | Inverse Kinematic | Calculate the joint position command , a six-dimension vector consisting of all the joint command of the 6-Axis robot manipulator, according to the robot end command in cartesian coordinate | |
| Servo System | Control Loop | Consist of position-control-loop, velocity-control-loop and current-control-loop | |
| Motor Model | A motor model with friction and inertia | ||
| Dynamic Disturbance | The inverse dynamic results are used as the dynamic disturbance for the servo system, to simulate the influence of inertia, gravity and friction in the real physical environment | ||
| Dynamic Feedforward Controller | Calculate the driving torque corresponding to the desired kinematic command according to Equation (36). Transform the driving torque to driving current by and compensate the dynamic disturbance | ||
| Conversion coefficient between disturbance torque and current | |||
| Conversion coefficient between dynamic feedforward torque and current | |||
| Forward Kinematic | Calculate the position of the robot end in cartesian coordinate according to the joint real position , a six-dimension vector consisting of real position of every joint of the 6-Axis robot manipulator | ||
| Simulate the external spring stiffness contacting with the end of robot | |||
| Force Sensor | Obtain the real contact force | ||
| Link | Joint Offset (d) (m) | Link Length (a) (m) | Link Twist () (rad) |
|---|---|---|---|
| 1 | 0 | 0 | 1.5708 |
| 2 | 0 | 0.4318 | 0 |
| 3 | 0.15005 | 0.0203 | −1.5708 |
| 4 | 0.4318 | 0 | 1.5708 |
| 5 | 0 | 0 | −1.5708 |
| 6 | 0 | 0 | 0 |
| (Kgm) | (Kgm) | (Kgm) | (Kgm) | (Kgm) | |
| 0 | 0 | 0 | 0 | 0 | |
| 0.13 | 0 | 0 | 0.524 | 0 | |
| 0.066 | 0 | 0 | 0.0125 | 0 | |
| (Kgm) | (Kgm) | (Kgm) | (Kgm) | m (Kg) | |
| 0.35 | 0 | 0 | 0 | 0 | |
| 0.539 | 1.1832 | 0.1044 | −0.2784 | 17..4 | |
| 0.066 | 0 | −0.336 | 0.0672 | 4.8 | |
| (Nm) | (Nm) | (Nms/rad) | G | (Kg m) | |
| 0.395 | −0.435 | 0.00148 | −62.61 | 0.000291 | |
| 0.126 | −0.071 | 0.000817 | 107.8 | 0.000409 | |
| 0.132 | −0.105 | 0.00138 | −53.71 | 0.00299 |
| Items | Brand and Model | Description |
|---|---|---|
| Robot manipulator | EFORT ERC20C-C10 | Degree-of-freedom: 6; Maximum load: 20 Kg; |
| Industrial computer | ADVANTECH | Main board: advantech AIMB-785; Processor: Intel Core i7-7700/ 3.6 GHz; |
| Servo drive | TSINO DYNATRON CoolDrive R6 | Maximum EtherCAT communication frequency: 4 KHz; |
| Force sensor | HPS-FT060E | Range in Z-axis: ±1000 N; Measurement accuracy: 0.4 N; Maximum EtherCAT communication frequency: 2 KHz; |
| Spring | Stiffness: 1293.83 N/m; |
| Link | Joint Offset (d) (m) | Link Length (a) (m) | Link Twist () (rad) |
|---|---|---|---|
| 1 | 0.504 | 0.16846 | 1.5708 |
| 2 | 0 | 0.78155 | 0 |
| 3 | 0 | 0.14034 | 1.5708 |
| 4 | 0.76039 | 0 | −1.5708 |
| 5 | 0 | 0 | 1.5708 |
| 6 | 0.125 | 0 | 0 |
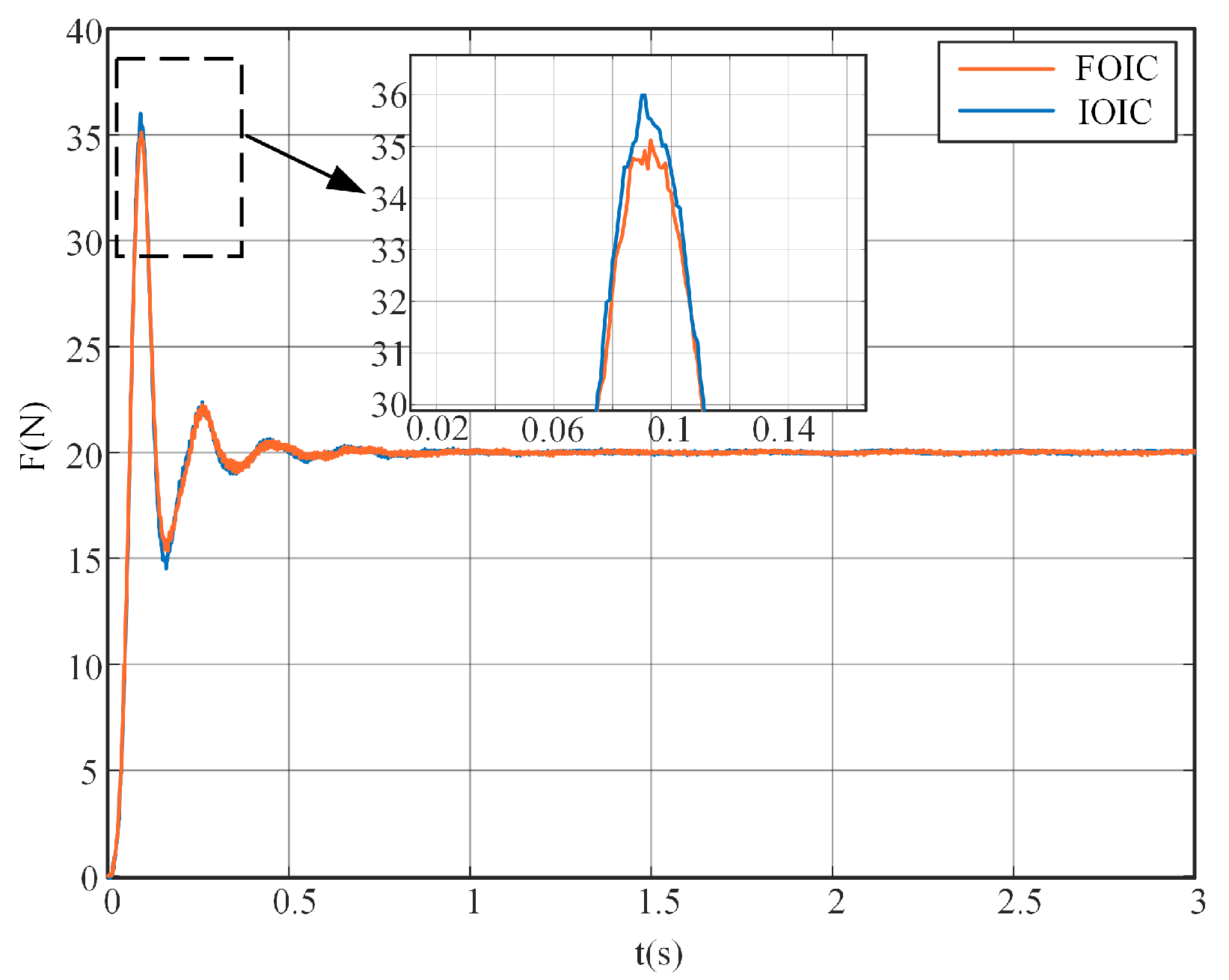
| IOIC | FOIC | Comparison | |
|---|---|---|---|
| Rising time (s) | 0.0614 | 0.0611 | 0.4886% |
| Overshoot (N) | 76.68% | 74.73% | 2.54% |
| Settling time (s) | 0.5359 | 0.4791 | 10.60% |
| ITAE | 0.3791 | 0.3478 | 8.2564% |
| IOIC | FOIC | Improvement Comparison of FOIC | |
|---|---|---|---|
| Settling time (s) | 0.7548 | 0.7051 | 6.5845% |
| ITAE | 0.2109 | 0.2081 | 1.3276% |
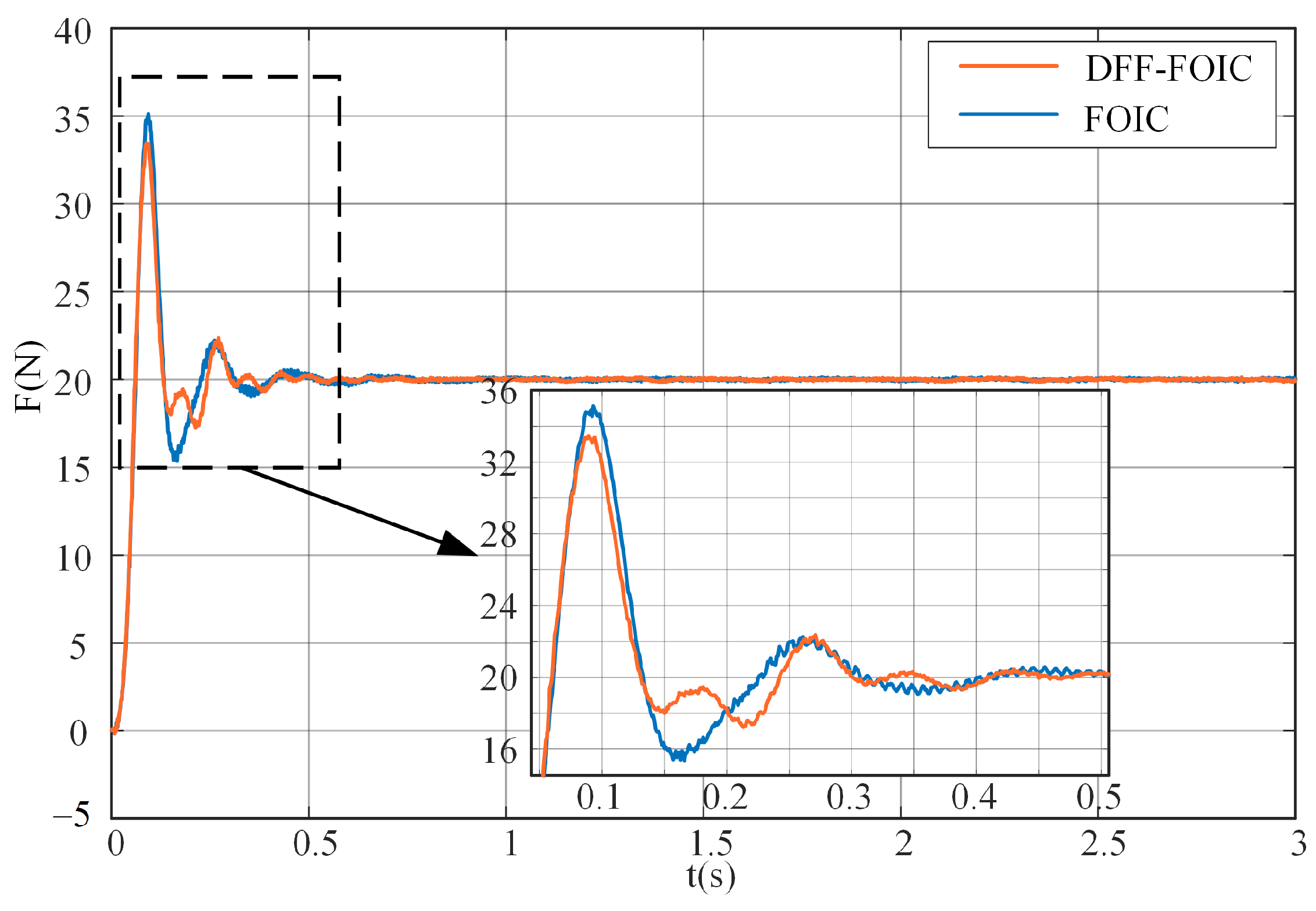
| FOIC | DFF-FOIC | Comparison | |
|---|---|---|---|
| Rising time (s) | 0.061 | 0.06 | 16.39% |
| Overshoot (N) | 75.62% | 67.33% | 10.96% |
| Settling time (s) | 0.474 | 0.431 | 9.07% |
| ITAE | 0.3619 | 0.317 | 12.41% |
| FOIC | DFF-FOIC | Comparison | |
|---|---|---|---|
| 0.0099 | 0.0055 | 44.44 % | |
| 0.004 | 0.0025 | 37.5 % |
| NSGA-IC | FOIC | DFF-NSAG | DFF-FOIC | |
|---|---|---|---|---|
| Rising time (s) | 0.083 | 0.074 | 0.083 | 0.074 |
| Overshoot (N% ) | 72.09% | 74.03% | 70.94% | 72.87% |
| Settling time (s) | 1.311 | 0.910 | 1.204 | 0.781 |
| ITAE | 2.751 | 1.813 | 2.599 | 1.260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Luo, Y.; Chen, Y. Dynamic Feedforward-Based Fractional Order Impedance Control for Robot Manipulator. Fractal Fract. 2023, 7, 52. https://doi.org/10.3390/fractalfract7010052
Ding Y, Luo Y, Chen Y. Dynamic Feedforward-Based Fractional Order Impedance Control for Robot Manipulator. Fractal and Fractional. 2023; 7(1):52. https://doi.org/10.3390/fractalfract7010052
Chicago/Turabian StyleDing, Yixiao, Ying Luo, and Yangquan Chen. 2023. "Dynamic Feedforward-Based Fractional Order Impedance Control for Robot Manipulator" Fractal and Fractional 7, no. 1: 52. https://doi.org/10.3390/fractalfract7010052
APA StyleDing, Y., Luo, Y., & Chen, Y. (2023). Dynamic Feedforward-Based Fractional Order Impedance Control for Robot Manipulator. Fractal and Fractional, 7(1), 52. https://doi.org/10.3390/fractalfract7010052







