Experimental Investigation of the Compaction-Crushing Characteristics of Graded Fractured Coal Gangue Based on Infill Mining

Abstract

The compaction and re-crushing characteristics of crushed gangue are important factors which affect the quality and effectiveness of the filling of the quarry. To study the compaction and re-crushing characteristics of the gangue particles, continuous grading and intermittent grading of two different structures were designed to study the bulk gangue particle size distribution. By conducting a side-limited uniaxial compression test on the crushed gangue, the compaction deformation parameters and particle re-crushing parameters of the samples under different axial pressure and grading conditions were calculated, the interaction between compaction and re-crushing was determined, and a compaction-re-crushing model of the crushed gangue was established. The following conclusions were obtained, (1) the axial displacement increment and fractal dimension of the graded crushed gangue are closely related to the graded structure of the skeletal particles; (2) the compaction stage of the graded crushed gangue can be divided into a fast compaction stage, a slow compaction stage, and a stable compaction stage—the fast compaction stage is significantly elastic, the slow compaction stage is more plastic, and the stable stage behavior approaches that of the original rock body; (3) the degree of crushing of the graded crushed gangue increases with an increase in axial stress, and the re-crushing of the specimen mainly occurs in the slow compaction stage; (4) the compaction-crushing-fractal evolution of the graded crushed gangue in the lateral limit compression process is established as the line of questioning. The physical significance of the parameters in the equation is discussed in this paper. The study can provide theoretical support and engineering guidance for the precise filling of a quarry and the prevention of later collapse.

1. Introduction

The compaction and re-crushing characteristics of quarry filling material are important factors which affect its filling effect and quality [1,2]. As the gangue filling material is widely-sourced, economical, and inexpensive, mine-filling accounts for most of its use, and the gangue material as a filling body can account for a large amount of gangue, reducing the land-take associated with its stockpiling, thereby reducing pollution of the environment [3,4]. On the other hand, the gradation of gangue for use as a bulk material for the filling of an extraction area is an important inherent factor which affects the filling effect [5,6]. The crushed gangue, in its natural state, is in a state of intermittent gradation [7]. To ensure the filling effect of the mining area and to protect the safety of coal production, the compaction and re-crushing characteristics of crushed gangue warrant investigation [8,9].

Intermittent grading is based on continuous grading and refers to a grading consisting of particles that are missing one, or several, particle size intervals [10]. In recent years, studies on continuously-graded rock particles have been carried out. Yu et al. [11] found that the larger the power index n of the gradation, the more particles of the rock undergo re-crushing during compression. Liu et al. [12] ascertained the relationship between the strain, compaction, and axial stress of crushed rock by conducting uniaxial compression tests on rocks. Yang et al. [13] carried out tests on sandstone samples under cyclic uniaxial compression loading and revealed the deformation process of the samples during cyclic loading. Zhou et al. [14] obtained the variation pattern of parameters such as strain rate, Poisson’s ratio, and elastic modulus of sandstone through tests and found that the degree of fragmentation of the samples was positively correlated with the pre-stress due to the degree of rock damage. Zhang et al. [15] and Gatumu et al. [16] concluded that the bearing capacity decreases with increasing ambient humidity, and, the greater the grading index, the greater the rate of change of the fragmentation rate.

Most studies of intermittently-graded rock particles have focused on permeability-driven instability [17,18,19], and Caquot et al. [20] identified the ‘wall effect’ and ‘interference effect’ as two factors which affect the porosity of the rock. The wall effect is the creation of additional pore space when particles make contact with the wall, and the interference effect is the forced separation of larger particles by the introduction of smaller ones. Based on these two effects, Francois et al. [21] and Liu et al. [22] suggested that the porosity of mixed, fractured rocks could be reduced when the ratio of the average size of fine particles to the average size of coarse particles was reduced. Cai et al. [23] studied the whole process of asphalt mixture skeleton formation experimentally by using three mixes with multi-stage design methods. Therefore, it is necessary to start from the grading structure, simulate the structural characteristics of crushed gangue in the initial state, explore the mechanical characteristics of the gangue particles and re-crushing characteristics during the bearing process, and establish a compaction-re-crushing model of graded crushed gangue to provide a theoretical basis for the filling management of a mining area [24,25,26].

In summary, scholars who previously worked on intermittent graded crushed rock investigated permeability-driven instability, and found that the graded bulk particles limit compaction and re-crushing characteristics, rendering intrinsic mechanism analysis less useful. The better method to reflect the changes in compressed crushed gangue, and conduct analyses of continuously-graded and intermittently-graded crushed gangue particles, is using the graded loading method for side limit uniaxial compression tests, which have been undertaken in this study. According to the test results, the compaction characteristics of the graded crushed gangue and re-crushing characteristics were studied using a graded crushed gangue compaction-re-crushing model. The limit-analysis method was used to determine the physical significance of the parameters of the formula, revealing the mechanical behavior of the graded crushed gangue and the interplay of the crushing behavior of the internal connections. According to the quantitative analysis of the graded compaction-crushing-fractal evolution, the qualitative understanding of the bulk filling material compaction and its re-crushing characteristics can be enriched to provide some theoretical reference for management of the empty area filling.

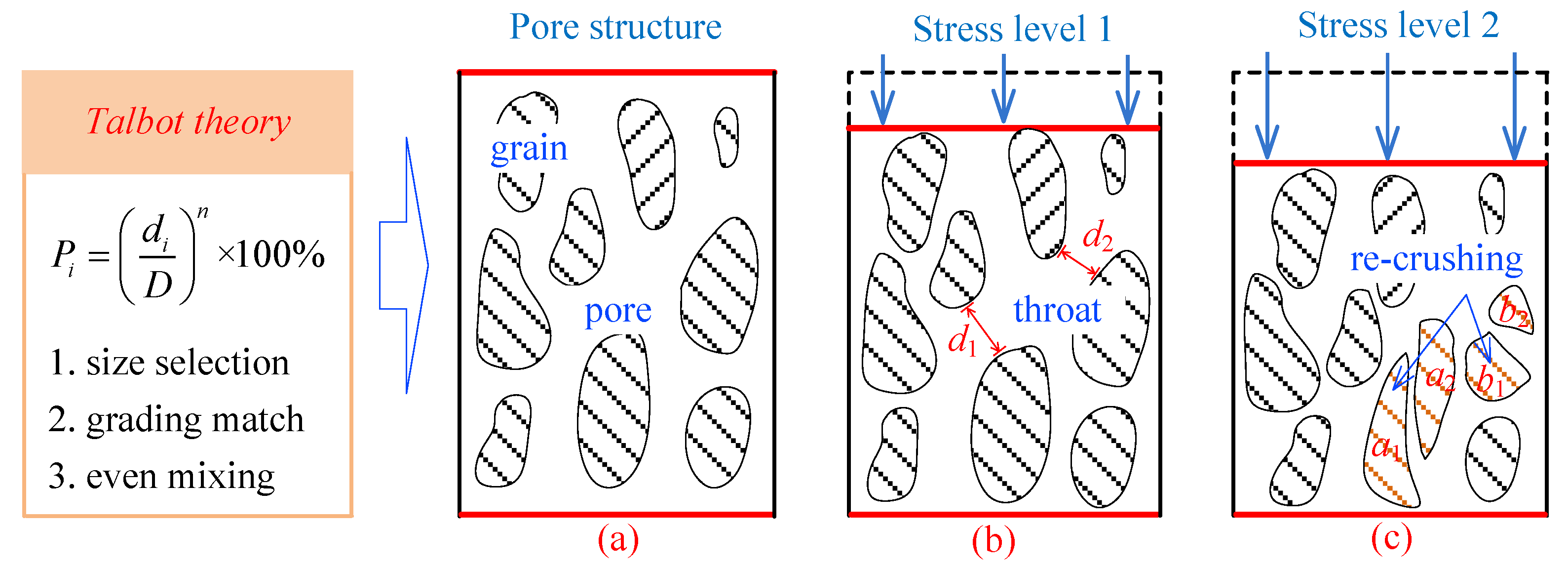
2. Compaction and Re-Crushing Process of Crushed Coal Gangue

Graded crushed gangue, in the compaction process, will be accompanied by the re-crushing of the particles, and the re-crushing of the particles will, in turn, affect its grading state, changing the compaction characteristics of the graded gangue and its bearing strength; that is, the granular re-crushing process will be presented to analyze the grade of crushed gangue compaction for, and re-crushing behavior of, the coupling effect between them. Therefore, the study of the re-crushing characteristics of the graded gangue can reveal its compaction and mechanical properties from another perspective.

2.1. Re-Crushing of Crushed Gangue

In the initial state, the crushed rock particles showed distinct and diverse shapes, which are generally prismatic or conical in shape, with all faces meeting at acute angles. After the lateral limit uniaxial compression test, point contact occurs between the more sharply angled particles, resulting in stress concentration, which eventually causes the asperities and sharp edges of the particles to fall off, forming smaller ellipsoidal or powder particles. The main types of damage during this process are fracture, crushing, and grinding. The general pattern of re-crushing of coal rock particles is shown in Figure 1.

Irregularly-fractured rock particles are broken into smaller particles by external loads. The breakage of the larger particles leads to the destruction of the entire skeleton structure, causing the external load to act directly on the smaller broken particles, decreasing the pore space between the rock particles and densifying the entire structure. In the subsequent pressure-bearing process, the smaller particles assume the skeletal role, and a series of complex effects of rupture, crushing, and grinding occur continuously, causing the smaller particles to become even further ellipsoidal or powdered, with the pores gradually decreasing and the particles nesting with each other. Therefore, crushed rock particles in the lateral limit uniaxial compression test undergo secondary crushing, which is the main form of crushing for the destruction of the skeleton and non-skeleton components in the grinding of fine particles.

From the macroscopic system consisting of crushed rock particles, the crushed rock particles are subjected to compression tests in the cylinder, mainly in the form of an increase in axial displacement and a decrease in volume of the entire crushed rock specimen. There are mainly three stages: 1. In the process of pressure compaction, the large gaps in the broken sample filled by granular rock particles are basically filled completely, and the internal friction between particles can no longer be overcome, thus changing the movement of particles to reduce the gaps. At this time, under the action of axial stress, the large particles are broken and become smaller particles to fill the remaining voids, which reduces the voids in the broken rock mass and leads to further compaction. 2. When the particles in the broken sample are broken to a certain extent, consolidation and bonding will occur under the action of high stress, so that the graded broken rock particles are compacted into the primitive rock mass close to the original rock mass. 3. Under the action of axial stress, the void of the whole broken sample decreases continuously, and the proportion of the skeleton in the whole acting system increases continuously, which leads to the reinforcement of the skeleton effect of the graded rock particles. The compaction-deformation process of the crushed structural coal rock particles is shown in Figure 2.

Therefore, the compaction process is also a process of increasing the compression resistance of the graded crushed rock particles until the whole system is completely occupied by the skeleton and a dense structure is achieved.

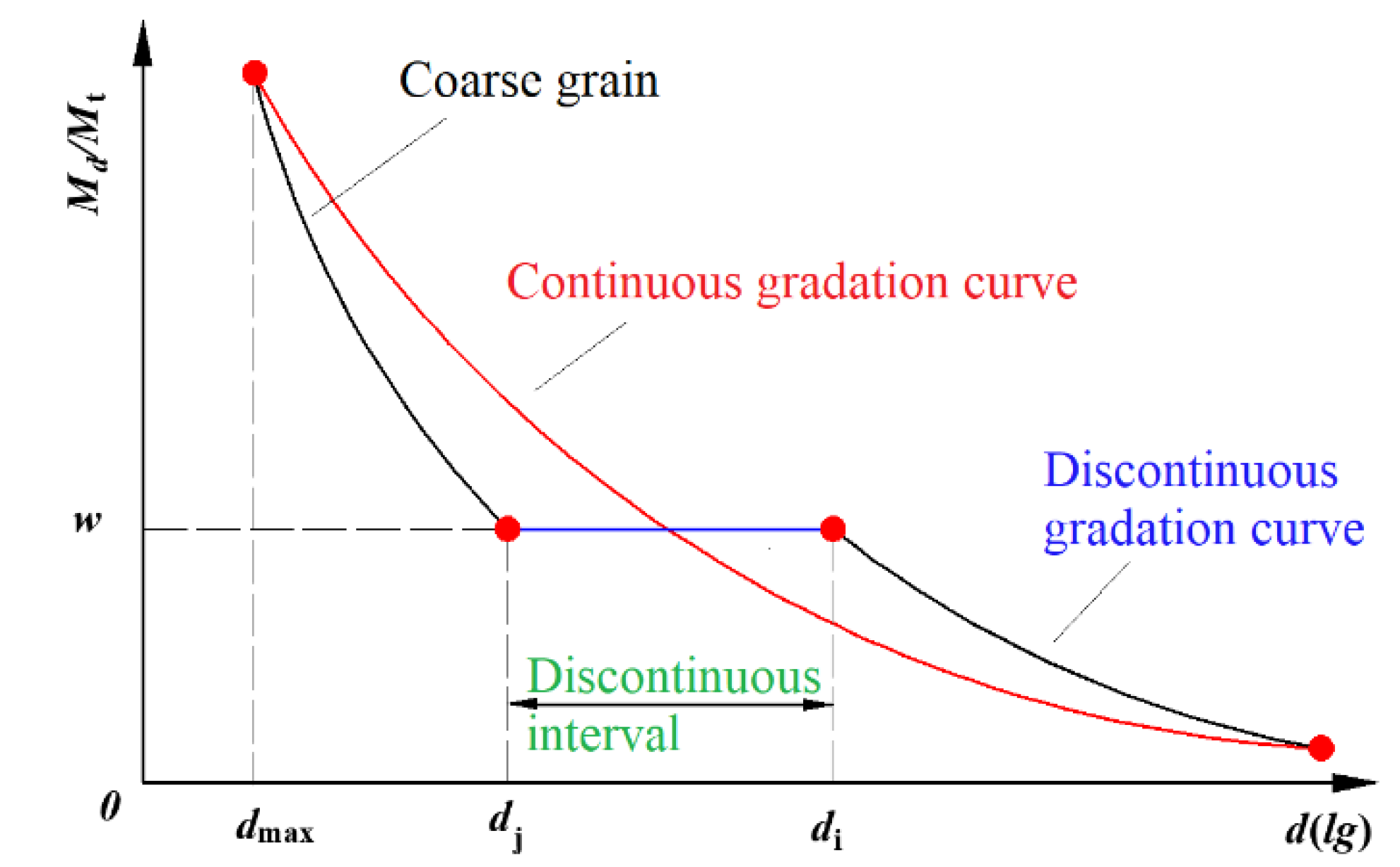
2.2. Particle Size Distribution Characteristics of Crushed Coal Gangue

The fractal dimension is a parameter that characterizes the complexity of the particle size fractal of crushed rock, where fractal refers to the microstructure of the object of study [27]. The intermittently-graded particle size is gradually supplemented by a continuous gradation structure during the compaction process, so that both intermittent and continuous gradations are in a single distribution during the re-crushing of crushed rock, i.e., a fractal dimension can characterize both of its mass distributions [28,29]. According to the basic defining equation of fractal dimension, the relationship between the number of saturated crushed rock particles and the characteristic scale can be expressed as:

$$N\left(x>d\right)=C{d}^{-D}$$

(1)

where d is the characteristic scale of crushed rock particles; N is the mass of crushed particles with a diameter greater than d; C denotes the characteristic constant; D is the fractal dimension.

According to the relationship between the particle mass of crushed rock and the characteristic scale, M ∝ d³, the mass of particles with a crushed particle scale smaller than d, can be expressed as:

$$M_d(x<d)=\left(x\right){\displaystyle {\int }_{d_{\mathrm{m}}}^d{\displaystyle \lambda \rho x^3}}dN$$

(2)

where λ is the shape factor of the crushed rock particles; d_m is the particle size of the crushed rock particles.

Substituting Equation (1) into Equation (2), let the largest particle of the broken coal rock body be d_m, then the total mass expression of the particle size fractal of the broken coal rock body is:

$$M_t=M_d\left(x<d_m\right)=\frac{CDs\rho }{3-D}\left(d_m^{3-D}-d_m^{3-D}\right)$$

(3)

The ratio of the mass M_d of the crushed rock particles with a particle size less than d to the overall total mass M_t of the specimen can be obtained from Equation (3), as given by:

$$\frac{M_d(x<d)}{M_t}=\frac{d^{3-D}-d_m^{3-D}}{d_m^{3-D}-d_m^{3-D}}$$

(4)

Broken rock particles will, under axial stress, undergo grinding between particles, thus producing some powder-like particles; compared with the largest particles in the broken specimen particles, the minimum particle size d_m can be defined as 0 mm, and, then, Equation (4) can be further expressed as:

$$\frac{M_d(x<d)}{M_t}={\left(\frac{d}{d_m}\right)}^{3-D}$$

(5)

where M_d is the total mass of particles in the crushed specimen with a particle size less than d, g; M_t is the total mass of the crushed rock specimen, g; d denotes the particle size of the crushed rock specimen, mm; d_m is the maximum particle size of the crushed test particles, mm; D is the particle size fractal dimension.

Taking the logarithm of both sides of Equation (5) simultaneously yields:

$$\lg \left(M_d/M_t\right)=\left(3-D\right)\lg \left(d/d_m\right)$$

(6)

From Equation (6), it can be seen that lg (M_d/M_t) and lg (d/d_m) satisfy a linear relationship with a slope of 3-D. Linear regression fitting lg(M_d/M_t) − lg(d/d_m) to the fractal dimension of the particle size distribution, D can be calculated from the sieving results of the crushed samples after compaction.

3. Materials and Methods

To study the re-crushing characteristics of graded crushed gangue, the use of self-designed crushed rock axial compression test system, from the gangue re-crushing particle size gradation and its fractal distribution characteristics, allowed for the comparative analysis of continuously-graded gangue and intermittently-graded gangue re-crushing particle size distribution characteristics. The graded compaction and re-crushing of the internal link between the two were investigated, then the particle size distribution evolution and crushing mechanism of graded gangue were further analyzed.

3.1. Materials

3.1.1. Research Background

Jiangjiahe Coal Mine is part of Binchang Mining Company and has a design capacity of 0.9 Mt/a. Today, the coal seam mined is a Jurassic soft rock coal seam, which can be buried to a depth of over 600 m and has entered the deep coal resource mining category. Deep mining makes the effects of high ground pressure and strong mining disturbances inevitable. The vertical stresses caused by gravity in deep mines are significantly increased, with complex tectonic stress fields and high ground stresses prevailing. The maximum horizontal principal stress at Jiangjiahe Mine is 16.46 MPa, the minimum horizontal principal stress is 9.13 MPa, the vertical stress is 15.34 MPa, and the maximum horizontal principal stress directions are N43.6 °E and N59.5 °E, respectively. Used in this study, 4# coal has an average strength of 16.84 MPa and is medium hard. There is a pseudo-roof in the local roof of the coal seam, which is carbonaceous mudstone less than 0.50 m, and mainly 20 m giant thick sandstone. The floor is mainly aluminous mudstone with carbonaceous mudstone pseudo-bottom distributed locally. Under high stress, the mining disturbance is strong and the surrounding rock is severely damaged. As a result of the burial depth, mining pressure and tectonic stresses, extensive channel deformation, slurry layer cracking, and delamination, shedding and bottom drops occurred in the main lane, downhill, and down-channel. During the excavation, geological changes such as associated faults, broken roof and coal body, fissure development, gas abnormalities, and water gushing abnormalities occurred.

3.1.2. Material Preparation

The crushed gangue loading test preparation was as follows: firstly, through the crushed rock screening device, particles with size ranges of d₁: 0~5 mm, d₂: 5~10 mm, d₃: 10~15 mm, d₄: 15~20 mm, and d₅: 20~25 mm were screened out as raw materials and constituted five groups of gangues. Secondly, according to the theory of continuous grading, the power index n was set to 0.2, 0.4, 0.6, and 0.8 for the preparation of three groups of samples, including one group of continuously-graded samples, and two groups of intermittently-graded samples. The mass of each group was 1000 g, and each group was packed into a different container, labelled, and stored. Finally, each group of samples was loaded to four stresses (2, 4, 8, and 12 MPa), at a rate of 0.05 MPa/s. To deform and re-crush the crushed samples, the stress-retention time was set at 30 min after loading to a certain stress.

In the process of screening crushed coal gangue in the different particle size ranges, to avoid errors caused by manual screening, a crushed coal rock body automatic screening device was used for screening. According to the test selected screen, and according to the particle size, as well as to install the corresponding particle size screen on the automatic screening device, the screen was fixed. Then, the top layer was loaded with crushed gangue particles, the power switch was turned on, and the equipment was run for 5 min to ensure that the particles were fully sieved (Figure 3).

3.2. Methodologies

3.2.1. Experiment Design

Based on the difference between continuous and intermittent gradation curves, intermittent gradation represents a gradation curve formed by removing particles in a certain size range from the base continuous gradation, where d_max is the maximum particle size in the test gradation, di is the minimum particle size in the intermittent particle size range, and d_j is the maximum particle size in the intermittent particle size range.

For the convenience of the subsequent mapping and analysis of this experiment, the intermittent interval (d_i to d_j) in the subsequent text refers to the missing gangue particle size in the intermittent gradation, that is, the test intermittent gradation of particle size d is greater than d_imm and less than or equal to d_jmm, such as in the intermittent 0~5 mm where it refers to the gradation missing particles with diameters less than or equal to 5 mm [30,31]. According to the continuous grading theory configuration of the crushed samples with different power index values n, the Talbot grading formula [32] can be used to calculate the total mass per 1000 g for each particle size interval:

$$\frac{M_d}{M_t}={\left(\raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$d_m$}\right.\right)}^n$$

(7)

where M_d is the mass of particles smaller than d, M_t denotes the total mass of the specimen, and d_m is the maximum particle size in the specimen.

According to the calculation results, the particle size mass distribution of crushed gangue particles under continuous grading is displayed in

Table 1. Mass distribution of particle size of crushed gangue under continuous grading.

Talbot Power Index n	Particle Size Interval Mass at Each Level/g
	0~5 mm	5~10 mm	10~15 mm	15~20 mm	20~25 mm
0.2	724.7	107.8	70.4	53.4	43.7
0.4	525.3	167.8	122.1	99.4	85.4
0.6	380.7	196.4	158.9	138.7	125.3
0.8	275.9	204.5	184.1	172.0	163.5

.

• The samples with intermittent grading structure are based on the samples with continuous grading structure, and the same quality of the control crushed samples and two grading structures are set under each power index n, intermittent 0~5 mm particle size, and intermittent 15~20 mm particle size, according to the principle of isometric scaling. The particles with sizes ranging from 0 to 5 mm are fine particles, and the particles with sizes greater than 5 mm are coarse particles. We let the mass of fine material be M_s, the mass of coarse material be M_l, and we use ω to express the fine material content:

$$\omega =\frac{M_s}{M_s+M_l}$$

(8)

The mass distribution of the particle size interval under intermittent grading is shown in

Table 2. Particle size interval mass distribution under intermittent grading.

Baseline Grading Power Index n	Particle Size Interval Mass at Each Level/g
	0~5 mm	5~10 mm	10~15 mm	15~20 mm	20~25 mm
0.2	0	391.6	257.0	194.0	158.7
0.2	765.6	113.9	74.4	0	46.1
0.4	0	353.5	257.2	209.3	180.0
0.4	583.3	186.3	135.6	0	94.8
0.6	0	317.1	256.6	224.0	202.3
0.6	442.0	228.0	184.5	0	145.5
0.8	0	282.4	254.2	237.5	225.9
0.8	333.2	247.0	222.3	0	197.5

.

3.2.2. Experimental Equipment

The DDL600 crushed rock compression system was used for uniaxial compression tests. This test system mainly consists of the electronic universal testing machine DDL600, a compaction device, an electronic analytical balance, and a main controlling computer. The crushed rock compression device consists of a cylinder, a piston, etc. The cylinder height and inner diameter are 200 mm and 100 mm, respectively. As the use of the load process is affected by radial stress and annular stress [33], to improve the accuracy of this test, the cylinder used in this test was made of a stiffer alloy material to reduce its influence as much as possible. The inner cylinder wall and piston were lubricated before the test was conducted, which, in turn, allowed for the frictional resistance of the cylinder in contact with the specimen to be ignored. The compression test equipment for breaking coal rock particles is shown in Figure 4.

3.2.3. Experimental Procedure

To study the compaction and re-crushing test characteristics of graded crushed gangue, the lateral limit uniaxial compression test was conducted by means of graded loading. The test process mainly included: specimen preparation, test loading, particle quality sieving statistics, and three modules. The specific test steps were as follows:

• Obtaining the raw material and specimen preparation. The laboratory crusher was used to crush the gangue particles, and then sieving gave five particle size intervals (0~5 mm, 5~10 mm, 10~15 mm, 15~20 mm, and 20~25 mm);
• According to Table 1 and Table 2 of the gradation test protocol, the gradation configuration of the different particle masses was conducted using an electronic scale and mixed well, and the configured samples were numbered in turn. The continuous grading power index of n = 0.2 was used as a benchmark for the intermittently-graded samples in the present work;
• Following the continuous and intermittent test programs, a graded loading program was established and saved in the axial pressure control system before specimen I was loaded into the cylinder, and the felt was placed on the upper surface of the specimen, followed by the displacement of the piston and its levelling using the piston to avoid errors caused by the loading process on the initial porosity;
• The prepared specimen was placed on the test bench so that the piston was facing the indenter. After the first level of the axial stress loading test was completed, the loaded gangue specimen was fully sieved using the automatic sieving device for crushed rock, the particle mass was weighed, and data were recorded using an electronic scale for each particle size interval;
• For the loading of the crushed specimen into the cylinder, the next level of stress loading was applied, and the above steps were repeated until all four levels of stress loading were completed; after the end of Group I grading, a Group II grading test and a complete grading test for each group were conducted in turn according to the test protocol; the above steps were repeated and the relevant test parameters were recorded.

4. Results and Discussion

To study the compaction-recompaction characteristics of graded crushed gangue, the authors started from the lateral limit compression test of crushed gangue, analyzing the relationship between its deformation and damage, and divided the compaction stages according to the distribution characteristics of particle size. The compaction-fractal relationship is listed. Based on the above study, the compaction-refragmentation model of crushed gangue was established. The reasonableness and feasibility of the model were verified.

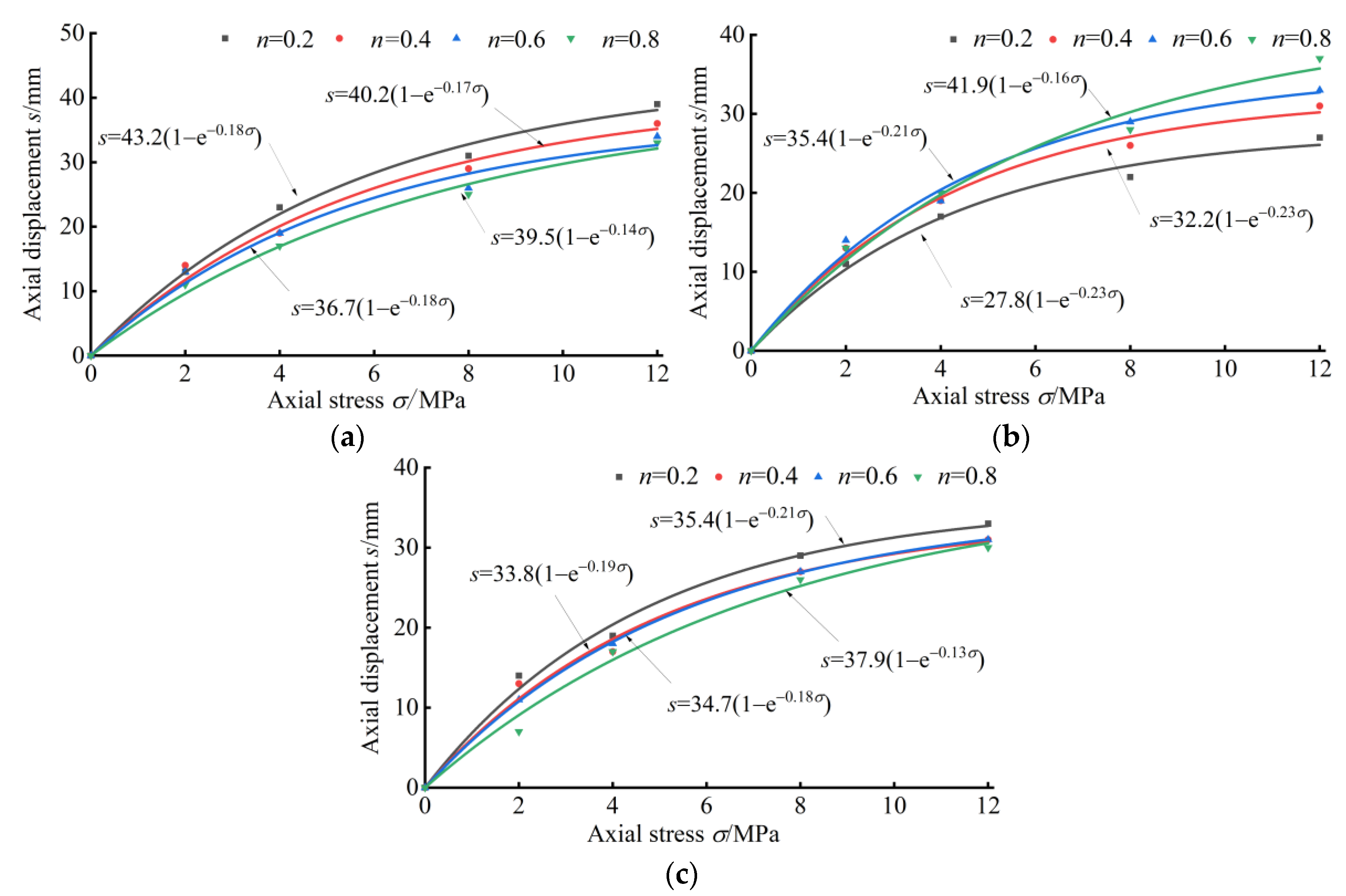
4.1. The Relationship between Deformation and Damage of Crushed Coal Gangue

The compaction characteristics of graded crushed gangue are influenced by external factors, many scholars have investigated the compaction and deformation characteristics of bulk gangue particles [34,35]. However, previous work has been limited by the test conditions, and the compaction characteristics of graded gangue under high stress and considerations for intermittent graded gangue compaction stage division research remains to be clarified.

Here, the limit method was used to analyze the compaction mechanical characteristics of the graded crushed gangue and to classify the compaction stages of the graded crushed gangue [36,37]. Among them, the axial displacement s was calculated by collecting the difference between the height h of the crushed specimen under all levels of stress and the initial specimen height h₀, that is:

$$s=h_0-h$$

(9)

The crushed gangue was laterally restrained in the cylinder with side limits, and, because the cylinder stiffness was large, its radial deformation can be neglected; therefore, only the resulting axial strain was considered. The axial strain is the ratio of the axial displacement and the initial height of the specimen under the action of axial stress [38]. That is, the axial strain can be calculated by the following formula.

$$\epsilon =s/h_0$$

(10)

The relationship between axial displacement s and axial stress in a continuously-graded fractured rock sample satisfies a negative exponential function:

$$s=a_1(1-{\mathrm{e}}^{b_1\sigma })$$

(11)

where a₁ and b₁ are both fitting parameters.

The relationship between strain and stress in a fractured rock sample can be obtained by dividing both sides of Equation (11) by h₀ at the same time:

$$\sigma =\frac{\ln \left(1-\raisebox{1ex}{$\epsilon h_0$}\!\left/ \!\raisebox{-1ex}{$a_1$}\right.\right)}{b_1}$$

(12)

Further differentiation of both sides of Equation (12) with respect to the strain ε gives the compression modulus E_S.

$$E_s=\frac{d\sigma }{d\epsilon }=-\frac{h_0}{b_1\left(a_1-s\right)}$$

(13)

Equation (13) shows that the compression modulus tends to infinity as the displacement s tends to a₁, the ultimate displacement at this point.

The effects of different intermittent particle size intervals on the compaction characteristics of intermittently-graded crushed gangue were investigated. According to the test results, the loading rate of 0.05 MPa/s, intermittent 0~5 mm particle size gradation, and intermittent 15~20 mm particle size gradation corresponding to the stress-displacement relationship were assessed. The axial displacement–axial stress curves for the crushed coal particles are shown in Figure 5.

From Figure 5, the axial displacement of the graded gangue and axial stress follow a positive exponential function, and the correlation coefficient exceeds 98%, indicating that the continuous grading and intermittent grading are applicable to Equation (11); with the increase in axial stress, crushed gangue axial displacement tends to increase. The axial displacement changes in two stages, between 0~4 MPa a rapid increase occurs and, at greater than 4 MPa, the increase is slow. About 60% of the displacement increment of the crushed gangue occurs in the rapidly-increasing stage. From Figure 5a, for the continuously-graded gangue specimen, the larger the power index n, the larger the ultimate displacement. Comparing Figure 5a,b, the overall gap-graded (missing the 0~5 mm particle size) displacement was larger.

According to the fitting results of the axial displacement–axial stress curve for the different grades of crushed gangue given in Figure 5, it can be seen that b₁ takes a negative value and the axial stress in Equation (11) is taken as the limit to obtain the limiting displacement slim, i.e.,

$$s_{\lim }=\underset{\sigma \to \infty }{\lim }{a}_1(1-e^{b_1\sigma })=a_1$$

(14)

From Equation (14), the axial displacement shows convergence characteristics with the change in axial stress, and the greater the value of b₁, the faster the convergence, i.e., the rate at which the axial displacement of the corresponding grade tends to stabilize when the change in stress is faster.

In its essence, the main stage of the dominant displacement increment is the rapid deformation stage, and the change in displacement of crushed gangue in the compaction process is mainly to fill the void by shifting the reorganization of broken particles; the greater the proportion of large particles, the larger the initial voids contained between the particles, and the greater the deformation.

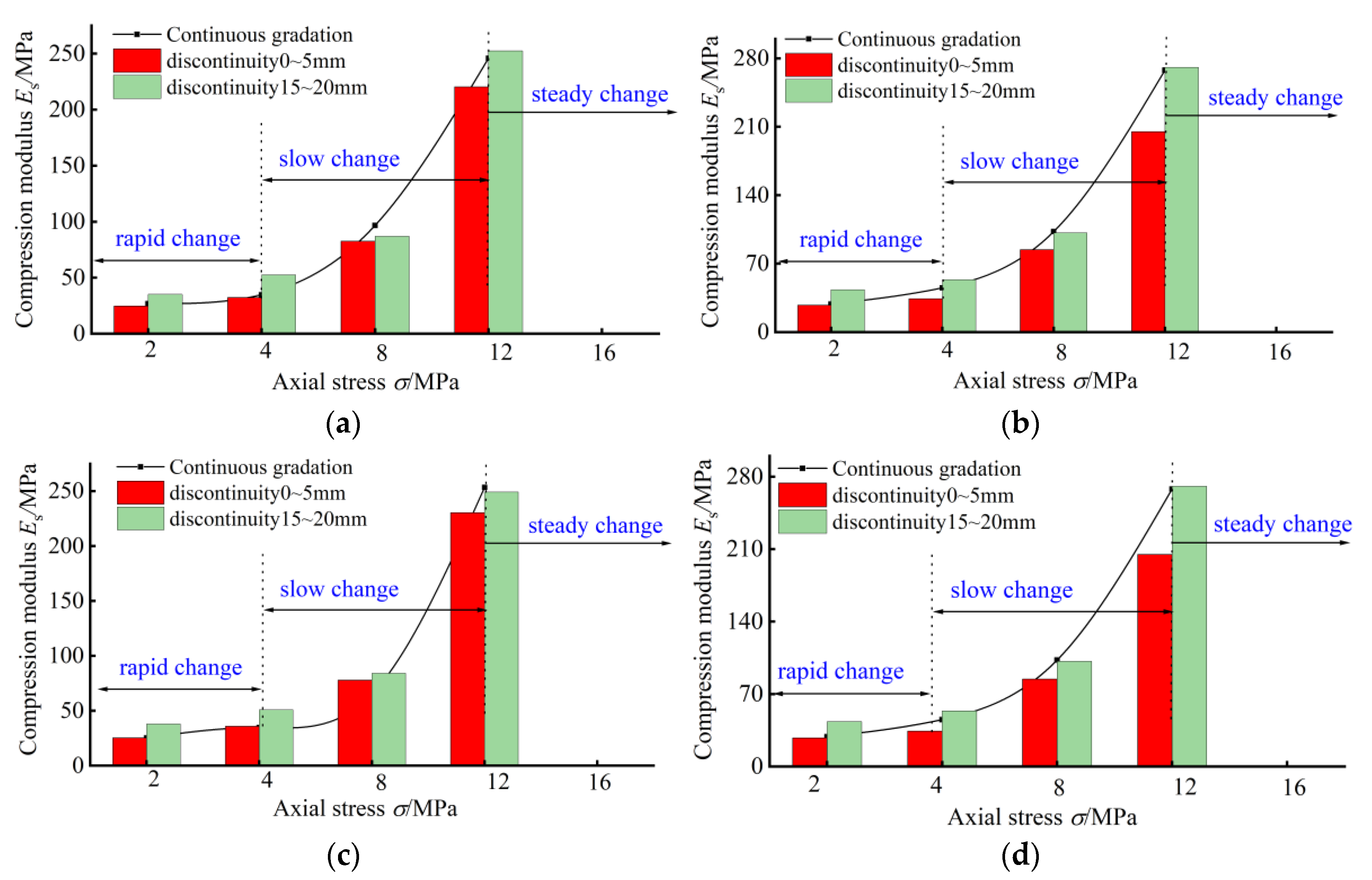
4.2. Analysis of Compaction and Re-Crushing Characteristics of Crushed Coal Gangue

4.2.1. Compaction and Re-Crushing Properties

Under the action of axial stress, the angular faces of the crushed gangue particles fall off and become smooth, the particle size is constantly reduced, and the specimen is densified. To examine the change in compression modulus during the compression of crushed gangue, according to Equations (1) and (4), the compression modulus and axial stress are plotted (Figure 6).

As seen in Figure 6, the trend of the compression modulus with axial stress for crushed samples with different grading structures can be divided into three stages: fast compaction, slow compaction, and stable compaction.

For stresses 0~4 MPa, the compression modulus was less than 50 and the compression modulus increased slowly with axial stress; this stage is accompanied by rapid compaction stage. When the stress is removed, there is a strong elastic effect and the modulus of compression is approximately linear with the change in axial stress. The work of axial stress in this stage is mainly used to overcome the friction between the particles, and the stress is concentrated near the void, causing a flow of particles into the void or increased embedding between particles. When the stress in the vicinity of the void exceeds the static friction, it will cause local instability in the vicinity of the void.

At stresses between 4 and 12 MPa, the compression modulus increases rapidly with increasing axial stress, and the compression resistance of the grading is significantly enhanced; the compression modulus undergoes rapid growth with increasing axial stress. The internal deformation rate of the specimen gradually decreases, and the compaction is slow throughout this stage. This is because, after the rapid compaction stage, the voids within the broken specimen are compressed and its internal structure is adjusted and optimized, the skeletal role of the internal particles is continuously improved, the particles in the load-bearing skeleton are broken in large quantities due to stress concentration, the broken small particles fill the voids, further reducing the voids ratio, and the load-bearing capacity of the specimen is greatly increased. At this stage, the specimen deformation shows strain hardening characteristics, with strong plasticity. There is a significant non-linear correlation between the compression modulus and plastic strain of the bulk particles during the plastic deformation stage.

Once the stress exceeds 12 MPa, the compression modulus exceeds 100. At this stage, the specimen forms a relatively stable skeletal bearing structure, with large particles being closely surrounded by small particles, reducing the stress concentration effect in the compaction process and making it difficult for larger particles to re-break. As a result, the possibility of instability damage to the load-bearing skeleton is low at this stage, and the focus is on structural fine-tuning and skeleton optimization. Gradation stability increases, the compaction is stable, and the behavior of the broken gangue rock body approaches that of the original rock body.

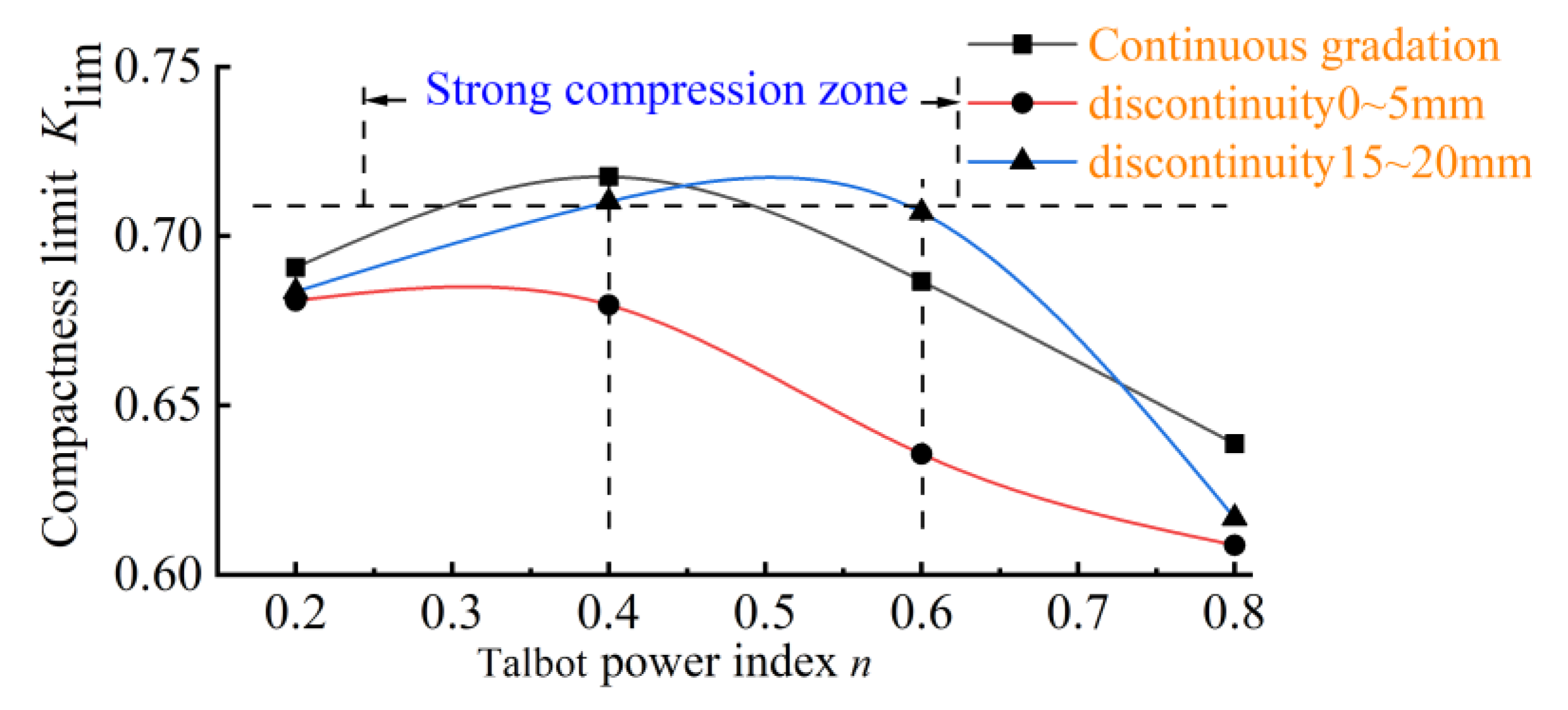
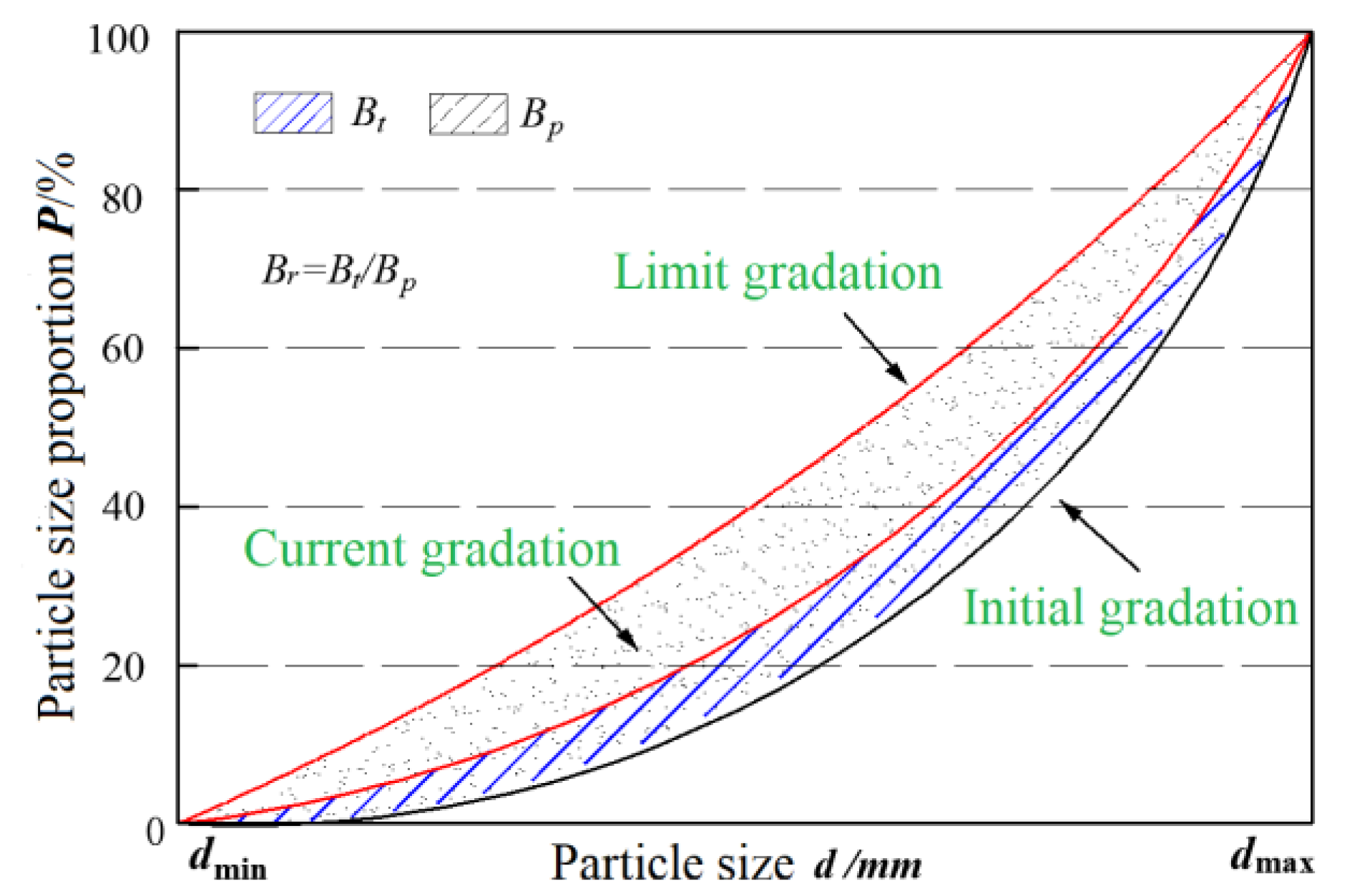
4.2.2. Compaction Limit Values

For precise filling of deep mines, the compaction at high stresses needs to be discussed. Therefore, this paper used ultimate displacement to explore the ultimate compaction of different gradations. Compaction can be used to characterize the degree of compaction of fractured rock under external forces, as characterized by the volume ratio of the samples before and after bearing compression [39]:

$$K=\raisebox{1ex}{$V_2$}\!\left/ \!\raisebox{-1ex}{$V_1$}\right.$$

(15)

where K is the degree of compaction, V₂ represents the volume after compression, and V₁ is the volume before compression.

For this uniaxial compression experiment, the cylinder bottom area was constant and, thus, the degree of compaction K can be simplified as:

$$K=\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$h_0$}\right.$$

(16)

The vertical joints are governed by Equation (9); Equations (14) and (16) introduce the limiting value of compaction, K_lim, as:

$$K_{\lim }=\frac{h_0-s_{{}_{\lim }}}{h_0}=\frac{h_0-a_1}{h_0}$$

(17)

To examine the compression resistance of different grades, the grades with compaction limit values greater than 0.7, i.e., those with no more than 30% deformation under high stress, are defined here as having strong compression resistance. The relationship between the compaction limiting value K_lim and the Talbot index n of the crushed samples is plotted according to Equation (17). The relationship curve between the compaction limit value and Talbot index is shown in Figure 7.

As can be seen from Figure 7, the compaction limit value K_min of intermittent 0~5 mm-graded samples decreases with the increase in power index n. The compaction limit values of continuously-graded and intermittently-15~20 mm-graded samples show a trend of increasing and then decreasing with the increase in power index n. The continuous grade with n = 0.4 has the maximum compaction limit, indicating the strongest compression resistance. At 0.4 < n < 0.6, the intermittent 15–20 mm grade has a compaction limit greater than 0.7 and a maximum value, indicating that the grade has good compression resistance at this stage. According to Table 2, the compaction limit value of 0–5 mm fine particles in the grading structure is always less than 0.7 and the compressibility is the weakest. This indicates that, for the compaction of crushed gangue, the absence of small particle size in the grading structure has much greater influence than the absence of intermediate particle size, while, due to the lack of intermediate particle size, the compaction of the particle grading structure may be improved.

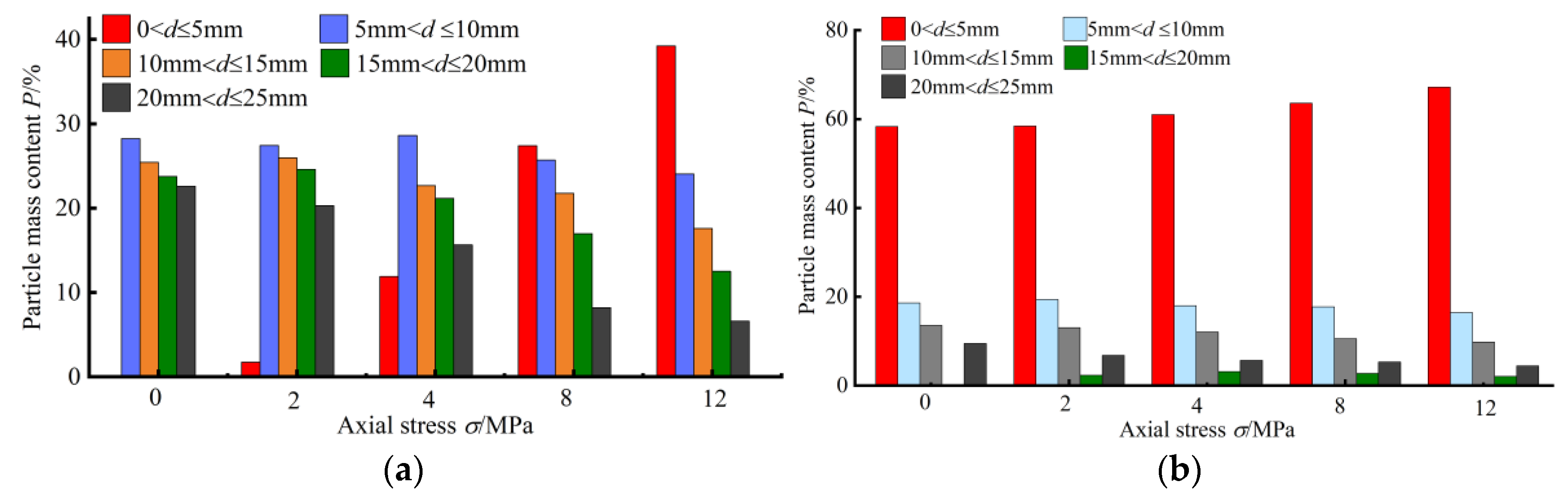
4.3. Particle Size Distribution Characteristics of Crushed Coal Gangue

4.3.1. Particle Size Interval Distribution

To study the crushed gangue compaction process missing small particle size and missing intermediate particle size on the crushed gangue re-crushing characteristics of the impact, according to the test results, the intermittent 0~5 mm and intermittent 15~20 mm grading compaction process of each particle size interval contained in the particle mass content P (expressed in percentage terms) and the relationship between axial stress are plotted in Figure 8.

Figure 8 shows that the crushed gangue in the compression process is mainly manifested as a continuous reduction in the percentage content of large particles and the percentage content of small particles increasing. When the stress was between 0 and 4 MPa, for intermittent 0~5 mm material, in the interval 0~5 mm in the graded samples in the particle, mass increased by 11.9%; for intermittent 15~20 mm fractions in the graded samples in the interval 0~5 mm in the particle, mass percentage increased by 2.8%. The mass of particles in the interval 0–5 mm increased by 27.4% for intermittent 0–5 mm-graded samples and by 6.2% for intermittent 15–20 mm-graded samples in the interval 0–5 mm at 4–12 MPa. The percentage of particles in the interval 0–5 mm increased more rapidly with axial stress than in the interval 15–20 mm, indicating that the absence of small particles makes the gradation more susceptible to re-fracture, and the re-fracture of particles in the samples occurred mainly at axial stresses of 4–12 MPa.

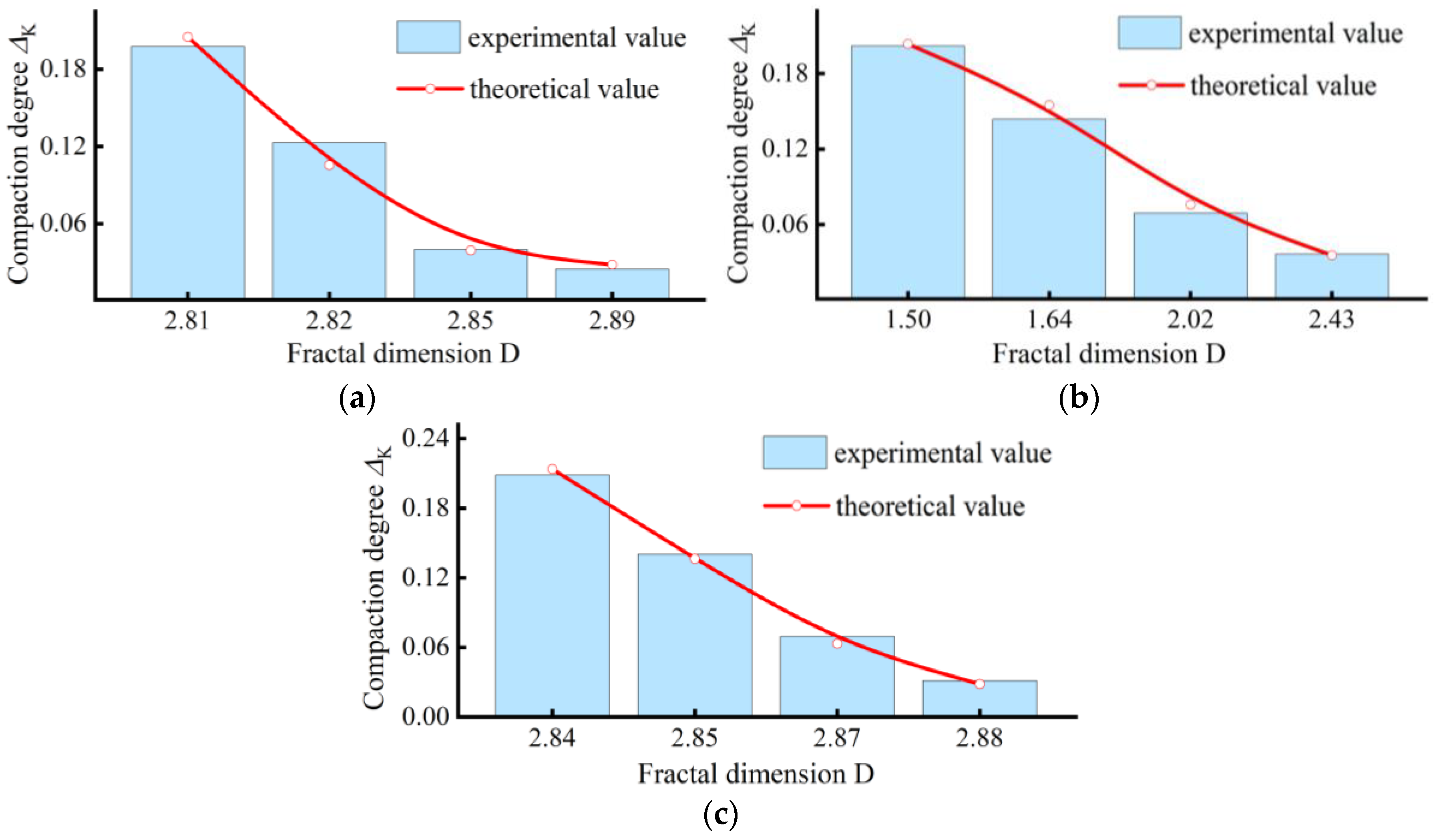
4.3.2. Changes in Fractal Dimension

The fractal dimension D is obtained from Equation (14). The relationship between the fractal dimension and the axial stress of a continuously-graded crushed sample can be expressed as follows.

$$D=a_2{\mathrm{e}}^{b_2\sigma }+c_2$$

(18)

where a₂, b₂, and c₂ are all fitted parameters.

To examine the variation in fractal dimension for samples with different grading structures under different axial pressures, the results of three sets of samples with n = 0.2 are used here as an example to plot the relationship between fractal dimension D and axial stress (Figure 9). As b₂ is negative in the fitted results in Figure 9, taking the axial stress in Equation (18) as the limit, the fractal dimension tends to c₂ with axial stress and b₂ characterizes the rate of convergence, i.e., the smaller the value of b₂, the faster it tends to c₂. The fractal dimension versus axial stress curve is shown in Figure 9.

As illustrated in Figure 9, the fractal dimension–axial stress relationship curve fitted with Equation (18) is good, with a correlation coefficient of over 99%. The fractal dimension of both continuously-graded and intermittently-graded crushed samples increases with the increase in axial stress. This is because many particles are broken during the compression process of the different grades; therefore, the different grades evolve towards an optimum grade. The fractal dimension of the intermittent 0–5 mm gradation is significantly influenced by the axial stress and the stability of the gradation is poor. The fractal dimension of intermittent 15–20 mm particles varies slowly with axial pressure. The fractal dimension of the intermittent 0–5 mm gradation is always smaller than the fractal dimension of the other two gradations, while the magnitude of the fractal dimension of the intermittent 15–20 mm gradation tends to be the same with increasing stress and the fractal dimension of the continuous gradation, with the difference between the two decreasing. This indicates that the absence of small particles in the gradation has a greater effect on the fractal dimension than the absence of intermediate particles.

4.4. Compaction-Crushing Modelling of Crushed Coal Gangue

Graded crushed gangue under the action of external load is affected by the occurrence of compaction and particle re-crushing processes; these are dynamic and mutually-influential. With the increase in axial stress, when the broken gangue particles constitute the whole system, the volume decreases; with the gap between the particles reduced, broken gangue is constantly compacted. From a statistical point of view, the gangue particles occur in the process of re-crushing and the particle size is constantly reduced, causing the redistribution of broken particles in a certain particle size range; thus, the compaction of broken gangue particles is also a particle re-crushing and particle size fractal evolution process, and two dynamic change processes are bound to be linked.

4.4.1. Size Distribution of Gangue Crushing

According to the study, with the increase in axial stress, the crushing of large particles will occur completely until all particles are less than 0.074 mm in size, at which point the grading curve will become a horizontal line. Based on this theory, the degree of crushing index B_r is proposed as the ratio between the degree of crushing and the crushing potential. The degree of crushing B_t represents the size of the area enclosed by the current particle grading curve and the initial grading curve before crushing, and the crushing potential B_p is the size of the area enclosed by the initial grading curve and the horizontal line. The gradation curve is illustrated in Figure 10. A diagram of the crushing potential is shown in Figure 11.

For stacked stone materials with fractal grading, the fragmentation index B_r is only related to the initial fractal dimension D₀, the current fractal dimension D and the fractal dimension limit D_u and are given by the following formula [40]:

$$B_r=\frac{D-D_0}{D_u-D_0}\frac{4-D_u}{4-D}$$

(19)

As seen from Equation (19), to calculate the degree of crushing index of crushed rock under the action of any axial stress, it is key to obtain the limit fractal dimension. To further explore the intrinsic link between the compaction of crushed gangue and re-crushing particle size distribution, and to obtain the limiting fractal dimension, the quantitative relationship between the compaction and fractal dimension was examined. The applicability of the relationship between axial displacement and axial stress for graded crushed gangue was verified in the axial displacement–axial stress curve, and, thus, the relationship between compaction and axial stress was obtained by deducing that:

$$K=1-\frac{a_1}{h_0}(1-{\mathrm{e}}^{b_1\sigma })$$

(20)

From Figure 9, the fractal dimension–axial stress curve given by Equation (9) can effectively predict the relationship between graded crushed gangue fractal dimension and axial stress; therefore, Equations (9) and (11) are combined in Equation (16) to obtain the axial stress, resulting in a compaction-fractal model characterizing the degree of compaction and fractal change in crushed gangue:

$$K=\frac{a_1}{h_0}{\left(\frac{D-c_2}{a_2}\right)}^{\frac{b_1}{b_2}}+1-\frac{a_1}{h_0}$$

(21)

To simplify Equation (21), the difference between the compaction under any axial stress and the compaction limit is defined as the compaction increment K, i.e.,

$${\Delta }_K=K-K_{\lim }$$

(22)

Combining Equations (17) and (22):

$${\Delta }_K=a{\left(D-c_2\right)}^b$$

(23)

where

$$\left\{\begin{array}{l}a=\raisebox{1ex}{$\left(1-K_{\lim }\right)$}\!\left/ \!\raisebox{-1ex}{${\left(a_2\right)}^{b_1/b_2}$}\right.\\ b=\raisebox{1ex}{$b_1$}\!\left/ \!\raisebox{-1ex}{$b_2$}\right.\end{array}\right.$$

(24)

where a₂, b₁, b₂, and c₂ are all fitted parameters, none of which is equal to zero.

To investigate the variation between the incremental compaction and the fractal dimension in Equation (23), the experimental and theoretical values for the three different gradations at n = 0.2 were plotted. The relationship between the compaction increments and the fractal dimension is shown in Figure 12.

As seen in Figure 12, the increment of compaction decreases as the fractal dimension increases. The similar trend between the experimental and theoretical values, and the relative error between the experimental and theoretical values, are less than 0.1, which, again, shows that the calculation of axial displacement and fractal dimension in the paper is reasonable within a certain tolerable error, and also indicates the validity of the compaction-fractal model characterized by Equation (23). The discrepancy between the theoretical and experimental values is mainly due to the difference between the irregularity of the particle shape and the regularity of the screen during the particle fractal statistics; as well as the loss of a small fraction of the particle mass the accuracy of the fit of the axial displacement and fractal dimension calculation is also an important cause of the discrepancy therein.

For the fitted parameters in the compaction-fractal model, it was found that a and b are non-zero and that the compaction increment K is a non-negative number. Therefore, the minimum value of K is obtained only when the fractal dimension D = c₂, and the minimum value is zero, when the difference between the current degree of compaction and the ultimate compaction is zero. The difference between the degree of compaction and its limiting value characterizes the existence of a certain compaction potential of the graded crushed gangue; when these are equal, the specimen is completely compacted. In the stable compaction stage, compaction deformation is mainly due to structure fine-tuning and skeletal optimization; large particles are rarer after continued crushing and, if this stage in the axial stress is large enough, it can also be considered that the specimen is completely compacted, putting a stop to further crushing. From the calculation of the crushing index, the change in fractal dimension can characterize the change in the degree of crushing of the gradation, and, as the fractal dimension increases, the degree of crushing also increases.

4.4.2. Compaction-Crushing Modelling

When the fractal dimension D tends to fractal dimension limit value, the specimen degree of crushing reaches the limiting value; that is, at this time, the broken gangue particles composed of the system no longer occur upon particle re-crushing, achieving an ideal state and a stable structure. Therefore, different grades of gangue have crushed particle size fractal dimensional D_u in the limiting case:

$$D_{\mathit{u}}=c_2$$

(25)

Equations (18) and (25) are combined in Equation (19) to obtain the formula for the degree of fragmentation under any axial stress:

$$B_r=\frac{a_2{e}^{b_2\sigma }+c_2-D_0}{c_2-D_0}\frac{4-c_2}{4-\left(a_2{e}^{b_2\sigma }+c_2\right)}$$

(26)

From Equation (26), we know that, for a graded structure under lateral limit compaction conditions with an initial fractal dimension determined, the index of fragmentation is only related to the axial stress. The degree of fragmentation increases with increasing axial stress, and, when the current fractal dimension of the fragmented specimen tends to the fractal dimension limit, the degree of re-fragmentation of the fragmented specimen also reaches its limiting value.

The crushing rate of a graded bulk particle can also be defined as the difference between the fractal dimension of the pile of stone particles after crushing has occurred and the fractal dimension before crushing [41]. Accordingly, the crushing potential is defined as the difference between the limiting value of the fractal dimension corresponding to the ultimate and initial gradation states and the initial fractal dimension, i.e., the fractal dimension increment:

$${\Delta }_D=D_u-D$$

(27)

The accuracy of the fit and its applicability to the fractal dimension D in Equation (18) is verified in Figure 12, which, when combined with Equations (18), (25), and (27), leads to:

$$b_2\sigma =\ln \left|\frac{{\Delta }_D}{a_2}\right|$$

(28)

Based on the defining equation for strain (Equation (10)) and a₁ as the limiting displacement, the limiting strain is derived as:

$${\epsilon }_{\lim }=\raisebox{1ex}{$a_1$}\!\left/ \!\raisebox{-1ex}{$h_0$}\right.$$

(29)

Figure 6 shows the compression modulus–axial stress relationship for different gradations, verifying the accuracy of the fitted equation and its applicability. Equation (12) is obtained from the deformation given by Equation (11), thus

$$b_1\sigma =\ln \left(1-\frac{\epsilon }{{\epsilon }_{\lim }}\right)$$

(30)

Dividing both sides of Equations (28) and (30) at the same time, eliminating the intermediate variable stress, and in combination with Equation (24), the compaction–re-fragmentation relationship is as follows:

$${\left|\frac{{\Delta }_D}{a_2}\right|}^b=1-\frac{\epsilon }{{\epsilon }_{\lim }}$$

(31)

From Equation (31), the left-hand side of the equation characterizes the graded re-crushing property and the right-hand side characterizes the graded compaction property; the particle crushing shows convergence with strain. In the initial unloaded state of the crushed specimen, i.e., when the strain is zero, a₁ is equal to the difference between the limiting value of the fractal dimension and the initial fractal dimension. In the completely-compacted state of the crushed specimen, that is, as the strain tends to its limiting value, the fractal dimension increment is zero and it, too, reaches its limiting value. Thus, for different grades of crushed gangue, the larger the absolute value of a₁, the greater the fractal dimension increment; that is, the greater the crushing potential and the more unstable the grade, the more likely it is that complete compaction is reached. Combined with the absolute value of a₁ in the fitting results, it is further confirmed that the continuous gradation is the most stable, while an intermittent 15~20 mm particle size ranks second, and the intermittent 0~5 mm particle size gradation stability is the worst.

In summary, for the quantified analysis of the compaction and re-crushing characteristics of graded crushed gangue under lateral limiting compaction conditions, a₁ can be used to characterize the size of the ultimate displacement, and b₁ can be used to characterize the rate at which the axial displacement tends to stabilize with the change in stress. Further, a₁ can be used to characterize the stability of the crushed gangue, b₂ can be used to characterize the rate of change in the fractal dimension with the change in stress as it tends to its limiting value, and c₂ can be used to characterize the fractal dimension limit value after re-crushing.

5. Conclusions

The axial displacement increment of graded crushed gangue is closely related to the fractal dimension and the gradation structure of the skeleton particles. Under high stress, the graded crushed gangue with a continuous gradation with n = 0.4 has strong compression resistance; when the proportion of fines is between 44.2% and 58.3%, the graded crushed gangue under with an intermittent 15–20 mm particle size gradation shows strong compression resistance; however, that with the intermittent 0–5 mm particle size gradation has poor compression resistance.

According to the change in compressive modulus with axial stress, the compaction stage of graded crushed gangue can be divided into fast compaction from 0~4 MPa, slow compaction from 4~12 MPa, and stable compaction stage above 12 MPa; the fast compaction stage is largely elastic in nature, the slow compaction stage exhibits plastic behavior, and, in the stable stage, the behavior approaches that of the original rock mass.

For graded crushed gangue, fragmentation increases with the increase in axial stress, and the re-crushing of the specimen mainly occurs at axial stresses of 4–12 MPa (i.e., in the slow compaction stage). Gap-graded materials are more prone to re-crushing and their stability is poor.

The compaction–fractal relationship was established using the compaction increment, which can be used to characterize the compaction potential, and the fractal dimension can be used to characterize the fractal characteristics. The strain induced by compaction deformation and the increment of fractal dimension characterize the re-crushing potential; these were used to establish the compaction–re-crushing relationship. The absolute value of the parameter a₂ in the equation can be used to characterize the stability of different gradations, and this further confirms that continuous gradation is the most stable, the intermittent 15~20 mm particle size ranks second, and the intermittent 0~5 mm particle size gradation is the least stable.