Numerical Solutions of Third-Order Time-Fractional Differential Equations Using Cubic B-Spline Functions
Abstract
1. Introduction
2. Cubic B-Spline Functions
New Approximation for
3. Temporal Discretization
- for ;
- ;
- ;
4. Description of Numerical Method
Initial Vector
- 1.
- ;
- 2.
- ;
- 3.
5. Stability and Convergence Analyses
5.1. Stability Analysis
5.2. Convergence Analysis
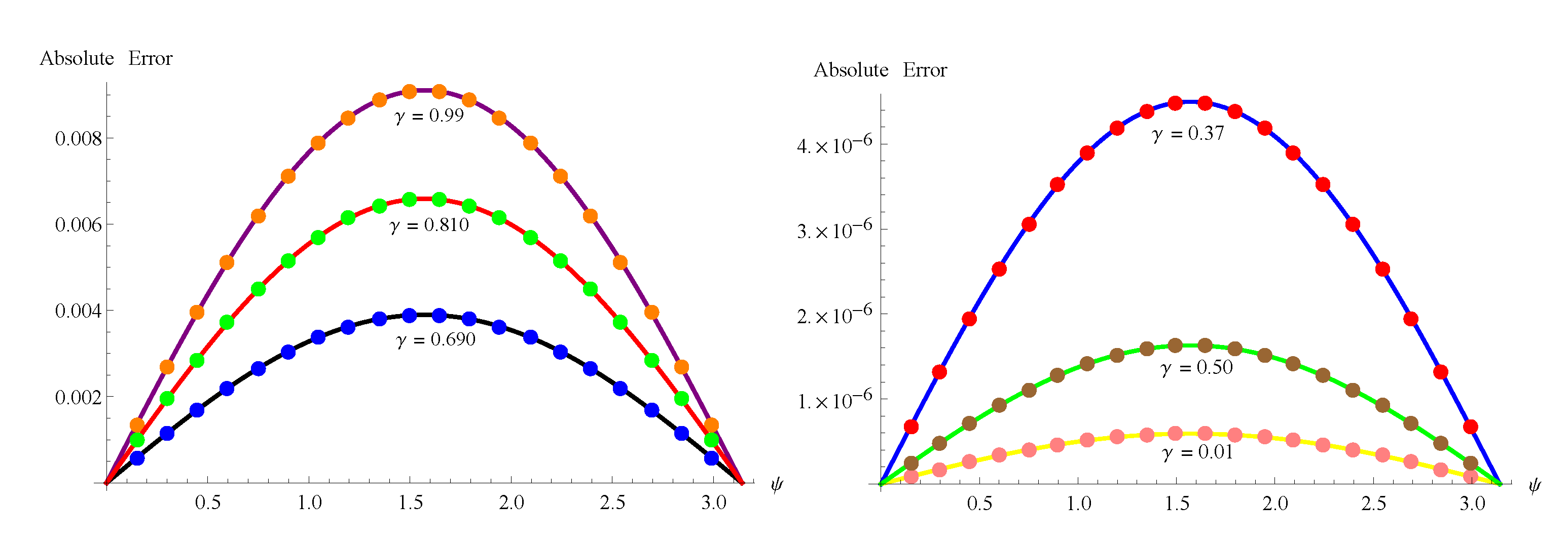
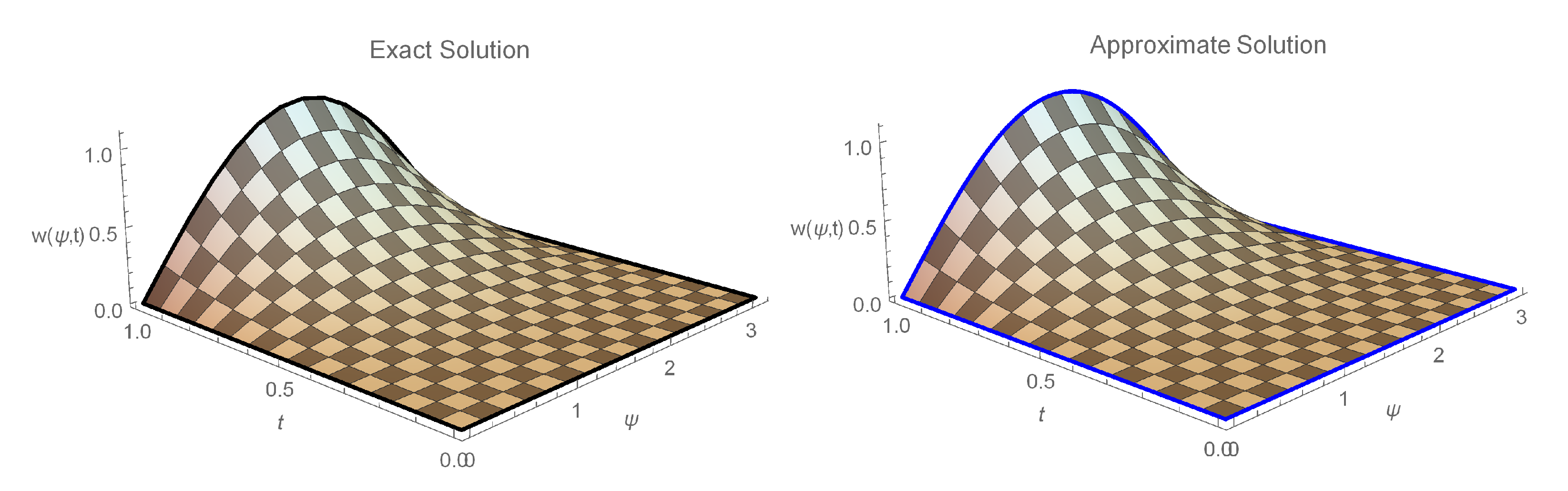
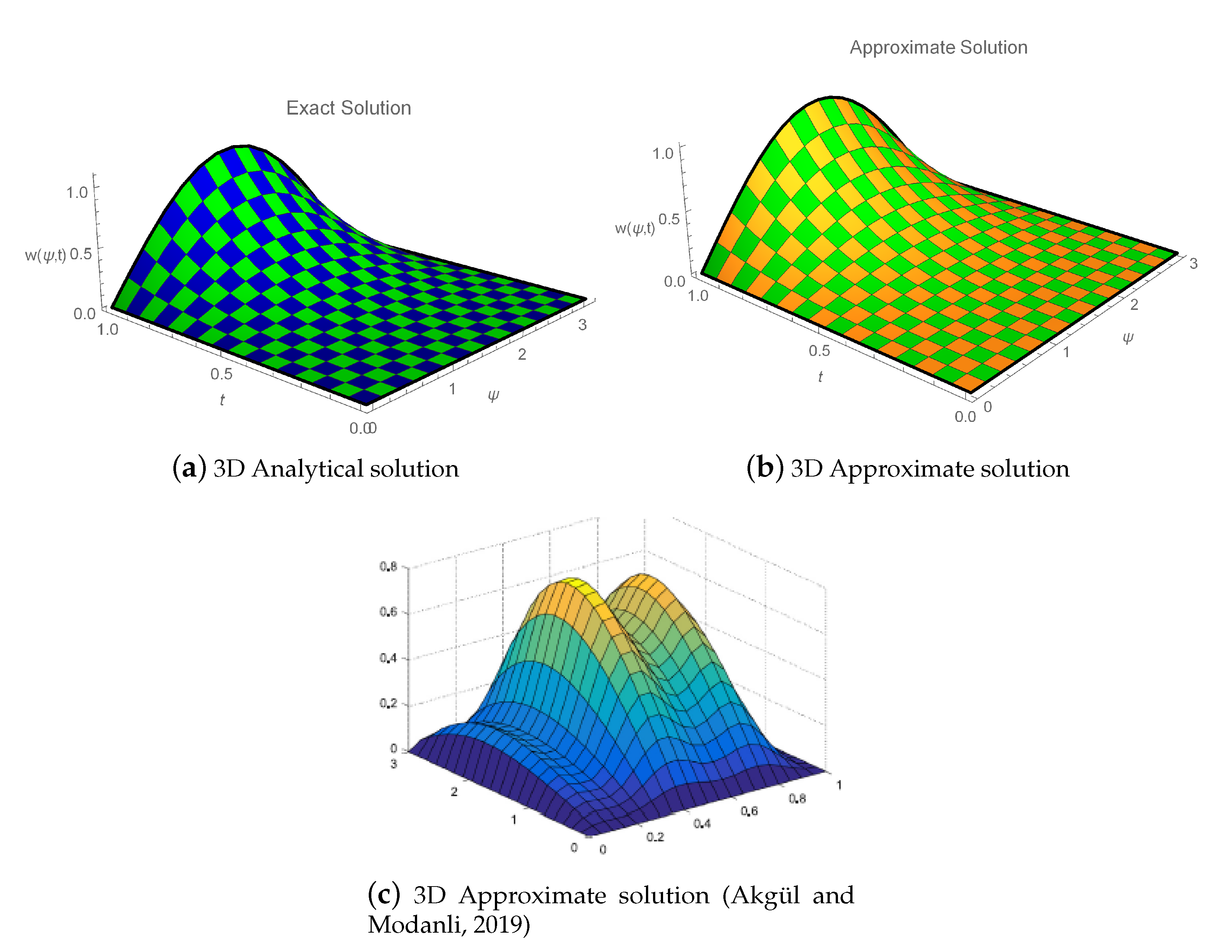
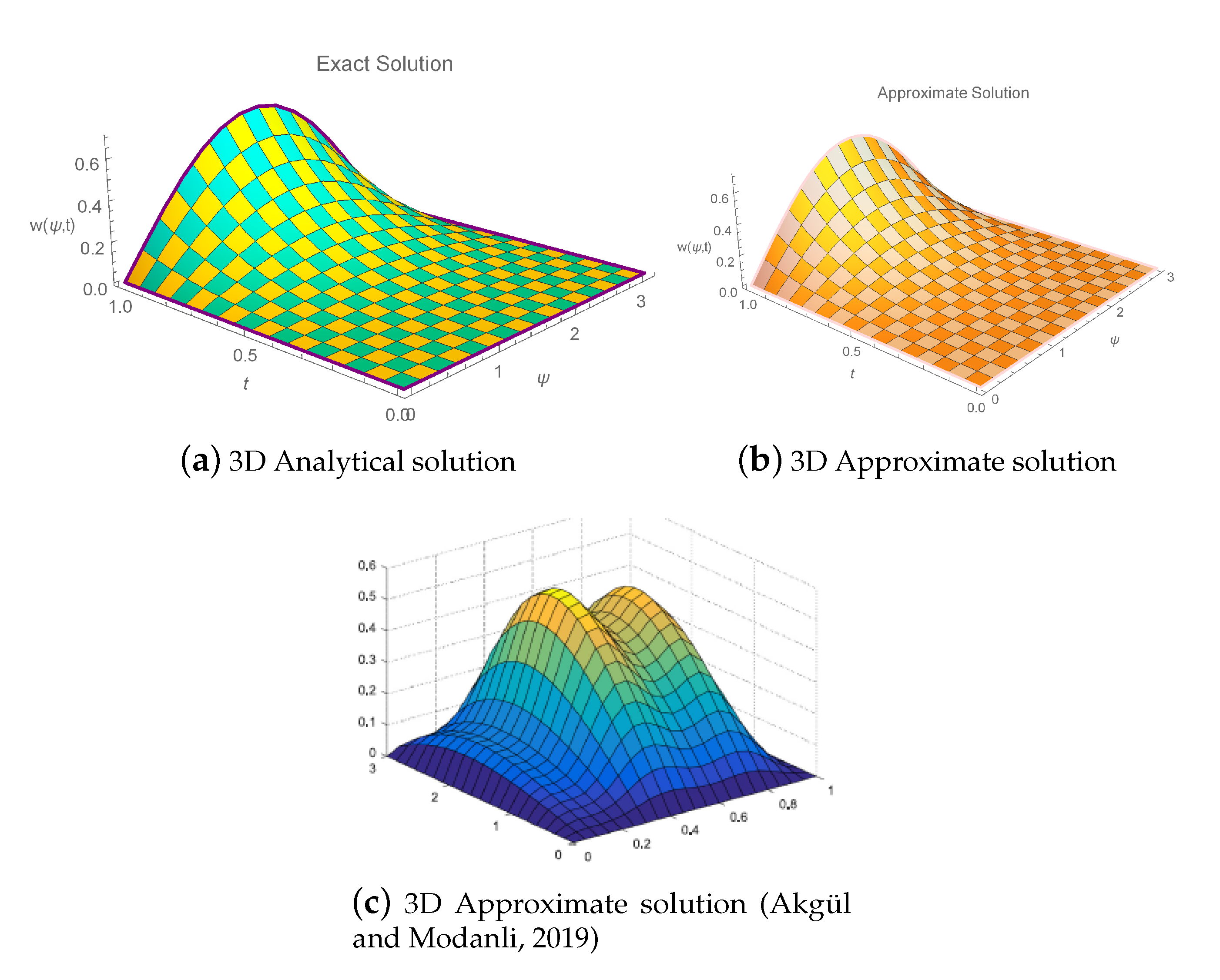
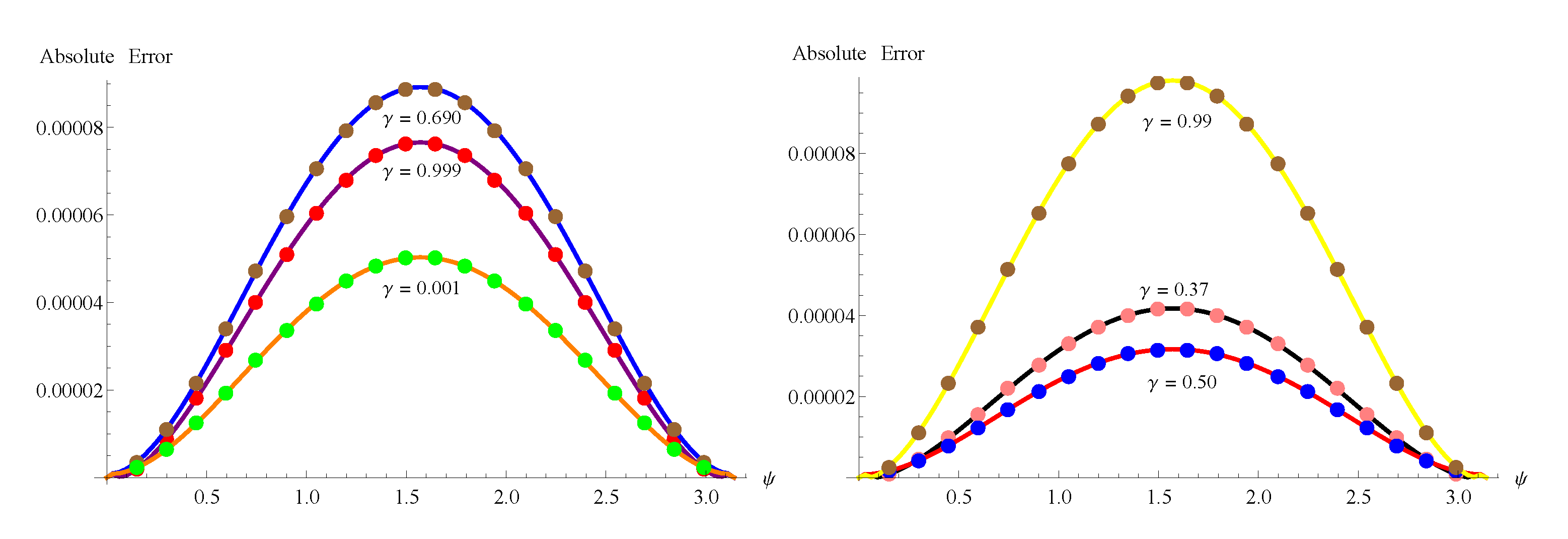
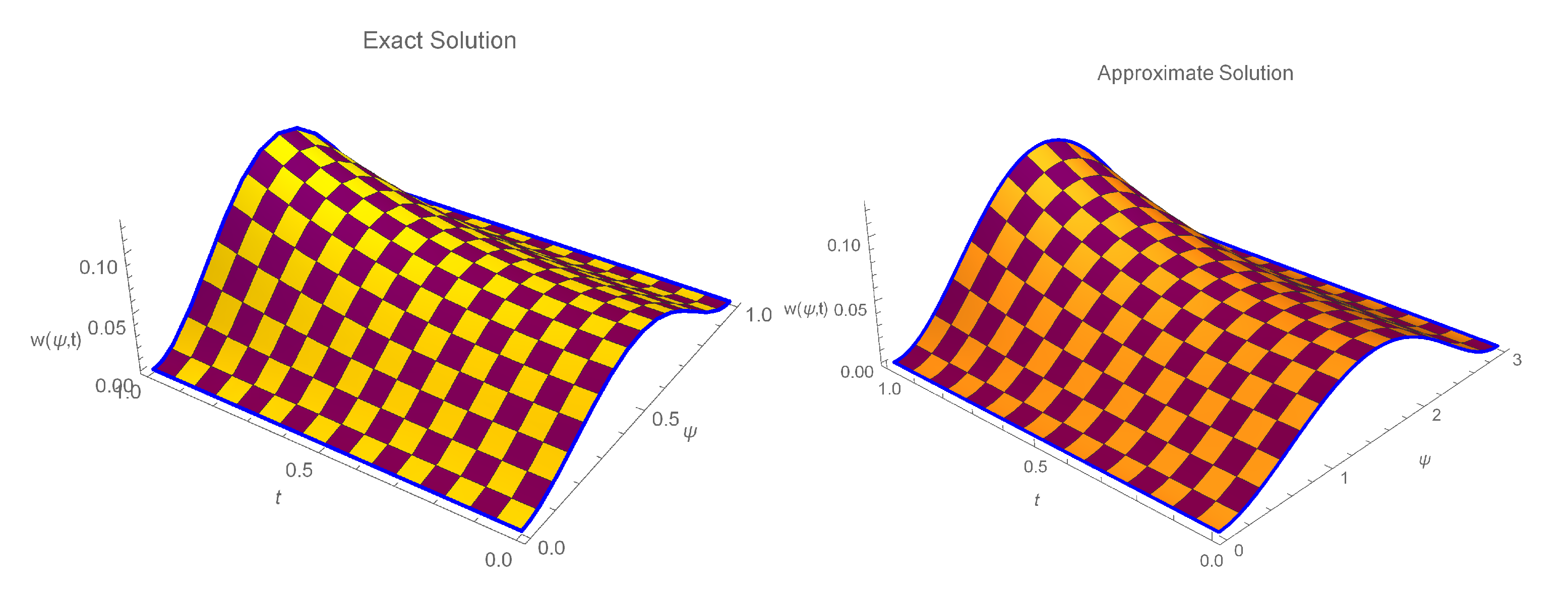
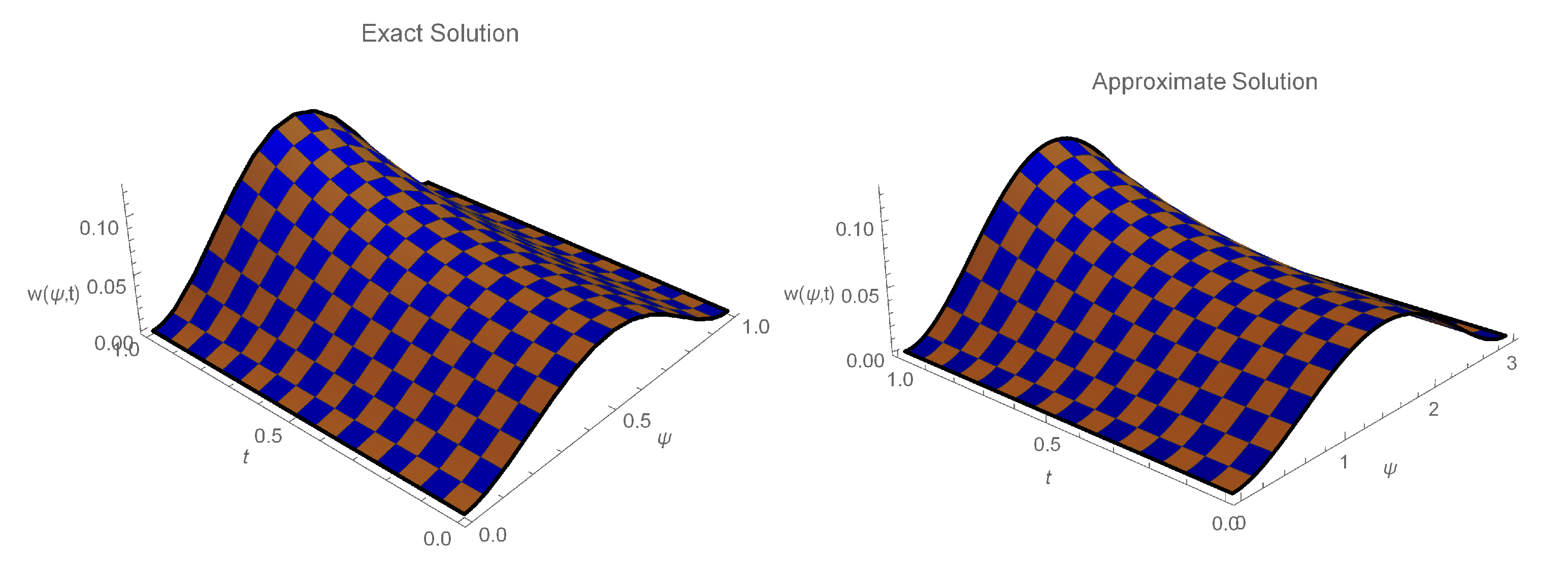
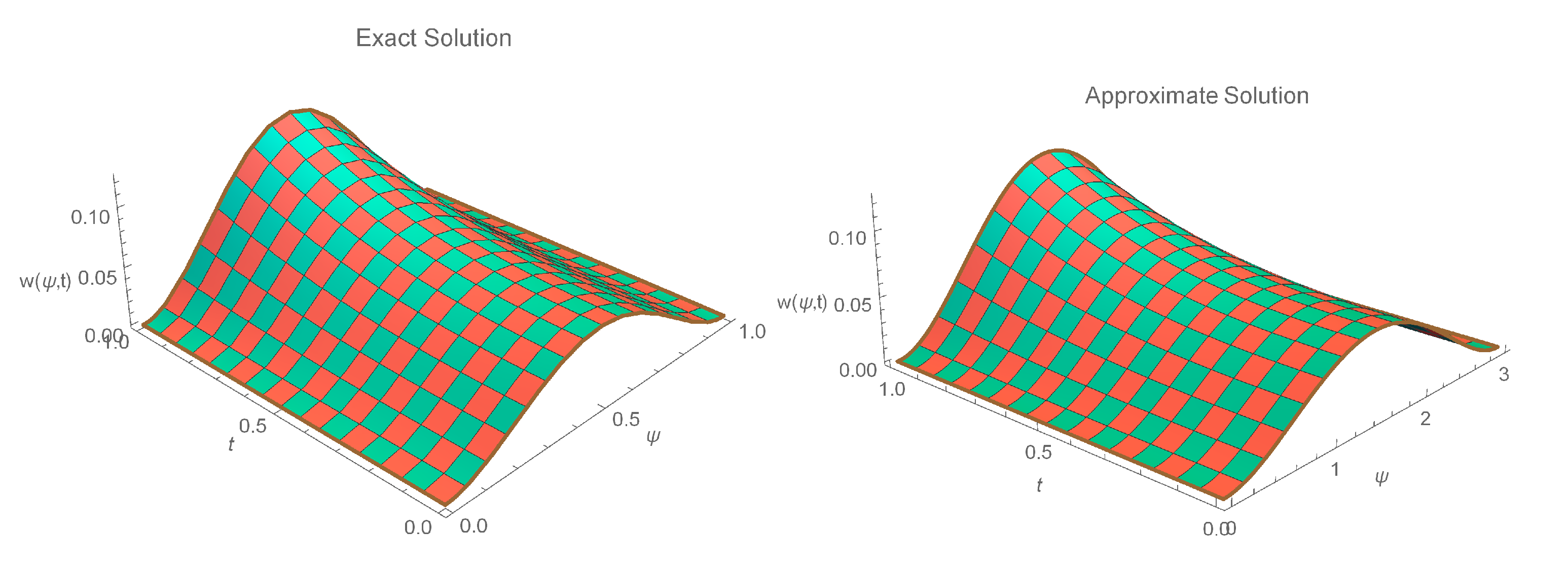
6. Numerical Implementation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diethelm, K.; Freed, A.D. On the solution of nonlinear fractional-order differential equations used in the modeling of viscoplasticity. Sci. Comput. Chem. Eng. 1999, 11, 217–224. [Google Scholar]
- Tariq, H.; Akram, G. Quintic spline technique for time fractional fourth-order partial differential equation. Numer. Methods Partial Differ. Equ. 2017, 33, 445–466. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 2000, 61, 132. [Google Scholar] [CrossRef] [PubMed]
- Van Beinum, W.; Meeussen, J.C.; Edwards, A.C.; Van Riemsdijk, W.H. Transport of ions in physically hetrogeneous systems; convection and diffusion in a column filled with alginate gel beads, predicted by a two-region model. Water Res. 2000, 34, 2043–2050. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus in Fractals and Fractional Calculus in Continuum Mechanics; Springer: Vienna, Austria, 1997; pp. 291–348. [Google Scholar]
- Zaslavsky, G.M.; Stevens, D.; Weitzner, H. Self-similar transport in incomplete chaos. Phys. Rev. E 1993, 48, 1683. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equations; Academic Press: London, UK, 1999. [Google Scholar]
- Ding, Z.; Xiao, A.; Li, M. Weighted finite difference methods for a class of space fractional partial differential equations with variable coefficients. J. Comput. Appl. Math. 2010, 233, 1905–1914. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, A.; Su, H. Convergence of the variational iteration method for solving multi-order fractional differential equations. Comput. Math. Appl. 2010, 60, 2871–2879. [Google Scholar] [CrossRef]
- Akgül, A.; Modanli, M. Crank-Nicholson difference method and reproducing kernel function for third order fractional differential equations in the sense of Atangana-Baleanu Caputo derivative. Choas Solitons Fractals 2019, 127, 10–16. [Google Scholar] [CrossRef]
- Ashyralyev, A.; Arjmand, D.; Koksal, M. Taylor’s decomposition on four points for solving third-order linear time-varying systems. J. Frankl. Inst. 2009, 346, 651–662. [Google Scholar] [CrossRef]
- Khalid, N.; Abbas, M.; Iqbal, M.K.; Baleanu, D. A numerical investigation of Caputo time fractional Allen-Cahn equation using redefined cubic B-spline functions. Adv. Differ. Equ. 2020, 1, 158. [Google Scholar] [CrossRef]
- Wu, G.C.; Zeng, D.Q.; Baleanu, D. Fractional impulsive differential equations: Exact solutions, integral equations and short memory case. Fract. Calc. Appl. Anal. 2019, 22, 180–192. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A.; Akgul, A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020, 8, 360. [Google Scholar] [CrossRef]
- Asif, N.A.; Hammouch, Z.; Riaz, M.B.; Bulut, H. Analytical solution of a Maxwell fluid with slip effects in view of the Caputo-Fabrizio derivative. Eur. Phys. J. Plus 2018, 133, 272. [Google Scholar] [CrossRef]
- Ghalib, M.M.; Zafar, A.A.; Riaz, M.B.; Hammouch, Z.; Shabir, K. Analytical approach for the steady MHD conjugate viscous fluid flow in a porous medium with nonsingular fractional derivative. Phys. A Stat. Mech. Its Appl. 2020, 554, 123941. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ismail, A.I.; Ali, N.H.M.; Baleanu, D. Extended cubic B-splines in the numerical solution of time fractional telegraph equation. Adv. Differ. Equ. 2019, 1, 365. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Akram, T.; Abbas, M.; Ismail, A.I.; Ali, N.H.M. A fully implicit finite difference scheme based on extended cubic B-spline for fractional advection-diffusion equation. Adv. Differ. Equ. 2018, 1, 109. [Google Scholar] [CrossRef]
- Shengjun, H.X.L. An extension of the cubic uniform B-spline curve. J. Comput. Aided Des. Comput. Graph. 2003, 5, 576–578. [Google Scholar]
- Abbas, M.; Iqbal, M.K.; Zafar, B.; Zin, S.B.M. New cubic B-spline approximations for solving non-linear third-order Korteweg-de vries equation. Indian J. Sci. Technol. 2019, 12, 1–9. [Google Scholar] [CrossRef]
- Fyfe, D. The use of cubic splines in the solution of two-point boundary value problems. Comput. J. 1969, 12, 188–192. [Google Scholar] [CrossRef]
- Iqbal, M.K.; Abbas, M.; Wasim, I. New cubic B-spline approximations for solving third-order Emden-Flower type equation. Appl. Math. Comput. 2018, 331, 319–333. [Google Scholar] [CrossRef]
- Lang, F.G.; Xu, X.P. A new cubic B-spline method for approximating the solution of a class of non-linear second order boundary value problem with two dependent variables. ScienceAsia 2014, 40, 444–450. [Google Scholar] [CrossRef][Green Version]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Sayevand, K.; Yazdani, A.; Arjang, F. Cubic B-spline collocation method and its applications for anomalous fractional diffusion equations in transport dynamic system. J. Vib. Control 2016, 22, 2173–2186. [Google Scholar] [CrossRef]

| Proposed Scheme | CNFDM [10] | |
|---|---|---|
| (0.001, 1.44) | ||
| (0.01, 1.44) | ||
| (0.37, 0.9) | ||
| (0.5, 0.529) | ||
| (0.69, 0.001) | ||
| (0.81, 0.01) | ||
| (0.99, 0.001) | ||
| (0.999, 0.001) |
| Proposed Scheme | CNFDM [10] | |
|---|---|---|
| (0.001, 1.33) | ||
| (0.01, 1.33) | ||
| (0.37, 0.648) | ||
| (0.5, 0.280) | ||
| (0.69, 0.010) | ||
| (0.81, 0.010) | ||
| (0.99, 0.001) | ||
| (0.999, 0.001) |
| & | & | |||
|---|---|---|---|---|
| 0.001 | ||||
| 0.01 | ||||
| 0.37 | ||||
| 0.5 | ||||
| 0.69 | ||||
| 0.81 | ||||
| 0.99 | ||||
| 0.999 |
| (0.5, 1.400) | |||
| (0.5, 0.900) | |||
| (0.5, 0.573) | |||
| (0.5, 0.432) |
| h | |||
|---|---|---|---|
| (0.5, 0.4348) | |||
| (0.5, 0.2580) | |||
| (0.5, 0.1970) | |||
| (0.5, 0.2105) |
| & | & | |||
|---|---|---|---|---|
| 0.001 | ||||
| 0.01 | ||||
| 0.37 | ||||
| 0.5 | ||||
| 0.69 | ||||
| 0.81 | ||||
| 0.99 | ||||
| 0.999 |
| & | & | |||
|---|---|---|---|---|
| 0.001 | ||||
| 0.01 | ||||
| 0.37 | ||||
| 0.5 | ||||
| 0.69 | ||||
| 0.81 | ||||
| 0.99 | ||||
| 0.999 |
| (0.5, 4.440) | |||
| (0.5, 5.380) | |||
| (0.5, 6.600) | |||
| (0.5, 8.475) |
| h | |||
|---|---|---|---|
| (0.5, 5.00) | |||
| (0.5, 10.50) | |||
| (0.5, 14.33) | |||
| (0.5, 17.49) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, M.; Bibi, A.; Alzaidi, A.S.M.; Nazir, T.; Majeed, A.; Akram, G. Numerical Solutions of Third-Order Time-Fractional Differential Equations Using Cubic B-Spline Functions. Fractal Fract. 2022, 6, 528. https://doi.org/10.3390/fractalfract6090528
Abbas M, Bibi A, Alzaidi ASM, Nazir T, Majeed A, Akram G. Numerical Solutions of Third-Order Time-Fractional Differential Equations Using Cubic B-Spline Functions. Fractal and Fractional. 2022; 6(9):528. https://doi.org/10.3390/fractalfract6090528
Chicago/Turabian StyleAbbas, Muhammad, Afreen Bibi, Ahmed S. M. Alzaidi, Tahir Nazir, Abdul Majeed, and Ghazala Akram. 2022. "Numerical Solutions of Third-Order Time-Fractional Differential Equations Using Cubic B-Spline Functions" Fractal and Fractional 6, no. 9: 528. https://doi.org/10.3390/fractalfract6090528
APA StyleAbbas, M., Bibi, A., Alzaidi, A. S. M., Nazir, T., Majeed, A., & Akram, G. (2022). Numerical Solutions of Third-Order Time-Fractional Differential Equations Using Cubic B-Spline Functions. Fractal and Fractional, 6(9), 528. https://doi.org/10.3390/fractalfract6090528







