New Numerical Approach of Solving Highly Nonlinear Fractional Partial Differential Equations via Fractional Novel Analytical Method

Abstract

In this work, the fractional novel analytic method (FNAM) is successfully implemented on some well-known, strongly nonlinear fractional partial differential equations (NFPDEs), and the results show the approach’s efficiency. The main purpose is to show the method’s strength on FPDEs by minimizing the calculation effort. The novel numerical approach has shown to be the simplest technique for obtaining the numerical solution to any form of the fractional partial differential equation (FPDE).

1. Introduction

In the 18th century, the work of Euler, D’Alembert, Laplace, and Lagrange heavily relied on the use of partial differential equations (PDEs) as a key tool for examining physical models and describing the mechanics of continua. Similarly, PDEs were a crucial tool for scientists throughout the middle of the nineteenth century, particularly in the work of Riemann. They are now essential for characterizing dynamical systems in the physical and mathematics sciences [1]. PDEs may be used to simulate many circumstances and phenomena in Physics, Fluid Mechanics, Heat and Wave Analysis, Quantum Mechanics, Engineering, Chemistry, and Electrodynamics [2,3]. In general, the dynamics of any physical system can be addressed by either linear or nonlinear PDEs [4,5].

Since there are not really any strategies that work for all equation types and each equation frequently needs to be addressed as a separate issue, it is challenging to solve nonlinear EDPs in general. With analytic solutions to PDEs, we may test and comprehend the numerical methods as well as the physical processes under consideration [6]. Finding an exact solution for nonlinear PDEs is tricky. As a result, over several decades, mathematicians and researchers have explored and presented novel numerical techniques and approaches for solving Nonlinear PDEs. Haar Wavelet Method (HWM), Homotopy Perturbation Method (HPM), Variational Iteration Method (VIM), Differential Transform Method (DTM), Homotopy Analysis Method (HAM), Least Squares Finite Element Method, Chebyshev and Fourier Spectral Methods, and Perturbation-Iteration Algorithm (PIA), are some recent numerical methods.

A robust technique is illustrated, and the Finite Approximation methodology is detailed in depth in [7]. The study in [8] discusses the Differential Transform approach to the physical application of electrical circuits. In [9], the Fishers Reaction Diffusion Equation is solved by utilizing the Least Squares Finite Element Approximation approach, whereas the authors of [10] applied the Haar Wavelet Method to the Fishers Reaction-Diffusion Equation.

The research in [11] contains a detailed description of how to solve Eigen Value Problems and Boundary Value Problems using Fourier Spectral Methods, Galerkin Methods, Chebyshev technique, Pseudospectral Methods, the Tau Method, Domain Decomposition Methods, and methods for unbounded intervals. The Homotopy Perturbation approach is used on both homogeneous and inhomogeneous PDE systems [12].

For semiconductor devices, the Poisson–Boltzmann Equation is discussed by Homotopy Analysis Method in [13]. In [14], the applicability of Adomain Decomposition Method (ADM) is demonstrated by solving non-integer PDEs in infinite domains.

PDEs of Fractional Order have also piqued the interest of mathematicians and physicists [15]. For example, in [16], a numerical approach known as PIA was used for several highly nonlinear PDEs, and quick convergence of these equations to their precise solutions was demonstrated. The interpolating element-free Galerkin method was applied to 2D generalized Benjamin–Bona–Mahony–Burgers (BBMB) and regularized Long-Wave Equations on non-rectangular domains in [17]. The Meshless approach using radial basis functions was used in [18] to determine a numerical solution to the nonlinear, high-dimensional, generalized BBMB problem. The test problems for different geometries of the two-dimensional and three-dimensional cases of the generalized Benjamin–Bona–Mahony–Burgers Equation (BBMBE) have been solved in this study.

The VIM and HPM are used to solve the Fornberg–Whitham Equation (FWE) in [19]. On Burgers Equation (BE), [20] implements a multi-symplectic box approach with two kinds of box schemes. Three approaches, namely ADM, VIM, and HPM, are used for the Fitzhugh–Nagumo problem in [21], and numerical results are produced. The material presented in [16,17,18,19,20,21] contains thorough information about the PDEs described and piques the reader’s curiosity. In [22,23], the authors have offered a full introduction to different types of PDEs and their solutions; also, several numerical techniques with different examples are offered in these two books. Several transformations are employed in the aforementioned numerical procedures.

In this article, some highly nonlinear fractional partial differential equations (NFPDEs) will be solved by the Fractional Novel Analytic Method (FNAM), introduced by [24,25,26]. In [26], this method was introduced as Novel Analytical Method. This approach is simple to use and saves time over other approaches. This paper is organized as follows: Section 3 discusses the mathematical formulation of this strategy, Section 4 contains the convergence of this method, Section 5 illustrates numerical examples, and the conclusion is presented in Section 6.

2. Preliminaries of Fractional Calculus

In this section, we introduce the fundamental concepts and features of fractional calculus [27,28,29].

Definition 1.

A real function $\mathcal{G}\left(\tau \right)$, $\tau >0$ is considered to be in space ${\mathbb{C}}_{\upsilon }$, $\upsilon \in \mathbb{R}$ if ∃ a real number $\rho >\upsilon$. s.t $\mathcal{G}\left(\tau \right)={\tau }^{\rho }{\mathcal{G}}_1\left(\tau \right)$ with ${\mathcal{G}}_1\left(\tau \right)\in \mathbb{C}(0,\infty )$ and it is said to be in the space ${\mathbb{C}}_{\upsilon }^{\aleph }$, $\aleph \in \mathbb{N}$.

Definition 2.

The Riemann–Liouville (RL) Fractional Integral (FI) operator of order α, of a function $\mathcal{G}\in {\mathbb{C}}_{\upsilon }$, $\upsilon >-1$, is defined as:

$$J^{\alpha }\mathcal{G}\left(\tau \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left[\alpha \right]}}{\int }_0^{\tau }{(\tau -\varsigma )}^{\alpha -1}\mathcal{G}\left(\varsigma \right)d\varsigma ,\alpha >0$$

$$J^0\mathcal{G}\left(\tau \right)=\mathcal{G}\left(\tau \right).$$

Numerous scholars have recently researched various RL-FI inequalities; for more details, see [27,28,29]. The features of operator $J^{\alpha }$ that we need in this study are: For $\mathcal{G}\in {\mathbb{C}}_{\upsilon }$, $\upsilon \ge -1$, $\alpha ,\beta \ge 0$

$$J^{\alpha }{J}^{\beta }\mathcal{G}\left(\tau \right)=J^{\alpha +\beta }\mathcal{G}\left(\tau \right),$$

$$J^{\alpha }{\tau }^p={\displaystyle \frac{\mathsf{\Gamma }[p+1]}{\mathsf{\Gamma }[p+\alpha +1]}}{\tau }^{\alpha +p}.$$

Definition 3.

The Fractional Derivative (FD) of $\mathcal{G}\left(\tau \right)$ in the Caputo sense [30] is defined as:

$$D^{\alpha }\mathcal{G}\left(\tau \right)=J^{m-\alpha }{D}^m\mathcal{G}\left(\tau \right).$$

For $m-1<\alpha \le m$, $m\in \mathbb{N}$, $\tau >0$, and $\mathcal{G}\in {\mathbb{C}}_{-1}^m$. In Caputo FD, an ordinary derivative is estimated, followed by a FI, to attain the desired order of FD. The RL-FI operator is a linear operation, defined as:

$$J^{\alpha }\left(\sum _{\ell =1}^h{C}_{\ell }{\mathcal{G}}_{\ell }\left(\tau \right)\right)=\sum _{\ell =1}^h{C}_{\ell }{J}^{\alpha }{\mathcal{G}}_{\ell }\left(\tau \right),$$

where ${\left\{C_{\ell }\right\}}_{\ell }^h$ are constants. The FDs are considered in the Caputo sense in this study.

Lemma 1.

[31] If $\mathcal{G}\left(\tau \right)\in {\mathbb{C}}^n[a,b]$, then

$$\left(J_{a+}^{\alpha }{D}_{a+}^{\alpha }\mathcal{G}\right)\left(\tau \right)=\mathcal{G}\left(\tau \right)-\sum _{l=0}^{n-1}{\displaystyle \frac{{\mathcal{G}}^{\left(l\right)}\left(a\right)}{l!}}{(\tau -a)}^l,$$

and

$$\left(J_{b-}^{\alpha }{D}_{b-}^{\alpha }\mathcal{G}\right)\left(\tau \right)=\mathcal{G}\left(\tau \right)-\sum _{l=0}^{n-1}{\displaystyle \frac{{(-1)}^l{\mathcal{G}}^{\left(l\right)}\left(b\right)}{l!}}{(b-\tau )}^l.$$

In particular, if $0<R\left(\alpha \right)\le 1$ and $\mathcal{G}\left(\tau \right)\in {\mathbb{C}}^n[a,b]$, then

$$\left(J_{a+}^{\alpha }{D}_{a+}^{\alpha }\mathcal{G}\right)\left(\tau \right)=\mathcal{G}\left(\tau \right)-\mathcal{G}\left(a\right)and\left(J_{b-}^{\alpha }{D}_{b-}^{\alpha }\mathcal{G}\right)\left(\tau \right)=\mathcal{G}\left(\tau \right)-\mathcal{G}\left(b\right).$$

3. Highly Nonlinear Partial Differential Equations of Fractional Order via Fractional Novel Analytical Method

In this section, we will go through the fundamental ideas behind implementing an FNAM for the NFPDE. Let us consider the following general Fractional Order PDE:

$$D_{\xi }^{2\beta }\varpi (\tau ,\xi )=\mathcal{F}\left(D_{\xi }^{\beta }\varpi ,\varpi ,D_{\tau }^{\beta }\varpi ,D_{\tau }^{2\beta }\varpi ,\cdots \right),$$

(1)

with initial condition

$$\varpi (\tau ,0)={\phi }_0\left(\tau \right),D_{\xi }^{\beta }\varpi (\tau ,0)={\phi }_1\left(\tau \right).$$

(2)

Taking the Fractional Integral (FI) for both sides of Equation (1) from 0 to $\xi$, we get

$$D_{\xi }^{\beta }\varpi (\tau ,\xi )-D_{\xi }^{\beta }\varpi (\tau ,0)=I_{\xi }^{\beta }\mathcal{F}\left[\varpi \right],$$

$$D_{\xi }^{\beta }\varpi (\tau ,\xi )={\phi }_1\left(\tau \right)+I_{\xi }^{\beta }\mathcal{F}\left[\varpi \right],$$

(3)

where $\mathcal{F}\left[\varpi \right]=\mathcal{F}\left(D_{\xi }^{\beta }\varpi ,\varpi ,D_{\tau }^{\beta }\varpi ,D_{\tau }^{2\beta }\varpi ,\cdots \right)$. Then, again taking the FI from 0 to $\xi$, on both sides of Equation (3). We obtain,

$$\varpi (\tau ,\xi )-\varpi (\tau ,0)={\phi }_1\left(\tau \right){\displaystyle \frac{{\xi }^{\beta }}{\mathsf{\Gamma }(\beta +1)}}+I_{\xi }^{2\beta }\mathcal{F}\left[\varpi \right].$$

Thus,

$$\varpi (\tau ,\xi )={\phi }_0\left(\tau \right)+{\phi }_1\left(\tau \right){\displaystyle \frac{{\xi }^{\beta }}{\mathsf{\Gamma }(\beta +1)}}+I_{\xi }^{2\beta }\mathcal{F}\left[\varpi \right].$$

(4)

For $\mathcal{F}\left[\varpi \right]$ the Fractional Taylor Series (FTS) is extended to about $\xi =0$.

$$\mathcal{F}\left[\varpi \right]=\sum _{k=0}^{\infty }{\displaystyle \frac{D_{\xi }^{k\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[k\beta +1]}}{\xi }^{k\beta },\beta >0$$

$$\mathcal{F}\left[\varpi \right]=\mathcal{F}\left[{\varpi }_0\right]+{\displaystyle \frac{D_{\xi }^{\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[\beta +1]}}{\xi }^{\beta }+{\displaystyle \frac{D_{\xi }^{2\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[2\beta +1]}}{\xi }^{2\beta }+{\displaystyle \frac{D_{\xi }^{3\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[3\beta +1]}}{\xi }^{3\beta }+\cdots +{\displaystyle \frac{D_{\xi }^{k\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[k\beta +1]}}{\xi }^{k\beta }+\cdots .$$

(5)

Substituting Equation (5) with Equation (4), we obtain

$$\varpi (\tau ,\xi )={\phi }_0\left(\tau \right)+{\phi }_1\left(\tau \right){\displaystyle \frac{{\xi }^{\beta }}{\mathsf{\Gamma }(\beta +1)}}+I_{\xi }^{2\beta }\left[\mathcal{F}\left[{\varpi }_0\right]+{\displaystyle \frac{D_{\xi }^{\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[\beta +1]}}{\xi }^{\beta }+{\displaystyle \frac{D_{\xi }^{2\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[2\beta +1]}}{\xi }^{2\beta }+\cdots +{\displaystyle \frac{D_{\xi }^{k\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }[k\beta +1]}}{\xi }^{k\beta }+\cdots \right],$$

$$\varpi (\tau ,\xi )={\phi }_0\left(\tau \right)+{\phi }_1\left(\tau \right){\displaystyle \frac{{\xi }^{\beta }}{\mathsf{\Gamma }(\beta +1)}}+{\displaystyle \frac{\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }(2\beta +1)}}{\xi }^{2\beta }+{\displaystyle \frac{D_{\xi }^{\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }(3\beta +1)}}{\xi }^{3\beta }+{\displaystyle \frac{D_{\xi }^{2\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }(4\beta +1)}}{\xi }^{4\beta }+\cdots +{\displaystyle \frac{D_{\xi }^{k\beta }\mathcal{F}\left[{\varpi }_0\right]}{\mathsf{\Gamma }\left(\right(k+2)\beta +1)}}{\xi }^{(k+2)\beta }+\cdots ,$$

$$\varpi (\tau ,\xi )={\mathfrak{a}}_0+{\mathfrak{a}}_1{\displaystyle \frac{{\xi }^{\beta }}{\mathsf{\Gamma }(\beta +1)}}+{\mathfrak{a}}_2{\displaystyle \frac{{\xi }^{2\beta }}{\mathsf{\Gamma }(2\beta +1)}}+{\mathfrak{a}}_3{\displaystyle \frac{{\xi }^{3\beta }}{\mathsf{\Gamma }(3\beta +1)}}+{\mathfrak{a}}_4{\displaystyle \frac{{\xi }^{4\beta }}{\mathsf{\Gamma }(4\beta +1)}}+\cdots +{\mathfrak{a}}_k{\displaystyle \frac{{\xi }^{k\beta }}{\mathsf{\Gamma }(k\beta +1)}}+\cdots ,$$

(6)

where

$$\begin{array}{cc}\hfill {\mathfrak{a}}_0& ={\phi }_0\left(\tau \right),\hfill \\ \hfill {\mathfrak{a}}_1& ={\phi }_1\left(\tau \right),\hfill \\ \hfill {\mathfrak{a}}_2& =\mathcal{F}\left[{\varpi }_0\right],\hfill \\ \hfill {\mathfrak{a}}_3& =D_{\xi }^{\beta }\mathcal{F}\left[{\varpi }_0\right],\hfill \\ \hfill {\mathfrak{a}}_4& =D_{\xi }^{2\beta }\mathcal{F}\left[{\varpi }_0\right],\hfill \\ \hfill ⋮\\ \hfill {\mathfrak{a}}_k& =D_{\xi }^{(k-2)\beta }\mathcal{F}\left[{\varpi }_0\right],\hfill \end{array}$$

such that the highest derivative of $\varpi$ is k. The endorsement of Equation (6) is to extend FTS for $\varpi$ about $\xi =0$. It means that,

$$\begin{array}{cc}\hfill {\mathfrak{a}}_0& =\varpi (\tau ,0),\hfill \\ \hfill {\mathfrak{a}}_1& =D_{\xi }^{\beta }\varpi (\tau ,0),\hfill \\ \hfill {\mathfrak{a}}_2& =D_{\xi }^{2\beta }\varpi (\tau ,0),\hfill \\ \hfill {\mathfrak{a}}_3& =D_{\xi }^{3\beta }\varpi (\tau ,0),\hfill \\ \hfill {\mathfrak{a}}_4& =D_{\xi }^{4\beta }\varpi (\tau ,0),\hfill \\ \hfill ⋮\\ \hfill {\mathfrak{a}}_k& =D_{\xi }^{k\beta }\varpi (\tau ,0),\hfill \end{array}$$

thus we simply obtain our wanted numerical solution.

4. Novel Analytical Method Convergence Analysis

Let us examine the following PDE

$$\varpi (\tau ,\xi )=\mathcal{G}\left(\varpi (\tau ,\xi )\right),$$

(7)

where a nonlinear operator is $\mathcal{G}$. Using the approach outlined, the achieved solution is identical to the following sequence

$${\mathfrak{S}}_n=\sum _{i=0}^n{\varpi }_i=\sum _{i=0}^n{\sigma }_i{\displaystyle \frac{{\left(\mathsf{\Delta }t\right)}^i}{i!}}.$$

(8)

Theorem 1.

Let $\mathcal{G}$ be an operator from $\mathfrak{H}\mapsto \mathfrak{H}$ (Hilbert space) and ϖ be the exact solution of Equation (7). The estimated solution

$$\sum _{i=0}^n{\varpi }_i=\sum _{i=0}^n{\sigma }_i{\displaystyle \frac{{\left(\mathsf{\Delta }t\right)}^i}{i!}}$$

is converged to ϖ, when ∃ a σ$(0\le \sigma <1)$, $\parallel {\varpi }_{i+1}\parallel \le \sigma \parallel {\varpi }_i\parallel$$\forall i\in \mathbb{N}\cup \left\{0\right\}$.

Proof of Theorem 1.

We seek to demonstrate that ${\left\{{\mathfrak{S}}_n\right\}}_{n=0}^{\infty }$ is a converged Cauchy Sequence,

$$\parallel {\mathfrak{S}}_{n+1}-{\mathfrak{S}}_n\parallel =\parallel {\varpi }_{n+1}\parallel \le \sigma \parallel {\varpi }_n\parallel \le {\sigma }^2\parallel {\varpi }_{n-1}\parallel \le \cdots \le {\sigma }^n\parallel {\varpi }_1\parallel \le {\sigma }^{n+1}\parallel {\varpi }_0\parallel .$$

(9)

Now for $n,m\in \mathbb{N}$, $n\ge m$, we obtain

$$\begin{array}{cc}\hfill \parallel {\mathfrak{S}}_n-{\mathfrak{S}}_m\parallel & =\parallel ({\mathfrak{S}}_n-{\mathfrak{S}}_{n-1})+({\mathfrak{S}}_{n-1}-{\mathfrak{S}}_{n-2})+\cdots +({\mathfrak{S}}_{m+1}-{\mathfrak{S}}_m)\parallel \hfill \\ \hfill & \le \parallel {\mathfrak{S}}_n-{\mathfrak{S}}_{n-1}\parallel +\parallel {\mathfrak{S}}_{n-1}-{\mathfrak{S}}_{n-2}\parallel +\cdots +\parallel {\mathfrak{S}}_{m+1}-{\mathfrak{S}}_m\parallel \hfill \\ \hfill & \le {\sigma }^n\parallel {\varpi }_0\parallel +{\sigma }^{n-1}\parallel {\varpi }_0\parallel +\cdots +{\sigma }^{m+1}\parallel {\varpi }_0\parallel \hfill \\ \hfill & \le \left({\sigma }^{m+1}+{\sigma }^{m+2}+\cdots +{\sigma }^n\right)\parallel {\varpi }_0\parallel ={\sigma }^{m+1}{\displaystyle \frac{1-{\sigma }^{n-m}}{1-\sigma }}\parallel {\varpi }_0\parallel .\hfill \end{array}$$

(10)

Hence ${\displaystyle \underset{n,m\to \infty }{lim}\parallel {\mathfrak{S}}_n-{\mathfrak{S}}_m\parallel =0}$, i.e., ${\left\{{\mathfrak{S}}_n\right\}}_{n=0}^{\infty }$ is a Cauchy Sequence in the $\mathfrak{H}$. Thus, ∃ a $\mathfrak{S}\in \mathfrak{H}$ s.t ${\displaystyle \underset{n\to \infty }{lim}{\mathfrak{S}}_n=\mathfrak{S}}$, where $\mathfrak{S}=\varpi$. □

Definition 4.

We define for every $n\in \mathbb{N}\cup \left\{0\right\}$,

$${\sigma }_n=\left\{\begin{array}{cc}{\displaystyle \frac{\parallel {\varpi }_{n+1}\parallel }{\parallel {\varpi }_n\parallel }}\hfill & \parallel {\varpi }_n\parallel \ne 0\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

(11)

Corollary 1.

From Theorem 1,

$$\sum _{i=0}^n{\varpi }_i=\sum _{i=0}^n{\sigma }_i{\displaystyle \frac{{\left(\mathsf{\Delta }t\right)}^i}{i!}}$$

is converged to ϖ when $0\le {\sigma }_i<1$, $i=0,1,2,3,\cdots$ for further details, see [22,23].

5. Numerical Application for Fractional Novel Analytical Method for Highly Nonlinear Partial Differential Equations

Four problems are addressed in this section utilizing the suggested Fractional Novel Analytical Method.

Example 1.

The Gardner Equation, which is used to describe internal solitary waves in shallow water, was generated by combining the KdV and modified KdV Equations [32]. Consider the Nonlinear Time Fractional Gardner Equation [33],

$$D_{\xi }^{\alpha }\varpi (\tau ,\xi )=-2\lambda \varpi (\tau ,\xi ){\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}+3\beta {\varpi }^2(\tau ,\xi ){\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}-{\displaystyle \frac{{\partial }^3\varpi (\tau ,\xi )}{\partial {\tau }^3}},$$

$$\varpi (\tau ,0)={\displaystyle \frac{\lambda }{3\beta }}\left(1+tanh\left({\displaystyle \frac{\lambda \tau }{3\sqrt{2\beta }}}\right)\right),$$

where $0<\alpha \le 1$. By carefully following the steps involved in the Fractional Novel Analytical approach, we obtain,

$$\varpi (\tau ,\xi )={\displaystyle \frac{\lambda }{3\beta }}+{\displaystyle \frac{{\xi }^{\alpha }{\lambda }^{4}sec{h}^2\left({\displaystyle \frac{\lambda \tau }{3\sqrt{2\beta }}}\right)}{27\sqrt{2}{\beta }^{{\displaystyle \frac{5}{2}}}\mathsf{\Gamma }(1+\alpha )}}-{\displaystyle \frac{\sqrt{2}{\xi }^{\alpha }{\lambda }^{4}sec{h}^2\left({\displaystyle \frac{\lambda \tau }{3\sqrt{2\beta }}}\right)}{27{\beta }^{{\displaystyle \frac{5}{2}}}\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{{\xi }^{\alpha }{\lambda }^{4}sec{h}^4\left({\displaystyle \frac{\lambda \tau }{3\sqrt{2\beta }}}\right)}{81\sqrt{2}{\beta }^{{\displaystyle \frac{5}{2}}}\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{{\xi }^{2\alpha }{\lambda }^{7}sec{h}^4\left({\displaystyle \frac{\lambda \tau }{3\sqrt{2\beta }}}\right)}{243{\beta }^4\mathsf{\Gamma }(1+2\alpha )}}+\cdots .$$

When $\alpha =1$, the exact solution of this problem is

$$\varpi (\tau ,\xi )={\displaystyle \frac{\lambda }{3\beta }}\left(1+tanh\left({\displaystyle \frac{\lambda }{3\sqrt{2\beta }}}\left(\tau -{\displaystyle \frac{2{\lambda }^2\xi }{9\beta }}\right)\right)\right)$$

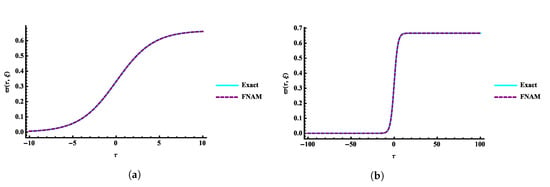
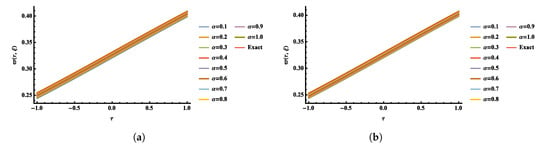
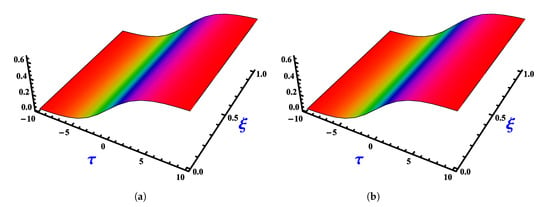
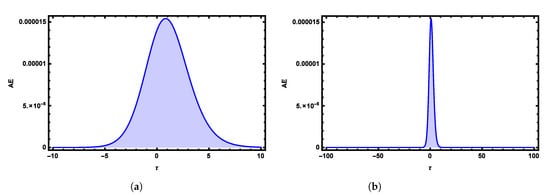
where $\beta ,\lambda >0$. Comparisons between exact and numerical solutions are plotted in Figure 1 by using the third terms of FNAM with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\xi =0.2$, $\beta =\lambda =1$. The obtained numerical solutions at different values of α’s with $\tau \in [-1,1]$ at $\xi =0.1$ and $\xi =0.2$ are shown in Figure 2. In Figure 3, 3D plots of the exact and obtained results at $\tau \in [-10,10]$ and $\xi \in [0,1]$ are plotted. Figure 4 and Figure 5 show the Absolute Error 2D and 3D graphs of the obtained result with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\beta =\lambda =1$, respectively.

Figure 1. Comparison between the exact and numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.2$ and $\beta =\lambda =1$ for Example 1.

Figure 2. Two-dimensional plots of the numerical solution at different $\alpha$’s values by using FNAM verses $\tau$ at time (a) $\xi =0.1$ and (b) $\xi =0.2$ for Example 1.

Figure 3. Three-dimensional plots of (a) the exact solution and (b) FNAM solution at $\tau \in [-10,10]$ and $\xi \in [0,1]$ for Example 1.

Figure 4. Absolute Error (AE) 2D graph of obtained numerical solutions using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.1$ and $\beta =\lambda =1$ for Example 1.

Figure 5. Absolute Error (AE) 3D graph of obtained numerical solutions using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.1$ and $\beta =\lambda =1$ for Example 1.

Example 2.

Whitham first presented the Fornberg–Whitham Equation in 1967. It is a fluid velocity function of independent variables τ and ξ. The equation served as an explanation for the qualitative aspect of the wave-breaking investigation and produced an exact solution that is a wave-like solution [34]. Consider the Nonlinear Time Fractional Fornberg–Whitham Equation [35,36],

$$D_{\xi }^{\alpha }\varpi (\tau ,\xi )-{\displaystyle \frac{{\partial }^2\varpi (\tau ,\xi )}{\partial \xi \partial {\tau }^2}}+{\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}=\varpi (\tau ,\xi ){\displaystyle \frac{{\partial }^3\varpi (\tau ,\xi )}{\partial {\tau }^3}}-\varpi (\tau ,\xi ){\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}+3{\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}{\displaystyle \frac{{\partial }^2\varpi (\tau ,\xi )}{\partial {\tau }^2}},$$

$$\varpi (\tau ,0)=e^{{\displaystyle \frac{\tau }{2}}},$$

where $0<\alpha \le 1$. By carefully following the steps involved in the Fractional Novel Analytical approach, we obtain,

$$\varpi (\tau ,\xi )=e^{{\displaystyle \frac{\tau }{2}}}-{\displaystyle \frac{{\xi }^{\alpha }{e}^{{\displaystyle \frac{\tau }{2}}}}{2\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{{\xi }^{2\alpha }{e}^{{\displaystyle \frac{\tau }{2}}}}{4\mathsf{\Gamma }(1+2\alpha )}}-{\displaystyle \frac{{\xi }^{3\alpha }{e}^{{\displaystyle \frac{\tau }{2}}}}{8\mathsf{\Gamma }(1+3\alpha )}}+{\displaystyle \frac{{\xi }^{4\alpha }{e}^{{\displaystyle \frac{\tau }{2}}}}{16\mathsf{\Gamma }(1+4\alpha )}}-{\displaystyle \frac{{\xi }^{5\alpha }{e}^{{\displaystyle \frac{\tau }{2}}}}{32\mathsf{\Gamma }(1+5\alpha )}}+\cdots .$$

When $\alpha =1$, the exact solution of this problem is $\varpi (\tau ,\xi )=e^{\left({\displaystyle \frac{\tau }{2}}-{\displaystyle \frac{2\xi }{3}}\right)}$.

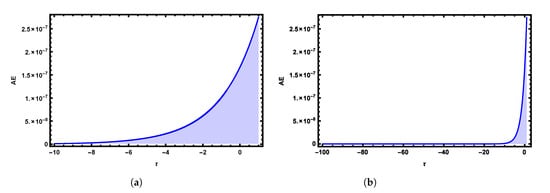
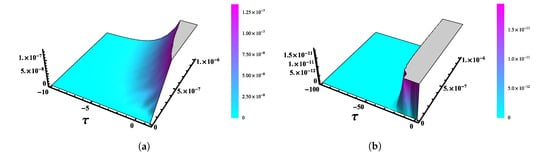
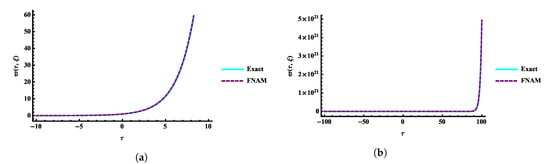
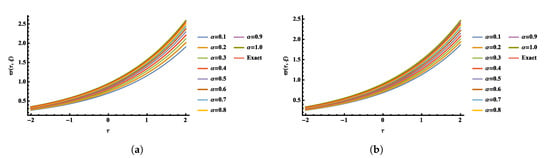
Figure 6 and Figure 7 show the 2D and 3D absolute error graphs of the obtained numerical solution with $\tau \in [-10,1]$ and $\tau \in [-100,1]$ at ξ, respectively. The simulation is realized by using the fifth terms of FNAM with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\xi =0.1$, as shown in Figure 8. The obtained solutions are plotted in Figure 9 at different values of α’s with τ at $\xi =0.1$ and $\xi =0.2$. Three-dimensional plots of the exact and obtained results with $\tau \in [-10,10]$ at $\xi \in [0,1]$ are shown in Figure 10.

Figure 6. Absolute Error (AE) 2D graphs of obtained numerical solutions by using FNAM verses (a) $\tau \in [-10,1]$ and (b) $\tau \in [-100,1]$ at time $\xi ={10}^{-6}$ for Example 2.

Figure 7. Absolute Error (AE) 3D graph of obtained numerical solutions by using FNAM verses (a) $\tau \in [-10,1]$ and (b) $\tau \in [-100,1]$ and $\xi \in [0,{10}^{-6}]$ for Example 2.

Figure 8. Comparison 2D Plots of exact and numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.1$ for Example 2.

Figure 9. Two-dimensional plots of numerical solutions at different $\alpha$’s values by using FNAM verses $\tau$ at time (a) $\xi =0.1$ and (b) $\xi =0.2$ for Example 2.

Figure 10. Three-dimensional plots of (a) the exact and (b) FNAM solutions at $\tau \in [-10,10]$ and $\xi \in [0,1]$ for Example 2.

Example 3.

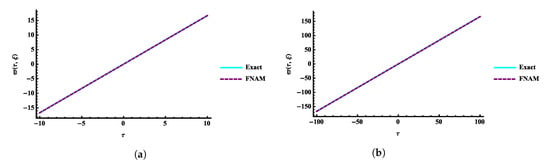
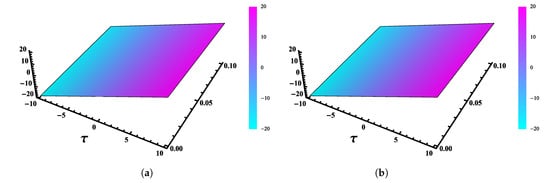
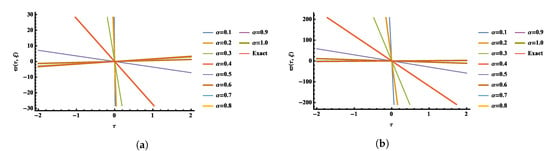
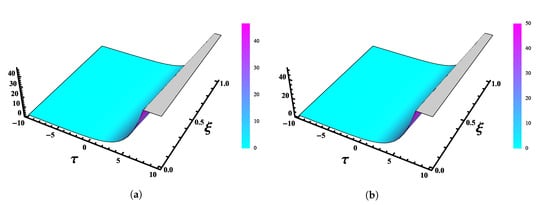
Burger’s equation develops as a model equation for the viscosity-induced smoothing of a shock wave. Consider the following Nonlinear Burger’s Equation of fractional order [37,38],

$$D_{\xi }^{\alpha }\varpi (\tau ,\xi )=-a\varpi (\tau ,\xi ){\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}+c{\displaystyle \frac{{\partial }^2\varpi (\tau ,\xi )}{\partial {\tau }^2}},$$

$$\varpi (\tau ,0)=2\tau ,$$

where $0<\alpha \le 1$. By carefully following the steps elaborate in the FNAM, the approximate solution is then,

$$\varpi (\tau ,\xi )=2\tau -{\displaystyle \frac{4a\tau {\xi }^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{16a^2\tau {\xi }^{2\alpha }}{\mathsf{\Gamma }(1+2\alpha )}}-{\displaystyle \frac{96a^3\tau {\xi }^{3\alpha }}{\mathsf{\Gamma }(1+3\alpha )}}+{\displaystyle \frac{768a^4\tau {\xi }^{4\alpha }}{\mathsf{\Gamma }(1+4\alpha )}}-{\displaystyle \frac{7680a^5\tau {\xi }^{5\alpha }}{\mathsf{\Gamma }(1+5\alpha )}}+\cdots .$$

When $\alpha =1$ the exact solution of this problem is $\varpi (\tau ,\xi )={\displaystyle \frac{2\tau }{1+2\xi }}$.

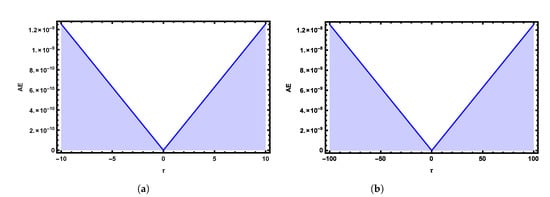
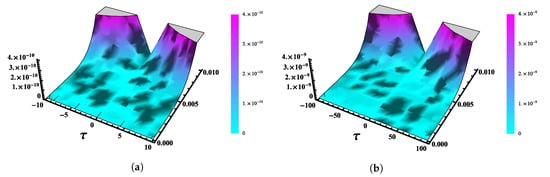
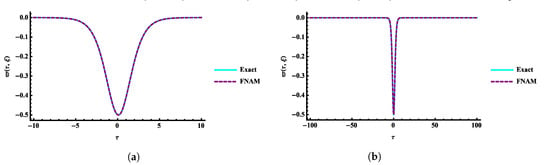
Comparisons among the exact and obtained numerical solutions by using the fifth terms of FNAM with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\xi =0.2$ and $a=c=1$ are shown in Figure 11. Three-dimensional plots of the exact and obtained numerical result with $\tau \in [-10,10]$ at $\xi \in [0,0.1]$ are shown in Figure 12. The obtained solutions are plotted in Figure 13 at different values of α’s with $\tau \in [-2,2]$ and $a=c=1$ at $\xi =0.1$ and $\xi =0.2$. Figure 14 shows the AE 2D graph of the obtained numerical solutions with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at time $\xi =0.01$ and $a=c=1$. AE 3D graphs are shown in Figure 15 with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at time $\xi \in [0,0.1]$ and $a=c=1$.

Figure 11. Comparison 2D plots of numerical and exact solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.2$ and $a=c=1$ for Example 3.

Figure 12. Three-dimensional plots of (a) the exact and (b) FNAM solutions at $\tau \in [-10,10]$, $\xi \in [0,0.1]$ and $a=c=1$ for Example 3.

Figure 13. Three-dimensional plots of (a) the exact and (b) FNAM solutions at $\tau \in [-10,10]$, $\xi \in [0,0.1]$ and $a=c=1$ for Example 3.

Figure 14. Absolute Error (AE) 2D graphs of obtained numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.01$ and $a=c=1$ for Example 3.

Figure 15. Absolute Error (AE) 3D graph of the obtained numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi \in [0,0.01]$ and $a=c=1$ for Example 3.

Example 4.

Consider the following Time Fractional Nonlinear KdV-Burger’s Equation [37]

$$D_{\xi }^{\alpha }\varpi (\tau ,\xi )=6\varpi (\tau ,\xi ){\displaystyle \frac{\partial \varpi (\tau ,\xi )}{\partial \tau }}-{\displaystyle \frac{{\partial }^3\varpi (\tau ,\xi )}{\partial {\tau }^3}},$$

$$\varpi (\tau ,0)={\displaystyle \frac{-2k{e}^{k\tau }}{{(1+e^{k\tau })}^2}},$$

where $0<\alpha \le 1$. By carefully following the steps elaborate in the FNAM, the approximate solution is then,

$$\begin{array}{cc}\hfill \varpi (\tau ,\xi )=& {\displaystyle \frac{-2k{e}^{k\tau }}{{(1+e^{k\tau })}^2}}+{\displaystyle \frac{{\xi }^{\alpha }\left({\displaystyle \frac{-48k^3{e}^{3k\tau }}{{(1+e^{k\tau })}^5}}+{\displaystyle \frac{24k^3{e}^{2k\tau }}{{(1+e^{k\tau })}^4}}-{\displaystyle \frac{48k^4{e}^{4k\tau }}{{(1+e^{k\tau })}^5}}+{\displaystyle \frac{72k^4{e}^{3k\tau }}{{(1+e^{k\tau })}^4}}-{\displaystyle \frac{28k^4{e}^{2k\tau }}{{(1+e^{k\tau })}^3}}+{\displaystyle \frac{2k^4{e}^{k\tau }}{{(1+e^{k\tau })}^2}}\right)}{\mathsf{\Gamma }(1+\alpha )}}+\hfill \\ \hfill & {\displaystyle \frac{{\xi }^{2\alpha }\left({\displaystyle \frac{-4032k^5{e}^{5k\tau }}{{(1+e^{k\tau })}^8}}+{\displaystyle \frac{4032k^5{e}^{4k\tau }}{{(1+e^{k\tau })}^7}}-{\displaystyle \frac{864k^5{e}^{3k\tau }}{{(1+e^{k\tau })}^6}}-{\displaystyle \frac{14112k^6{e}^{6k\tau }}{{(1+e^{k\tau })}^8}}+{\displaystyle \frac{28224k^6{e}^{5k\tau }}{{(1+e^{k\tau })}^7}}-{\displaystyle \frac{18336k^6{e}^{4k\tau }}{{(1+e^{k\tau })}^6}}+\cdots \right)}{\mathsf{\Gamma }(1+2\alpha )}}+\cdots .\hfill \end{array}$$

When $\alpha =1$ the Exact solution of this problem is $\varpi (\tau ,\xi )={\displaystyle \frac{-2k^2{e}^{k(\tau -k^2\xi )}}{{\left(1+e^{k(\tau -k^2\xi )}\right)}^2}}$.

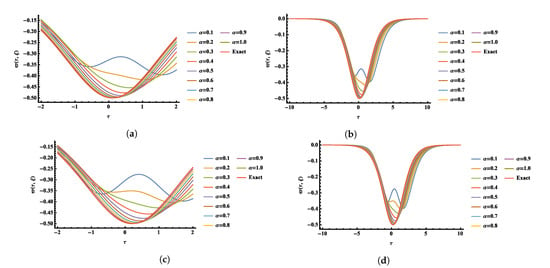
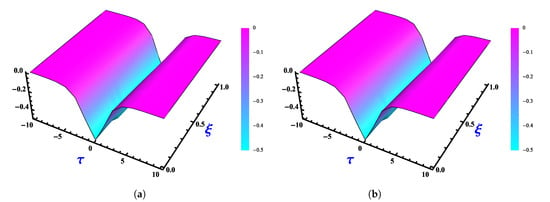
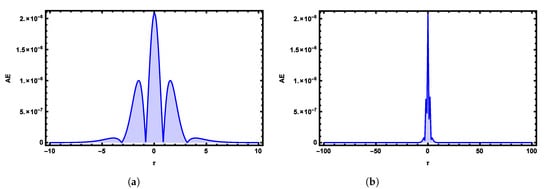
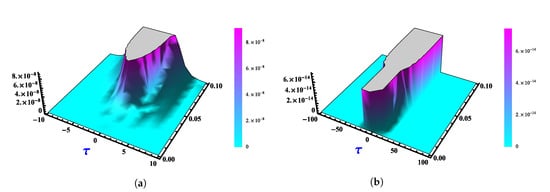
Comparisons between the exact and numerical solutions are plotted in Figure 16 by using the third terms of FNAM with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\xi =0.1$, $k=1$. The obtained numerical solutions at different values of α’s with $\tau \in [-2,2]$ and $\tau \in [-10,10]$ at $\xi =0.1$ and $\xi =0.2$ are shown in Figure 17. In Figure 18, 3D plots of the exact and obtained results at $\tau \in [-10,10]$ and $\xi \in [0,1]$ are plotted. Figure 19 shows the Absolute Error 2D graphs of the obtained result with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\xi =0.1$, $k=1$. A three-dimensional graph of the Absolute Error of the obtained numerical solution with $\tau \in [-10,10]$ and $\tau \in [-100,100]$ at $\xi \in [0,0.1]$, $k=1$ is illustrated in Figure 20.

Figure 16. Comparison between the exact and numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.1$ and $k=1$ for Example 4.

Figure 17. Two-dimensional plots of the numerical solution at different $\alpha$’s values by using FNAM verses $\tau$ at time (a) $\xi =0.1$ and $\tau \in [-2,2]$, (b) $\xi =0.1$ and $\tau \in [-10,10]$, (c) $\xi =0.2$ and $\tau \in [-2,2]$ and (d) $\xi =0.2$ and $\tau \in [-10,10]$ for Example 4.

Figure 18. Plots of (a) the exact solution and (b) FNAM solution at $k=1$, $\tau \in [-10,10]$ and $\xi \in [0,1]$ for Example 4.

Figure 19. Absolute Error (AE) 2D graphs of obtained numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi =0.1$ and $k=1$ for Example 4.

Figure 20. Absolute Error (AE) 3D graph of the obtained numerical solutions by using FNAM verses (a) $\tau \in [-10,10]$ and (b) $\tau \in [-100,100]$ at time $\xi \in [0,0.1]$ and $k=1$ for Example 4.

6. Conclusions

The numerical approach provided here has been utilized to solve highly nonlinear fractional partial differential equations. The purposed method is very efficient at finding and comparing the results of nonlinear FPDEs with the exact solution. Based on the numerical solutions obtained, we can affirm that there is an excellent agreement with the existing solutions and demonstrate that this technique can be utilized to tackle the proposed problems effectively. By adding appropriate terms to the solution’s series, the error can be reduced. The solution obtained at each fractional order is found to be converging to the integer order. We have compared the provided numerical solutions with exact solutions to demonstrate the validity and vast potential of the suggested numerical approach. The proposed technique is more reliable, efficient, and easy to use; it is also less computationally intense to find the solution to the nonlinear partial differential equation of the non-integer order. This method could be applied to a system of fractional differential equations, fractional oscillators, fractional integro-differential equations, etc.