Fractal Characteristics of Deep Shales in Southern China by Small-Angle Neutron Scattering and Low-Pressure Nitrogen Adsorption

Abstract

The occurrence and flow of shale gas are substantially impacted by nanopore structures. The fractal dimension provides a new way to explore the pore structures of shale reservoirs. In this study, eight deep shale samples from Longmaxi Formation to Wufeng Formation in Southern Sichuan were selected to perform a series of analysis tests, which consisted of small-angle neutron scattering, low-pressure nitrogen adsorption, XRD diffraction, and large-scale scanning electron microscopy splicing. The elements that influence the shale fractal dimension were discussed from two levels of mineral composition and pore structures, and the relationship between the mass fractal dimension and surface fractal dimension was focused on during a comparative analysis. The results revealed that the deep shale samples both had mass fractal characteristics and surface fractal characteristics. The mass fractal dimension ranged from 2.499 to 2.991, whereas the surface fractal dimension ranged from 2.814 to 2.831. The mass fractal dimension was negatively correlated with the surface fractal dimension. The mass fractal dimension and the surface fractal dimension are controlled by organic matter pores, and their development degree significantly affects the fractal dimension. The mass fractal dimension increases with the decrease of a specific surface area and pore volume and increases with the increase of the average pore diameter. The permeability and surface fractal dimension are negatively correlated, but no significant correlation exists between the permeability and mass fractal dimension, and the internal reason is the dual control effect of organic matter on shale pores. This study comprehensively analyses the mass fractal characteristics and surface fractal characteristics, which helps in a better understanding of the pore structure and development characteristics of shale gas reservoirs.

1. Introduction

The “shale revolution” in the United States has piqued global interest in shale gas exploration and development [1]. In 2012, China began exploring and developing shale gas, and it is currently carrying out large-scale commercial development in the Sichuan Basin. The output will reach 23 billion cubic meters in 2021, ranking second in the world. With the continuous expansion of the development area, the deep shale, which has a burial depth of more than 4000 m, has also been gradually developed [2]. China is rich in deep shale gas resources and has huge development potential; therefore, it is becoming a key area of shale gas production in the future [3]. Statistics revealed that the shale gas resources in China are estimated to be 144.5 × 10¹² m³, with 36.1 × 10¹² m³ recoverable resources, and the deep shale gas resources buried below 3500 m account for more than 65% of the total [4]. The Sichuan Basin is one of China’s major shale gas producing areas. The deep shale gas reserves exceeding 3500 m reach 11.2 × 10¹² m³, primarily distributed in the South-eastern, Southern, and Northern Sichuan regions [5,6]. The shale of this stratum has generally experienced a complex tectonic evolution process, which is affected by deep burial, strong uplift, strong denudation, and strong deformation, leading to a complex nanoscale pore structure and diverse pore types [7,8]. As a result, it is obvious that the deep layers of the Sichuan Basin in the pore structure of shale are of great significance.

The fractal theory has recently been introduced as a new method for studying shale pore structures by Chinese and foreign researchers [9,10,11]. The fractal dimension can quantitatively describe the complexity and heterogeneity of a pore structure. However, because the heterogeneity of shale pores does not conform to the traditional Euclidean set law, Mandelbrot put forward the fractal geometry theory in order to characterise special structures that do not conform to the Euclidean geometry law and have a certain self-similarity [12]. It has been widely promoted and applied in the field. Pfeifer (1983) made use of the adsorption method to study the fractal characteristics of the reservoir [13]. Katz (1985) and Krohn (1988) used scanning electron microscope images to investigate the fractal characteristics of sandstone pores successively and came to the conclusion that sandstone, shale, and carbonate rock have certain fractal features at the pore scale [14,15]. The fractal characteristics of coals of various maturity levels were studied by Yao et al., and the relationship between coal composition and coal rank and fractal dimension was discussed [16]. Shao (1988) used the FHH model to calculate the fractal dimension of pores in shale based on a low-temperature nitrogen adsorption experiment and also achieved good fitting results [17]. Longfei Xu (2020) used nitrogen adsorption experiments to investigate the fractional characteristics of shale with different lithofacies, as well as explored the surface fractal characteristics of shale and the correlation among the surface fractal dimension and pore structure [18]. Scholars primarily study the fractal characteristics of shale through the image method and the low-pressure nitrogen adsorption method.

The fractal phenomenon is the fractal behaviour that occurs in the actual three-dimensional space, but only one plane can be seen through the image observation, making intuitive observation difficult to completely and effectively portray the irregular behaviour of the three-dimensional space. Fractals can usually be divided into surface fractals and mass fractals [19]. The fractal dimension calculated by low-pressure nitrogen adsorption (LPNA) is the surface fractal dimension, which is able to efficiently characterise the surface intricacy of the three-dimensional shale pore structure. Nevertheless, it is unable to characterise the characteristics of the pore distribution. The experimental method of small-angle neutron scattering was introduced in the research, which can effectively test the three-dimensional information describing the pore distribution of shale, and then study the mass fractal behaviour in the pore space.

The pore structure of shale has been characterised through small-angle neutron scattering (SANS) technology, and it has unique advantages in comparison to the fluid injection and image analysis methods: (1) a high measurement accuracy, with the highest measurement accuracy reaching 1 nm. (2) While characterising the samples with high precision, the size of the samples is large, which can reach up to 10¹¹ μm³. (3) It can comprehensively characterise the total pore information (open pores + closed pores) of shale [20,21,22,23,24,25,26,27]. Radlinski (2000) was the first to establish a relationship between pore size (R) and scattering vector (Q) for a broad particle size distribution in shale, namely R ≈ 2.5/Q [28]. Sun (2018) further employed SANS to study the pore size distribution of nanopores in Southern Sichuan shale, applying the Porod invariant equation and polydisperse sphere (PDSP) model for calculating the porosity, pore size distribution, and fractal dimension of shale [29].

This study aims to investigate the fractal characteristics of deep shale using deep shale reservoirs in Southern Sichuan, China. The mass fractal dimension is calculated by small-angle neutron scattering technology, whereas a low-pressure nitrogen adsorption experiment is used to calculate the surface fractal dimension. The two aspects are combined to explore the separation characteristics of deep shale. The relationships between parameters such as the TOC, clay mineral content, pore structure, and fractal dimension were then analysed. Finally, the correlation between the mass fractal of the deep shale samples and the surface fractal and its impact on production development are discussed. Therefore, the small-angle neutron scattering experimental method can obtain the fractal characteristics and pore structure parameters of the total pores of the shale, which are different from the scanning electron microscope and nitrogen adsorption.

2. Materials and Methods

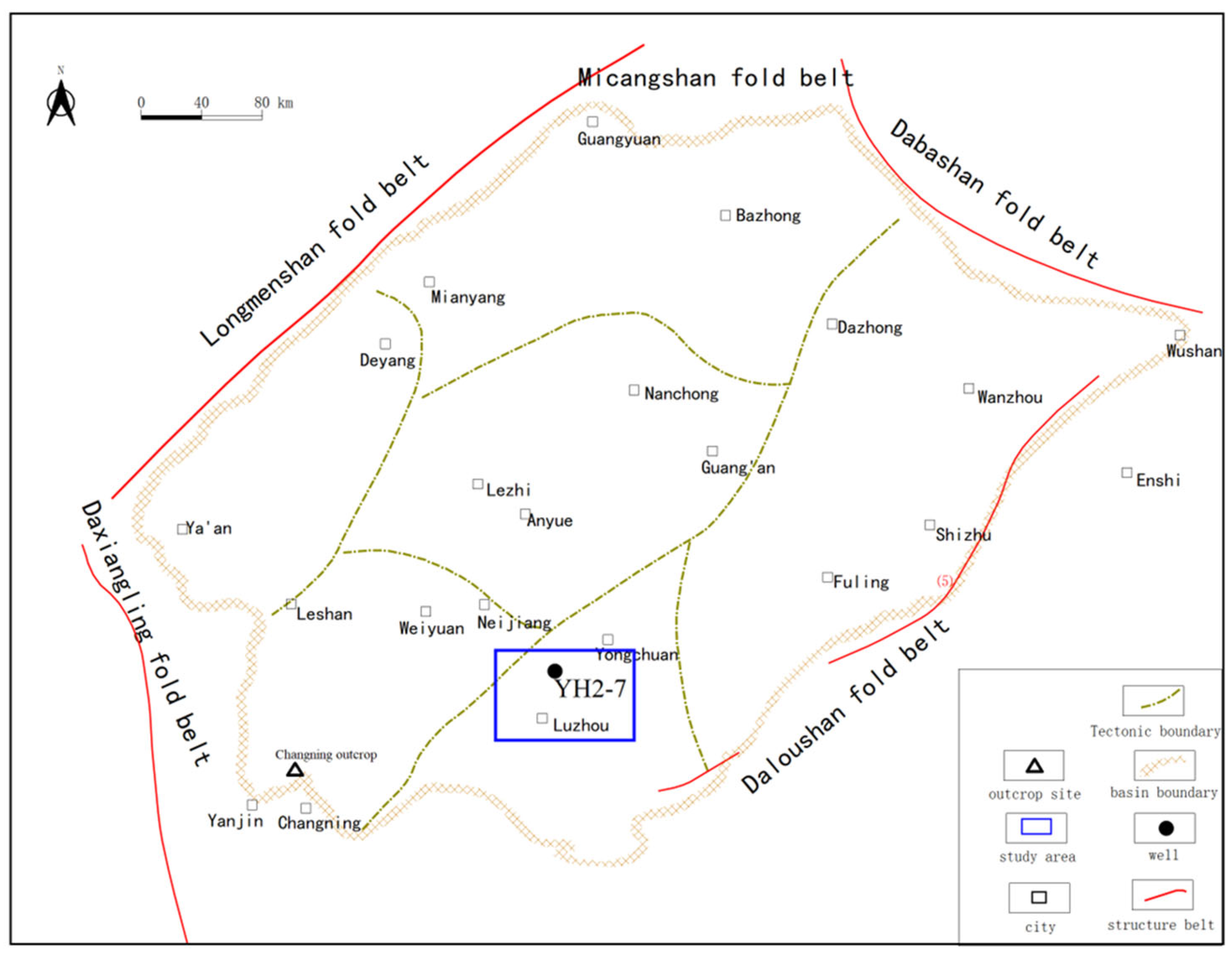
2.1. Samples

Fresh shale samples were obtained from the Southern Sichuan Basin in China (Figure 1). Their burial depths are more than 4000 m. Eight shale samples from the YH2 coring wells were chosen for this study, and they were given the numbers L1–L8, depending on the burial depth of the samples from shallow to deep. The block’s stratigraphic sequence is normal, and the Lower Silurian Longmaxi Formation shale is in contact with the underlying Upper Ordovician Wufeng Formation. The black carbonaceous shale and black silty shale dominate the Longmaxi Formation. The strata at the bottom of the Longmaxi Formation in the study area are buried at a depth of 3500–4500 m, and black carbonaceous shale is developed. Graptolite and pyrite are common in cross-sections.

In this study, the basic parameters such as the TOC, whole-rock mineral composition, and permeability were initially measured for all samples. Pulse decay permeability tests were performed on the core column. Permeability measurements were performed using a pulse decay osmometer (PDP-200, Thermo Fisher Scientific, Waltham, MA, USA) with dry nitrogen as the medium. XRD analysis and the TOC content test were done by using a TTR3 X-ray diffractometer (Rigaku Corporation, Tokyo, Japan) and LECO CS230 carbon/sulphur analyser (LECO, San Jose, CA, USA), respectively. In order to ensure the comparability of small-angle neutron scattering and nitrogen adsorption, the samples were crushed to 40–80 mesh and then subjected to small-angle neutron scattering and nitrogen adsorption tests, respectively.

2.2. Methods

2.2.1. Small-Angle Neutron Scattering

Small-angle neutron scattering (SANS) measurements were performed on the small-angle neutron scattering instrument at the China Spallation Neutron Source (CSNS) [31,32], located in Dongguan, China. Samples were prepared into thin wafers with thicknesses lower than 1 mm to avoid multiple scattering. Prior to the commencement of the experiment, the samples were dried in the oven at 105 °C for over 24 h until the mass of the samples stop decreasing. The samples were then mounted on the automatic sample changer with Kapton tape. The scattering profiles of the shale samples were collected by a 1 m × 1 m area detector placed 4 m behind the sample position. The scattering data were further corrected for detector efficiency, sample thickness, and transmission, with background scattering from the empty beam and Kapton tape subtracted. The data were calibrated to absolute scaling based on a secondary standard sample provided by the beamline. The data analysis was performed using IGOR Pro (Portland, OR, USA).

2.2.2. Low-Pressure Nitrogen Adsorption

A Micromeritics ASAP 2420-specific surface area and porosity analyser (Norcross, GA, USA) were used to examine the samples, with an equilibration time set to 10 s [33]. The sample used was 40–80 mesh grain shale. The measuring range of the instrument’s pore diameter was 0.35–400 nm, the specific surface area was 0.005 m²/g, and the pore volume was 0.0001 cm³/g. The nitrogen adsorption and desorption isotherms of different partial pressures were measured at −196.15 °C, with the nitrogen having a purity greater than 99.99% as the adsorbate.

2.2.3. Large Field of View Mosaic Scanning Electron Microscope

A FEI Helios 650 focused ion beam double-beam scanning electron microscope (FIB-SEM, Thermo Fisher Scientific, Waltham, MA, USA) was used for the large field of view splicing scanning electron microscope imaging. The sample was first sectioned and mechanically sectioned with 9 μm–2 μm–0.5 μm sandpaper, and then, argon was utilised. The imaged regions were created by ion profiling techniques. For the imaging area, a series of high-precision (resolution 100 nm), small field of view (pixels 1000 × 1000) SEM images arranged in a matrix and, overlapping each other, were continuously captured. Finally, these images are stitched together through Atlas software and an image alignment algorithm to create a high-precision (resolution 15 nm) and large field of view (pixels 12000 × 6000) SEM image.

3. Results

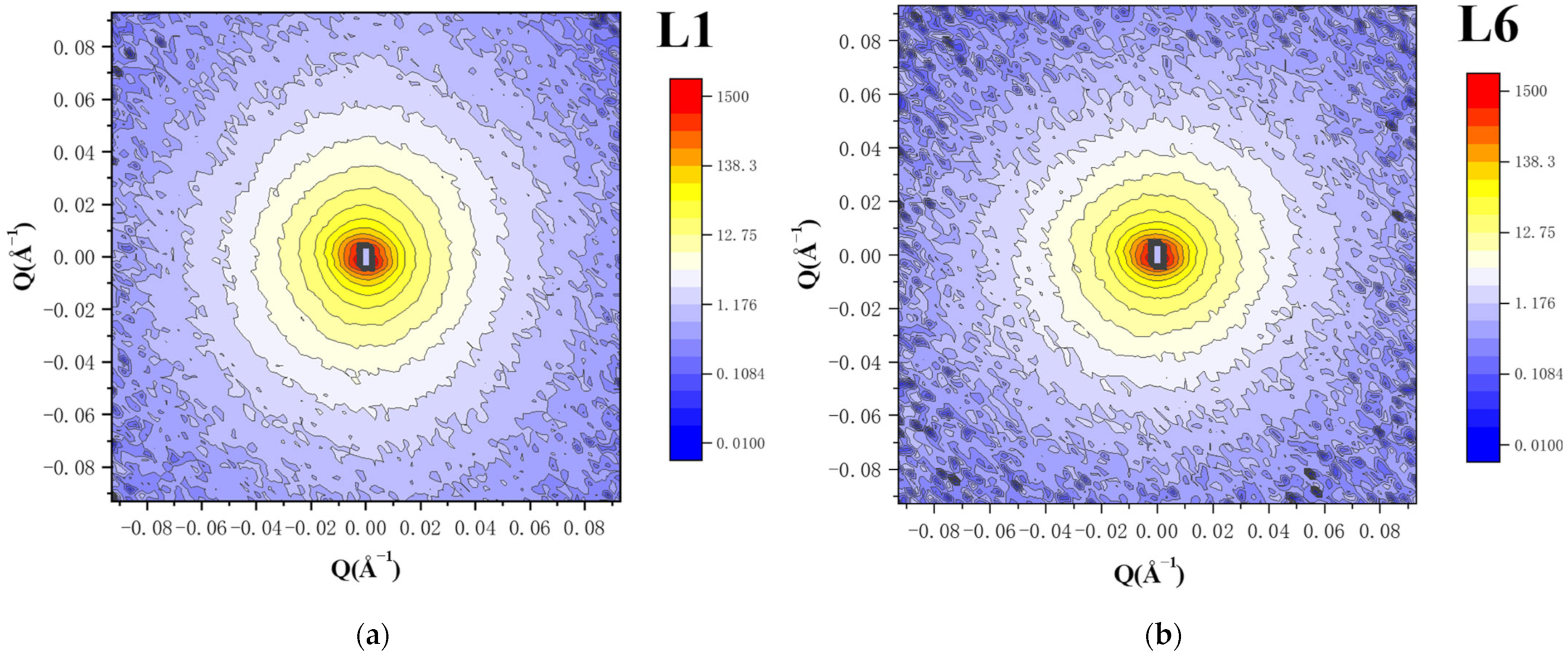
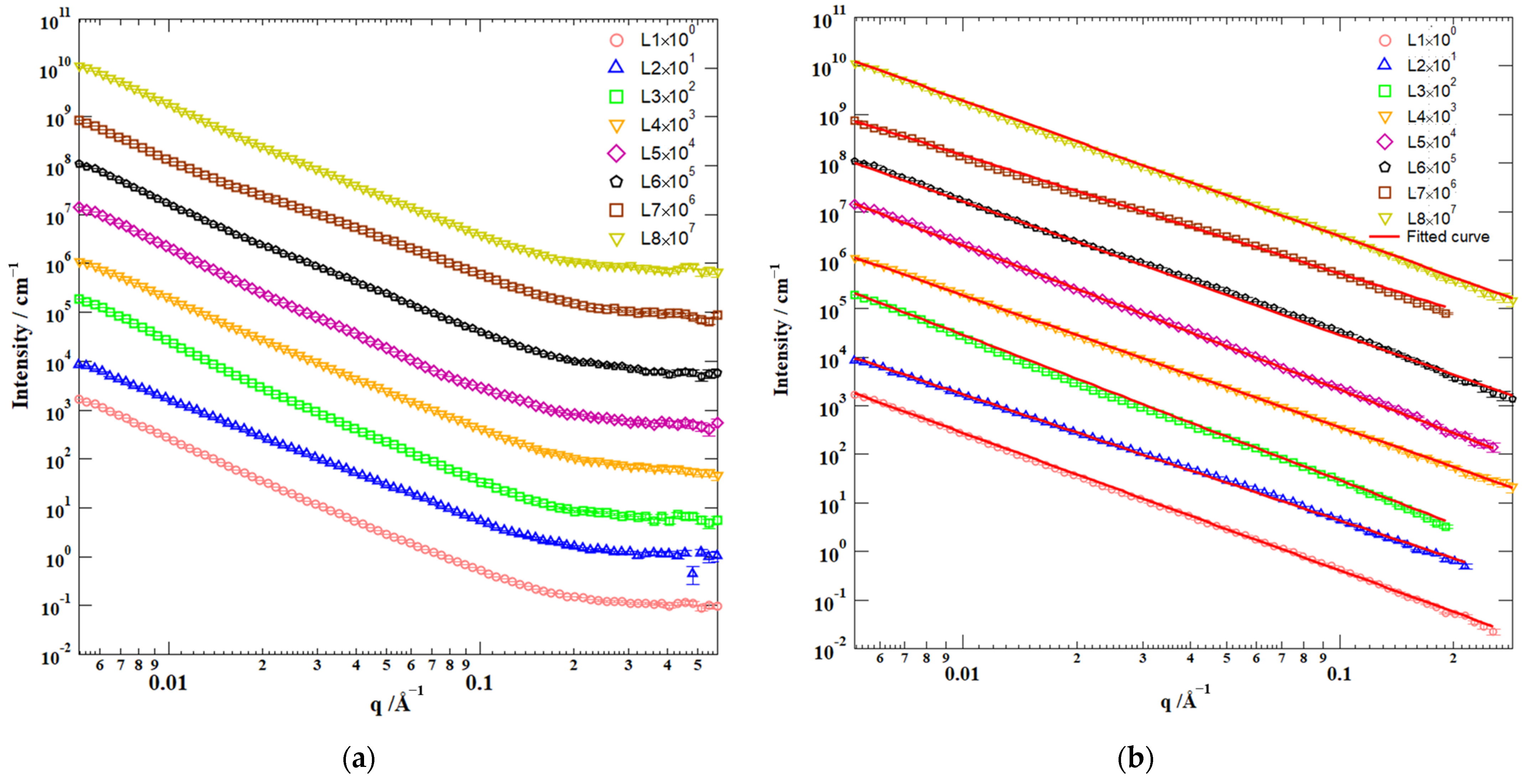
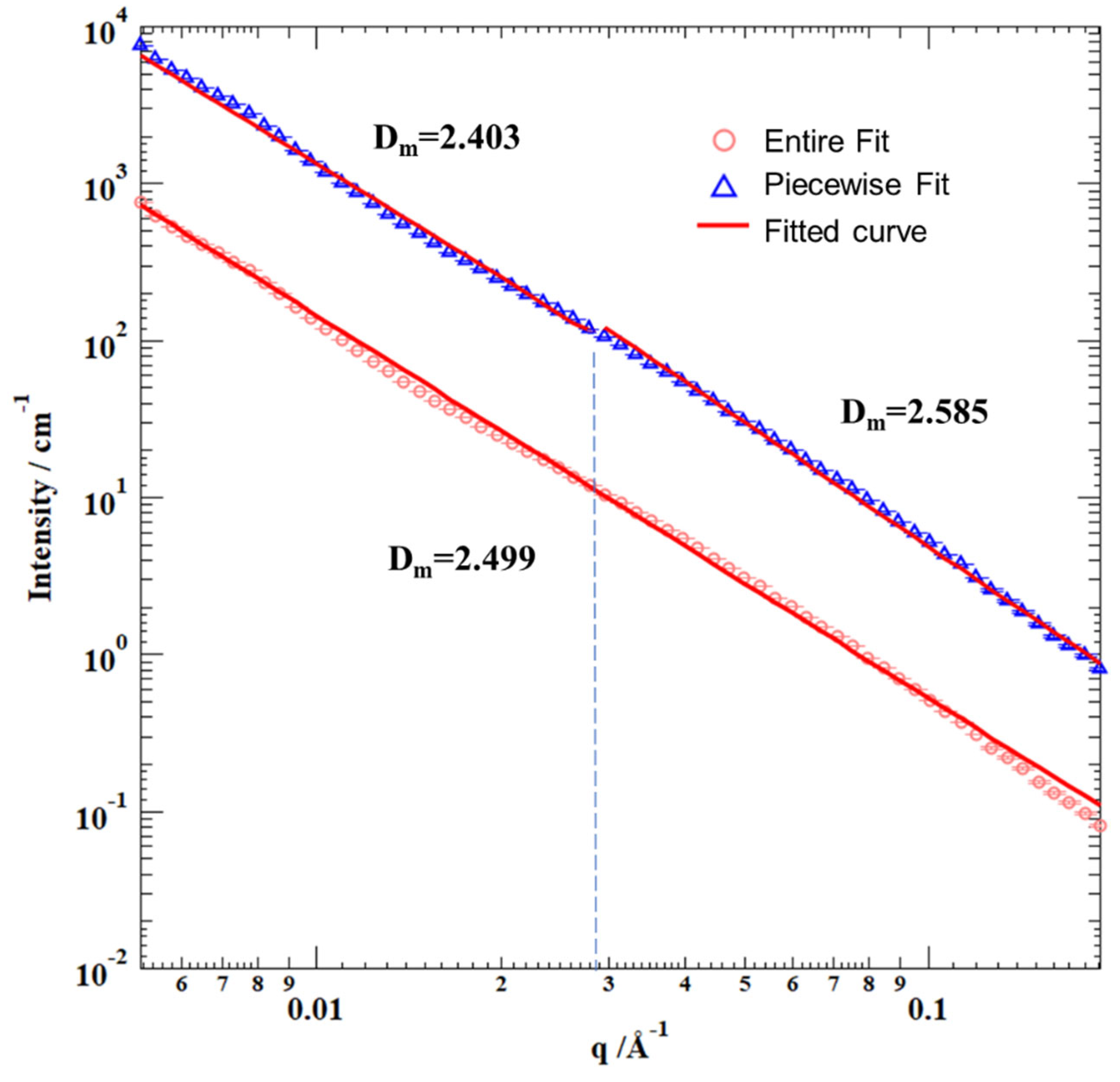
3.1. SANS Experimental Results

3.1.1. Calculation of Scattering Length Density (SLD)

The total organic carbon (TOC) and mineral compositions of the samples are listed in

Table 1. The total organic carbon (TOC) and mineral content of shale [34].

Sample	TOC	Quartz (%)	Calcite (%)	Dolomite (%)	Plagioclase (%)	Pyrite (%)	Illite (%)	Montmorillonite (%)	Chlorite (%)	SLD (1010·cm−2)
L1	2.81	61.34	2.52	3.69	6.34	4.11	16.04	2.82	3.14	4.11
L2	3.99	45.30	5.60	6.80	4.80	6.90	23.10	4.13	3.37	4.12
L3	3.07	56.98	7.57	12.10	2.52	3.02	14.72	2.50	0.59	4.26
L4	3.78	57.86	8.96	18.41	3.11	3.97	5.85	1.00	0.83	4.37
L5	1.92	55.84	9.91	20.86	4.19	2.60	4.69	0.87	1.05	4.43
L6	3.32	43.81	8.87	20.46	2.73	2.57	17.65	2.09	1.82	4.36
L7	3.67	36.12	1.41	9.41	11.21	10.85	24.70	3.50	2.80	4.10
L8	2.47	45.10	6.93	5.24	1.95	0.68	29.57	4.83	5.71	4.11

. The calculation of a shale pore structure by small-angle neutron scattering generally assumes that the shale is a two-phase porous medium (i.e., pores and components). Considering the scattering length density (SLD) of the pore (air) phase as 0, the SLD of the shale solid can be calculated by the content of each component of the shale, with the experimental results indicated in Table 1 [34].

$$SLD\left(shale\right)={{\displaystyle \sum }}_i^{n}vol\%\left(i\right)SLD\left(i\right)$$

(1)

where i is the component, and n is the total number of components.

3.1.2. Calculation of SANS Experimental Results

Figure 2 illustrates the two-dimensional SANS data of two typical samples in this experiment. The variations of the scattering intensities are represented by colour scales. The orientation of the pores can be qualitatively analysed through the anisotropicity two-dimensional scattering intensity data, as shown in Figure 2.

In this study, the absolute scattering intensities measured by all detection units on the same radius R are added, and the multipoint data on the ring will be accumulated into one data point. By constantly changing the value of R in this way, the two-dimensional absolute scattering intensity can be converted into the one-dimensional absolute scattering intensity. This data averaging method is known as circular data averaging. As a result, the scattering intensity $I\left(R\right)$ of the radius R in the two-dimensional scattering image is described as follows:

$$I\left(R\right)=\underset{x^2+y^2=R^2}{{\displaystyle \mathit{∯}}}{I}_s\left(x,y\right)dxdy$$

(2)

The actual two-dimensional detector consists of square receiving units with a side length of $∆R_x$ organised neatly. Considering that the counting position of the detecting unit is the centre coordinate of the square, the size of the scattering vector corresponding to the ring with radius R is:

$$Q=\frac{4\pi }{\lambda }\sin \left[\frac{1}{2}{\tan }^{-1}\left(\frac{R-0.5∆R_x}{L}\right)\right]$$

(3)

where $Q$ is the scattering vector, representing the distance of the two-dimensional detector in the sample cell, and the neutron wavelength, $∆R_x$, denotes the side length of the smallest unit of the neutron receiver.

Through Equations (3) and (4), the scattering intensity corresponding to each scattering vector can be calculated. The SANS scattering intensity curves of all the samples after the circular data averaging method are shown in Figure 3a. For the purpose of distinguishing the scattering intensity curves of various samples in the figure, the scattering intensity value drawn in the figure is three times that of the actual scattering intensity multiplied by the sample number. For instance, the scattering intensity of the L7 sample in the figure is the actual scattering intensity, which is multiplied by 21. When Q is greater than 0.2, there is a clear deflection in the scattering curve. This phenomenon may be the representation of the multifractal structure or be caused by an error in the experimental findings [35,36]. Existing research results revealed that, when the scattering vector is large, the scattering intensity is coherent with the background signal [37]. This is due to the hydrogen atoms in shale. Therefore, the background interference can be calculated by the shale composition.

Figure 3b is a plot of SANS scattering intensity after subtracting background values from the original experimental data. Since the fractal characteristics ought to be very linear within a specific range of Q (Å⁻¹) in the double logarithmic coordinates, data that do not conform to the fractal characteristics will be disqualified according to the characteristics of scattering intensity curves of dissimilar samples, so as to ascertain the correctness of the study, as shown in

Table 2. SANS measurement of the physical parameters of deep shale.

Sample	Mass Fractal Dimension	R2	Porod Porosity (%)	Qmin (Å−1)	Qmax (Å−1)
L1	2.831	0.9988	5.81	0.00515	0.254
L2	2.597	0.9977	5.69	0.00515	0.214
L3	2.991	0.9981	4.82	0.00515	0.191
L4	2.715	0.9982	4.83	0.00515	0.287
L5	2.989	0.9977	4.25	0.00515	0.255
L6	2.747	0.9976	4.25	0.00515	0.287
L7	2.499	0.9968	5.70	0.00515	0.191
L8	2.794	0.9985	4.39	0.00515	0.287

. Having subtracted the unacceptable data, the SANS curve of the sample approximately follows a power–law correlation (I (Q)~Q^−p, where p is the Porod exponent) [38,39]. The standard correlation coefficient (R²) of the fitting curves of all the samples is as high as 0.998 due to the strong fractal characteristics caused by the pore size in the shale. Among them, the Porod exponent (P) can characterise the fractal features in the shale. The Porod exponent (P) in this study is less than 3, indicating that the deep shale sample conforms to the mass fractal (pore fractal), and the mass fractal dimension ($D_m$) can quantify the way the mass of the object rises with the length. The number characterises the tightness of the mass fractal body and the inhomogeneity of the mass distribution. Its fractal dimension is equal to P, and the larger the $D_m$, the more inhomogeneous the system mass or density is. For the shale pore system, the mass fractal dimension can be thought of as the degree of uniformity in the development of shale pores. The larger the $D_m$, the more uneven the distribution of pores in shale. The fractal dimension results of all the shale samples in this study are reported in Table 2.

Considering shale as a two-phase system composed of shale matrix and pores, the porosity ($\varnothing$) of shale can be calculated via the Porod invariant method using the scattering contrast ($∆\rho$) [40]:

$${{\displaystyle \int }}_0^{\infty }{Q}^{2}I\left(Q\right)dQ=2{\pi }^2{\left(∆\rho \right)}^2\varnothing \left(1-\varnothing \right)$$

(4)

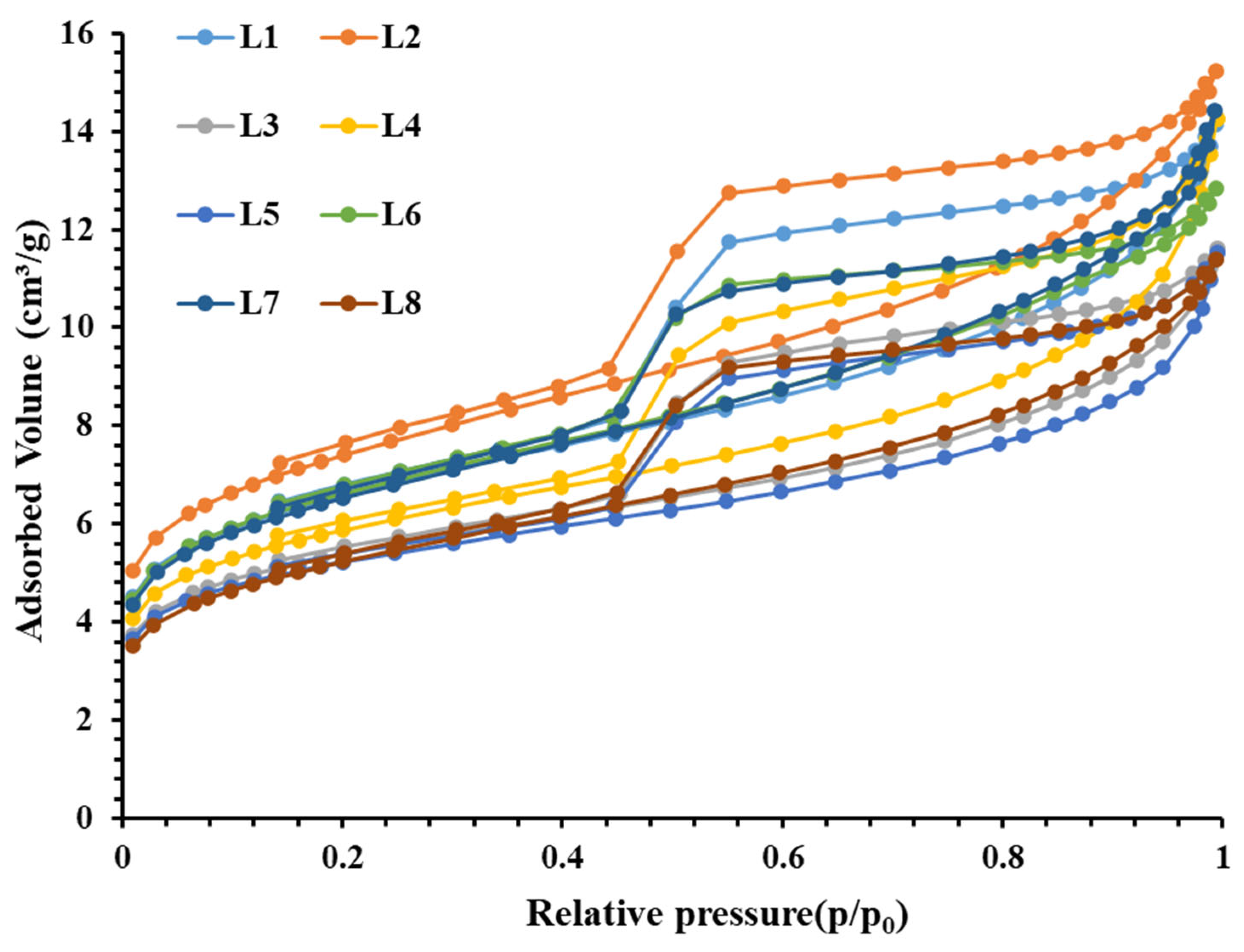
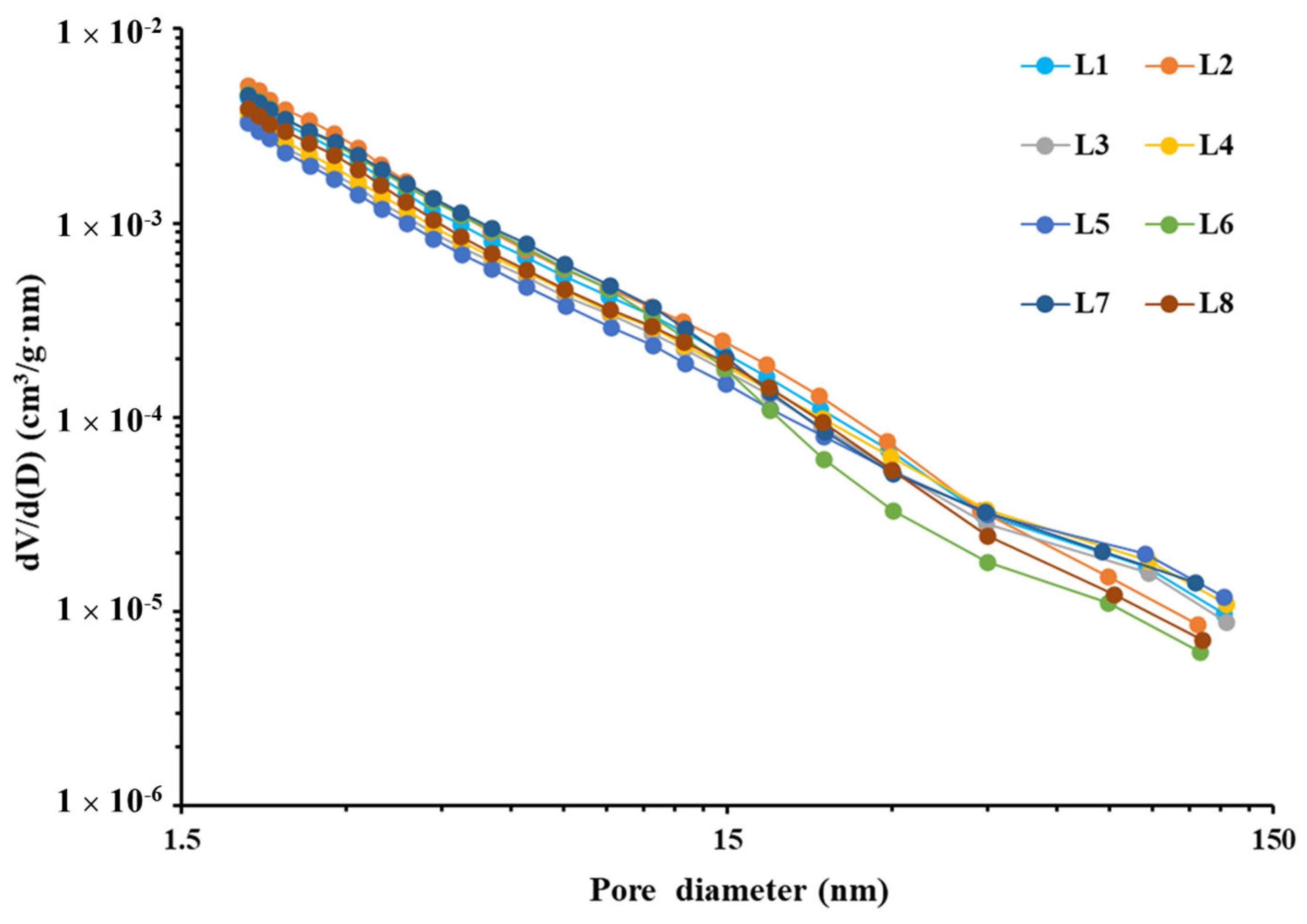
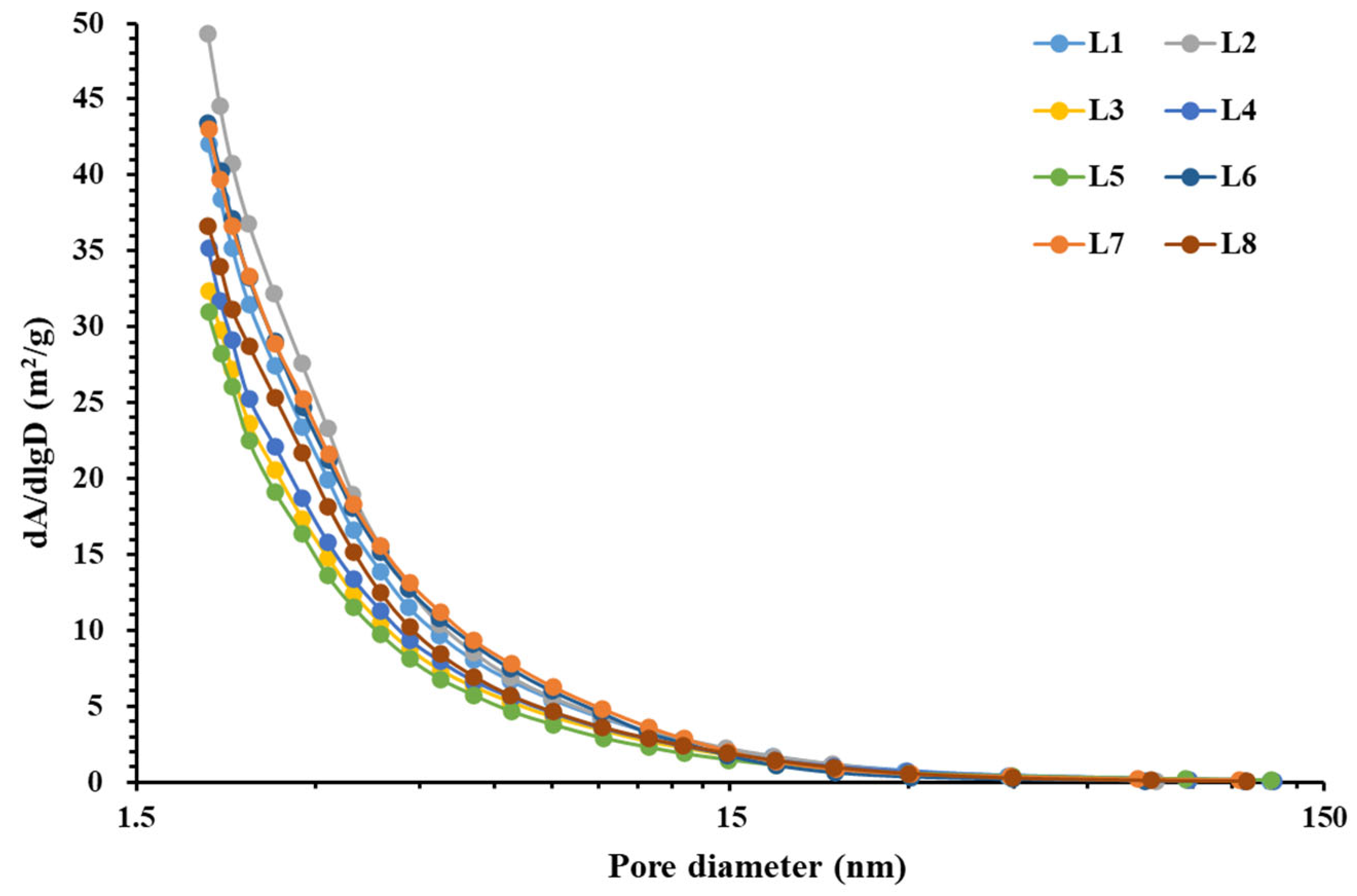
3.2. Low-Pressure Nitrogen Adsorption Experiment Results

The nitrogen adsorption curves of the shale samples are depicted in Figure 4. According to the IUPAC classification, this low-pressure nitrogen adsorption isotherm is classified as type IV [41]. The pore volume and pore size distribution of shale can be calculated from the nitrogen adsorption/desorption curve. This study is based on the BJH model, and the effective pore size ranges from 1.48 to 117.00 nm [42,43,44].

Based on the nitrogen adsorption data, the surface fractal dimension of the shale was calculated using Pfeifer’s Frenkel–Halsey–Hill (FHH) model. The surface fractal dimension is usually 2 to 3. When the value of the surface fractal dimension is close to 2, the solid surface is smooth and uniform; when the value is close to 3, it reflects the complex pore structure, the pore surface is extremely irregular and uneven, and the fluid flow resistance is high.

$$ln\left(\frac{V}{V_0}\right)=K\left[ln\left[ln\frac{p_0}{p}\right]\right]+C$$

(5)

where V is the adsorption volume of the sample at the equilibrium pressure P, V₀ depicts the monolayer coverage volume, P₀ is the saturation vapour pressure of the adsorbed gas, P illustrates the equilibrium pressure of the system, K is a characteristic constant, and C is a constant. In this study, the adsorption isotherm has a detailed hysteresis loop. Therefore, the surface fractal dimension is calculated by Equation (6).

$$D_s=K+3$$

(6)

The physical parameters of nitrogen adsorption of all the samples are shown in

Table 3. Measurement of the physical parameters of deep shale by nitrogen adsorption.

Sample	Fractal Fitting Equation	R2	Surface Fractal Dimension	N2 Porosity (%)	Median Pore size (nm)	Specific Surface Area (m2/g)
L1	Y = −0.1822X + 1.9676	0.945	2.828	4.21	6.38	22.57
L2	Y = −0.1700X + 2.0869	0.927	2.830	4.09	5.51	25.45
L3	Y = −0.1787X + 1.7620	0.955	2.821	3.50	7.52	18.33
L4	Y = −0.1761X + 1.8918	0.962	2.824	3.85	6.34	19.63
L5	Y = −0.1819X + 1.7262	0.965	2.818	3.70	7.55	17.76
L6	Y = −0.1750X + 1.9730	0.907	2.825	3.98	6.21	22.76
L7	Y = −0.1818X + 1.9674	0.926	2.828	4.85	5.41	24.40
L8	Y = −0.1821X + 1.7481	0.922	2.818	3.68	6.39	18.08

.

4. Discussion

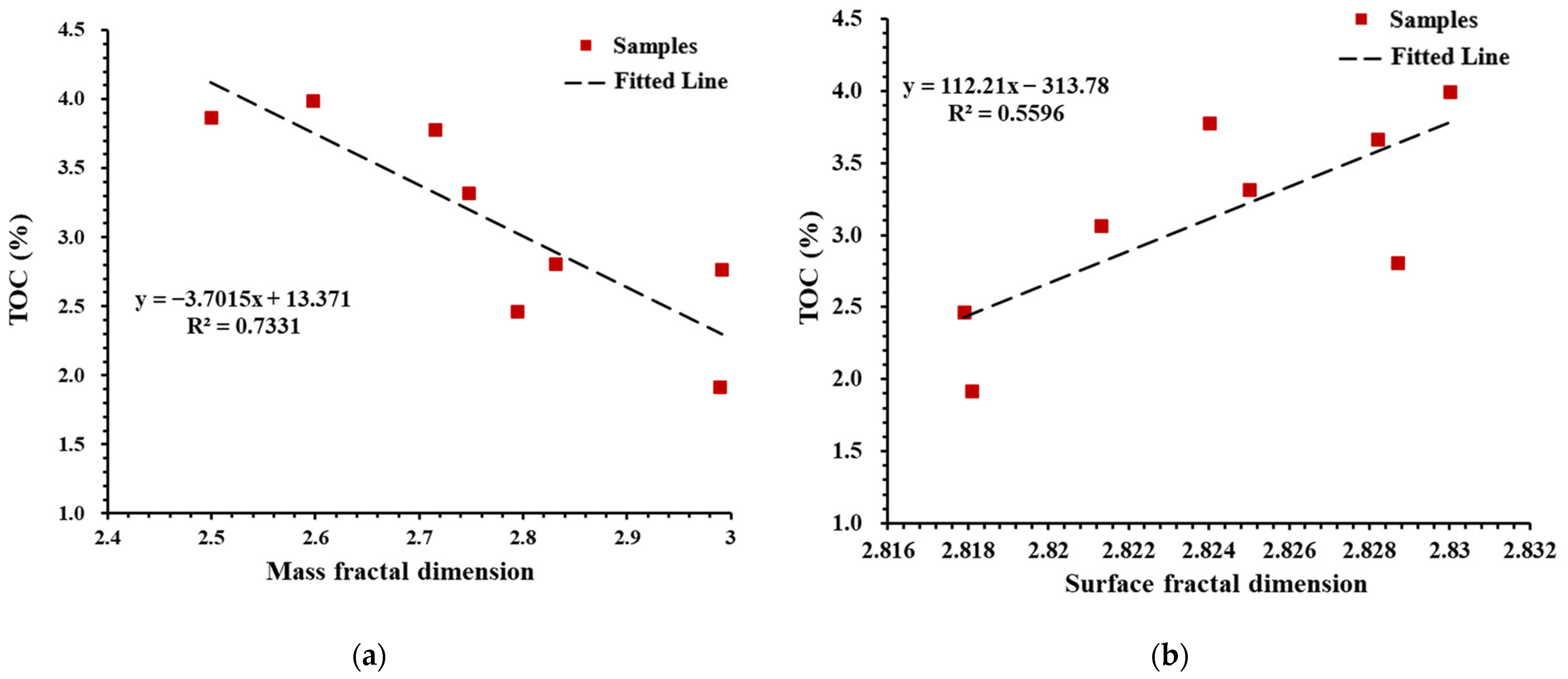
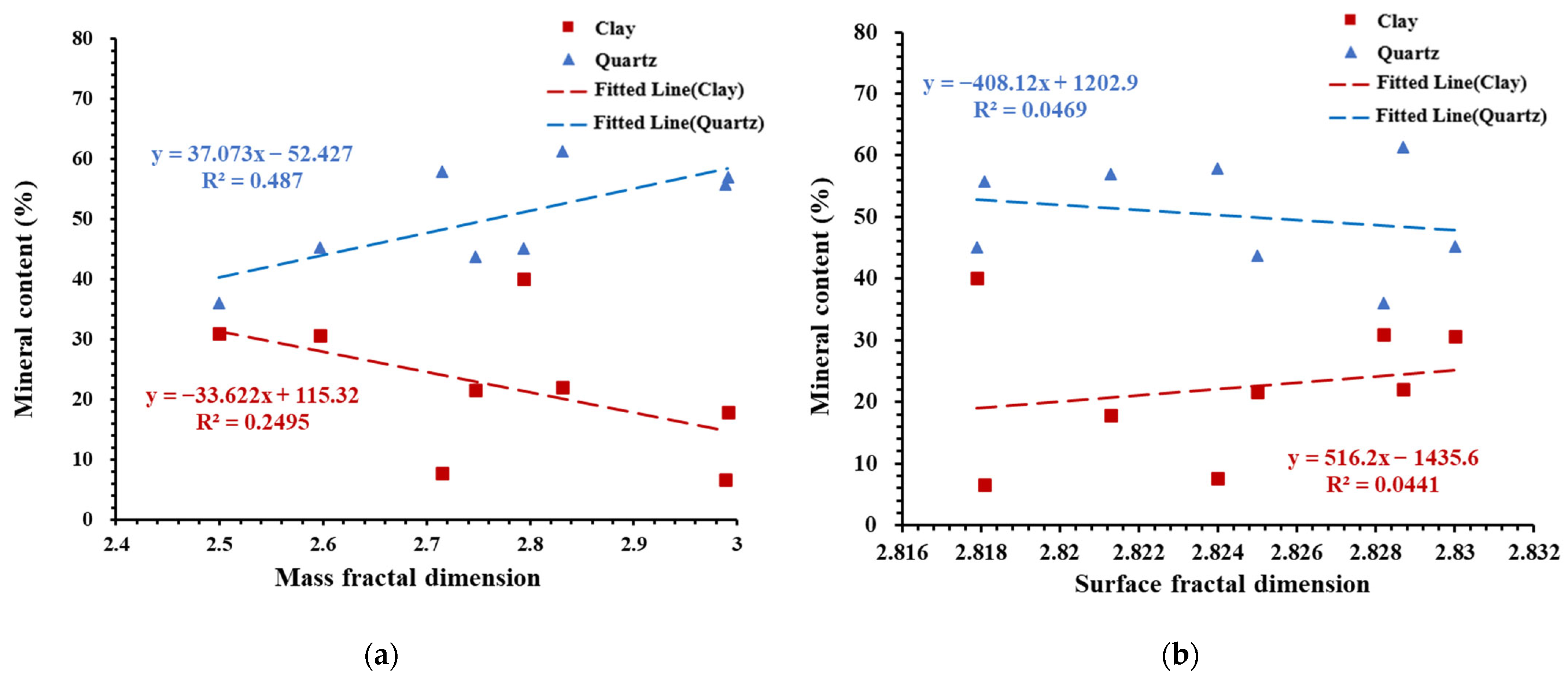
4.1. The Relationship between Fractal Dimensions and the Composition and TOC Content of Deep Shales

Figure 5a shows the correlation among the total organic carbon (TOC) content of shale and the fractal dimension of the mass. A negative correlation can be seen between the TOC content and mass fractal dimension (R² = 0.73). When the TOC content increases, the mass fractal dimension that characterises the distribution of shale pores decreases, indicating that the nanopores of shale are dominated by organic pores. The higher the organic matter content, the more organic matter pores are the main body of nanopores, the more concentrated the pore distribution, and the lower the mass fractal dimension. Scanning electron microscope observation revealed that a considerable number of nanoscale organic pores have developed in the deep shale of Southern Sichuan, including independent organic pores, clay mineral-associated organic pores, and pyrite-associated organic pores.

Figure 5b highlights the correlation between the total organic carbon (TOC) content of shale, as well as the surface fractal dimension. The TOC content is found to have a positive correlation with the surface fractal dimension (R² = 0.56). The surface fractal dimension characterises the surface roughness of shale pores. As presented in Figure 6, the surface structure of the organic matter pores in the experimental samples is complex. The thermal maturity of the organic matter in this experiment is relatively high, averaging 3.27%, which is consistent with the characteristics of the high thermal maturity of shale in the Longmaxi Formation in Southern Sichuan, China. Honeycomb-like organic pores of various sizes are often developed in high thermal maturity organic matter, significantly improving the surface roughness of shale pores. Therefore, as the organic matter increases, the fractal dimension of the shale surface will increase dramatically.

Figure 7 shows the correlation star map of the shale fractal dimension, clay content, and content of the main inorganic minerals such as quartz. As can be observed, the fractal dimension of the mass and fractal dimension of the surface have no significant correlation with the contents of inorganic minerals. This suggests that the intergranular pores and intragranular pores formed by inorganic minerals are not developed in the shale reservoir of the experimental sample.

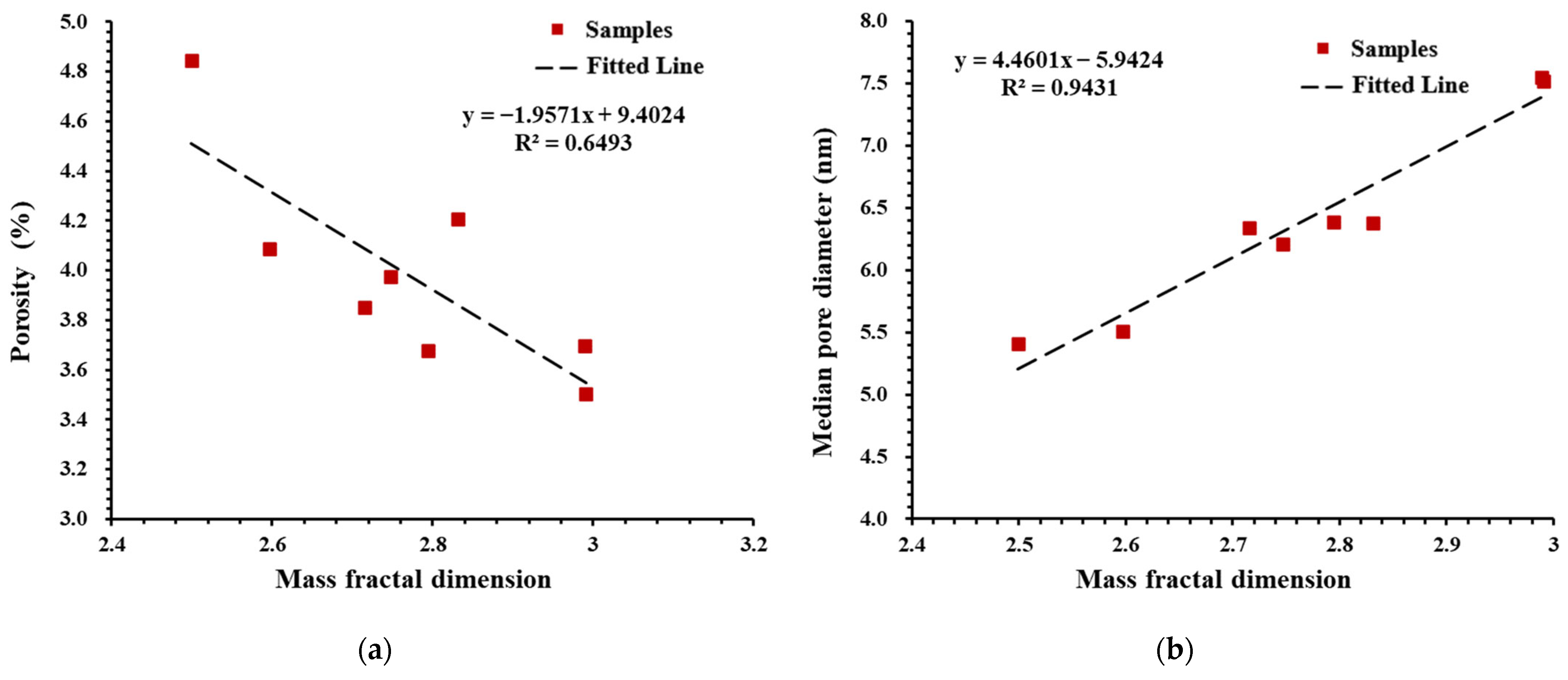
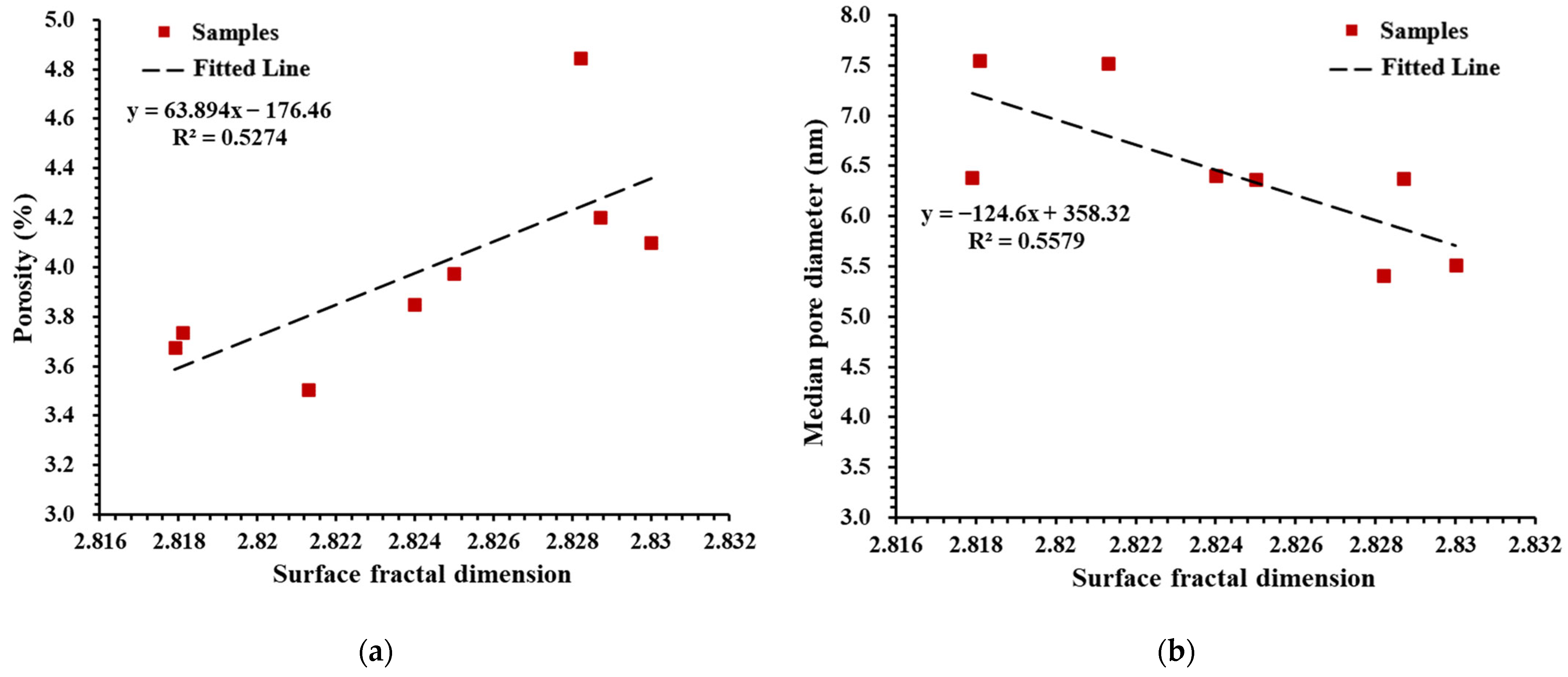
4.2. The Relationship between Fractal Dimension and Pore Structure of Deep Shale

Figure 8a illustrates a correlation analysis diagram of the shale porosity and fractal dimension. In this study, the shale structural parameters such as porosity and specific surface area calculated by the low-pressure nitrogen adsorption method were used for a comparative analysis to ensure the consistency and reliability of the analysis results. The porosity and mass fractal dimension (R² = 0.65) have a certain negative correlation. In general, when the porosity of shale decreases, the fractal dimension of its mass increases. However, this moderate correlation between the porosity and mass fractal dimension suggests that there are other factors that influence the relationship. A complex link between the porosity and fractal dimension will result from the combined relationship between the macropores and micropores in the sample. Therefore, in this study, the shale median pore diameter represents the pore distribution homogeneity with a pore diameter of 1–100 nm, and the median pore diameter is the pore diameter corresponding to when the cumulative pore volume reaches 50% of the total shale volume. Small signifies that the shale has smaller pore size pores and vice versa. Furthermore, the model of polydisperse pore size distribution opposes the supposition of the fractal behaviour. In this study, pores with a diameter of 1–150 nm were studied by means of low-pressure nitrogen adsorption, the pores being divided into two parts according to their sizes. Micropores and mesopores with a diameter of less than 10 nm are artificially referred to as small pores. The 10-nanometer mesopores and macropores are known as large pores.

The relationship between the median pore size and mass fractal dimension of the shale samples is shown in Figure 8b. The shale median pore size and mass fractal dimension are shown to have a highly positive correlation, and the correlation coefficient R² is as high as 0.94. The mass fractal dimension increases with the average pore size. The mass fractal dimension is a measure to characterise the complexity of the shale pore distribution; thus, the relationship between the fractal dimension and median pore size can be explored through the shale pore size distribution curve.

Figure 9 depicts the pore size distribution curve of the deep sample characterised by low-pressure nitrogen adsorption. The pores of deep shale compressed by the overlying rock’s intense mechanical compaction, particularly the small-diameter nanopores with organic matter as the main body, which lack high-hardness inorganic minerals to support pores, so they will be severely impacted. Due to the influence of compaction, a large number of small-diameter pores are developed, which are shown in Figure 6. The special development of small-diameter pores will ensure that the pore distribution of shale is uniform and will decrease the shale’s mass fractal dimension. Thus, the shale pore volume distribution represented by the median diameter is a direct determinant of the mass fractal dimension. Hence, the shale pore volume distribution represented by the median diameter is a direct determinant of the mass fractal dimension. Since the porosity of deep shale is primarily provided by small pore sizes, for all the samples, pores with a pore size of less than 10 nm contributed an average of 61.52% of the pore volume, so there is also a certain negative correlation between the porosity and median pore size., resulting in a moderate correlation between the shale porosity and mass fractal dimension.

The correlation between the surface fractal dimension and porosity and median pore size is shown in Figure 10. It can be noticed that the fractal dimension of the surface has a moderate correlation with the porosity, as well as the median pore size. Among them, the porosity has a positive association with them, while the median pore size has a negative correlation. This means that neither the porosity or the pore distribution represented by the median pore size is a direct factor that impacts the fractal dimension of the shale surface; nevertheless, it is still affected by other factors.

The relationship between the fractal dimension and specific surface area of the shale samples is shown in Figure 11. The fractal dimension and total specific surface area exhibit a good negative association, and shale samples with larger fractal dimensions invariably have a larger total specific surface area. The correlation coefficient is 0.64. However, there is a highly positive correlation between the surface fractal dimension and specific surface area, with a correlation coefficient as high as 0.88. As a result, the size of a specific surface area is a direct influencing factor of the surface fractal dimension. More shale pore surface per unit volume of the sample is represented by a larger specific surface area, which will make the shale pores rougher, eventually leading to an increase in its surface fractal dimension. This also explains the correlation between the median pore size and the specific surface area. From the specific surface area distribution curve (Figure 12), it can be seen that 91.02% of the specific surface area in the shale reservoir is provided by pores with a pore diameter of less than 10 nm. Therefore, the smaller the median pore size, the tinier the pores contained in the shale, the rougher the pore surface, and, thus, the larger the surface fractal dimension.

Figure 13 illustrates the association between the fractal dimension and burial depth of the shale samples. Vertically, there is no obvious correlation between the mass fractal dimension and burial depth. This demonstrates that the pore distribution of deep shale has a strong consistency in the vertical direction. The surface fractal dimension is negatively associated with the burial depth, and the surface fractal dimension of shale decreases as the sample depth increases. This depicts the lower complexity and better connectivity of the pore surface structure at the bottom of deep Longmaxi formation shale.

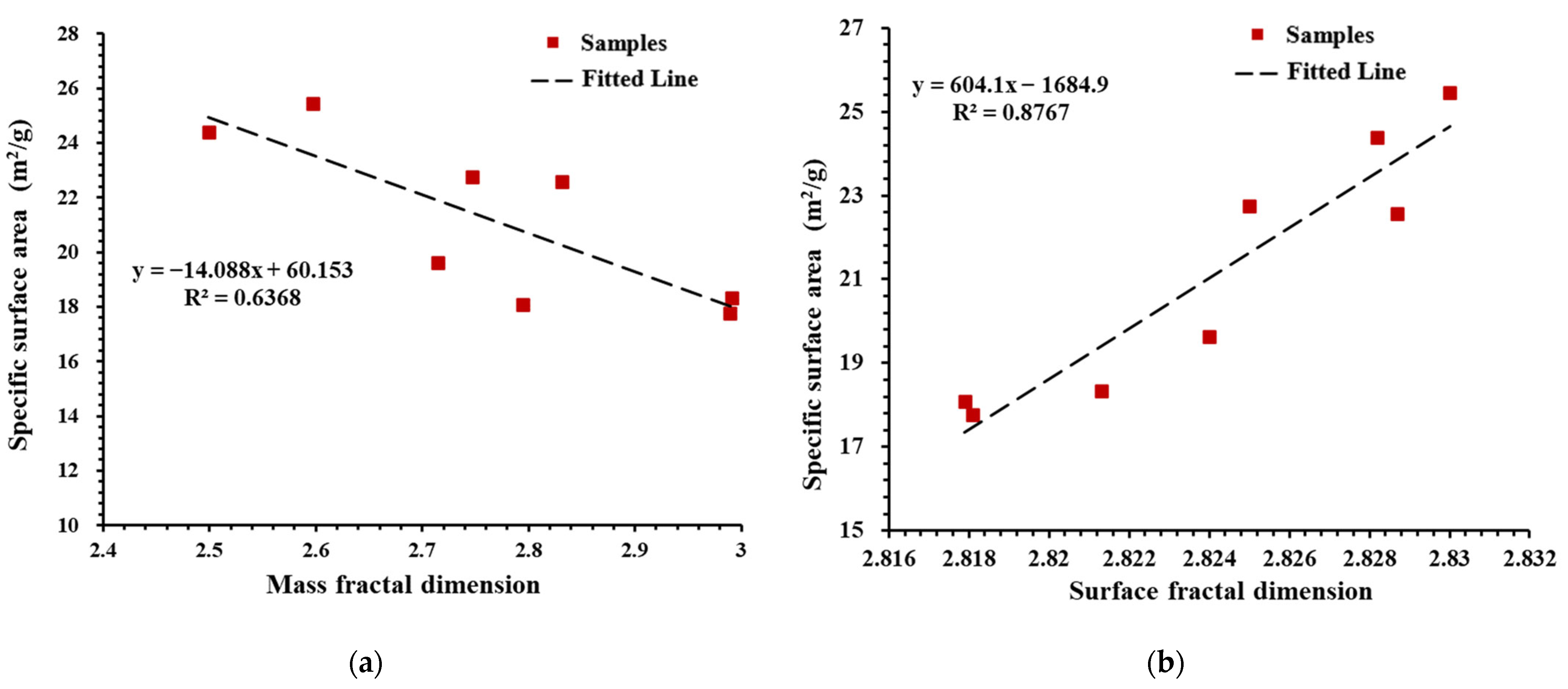
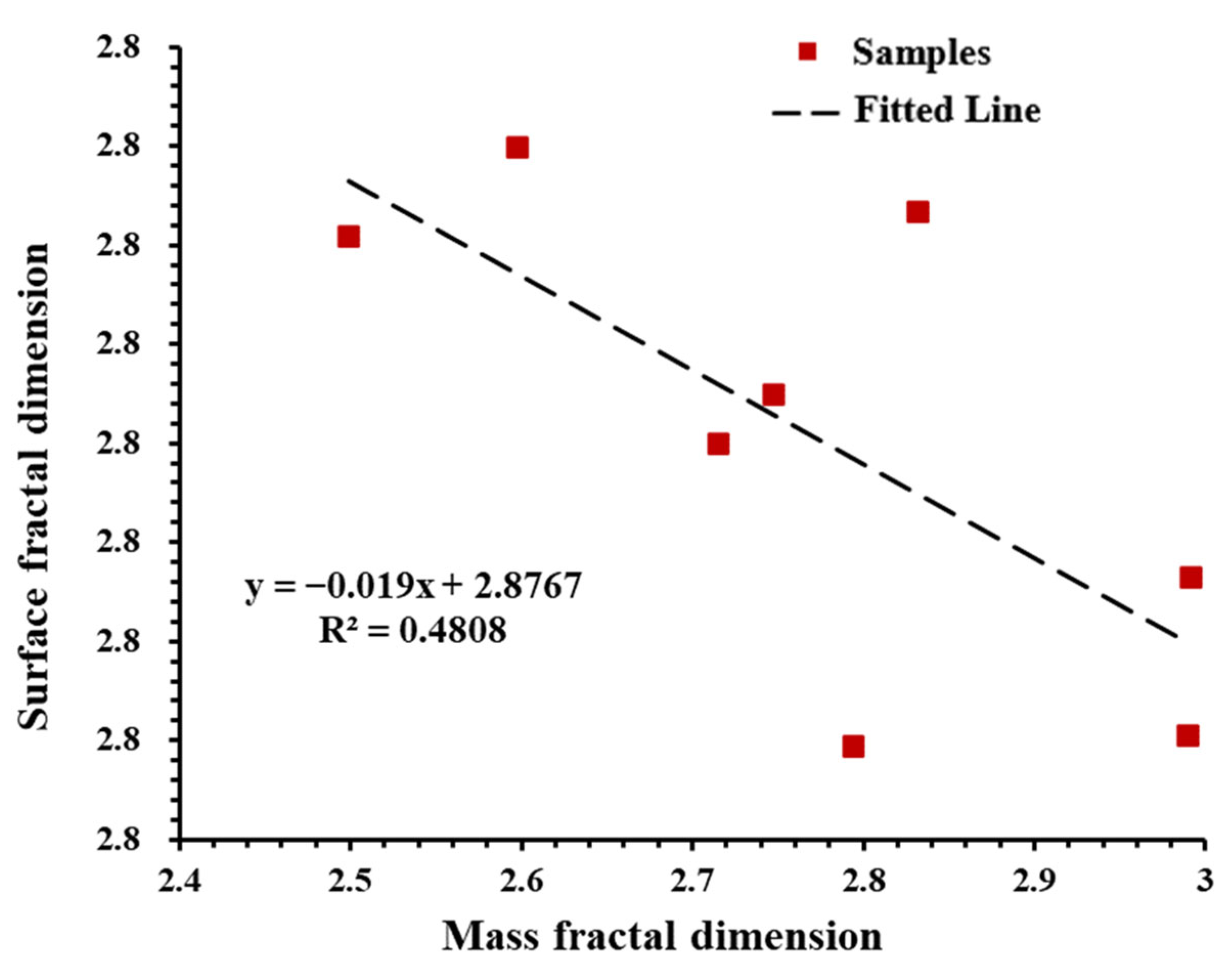
4.3. The Relationship between Mass Fractal Dimension and Surface Fractal Dimension

The roughness of the pore surface of the rock is characterised by the surface fractal, and the distribution features of the rock pores are characterised by the mass fractal. Therefore, conceptually, both the surface fractal features and mass fractal features can exist in rocks. Since the two fractal dimensions represent different shale pore structure characteristics, in this study, they are utilised to comprehensively characterise the shale pore structure characteristics. Deep shale possesses double fractal characteristics, with a mass distribution dimension of 2.499–2.991 and a surface fractal dimension of 2.814–2.831, indicating that both the pore distribution and the pore surface of the shale are heterogeneous. Existing studies have revealed that shale reservoirs will show vertical heterogeneity and lateral homogeneity. For the samples in this experiment, it can be seen that the distribution range of the mass fractal dimension is large, with a standard deviation of 0.161, whereas the surface fractal distribution of the dimensions is smaller, with a standard deviation of only 0.004. This demonstrates that the pore distribution of deep shale varies greatly vertically, and the pore surface roughness of deep shale always maintains a high level.

Figure 14 is a correlation diagram between the mass fractal dimension and surface fractal dimension. A negative correlation can be seen between the mass fractal dimension and surface fractal dimension for deep shale reservoirs (R² = 0.48). This is because the pores of deep shale are dominated by small-diameter pores, so when the mass fractal dimension is small, a large number of micropores develop in the shale, and the micropores are the primary contributor to the specific surface area, so the shale pore walls are rougher, which leads to an increase in the fractal dimension of the surface.

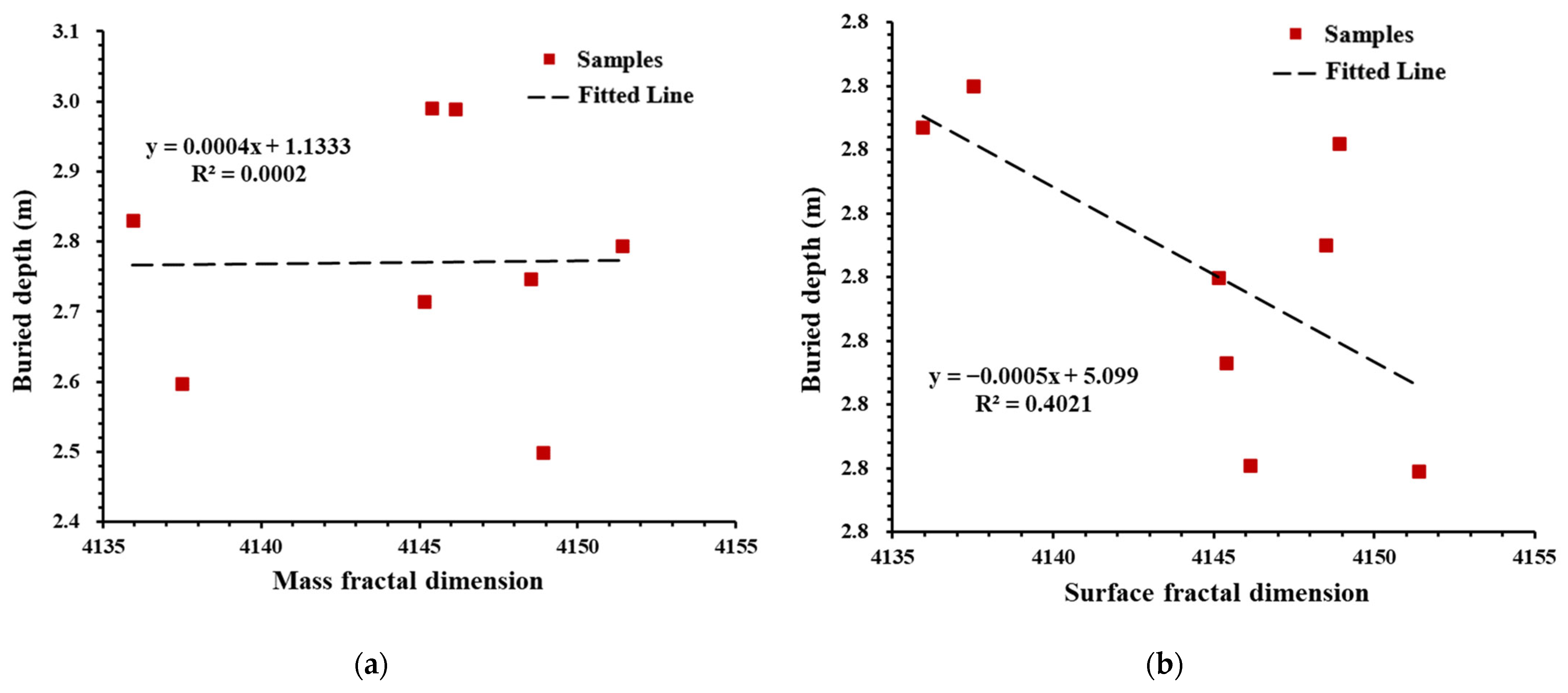
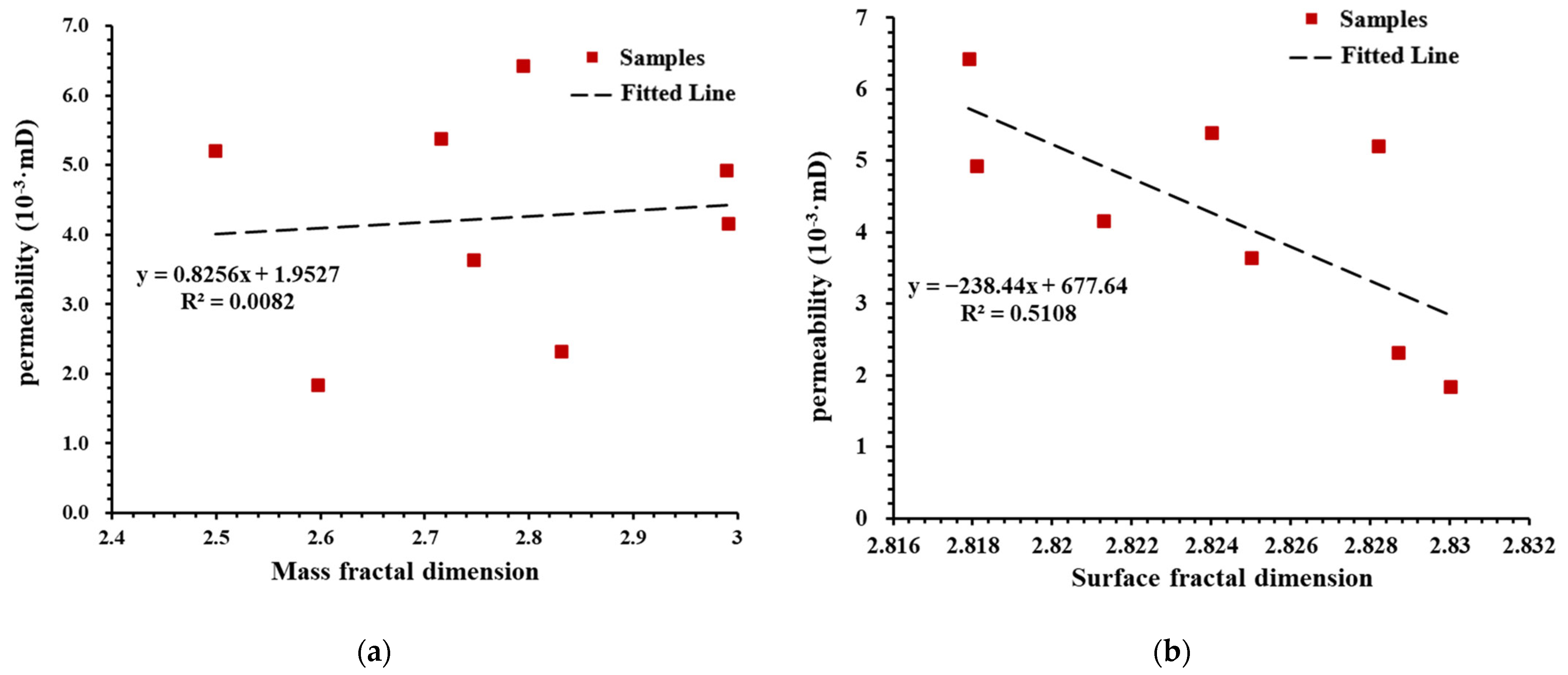
4.4. The Relationship between the Fractal Dimension and Deep Shale Connectivity

The contents of micropores and small pore size mesopores in organic matter is the key factors affecting the mass fractal characteristics and surface fractal characteristics of deep shale samples. Consequently, the contents of small and medium-sized pores in organic matter are the main reason for the structural heterogeneity of deep shale. For deep shale reservoirs, small pore sizes not only provide the main pore volume of the shale but likewise provide a large amount of surface area. This highlights that, in deep shale reservoirs, small pores constitute the primary storage space for free gas and adsorbed gas at the same time.

Figure 15 shows the correlation between the permeability and fractal dimension. It can be seen that the fractal dimension of the surface is inversely proportional to the permeability, which corresponds to the traditional understanding. As the fractal dimension of the surface increases, the pores increase, and the shale pore walls are rougher and more complicated, leading to an increase in the flow resistance of the gas and a decrease in the permeability. On the other hand, there is no correlation between the permeability and mass fractal dimension. This is inconsistent with the conventional wisdom that an increase in the number of micropores (i.e., a decrease in the fractal dimension of the mass) will lead to narrower connections between the macropores, resulting in a lower permeability. However, this is inconsistent with the findings of this study. In this study, with the reduction of the mass fractal dimension, the contents of the micropores increased, and the permeability was mainly unchanged. Consequently, the L2 and L7 samples with comparable mass fractal dimensions but different permeabilities were selected for analysis.

The mass fractal dimensions of the L2 and L7 samples were 2.60 and 2.50, respectively, and their TOC contents were similar: 3.99% and 3.87%, respectively, but the permeability was 0.0184 mD and 0.0521 mD, respectively. As can be seen, the mass fractal dimensions of the two samples are similar, but the permeability is very different. Figure 16 and Figure 17 are the large-scale mosaic SEM images of the microscopic pore structures of the two samples, respectively, with image recognition technology marking the organic matter in blue. Previous researchers have demonstrated a strong connectivity between organic pores within organic matter, and the connectivity increases with thermal maturity [45]. All of the samples utilised in this study have high thermal maturity (average 3.27). When connected, this can be substituted by observing the distribution of organic matter.

The organic matter development in shale mainly presents two states: namely, organic matter strips distributed along bedding fractures (Figure 16) and massive organic matter agglomerates (Figure 17). As illustrated in Figure 15, the organic matter of the L7 shale sample with high permeability develops in sheets along the horizontal bedding direction, and there is good communication between adjacent organic matter pores. In addition, the adjacent organic matter pore network has matrix mineral fracture pairs in the middle. Even though there are still a certain number of organic pores that are not fully communicated in the 2D SEM images, it is possible to communicate in the actual 3D space by observing their pore morphology. Hence, a large-scale three-dimensional pore network will be formed, which effectively improves the connectivity of shale pores. As shown in Figure 16, the organic matter distribution in the L2 shale samples with low permeability is blocky and scattered in the shale mineral matrix. Despite the fact that organic matter is developed, each organic matter development area only contains a small-scale pore network, and each organic matter development area is isolated from one another, and there are not enough matrix mineral fractures to communicate with it effectively. Therefore, its closed porosity rate is high, and the pore connectivity is poor.

Therefore, the content and distribution of organic pores jointly control the connectivity of shale. The shale distribution of small-diameter organic pores along the bedding direction will also significantly enhance the connectivity of shale, so the connectivity of the samples with micropores is quite different. This also emphasises the necessity of comprehensively exploring the fractal characteristics of shale through two fractal dimensions. A single-surface fractal dimension or mass fractal dimension is difficult to use to fully characterise the physical properties of shale reservoirs.

Based on the fractal characteristics and pore structure characteristics of the deep shale samples, it can be seen that the deep shale reservoirs exhibit characteristics of micropore development and poor connectivity. In addition, since the burial depth of deep shale is greater than 4000 m and the pressure coefficient is often larger than 2.0, it tends to have better gas-bearing properties. As a result of their good gas-bearing qualities, deep shale gas wells usually have a higher initial production, but due to poor connectivity, the production capacity will decline rapidly, and their production capacity per unit pressure difference will be low.

4.5. Experimental Error Analysis

This study uses fractal dimension calculations to evaluate rock samples such as shale [29,40,46]. This method can characterise the general fractal characteristics of shale pores. However, this method does not fully consider the multifractal elements that may exist in the shale samples. For instance, the L7 sample in this study shows that the fitting correlation coefficient can reach 0.9968. However, the fitting model line is not strictly consistent with the data sample in Figure 3b and may have several different fractal characteristics. For instance, Figure 18 details the L7 sample description with dual fractal characteristics. Unlike the mass fractal dimension of 2.443 fitted by the overall data of the L7 sample, the mass fractal dimension fitted by the first data is 2.403. Moreover, the mass fractal dimension fitted by the second data is 2.585, indicating two forms of pore distribution in the L7 sample. Moreover, the small aperture pore distribution is denser than that of the large apertures. In short, the general fractal dimension calculation results presented in this chapter is similar to the average of two data segments. However, this method is a rough estimate of the samples with multifractal dimensions similar to the L7 sample and can result in experimental errors. To address this issue, future studies should analyse the specific characteristics and significance of multifractality in shale pore structures.

5. Conclusions

In this paper, the mass fractal characteristics and surface fractal characteristics of shale are analysed by small-angle neutron scattering and low-pressure nitrogen adsorption. The relationship between fractal dimension and pore structure was investigated. Furthermore, the similarities and differences between mass fractal dimension and surface fractal dimension are discussed, as well as the primary controlling factors of the two fractal dimensions.

• Deep shale has double the fractal characteristics, meaning that its pore distribution has mass fractal characteristics, and its pore surface has surface fractal characteristics. The deep shale’s mass distribution dimension ranges from 2.499 to 2.991, while the surface fractal dimension ranges from 2.814 to 2.831, indicating that both the pore distribution and the pore surface of the shale are heterogeneous. Moreover, the mass fractal dimension of deep shale is negatively related to the surface fractal dimension. Therefore, the characteristics of the shale reservoirs can be more comprehensively characterised by studying shale reservoirs in terms of mass fractal dimension and surface fractal dimension.
• The organic matter content is the controlling factor of the fractal dimension of deep shale, and the small-diameter organic pores generated in the organic matter will control the fractal characteristics of the shale. Among them, the TOC content is negatively correlated with the mass fractal dimension; however, it is positively related to the surface fractal dimension. There is no evident correlation between the fractal dimension and inorganic mineral content.
• The mass fractal dimension displays a highly negative correlation with the median pore size (R² = 0.94) and has a moderate correlation with the porosity and specific surface. This suggests that the mass fractal dimension is directly influenced by the distribution of the shale pore volume. Similarly, the specific surface area is the direct influencing factor of the surface fractal dimension. This points out that the direct influencing factors of various fractal dimensions are different, necessitating the distinction and discussion of the fractal characteristics of shale.
• The permeability and the surface fractal dimension are negatively correlated. The larger the surface fractal dimension, the more complex the shale surface, and the greater the gas flow resistance. No significant correlation exists between the mass fractal dimension and permeability. The distribution of organic matter substantially impacts the shale connectivity, which is enhanced when the organic matter is distributed along the bedding, thereby resulting in some samples of low-mass fractal dimensions with high permeability.