Fuzzy Fractional-Order PD Vibration Control of Uncertain Building Structures
Abstract
:1. Introduction
2. Preliminary Concepts and Model Description
2.1. Fractional Calculus
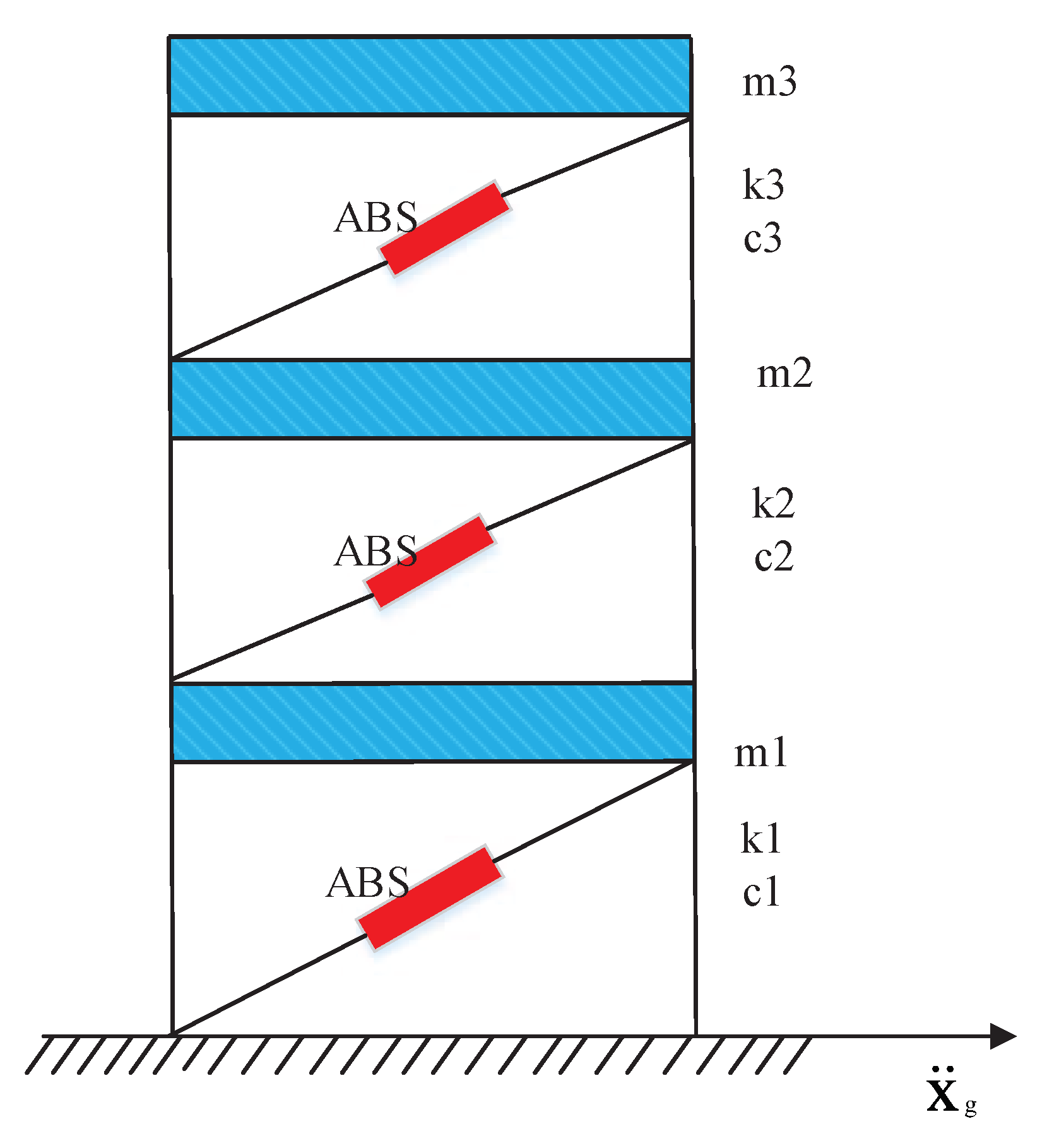
2.2. Vibration Control System of Uncertain Building Structures
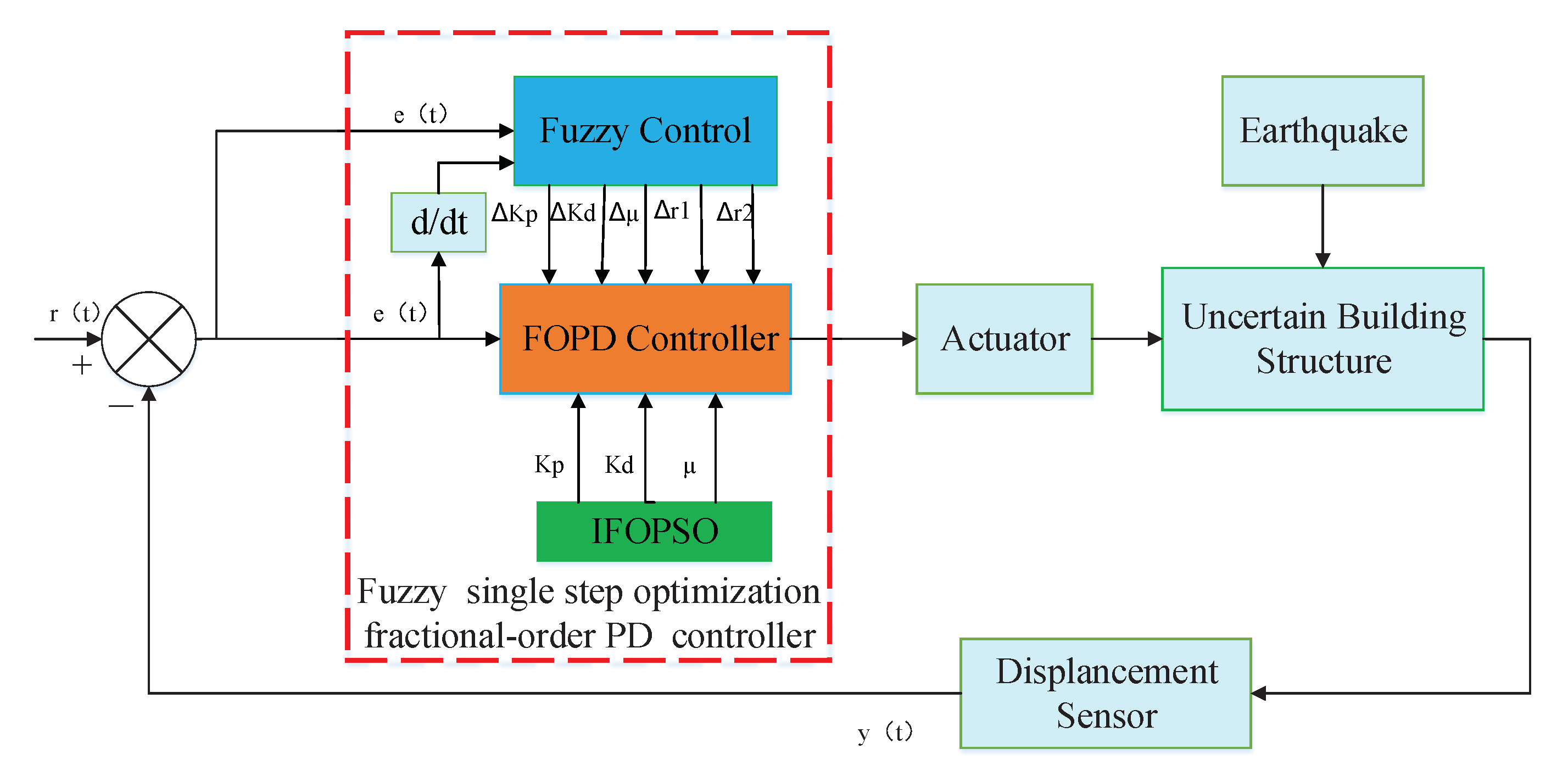
3. Control Strategy
3.1. Improved Discrete FOPD Control
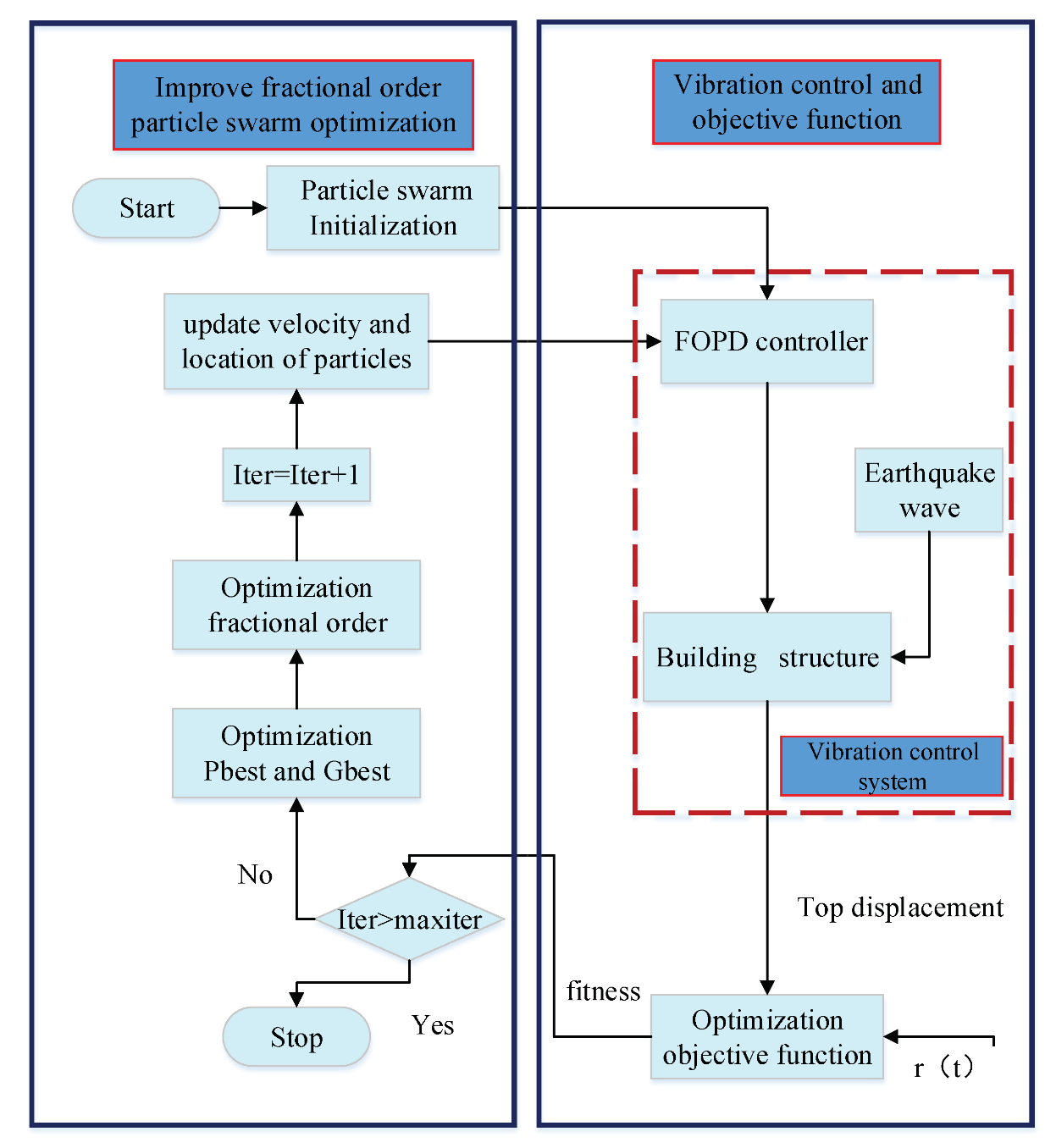
3.2. Improved FO Particle Swarm Optimization
- Step 1. Initialize the particle swarm. Randomly generate and of the particles, and determine of each particle and of the swarm;
- Step 2. Calculate the fitness value of each particle. If it is good, then update and ;
- Step 3. Use Equations (12) and (16) to update the velocity and location of the particles;
- Step 4. Use Equations (18)–(20) to calculate the fractional-order ;
- Step 5. Use Equation (17) to update the weight ;
- Step 6. Check stop conditions. If they are satisfied, then stop the search and output the results; Otherwise, return back to Step 2.
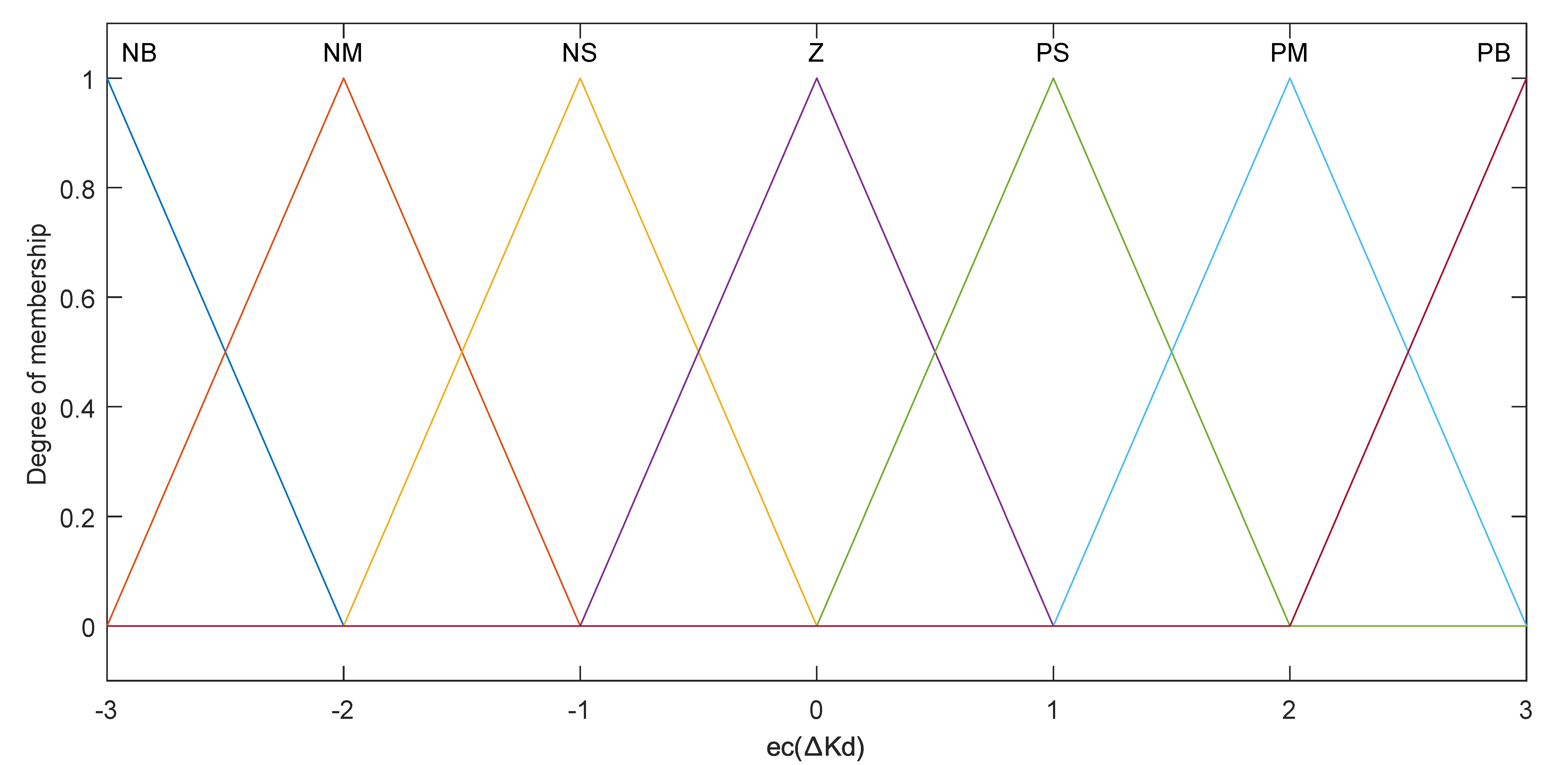
3.3. FFOPD Controller
- Based on the established fuzzy rules, the outputs of the adjusting values are obtained;
- The actual real-time control parameters are calculated by the Equation (24);
- The discrete FOPD controller and the fuzzy single step optimization control force at the k-th time instant are calculated by Equation (22).
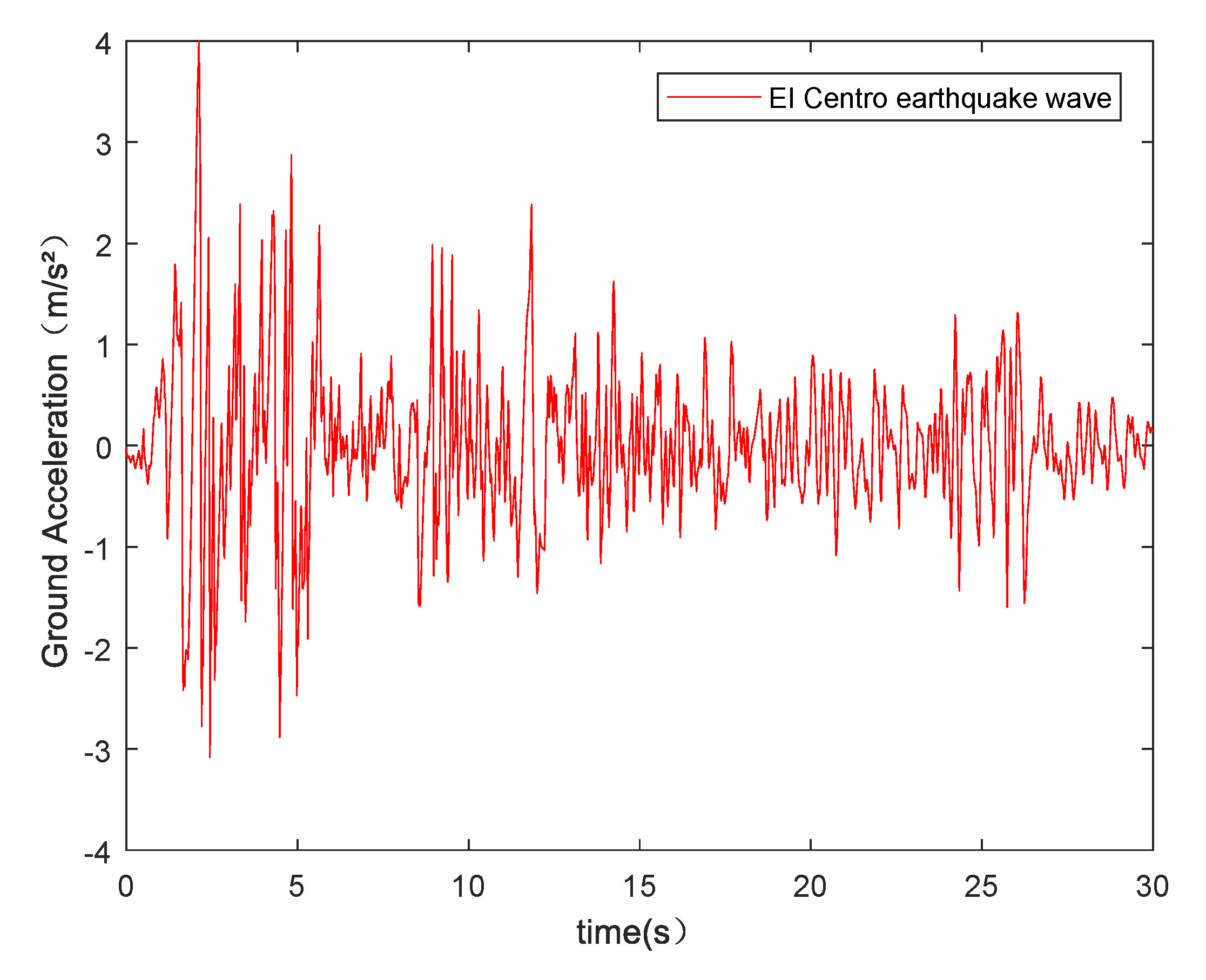
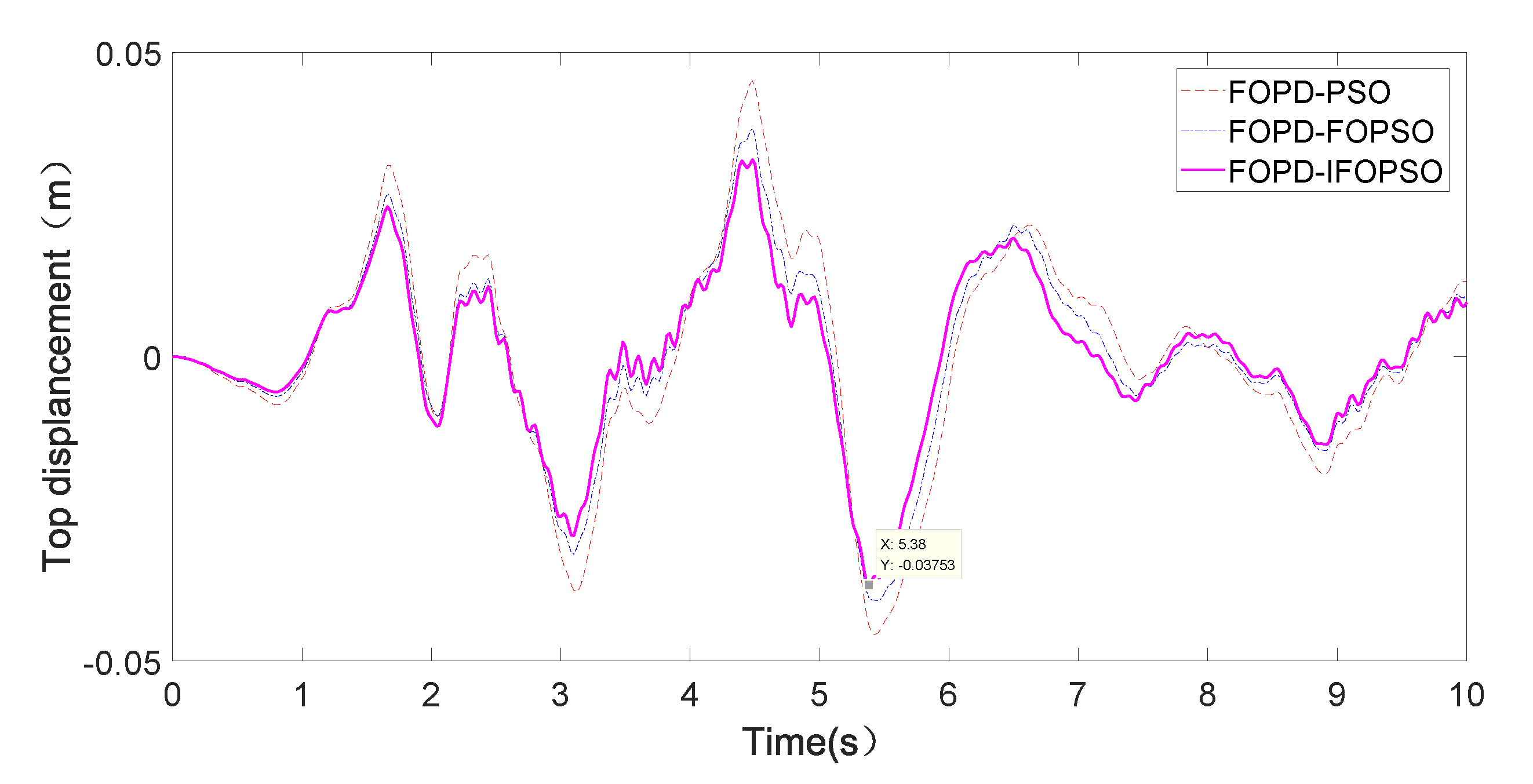
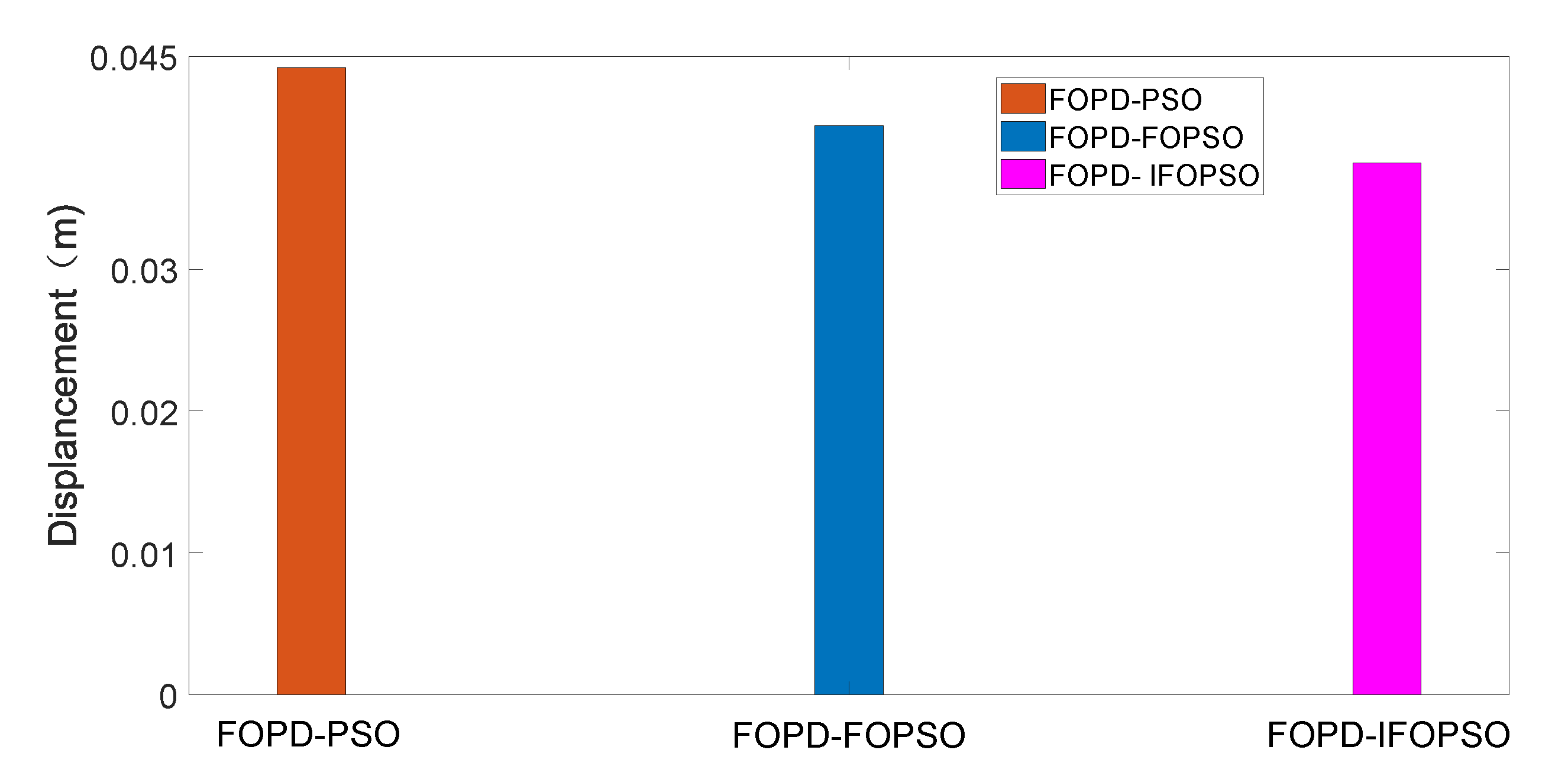
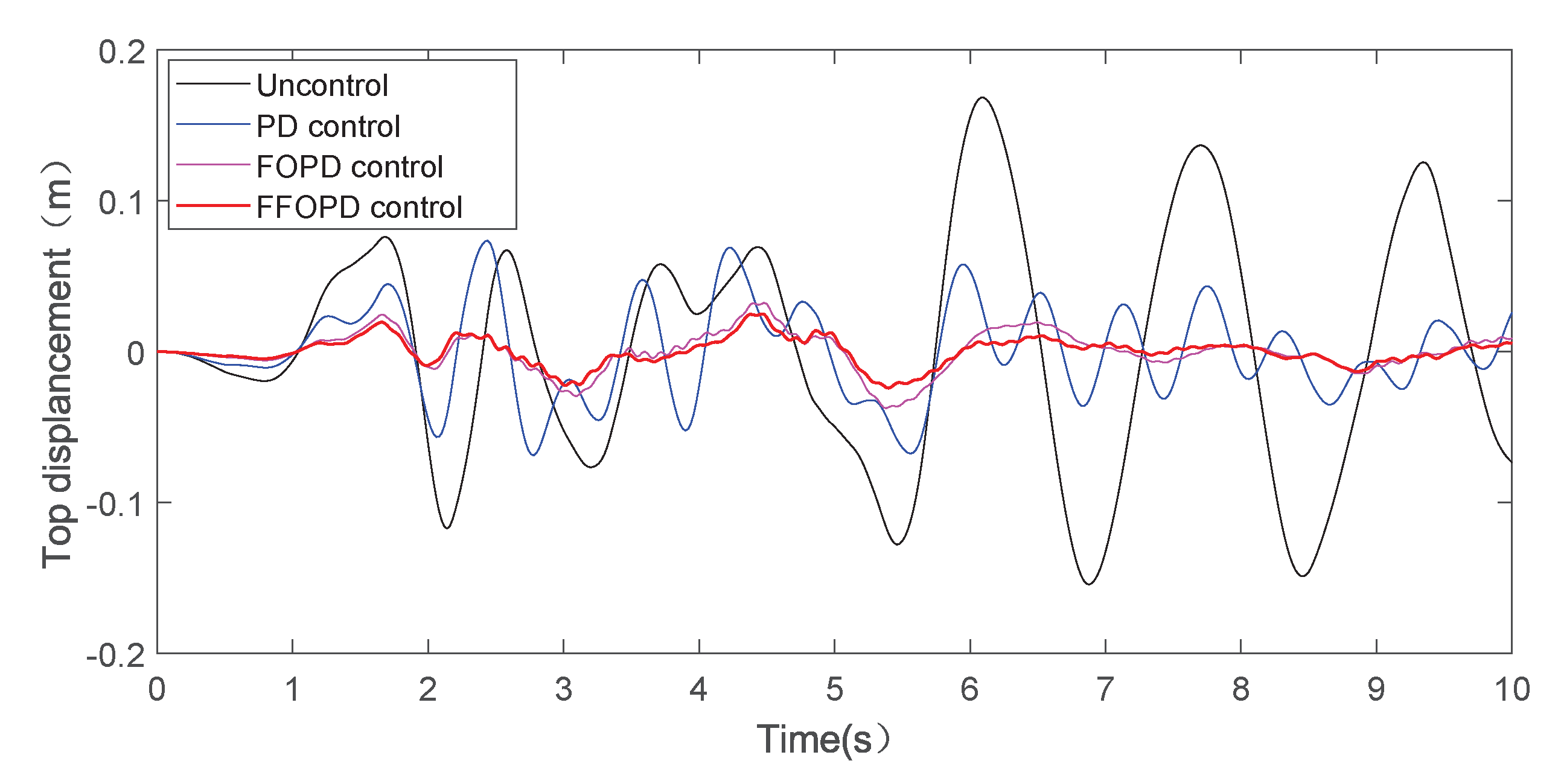
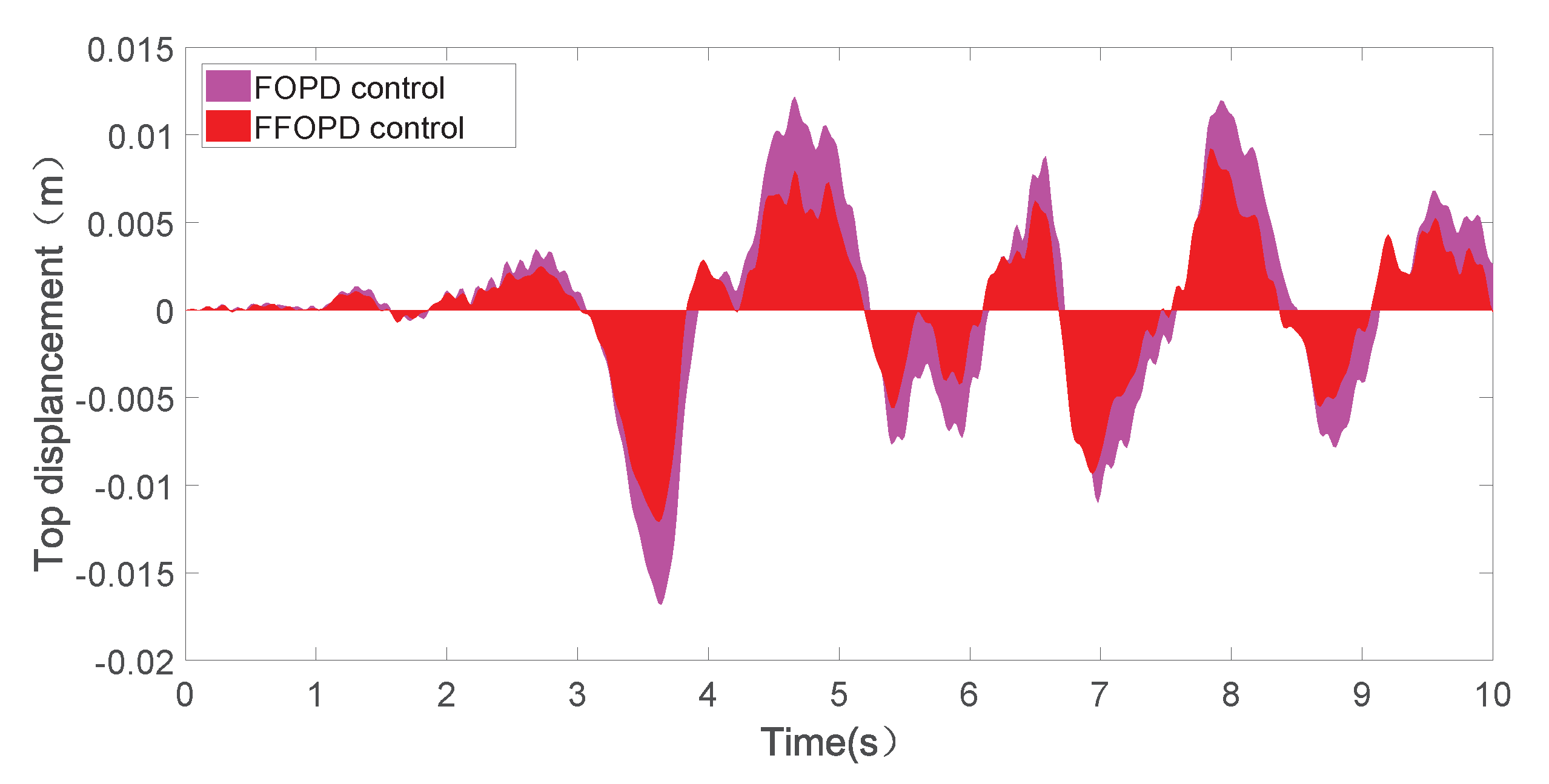
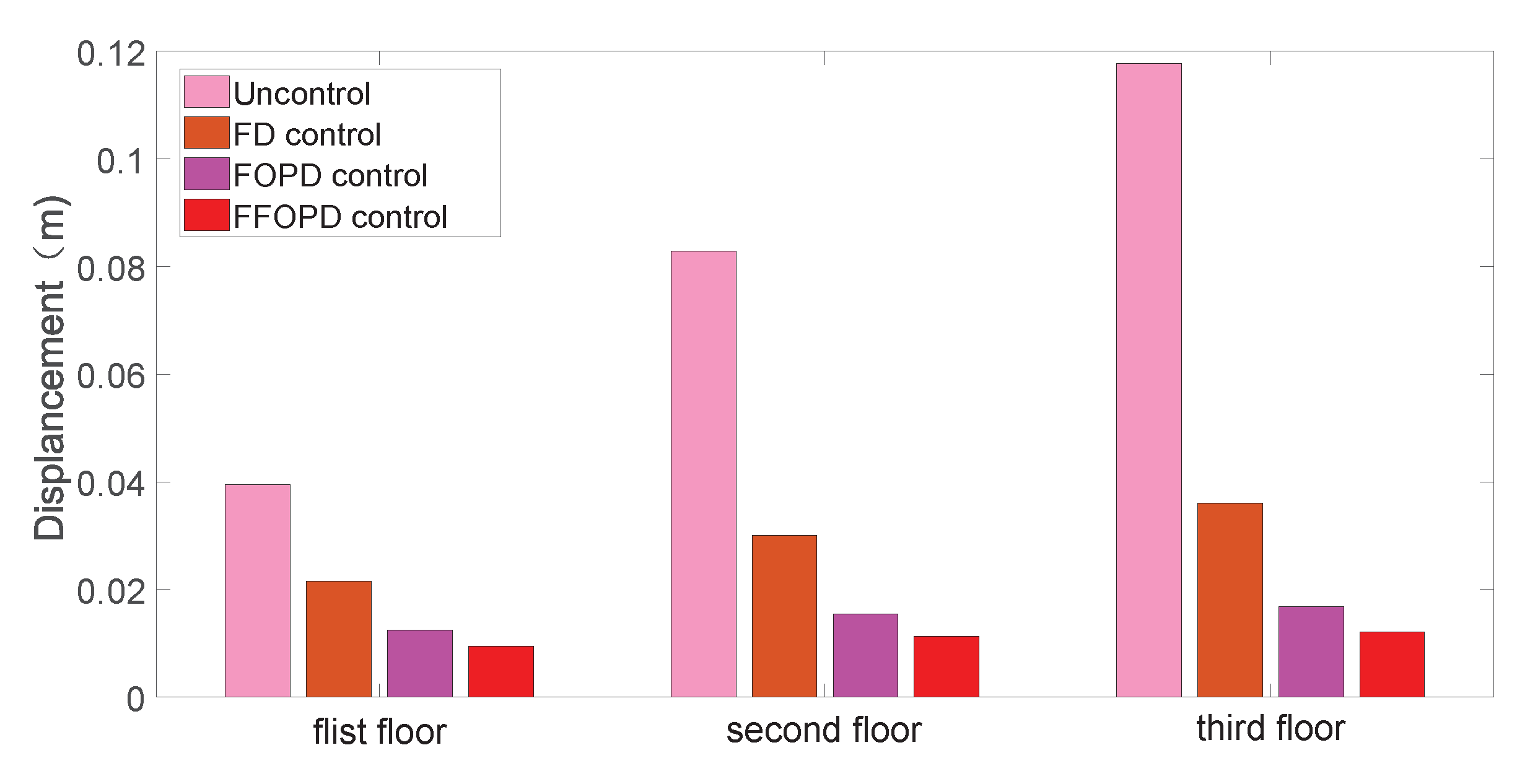
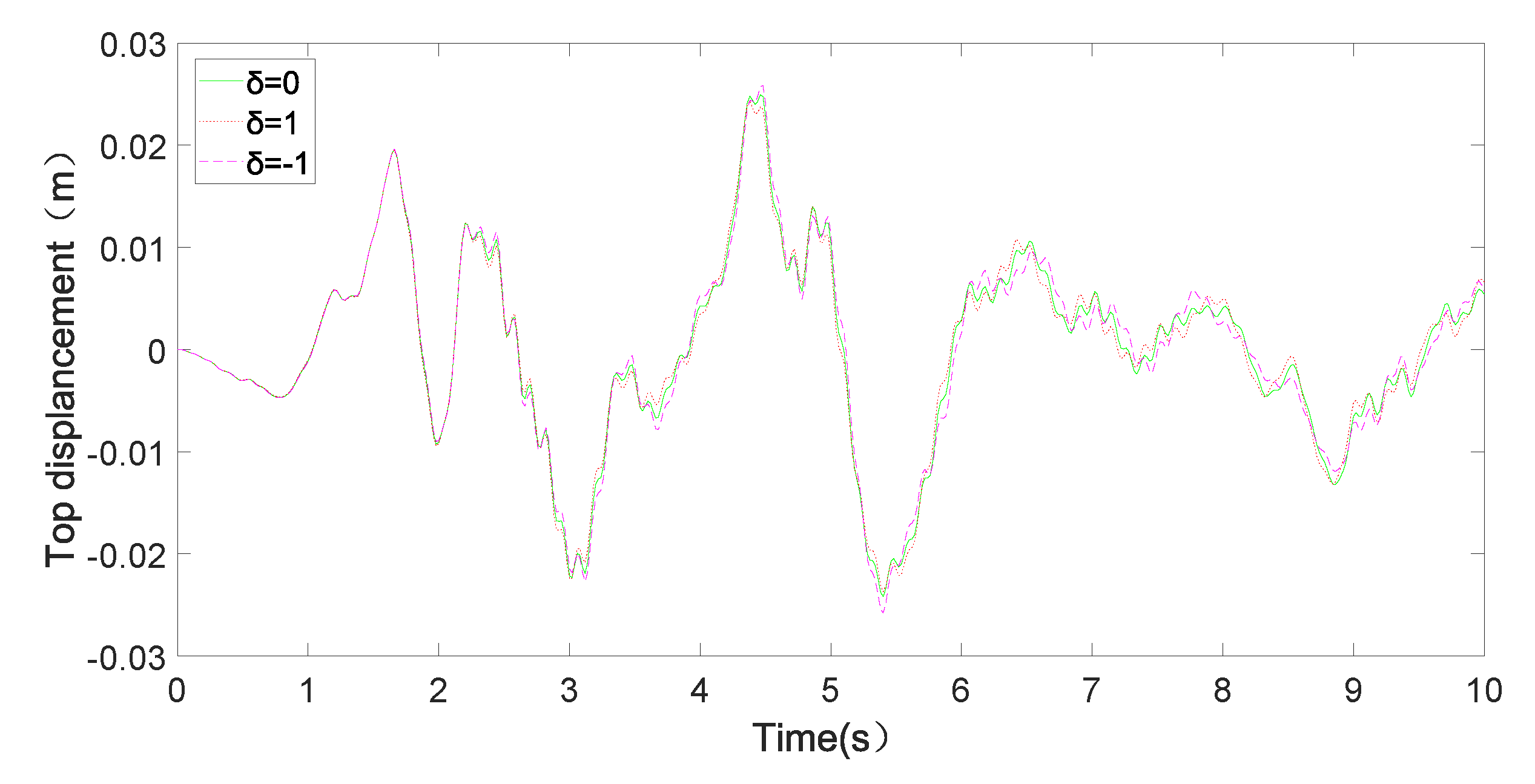
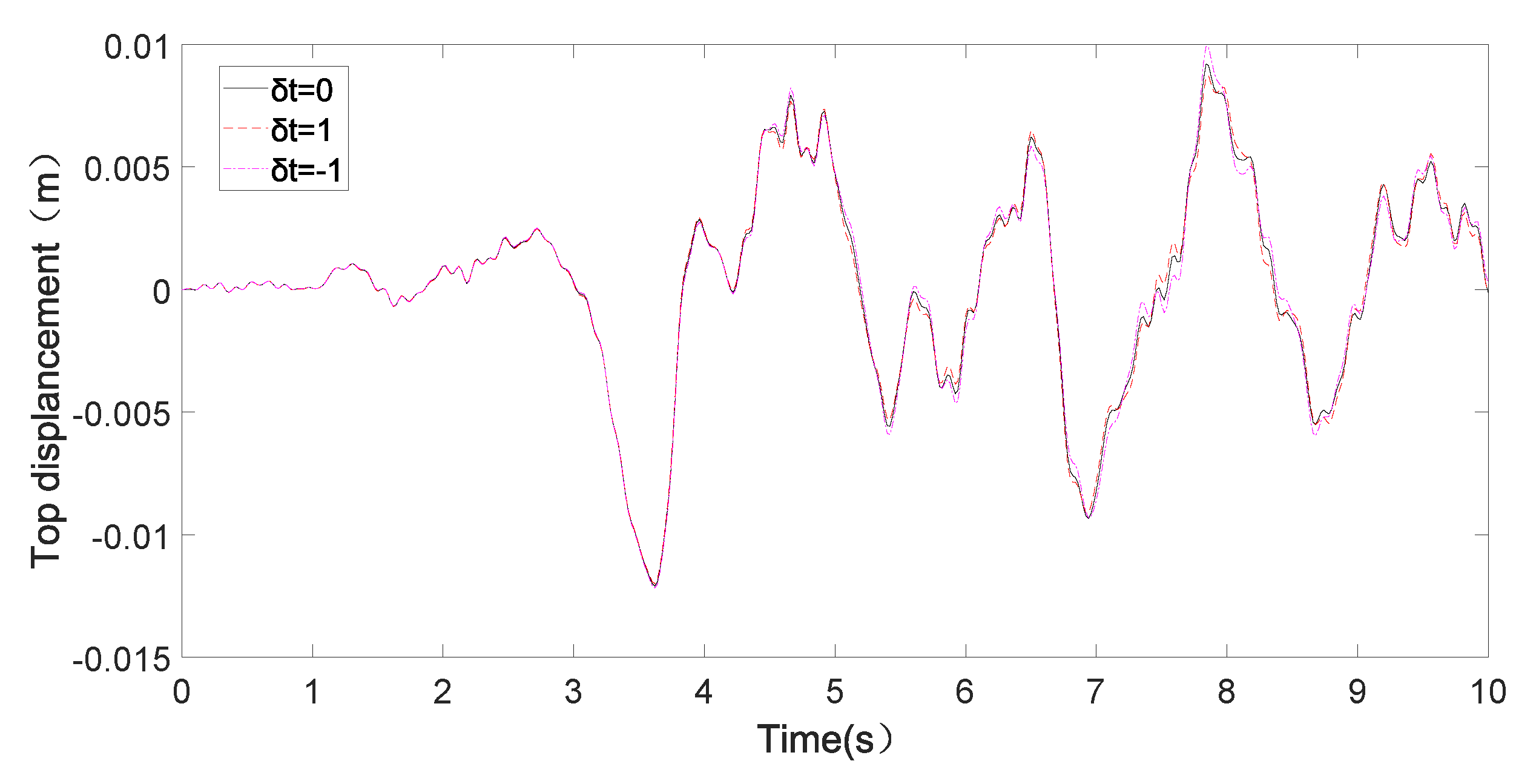
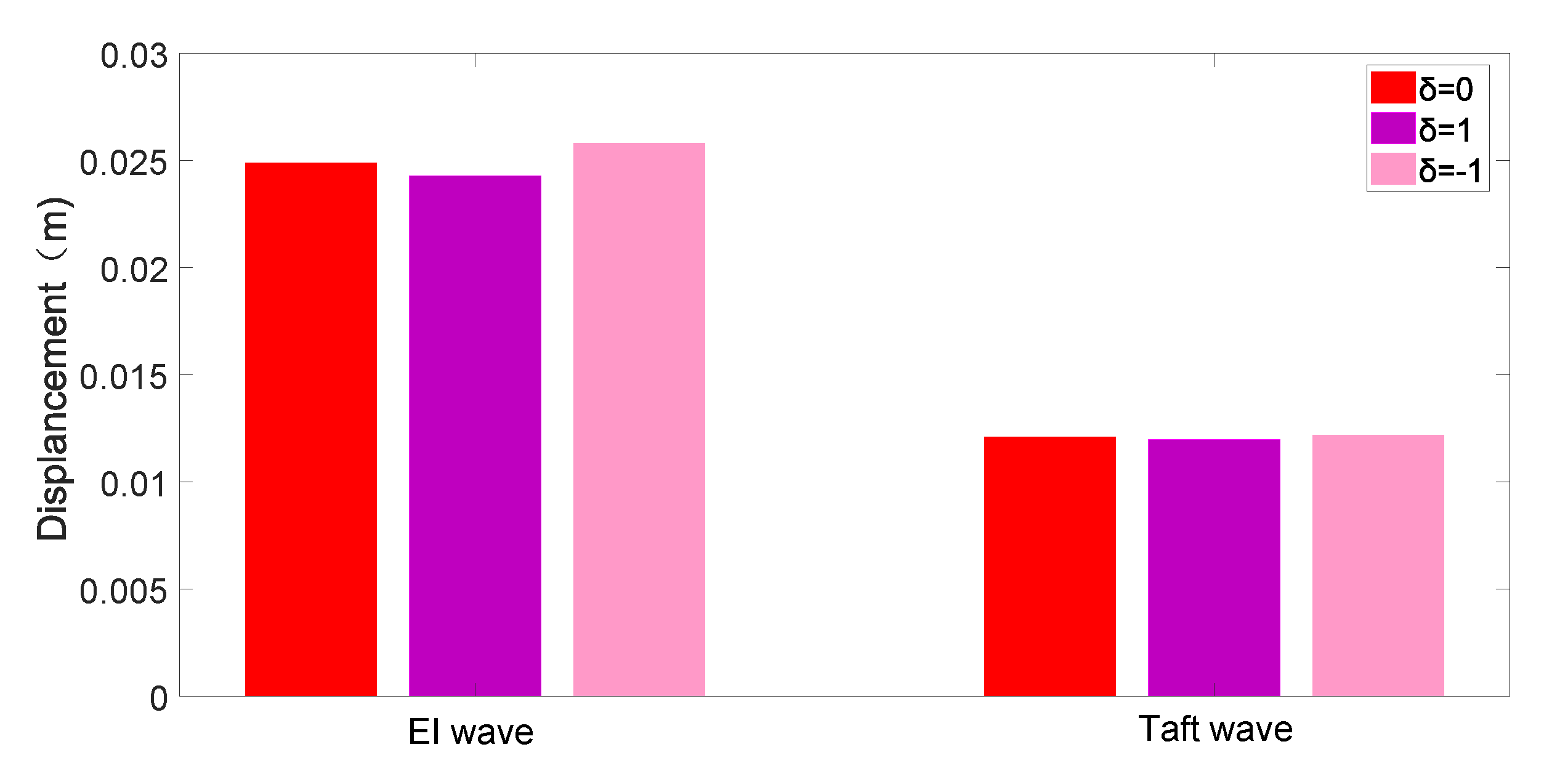
4. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, H.; Liang, H.; Tong, G.; Liu, F.; Liu, Y.; Liu, X.; Jia, Z.; Paul, J. Research on vibration mechanism and control technology of building structure under earthquake action. J. Vibroeng. 2021, 23, 1395–1406. [Google Scholar]
- Huang, J.; Rao, Y.; Qiu, H.; Lei, Y. Generalized algorithms for the identification of seismic ground excitations to building structures based on generalized Kalman filtering under unknown input. Adv. Struct. Eng. 2020, 23, 2163–2173. [Google Scholar] [CrossRef]
- He, Q.; Yin, A.; Fan, Z.; He, L. Seismic responses analysis of multi-story suspended floors system. J. Vibroeng. 2021, 23, 167–182. [Google Scholar] [CrossRef]
- Maruani, J.; Bruant, I.; Pablo, F.; Gallimard, L. Active vibration control of a smart functionally graded piezoelectric material plate using an adaptive fuzzy controller strategy. J. Intell. Mater. Syst. Struct. 2019, 30, 2065–2078. [Google Scholar] [CrossRef]
- Hu, W.; Gao, Y.; Yang, B. Semi-active vibration control of two flexible plates using an innovative joint mechanism. Mech. Syst. Signal Process. 2019, 130, 565–584. [Google Scholar] [CrossRef]
- Yang, X.; Gao, J. Linear–quadratic uncertain differential game with application to resource extraction problem. IEEE Trans. Fuzzy Syst. 2015, 24, 819–826. [Google Scholar] [CrossRef]
- Guo, S.X.; Li, Y. Non-probabilistic reliability method and reliability-based optimal LQR design for vibration control of structures with uncertain-but-bounded parameters. Acta Mech. Sin. 2013, 29, 864–874. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, S.Q.; Wang, Z.X.; Qin, X.S.; Wang, R.X.; Schmidt, R. Disturbance rejection control with H∞ optimized observer for vibration suppression of piezoelectric smart structures. Mech. Ind. 2019, 20, 202. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, X.; Shi, X.; Jin, Y. Variable fractional order sliding mode control for seismic vibration suppression of uncertain building structure. J. Vib. Eng. Technol. 2021, 10, 299–312. [Google Scholar] [CrossRef]
- Kumar, G.; Kumar, A.; Jakka, R.S. The Particle Swarm modified quasi bang-bang controller for seismic vibration control. Ocean. Eng. 2018, 166, 105–116. [Google Scholar] [CrossRef]
- Paul, S.; Yu, W.; Li, X. Bidirectional active control of structures with type-2 fuzzy PD and PID. Int. J. Syst. Sci. 2018, 49, 766–782. [Google Scholar] [CrossRef]
- Zizouni, K.; Fali, L.; Sadek, Y.; Bousserhane, I.K. Neural network control for earthquake structural vibration reduction using MRD. Front. Struct. Civ. Eng. 2019, 13, 1171–1182. [Google Scholar] [CrossRef]
- Ma, T.; Bi, F.; Wang, X.; Tian, C.; Lin, J.; Wang, J.; Pang, G.; Sciubba, E. Optimized fuzzy skyhook control for semi-active vehicle suspension with new inverse model of magnetorheological fluid damper. Energies 2021, 14, 1674. [Google Scholar] [CrossRef]
- Metered, H.; Elsawaf, A.; Vampola, T.; Sika, Z. Vibration control of MR-damped vehicle suspension system using PID controller tuned by particle swarm optimization. SAE Int. J. Passeng. Cars-Mech. Syst. 2015, 8, 426–435. [Google Scholar] [CrossRef]
- Jin, X.; Chen, K.; Zhao, Y.; Ji, J.; Jing, P. Simulation of hydraulic transplanting robot control system based on fuzzy PID controller. Measurement 2020, 164, 108023. [Google Scholar] [CrossRef]
- Ab Talib, M.H.; Mat Darus, I.Z.; Mohd Samin, P.; Mohd Yatim, H.; Ardani, M.I.; Shaharuddin, N.M.R.; Hadi, M.S. Vibration control of semi-active suspension system using PID controller with advanced firefly algorithm and particle swarm optimization. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 1119–1137. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Das, S.; Gupta, A. A novel fractional order fuzzy PID controller and its optimal time domain tuning based on integral performance indices. Eng. Appl. Artif. Intell. 2012, 25, 430–442. [Google Scholar] [CrossRef]
- Etedali, S.; Zamani, A.A.; Tavakoli, S. A GBMO-based PIλDμ controller for vibration mitigation of seismic-excited structures. Autom. Constr. 2018, 87, 1–12. [Google Scholar] [CrossRef]
- Xiao, M.; Tao, B.; Zheng, W.X.; Jiang, G. Fractional-order PID controller synthesis for bifurcation of fractional-order small-world networks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4334–4346. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y. A two-degree-of-freedom controller design satisfying separation principle with fractional-order PD and generalized ESO. IEEE/ASME Trans. Mechatronics 2021, 27, 137–148. [Google Scholar] [CrossRef]
- Tepljakov, A.; Gonzalez, E.A.; Petlenkov, E.; Belikov, J.; Monje, C.A.; Petráš, I. Incorporation of fractional-order dynamics into an existing PI/PID DC motor control loop. ISA Trans. 2016, 60, 262–273. [Google Scholar] [CrossRef] [PubMed]
- Munoz, J.; Monje, C.A.; Santiago, M.; Balaguer, C. Joint position control based on fractional-order PD and PI controllers for the arm of the humanoid robot TEO. Int. J. Humanoid Robot. 2019, 16, 1950042. [Google Scholar] [CrossRef]
- Xu, K.; Chen, L.; Wang, M.; Lopes, A.M.; Tenreiro Machado, J.; Zhai, H. Improved decentralized fractional PD control of structure vibrations. Mathematics 2020, 8, 326. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Pan, G.; Zhang, S. Robust yaw control of autonomous underwater vehicle based on fractional-order PID controller. Ocean. Eng. 2022, 257, 111493. [Google Scholar] [CrossRef]
- Chen, L.; Chen, G.; Wu, R.; Lopes, A.M.; Tenreiro Machado, J.A.; Niu, H. Variable coefficient fractional-order PID controller and its application to a SEPIC device. IET Control Theory Appl. 2020, 14, 900–908. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M.; Kanagaraj, N.; Nisar, K. Fuzzy fractional-order PID controller for fractional model of pneumatic pressure system. Math. Probl. Eng. 2018, 2018, 5478781. [Google Scholar] [CrossRef]
- Swethamarai, P.; Lakshmi, P. Adaptive-fuzzy fractional order PID controller-based active suspension for vibration control. IETE J. Res. 2020, 1–16. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Das, S.; Gupta, A. Improved model reduction and tuning of fractional-order PIλDμ controllers for analytical rule extraction with genetic programming. ISA Trans. 2012, 51, 237–261. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y.; Wang, T.; Zhang, C.; Liu, Y.H. Fuzzy finite-time stable compensation control for a building structural vibration system with actuator failures. Appl. Soft Comput. 2020, 93, 106372. [Google Scholar]
- Li, Z.; Ding, J.; Wu, M.; Lin, J. Discrete fractional order PID controller design for nonlinear systems. Int. J. Syst. Sci. 2021, 52, 3206–3213. [Google Scholar] [CrossRef]
- Lavassani, S.H.H.; Shangapour, S.; Homami, P.; Gharehbaghi, V.; Farsangi, E.N.; Yang, T. An innovative methodology for hybrid vibration control (MR+ TMD) of buildings under seismic excitations. Soil Dyn. Earthq. Eng. 2022, 155, 107175. [Google Scholar] [CrossRef]
- Soleymani, M.; Abolmasoumi, A.H.; Bahrami, H.; Khalatbari-S, A.; Khoshbin, E.; Sayahi, S. Modified sliding mode control of a seismic active mass damper system considering model uncertainties and input time delay. J. Vib. Control 2018, 24, 1051–1064. [Google Scholar] [CrossRef]
- El Ouni, M.H.; Kahla, N.B.; Ahmed, M.; Islam, S.; Ayed, H.; Khedher, K.M. Comparative study of different active control systems of high rise buildings under seismic excitation. Period. Polytech. Civ. Eng. 2019, 63, 1092–1102. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Pires, E.; Machado, J.; Oliveira, P.; Cunha, J.B.; Mendes, L. Particle swarm optimization with fractional-order velocity. Nonlinear Dyn. 2010, 61, 295–301. [Google Scholar] [CrossRef]
- Yang, P.Y.; Chou, F.I.; Tsai, J.T.; Chou, J.H. Adaptive-uniform-experimental-design-based fractional-order particle swarm optimizer with non-linear time-varying evolution. Appl. Sci. 2019, 9, 5537. [Google Scholar] [CrossRef]
- Liu, L.; Pan, F.; Xue, D. Variable-order fuzzy fractional PID controller. ISA Trans. 2015, 55, 227–233. [Google Scholar] [CrossRef]
- Oussama, M.; Abdelghani, C.; Lakhdar, C. Efficiency and robustness of type-2 fractional fuzzy PID design using salps swarm algorithm for a wind turbine control under uncertainty. ISA Trans. 2022, 125, 72–84. [Google Scholar] [CrossRef]





| Range | |
|---|---|
| Name of the Optimization Algorithm | Control System Parameter Value |
| FOPD-PSO | |
| FOPD-FOPSO | |
| FOPD-IFOPSO |
| Floor | 1 | 2 | 3 |
|---|---|---|---|
| Height (m) | 3.2 | 3.0 | 3.0 |
| Quality (kg) | 2762 | 2760 | 2300 |
| Rigidity ( N/m) | 2.485 | 1.921 | 1.522 |
| Name of Various | Parameter Values | ||
| uncertain parameters | |||
| various of | |||
| various of |
| Variables of Fuzzy Algorithm | Fuzzy Logic Parameter Value |
|---|---|
| Fuzzy domain variables (input) | |
| Fuzzy domain variables (output) | ; |
| ; ; | |
| Input quantization factors | ; |
| Output proportion factors |
| ec | |||||||
|---|---|---|---|---|---|---|---|
| e | NB | NM | NS | Z | PS | PM | PB |
| NB | PB/PS | PB/NS | PM/NB | PM/NB | PS/NB | Z/NM | Z/PS |
| NM | PB/PS | PB/NS | PM/NB | PS/NM | PS/NM | Z/NS | NS/Z |
| NS | PM/Z | PM/PS | PM/PM | PS/PM | Z/PS | NS/PS | NS/Z |
| Z | PM/Z | PM/NS | PS/NS | Z/NS | NS/NS | NM/NS | NM/Z |
| PS | PS/Z | PS/Z | Z/Z | NS/Z | NS/Z | NM/Z | NM/Z |
| PM | PS/PB | Z/PS | NS/PS | NM/PS | NM/PS | NM/PS | NB/PB |
| PB | Z/PB | Z/PM | NM/PM | NM/PM | NM/PS | NB/PS | NB/PB |
| ec | |||||||
|---|---|---|---|---|---|---|---|
| e | NB | NM | NS | Z | PS | PM | PB |
| NB | NS | PS | PB | PB | PB | PM | NS |
| NM | PS | PS | PB | PM | PM | PS | Z |
| NS | Z | NS | NM | NM | NS | NS | Z |
| Z | Z | PS | PS | PS | PS | PS | Z |
| PS | Z | Z | Z | Z | Z | Z | Z |
| PM | NB | NS | NS | NS | NS | NS | NM |
| PB | NB | NM | NM | NM | NS | NS | NB |
| Name of the IFOPSO Parameters | Value of the Parameters |
|---|---|
| Particle number | |
| Number of iterations/Repeated experiments | |
| Scaling factors | |
| Range | |
| Name of the Control System | Control System Parameter Value |
| PD | |
| FOPD | |
| FFOPD |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Cheng, T.; Lopes, A.M.; Chen, L.; Zhu, X.; Wang, M. Fuzzy Fractional-Order PD Vibration Control of Uncertain Building Structures. Fractal Fract. 2022, 6, 473. https://doi.org/10.3390/fractalfract6090473
Xu K, Cheng T, Lopes AM, Chen L, Zhu X, Wang M. Fuzzy Fractional-Order PD Vibration Control of Uncertain Building Structures. Fractal and Fractional. 2022; 6(9):473. https://doi.org/10.3390/fractalfract6090473
Chicago/Turabian StyleXu, Kang, Tingli Cheng, António M. Lopes, Liping Chen, Xiaoxuan Zhu, and Minwu Wang. 2022. "Fuzzy Fractional-Order PD Vibration Control of Uncertain Building Structures" Fractal and Fractional 6, no. 9: 473. https://doi.org/10.3390/fractalfract6090473
APA StyleXu, K., Cheng, T., Lopes, A. M., Chen, L., Zhu, X., & Wang, M. (2022). Fuzzy Fractional-Order PD Vibration Control of Uncertain Building Structures. Fractal and Fractional, 6(9), 473. https://doi.org/10.3390/fractalfract6090473








