Abstract
This brief investigates the Mittag–Leffler formation bounded control problem for second-order fractional multi-agent systems (FMASs), where the dynamical nodes of followers are modeled to satisfy quadratic (QUAD) condition. Firstly, under the undirected communication topology, for the considered second-order nonlinear FMASs, a distributed event-triggered control scheme (ETCS) is designed to realize the global Mittag–Leffler bounded formation control goal. Secondly, by introducing adaptive weights into triggering condition and control protocol, an adaptive event-triggered formation protocol is presented to achieve the global Mittag–Leffler bounded formation. Thirdly, a five-step algorithm is provided to describe protocol execution steps. Finally, two simulation examples are given to verify the effectiveness of the proposed schemes.
1. Introduction
In the past few decades, there has been increasingly attention for the cooperative control of multi-agent systems (MASs) from various application fields, such as social sciences, artificial intelligence, and military, and so on [1,2,3,4,5,6]. As an important component of cooperative control, the formation control, which aims to motivate agents to achieve a predefined configuration under the designed control protocols, has been widely applied in many practical fields, for example, unmanned aerial vehicle [7], multi-robot systems [8], and biological system [9].
Recently, a lot of scholars have paid their attention to the formation control of multi-agent systems (MASs), and some significant works have been reported. Such as in [10], a neuro-adaptive formation scheme for nonlinear MASs with time-delay was designed to realize target tracking. In [11], under the directed communication graphs, by equipping the event-triggered approach and applying complex Laplace transform, a distributed control scheme was presented to achieve the time-invariant formation control (TIFC) for networked MASs. In [12], the authors developed the design method of the TIFC protocol for second-order MASs based on sampled data on a fixed directed communication topology. In [13], the formation-containment target was achieved for general linear MASs under a discontinuous protocol, where the dynamics of leader is influenced by unknown input. In [14], by applying an adaptive output–feedback approach, Wang investigated the time-variant formation control (TVFC) of nonlinear MASs with switching networks. In [15], by using a sliding mode method, under the influence of random disturbances, a novel ETCS was proposed to analyze the stability of error system for second-order MASs.
It is worth noting that, in the above mentioned literature [10,11,12,13,14,15], the obtained results focus on the integer-order MASs. However, in practical applications, such as engineering, manufacturing, aerospace, and artificial intelligence, the fractional systems can give a more accurate description for various processes with the characterization of hereditary and memory properties [16], and many results have been derived [17,18,19,20,21,22]. Recently, some achievements have emerged in regard to the formation control of fractional-order MASs. For example, in [23], by applying a frequency-domain analytical method, the formation problem was studied for double-integrator FMASs. Liu et al. in [24] designed an active reconfigurable control scheme to address the distributed formation tracking control problem for MASs with multiple leaders under actuator faults and constraints. In [25], Gong proposed an observer-based protocol to address the TVFC problem for FMASs with general linear dynamics, where the topology structure is selected as fixed and switched, respectively. In [26], by using the sliding mode strategy, a distributed feedback control scheme was designed to solve the problems of consensus and formation for FMASs.
On the one hand, in most traditional formation control strategies, such as a sliding mode scheme, impulsive strategy, and periodic sampling scheme, agents are always assumed to obtain continuous information from their neighbors, and information transmission occurs in either continuous or cyclical time. However, in practical applications, continuous exchange of information cannot be guaranteed because of the limitations of communication bandwidth and energy supply, which brings a lot of inconvenience. In addition, the continual monitoring of information might result in an enormous energy and financial waste. Therefore, researchers proposed an event-triggered control strategy (ETCS). Under this control mechanism, information communication proceeds after a predetermined event occurred, which can guarantee the expected performance and reduce communication costs. Based on the above advantages, ETCS have been widely used in the study of MASs in [27,28,29,30,31]. In [28], the authors applied stability theory of FMASs and developed a differential inequality convex function to address the consensus problem for discontinuous singularly perturbed MASs based on ETCS. In [29], under interplay between control gains and parameters, by employing the discrete-time signals from neighbors and co-design approach, two novel ETCS were presented to investigate the consensus issue of general MASs with linear growth. In [31], under the periodic DoS attacks, the problem of MASs formation was discussed via novel attack-resilient ETCS, and the generalized Nyquist stability criterion was used to analyze the error systems.
It should be pointed out that, in literature [28,29,31], the design of control protocols is related to some global or unknown knowledge, such as the Laplacian matrix eigenvalue information, and the knowledge of the unknown nonlinear dynamics. To overcome this drawback, the distributed adaptive updating law is proposed. Recently, some scholars have combined the advantages of ETCS and adaptive control to design the adaptive event-triggered control. In addition, some admirable results were obtained [32,33,34,35]. For example, in [34], the TVFC issue of linear MASs was considered under the proposed adaptive ETCS with adjustable time-variant parameters. In [35], the authors developed an adaptive ETCS and a novel Lyapunov function to handle the asymptotic tracking problem for uncertain nonlinear systems with unknown virtual control coefficients.
It should be pointed out that most of works in [27,28,29,30,31,32,33,34,35] are concerned with the formation control of first-order integer system, which can not accurately characterize some complex dynamic behaviors in practical application. To the best of our knowledge, a few results are concerned with the formation control problem of second-order FMASs. Particularly, the distributed event-triggered control protocol and adaptive event-triggered mechanism are adopted to address the formation problem of second-order FMASs.
Motivated by the above discussion, in this paper, our objective is to address the global Mittag–Leffler bounded formation control issue for second-order FMASs with QUAD inherent dynamics under the designed event-triggered and adaptive event-triggered control mechanisms. Compared with the previous results, the significant innovations are demonstrated as follows:
- This paper extends the formation control problem for MASs to the case of fractional order. In the existing works [36,37], the results mainly focus on the integer order MASs, which can be regarded as special cases of this paper. Therefore, the results in this paper are more general.
- The system model is modeled to second-order MASs, which is not only related to position information but also to velocity information. Compared with literature [34,38], where the system model only considers position information, the established system model is more realistic.
- An adaptive event-triggered control protocol is developed, where the global information of Laplacian matrix is not required. Different from the proposed state-dependent triggering conditions in [27,28,29,30,31], a constant is introduced into triggering conditions in this paper to address the formation control issue and avoid the occurrence of Zeno behavior.
The remainder of this brief is organized as follows: in Section 2, some preliminary knowledge and the problem formulation are introduced. The main results are proposed in Section 3. The executive flow algorithm in regard to protocol is presented in Section 4. Two numerical simulations are given in Section 5. Finally, the conclusions are listed in Section 6.
Notation: see Table 1.

Table 1.
Notations.
2. Preliminaries and Problem Formulation
2.1. Basic Graph Theory
The topology between follower agents and can be described by an undirected graph g , where denotes the set of N followers in g; intends the set of edge in g, where edge shows the information communication between and ; is the weighted adjacency matrix of g. For an undirected graph, the elements of adjacency satisfy that if and only if , and , otherwise. Moreover, we suppose there is no self-loops, i.e., in g for all . The adjacency matrix for the leader is defined , represents connected weight between the leader and the follower i. The neighbor set of is denoted . The in-degree of is defined as . The Laplacian matrix corresponding to g is , where . There is a path from to if there exists a finite ordered edge belongs to the edge set such that holds. If there exists at least a path between any two nodes, the undirected graph is said to be connected. In this paper, the graph g is assumed undirected.
Lemma 1
([39]). For any , and , the following inequality holds:
Lemma 2
([28]). Let , , and . The following inequalities hold:
Definition 1
([40]). (QUAD condition) The function is QUAD, if for any and , there exists , , and such that
2.2. Fractional Calculus
Definition 2
([16]). For an integrable function , the Riemann–Liouville fractional integral of order is defined by:
where is Gamma function.
Definition 3
([16]). The Caputo’s fractional derivative of order for is defined by
where and . Particularly,
In the following, represents .
Property 1.
Let , and be any constants. Then,
| ; . |
Lemma 3
([39]). Let be a continuously differentiable function, and , then
Lemma 4
([39]). If functions , are continuously differentiable, and φ is convex on R. Then, for any , we obtain
Lemma 5
([17]). Let be a continuously differentiable function on , , and . If, for any , holds, then
where is constant, C is defined as in [28], and is the Mittag–Leffler function, , is constant, and z is a complex variable.
Definition 4.
Let , if there exist constants , , and >0, such that
then is said to be Mittag–Leffler convergent to .
Lemma 6.
Let . If is continuously differentiable on any compact interval of , is C-regular and . If there exist constants , , and , for any satisfying
then is said to be Mittag–Leffler convergent to , where .
| , |
Proof.
On the basis of condition (ii) and Lemma 6, it yields that
Combined with condition (i) and the above-mentioned inequality, we obtain
Applying Lemma 2, we have
where . Definition 4 shows is Mittag–Leffler convergent to . The proof is completed. □
2.3. Problem Formulation
Consider the MASs consisting of one leader and N followers. The dynamics of each follower i can be described by the following second-order differential equations:
where , for , and denote the position and velocity of ith-follow at time t, respectively; represents the control input; the nonlinear mapping : depicts the inherent dynamics of follower i.
The dynamics of the leader is formulated as
where and are the position and velocity of ith-leader at time t; : depicts the inherent dynamics of leader.
In order to obtain the main results, we made the assumptions as follows:
Assumption A1.
The undirected network topology of g is connected.
Assumption A2.
is QUAD.
For systems (1) and (2), a desired geometric formation tracking vector is specified by . To achieve the desired formation between follows and leader, define error state as , where ; furthermore, we obtain
where , and , .
Definition 5.
Given a desired geometric formation, . Under control protocol , if for ,
holds, then systems (1) and (2) are said to realize the desired formation.
Remark 1.
In Definition 5, stands for the relative offset vector between and , if , then systems (1) and (2) are said to realize the consensus tracking.
Definition 6.
Under control protocol , , if there exist constants and , such that
then systems (1) and (2) are called to realize the global Mittag–Leffler bounded formation.
3. Main Results
In this section, we presented two distributed protocols based on event-triggered mechanism to achieve desired formation. In addition, Zeno behavior is excluded for designed event-triggered control scheme. Moreover, the executive algorithm in regard to protocol is proposed.
Denote a triggering instants sequence of agent i as , which is determined by the triggering function. Let state information , where . Denote , and .
Denote the state measurement errors of follower and leader, respectively,
Furthermore, we denote
3.1. Global Mittag–Leffler Formation with Event-Triggered Protocol
In this subsection, the global Mittag–Leffler bounded formation of systems (1) and (2) is discussed under the proposed control protocol based on predefined ETCS, and the formation condition is derived in terms of linear matrix inequalities (LMIs). In addition, Zeno behavior is excluded.
The distributed ETCS for agent is designed as
where is the feedback gain matrices to be determined later, and the triggering instant sequence of the agent will be determined by the following event-triggered condition
where is a threshold parameter, and . Figure 1 shows a schematic of the designed ETCS protocol.
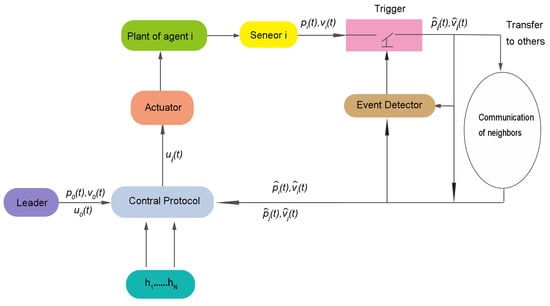
Figure 1.
Schematic of ETCSl.
Using (4)–(6), we obtain
Set . Furthermore, the error system (7) can be written as
Theorem 1.
Suppose that Assumptions 1 and 2 hold, and . If there exist scalars , and , matrices , and , such that
holds, then FMASs (1) and (2) can realize the global Mittag–Leffler bounded formation under designed protocol (5) with (6).
Proof.
Consider the following candidate Lyapunov function:
For , according to Lemma 3, the Caputo’s fractional derivative of along of the trajectories of error system (8) is calculated as
According to the Assumption 2 that is QUAD, we obtain
By Lemma 1, we obtain
Substituting (6), and (10) to (13), it yields that
where , and . By utilizing Lemma 6, it can derive
where . According to Definition 6, it shows that the global Mittag–Leffler bounded formation of FMASs (1) and (2) is realized. The proof is completed. □
As is known to all, “Zeno behavior” means that the limitless number of event-triggering times is proceeded in finite time, it causes the ETCS protocol to be invalid. Consequently, the following theorem is to verify that the intervals between any two event-triggering instants are lower-bound.
Theorem 2.
For FMASs (1) and (2), under the scheme (5), the Zeno behavior can be excluded.
Proof.
According to Theorem 1, we can obtain that is bounded. Hence, for , there is a positive scalar , such that . Because of , and , we have and . Thus, we also derive
In line with event-triggered condition (6), when , it is easy to derive that . Furthermore, it follows from (15) that . If , then . If , then . Therefore, we can draw the conclusion that Zeno behavior is excluded. The proof is completed. □
3.2. Global Mittag–Leffler Bounded Formation with Adaptive Event-Triggered Protocol
In this subsection, the global Mittag–Leffler bounded formation is discussed under an adaptive protocol based on ETCS. In addition, Zeno behavior is excluded.
We consider the following adaptive ETCS formation protocol:
where and are the feedback gain matrices, are the adaptive coupling weights with , are positives satisfying that .
The triggering instant sequence of the agent will be determined iteratively by the following trigger function
where . The triggering function in triggering mechanisms (17) is designed as , thereinto , and
Remark 2.
It is worth noting that, if the adaptive coupling weight and in (16) and (17) are constants, then determination of these scalar gains requires global information of the Laplacian matrix. Hence, in this paper, and are introduced, which are adaptive rather than being prefixed.
For the follower, substituting the control protocol (17) into the error system (3), it yields that
Theorem 3.
Suppose that Assumptions 1 and 2 hold, and . If there exist scalars , , and , matrices , , and , such that
holds, then FMASs (1) and (2) can realize the global Mittag–Leffler bounded formation under designed adaptive protocol (16) with ETCS (17).
Proof.
Consider the following candidate Lyapunov function:
For , by employing Lemmas 3 and 4, the Caputo’s fractional derivative of is listed as
It follows from (23) that
where . Based on (16), it can be derived that
In addition, by use of (16), we also obtain
Based on Lemma 1, it yields that
Form (12), we have
Based on the above calculations, we obtain
In light of Lemma 1, we can obtain
According to expression (4), we have
It is easy to obtain
Substituting (24) and (25) into (23), we can derive
where , , . Apply Lemma 5, we can obtain
where . According to Definition 6, it implies that FMASs (1) and (2) can achieve the Mittag–Leffler bounded formation under designed control protocol (16) with the ETCS (17). The proof is completed. □
Theorem 4.
For FMASs (1) and (2), under the control scheme (16), Zeno behavior is avoided.
Proof.
According to Theorem 3, we obtain that is bounded. Hence, for , there has positive scalar , such that , which utilizes the fact that . According to Definition 2, we can obtain .
In light of the the triggering function in triggering mechanisms (17), when , we have
In addition,
Because the adaptive coupling weight and will have convergent constants, then and are constants. Let and . Furthermore, combining with
and (3.24), we have . Hence, it yields that . This implies that Zeno behavior is excluded in Theorem 3. The proof is completed. □
Remark 3.
In the designed control protocol (5), the control gain and triggering condition parameter are required to satisfy condition (9). Because the term may be negative, then does not need to be large. In the designed control protocol (5), the control gains and Λ are applied to satisfy inequality condition in Theorem 3. It should be pointed out that adaptive ETCS means that coupling weight is adaptively adjusted with error state . The gain is still determined from precisely known agent dynamics, which is not adaptive.
Remark 4.
In the existing works [27,28,29,30,31], the triggering function is designed as state-dependent that is . It is worth noting that this may lead to some limitations, such as the requirement on continuous communication and occurrence of Zeno behavior. To circumvent this drawback, some scholars proposed a state-independent triggering function [41], i.e., . However, the triggering function does not include the information from the system states, which would lead to the change of the system performance. For the design of the distributed event-triggered scheme, how to avoid Zeno behavior while ensuring control performance is a challenge. In this paper, constants and are introduced into triggering conditions (6) and (17) to address this problem, respectively.
4. Process of the Event-Triggered Scheme
In this section, we present the workflow description of the ETCS executive process.
| Event-triggered protocol execution: |
| Step 1: For , choose the desired information of formation . |
| Step 2: if , apply the state information of leader and . |
| Step 3: if function , share its state information of position |
| and velocity , moreover including triggered instant . |
| Step 4: update state information , and control input signal. |
| Step 5: if updated state information and are received from their neighbors, |
| then update the state information , and control input signal. |
5. Numerical Simulations
In this section, to validate the correctness of the proposed results, two simulation examples are given. The efficiency of distributed event-triggered protocol and adaptive event-triggered scheme is illustrated in Examples 1 and 2, respectively.
Example 1.
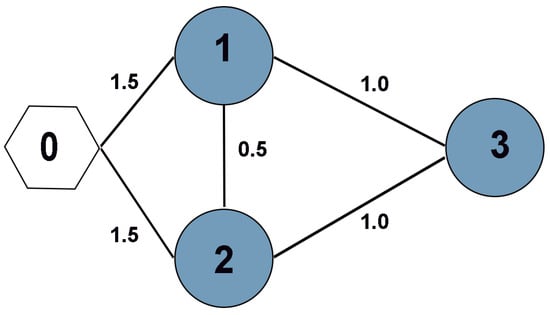
The second-order FMASs with QUAD inherent dynamics is employed to simulate a traffic scenario in the rough sand, which consists of three followers labeled 1–3 and a leader labeled 0. Suppose that each agent denotes a robot, where leader is called as a guidance robot. Our objective is that multiple autonomous robots finally shape a formation pattern of a triangle. Figure 2 shows the corresponding topologly structure.

Figure 2.
Interaction topology between agents.
Moreover, let and are the position error and velocity error between leader and followers i.
According to Figure 2, the weighted adjacency matrix of this system is:
The weight of communication between leaders and followers , and parameter .
Select the dynamic function , it is easy to check that Assumption 2 holds. Let scalars , , , , , , and . Set the predesigned formation compensation vector as:
For protocol (5), select the control gain matrix
According to inequality (9), the following matrixes are derived:
The triggering interval of the three followers under the triggering function (6) is shown in Figure 3; it can be seen that there is no Zeno behavior occurs. The trajectories of control input are shown in Figure 4. Figure 5 shows the formation tracking errors of and within 6 s. From Figure 5, it can be found that errors and asymptotically approach 0. Figure 6 shows the formation of leader and followers at different times, and they finally perform and maintain an obtuse triangle formation. Thus, it can be verified that, under the event-triggered strategy (6), the control protocol (5) for the shape of the desired formation is effective.
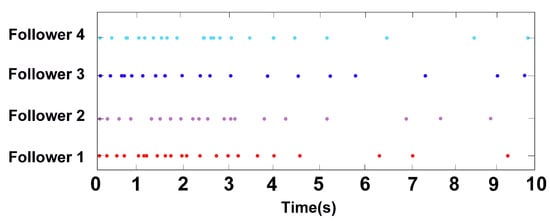
Figure 3.
The triggered instants of all followers in Example 1.
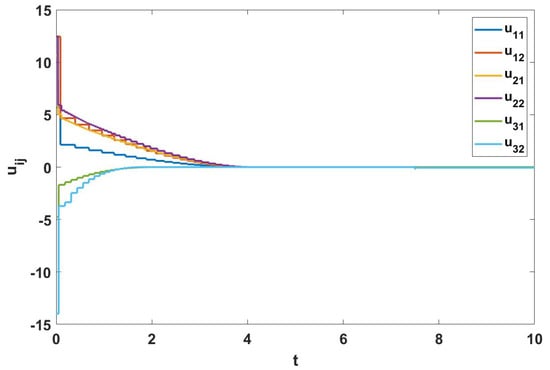
Figure 4.
The trajectories of control input in Example 1.
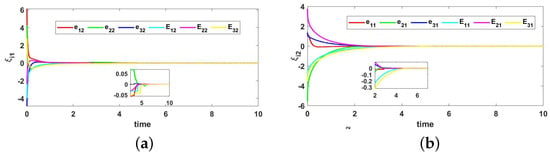
Figure 5.
Formation tracking errors in Example 1. (a) formation tracking errors of ; (b) formation tracking errors of .
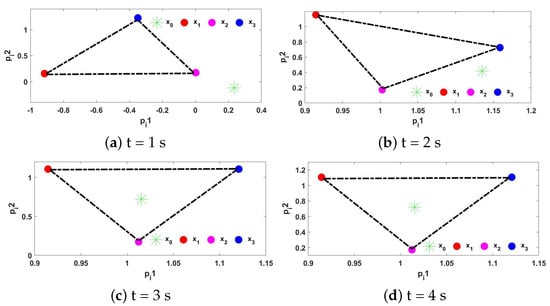
Figure 6.
States trajectory snapshots of agents at different times.
Example 2.
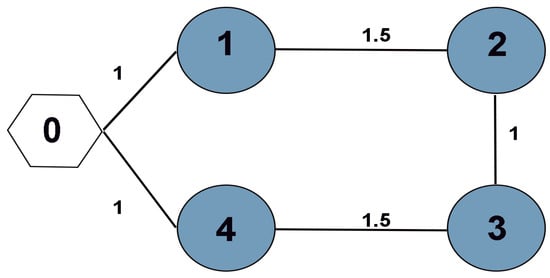
Consider a second-order FMASs with QUAD inherent dynamics, which consists of 4 followers labeled 1–4 and a leader labeled 0. Figure 7 shows the corresponding topology. Moreover, let and are the position error and velocity error between leader and followers i.

Figure 7.
Interaction topology between agents.
According to Figure 6, the weighted adjacency matrix of this system is
The weight of communication between leaders and followers , and parameter . Select the dynamic function , it is easy to check that Assumption 2 holds. Let scalars , , and . Set the predesigned formation compensation vector as:
For protocol (16), select the control gain matrixes
According to inequality condition, the following matrixes are derived:
The triggering interval of the four followers under the triggering function (17) is shown in Figure 8, it can be seen that there is no Zeno behavior occurs. Figure 9 describes the trajectories of control input (16), and the trajectories of adaptive coupling weight are displayed in Figure 10. From Figure 10, we can find that the adaptive coupling weight is convergent to constant. Figure 11 shows the formation tracking errors of and within 8 s, and we find errors and asymptotically approach 0. Figure 12 shows the formation of leader and followers at different times, and they perform and maintain a rectangle formation finally. Thus, it can be verified that, under the ETCS (17), the control protocol (16) for the shape of the desired formation is efficient.
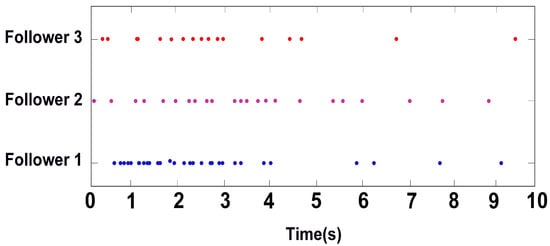
Figure 8.
The triggered instants of all followers in Example 2.
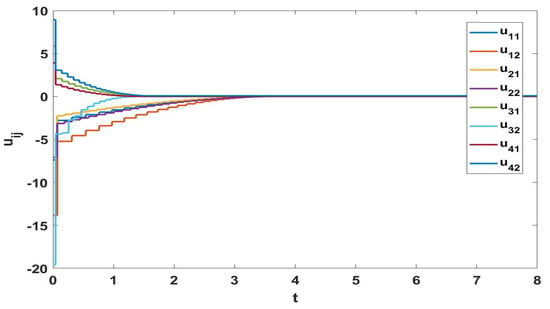
Figure 9.
The trajectories of control input in Example 1.
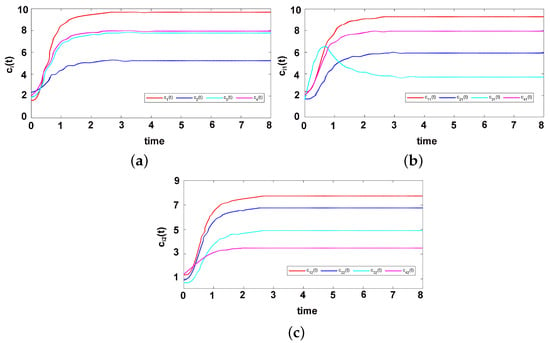
Figure 10.
Formation tracking errors in Example 2. (a) formation tracking errors of ; (b) formation tracking errors of ; (c) formation tracking errors of .
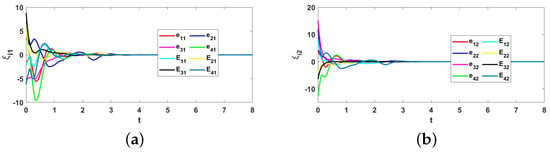
Figure 11.
Formation tracking errors in Example 2. (a) formation tracking errors of ; (b) formation tracking errors of .
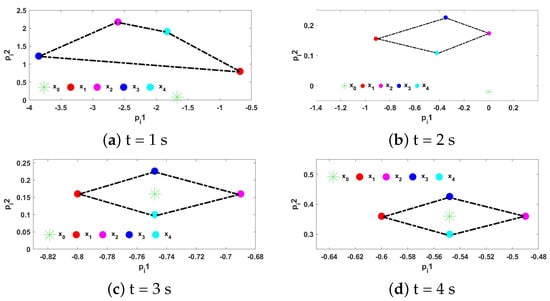
Figure 12.
States trajectory snapshots of agents at different times.
6. Conclusions
This paper has disscussed the global Mittag–Leffler formation for FMASs with QUAD inherent dynamics. Two distributed control schemes based on event-triggered strategies have been proposed by utilizing local information from the neighbors. The global Mittag–Leffler (bounded) formation conditions have been obtained in the form of LMIs. Future research interests is to focus on the time-varying formation in finite/fixed time for FMASs.
Author Contributions
Conceptualization, Y.W. and H.W.; methodology, Y.W.; software, J.Z.; validation, Y.W., J.Z. and H.W.; formal analysis, H.W.; investigation, Y.W.; resources, H.W.; data curation, Y.W.; writing—original draft preparation, J.Z.; writing—review and editing, J.Z.; visualization, Y.W.; supervision, H.W.; project administration, H.W.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of China (No. 12171416).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Editors and Reviewers for their insightful and constructive comments, which help to enrich the content and improve the presentation of the results in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dusit, N.; Wang, P.; Walid, S.; Are, H. Controlled coalitional games for cooperative mobile social networks. IEEE Trans. Veh. Technol. 2011, 60, 1812–1824. [Google Scholar]
- Chen, X.; Gong, X.; Yang, L.; Zhang, J. Exploiting social tie structure for cooperative wireless networking: A social group utility maximization framework. IEEE-ACM Trans. Netw. 2016, 24, 3593–3606. [Google Scholar] [CrossRef]
- Wang, X.; Vivek, Y.; Balakrishnan, S. Cooperative UAV formation flying with obstacle/collision avoidance. IEEE Trans. Control Syst. Technol. 2007, 15, 672–679. [Google Scholar] [CrossRef]
- Hamed, R.; Farzaneh, A. A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots. IEEE Trans. Ind. Electron. 2014, 61, 347–354. [Google Scholar]
- Zhang, Z.; Wu, H. Cluster synchronization in finite/fixed time for semi-Markovian switching T-S fuzzy complex dynamical networks with discontinuous dynamic nodes. AIMS Math. 2022, 7, 11942–11971. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, S.; Luo, D.; You, Y. Affine formation maneuver control of high-order multi-agent systems over directed networks. Automatica 2020, 118, 109004. [Google Scholar] [CrossRef]
- Wei, L.; Chen, M.; Li, T. Dynamic event-triggered cooperative formation control for UAVs subject to time-varying disturbances. IET Control Theory Appl. 2020, 14, 2514–2525. [Google Scholar] [CrossRef]
- Zong, C.; Ji, Z.; Tian, L.; Zhang, Y. Distributed multi-robot formation control based on bipartite consensus with time-varying delays. IEEE Access 2019, 7, 144790–144798. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Q.; Yang, X.; Yang, L. Passivity and optimal control of descriptor biological complex systems. IEEE Trans. Autom. Control 2008, 53, 122–125. [Google Scholar] [CrossRef]
- Kiarash, A.; Selmic, R. Neuro-Adaptive formation control and target tracking for nonlinear multi-agent systems with time-delay. IEEE Control Syst. Lett. 2021, 5, 791–796. [Google Scholar]
- Mojtaba, R.; Beheshti, M.; Sadegh, B. Event-Based Formation Control of Networked Multi-Agent Systems Using Complex Laplacian Under Directed Topology. IEEE Control Syst. Lett. 2021, 5, 1085–1090. [Google Scholar]
- Liu, C.; Wu, X.; Mao, B. Formation tracking of second-order multi-agent systems with multiple leaders based on sampled data. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 68, 331–335. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Han, L.; Li, Q.; Ren, Z. Formation-containment tracking for general linear multi-agent systems with a tracking-leader of unknown control input. Syst. Control Lett. 2018, 122, 67–76. [Google Scholar] [CrossRef]
- Wang, R. Adaptive output-feedback time-varying formation tracking control for multi-agent systems with switching directed networks. J. Frankl. Inst.-Eng. Appl. Math. 2020, 357, 551–568. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Xu, Y.; Yang, D. Time-Varying formation for high-order multi-agent systems with external disturbances by event-triggered integral sliding mode control. Appl. Math. Comput. 2019, 359, 333–343. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Bai, J.; Wu, H.; Cao, J. Secure synchronization and identification for fractional complex networks with multiple weight couplings under DoS attacks. Comput. Appl. Math. 2022, 41, 187. [Google Scholar] [CrossRef]
- Nehad, A.S.; Abderrahim, W.; Rasool, S.; Se-Jin, Y.; Bashir, S.; Yasir, M.; Kashif, H. Effects of fractional derivative and heat source/sink on MHD free convection flow of nanofluids in a vertical cylinder: A generalized Fourier’s law model. Case Stud. Therm. Eng. 2021, 28, 101518. [Google Scholar]
- Nehad, A.S.; Abderrahim, W.; Essam, R.E.; Thirupathi, T.; Se-Jin, Y. Heat transfers thermodynamic activity of a secondgrade ternary nanofluid flow over a vertical plate with Atangana-Baleanu time-fractional integral. Alex. Eng. J. 2022, 6, 10045–10053. [Google Scholar]
- Gong, P. Exponential bipartite consensus of fractional-order nonlinear multi-agent systems in switching directed signed networks. IET Control Theory Appl. 2020, 14, 2582–2591. [Google Scholar] [CrossRef]
- Li, R.; Wu, H.; Cao, J. Impulsive exponential synchronization of fractional-order complex dynamical networks with derivative couplings via feedback control based on discrete time state observations. Acta Math. Sci. 2022, 42B, 737–754. [Google Scholar] [CrossRef]
- Wang, X.; Wu, H.; Cao, J. Global leader-following consensus in finite time for fractional-order multi-agent systems with discontinuous inherent dynamics subject to nonlinear growth. Nonlinear Anal.-Hybrid Syst. 2020, 37, 100888. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Qi, L.; Chen, W. Distributed formation control of double-integrator fractional-order multi- agent systems with relative damping and nonuniform time-delays. J. Frankl. Inst.-Eng. Appl. Math. 2019, 356, 5122–5150. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, X.; Shi, P.; Ren, Z.; Liu, J. Distributed fault-tolerant formation tracking control for multiagent systems with multiple leaders and constrained actuators. IEEE Trans. Cybern. 2022, 1–10. [Google Scholar] [CrossRef]
- Gong, Y.; Wen, G.; Peng, Z.; Huang, T. Observer-based time-varying formation control of fractional-order multi-agent systems with general linear dynamics. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 67, 82–86. [Google Scholar] [CrossRef]
- Vahid, M.; Mahdi, S.; Davood, A.; Ehsan, S. Leader following distributed formation tracking in nonlinear fractional-order multi-agent systems by using adaptive integral sliding mode approach. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019. [Google Scholar]
- Chen, B.; Hu, J.; Zhao, Y.; Bijoy Kumar, G. Leader-following consensus of linear fractional-order multi-agent systems via event-triggered control strategy. IFAC-PapersOnLine 2020, 53, 2909–2914. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Cao, J. Global Mittag–Leffler consensus for fractional singularly perturbed multi-agent systems with discontinuous inherent dynamics via event-triggered control strategy. J. Frankl. Inst.-Eng. Appl. Math. 2021, 358, 2086–2114. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, F.; Wei, B. Event-Triggered control for multi-agent systems: Event mechanisms for information transmission and controller update. J. Syst. Sci. Complex. 2021, 35, 953–972. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, G. Periodic dynamic event-triggered cluster formation control of multi-agent systems. In Proceedings of the International Conference on Intelligent Automation and Soft Computing, Chicago, IL, USA, 26–28 May 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Wang, J.; Gao, J.; Wu, P. Attack-resilient event-triggered formation control of multi-agent systems under periodic DoS attacks using complex Laplacian. ISA Trans. 2021, in press. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G. Observer-based fuzzy adaptive event-triggered control codesign for a class of uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2018, 26, 1589–1593. [Google Scholar] [CrossRef]
- Liu, G.; Pan, Y.; Lam, H.; Liang, H. Event-triggered fuzzy adaptive quantized control for nonlinear multi-agent systems in nonaffine pure-feedback form. Fuzzy Sets Syst. 2021, 416, 27–46. [Google Scholar] [CrossRef]
- Deng, J.; Li, K.; Wu, S.; Wen, Y. Distributed adaptive time-varying formation tracking control for general linear multi-agent systems based on event-triggered strategy. IEEE Access 2020, 8, 13204–13217. [Google Scholar] [CrossRef]
- Li, Y.; Hu, X.; Che, W.; Hou, Z. Event-based adaptive fuzzy asymptotic tracking control of uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 29, 3003–3013. [Google Scholar] [CrossRef]
- Liu, J.; Fang, J.-A.; Li, Z.; Miao, Q. Event-Triggering formation tracking for second-order multi-agent systems subjected to input saturation. IEEE Access 2019, 7, 138378–138390. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, T. Leader-following formation control of second-order nonlinear systems with time-varying communication delay. Int. J. Control Autom. Syst. 2021, 19, 1729–1739. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Gao, Z.; Yang, L.; He, Q. Adaptive bipartite event-triggered time-varying output formation tracking of heterogeneous linear multi-agent systems under signed directed graph. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Cao, J. Group consensus in finite time for fractional multiagent systems with discontinuous inherent dynamics subject to Hölder growth. IEEE Trans. Cybern. 2020, 52, 4161–4172. [Google Scholar] [CrossRef]
- Marco, C.; Pietro, D.; Hogan, S.; Bernardo, M. Synchronization of networks of piecewise-smooth systems. IEEE Control Syst. Lett. 2018, 2, 653–658. [Google Scholar]
- Zhu, W.; Jiang, Z. Event-based leader-following consensus of multi-agent systems with input time delay. IEEE Trans. Autom. Control 2015, 60, 1362–1367. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).