On Sliding Mode Control for Singular Fractional-Order Systems with Matched External Disturbances
Abstract
:1. Introduction
- (1)
- A novel integral SMF and SMC with derivative terms are proposed for SFOS stabilization. The difference with [23] is that the system state is in the SMS from the initial moment, reducing the time required to reach the SMS. A sufficient condition for asymptotic stability is provided for normalization.
- (2)
- An innovative integral SMF and SMC for a class of SFOS that did not satisfy the normalization criterion and obtained an SANC for the admissibility of such closed-loop systems. Compared with [24], the results are more general.
- (3)
- We numerically verified the effectiveness of our scheme in two separate instances.
2. Preliminaries and Formulation of the Problem
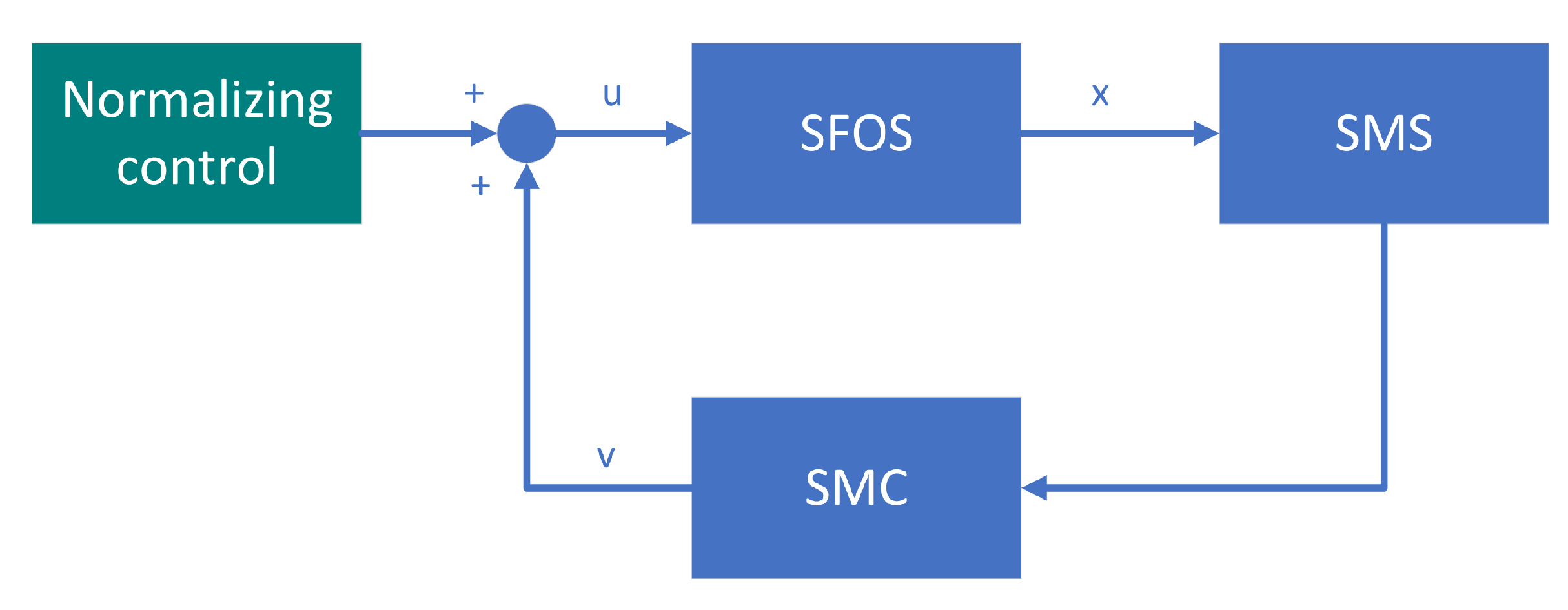
3. Synthesis of SMC of SFOS with Matched Uncertainties
3.1. Normalized-Based Integral SMC Method
3.2. Integral SMC Method
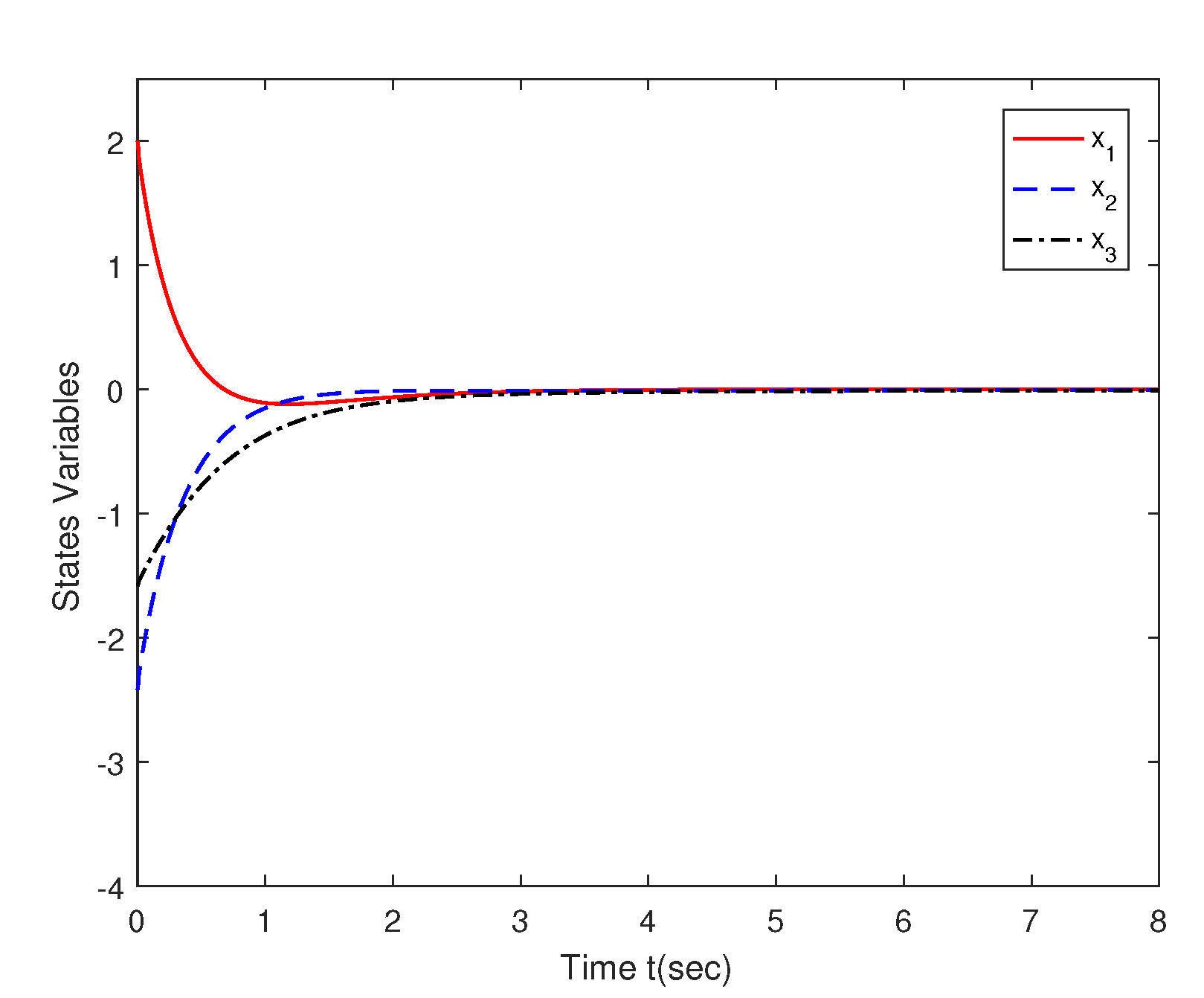
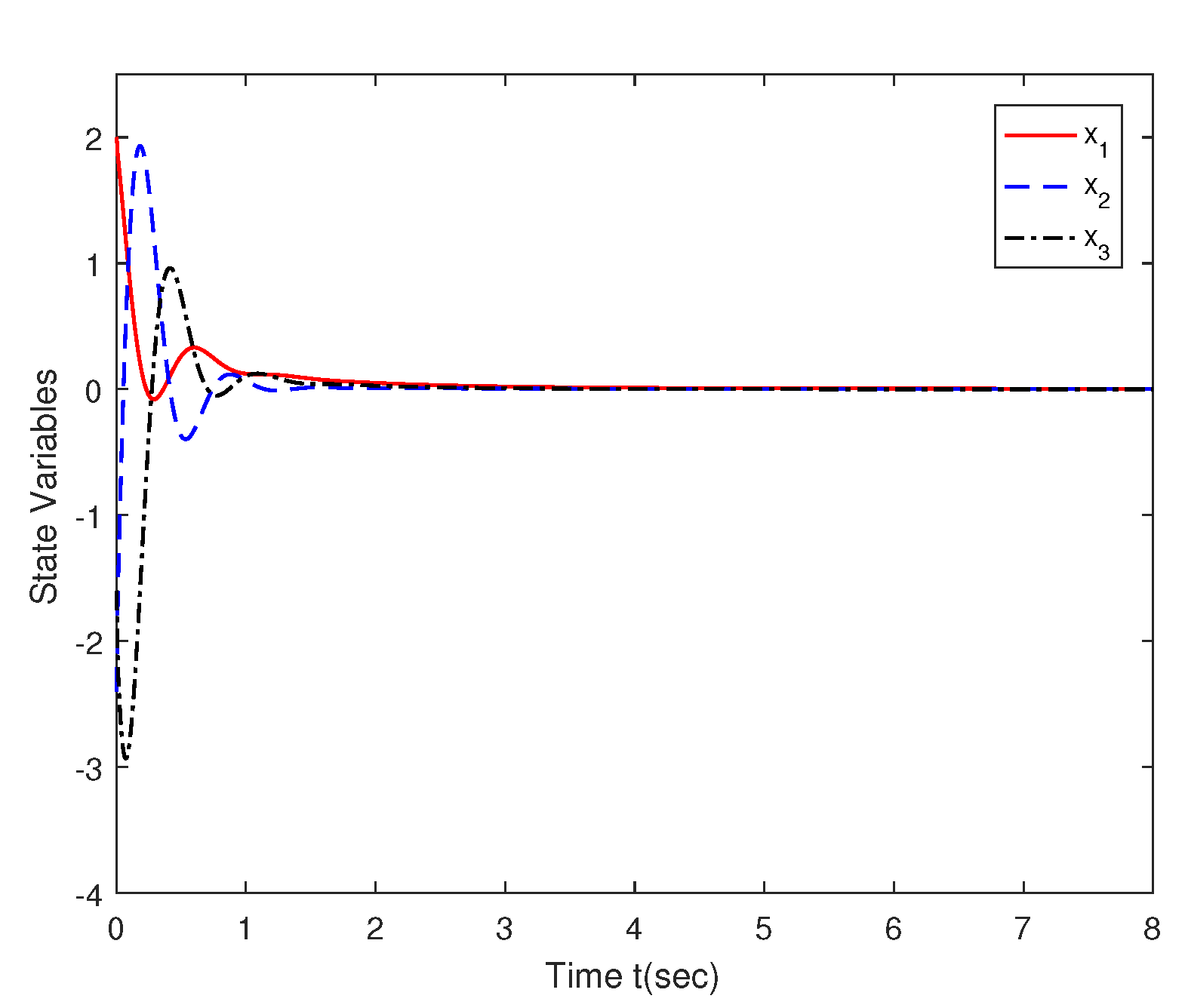
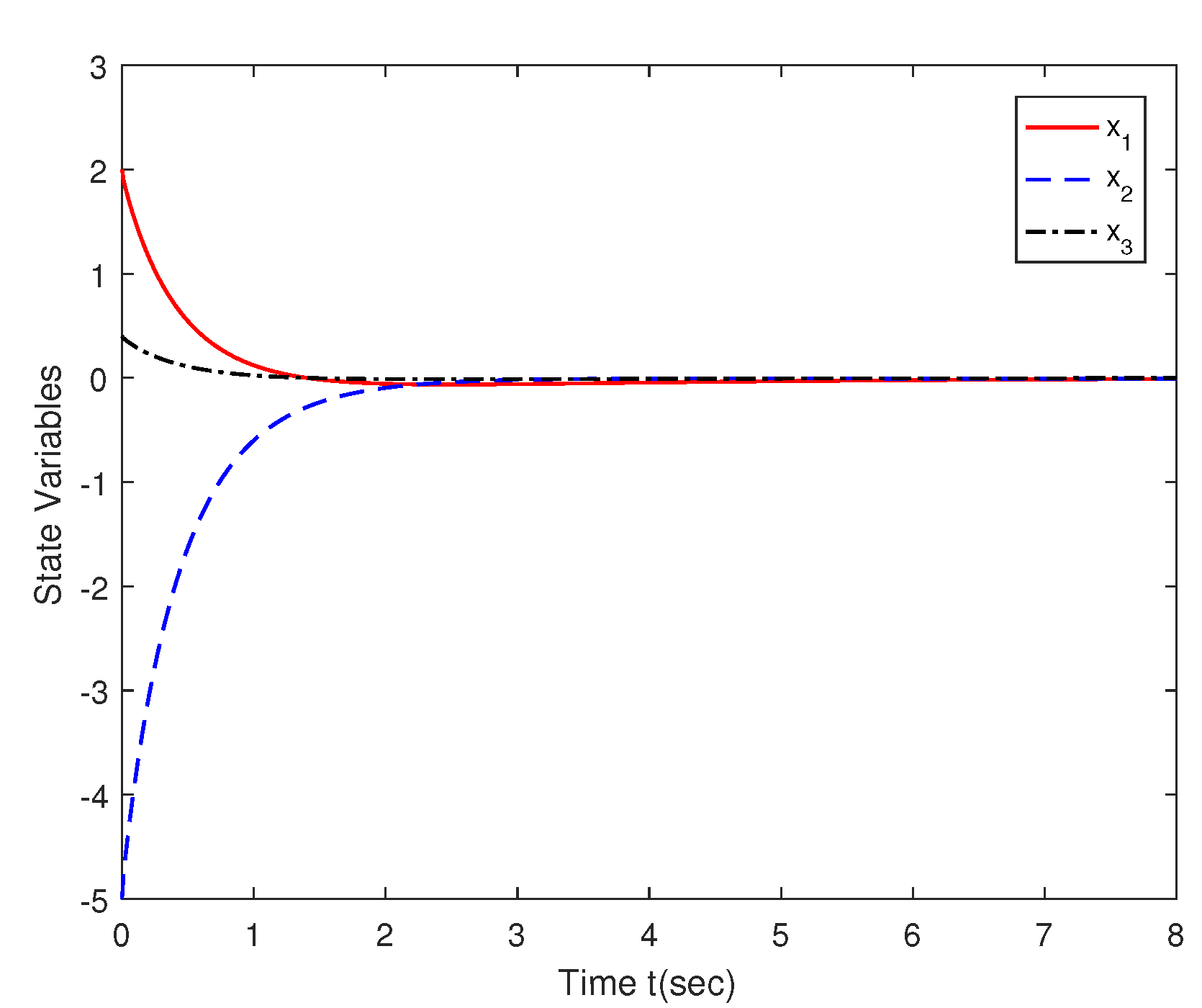
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SS | singular systems |
| SANC | sufficient and necessary conditions |
| SMC | sliding mode control |
| SFOSs | singular fractional-order systems |
| LMI | linear matrix inequality |
| SMF | sliding mode functions |
| SMS | sliding mode surface |
References
- Duan, G. Analysis and Design of Descriptor Linear Systems; Springer: New York, NY, USA, 2010. [Google Scholar]
- Müller, P.C. Linear mechanical descriptor systems: Identification, analysis and design. In Proceedings of the IFAC Conference on Control of Industrial Systems, Belfort, France, 20–22 May 1997; pp. 375–380. [Google Scholar]
- Narasimhamurthi, N.; Musavi, M. A generalized energy function for transient stability analysis of power systems. IEEE Trans. Circuits Syst. 1984, 31, 637–645. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J. Bifurcation and chaotic behavior of a discrete singular biological economic system. Appl. Math. Comput. 2012, 219, 2371–2386. [Google Scholar] [CrossRef]
- Dai, L. Singular Control Systems; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Xu, S.; Lam, J. Robust Control and Filtering of Singular Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Gao, R.; Zhai, D.; Li, T. Linear sliding variable-based sliding mode controller design of descriptor systems via output information. IET Contr. Theory Appl. 2019, 13, 1673–1682. [Google Scholar] [CrossRef]
- Yu, Y.; Jiao, Z.; Sun, C. Sufficient and necessary condition of admissibility for fractional-order singular system. Acta Autom. Sinica. 2013, 39, 2160–2164. [Google Scholar] [CrossRef]
- Wei, Y.; Du, B.; Chen, Y.; Cheng, S.; Wang, Y. Necessary and sufficient admissibility condition of singular fractional order systems. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 85–88. [Google Scholar]
- Zhang, X.; Chen, Y. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order alpha: The 0 < alpha < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [PubMed]
- Wei, Y.; Tse, P.W.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans. 2017, 69, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Qiu, J. Stabilization of fractional-order singular uncertain systems. ISA Trans. 2015, 56, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Lin, C.; Chen, B.; Wang, Q. Stabilization for singular fractional-order systems via static output feedback. IEEE Access. 2018, 6, 71678–71684. [Google Scholar] [CrossRef]
- Lin, C.; Chen, B.; Shi, P.; Yu, J. Necessary and sufficient conditions of observer-based stabilization for a class of fractional-order descriptor systems. Syst. Control Lett. 2018, 112, 31–35. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, J.; Liu, T.; Wang, Y. Sufficient and necessary conditions for stabilizing singular fractional order systems with partially measurable state. J. Frankl. Inst.-Eng. Appl. Math. 2019, 356, 1975–1990. [Google Scholar] [CrossRef] [Green Version]
- Kaczorek, T. Singular fractional linear systems and electrical circuits. Int. J. Appl. Math. Comput. Sci. 2011, 21, 379–384. [Google Scholar] [CrossRef]
- Itkis, U. Control System of Variable Structure; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; T. J. International Ltd.: Padstow, UK, 1998. [Google Scholar]
- Kao, Y.; Ma, S.; Xia, H.; Wang, C.; Liu, Y. Integral sliding mode control for a kind of impulsive uncertain reaction-diffusion systems. IEEE Trans. Autom. Control 2022. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, W. Adaptive sliding mode fault tolerant control for interval Type-2 fuzzy singular fractional-order systems. J. Vib. Control 2022, 28, 465–475. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Liu, Q. A New Adaptive Robust Sliding Mode Control Approach for Nonlinear Singular Fractional-Order Systems. Fractal Fract. 2022, 6, 253. [Google Scholar] [CrossRef]
- Meng, B.; Wang, X.; Zhang, Z.; Wang, Z. Necessary and sufficient conditions for normalization and sliding mode control of singular fractional-order systems with uncertainties. Sci. China-Technol. Sci. 2020, 63, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Babu, P.S.; Xavier, N.; Bandyopadhyay, B. Integral sliding mode control for fractional order descriptor systems. In Proceedings of the 18th European Control Conference, Naples, Italy, 25–28 June 2019; pp. 3601–3605. [Google Scholar]
- Monje, C.; Chen, Y.; Vinagre, B.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- N’Doye, I.; Darouach, M.; Zasadzinki, M.; Radhy, N.E. Robust stabilization of uncertain descriptor fractional-order systems. Automatica 2013, 49, 1907–1913. [Google Scholar] [CrossRef]
- Si, X.; Wang, Z.; Song, Z.; Zhang, Z. Asymptotic stabilization of delayed linear fractional-order systems subject to state and control constraints. Fractal Fract. 2022, 6, 67. [Google Scholar] [CrossRef]
| Normalized-Based Intrgral SMC | Integral SMC | ||
|---|---|---|---|
| Example 1 | ✓ | ✓ | ✓ |
| Example 2 | ✘ | ✘ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Meng, B.; Wang, Z. On Sliding Mode Control for Singular Fractional-Order Systems with Matched External Disturbances. Fractal Fract. 2022, 6, 366. https://doi.org/10.3390/fractalfract6070366
Song S, Meng B, Wang Z. On Sliding Mode Control for Singular Fractional-Order Systems with Matched External Disturbances. Fractal and Fractional. 2022; 6(7):366. https://doi.org/10.3390/fractalfract6070366
Chicago/Turabian StyleSong, Shubin, Bo Meng, and Zhen Wang. 2022. "On Sliding Mode Control for Singular Fractional-Order Systems with Matched External Disturbances" Fractal and Fractional 6, no. 7: 366. https://doi.org/10.3390/fractalfract6070366
APA StyleSong, S., Meng, B., & Wang, Z. (2022). On Sliding Mode Control for Singular Fractional-Order Systems with Matched External Disturbances. Fractal and Fractional, 6(7), 366. https://doi.org/10.3390/fractalfract6070366







