Sign Retention in Classical MF-DFA
Abstract
:1. Introduction
2. Methodology
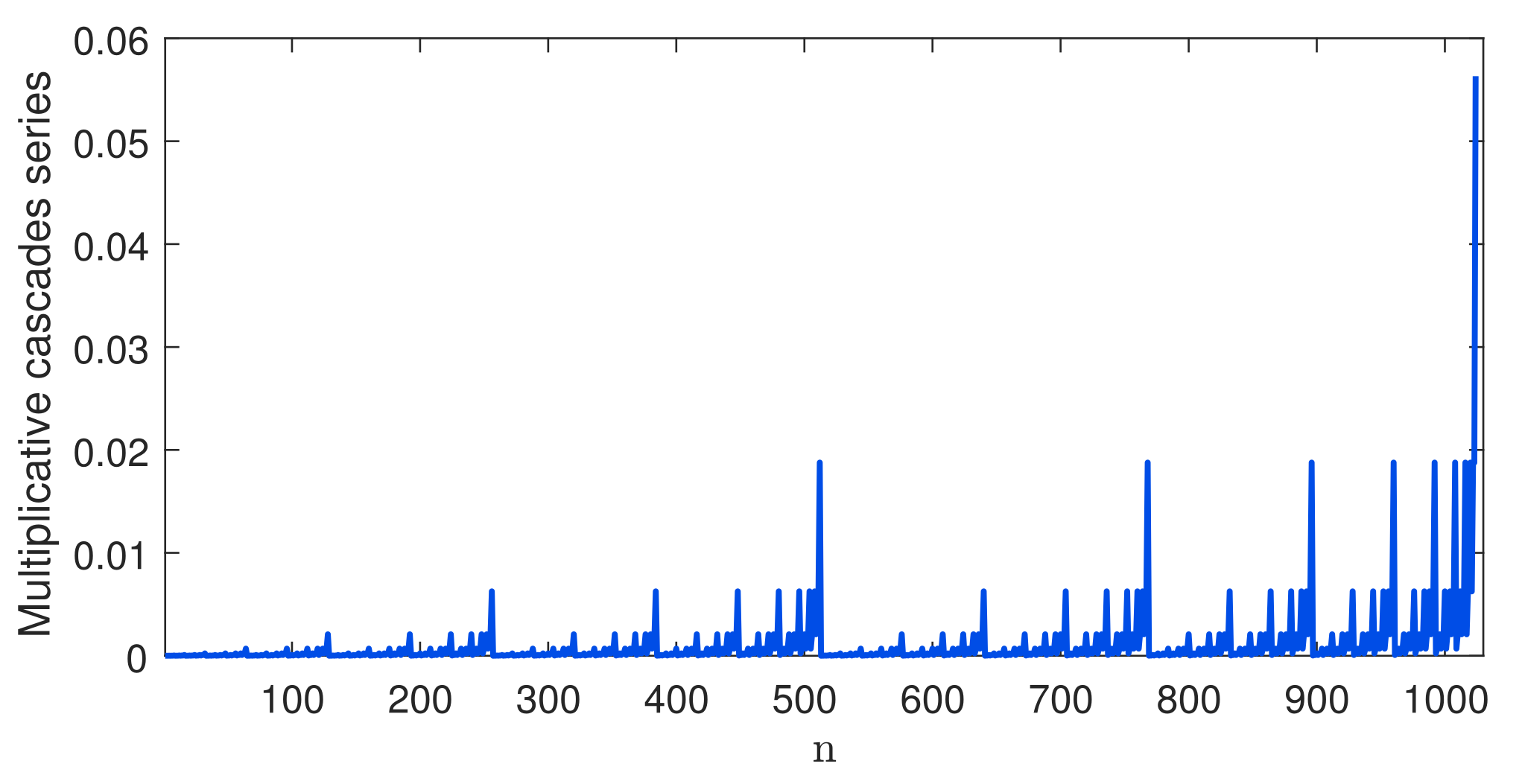
2.1. Multiplicative Cascades Series
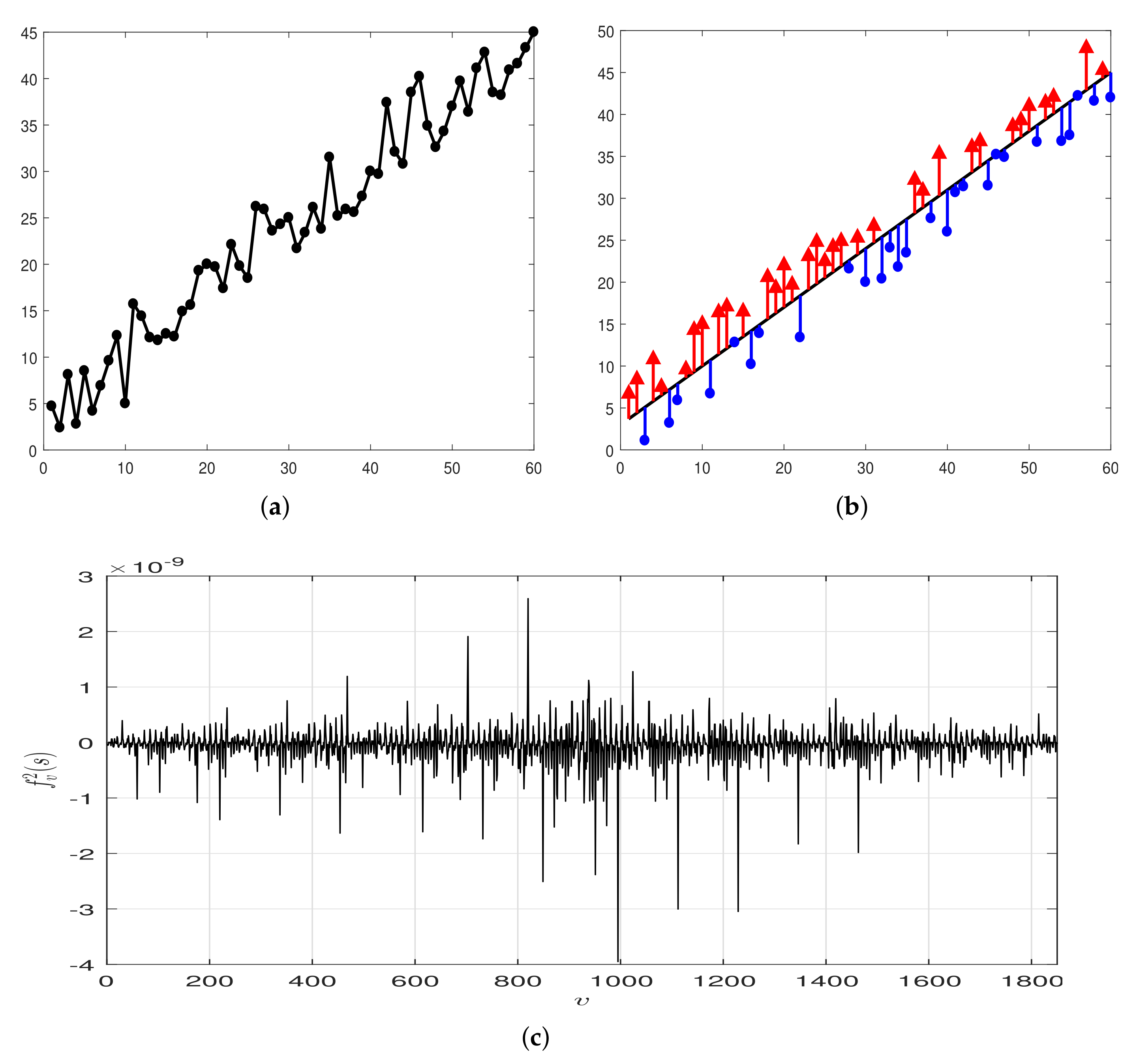
2.2. MF-S-DFA
3. Emperiment Results
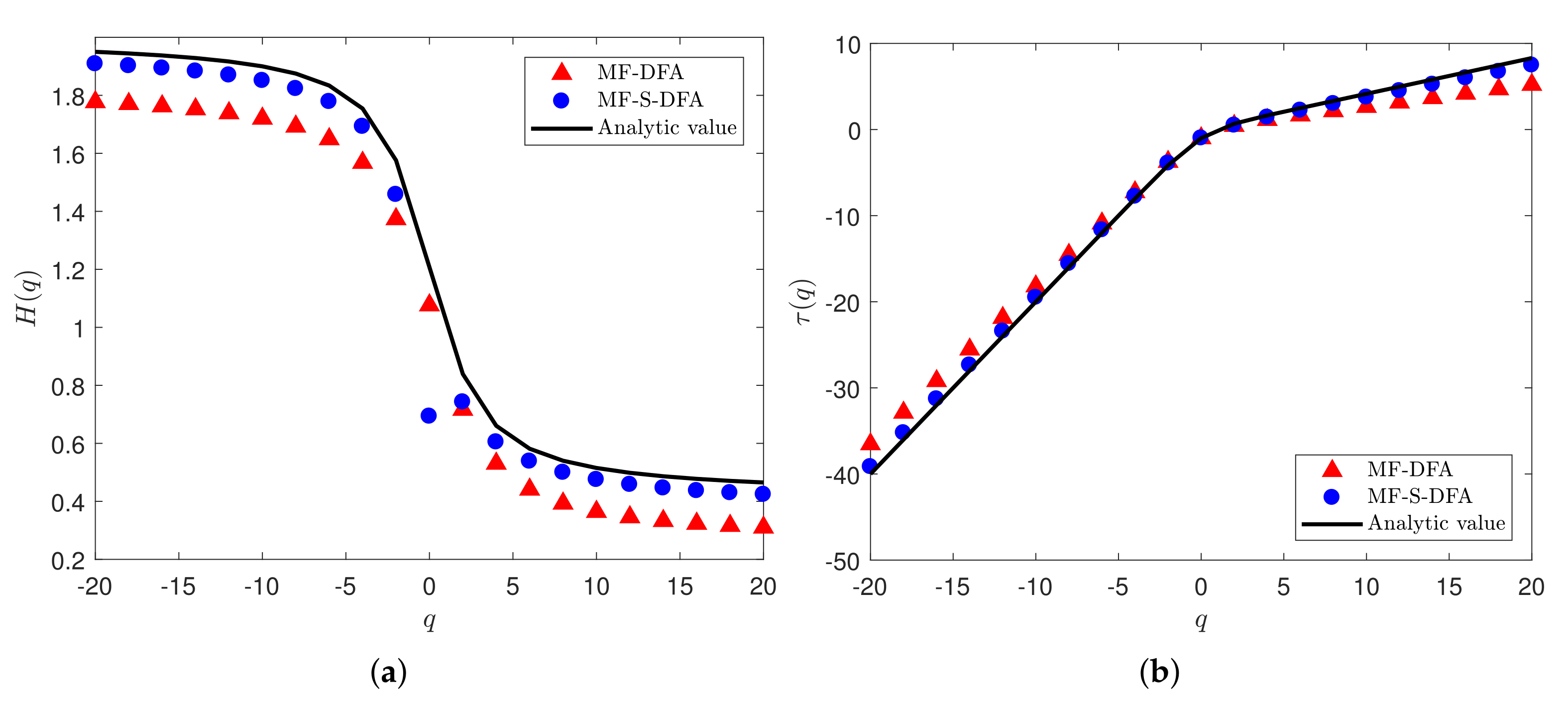
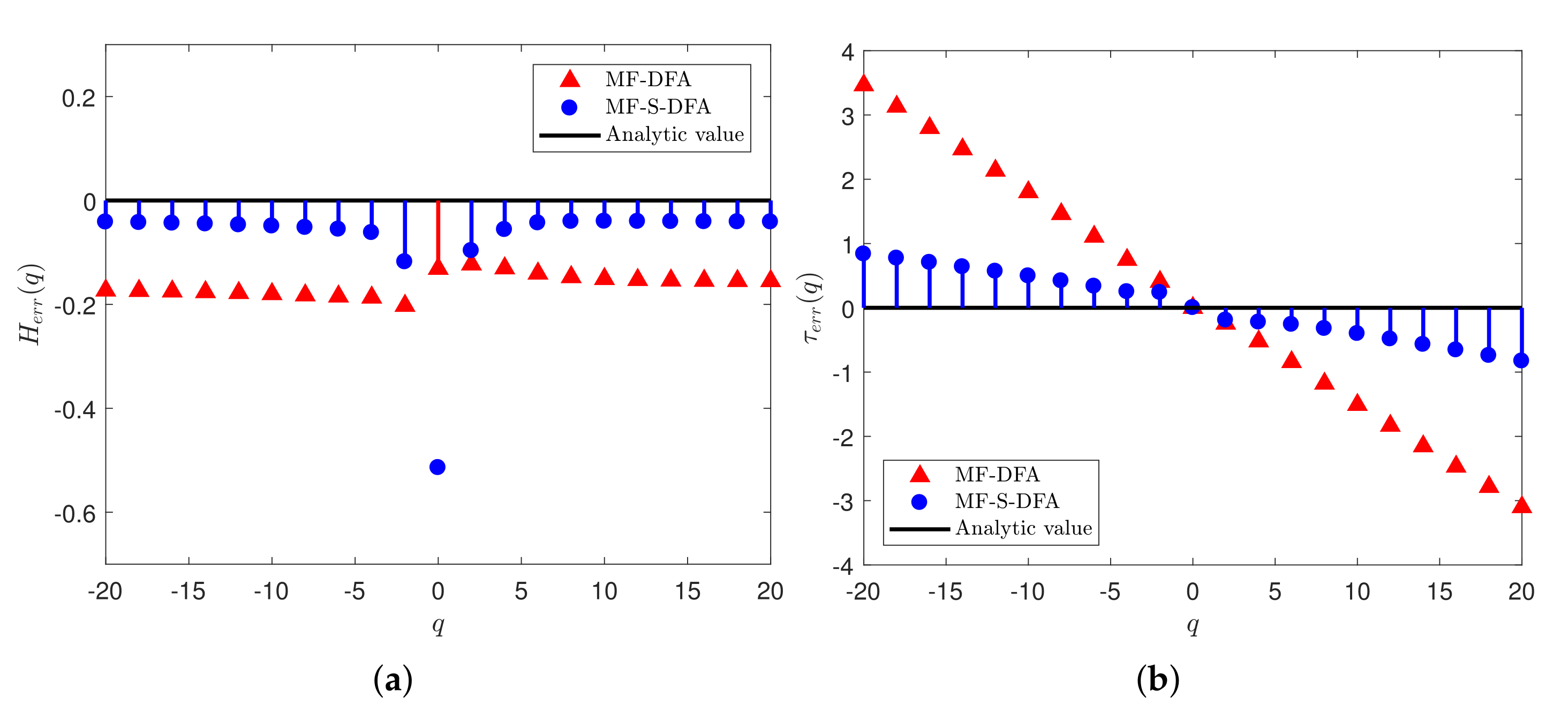
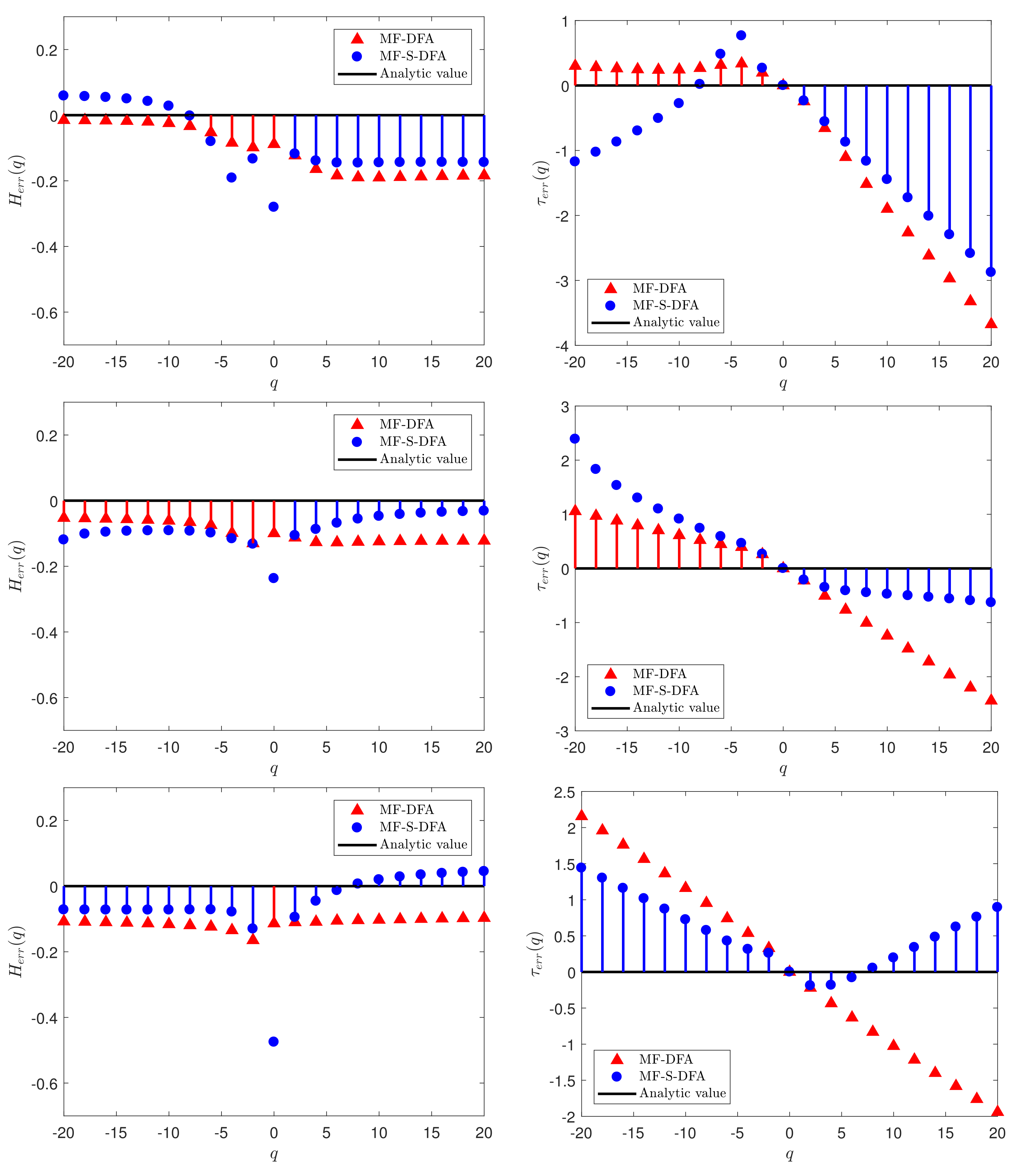
3.1. Multifractal Analysis with Different
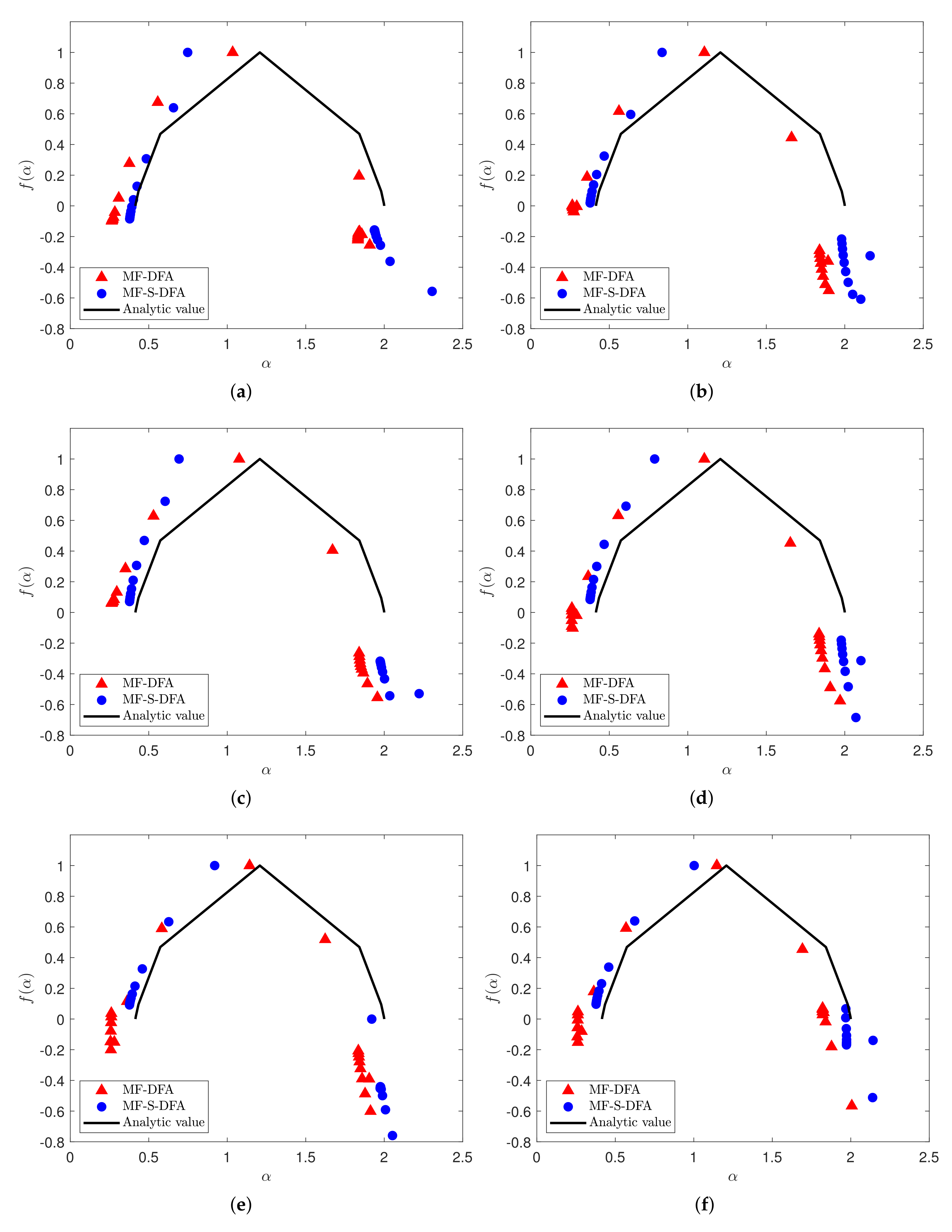
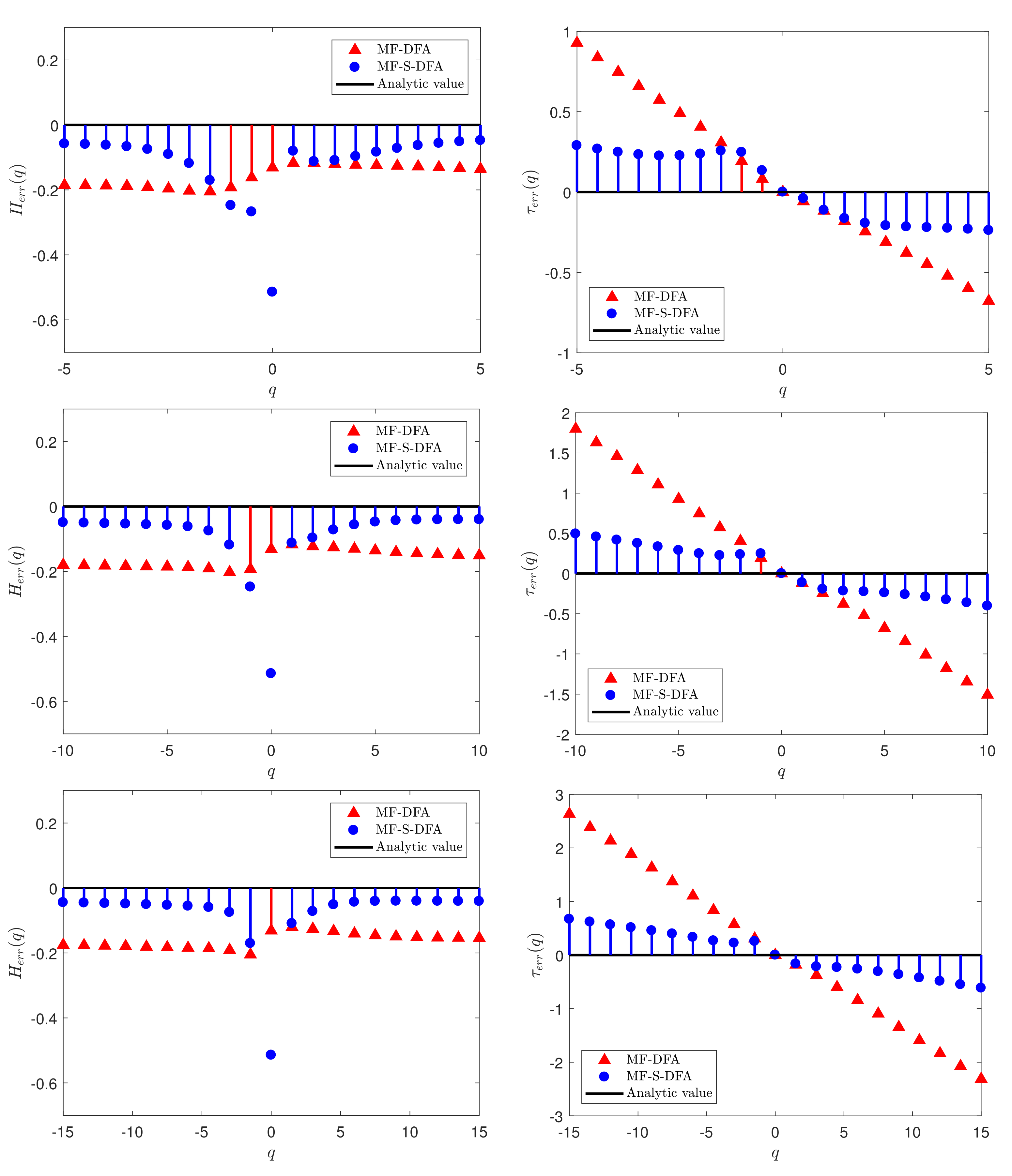
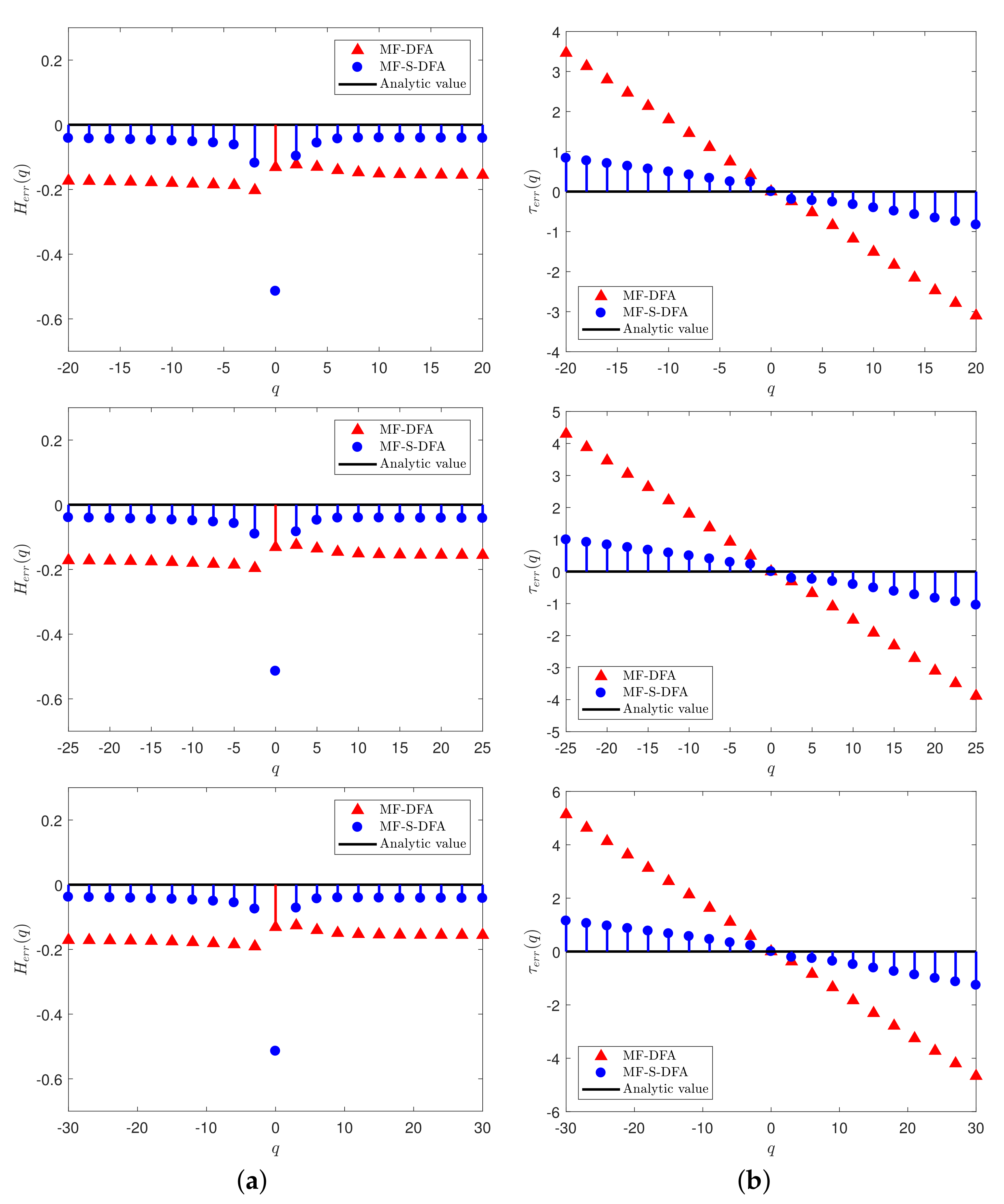
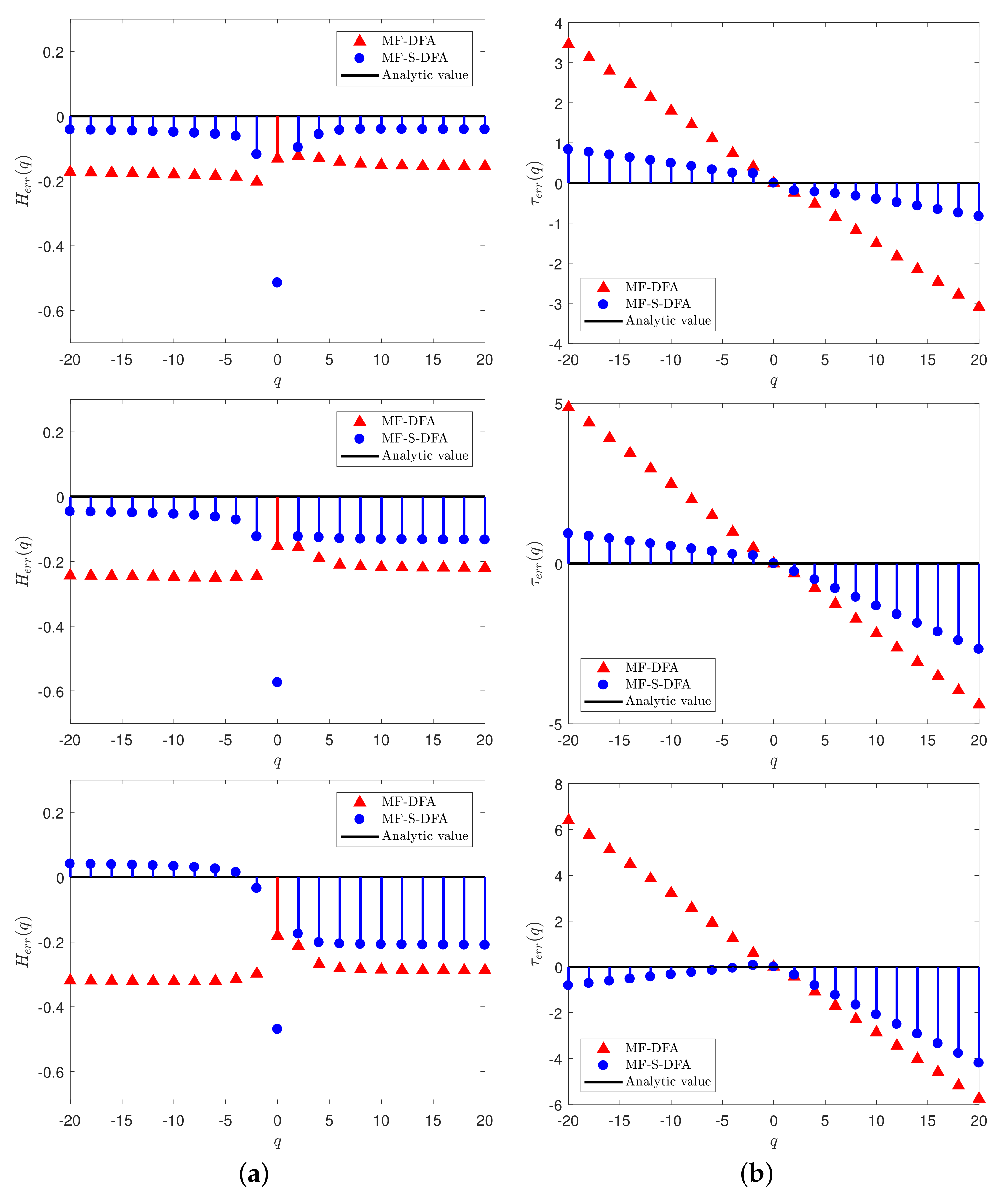
3.2. Multifractal Analysis with Different Domains of q
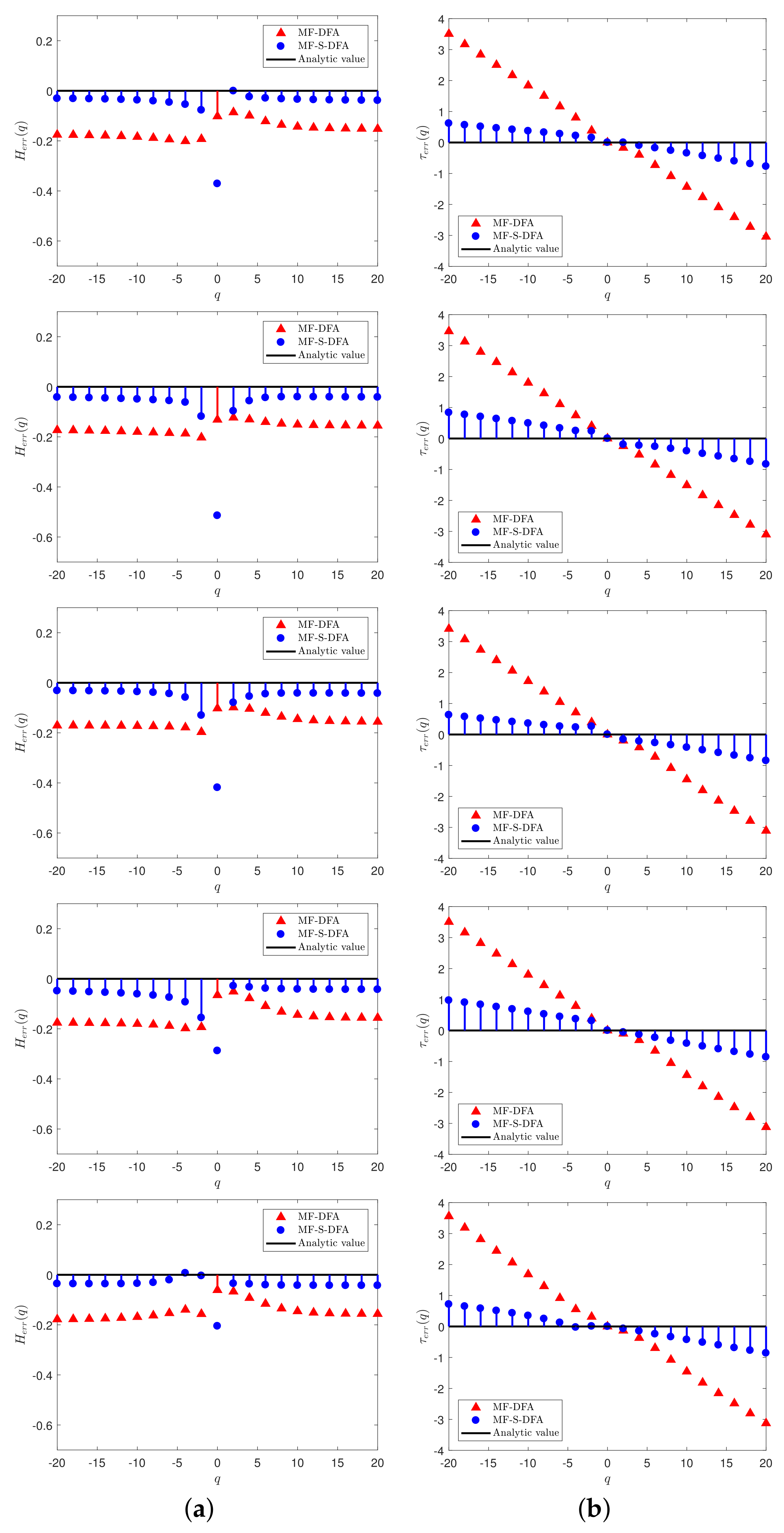
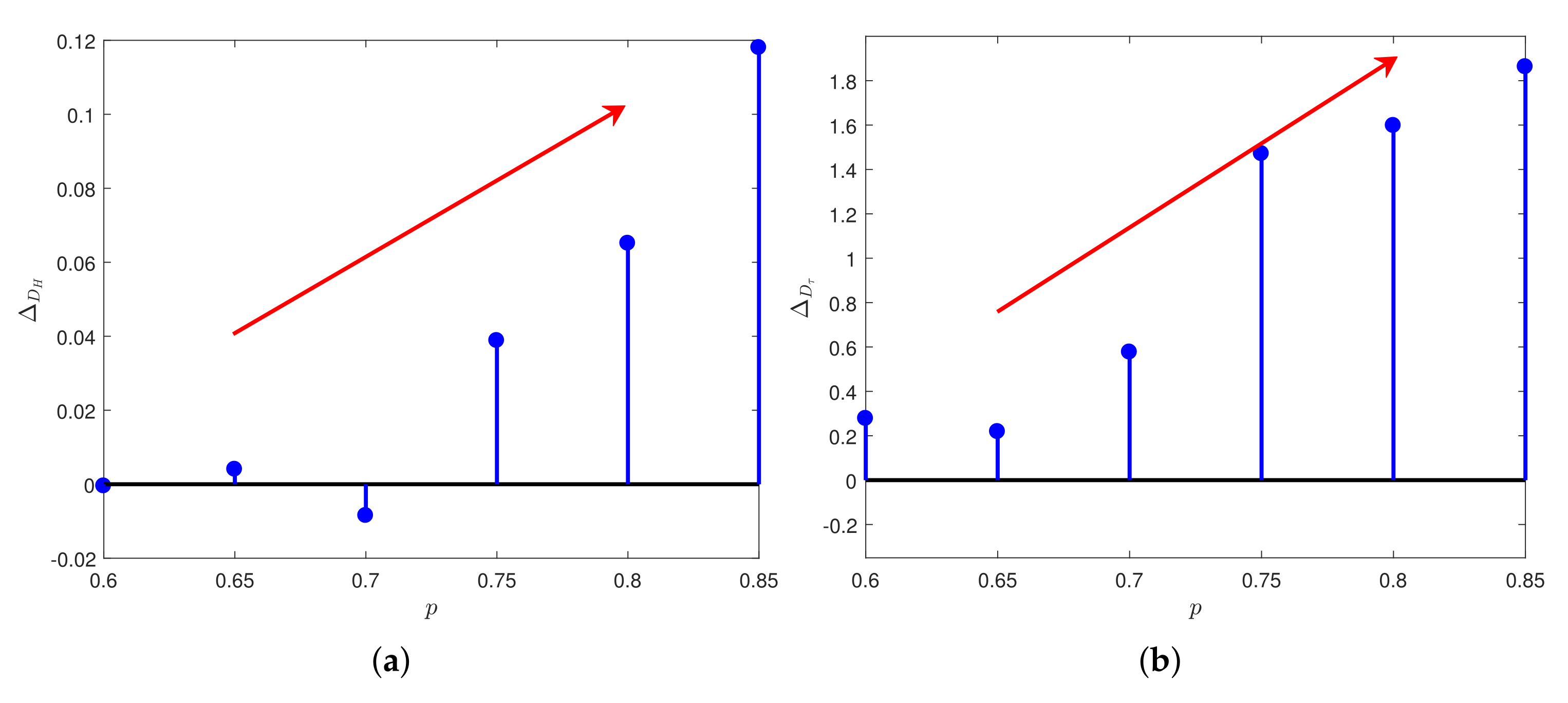
3.3. Multifractal Analysis with Different p
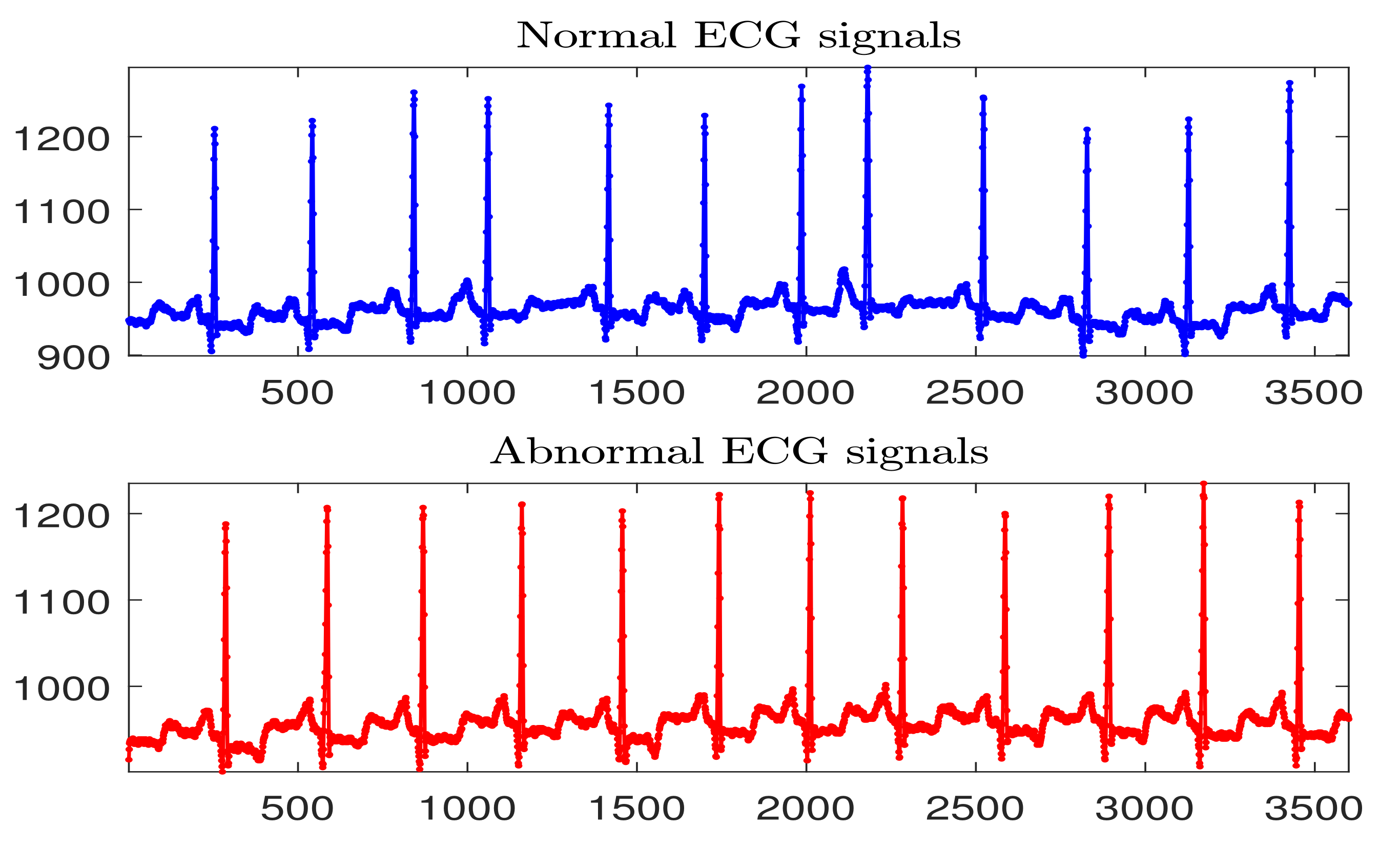
4. Application of MF-S-DFA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Ivanov, P.C.; Hu, K.; Chen, Z.; Carbone, A.; Stanley, H.E. Quantifying signals with power-law correlations: A comparative study of detrended fluctuation analysis and detrended moving average techniques. Phys. Rev. E 2005, 71, 051101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Z.Q.; Xie, W.J.; Zhou, W.X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pratviel, Y.; Deschodt-Arsac, V.; Larrue, F.; Arsac, L.M. Tool Embodiment Is Reflected in Movement Multifractal Nonlinearity. Fractal Fract. 2022, 6, 240. [Google Scholar] [CrossRef]
- Wang, J.; Shao, W.; Kim, J. Automated classification for brain MRIs based on 2D MF-DFA method. Fractals 2020, 28, 2050109. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E. 1994, 49, 1685. [Google Scholar] [CrossRef] [Green Version]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.X. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E. 2008, 77, 066211. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Zhuang, X.T.; Liu, Z.Y. Price—Volume multifractal analysis and its application in Chinese stock markets. Phys. A Stat. Mech. Its Appl. 2012, 391, 3484–3495. [Google Scholar] [CrossRef]
- Shao, W.; Wang, J. Does the “ice-breaking” of South and North Korea affect the South Korean financial market? Chaos Solitons Fractals 2020, 132, 109564. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, S.M. Multifractal features of financial markets. Phys. A Stat. Mech. Its Appl. 2004, 344, 272–278. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Zhao, Y.; Zhang, X. Multifractal detrended fluctuation analysis on air traffic flow time series: A single airport case. Phys. A Stat. Mech. Its Appl. 2019, 531, 121790. [Google Scholar] [CrossRef]
- Shang, P.; Lu, Y.; Kamae, S. Detecting long-range correlations of traffic time series with multifractal detrended fluctuation analysis. Chaos Solitons Fractals 2008, 36, 82–90. [Google Scholar] [CrossRef]
- Li, X.; Shang, P. Multifractal classification of road traffic flows. Chaos Solitons Fractals 2007, 31, 1089–1094. [Google Scholar] [CrossRef]
- Zhang, C.; Ni, Z.; Ni, L. Multifractal detrended cross-correlation analysis between PM2.5 and meteorological factors. Phys. A Stat. Mech. Its Appl. 2015, 438, 114–123. [Google Scholar] [CrossRef]
- Lee, C.K. Multifractal characteristics in air pollutant concentration time series. Water Air Soil Pollut. 2002, 135, 389–409. [Google Scholar] [CrossRef]
- Stan, C.; Cristescu, M.T.; Luiza, B.I.; Cristescu, C.P. Investigation on series of length of coding and non-coding DNA sequences of bacteria using multifractal detrended cross-correlation analysis. J. Theor. Biol. 2013, 321, 54–62. [Google Scholar] [CrossRef]
- Gutierrez, J.M.; Rodrıguez, M.A.; Abramson, G. Multifractal analysis of DNA sequences using a novel chaos-game representation. Phys. A Stat. Mech. Its Appl. 2001, 300, 271–284. [Google Scholar] [CrossRef]
- Mandal, S.; Sinha, N. Arrhythmia diagnosis from ECG signal analysis using statistical features and novel classification method. J. Mech. Med. Biol. 2021, 21, 2150025. [Google Scholar] [CrossRef]
- Wang, J.; Shao, W.; Kim, J. ECG Classification Comparison Between MF-DFA and MF-DXA. Fractals 2021, 29, 2150029. [Google Scholar] [CrossRef]
- Riedi, R. An improved multifractal formalism and self-similar measures. J. Math. Anal. Appl. 1995, 189, 462–490. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Jiang, W.; Shao, W. Convergence investigation of multifractal analysis based on Lp-norm constraint. Fractals 2022. [Google Scholar] [CrossRef]
- Lee, Y.J.; Kim, N.W.; Choi, K.H.; Yoon, S.M. Analysis of the informational efficiency of the EU carbon emission trading market: Asymmetric MF-DFA approach. Energies 2020, 13, 2171. [Google Scholar] [CrossRef]
- Wang, J.; Shao, W. Multifractal analysis with detrending weighted average algorithm of historical volatility. Fractals 2021, 29, 2150193. [Google Scholar] [CrossRef]
- Lavicka, H.; Kracik, J. Fluctuation analysis of electric power loads in Europe: Correlation multifractality vs. Distribution function multifractality. Phys. A Stat. Mech. Its Appl. 2020, 545, 123821. [Google Scholar] [CrossRef] [Green Version]
- Sosa-Herrera, J.A.; Rodriguez-Romo, S. Kernel density approach to error estimation of MF-DFA measures on time series. Phys. A Stat. Mech. Its Appl. 2019, 526, 120863. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]

| 8 | 9 | 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|---|---|
| MF-DFA | 0.1550 | 0.1598 | 0.1635 | 0.1557 | 0.1566 | 0.1488 | |
| MF-S-DFA | 0.1180 | 0.0894 | 0.1247 | 0.1044 | 0.0870 | 0.0570 | |
| MF-DFA | 1.9539 | 1.9897 | 1.9971 | 1.9585 | 1.9970 | 1.9816 | |
| MF-S-DFA | 0.6585 | 0.4278 | 0.5265 | 0.4661 | 0.5920 | 0.4746 |
| q | |||||||
|---|---|---|---|---|---|---|---|
| MF-DFA | 0.1597 | 0.1625 | 0.1635 | 0.1635 | 0.1632 | 0.1629 | |
| MF-S-DFA | 0.1595 | 0.1393 | 0.1294 | 0.1247 | 0.1225 | 0.1213 | |
| MF-DFA | 0.4910 | 1.0002 | 1.5024 | 1.9971 | 2.4893 | 2.9811 | |
| MF-S-DFA | 0.2129 | 0.3046 | 0.4139 | 0.5265 | 0.6397 | 0.7526 |
| p | |||||||
|---|---|---|---|---|---|---|---|
| MF-DFA | 0.1293 | 0.1016 | 0.1129 | 0.1635 | 0.2259 | 0.2942 | |
| MF-S-DFA | 0.1298 | 0.0976 | 0.1214 | 0.1247 | 0.1608 | 0.1762 | |
| MF-DFA | 1.5995 | 1.1609 | 1.2781 | 1.9971 | 2.8143 | 3.6819 | |
| MF-S-DFA | 1.3223 | 0.9430 | 0.7018 | 0.5265 | 1.2169 | 1.8197 |
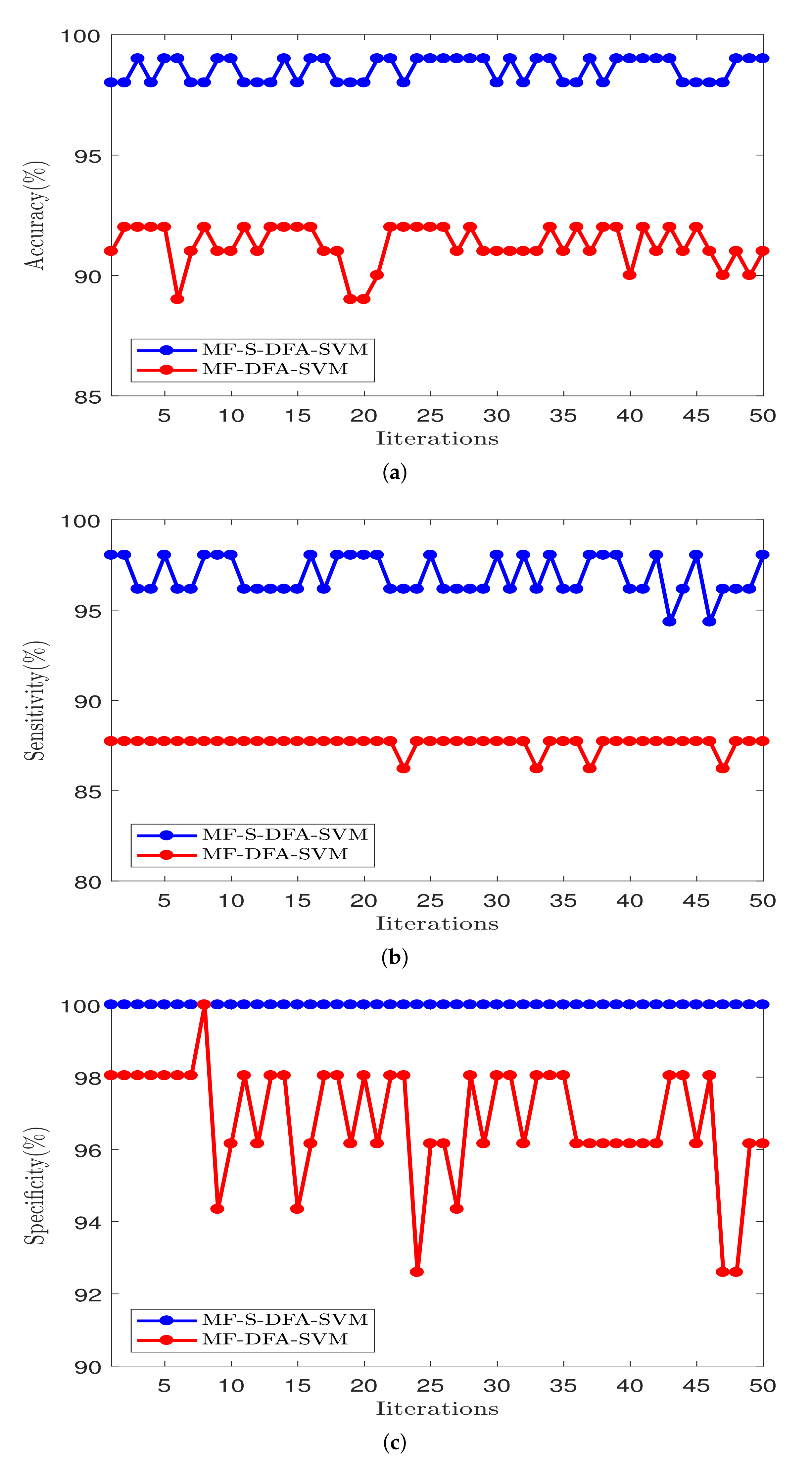
| Method | Accuracy | Sensitivity | Specificity |
|---|---|---|---|
| MF-S-DFA-SVM | |||
| MF-DFA-SVM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Zhang, Y.; Wang, J. Sign Retention in Classical MF-DFA. Fractal Fract. 2022, 6, 365. https://doi.org/10.3390/fractalfract6070365
Yang M, Zhang Y, Wang J. Sign Retention in Classical MF-DFA. Fractal and Fractional. 2022; 6(7):365. https://doi.org/10.3390/fractalfract6070365
Chicago/Turabian StyleYang, Mengdie, Yudong Zhang, and Jian Wang. 2022. "Sign Retention in Classical MF-DFA" Fractal and Fractional 6, no. 7: 365. https://doi.org/10.3390/fractalfract6070365
APA StyleYang, M., Zhang, Y., & Wang, J. (2022). Sign Retention in Classical MF-DFA. Fractal and Fractional, 6(7), 365. https://doi.org/10.3390/fractalfract6070365






