Fractal Properties of the Magnetic Polarity Scale in the Stochastic Hereditary αω-Dynamo Model
Abstract
:1. Introduction
2. Hereditary Two-Modes -Dynamo Model
3. Stochastic -Dynamo Model
4. Difference Scheme for Model
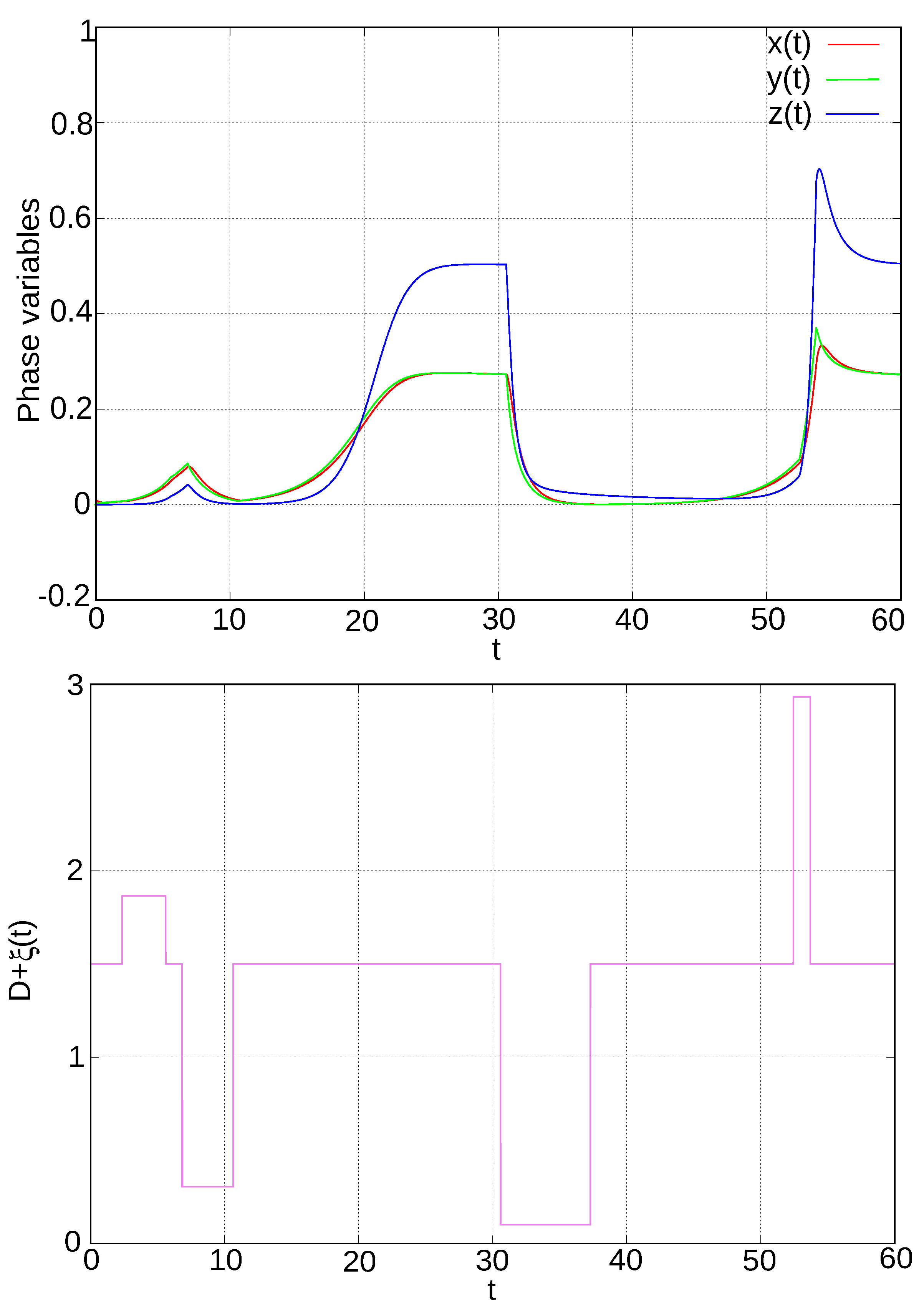
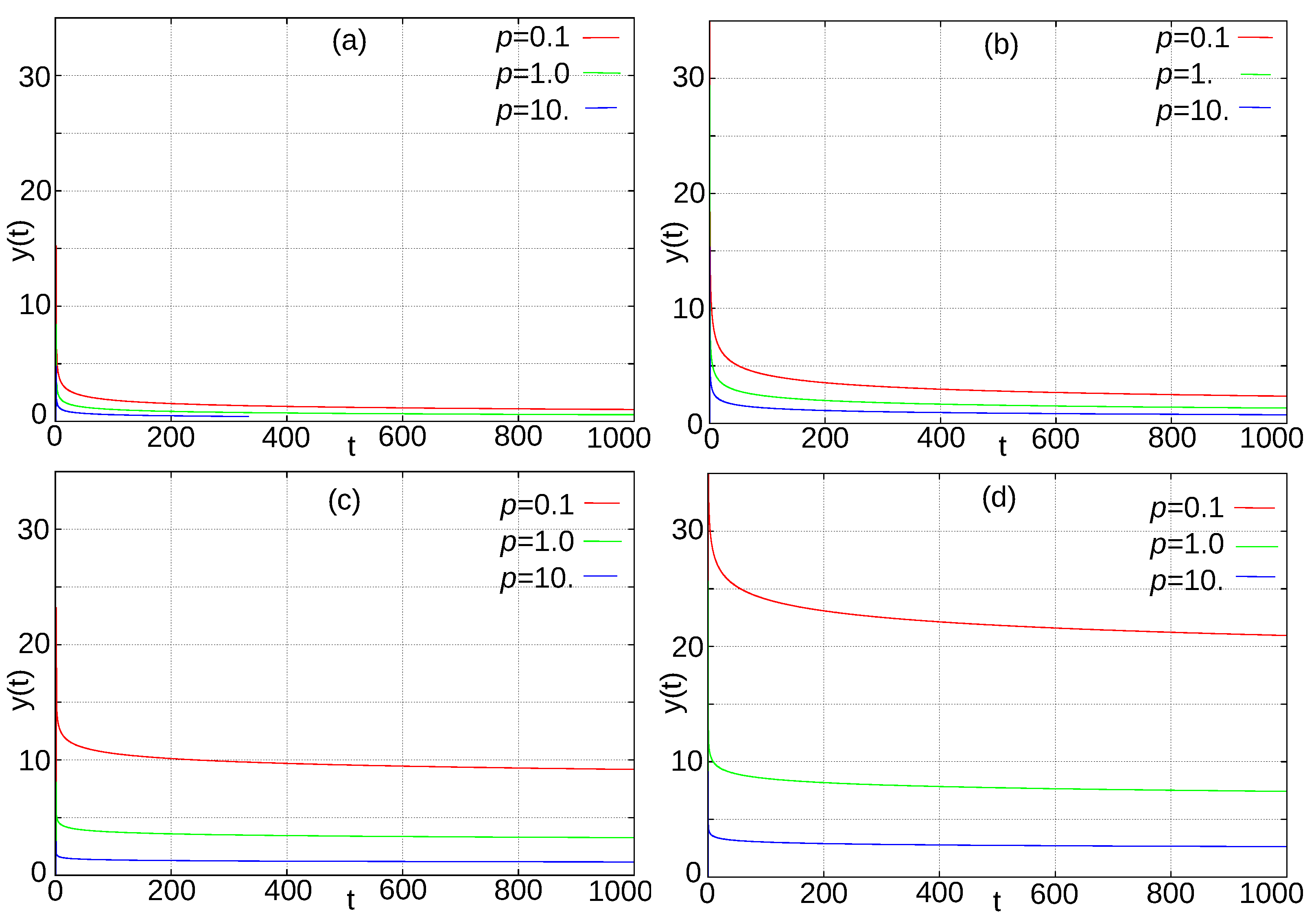
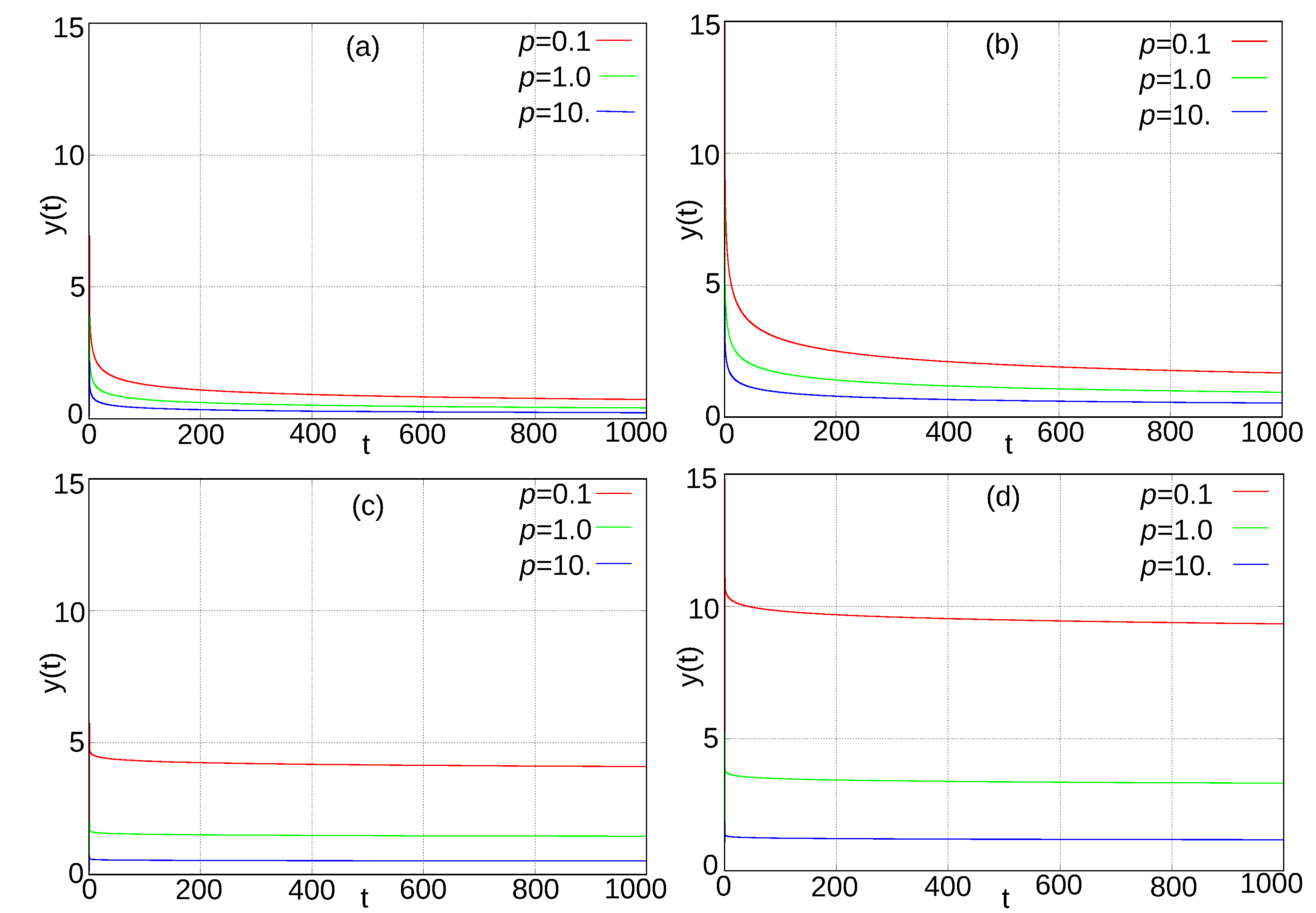
5. Fractional Stochastic -Dynamo Model–Simulation Results
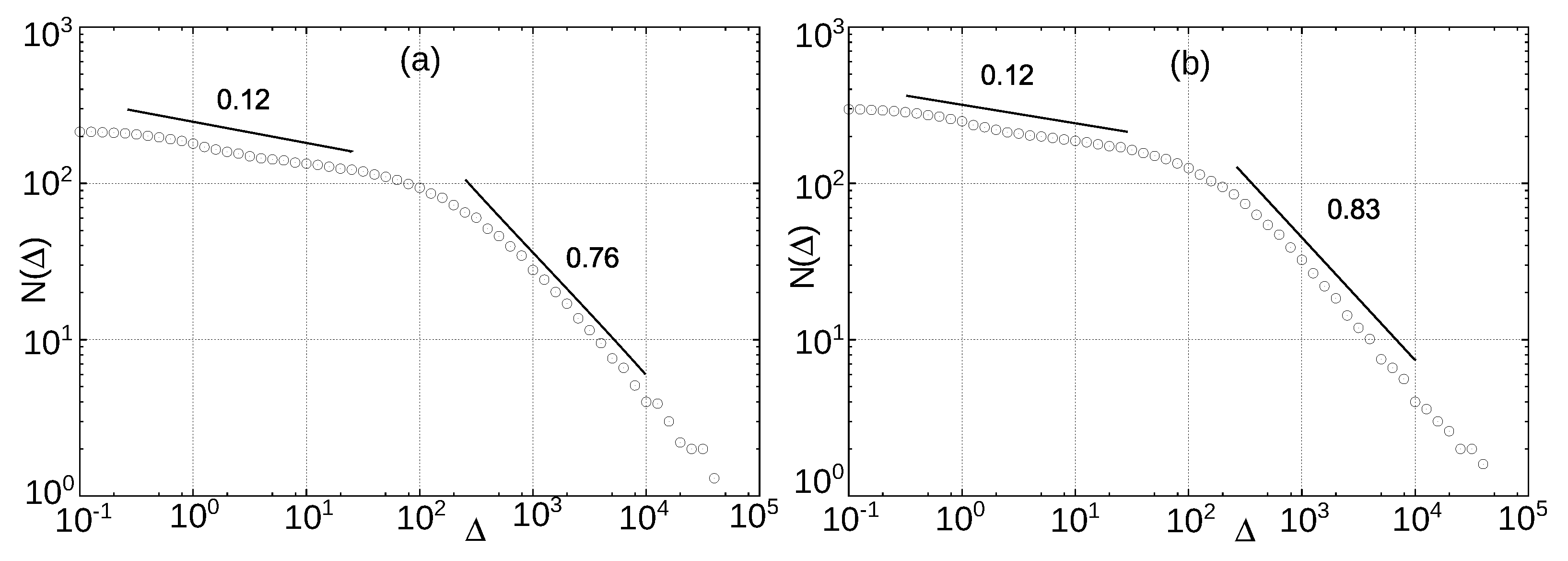
5.1. Hausdorff Dimension of the Polarity Timescale
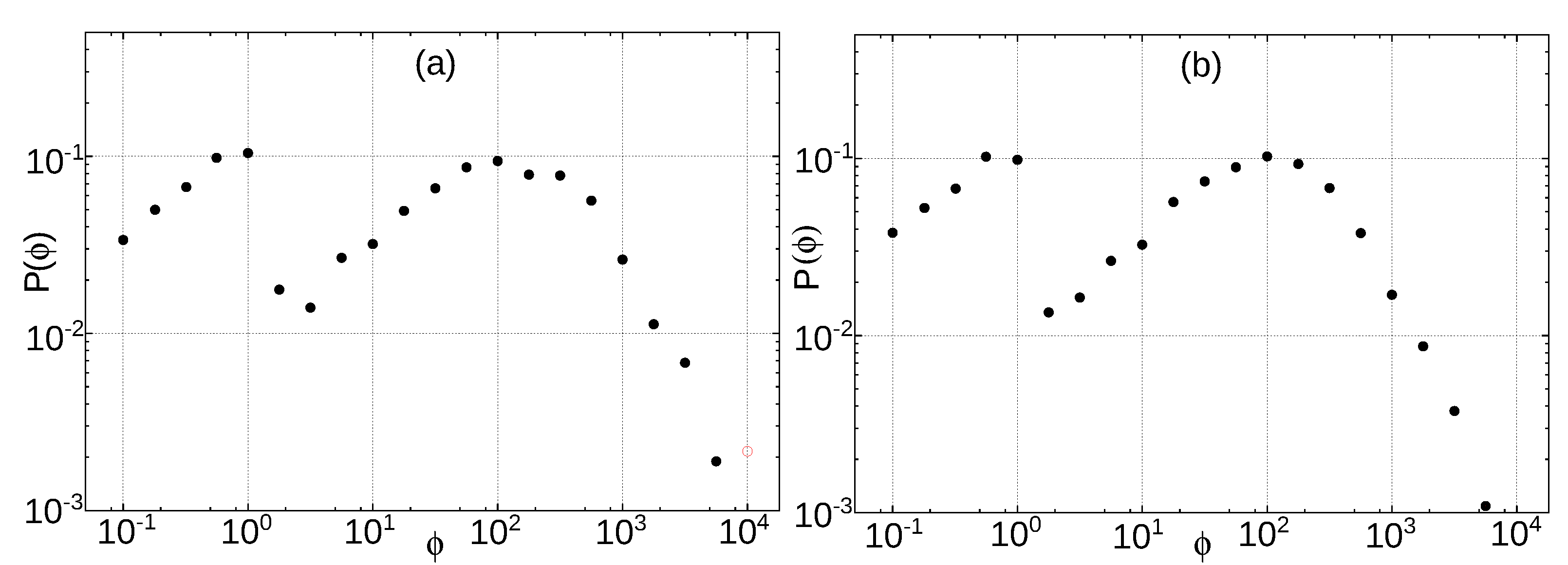
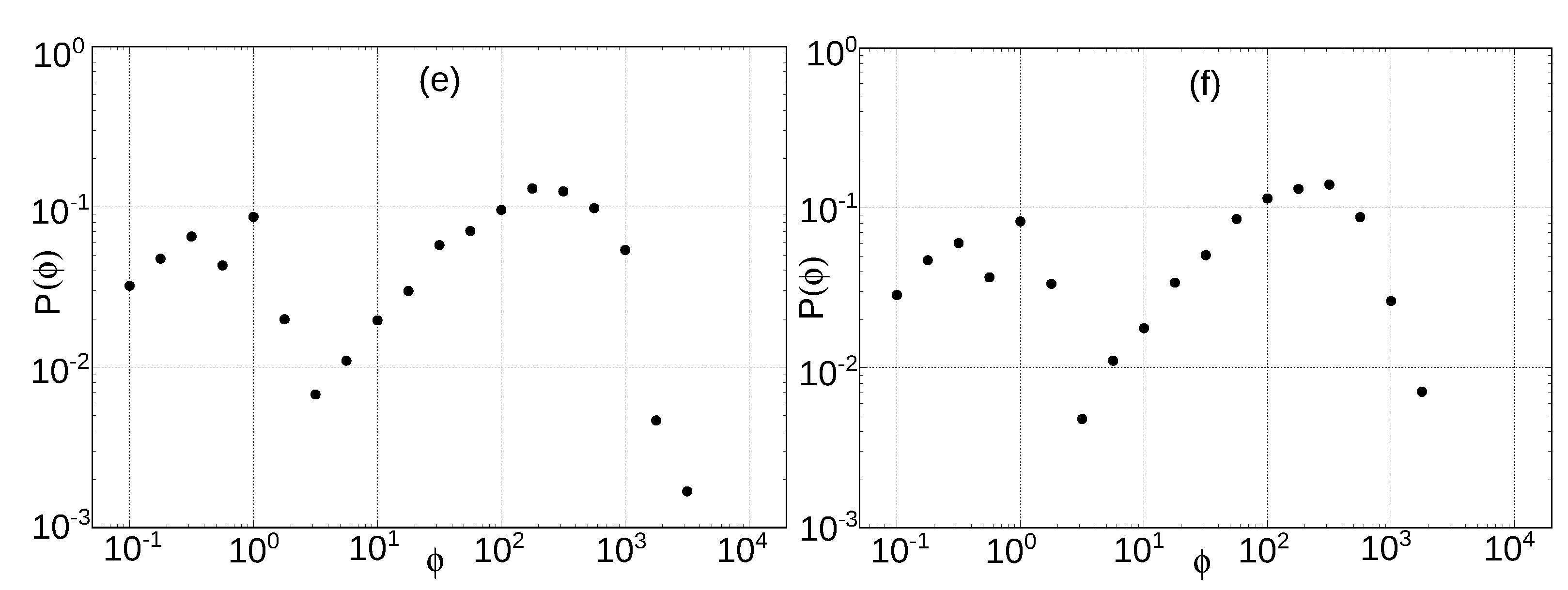
5.2. Distribution of the Polarity Intervals
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GMPTS | GeoMagnetic Polarity TimeScale |
Appendix A. Expressions for the Difference Scheme Coefficients
Appendix B. C++ Code for the Simulation
References
- Zeldovich, Y.B.; Rusmaikin, A.A.; Sokoloff, D.D. Magnetic Fields in Astrophysics. The Fluid Mechanics of Astrophysics and Geophysics; Gordon and Breach: New York, NY, USA, 1983. [Google Scholar]
- Merril, R.T.; McElhinny, M.W.; McFadden, P.L. The Magnetic Field of the Earth: Paleomagnetism, the Core, and the Deep Mantle; Academic Press: London, UK, 1996. [Google Scholar]
- Stix, M. The Sun. An Introduction; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1989. [Google Scholar]
- Parker, E.N. Hydromagnetic dynamo models. Astrophys. J. 1955, 122, 293–314. [Google Scholar] [CrossRef]
- Krause, F.; Rädler, K.-H. Mean-Filed Magnetohydrodynamics and Dynamo Theory; Academic-Verlag: Berlin, Germany, 1980. [Google Scholar]
- Hori, K.; Yoshida, S. Non-local memory effects of the electromotive force by fluid motion with helicity and two-dimensional periodicity. Geophys. Astrophys. Fluid Dyn. 2008, 102, 601–632. [Google Scholar] [CrossRef]
- Brandenburg, A. Memory effects in turbulent transport. Astrophys. J. 2009, 706, 712–726. [Google Scholar]
- Vodinchar, G. Hereditary Oscillator Associated with the Model of a Large-Scale αΩ-Dynamo. Mathematics 2020, 8, 2065. [Google Scholar] [CrossRef]
- Pechersky, D.M. Some characteristics of the geomagnetic field for 1700 Myears. Physica Zemli. 1997, 5, 3–20. (In Russian) [Google Scholar]
- Ermushev, A.V.; Rusmaikin, A.A.; Sokoloff, D.D. Fractal nature of the sequence of reverscals of the geomagnetic field. Magnetyhydrodynamics 1992, 4, 326–330. [Google Scholar]
- Gaffin, S. Analysis of scaling in the geomagnetic polarity reversal record. Phys. Earth Planet. Inter. 1989, 57, 284–290. [Google Scholar] [CrossRef]
- Anufriev, A.; Sokoloff, D. Fractal properties of geodynamo models. Geophys. Astrophys. Fluid Dyn. 1994, 74, 207–223. [Google Scholar] [CrossRef]
- Hollerbach, R.; Barenghi, C.; Lones, C. Taylor’s constraint in a spherical αω-dynamo. Geophys. Astrophys. Fluid Dyn. 1992, 67, 3–25. [Google Scholar] [CrossRef]
- Feschenko, L.; Vodinchar, G. Reversals in the large-scale αΩ-dynamo with memory. Nonlinear Process. Geophys. 2015, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Handbook of Fractional Calculus with Applications; Tenreiro, J.A.; De Gruyter, M. (Eds.) GmbH: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2014. [Google Scholar]
- Uchaikin, V. Fractional Derivatives Method; Artichoke: Ulyanovsk, Russia, 2008. (In Russian) [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Field, G.B.; Blackman, E.G. Quenching of the α2 Dynamo. Astrophys. J. 2002, 572, 685–692. [Google Scholar] [CrossRef] [Green Version]
- Brandenburg, A.; Sandin, C. Catastrophic alpha quenching alleviated by helicity flux and shear. Astron. Astrophys. 2004, 427, 13–21. [Google Scholar] [CrossRef]
- Ruzmaikin, A. The Solar Cycle a a Strange Attractor. Comments Astrophys. 1981, 9, 85–96. [Google Scholar]
- Knobloch, E. Chaos in the segmented disc dynamo. Phys. Lett. A 1981, 82, 439–440. [Google Scholar] [CrossRef]
- Vodinchar, G.; Kazakov, E. The Lorenz system and its generalizations as dynamo models with memory. E3S Web Conf. 2018, 62, 02011. [Google Scholar] [CrossRef]
- Kleeorin, K.; Ruzmaikin, A. Dynamics of the average turbulent helicity in a magnetic field. Magnetohydrodynamics 1982, 18, 116–122. [Google Scholar]
- Brandenburg, A.; Haugen, N.E.L.; Käpylä, P.J.; Sandin, C. The problem of small and large scale fields in the solar dynamo. Astron. Nachr. 2004, 326, 174–185. [Google Scholar] [CrossRef] [Green Version]
- Sur, S.; Subramanian, K. Galactic dynamo action in presence of stochastic α and shear. Mon. Not. R. Astron. Soc. Lett. 2008, 392, 6–10. [Google Scholar] [CrossRef] [Green Version]
- Dekker, K.; Verwer J., G. Stability of Runge-Kutta Methods for Stiff Nonlinear Differential Equations; North-Holland: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1984. [Google Scholar]
- Lorenz, E. Deterministic nonperiodic flow. J. Atm. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1982. [Google Scholar]
- Pchelintsev, A.N. Numerical and Physical Modeling of the Dynamics of the Lorenz System. Numer. Anal. Appl. 2014, 7, 159–167. [Google Scholar] [CrossRef]
- Sokoloff, D.; Nefedov, S. A small-mode approximation in the stellar dynamo problem. Numer. Methods Program. 2007, 8, 142–149. [Google Scholar]
- Roberts, P.H. Kinematic dynamo models. Phil. Trans. R. Soc. A 1972, 272, 663–668. [Google Scholar]
- Reshetnyak, M. Simulation of Dynamo Processes in Geophysics. Ph.D. Thesis, G. A. Gamburtsev Institute of Physics of the Earth, Moscow, Rusia, 2003. [Google Scholar]
- Pechersky, D.M.; Reshetnyak, M.Y.; Sokoloff, D.D. Fractal analysis of the geomagnetic polarity time scale. Geomagn. Aeron. 1997, 37, 132–142. (In Russian) [Google Scholar]
- Ivanov, S.S. Self-similarity of the geomagnetic field reversal sequence. Geomagn. Aeron. 1993, 33, 181–186. (In Russian) [Google Scholar]
- Schmitt, D.; Ossendrijver, M.A.J.H.; Hoyng, P. Magnetic field reversals and secular variation in a bistable dynamo model. Phys. Earth Planet. Inter. 2001, 125, 119–124. [Google Scholar] [CrossRef]
- Pétrélis, F.; Fauve, S.; Dormy, E.; Valet, J.P. Simple Mechanism for Reversals of Earth’s Magnetic Field. Phys. Rev. Lett. 2009, 102, 144503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rikitake, T. Electromagnetism and the Earth’s Interior; Elsevier: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Chossat, P.; Ambruster, D.; Oprea, I. A heteroclinic Model of Geodynamo Reversals and Excursions. In Dynamo and Dynamics, a Mathematical Challenge; Kluwer Academic: Dordrecht, The Netherlands, 2001. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vodinchar , G.; Feshchenko, L. Fractal Properties of the Magnetic Polarity Scale in the Stochastic Hereditary αω-Dynamo Model. Fractal Fract. 2022, 6, 328. https://doi.org/10.3390/fractalfract6060328
Vodinchar G, Feshchenko L. Fractal Properties of the Magnetic Polarity Scale in the Stochastic Hereditary αω-Dynamo Model. Fractal and Fractional. 2022; 6(6):328. https://doi.org/10.3390/fractalfract6060328
Chicago/Turabian StyleVodinchar , Gleb, and Lyubov Feshchenko. 2022. "Fractal Properties of the Magnetic Polarity Scale in the Stochastic Hereditary αω-Dynamo Model" Fractal and Fractional 6, no. 6: 328. https://doi.org/10.3390/fractalfract6060328
APA StyleVodinchar , G., & Feshchenko, L. (2022). Fractal Properties of the Magnetic Polarity Scale in the Stochastic Hereditary αω-Dynamo Model. Fractal and Fractional, 6(6), 328. https://doi.org/10.3390/fractalfract6060328





