Bazilevič Functions of Complex Order with Respect to Symmetric Points

Abstract

In this paper, we familiarize a class of multivalent functions with respect to symmetric points related to the differential operator and discuss the impact of Janowski functions on conic regions. Inclusion results, the subordination property, and coefficient inequalities are obtained. Further, the applications of our results that are extensions of those given in earlier works are presented as corollaries.

1. Introduction

Let $\mathbb{C},{\mathbb{Z}}^{-}$, and $\mathbb{N}$ denote the sets of complex numbers, negative integers, and natural numbers, respectively. Let ${\Lambda }_p$ denote the class of all analytic functions defined in the unit disc $\mathbb{E}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}$, which has the series representation of the form

$$\chi \left(z\right)=z^p+\sum _{k=1}^{\infty }{a}_{p+k}{z}^{p+k},(p=1,2,3,\dots ),$$

(1)

and let $\Lambda ={\Lambda }_1$. Further, let ${\mathcal{R}}_p$ denote the class of functions $r\left(z\right)$ that is analytic in the disc and that satisfies $\vartheta \left(0\right)=p$, $Re\left\{\vartheta \left(z\right)\right\}>0$ for all z in $\mathbb{E}$ and $\mathcal{R}={\mathcal{R}}_1$. The convolution (or Hadamard product) of two analytic functions $\chi \left(z\right)$ defined as in (1) and $g\left(z\right)=z^p+{\sum }_{k=1}^{\infty }{\Theta }_{p+k}{z}^{p+k}$ is defined by $(\chi *g)\left(z\right)=z^p+{\sum }_{k=1}^{\infty }{a}_{p+k}{\Theta }_{p+k}{z}^{p+k}$. In [1], Breaz et al. represented an operator ${\mathcal{T}}_{\lambda ,\delta }^m\chi \left(z\right)$ using the Hadamard product as follows.

$${\mathcal{T}}_{\lambda ,\delta }^m\chi \left(z\right)=z^p+\sum _{k=1}^{\infty }{\left[\frac{p+\lambda k}{p}\right]}^m{\mathrm{Y}}_{\delta }^k{a}_{p+k}{z}^{p+k},$$

(2)

where ${\mathrm{Y}}_{\delta }^k=\frac{{\prod }_{i=2}^{k+1}(i-2\delta )}{k!}$, $(0\le \delta <1,p=1,2,3,\dots )$, $m\in {\mathbb{N}}_0=\mathbb{N}\cup \left\{0\right\}$, and $0\le \lambda \le 1$. To add more versatility to our present study, we let ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ denote the operator defined by replacing ${\mathrm{Y}}_{\delta }^k$ with a arbitrary non-zero complex coefficient ${\Theta }_{p+k}$ in (2). Precisely, ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right):{\Lambda }_p⟶{\Lambda }_p$ is defined by

$${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)=z^p+\sum _{k=1}^{\infty }{\left[\frac{p+\lambda k}{p}\right]}^m{\Theta }_{p+k}{a}_{p+k}{z}^{p+k},$$

(3)

where $m\in N_0=N\cup \left\{0\right\}$ and $0\le \lambda \le 1$. From (3), we can easily see that

$${\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)=(1-\lambda ){\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)+\frac{\lambda }{p}z{\left({\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)\right)}^{{}^{\prime }}.$$

(4)

It can be easily seen that ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ reduces to new and well-known operators by assigning appropriate values to m, $\lambda$, and ${\Theta }_{p+k}$; see [2,3,4,5,6,7,8].

We let ≺ and ${\prec }_q$ denote the subordination and quasi-subordination, respectively. Note that $\chi /\ell \prec g$ implies $\chi {\prec }_{q}g$. For a detailed discussion and a formal definition of the quasi-subordination, the reader is referred to [9,10]. Throughout this paper, we let $\ell \left(z\right)=d_0+d_{1}z+d_2{z}^2+\cdots (d_0\ne 0)$ and $|d_0|\le 1$.

Motivated by the studies of Ahuja et al. [2] and Aouf et al. [11], we now define the following.

Definition 1.

For $t\in \mathbb{C}$, with $\left|t\right|\le 1$, $t\ne 1$, $\alpha >0$, and $\gamma \in \mathbb{C}\backslash \left\{0\right\}$, and ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ is defined as in (3), we say that the function $\chi \in {\Lambda }_p$ belongs to the class ${\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ if it satisfies the subordination condition

$$\frac{1}{\gamma }\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right]{\prec }_q\psi \left(z\right)-1,$$

(5)

where $\psi \in \mathcal{R}$, and ψ, which has a power series expansion of the form

$$\psi \left(z\right)=1+L_{1}z+L_2{z}^2+L_3{z}^3+\cdots ,z\in \mathbb{E},L_1>0.$$

(6)

Remark 1.

The class ${\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ reduces to the following classes of functions, which are well known in this field of research:

1. 

Setting $m=t=0$, ${\Theta }_{p+k}=1$, $\ell \left(z\right)=1$, and $\lambda =p=1$, we get

$${\mathcal{B}}_{\alpha }(\gamma ;\psi )=\left\{\chi \in \Lambda ;1+\frac{1}{\gamma }\left(\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}{\left(\frac{\chi \left(z\right)}{z}\right)}^{\alpha }-1\right)\prec \psi \left(z\right)\right\}.$$

Further, if we let $\gamma =0$ and $\psi \left(z\right)=\frac{1+z}{1-z}$ in ${\mathcal{B}}_{\alpha }(\gamma ;\psi )$, we get the well-known Bazilevič class of functions introduced by Bazilevič in [12].

2. 

If we let p = λ = 1, t = $-1$, α = 0, $\ell \left(z\right)$ = 1, and $\psi \left(z\right)=\frac{1+Az}{1+Bz}$, the class ${\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ reduces to

$${\mathcal{Q}}_s^{\gamma }(A,B,m)=\left\{\chi \in \Lambda :1+\frac{1}{\gamma }\left(\frac{2D^{m+1}\chi \left(z\right)}{D^m\chi \left(z\right)-D^m\chi (-z)}-1\right)\prec \frac{1+Az}{1+Bz}\right\},$$

where $D^m\chi$ denotes the Sălăgean derivative of χ. The class ${\mathcal{Q}}_s^{\gamma }(A,B,m)$ was recently introduced by Arif et al. in [13].

Motivated by [11,14,15,16,17], also we define the following.

Definition 2.

For $t\in \mathbb{C}$, with $\left|t\right|\le 1$, $t\ne 1$, $\alpha >0$, $\mu \in \mathbb{C}$, and $\gamma \in \mathbb{C}\backslash \left\{0\right\}$, and ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ is defined as in (3), we say that the function $\chi \in {\Lambda }_p$ belongs to the class ${\mathcal{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ if it satisfies the subordination condition

$$\begin{array}{c}(1+\mu ){\left(\frac{(1-t^p)z^p}{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}\right)}^{\alpha }\\ -\frac{\mu }{p}\frac{{(1-t^p)}^{\alpha }{z}^{p\alpha +1}{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)\right]}^{\prime }}{{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)\right]}^{\alpha +1}}{\prec }_q\psi \left(z\right),\end{array}$$

(7)

where $\psi \in \mathcal{R}$ is of the form (6).

Remark 2.

In [11], Aouf et al. listed five special cases of their function class; it could be easily seen that all of those classes are special cases of ${\mathcal{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$.

2. Prelimanries

Let $\mathcal{H}(a,n)$ be the subclass of $\Lambda$ consisting of functions of the form $\chi \left(z\right)=a+a_n{z}^n+a_{n+1}{z}^{n+1}+\dots$.

Now, we will state some results that we will be using to establish our main results.

Lemma 1

([18]). Let g be convex in $\mathbb{E}$, with $g\left(0\right)=a$, $\delta \ne 0$, and $Re\left\{\delta \right\}>0$. Suppose that $\vartheta \left(z\right)$ is analytic, and $\mathbb{E}$ is given by

$$\vartheta \left(z\right)=a+{\vartheta }_n{z}^n+{\vartheta }_{n+1}{z}^{n+1}+\cdots ,z\in \mathbb{E}.$$

(8)

If

$$\vartheta \left(z\right)+\frac{z{\vartheta }^{{}^{\prime }}\left(z\right)}{\delta }\prec g\left(z\right),$$

then

$$\vartheta \left(z\right)\prec q\left(z\right)\prec g\left(z\right),$$

where

$$q\left(z\right)=\frac{\delta }{n{z}^{\delta /n}}{\int }_0^{z}g\left(\zeta \right){\zeta }^{(\delta /n)-1}d\zeta .$$

The function q is convex and is the best $(a,n)$-dominant.

Lemma 2

([19], p. 76). Let g be starlike in $\mathbb{E}$, with $g\left(0\right)=0$. If $\vartheta \in \mathcal{H}(a,n)$ satisfies

$$z{\vartheta }^{{}^{\prime }}\left(z\right)\prec g\left(z\right),$$

then

$$\vartheta \left(z\right)\prec q\left(z\right)=a+n^{-1}{\int }_0^{z}g\left(\zeta \right){\zeta }^{-1}d\zeta .$$

The function q is convex and is the best $(a,n)$-dominant.

Remark 3.

Lemma 1 for the case of $n=1$ was earlier given by Suffridge [20].

Lemma 3

([21]). If $\vartheta \left(z\right)=1+{\displaystyle \sum _{k=1}^{\infty }}{\vartheta }_k{z}^k\in \mathcal{R}$, then $\left|{\vartheta }_k\right|\le 2$ for all $k\ge 1$, and the inequality is sharp for ${\displaystyle {\vartheta }_{\mu }\left(z\right)=\frac{1+\mu z}{1-\mu z},\left|\mu \right|\le 1}$.

Lemma 4

([22]). Let $\vartheta \left(z\right)=1+{\displaystyle \sum _{k=1}^{\infty }}{\vartheta }_k{z}^k\in \mathcal{R}$, and also let v be a complex number; then,

$$|{\vartheta }_2-v{\vartheta }_1^2|\le 2max\left\{1,|2v-1|\right\},$$

the result is sharp for functions given by

$$\vartheta \left(z\right)=\frac{1+z^2}{1-z^2},\vartheta \left(z\right)=\frac{1+z}{1-z}.$$

We define the function $\vartheta \left(z\right)$ by

$$\vartheta \left(z\right)=1+{\vartheta }_{1}z+{\vartheta }_2{z}^2+\cdots =\frac{1+w\left(z\right)}{1-w\left(z\right)}\prec \frac{1+z}{1-z},(z\in \mathbb{E}).$$

(9)

We can note that $\vartheta \left(0\right)=1$ and $\vartheta \in \mathcal{R}$ (see Lemma 3). Using (9), it is easy to see that

$$w\left(z\right)=\frac{\vartheta \left(z\right)-1}{\vartheta \left(z\right)+1}=\frac{1}{2}\left[{\vartheta }_{1}z+\left({\vartheta }_2-\frac{{\vartheta }_1^2}{2}\right)z^2+\left({\vartheta }_3-{\vartheta }_1{\vartheta }_2+\frac{{\vartheta }_1^3}{4}\right)z^3+\cdots \right].$$

For some $\ell \left(z\right)=d_0+d_{1}z+d_2{z}^2+\cdots (d_0\ne 0$ and $|d_0|\le 1$), we have (see [10])

$$\begin{array}{c}\hfill 1+\gamma \ell \left(z\right)\left\{\psi \left[w\right(z\left)\right]-1\right\}=1+\frac{1}{2}\gamma L_1{d}_0{\vartheta }_{1}z\\ \hfill +\gamma \left[d_0\left(\frac{1}{2}{L}_1\left({\vartheta }_2-\frac{{\vartheta }_1^2}{2}\right)+\frac{1}{4}{L}_2{\vartheta }_1^2\right)+\frac{d_1{L}_1{\vartheta }_1}{2}\right]z^2+\cdots .\end{array}$$

(10)

3. Main Results

It is well known that functions in $\mathcal{R}$ need not be convex or univalent. However, in this section, we will work with the restriction that $\psi \in \mathcal{R}$ is convex and univalent in $\mathbb{E}$.

We begin with the following.

Theorem 1.

Let ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)\in {\Lambda }_p$ with ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ and ${\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. In addition, let $\psi \left(z\right)$ be convex univalent in $\mathbb{E}$ with $\psi \left(0\right)=1$ and $Re\psi \left(z\right)>0$. Further, suppose that

$$\begin{array}{c}\frac{1}{\gamma \ell \left(z\right)}\left[\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}}{z^{p\alpha }{(1-t^p)}^{\alpha -1}}-1\right][1-\frac{z{\ell }^{\prime }\left(z\right)}{\ell \left(z\right)}-p\alpha -\frac{p\alpha {(1-t^p)}^{\alpha -1}{z}^{p\alpha -1}}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}-z^{p\alpha }{(1-t^p)}^{\alpha -1}}\hfill \\ +\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}-z^{p\alpha }{(1-t^p)}^{\alpha -1}}\left(\frac{z{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\right]}^{\prime }}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}+\frac{(\alpha -1)z{\Gamma }^{\prime }\left(z\right)}{\Gamma \left(z\right)}\right)]+1\prec \psi \left(z\right),\hfill \end{array}$$

(11)

where $\Gamma \left(z\right)={\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)$. Then,

$$\frac{1}{\gamma }\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right]{\prec }_{q}Q\left(z\right)-1$$

(12)

where

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\psi \left(\zeta \right)d\zeta$$

and Q is convex and is the best dominant.

Proof. 

Let

$$k\left(z\right)=1+\frac{1}{\gamma \ell \left(z\right)}\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right](z\in \mathbb{E}),$$

then $k\left(z\right)=1+k_{1}z+k_2{z}^2+\cdots \in \mathcal{H}(1,1)$ with $k\left(z\right)\ne 0$ in $\mathbb{E}$. Since $\psi \left(z\right)$ is convex, it can be easily seen that Q is convex and univalent in $\mathbb{E}$. On computation, we have

$$\begin{array}{c}\frac{z{k}^{{}^{\prime }}\left(z\right)}{k\left(z\right)-1}=[\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}-z^{p\alpha }{(1-t^p)}^{\alpha -1}}\left(\frac{z{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\right]}^{\prime }}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}+\frac{(\alpha -1)z{\Gamma }^{\prime }\left(z\right)}{\Gamma \left(z\right)}\right)\\ -\frac{z{\ell }^{\prime }\left(z\right)}{\ell \left(z\right)}-p\alpha -\frac{p\alpha {(1-t^p)}^{\alpha -1}{z}^{p\alpha -1}}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}-z^{p\alpha }{(1-t^p)}^{\alpha -1}}].\end{array}$$

Thus, by (11), we have

$$k\left(z\right)+z{k}^{{}^{\prime }}\left(z\right)\prec \psi \left(z\right)(z\in \mathbb{E}).$$

(13)

Now, by Lemma 1, we deduce that $k\left(z\right)\prec Q\left(z\right)\prec \psi \left(z\right)$. Since $Re\left\{\psi \left(z\right)\right\}>0$ and $Q\left(z\right)\prec \psi \left(z\right)$, we also have $ReQ\left(z\right)>0$. Since subordination is invariant under translation and using the fact that $k\left(z\right)/\ell \left(z\right)\prec \psi \left(z\right)$ implies $k\left(z\right){\prec }_q\psi \left(z\right)$, we have

$$\frac{1}{\gamma }\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right]{\prec }_{q}Q\left(z\right)-1,$$

and the proof is complete. □

Letting $\alpha =0$ and $\ell \left(z\right)=1$ in Theorem 1, we get the following result.

Corollary 1.

Let ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)\in {\Lambda }^p$ with ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ and ${\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. In addition, let $\psi \left(z\right)$ be convex univalent in $\mathbb{E}$ with $\psi \left(0\right)=1$ and $Re\psi \left(z\right)>0$. Further, suppose that

$$\begin{array}{c}\frac{1}{\gamma }\left(\frac{(1-t^p){\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{\Gamma \left(z\right)}-1\right)[1+\frac{(1-t^p){\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{(1-t^p){\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)-\Gamma \left(z\right)}\\ \left(\frac{z{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\right]}^{\prime }}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}-\frac{z{\left[\Gamma \left(z\right)\right]}^{\prime }}{\Gamma \left(z\right)}\right)]+1\prec \psi \left(z\right),\end{array}$$

where $\Gamma \left(z\right)={\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)$. Then,

$$1+\frac{1}{\gamma }\left(\frac{(1-t^p){\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)\right]}-1\right)\prec Q\left(z\right)$$

where

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\psi \left(\zeta \right)d\zeta$$

and Q is convex and is the best dominant.

If we let $p=\lambda =1$, $t=-1$, $m=0$, and ${\Theta }_{p+k}=1$ in Corollary 1, we get the following.

Corollary 2.

Let $\chi \left(z\right)\in \Lambda$ with $\chi \left(z\right)$ and ${\chi }^{\prime }\left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. In addition, let $\psi \left(z\right)$ be convex univalent in $\mathbb{E}$ with $\psi \left(0\right)=1$ and $Re\psi \left(z\right)>0$. Further, suppose that

$$\begin{array}{c}\frac{1}{\gamma }\left(\frac{2z{\chi }^{\prime }\left(z\right)}{\left[\chi \left(z\right)-\chi (-z)\right]}-1\right)(1+\frac{2z^2{\chi }^{″}\left(z\right)}{2{\chi }^{\prime }\left(z\right)-\chi \left(z\right)+\chi (-z)}\\ -\frac{2z^2{\chi }^{\prime }\left(z\right){\left[\chi \left(z\right)-\chi (-z)\right]}^{\prime }}{\left[\chi \left(z\right)-\chi (-z)\right]\left\{2{\chi }^{\prime }\left(z\right)-\chi \left(z\right)+\chi (-z)\right\}})+1\prec \psi \left(z\right).\end{array}$$

Then,

$$1+\frac{1}{\gamma }\left(\frac{2z{\chi }^{\prime }\left(z\right)}{\left[\chi \left(z\right)-\chi (-z)\right]}-1\right)\prec Q\left(z\right)$$

where

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\psi \left(\zeta \right)d\zeta$$

and Q is convex and is the best dominant.

If we let $p=\lambda =1$, $t=0$, $m=0$, and ${\Theta }_{p+k}=1$ in Corollary 1, we get the following.

Corollary 3.

Let $\chi \left(z\right)\in \Lambda$ with $\chi \left(z\right)$ and ${\chi }^{\prime }\left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. In addition, let $\psi \left(z\right)$ be convex univalent in $\mathbb{E}$ with $\psi \left(0\right)=1$ and $Re\psi \left(z\right)>0$. Further, suppose that

$$\begin{array}{c}\frac{1}{\gamma }\left(\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}-1\right)\left(1+\frac{z^2{\chi }^{″}\left(z\right)}{z{\chi }^{\prime }\left(z\right)-\chi \left(z\right)}-\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\right)+1\prec \psi \left(z\right).\end{array}$$

Then,

$$1+\frac{1}{\gamma }\left(\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}-1\right)\prec Q\left(z\right)$$

where

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\psi \left(\zeta \right)d\zeta$$

and Q is convex and is the best dominant.

Theorem 2.

Let $\psi \left(z\right)$ be convex univalent in $\mathbb{E}$ with $\psi \left(0\right)=1$ and $Re\psi \left(z\right)>0$. If $\chi \left(z\right)\in {\mathcal{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ with $Re\left(\mu \right)>0$, then

$${\left(\frac{(1-t^p)z^p}{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}\right)}^{\alpha }\prec Q\left(z\right)$$

(14)

where the function

$$Q\left(z\right)=\frac{1}{z}{\int }_0^z\psi \left(t\right)dt$$

and Q is convex and is the best dominant.

Proof. 

Let

$$k\left(z\right)={\left(\frac{(1-t^p)z^p}{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}\right)}^{\alpha }(z\in \mathbb{E}),$$

then $k\left(z\right)=1+k_{1}z+k_2{z}^2+\cdots \in \mathcal{H}(1,1)$ with $k\left(z\right)\ne 0$ in $\mathbb{E}$. Since $\psi \left(z\right)$ is convex, it can be easily seen that Q is convex and univalent in $\mathbb{E}$. On computation, we have

$$\begin{array}{c}(1+\mu ){\left(\frac{(1-t^p)z^p}{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}\right)}^{\alpha }-\frac{\mu }{p}\frac{{(1-t^p)}^{\alpha }{z}^{p\alpha +1}{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)\right]}^{\prime }}{{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)\right]}^{\alpha +1}}\\ =k\left(z\right)+\frac{\mu }{p\alpha }z{k}^{\prime }\left(z\right).\end{array}$$

Now, by Lemma 1, we deduce that $k\left(z\right)\prec Q\left(z\right)\prec \psi \left(z\right)$. Since $Re\psi \left(z\right)>0$ and $Q\left(z\right)\prec \psi \left(z\right)$, we also have $ReQ\left(z\right)>0$, and the proof is complete. □

The following corollary is a consequence of Theorem 2, which is closer to the result recently obtained by Aouf et al. [11] (Theorem 1).

Corollary 4.

If $\chi \left(z\right)\in {\mathcal{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ with $\psi =\frac{1+Az}{1+Bz},(-1\le B<A\le 1)$, then

$${\left(\frac{(1-t^p)z^p}{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}\right)}^{\alpha }\prec Q\left(z\right)\prec \frac{1+Az}{1+Bz}$$

(15)

where the function Q is given by

$$Q\left(z\right)=\left\{\begin{array}{cc}\frac{A}{B}+\left(1-\frac{A}{B}\right){(1+Bz)}^{-1}{}_2{F}_1\left(1,1;\frac{p\alpha }{\mu }+1;\frac{Bz}{1+Bz}\right),\hfill & B\ne 0\hfill \\ 1+\frac{p\alpha }{p\alpha +\mu }Az,\hfill & B=0.\hfill \end{array}\right.$$

The function Q is convex and is the best dominant of (15). Furthermore,

$$Re{\left(\frac{(1-t^p)z^p}{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}\right)}^{\alpha }>\delta ,(z\in \mathbb{E}),$$

where

$$\delta =\left\{\begin{array}{cc}\frac{A}{B}+\left(1-\frac{A}{B}\right){(1-B)}^{-1}{}_2{F}_1\left(1,1;\frac{p\alpha }{\mu }+1;\frac{B}{B-1}\right),\hfill & B\ne 0\hfill \\ 1\frac{p\alpha }{p\alpha +\mu }A,\hfill & B=0.\hfill \end{array}\right.$$

Proof. 

The function $\psi \left(z\right)=\frac{1+Az}{1+Bz}$ is convex and univalent in $\mathbb{E}$ provided that $-1\le B<A\le 1$. Now, replacing $\psi \left(z\right)=\frac{1+Az}{1+Bz}$ in Theorem 11 and retracing the computation as Aouf et al. [11] (Theorem 1) did, we can establish the assertion of the Corollary. □

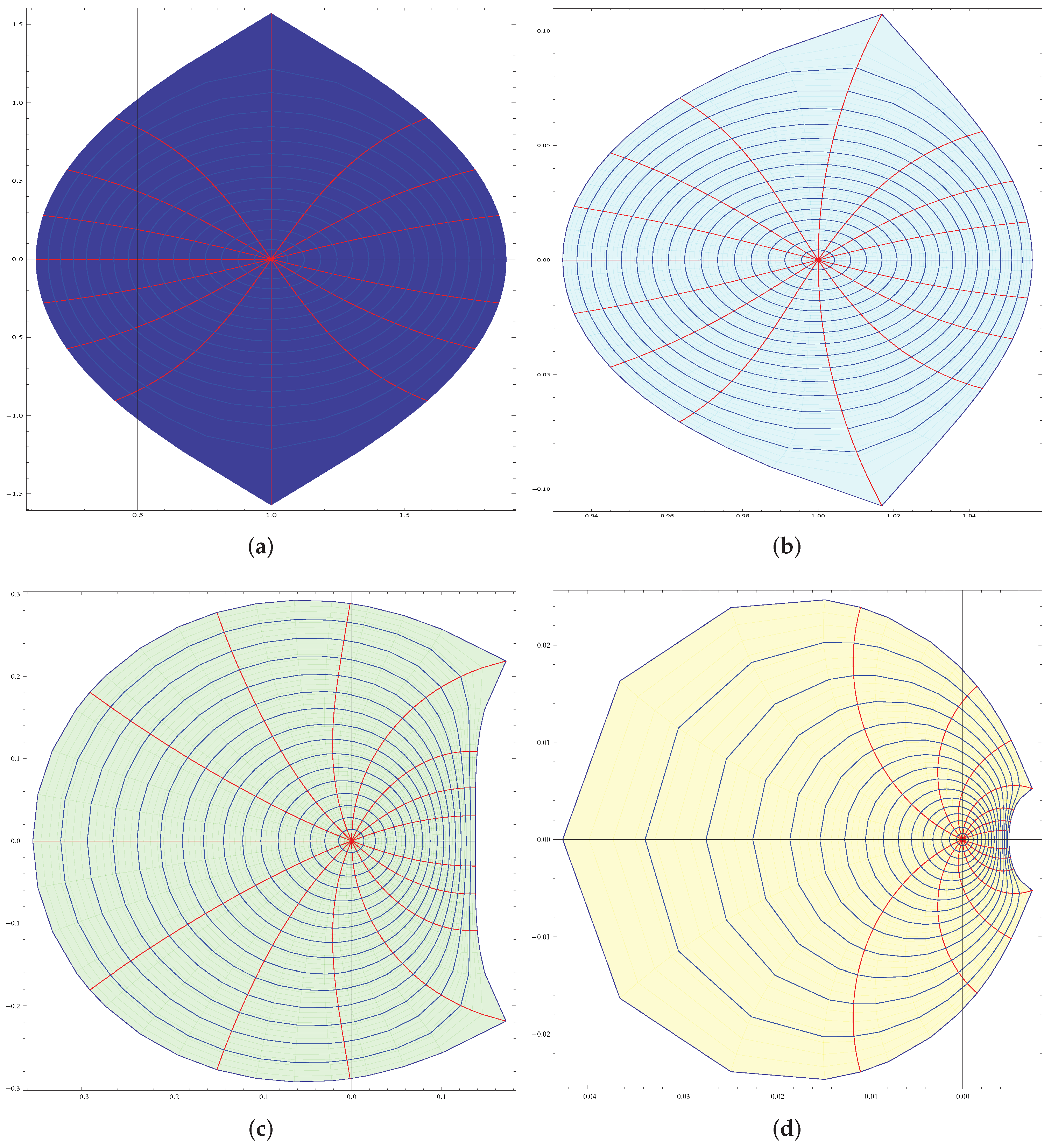
Applications to a Petal-Shaped Domain

The study of classes of analytic functions restricted to a conic domain was reignited by Dziok et al. [23,24,25] (also see [26,27,28,29,30]). The reader is referred to Mendiratta et al. [31], in which the authors have summarized recent developments. To obtain the applications of our main results to a conic region, here, we choose the function $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$, as it satisfies the conditions of Theorem 1. The function $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$ is convex univalent in $\mathbb{E}$ and has a Maclaurin series of the form

$$1+{sinh}^{-1}\left(z\right)=1+z-\frac{z^3}{6}+\frac{3z^5}{40}-\frac{5z^7}{112}+\frac{35z^9}{1152}-\frac{63z^{11}}{2816}+\cdots .$$

The function $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$ maps the unit disc onto a petal shaped region in the w-plane (see Figure 1a). From Figure 1a, it can be seen that $\psi \left(0\right)=1$ and $Re\left[\psi \right(z\left)\right]>0$ for all $z\in \mathbb{E}$. For studies related to starlike functions that are related to the petal-shaped domain, the reader is referred to [32,33,34]. Replacing $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$, $p=\lambda =1$, $t=-1$$\alpha =m=0$, ${\Theta }_{p+k}=1$, and $\gamma =1+0i$ in Theorem 1, we have the following result.

Corollary 5.

Let $\chi \left(z\right)\in \Lambda$ with $\chi \left(z\right)$ and ${\chi }^{\prime }\left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. Further, suppose that

$$\begin{array}{c}\left(\frac{2z{\chi }^{\prime }\left(z\right)}{\left[\chi \left(z\right)-\chi (-z)\right]}\right)\left(2+\frac{z{\chi }^{″}\left(z\right)}{{\chi }^{\prime }\left(z\right)}-\frac{z{\left[\chi \left(z\right)-\chi (-z)\right]}^{\prime }}{\left[\chi \left(z\right)-\chi (-z)\right]}\right)\prec 1+{sinh}^{-1}\left(z\right).\end{array}$$

Then,

$$\frac{2z{\chi }^{\prime }\left(z\right)}{\left[\chi \left(z\right)-\chi (-z)\right]}\prec 1+{sinh}^{-1}\left(z\right)+\frac{1-\sqrt{1+z^2}}{z}.$$

The impact of the famous Janowski function on the conic region was first found by Noor and Malik in [35]. Subsequently, it was studied by other researchers (the reader is referred to [1,10,36,37] and the references provided therein). Let the function $N(A,B,\psi )$ be defined as

$$N(A,B,\psi )=\frac{(A+1)\psi \left(z\right)-(A-1)}{(B+1)\psi \left(z\right)-(B-1)}.$$

The convex domain $1+{sinh}^{-1}\left(z\right)$ becomes starlike with respect to the point 0 under the impact of $N(A,B,\psi )-1$ (see Figure 1). Notice that the top tip of the petal is tilted in the clockwise direction and the bottom tip of the petal is tilted in the counter-clockwise direction, which makes the petal-shaped domain into a lune-shaped domain.

Remark 4.

The purpose of choosing $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$ over other conic region is that, on the impact of $N(A,B,\psi )$, the function $1+{sinh}^{-1}\left(z\right)$ that maps unit disc onto convex domain becomes convex with respect to the point 0 (starlike).

Theorems 1 and 2 require the superordinate function to be convex, and it should be mapped onto the right half plane. If the superordinate function is starlike along with the condition that it will be zero at $z=0$, we will use Lemma 2 to obtain the sufficient conditions for starlikeness.

Theorem 3.

Let $\chi \left(z\right)\in \Lambda$ with ${\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)$ and ${\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. In addition, let $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$ be defined in $\mathbb{E}$. Further, suppose that

$$\begin{array}{c}\frac{1}{\gamma \ell \left(z\right)}\left[1-\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}}{z^{p\alpha }{(1-t^p)}^{\alpha -1}}\right][\frac{z{\ell }^{\prime }\left(z\right)}{\ell \left(z\right)}+p\alpha +\frac{p\alpha {(1-t^p)}^{\alpha -1}{z}^{p\alpha -1}}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}-z^{p\alpha }{(1-t^p)}^{\alpha -1}}\\ -\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left[\Gamma \left(z\right)\right]}^{\alpha -1}-z^{p\alpha }{(1-t^p)}^{\alpha -1}}\left(\frac{z{\left[{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)\right]}^{\prime }}{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}+\frac{(\alpha -1)z{\Gamma }^{\prime }\left(z\right)}{\Gamma \left(z\right)}\right)]\\ {\prec }_q\frac{(A+1)\psi \left(z\right)-(A-1)}{(B+1)\psi \left(z\right)-(B-1)}-1,\end{array}$$

where $\Gamma \left(z\right)={\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)$. Then,

$$1+\frac{1}{\gamma }\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right]{\prec }_{q}M\left(z\right),$$

where

$$M\left(z\right)=1+{\int }_0^z\left[\frac{(A+1)\psi \left(\zeta \right)-(A-1)}{(B+1)\psi \left(\zeta \right)-(B-1)}-1\right]{\zeta }^{-1}d\zeta .$$

M is convex and is the best dominant.

Proof. 

Here, the function $h\left(z\right)=\frac{(A+1)\psi \left(z\right)-(A-1)}{(B+1)\psi \left(z\right)-(B-1)}-1$ is starlike with respect to 0, but the real part of $h\left(z\right)$ is not greater than zero. So, we will use Lemma 2 to establish the assertion of the Corollary. □

Setting $p=\lambda =1$, $t=0$, $\alpha =m=0$, ${\Theta }_{p+k}=1$, and $\gamma =1$ in Theorem 3, we get the following.

Corollary 6.

Let $\chi \left(z\right)\in \Lambda$ with $\chi \left(z\right)$ and ${\chi }^{\prime }\left(z\right)\ne 0$ for all $z\in \mathbb{E}\backslash \left\{0\right\}$. In addition, let $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$ be defined in $\mathbb{E}$. Further, suppose that

$$\begin{array}{c}\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\left[1+\frac{z{\chi }^{″}\left(z\right)}{{\chi }^{\prime }\left(z\right)}-\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\right]\prec \frac{(A+1)\psi \left(z\right)-(A-1)}{(B+1)\psi \left(z\right)-(B-1)}-1\end{array}$$

with $\psi \left(z\right)=1+{sinh}^{-1}\left(z\right)$. Then,

$$\frac{z{\chi }^{\prime }\left(z\right)}{\chi \left(z\right)}\prec M\left(z\right),$$

where

$$M\left(z\right)=1+{\int }_0^z\left[\frac{(A+1)\psi \left(\zeta \right)-(A-1)}{(B+1)\psi \left(\zeta \right)-(B-1)}-1\right]{\zeta }^{-1}d\zeta .$$

M is convex and is the best dominant.

4. Coefficient Estimates for Functions in ${\mathfrak{N}}_{\mathbf{p}}^{\mathbf{m}}(\mathbf{\alpha };\mathbf{t};\mathbf{\lambda };\mathbf{\gamma };\mathbf{\psi };{\Theta }_{\mathbf{p}+\mathbf{k}})$ and ${\mathcal{N}}_{\mathbf{p}}^{\mathbf{m}}(\mathbf{\alpha };\mathbf{t};\mathbf{\lambda };\mathbf{\gamma };\mathbf{\psi };{\Theta }_{\mathbf{p}+\mathbf{k}})$

Let $\mathcal{L}$ denote the class of all functions $\ell \left(z\right)$ that are analytic in $\mathbb{E}$ and that satisfy $|\ell (z\left)\right|\le 1$.

Unlike in the previous section, here, we do not restrict $\psi$ to being convex or starlike.

Theorem 4.

Let $\ell \left(z\right)=d_0+d_{1}z+d_2{z}^2+\cdots \in \mathcal{L}$ with $d_n\in \mathbb{C}\forall n\ge 0;d_0\ne 0\mathrm{and}\left|d_0\right|\le 1$. If the function $\chi \left(z\right)$ is given by (1) and if $\chi \in {\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ with $\psi \left(z\right)=1+L_{1}z+L_2{z}^2+L_3{z}^3+\cdots ,(L_1>0;z\in \mathbb{E})$, then the estimates of the initial coefficients of χ are

$$\left|a_{p+1}\right|\le \frac{L_1\left|\gamma \right|}{{\left(\frac{p+\lambda }{p}\right)}^m\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]\left|{\Theta }_{p+1}\right|}$$

(16)

and

$$\begin{array}{c}\hfill |a_{p+2}|\le \frac{L_1\left|\gamma \right|}{{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]\left|{\Theta }_{p+2}\right|}\left[\left|\frac{d_1}{d_0}\right|+max\left\{1,\left|\frac{L_2}{L_1}\right.\right.\right.\\ \hfill \left.\left.\left.-L_1\frac{\gamma d_0(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}{{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2}\right|\right\}\right].\end{array}$$

(17)

In addition, for all $\mu \in \mathbb{C}$, we have

$$\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{L_1\left|\gamma \right|}{{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]\left|{\Theta }_{p+2}\right|}\left[\left|\frac{d_1}{d_0}\right|+max\left\{1,\left|2{\mathcal{H}}_1-1\right|\right\}\right],$$

(18)

where ${\mathcal{H}}_1$ is given by

$$\begin{array}{c}\hfill {\mathcal{H}}_1=\frac{1}{2}\left(1-\frac{L_2}{L_1}+L_1\frac{\gamma d_0(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}{{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2}\right.\\ \hfill \left.+\frac{\mu d_0\gamma L_1{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]{\Theta }_{p+2}}{{\left(\frac{p+\lambda }{p}\right)}^{2m}{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2{\Theta }_{p+1}^2}\right).\end{array}$$

The inequality is sharp for each $\mu \in \mathbb{C}$.

Proof. 

Let $\chi \in {\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$. Then, by the definition of quasi-subordination of analytic functions, there is a function $\ell \left(z\right)=d_0+d_{1}z+d_2{z}^2+\cdots (d_0\ne 0)$ such that

$$\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}=1+\gamma \ell \left(z\right)\left\{\psi \left[w\right(z\left)\right]-1\right\},$$

(19)

where $w\left(z\right)$ is the Schwartz function. The left-hand side of (19) will be

$$\begin{array}{c}\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right){\left({\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)\right)}^{\alpha -1}}{{(1-t^p)}^{\alpha -1}{z}^{p\alpha }}=1+{\left(\frac{p+\lambda }{p}\right)}^m\left[\left(\frac{p+\lambda }{p}\right)+\right.\\ \left.(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]a_{p+1}{\Theta }_{p+1}z+\{{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]a_{p+2}{\Theta }_{p+2}\\ +(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right){\left(\frac{p+\lambda }{p}\right)}^{2m}\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]a_{p+1}^2{\Theta }_{p+1}^2\}{z}^2+\cdots \end{array}$$

(20)

where ${\Theta }_{p+k}$s are the corresponding coefficients from the power series expansion of h, which may be real or complex. By using (10) and (20), we have

$$a_{p+1}=\frac{d_0\gamma L_1{\vartheta }_1}{2{\left(\frac{p+\lambda }{p}\right)}^m\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]{\Theta }_{p+1}},$$

(21)

$$\begin{array}{c}\hfill a_{p+2}=\frac{L_1{d}_0\gamma }{2{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]{\Theta }_{p+2}}\left[{\vartheta }_2-\frac{1}{2}\left(1-\frac{L_2}{L_1}\right.\right.\\ \hfill \left.\left.+L_1\frac{\gamma d_0(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}{{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2}\right){\vartheta }_1^2+\frac{d_1{\vartheta }_1}{d_0}\right].\end{array}$$

(22)

Applying Lemma 3 in (21) and (22), we can establish the respective inequalities (16) and (17). In view of (21) and (22), we have for $\mu \in \mathbb{C}$ (see [10] (Theorem 4.1)):

$$\begin{array}{c}\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{L_1\left|\gamma \right|}{2{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]\left|{\Theta }_{p+2}\right|}\left[2+2\left|\frac{d_1}{d_0}\right|+\right.\\ \frac{1}{2}{\left|{\vartheta }_1\right|}^2\left(\left|\frac{L_2}{L_1}-L_1\frac{\gamma d_0(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}{{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2}\right.\right.\\ \left.\left.\left.-\frac{\mu d_0\gamma L_1{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]{\Theta }_{p+2}}{{\left(\frac{p+\lambda }{p}\right)}^{2m}{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2{\Theta }_{p+1}^2}\right|-1\right)\right].\end{array}$$

(23)

Let us denote

$$\begin{array}{c}\hfill X=\left|\frac{L_2}{L_1}-L_1\frac{\gamma d_0(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}{{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2}\right.\\ \hfill \left.-\frac{\mu d_0\gamma L_1{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]{\Theta }_{p+2}}{{\left(\frac{p+\lambda }{p}\right)}^{2m}{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2{\Theta }_{p+1}^2}\right|.\end{array}$$

Now, if $X\le 1$, then (4) reduces to

$$\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{L_1\left|\gamma \right|}{{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]\left|{\Theta }_{p+2}\right|}\left[1+\left|\frac{d_1}{d_0}\right|\right].$$

(24)

Now, if $X\ge 1$, then (4) reduces to

$$\begin{array}{c}\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{L_1\left|\gamma \right|}{{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]\left|{\Theta }_{p+2}\right|}\left[\left|\frac{d_1}{d_0}\right|+\right.\\ \left|\frac{L_2}{L_1}-L_1\frac{\gamma d_0(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\left[\left(\frac{p+\lambda }{p}\right)+\frac{(\alpha -2)}{2}\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}{{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2}\right.\\ \left.\left.-\frac{\mu d_0\gamma L_1{\left(\frac{p+2\lambda }{p}\right)}^m\left[\frac{p+2\lambda }{p}+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]{\Theta }_{p+2}}{{\left(\frac{p+\lambda }{p}\right)}^{2m}{\left[\left(\frac{p+\lambda }{p}\right)+(\alpha -1)\left(\frac{1-t^{p+1}}{1-t^p}\right)\right]}^2{\Theta }_{p+1}^2}\right|\right].\end{array}$$

(25)

The equality holds for (24) if ${\vartheta }_1=0,{\vartheta }_2=2$. Equivalently, we have $\vartheta \left(z\right)={\vartheta }_2\left(z\right)=\frac{1+z^2}{1-z^2}$ by Lemma 4. Therefore, the extremal function in ${\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k}),(z\in \mathbb{E})$ is given by

$$\begin{array}{c}\hfill \frac{1}{\gamma }\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right]\\ \hfill =\ell \left(z\right)\left(\frac{{\vartheta }_2\left(z\right)-1}{{\vartheta }_2\left(z\right)+1}\right)=\ell \left(z\right)\left[\psi \left(z^2\right)-1\right],(z\in \mathbb{E}).\end{array}$$

Similarly, the equality holds for (4) if ${\vartheta }_2=2$. Equivalently, we have $p\left(z\right)=p_1\left(z\right)=\frac{1+z}{1-z}$ by Lemma 4. Therefore, the extremal function in ${\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k}),(z\in \mathbb{E})$ is given by

$$\begin{array}{c}\hfill \frac{1}{\gamma }\left[\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^{m+1}\chi \left(z\right)}{z^p}\right){\left(\frac{{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(z\right)-{\mathcal{T}}_{{\Theta }_{p+k}}^m\chi \left(tz\right)}{(1-t^p)z^p}\right)}^{\alpha -1}-1\right]\\ \hfill =\ell \left(z\right)\left(\frac{{\vartheta }_1\left(z\right)-1}{{\vartheta }_1\left(z\right)+1}\right)=\ell \left(z\right)\left[\psi \left(z\right)-1\right],(z\in \mathbb{E}).\end{array}$$

□

Theorem 5.

Let $\ell \left(z\right)=d_0+d_{1}z+d_2{z}^2+\cdots \in \mathcal{L}$ with $d_n\in \mathbb{C}\forall n\ge 0;d_0\ne 0\mathrm{and}\left|d_0\right|\le 1$. If the function $\chi \left(z\right)$ is given by (1) and if $\chi \in {\mathfrak{N}}_p^m(\alpha ;t;\lambda ;\gamma ;\psi ;{\Theta }_{p+k})$ with $\psi \left(z\right)=1+L_{1}z+L_2{z}^2+L_3{z}^3+\cdots ,(L_1>0;z\in \mathbb{E})$, then the estimates of the initial coefficients of χ are

$$\left|a_{p+1}\right|\le \frac{p^{m+1}(1-t^p)L_1\left|\gamma \right|}{\left(1-t^{p+1}\right){\left(p+\lambda \right)}^m\left(\mu +p\alpha \right)\left|{\Theta }_{p+1}\right|}$$

and

$$\begin{array}{c}\hfill |a_{p+2}|\le \frac{(1-t^p)p^{m+1}{L}_1\left|\gamma \right|}{\left(1-t^{p+1}\right){\left(p+2\lambda \right)}^m\left(\mu +p\alpha \right)\left|{\Theta }_{p+2}\right|}\left[\left|\frac{d_1}{d_0}\right|+max\left\{1,\left|\frac{L_2}{L_1}\right.\right.\right.\\ \hfill \left.\left.\left.-L_1\frac{2p\gamma d_0(1-t^p)}{{(\mu +p\alpha )}^2\left[2\mu (\alpha +1)+p\alpha (\alpha +1)\right]}\right|\right\}\right].\end{array}$$

In addition, for all $\mu \in \mathbb{C}$, we have

$$\left|a_{p+2}-\mu a_{p+1}^2\right|\le \frac{(1-t^p)p^{m+1}{L}_1\left|\gamma \right|}{\left(1-t^{p+1}\right){\left(p+2\lambda \right)}^m\left(\mu +p\alpha \right)\left|{\Theta }_{p+2}\right|}\left[\left|\frac{d_1}{d_0}\right|+max\left\{1,\left|2{\mathcal{H}}_2-1\right|\right\}\right],$$

where ${\mathcal{H}}_2$ is given by

$$\begin{array}{c}\hfill {\mathcal{H}}_2=\frac{1}{2}\left(1-\frac{L_2}{L_1}+\frac{2p\gamma L_1{d}_0(1-t^p)}{{(\mu +p\alpha )}^2\left[2\mu (\alpha +1)+p\alpha (\alpha +1)\right]}+\frac{\mu d_0\gamma L_1(1-t^p)p^{m+1}{(p+2\lambda )}^m{\Theta }_{p+2}}{(1-t^{p+1}){(p+\lambda )}^{2m}(\mu +p\alpha ){\Theta }_{p+1}^2}\right).\end{array}$$

The inequality is sharp for each $\mu \in \mathbb{C}$.

Remark 5.

It can be seen that by setting different values for the parameters involved, we can obtain several results as special cases of our main results. The reader is referred to [37] for various applications of our main results.

5. Conclusions

We have demarcated a different family of multivalent Bazilevič functions that connect the convex combinations of analytic functions. We have used a comprehensive differential operator to define multivalent functions of complex order with respect to symmetric points to amalgamate the study of several classes of p-valent functions. Solutions to the Fekete–Szegö problem and sufficient conditions for starlikeness are the foremost results of this paper. Applications involving a conic domain were deliberated in detail. We also pointed out appropriate connections that we investigated here, together with those in several interconnected earlier works on this subject.

Lemma 1 and 2 do not hold true if the classical derivative is replaced with a quantum derivative, so the results that we obtained in Section 3 cannot be easily translated into the corresponding results involving the quantum derivative. Hence, there is a need to develop some tools or methods to obtain the subordination condition for starlikeness involving the quantum derivative. In addition, we note that the impact of $N(A,B,\psi )$ (see Section 3) is not the same in all conic regions. So, the following question arises: Are there any specific specialized regions in which the impact of $N(A,B,\psi )$ will be the same?

Further, the study considered in this article can be extended by taking an exponential function, Legendre polynomial, Chebyshev polynomial, Fibonacci sequence, or q-Hermite polynomial instead of considering $\psi \left(z\right)$ as in (6).