1. Introduction
In this paper, we continue the study of efficient algorithms for computation of the Riemann zeta function over the complex plane, introduced by Borwein [
1] and extended by Belovas et al., (see [
2,
3] and references therein). Šleževičienė [
4], Vepštas [
5], and Coffey [
6] applied this methodology for the computation of Dirichlet
L-functions, Hurwitz zeta function, and polylogarithm. Belovas et al. obtained limit theorems, which allowed the introduction of asymptotic approximations for the coefficients of the series of the algorithms. A preliminary presentation of computational aspects of the approach has been presented in [
3]. Theoretical aspects of the approach (as well as more subtle proofs of the limit theorems) have been discussed in [
7].
Fractal geography of the Riemann zeta function (and other zeta functions) was addressed by King [
8]. Woon [
9] and Tingen [
10] computed Julia and Mandelbrot sets of the Riemann zeta function and Hurwitz zeta function, respectively, and studied the properties of these fractals. Recently Blankers et al. [
11] investigated the analogs of Julia and Mandelbrot sets for dynamical systems over the hyperbolic numbers. In the present study, we enhance algorithms for the calculation of the Riemann zeta function, proposed in [
2,
3]. We specify the convergence rate to the limiting distribution for the coefficients of the series, identify the error term, and discuss computational complexity. The algorithms are compared against the recently proposed
Zetafast algorithm [
12] and are applied for the investigation of underlying fractal structures associated with the Riemann zeta function.
The paper is organized as follows. The first part is the introduction. In
Section 2, we describe algorithms and present theoretical results.
Section 3 is devoted to the visual investigation of the underlying fractal background of the Riemann zeta function. Pseudocodes of the algorithms for the computation and the visualization are given in
Section 4.
Section 5 and
Section 6 are devoted to presenting the results and conclusions, respectively.
Throughout this paper, stands for the Cartesian product of sets U and V. We denote by the cumulative distribution function of the standard normal distribution, and by we denote the gamma function. Next, and stand for the floor function and the ceiling functions, respectively. All limits in the paper, unless specified, are taken as .
2. MB- and BLC-Algorithms for the Computation of the Riemann Zeta Function
Let
be a complex variable. The Riemann zeta-function is defined on the half-plane
by the ordinary Dirichlet series or the Euler product formula,
and by analytic continuation for other complex values. The Riemann zeta function is a meromorphic function (holomorphic on the whole complex plane except for a simple pole at
with residue 1). The Riemann zeta function satisfies the functional equation
implying that
has simple zeros at
,
, known as the trivial zeros. Other zeroes are called nontrivial. The famous Riemann hypothesis states that all the nontrivial zeros lie on the critical line
. The hypothesis is closely related to the distribution of prime numbers, implying the best possible error term in the prime number theorem,
Here
is the prime-counting function, i.e., the number of primes less than or equal to
x,
. A summary of the literature covering the problems related to the Riemann zeta function and its applications is presented in [
13,
14] and the references therein.
2.1. MB-Algorithm
In [
3] Belovas et al., proposed a modification of Borwein’s efficient algorithm (
-algorithm) for the computation of the Riemann zeta function [
1]. The algorithm applies to complex numbers with
and arbitrary
t. The Riemann zeta function is represented by the alternating series
Here (case
in
corresponds
-series), by Theorem 1 from [
3], we have
while
The algorithm is nearly optimal in the sense that there is no sequence of
n-term exponential polynomials that converge to the Riemann zeta function much faster than of the algorithm (see Theorem 3.1 in [
1]).
2.2. BLC-Algorithm
This algorithm, introduced in [
2], also uses series (
1) (case
in
corresponds
-series), but with different binomial-like coefficients,
Here
stands for the regularized incomplete beta function,
The error terms of these methods are discussed in the following subsection.
2.3. Error Terms and Computational Complexity
First we formulate an auxiliary lemma, aiming to investigate the behaviour of the series in the neighbourhoods of critical points
,
Note that in (
1) the denominator
if and only if
,
and
.
Lemma 1. Let be defined by (5) and be the circle Then, for and , Proof of Lemma 1. Parametrizing the complex function
for the circle
, we obtain
The function
is periodic with period
and symmetric with respect to
(indeed,
). Hence the statement of the lemma reduces to solving
Differentiating
, we get for
Indeed, with and
, we have
For
, we have
We have shown that
for
. Note that
for
. Thus the function
is monotonically increasing and
with (
7) and (
8) yielding us the statement of the lemma. □
The error term and the computational complexity are closely linked to the problem of the selection of the minimal number of terms in the series (
1). Let us formulate the following theorem.
Theorem 1. Let , , and , then
- (i)
the error term of the series (1) is - (ii)
the series (1) to compute the Riemann zeta-function with d decimal digits of accuracy, require a number of terms with coefficients of expressions (9) and (10) presented in Table 1.
Proof of Theorem 1. Let us start with
-series. The error term of the series (
1) is (cf. Algorithm 2 in [
1])
Considering the function
, we have
By a product representation of the gamma function (cf. 8.326.1 in [
15]),
The product is decreasing by
, hence (cf. 8.332.2 in [
15]),
In view of (
14), to compute the Riemann zeta-function with
d decimal digits of accuracy, the approach requires a number
n of terms not less than
. Let
. We have
. Let
and
. By applying the maximum modulus principle and Lemma 1, we receive
thus concluding the proof. The deduction for
-series is analogical. □
Corollary 1. Under the conditions of Theorem 1, for , , the series (1) to compute the Riemann zeta-function with d decimal digits of accuracy, requires the number of terms Proof of Corollary 1. The result (
18) follows immediately, if we notice that for
we have
□
2.4. NA-Modifications of MB- and BLC-Algorithms
Limit theorems for coefficients of
- and
-series enable us to derive a normal approximation for coefficients
(cf. (24) in [
3]). We can formulate the following theorem.
Theorem 2. Coefficients of the series (1) satisfy Coefficients and are presented in Table 2. Proof of Theorem 2. Let us start with
-series coefficients. Suppose
is an integral random variable with the probability mass function
Let
be the cumulative distribution function of the random variable
(
20), then (cf. Theorem 3 in [
7])
Note that the cumulative distribution function
Denoting
and taking into account (
22) and (
23), we obtain
The first part of the theorem follows. Similar result for
-coefficients
has been proven in [
2]. □
Theorem 2 allows us to choose the number of terms
for the series (
1),
for
n large enough. Here
. Note that
for fixed
and
d. The refined version of
-modification based methodology is summarized in
Section 4.
2.5. Empirical Insights for NA-Modifications
While performing practical computations using
-algorithms, we have noticed that the values produced were significantly more accurate than otherwise implied by
d in the analytic estimate (
10). In order to increase the performance and to have a clear course for future theoretical refinements, we propose empirical formulae for the minimum number of terms in the series (
1) to compute the Riemann zeta-function with
d decimal digits of accuracy.
Kuzma has proposed the following empirically-based estimate for the number of terms for the
-series (
),
In the present section, we offer an improvement to this estimate.
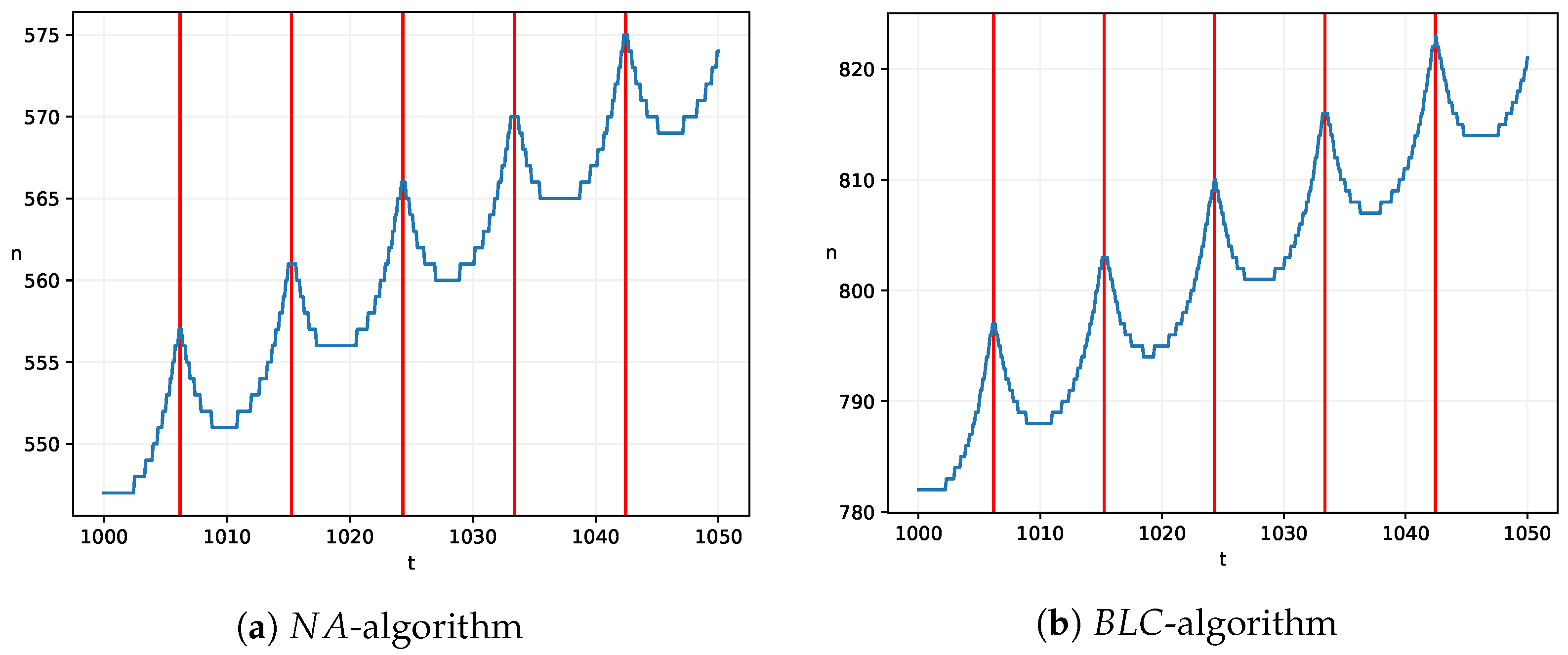
Figure 1 displays the minimum
n required to calculate the Riemann zeta function with
digits of accuracy using
- and
-algorithms at
,
(the blue curve). The curves have clearly visible periodic peaks (marked by red vertical lines). The peaks have a period of
, which correspond
special points of Theorem 1. Since we are interested in the upper bound of this empirical curve, for the following calculations we use the points
,
.
Figure 2 shows regression models
derived for
using the points
(0, 10,000). Each graph represents a fitted curve for a different
d value.
Figure 3 illustrates fluctuations of the coefficients of the regression models (
26) by
d. Here we can clearly see that
has no correlation with
d while
and
does.
Fitting
with
and
with
we obtain the following coefficients for (
26) (see
Table 3):