Modification of the Optimal Auxiliary Function Method for Solving Fractional Order KdV Equations
Abstract
:1. Introduction
2. Basic Definitions
3. Analysis of OAFM for Fractional Order PDEs
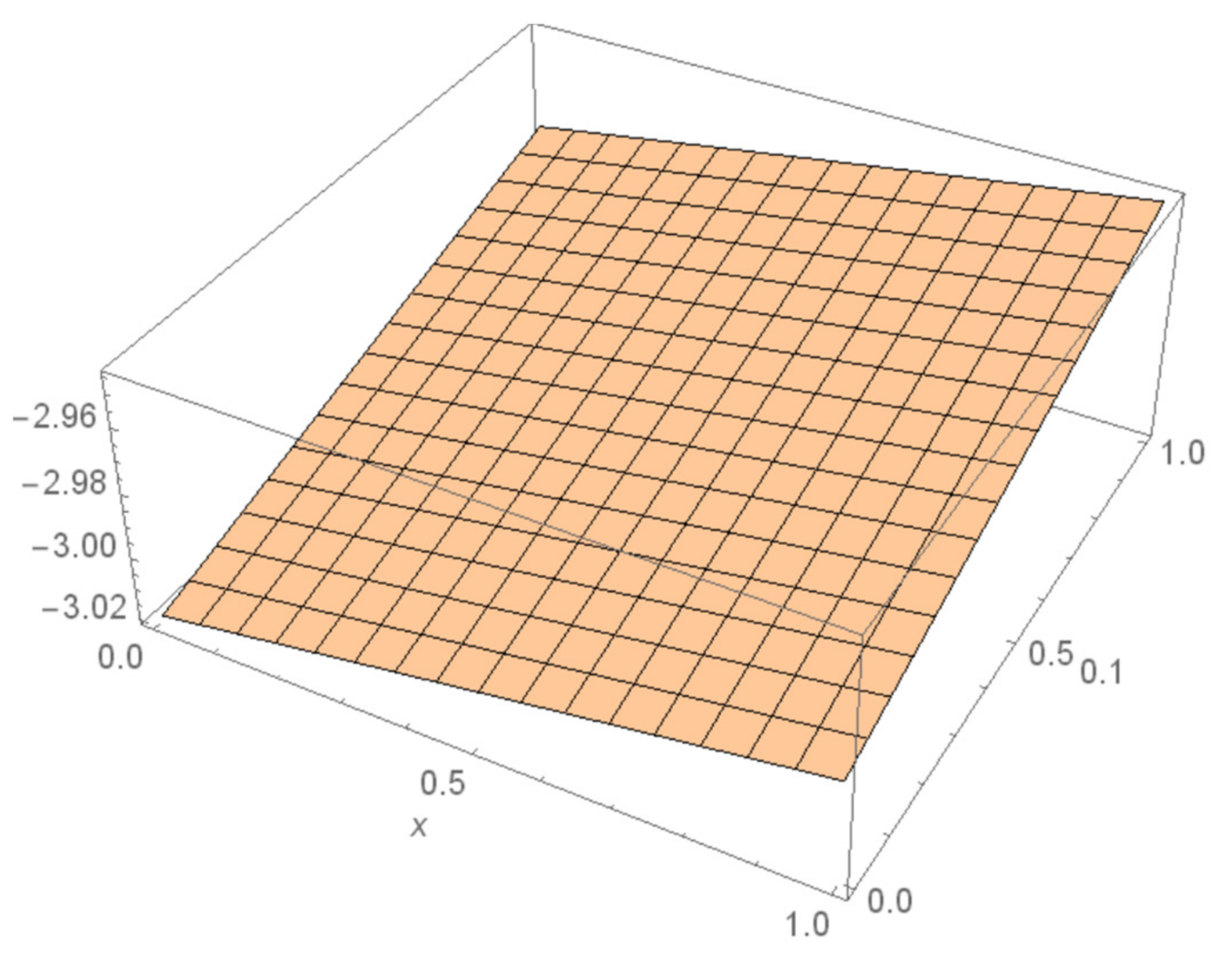
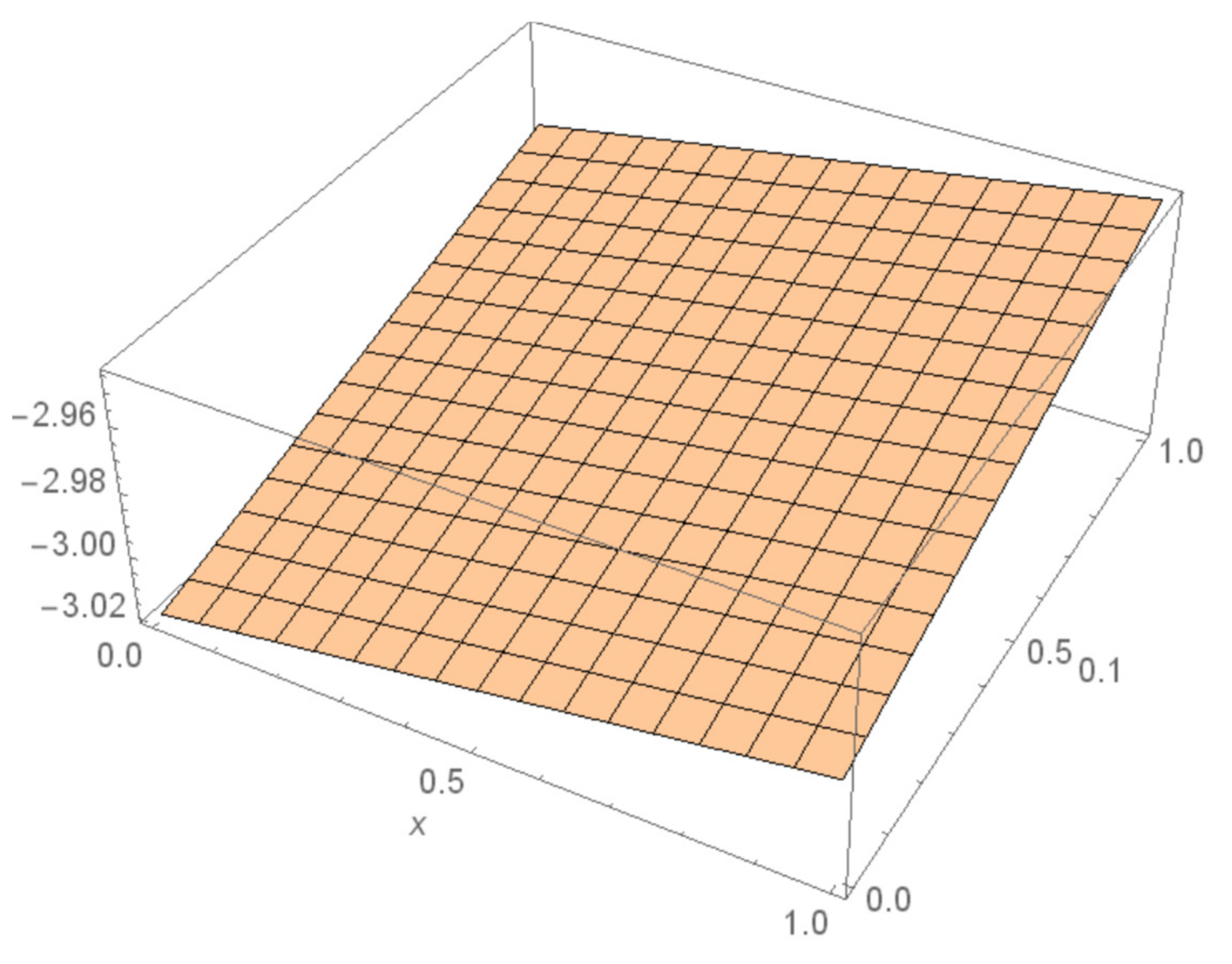
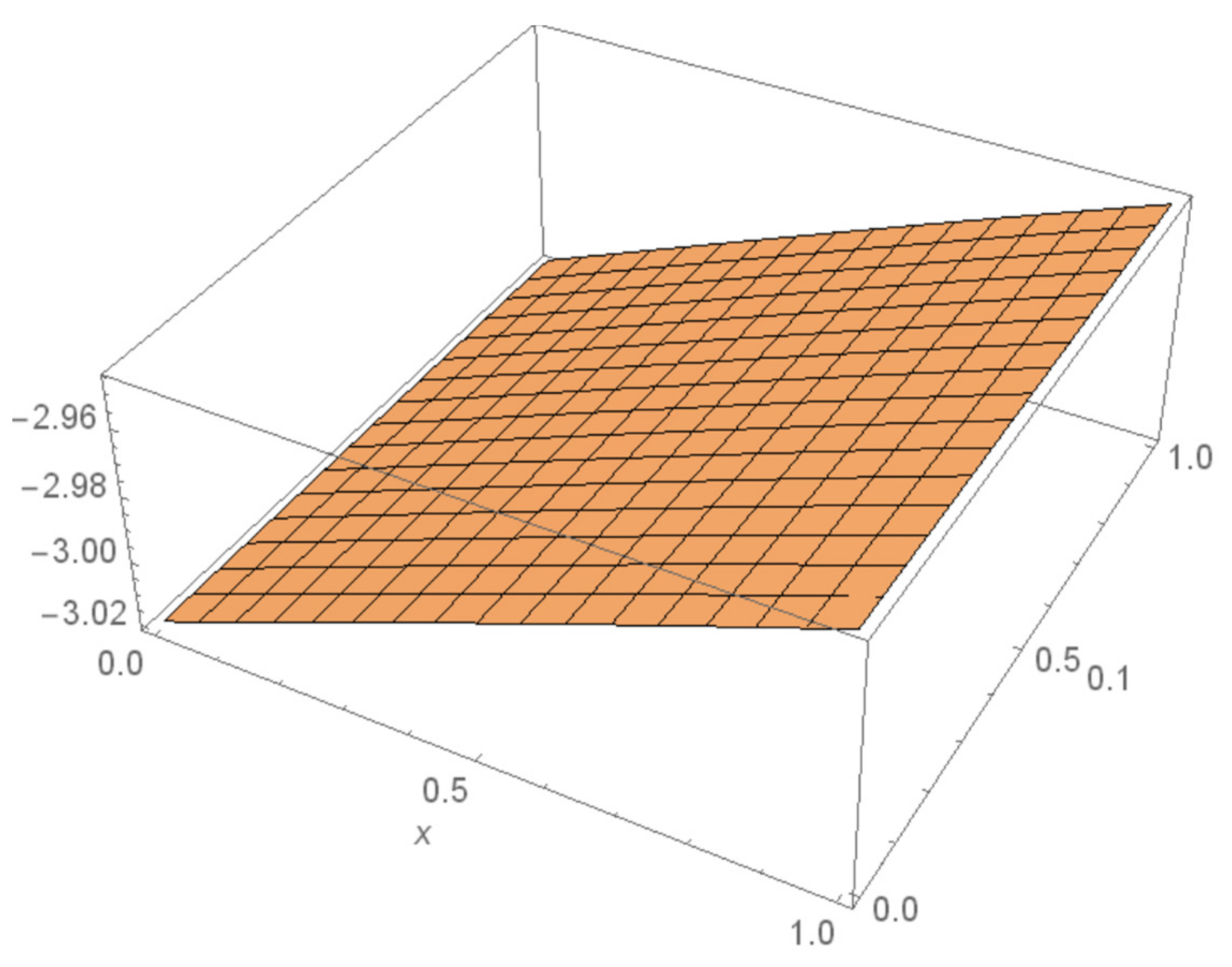
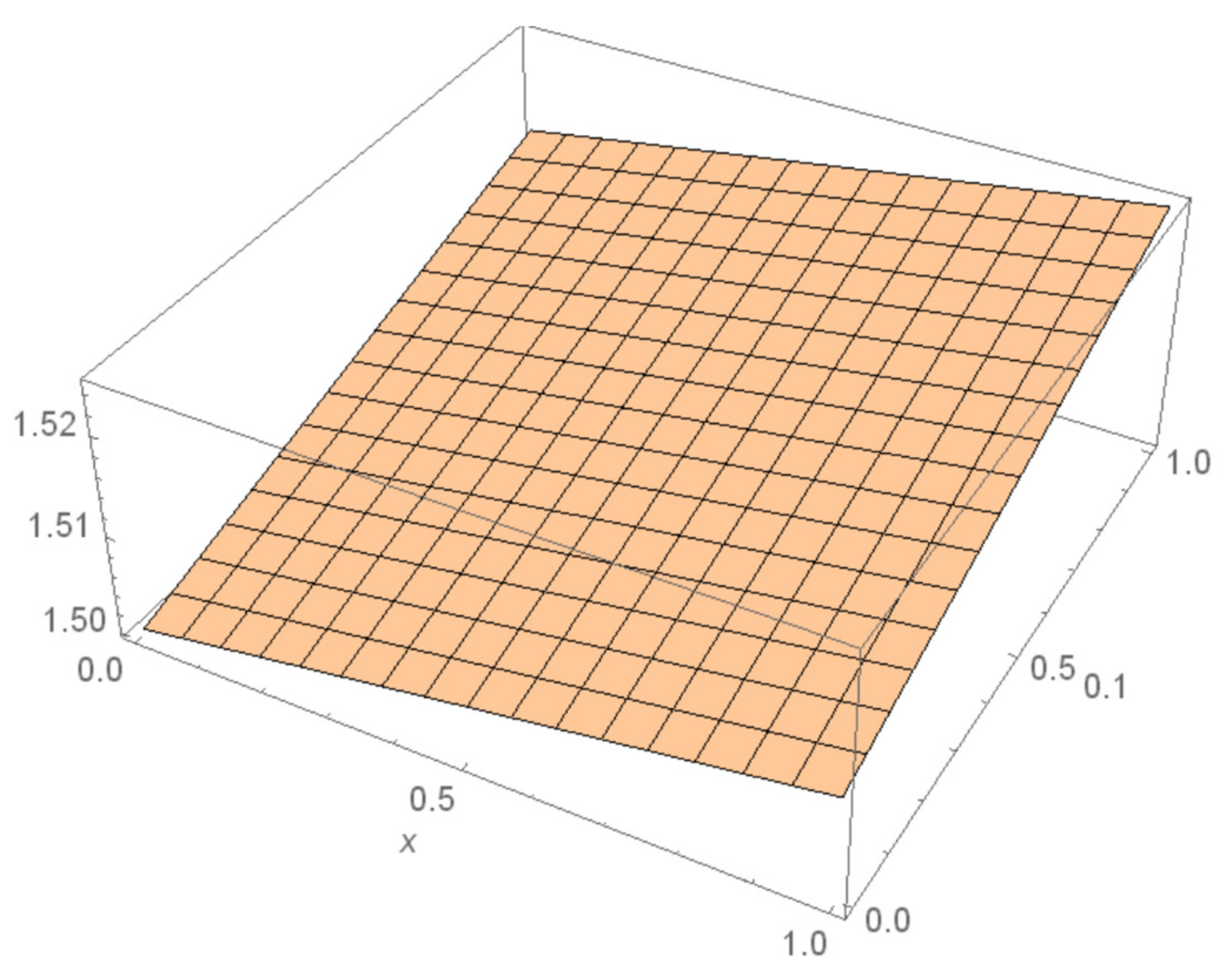
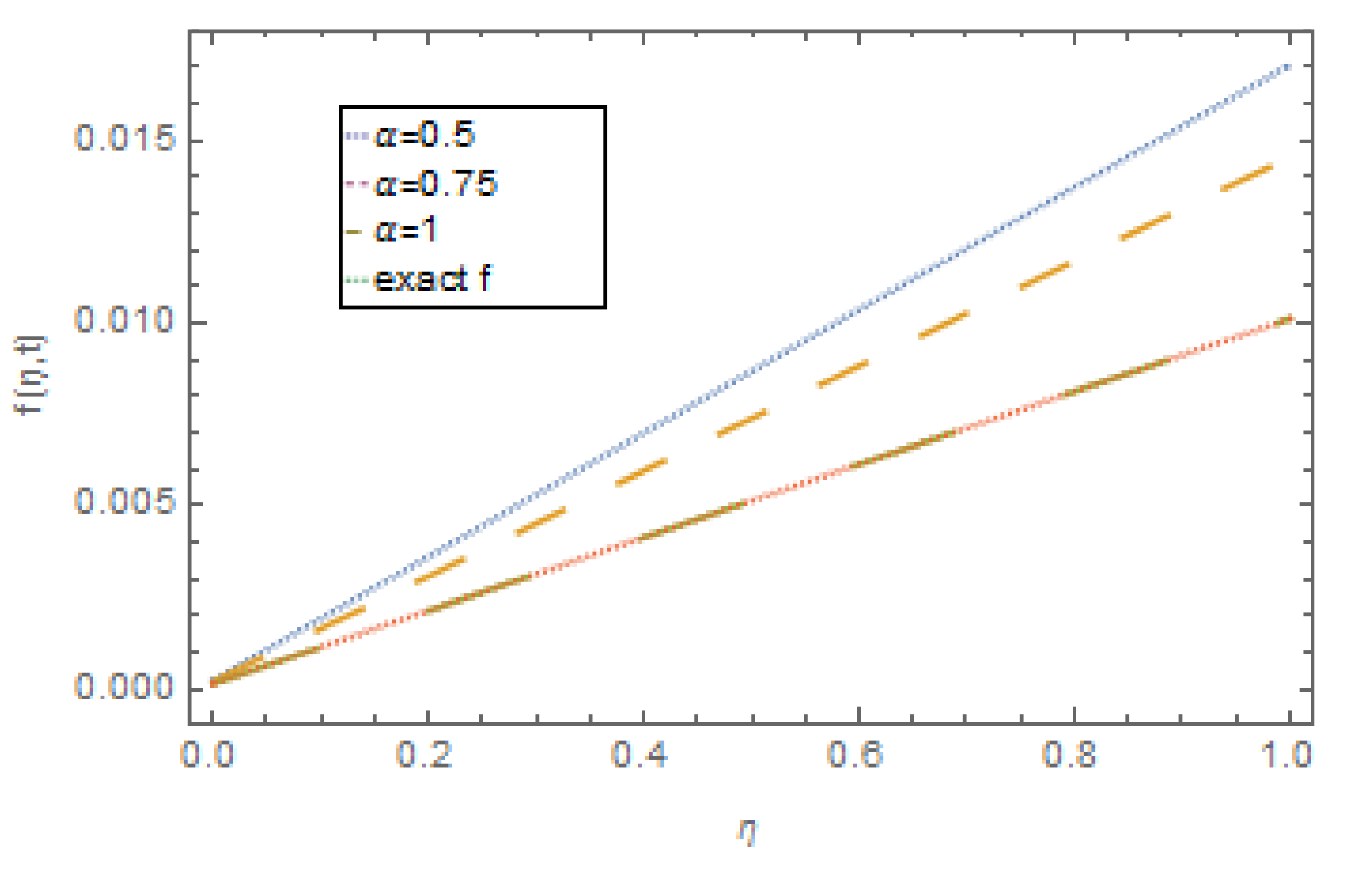
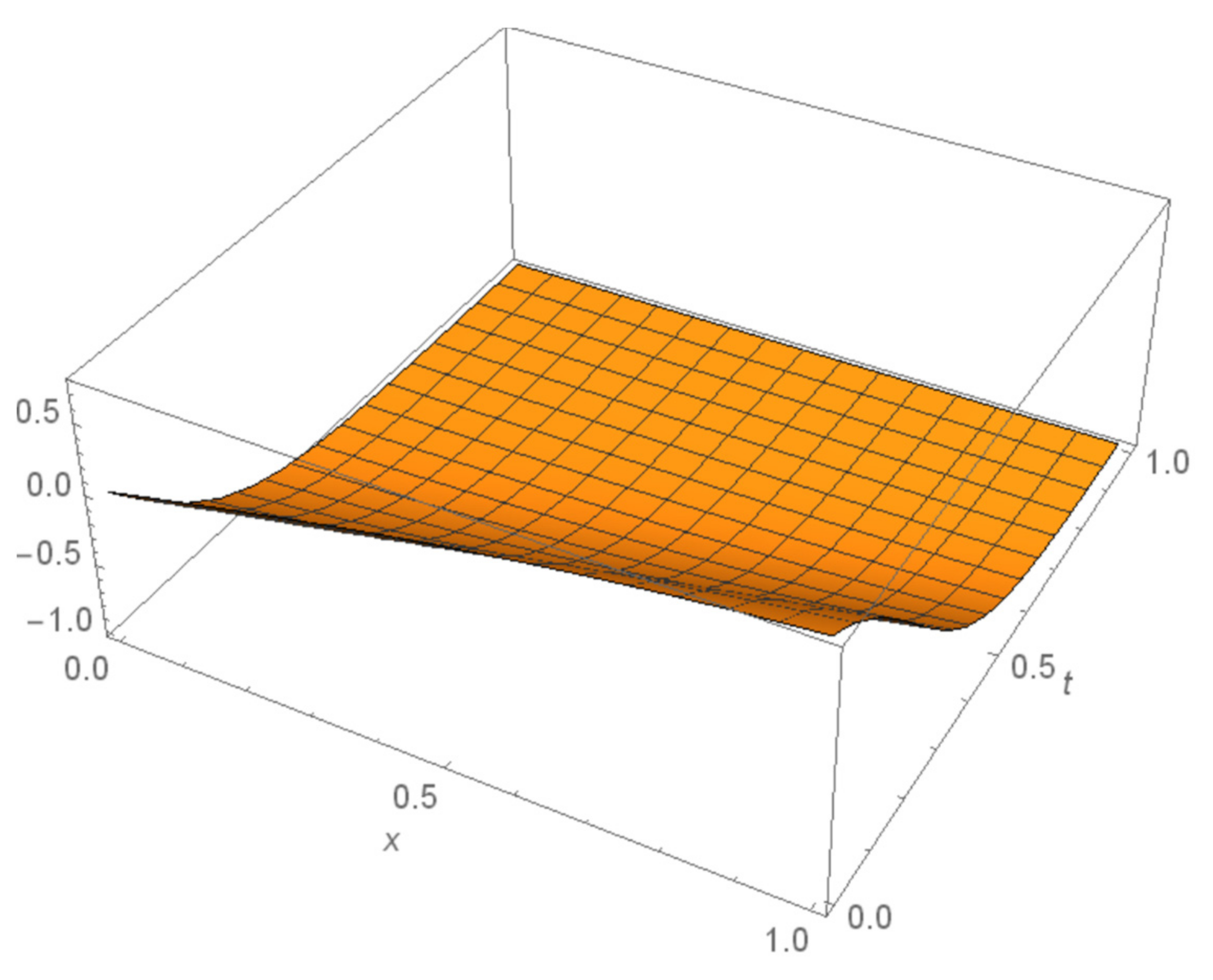
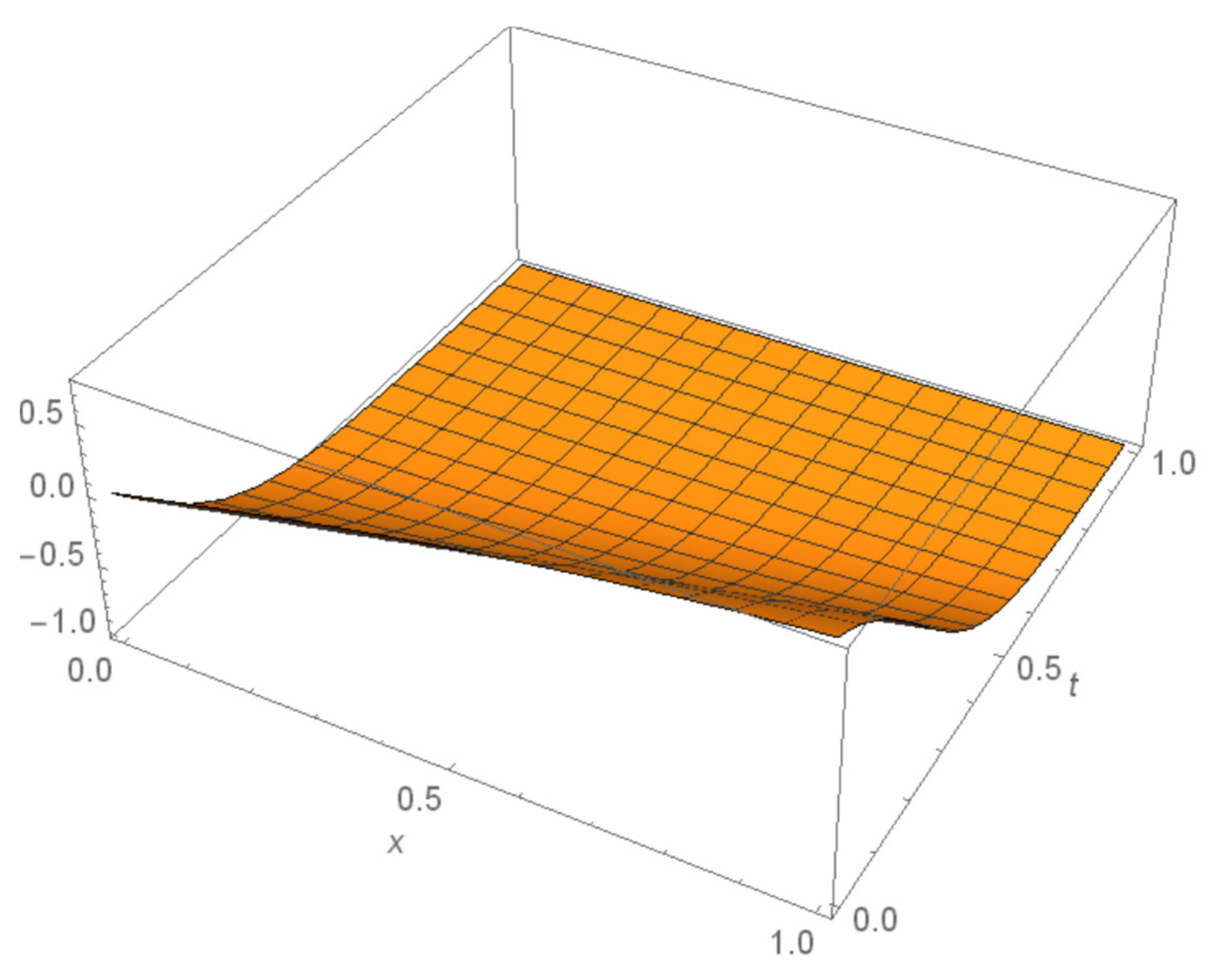
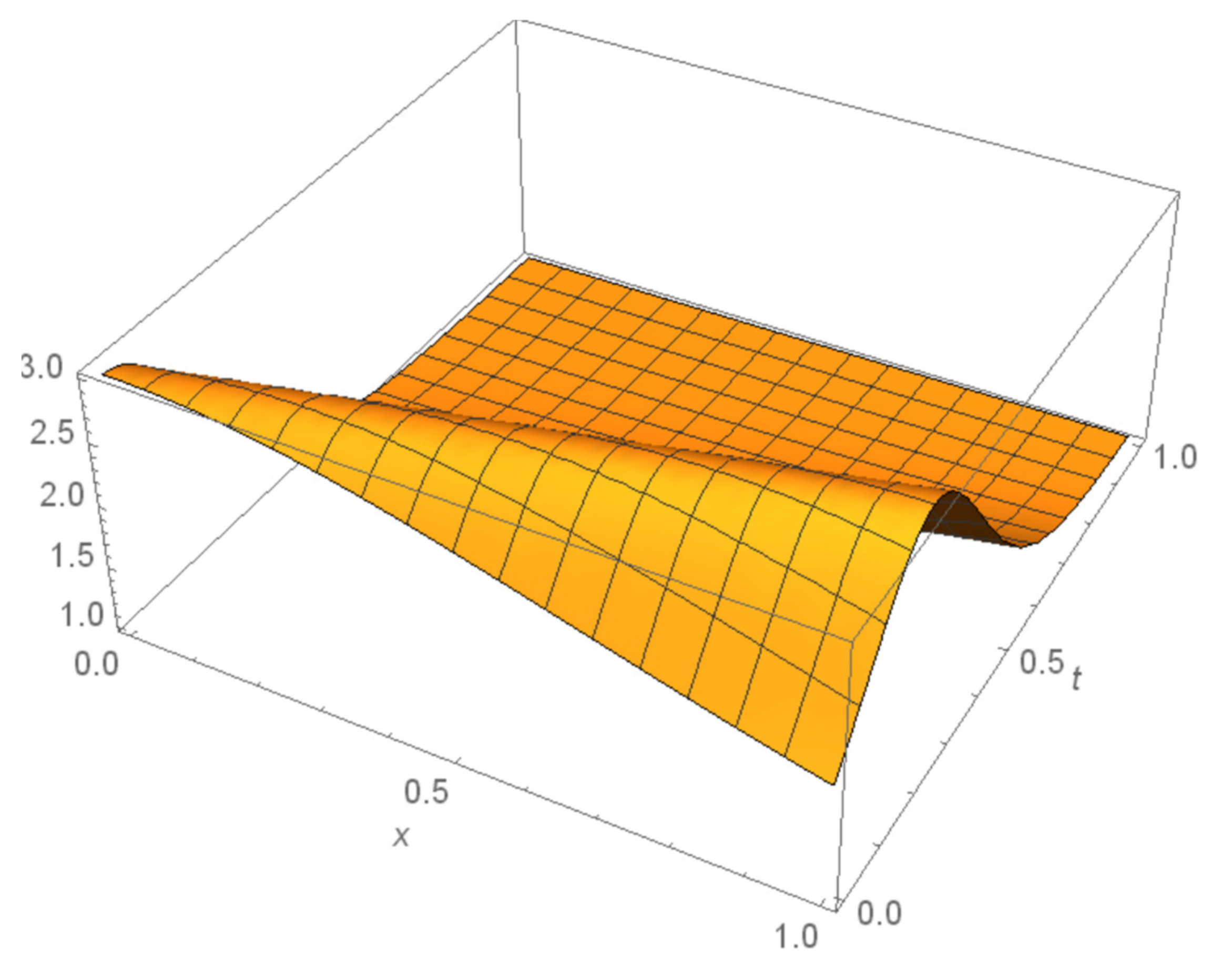
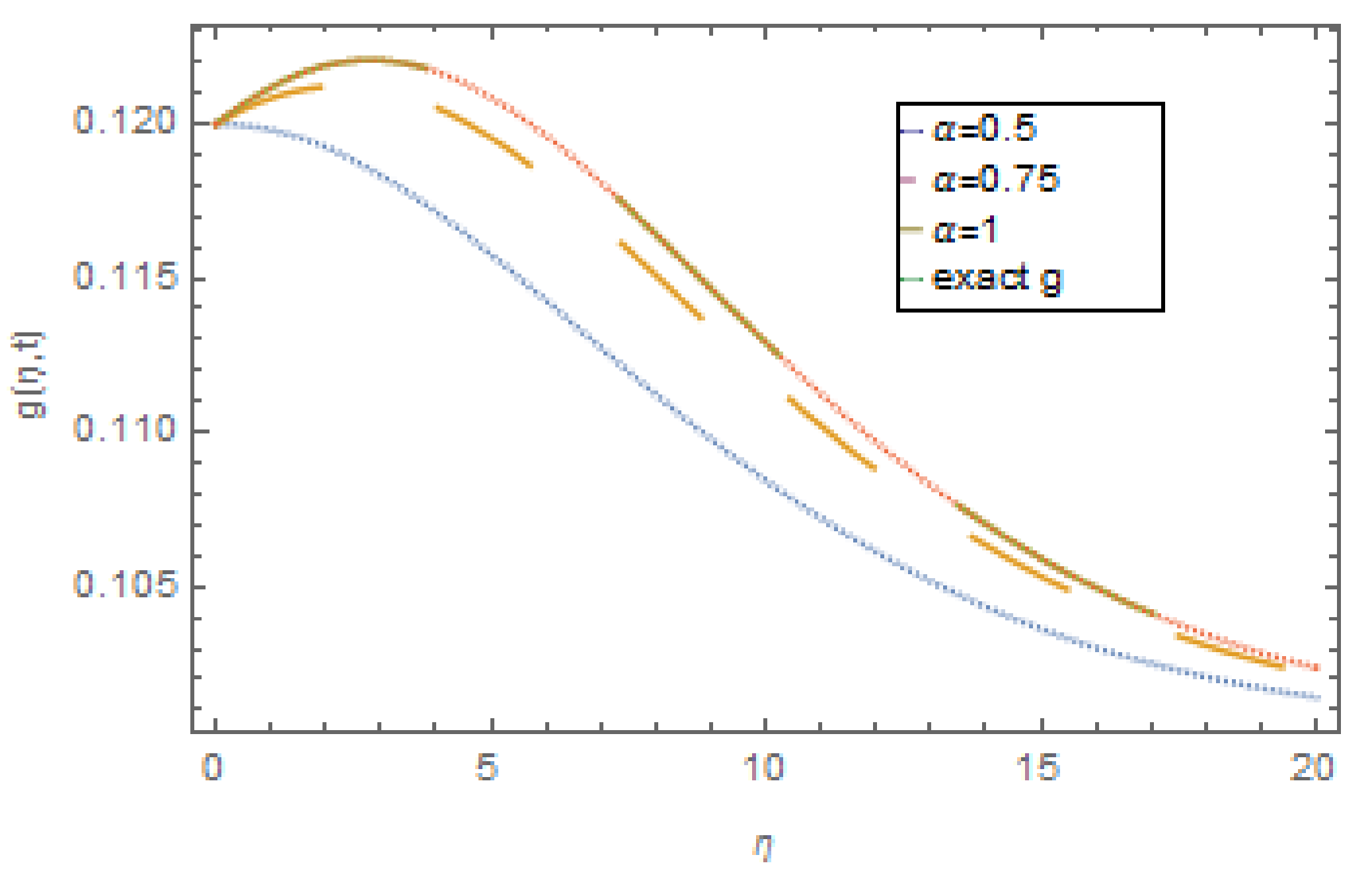
4. Numerical Examples
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fellah, Z.E.A.; Depollier, C.; Fellah, M. Application of fractional calculus to sound wave propagation in rigid porous materials, validation via ultrasonic measurements. Acta Acustic United Acust. 2002, 88, 34–39. [Google Scholar]
- Sebaa, N.; Fellah, Z.; Lauriks, W.; Depollier, C. Application of fractional calculus to ultrasonic wave propagation in human cancellous bone. Signal Process. 2006, 86, 2668–2677. [Google Scholar] [CrossRef]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional calculus in viscoelastic an experimental study. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Sua´rez, J.I.; Vinagre, B.M.; Calder´on, A.J.; Monje, C.A.; Chen, Y.Q. Using fractional calculus for lateral and longitudinal control of autonomous vehicles. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2004. [Google Scholar]
- Oldham, K.B.; Spanier, J. e Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Meerschaert, M.M.; Scheffler, H.-P.; Tadjeran, C. Finite difference methods for two-dimensional fractional dispersion equation. J. Comput. Phys. 2006, 211, 249–261. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 2004, 37, 161–208. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Schneider, W.R.; Wyess, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Torrisi, M.; Tracina, R.; Valenti, A. A group analysis approach for a nonlinear differential system arising in diffusion phenomena. J. Math. Phys. 1996, 37, 4758–4767. [Google Scholar] [CrossRef]
- Drzain, P.G.; Johnson, R.S. An Introduction Discussion the Theory of Solution and Its Diverse Applications; Cambridge Unversity Press: Cambridge, UK, 1989. [Google Scholar]
- Abdel-Hamid, B. Exact solutions of some nonlinear evolution equations using symbolic computations. Comput. Math. Appl. 2000, 40, 291–302. [Google Scholar] [CrossRef] [Green Version]
- Bluman, G.; Kumei, S. On the remarkable nonlinear diffusion equations. J. Math. Phys. 2003, 21, 1019–1023. [Google Scholar] [CrossRef]
- Chun, L.C. Fourier series based variational iteration method for a reliable treatment of heat equations with variable coefficients. Int. J. Nonlinear Sci. Numer. Simul. 2007, 10, 1383–1388. [Google Scholar] [CrossRef]
- Chowdhury, S.H. A comparison between the Extended homotopy perturbation method and adomian decomposition method for solving nonlinear heat transfer equations. J. Appl. Sci. 2011, 11, 1416–1420. [Google Scholar] [CrossRef]
- Yaghoobi, H.; Tirabi, M. The application of differential transformation method to nonlinear equation arising in heat transfer. Int. Commun. Heat Mass Transf. 2011, 38, 815–820. [Google Scholar] [CrossRef]
- Ganji, D.D. The application of He’s homotopy perturbation method to nonlinear equation arising in heat transfer. Phys. Lett. A 2006, 355, 337–341. [Google Scholar] [CrossRef]
- Bellman, R. Perturbation techniques in Mathematics. In Physics and Engineering; Rinehart and Winston: New York, NY, USA, 1964. [Google Scholar]
- Cole, J.D. Perturbation Methods in Applied Mathematics; Blaisedell: Waltham, MA, USA, 1968. [Google Scholar]
- O’Malley, R.E. Introduction to Singular Perturbation; Acadmeic Press: New York, NY, USA, 1974. [Google Scholar]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Marinca, V.; Herisanu, N.; Nemes, I. Optimal homotopy asymptotic method with application to thin film flow. Cent. Eur. J. Phys. 2008, 6, 648–653. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Explicit analytical approximation to large amplitude nonlinear osciallation of a uniform contilaver beam carrying an intermediate lumped mass and rotary inertia. Meccanica 2010, 45, 847–855. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. An optimal homotopy asymptotic method applied to the steady flow of a fourth-grade fluid past a porous plate. Appl. Math. Lett. 2009, 22, 245–251. [Google Scholar] [CrossRef] [Green Version]
- Marinca, V.; Herisanu, N.; Nemes, I. A New Analytic Approach to Nonlinear Vibration of an Electrical Machine. Proceeding Rom. Acad. 2008, 25, 9229–9236. [Google Scholar]
- Marinca, V.; Herisanu, N. Determination of periodic solutions for the motion of a particle on a rotating parabola by means of the Optimal Homotopy Asymptotic Method. J. Sound Vib. 2009, 11, 005. [Google Scholar] [CrossRef]
- Ullah, H.; Islam, S.; Fiza, M. An Extension of the Optimal Homotopy Asymptotic Method to Coupled Schrödinger-KdV. E Quation. Int. J. Differ. Equ. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Ullah, H.; Islam, S.; Idrees, M.; Arif, M. Solution of Boundary Layer Problems with Heat Transfer by Optimal Homotopy Asymptotic Method. Abstr. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Ullah, H.; Islam, S.; Idrees, M.; Arif, M. Application of Optimal Homotopy Asymptotic Method to Doubly Wave Solutions of the Coupled Drinfel’d-Sokolov-Wilson Equations. Math. Probl. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Ullah, H.; Islam, S.; Sharidan, S.; Khan, I.; Fiza, M. Formulation and application of Optimal Homotopy Asymptotic Method for coupled Differential Difference Equations. PLoS ONE 2015, 10, e0120127. [Google Scholar] [CrossRef] [PubMed]
- Ullah, H.; Islam, S.; Khan, I.; Dennis, L.C.C.; Fiza, M. Approximate Solution of Two-Dimensional Nonlinear Wave Equation by Optimal Homotopy Asymptotic Method. Math. Probl. Eng. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Marinca, B.; Marinca, V. Approximate analytical solutions for thin film flow of fourth grade fluid down a vertical cylinder. Proceeding Rom. Acad. Ser. A 2018, 19, 69–76. [Google Scholar]
- Abbasbandy, S. The application of homotopy analysis method to a generalized Hirota-Satsuama coupled KdV equations. Phys. Lett. A 2007, 361, 478–483. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical comparison of method for solving linear differntial equation, of fractional order. Chaos Solitons Fractals 2007, 31, 1248–1255. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical approach to differential equations of fractional order. J. Comput. Appl. Math. 2007, 207, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Odibat, Z.; Momani, S. Numerical methods for nonlinear partial differential equations of fractional order. Appl. Math. Moddeling 2008, 32, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Korteweg, D.; Vries, D.G. On the change of from of long waves advancing in a rectangular canal and on a new type of long statiionary waves. Philosphical Mag. 1895, 39, 422–428. [Google Scholar] [CrossRef]
- Fung, M.K. KdV equation as an Euler-Poincare equation. Chin. J. Phys. 1997, 35, 789–798. [Google Scholar]
- El-Wakil, S.A.; Abulwafa, E.M. Formulation and solution of space-time fractional Boussinesq equation. Nonlinear Dyn. 2015, 80, 167–175. [Google Scholar] [CrossRef]
- Nazari-Golshan, N.A.; Nourazar, S.S. Effect of trapped electron on the dust ion acoustic waves in dusty plasma using time fractional modified Korteweg-de Vries equation. Phys. Plasmas 2013, 20, 103701. [Google Scholar] [CrossRef]
- El-Shewy, E.K.; Mahmoud, A.A.; Tawfik, A.M.; Abulwafa, E.M.; Elgarayhi, A. Space—Time fractional KdV-Burgers equation for dust acoustic shock waves in dusty plasma with non-thermal ions. Chin. Phys. B 2014, 23, 070505. [Google Scholar] [CrossRef]
- Ghosh, U.; Sengupta, S.; Sarkar, S.; Das, S. Analytical solution with tanh-method and fractional subequation method for non-linear partial differential equations and corresponding fractional differential equation composed with Jumarie fractional derivative. Int. J. Appl. Math. Stat. 2016, 54, 11–31. [Google Scholar]
- Alzaidy, J.F. The fractional sub–equation method and exact analytical solutions for some non-linear fractional PDEs. Am. J. Math. Anal. 2013, 1, 14–19. [Google Scholar]
- Yomba, E. The extended Fan’s sub-equation method and its application to KdV–MKdV, BKK and variant Boussinesq equations. Phys. Lett. A 2005, 336, 463–476. [Google Scholar] [CrossRef]




| HAM [33] | ClosedFormSol | OAFM | OHAM | |
|---|---|---|---|---|
| 0 | 0.5478591 | 0.5478594 | 0.5478594 | 0.5478591 |
| 20 | 0.5468792 | 0.5468793 | 0.5468793 | 0.5468792 |
| 40 | 0.5145785 | 0.5145789 | 0.5145789 | 0.5145785 |
| 60 | 0.5125476 | 0.5125478 | 0.5125478 | 0.5125476 |
| 80 | 0.5132221 | 0.5132222 | 0.5132222 | 0.5132221 |
| 100 | 0.5144442 | 0.5144444 | 0.5144444 | 0.5144442 |
| HAM [33] | ClosedFormSol | OAFM | OHAM | |
|---|---|---|---|---|
| 0 | 0.334666 | 0.343533 | 0.343533 | 0.334666 |
| 20 | 0.706405 | 0.713534 | 0.713534 | 0.706405 |
| 40 | 0.734121 | 0.734269 | 0.734269 | 0.734121 |
| 60 | 0.734655 | 0.734659 | 0.734659 | 0.734655 |
| 80 | 0.734664 | 0.734667 | 0.734667 | 0.734664 |
| 100 | 0.734665 | 0.734667 | 0.734667 | 0.734665 |
| OAFM | ClosedFormSol | HAM [33] | OHAM | |
|---|---|---|---|---|
| 0 | 1.5 | 1.50222 | 1.50221 | 1.50221 |
| 20 | 1.59392 | 1.59472 | 1.5947 | 1.5947 |
| 40 | 1.59985 | 1.5999 | 1.5998 | 1.5998 |
| 60 | 1.6 | 1.6 | 1.6 | 1.6 |
| 80 | 1.6 | 1.6 | 1.6 | 1.6 |
| 100 | 1.6 | 1.6 | 1.6 | 1.6 |
| 0 | 0.00012458 | 0.000014578 | 0.000000457 | 1.99865 × 10−18 |
| 20 | 0.000012456 | 0.000004578 | 0.000000457 | 2.99865 × 10−18 |
| 40 | 0.0000001245 | 0.0000000014 | 0.0000000245 | 1.58421 × 10−19 |
| 60 | 1.34118 × 10−8 | 5.63709 × 10−9 | 2.54789 × 10−10 | 5.90535 × 10−19 |
| 80 | 2.71092 × 10−10 | 2.3988 × 10−12 | 3.66673 × 10−14 | 2.32147 × 10−20 |
| 100 | 2.13366 × 10−12 | 4.562 × 10−14 | 7.54742 × 10−16 | 1.74665 × 10−20 |
| 0 | 0.012458 | 0.164870 | 0.00012458 | 5.12478 × 10−18 |
| 20 | 0.012456 | 0.00012458 | 0.00004789 | 3.14586 × 10−19 |
| 40 | 0.000004578 | 0.000012458 | 0.000045786 | 3.24578 × 10−20 |
| 60 | 9.34118 × 10−8 | 7.63709 × 10−8 | 2.5478 × 10−10 | 2.90535 × 10−20 |
| 80 | 1.71092 × 10−9 | 1.3988 × 10−10 | 4.6667 × 10−12 | 5.32146 × 10−21 |
| 100 | 3.1336 × 10−10 | 2.562 × 10−11 | 8.54741 × 10−14 | 9.74660 × 10−21 |
| 0 | 0.0045789 | 0.004578566 | 0.00002145 | 3.22115 × 10−18 |
| 20 | 0.000124578 | 0.000045789 | 0.000004586 | 5.11245 × 10−19 |
| 40 | 0.000000024 | 0.000004578 | 0.000004586 | 5.64850 × 10−20 |
| 60 | 1.45789 × 10−8 | 3.45789 × 10−8 | 3.4586 × 10−10 | 3.54691 × 10−21 |
| 80 | 2.45789 × 10−9 | 3.2145 × 10−10 | 3.4586 × 10−12 | 3.45879 × 10−21 |
| 100 | 3.1457 × 10−10 | 3.1245 × 10−11 | 2.3546 × 10−14 | 3.25460 × 10−21 |
| 0 | 0.0164508 | 0.008144 | 0.000449177 | 4.55951 × 10−16 |
| 20 | 0.00217387 | 0.00190041 | 0.000754522 | 0.00008 × 10−16 |
| 40 | 0.000273879 | 0.0000265752 | 0.0000147276 | 1.59572 × 10−16 |
| 60 | 5.14463 × 10−6 | 4.83366 × 10−7 | 2.70061 × 10−7 | 2.92649 × 10−18 |
| 80 | 9.42707 × 10−8 | 8.85201 × 10−9 | 4.94645 × 10−9 | 5.36017 × 10−20 |
| 100 | 1.72664 × 10−9 | 1.6213 × 10−10 | 9.05975 × 10−11 | 9.81748 × 10−21 |
| 0 | 0.0164508 | 0.008144 | 0.000449177 | 4.55951 × 10−16 |
| 20 | 0.00217387 | 0.00190041 | 0.000754522 | 0.00008 × 10−16 |
| 40 | 0.000273879 | 0.0000265752 | 0.0000147276 | 1.59572 × 10−16 |
| 60 | 5.14463 × 10−6 | 4.83366 × 10−7 | 2.70061 × 10−7 | 2.92649 × 10−18 |
| 80 | 9.42707 × 10−8 | 8.85201 × 10−9 | 4.94645 × 10−9 | 5.36017 × 10−20 |
| 100 | 1.72664 × 10−9 | 1.6213 × 10−10 | 9.05975 × 10−11 | 9.81748 × 10−21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, H.; Fiza, M.; Khan, I.; Alshammari, N.; Hamadneh, N.N.; Islam, S. Modification of the Optimal Auxiliary Function Method for Solving Fractional Order KdV Equations. Fractal Fract. 2022, 6, 288. https://doi.org/10.3390/fractalfract6060288
Ullah H, Fiza M, Khan I, Alshammari N, Hamadneh NN, Islam S. Modification of the Optimal Auxiliary Function Method for Solving Fractional Order KdV Equations. Fractal and Fractional. 2022; 6(6):288. https://doi.org/10.3390/fractalfract6060288
Chicago/Turabian StyleUllah, Hakeem, Mehreen Fiza, Ilyas Khan, Nawa Alshammari, Nawaf N. Hamadneh, and Saeed Islam. 2022. "Modification of the Optimal Auxiliary Function Method for Solving Fractional Order KdV Equations" Fractal and Fractional 6, no. 6: 288. https://doi.org/10.3390/fractalfract6060288
APA StyleUllah, H., Fiza, M., Khan, I., Alshammari, N., Hamadneh, N. N., & Islam, S. (2022). Modification of the Optimal Auxiliary Function Method for Solving Fractional Order KdV Equations. Fractal and Fractional, 6(6), 288. https://doi.org/10.3390/fractalfract6060288







