1. Introduction
The development of fractal theory provides a new theoretical basis for the study of soil with a complex internal structure [
1,
2]. Fractal theory is widely used in research on geotechnical materials as a theoretical method to describe the geometric characteristics of porous media [
3,
4]. There are extensive experimental data and theoretical research in this field showing that the pore distribution in soil has obvious fractal characteristics [
5,
6]. At present, the research mainly focuses on the pore–solid model, while there is less research on the seepage–fractal model.
Soil is a loose, porous three-phase medium composed of soil particles, air, and water. Soil particles form the skeleton of soil, while air and water exist in the interconnected pores between soil particles in the soil. In nature, the hydraulic parameters of soil have strong spatial variability at different scales. The pore structure and its connectivity are very complex, and pore scale ranges from millimeters to microns. The process of fluid migration depends on the multiscale pore structure of soil [
7,
8]. Wang [
9] measured the pore size of soil with high-resolution computed tomography (CT) imaging technology, calculated the soil porosity, reconstructed the soil pores in three-dimensional space, and studied the spatial distribution law of soil pores based on their fractal characteristics. Rainfall will introduce changes to the pore structure in the soil surface, and soil particles’ transportation caused by infiltration will clog soil pores and reduce the porosity of surface soil, causing a continuous change in soil pore micro characteristics consequently affecting the mechanical properties of soil [
10]. The pore structure of soil is affected by many factors, and soil conditioner can significantly increase the number of macro and small pores to improve the soil structure and porosity [
11].
Seepage refers to the phenomenon of pore water in the soil flowing through the interconnected pores in the soil particle skeleton under the action of water [
12]. Soil permeability represents the ability to allow water or other fluids to flow through its interior. The study of soil permeability is very important in many engineering fields, including studies on the seepage instability of embankments, waterproof foundation pits, etc. [
13,
14,
15]. There are interconnected pores in the soil particle skeleton, which explains the soil permeability. Therefore, the shape, size, and connection mode of pores have an important impact on the permeability of the soil. Many scholars around the world have done meaningful research on the characteristics of soil permeability; they have explored the internal connection between hydraulic conductivity and other physical parameters and tried to establish a model to determine the hydraulic conductivity [
16,
17].
Soil particle size distribution refers to the percentage of particles of different sizes in the total particles. It is one of the basic parameters of soil and has a strong impact on the hydraulic properties. Graded entropy can be used to represent the particle size distribution of soil. Through soil particle size, the relationship between hydraulic conductivity and graded entropy can be established. This approach can be applied to predict the hydraulic conductivity of various soils [
18].
Darcy’s law describes the linear function between the seepage velocity of water in saturated soil and the hydraulic gradient, also known as the linear seepage law. However, according to test results, this linear function is only applicable under certain conditions. With increased soil viscosity, the linear relationship no longer exists. Therefore, a new method is needed to calculate the hydraulic conductivity of cohesive soil. The plasticity index, average pore diameter, and particle size distribution of cohesive soil affect its permeability, resulting in changes to the hydraulic gradient and seepage velocity. The function describing the relationship between these influencing factors and hydraulic conductivity can be obtained with the single factor test. Scholars have studied the internal relationship between the physical indices and hydraulic conductivity of cohesive soil and have tried to find the optimal method to calculate the hydraulic conductivity [
19].
Stress in the soil causes consolidation and deformation, which leads to changes in the pore structure and affects the distribution of hydraulic conductivity. This phenomenon is more obvious in the construction of pile foundations [
20]. The pore fractal dimension refers to the size and development degree of pore channels, indicating the distribution characteristics of soil pores [
21]. In the process of seepage failure in porous media, movable fine particles are continuously lost from the pore channels, and physical and mechanical parameters such as hydraulic conductivity, porosity, and the nonuniformity coefficient change, resulting in changes to the fractal dimension [
22,
23,
24,
25]. Studying the fractal characteristics of porous soil seepage and predicting and controlling the formation and development of seepage failure are significance for the long-term and safe operation of dam engineering. Capillary curvature, pressure, and wall roughness are closely related to soil hydraulic conductivity. When the capillary structure changes, the fractal dimension changes. Therefore, hydraulic conductivity can be expressed as an equation of capillary state and the fractal dimension [
26]. Computer tomography and three-dimensional modeling technology can eliminate the influence of geometric size, establish relationships between soil parameters and the fractal dimension, reflect the fractal characteristics of the model in real time and reduce the error [
27]. Meanwhile, the shrinkage crack caused by water loss changes the fractal characteristics, and permeability is obviously affected [
28]. The expansive agent reduces the cracks of porous media, and leads to the decrease in permeability [
29,
30]. Soil properties can be explained by fractal theory; however, under the action of many factors, soil physical indices are not ideally fractal [
31]. For complex models, the fractional Adams–Bashforth method can quickly obtain the approximate solution, which plays a positive role in the application of fractal theory [
32].
At present, the study of seepage by fractal theory is less related to the permeability of embankment soil. Research on hydraulic conductivity, hydraulic gradient, and its influencing factors is still insufficient, and the functional relationship between hydraulic conductivity, hydraulic gradient, and fractal dimension needs to be studied further. Based on the fractal characteristics of embankment soil, an analytical formula of the relationship between hydraulic conductivity, porosity, and fractal dimension is derived. Considering the influence of randomness, the seepage fractal model of embankment soil was established. Combined with engineering practice, the relationship between hydraulic conductivity, hydraulic gradient, and fractal dimension was further studied, and the internal relationship between seepage failure and fractal dimension of porous media soil is revealed.
2. Methodology
2.1. Hydraulic Conductivity Based on Pore Radius and Fractal Dimension
Soil is a typical porous medium. Spaces without a solid skeleton are called pores, which are occupied by liquid or gas, and are connected to each other to form channels. Water can flow through these pores in the soil. Therefore, the structure and scale of pores affect the hydraulic characteristics of the soil.
When there is seepage failure of soil, such as with piping, movable fine particles are continuously lost from the pore channels, resulting in changes in pore size and internal structure, and then in the fractal dimension of the soil. Under the action of seepage, some soil particles are brought to other positions by the seepage water, and the pore radius and permeability of soil change. It can be seen that pore size has an effect on the fractal dimension and hydraulic conductivity, resulting in a function that describes the relationship between them.
Hydraulic conductivity reflects the permeability of porous medium. Due to the irregularity and complexity of soil structure, a unified analytical mathematical formula cannot be used to express hydraulic conductivity at present. In engineering, some empirical values or formulas are usually used, or hydraulic conductivity is determined according to indoor geotechnical tests, in situ tests, and numerical test inversion. Considering that soil particles and pores show fractal characteristics from the atomic scale to grain size, the micro pore structure of soil is analyzed, and the analytical relationship between fractal dimension and hydraulic conductivity and porosity is deduced to further explore seepage and fractal characteristics of porous soil media.
In order to describe the characteristic of soil, a cluster of capillaries with different radiuses is introduced to simulate the pores in soil. Take a cylinder in the soil with a radius of
R and a length of
L. Suppose that in the cylinder, interconnected pores can be replaced by capillaries, and the radius (
r) values of capillaries differ from each other. When the capillary radius satisfies
, the total number of capillaries with radius greater than r in the unit section of soil approximately obeys Equation (1) [
33]:
where
D is the fractal dimension of capillaries in porous media. Since capillaries are composed of interconnected pores, their fractal dimension is equivalent to the fractal dimension of pores in porous media.
R and
r are the radius of the cylinder and capillary. The fractal dimension of capillaries in soil can be obtained by Equation (2):
where
d is the fractal dimension of Euclidean space, and
n is the porosity of porous media. Obviously, the fractal dimension of a plane in Euclidean space is 2, and the fractal dimension of capillaries in soil meets
. The fractal dimension of three-dimensional Euclidean space is 3, and the fractal dimension of capillaries in soil meets
.
By differentiating Equation (1), when the capillary radius changes from
r to
r +
dr, the cumulative number of capillaries can be obtained. As shown in Equation (3), it is obvious that the cumulative number of capillaries in the interval decreases with increased pore size:
According to Poiseuille’s law, when fluid moves in a laminar flow in a horizontal circular pipe, such as capillary, the difference between the volume flow and the pressure at both ends of the pipe, the radius and length of the pipe, and the viscosity coefficient of the fluid meets Equation (4):
where
and
are the gravity and viscosity coefficient of fluid, respectively;
r and
L are the radius and length of the pipe, respectively, and
is the head difference.
Assuming that the minimum and maximum capillary apertures in a section are
and
, respectively, and the aperture is continuously distributed, the total flow through the section can be obtained by integrating the flow through each capillary in the section in the interval
. The total flow is shown in Equation (5):
Bringing Equations (3) and (4) into Equation (5), we obtain Equation (6):
Based on Darcy’s law, the hydraulic conductivity (
k) of soil is shown in Equation (7):
where
is the seepage velocity, and
is the hydraulic gradient. Bringing Equation (6) into Equation (7), after sorting, hydraulic conductivity meets Equation (8):
Soil porosity is the ratio of the pores volume to the total volume. In this study, the pores volume in soil can be expressed by the volume of capillary clusters in the interval
, and the total soil volume is equal to the volume of a hypothetical cylinder. Therefore, the soil porosity can be expressed by Equation (9):
where
n is the porosity,
is the total soil volume, and
is the pore volume in the capillary cluster. By introducing Equation (3) into Equation (9), we obtain Equation (10):
In nature, soil is a typical porous medium. In Equations (8) and (10), the hydraulic conductivity and porosity of soil are functions of the capillary cluster radius and fractal dimension. If the fractal dimension and pore size are different, the hydraulic conductivity and porosity are also different. Strictly speaking, due to the assumption, the relationship between hydraulic conductivity and porosity is difficult to express analytically. Considering the complexity and irregularity of soil pores, the maximum pore radius is much larger than the minimum pore radius. At this time, the relationship between maximum and minimum pore radius can be expressed by Equation (11):
By introducing Equation (11) into Equations (8) and (10), the hydraulic conductivity and porosity of soil can be expressed by Equations (12) and (13):
Obviously, the hydraulic conductivity of soil is affected by the fractal dimension, pore size, water viscosity coefficient, and other factors.
2.2. Randomness of Hydraulic Conductivity of Embankment Soil
Due to the differences in internal structure and pore distribution, soil hydraulic conductivity has a certain spatial variability, resulting in different values throughout the soil. In embankment engineering, due to the influence of time and space, the hydraulic conductivity of soil shows strong randomness, which cannot be ignored. It has a significant impact on the safe operation and early risk warning of embankments. Deterministic research cannot meet the requirements of the development of modern science and technology. More engineering applications need to consider the randomness of hydraulic conductivity in order to meet the needs of design and risk protection.
The randomness of hydraulic conductivity is affected by many factors, such as pore structure, plasticity index, and compactness. The relationship between these factors is complex and difficult to study at the same time. Some scholars try to use statistical methods to study the random characteristics of hydraulic conductivity, testing multiple groups of soil samples, counting the mean and variance, and obtaining an approximate expression of the probability density function through regression analysis. The concept of randomness is introduced in these studies. Soil hydraulic conductivity is regarded as a random variable that follows a certain distribution law. It is generally believed that the log normal distribution has good adaptability and can reflect the spatial structure of soil hydraulic conductivity better, and it has been applied in some studies [
34,
35,
36,
37].
In embankment engineering, when measuring the hydraulic conductivity of multiple groups of soil samples and counting the mean and variance, the mean and variance of logarithmic hydraulic conductivity can be expressed by Equation (14):
In the discrete random field, the hydraulic conductivity of the
jth soil element can be expressed by Equation (15):
where
is the local average of the standard normal random field in the
jth soil element. There is a certain correlation between the points in the random field, which can be described by the correlation function. The exponential correlation function can represent the random characteristics of embankment soil better as shown in Equation (16):
The fluctuation scale () can be regarded as the maximum distance beyond which points in the random field are almost irrelevant. Linear distance () between any points in the random field is closely related to correlation. The randomness of hydraulic conductivity is affected by the coefficient of variation (COV) and . With increased COV, randomness increases. With increased , the correlation between points is enhanced, randomness is reduced, and the soil tends to be uniform.
As shown in
Figure 1, a hydraulic conductivity random field is generated based on the random field model in this paper. The shape of the random field is a 40 m square. There are two soil layers in the random field with the same thickness. Assume that the mean of soil hydraulic conductivity is 1 × 10
−5 cm/s and the fluctuation scale of the random field in any direction is fixed at 3 m. Different COV values result in changes in the dispersion degree and spatial structure of hydraulic conductivity, while the mean of hydraulic conductivity of soil is the same. In order to show this spatial distribution characteristic, different COV values were selected to generate the hydraulic conductivity random field: COV of 0.1 and 0.3 (
Figure 1a) and 0.2 and 0.3 (
Figure 1b). There are 1600 elements in the random field, and the element size is a 1 m square. Hydraulic conductivity is expressed in gray scale; from pure black to pure white, the scale represents hydraulic conductivity from minimum to maximum. According to the principle of minimum potential energy, groundwater mainly flows through light colored units.
In
Figure 1a, the gray levels of the upper soil units are close to each other, the overall color difference is small, the distribution is relatively uniform, and the gray levels of the units are far away from pure white or pure black, which shows that the gray value is concentrated in the middle part. Correspondingly, in this case, the value of hydraulic conductivity changes little, and the deviation from its mean value is small. The COV of upper soil is 0.1, which means that the deviation of unit hydraulic conductivity from its mean value is small. There are obvious differences in the gray level of subsoil units; it is close to pure black or pure white, and the gray difference increases. Based on the definition of COV, the greater the value, the higher the deviation of hydraulic conductivity from its mean value. Relatively, the unit can be assigned a larger or smaller value of hydraulic conductivity. In
Figure 1a, the random field reflects the spatial distribution of hydraulic conductivity, and similar results can be seen in
Figure 1b. In this model, the dispersion degree and spatial structure of hydraulic conductivity of embankment soil will change, although the mean values are equal.
Obviously, it is difficult to characterize the spatial variation of hydraulic conductivity in the fractal dimension, which limits the application of fractal theory in engineering, particularly embankment engineering. Therefore, embankment soil is divided into several basic units, the soil hydraulic conductivity random field is generated, the fractal dimension of each soil unit is calculated, and then the influence of fractal dimension on hydraulic gradient is studied, which has positive significance for engineering practice.
3. Case Study
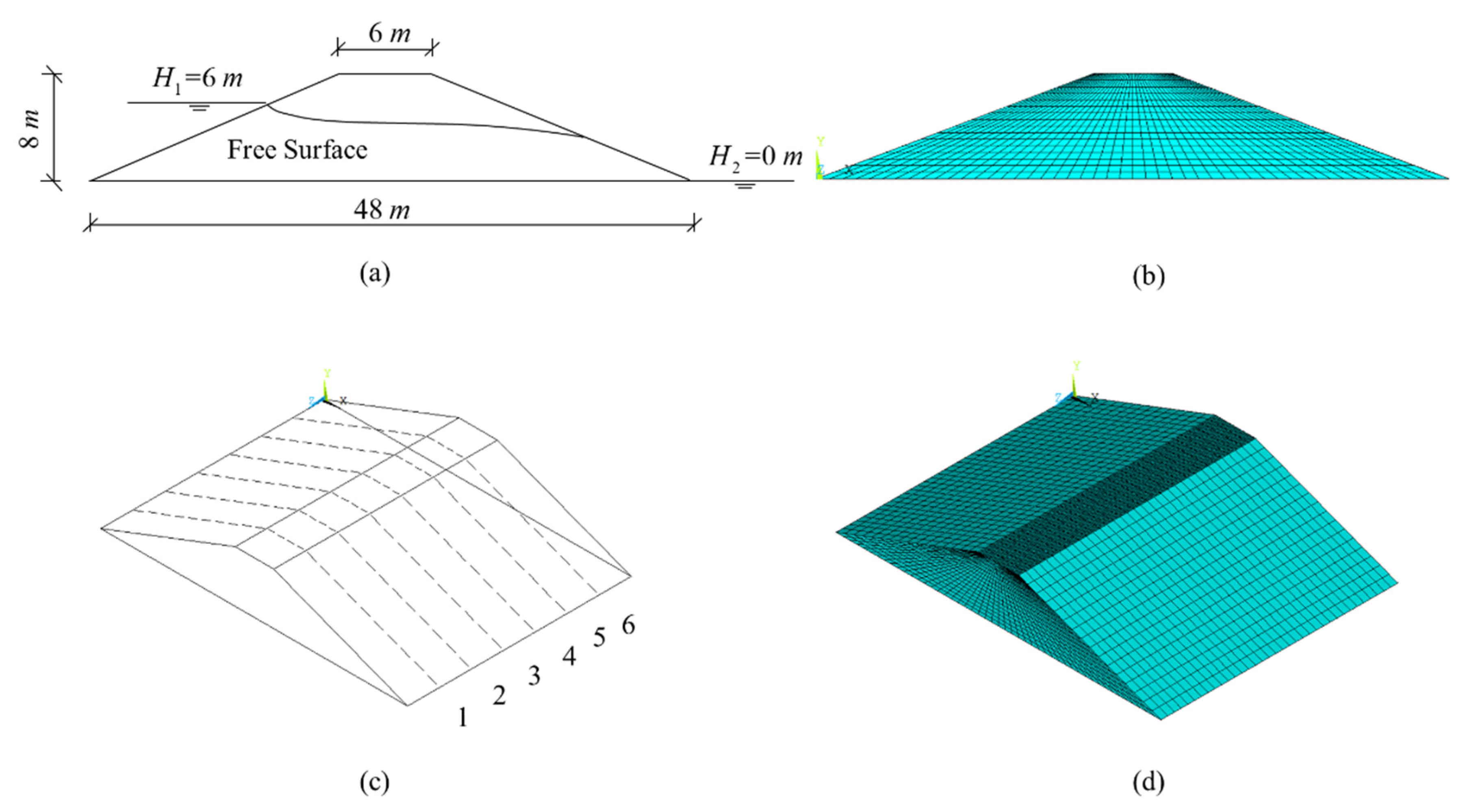
In recent years, within the general trend of global warming, extreme weather has occurred frequently. In order to ensure the stability of lake embankments, the embankments of Shijiu and Gucheng Lakes in Nanjing City, Jiangsu Province, are reinforced. During the reinforcement process, the hydraulic conductivity of many embankment soil samples was measured. Based on this, the embankment section of Shijiu Lake was selected for analysis. It is located at K19 + 400 stake in Lishui District, near Lianhewei drainage station (shown in
Figure 2). In Lishui District, the width of the embankment top is generally 5–7 m, and some embankment tops are earth roads. The lower part of the upstream slope has dry masonry and riprap toe protection, and the upper part has mortar masonry or concrete protection. The downstream slope is basically natural grassland or shrub, and there are berms on the downstream slope of some embankment sections; there is a mortar masonry wave wall approximately 0.3–1.5 m in size near the water.
Due to the length of time the embankment has been there, the upstream–downstream slopes have been eroded to varying degrees. In studying the randomness of hydraulic conductivity, the analysis model was established according to the engineering practice without considering the erosion effect on both sides. In this section, the embankment soil is not layered and is composed of heavy silty loam.
Figure 3 shows the embankment model of Shijiu Lake. According to the engineering practice, the generalized model of the lake embankment was established. The width of the embankment top and bottom was 6 and 48 m, the vertical distance from the top to the foundation was 8 m, and the model was 35 m long in the z-direction. The model was divided into 26,880 elements and 59,976 nodes. The dimensions of the elements in the y-and z-directions were 0.5 and 1 m, and the cell size was not fixed in the x-direction. Six sections were chosen to study the variation of soil hydraulic conductivity and fractal dimension: z = 5, 10, 15, 20, 25, and 30.
In this study, through on-site borehole sampling, indoor permeability tests were carried out on several samples of embankments in Lishui District. A total of 54 undisturbed soil samples were obtained in the soil layers inside and outside the impervious core of the embankment section. The undisturbed soil sample was 20 cm long. Each sample was measured three times, and then the hydraulic conductivity of embankment soil samples in Lishui District was obtained. The mean value measured in the test was compared with the hydraulic conductivity provided in the survey report and analyzed to determine the hydraulic conductivity of each soil layer as shown in
Table 1.
Based on the data in
Table 1, a random field of hydraulic conductivity was generated, with a mean of 3.32 × 10
−6 cm/s and COV of 0.3, and then the fractal dimension of soil element was calculated according to the relationship between soil fractal dimension and hydraulic conductivity. There were three important boundary conditions: (1) the upstream slope was permeable, and the total head was 6 m; (2) the downstream slope was permeable, and the total head was 0 m; (3) without considering the influence of unsaturated zone, the bottom of the embankment was impervious.
4. Results and Discussion
A gray scale diagram of hydraulic conductivity and fractal dimension of six sections in the embankment are shown in
Figure 4.
Figure 4a shows the distribution law of the hydraulic conductivity of each unit in
Section 1. In the section, the gray values of the units in the middle and upper left areas are similar, showing darker colors, and the hydraulic conductivity in this area was low. On both sides of the section, the gray values of the units were close to each other and the color was light, which means the hydraulic conductivity of the soil was high. It can be seen that dark and light soil units appeared as irregular blocks. In the junction area of blocks, there was no sudden change in gray level, but an obvious transition state, gradually changing from pure white to pure black.
Figure 4b shows the distribution law of the fractal dimension of each unit in
Section 1. In this section, the gray values of the units in the middle and upper left regions were similar, showing lighter colors. The unit fractal dimension in this region was large; according to the statistics, the soil fractal dimension was mainly distributed in the interval (1.7, 1.8), which was close to two. In a plane, the soil fractal dimension was distributed in the interval (1, 2); therefore, in this part of the region, it was large. On both sides of the section, the gray values of the units were also close to each other, but the color in this part was dark. According to the statistics, in this part of the area, the soil fractal dimension was mainly distributed in the interval (1.55, 1.6), which means that it was small. At the same time, it can be seen that the dark and light units appeared as irregular blocks. In the junction area of the blocks, there was no sudden change in the gray, but an obvious shift from pure white to pure black.
Comparing
Figure 4a,b, the unit distribution area with dark color in
Figure 4a was close to the unit distribution area with light color in
Figure 4b, and the unit distribution area with light color in
Figure 4a was close to the unit distribution area with medium dark color in
Figure 4b, indicating that the unit gray levels of hydraulic conductivity and fractal dimension present opposite characteristics. In
Figure 4a, the soil units with low hydraulic conductivity were represented by dark color, and the units with high hydraulic conductivity were represented by light color. In
Figure 4b, the soil units with small fractal dimension were represented by dark color, and the units with large fractal dimension were represented by light color. In a unit at the same point, when the hydraulic conductivity was low, the corresponding fractal dimension was large, and when the hydraulic conductivity was high, the corresponding fractal dimension was small.
The reasons for this phenomenon are as follows: The fractal dimension of two-dimensional Euclidean space is 2. For the soil distributed in this space, considering the influence of pore structure, the fractal dimension is . Assuming that the structure of pores in the soil tends to be consistent, a single-direction seepage channel is formed, and groundwater can only flow through this channel. Based on the meaning of fractal, the fractal dimension of soil is infinitely close to 1. In this case, the seepage path of water is a straight line. In the flow process, it is rarely hindered by soil particles or soil particle agglomerates, the flow rate is high, and the hydraulic conductivity of soil can reach the maximum value.
Correspondingly, it is assumed that there is no rule governing the structure of pores. At any point, the seepage channel can point in any direction and water can flow in any direction. In this case, the fractal dimension of the soil is infinitely close to 2, and the seepage path of water is no longer a straight line but a curve related to the head difference. In the process of flow, soil particles or soil particle agglomerates form the greatest obstruction to seepage, the hydraulic conductivity and flow rate are reduced and can reach the minimum value. In nature, the two extreme working conditions are almost impossible. In the section, when the fractal dimension of soil increases, the hydraulic conductivity decreases, and when the fractal dimension decreases, the hydraulic conductivity increases.
Figure 4c,d show similar laws. Comparing
Figure 4a,c, due to the randomness of hydraulic conductivity, although the laws are consistent, its distribution in the two sections differs. In
Figure 4e,g, the dark areas are widely distributed, which indicates that most of the unit hydraulic conductivity is low in the two sections. In
Figure 4f,h, there are many units with light color, which means that the fractal dimension of most units is large. Consistent results can also be seen in
Figure 4i–l. Obviously, hydraulic conductivity can be explained by fractal theory; however, it is not an ideal fractal, which leads to the fractal dimension of soil properties always being greater than 1.5 [
31,
38]. Similar explanations can be found in this study.
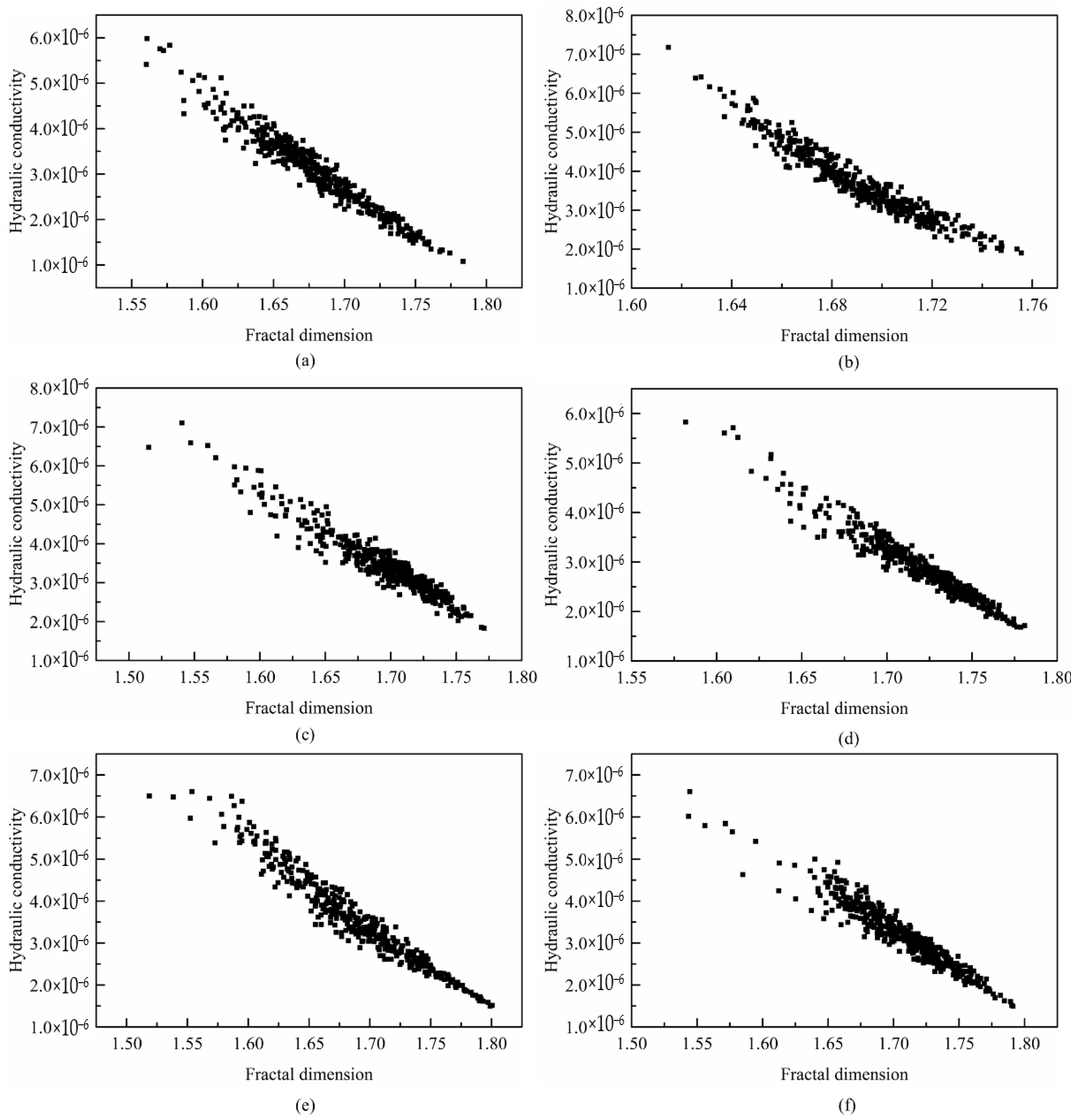
Figure 5 shows the variations in hydraulic conductivity with fractal dimension in different sections. In the sections, hydraulic conductivity decreases with increased fractal dimension. For the same fractal dimension, some of the unit hydraulic conductivity is not unique, and its value changes within a range. The reason is that the unit permeability is affected by the maximum pore diameter and porosity, and these are random variables, which will affect the fractal dimension and hydraulic conductivity values.
The fractal dimension values in each section are in the interval [1.5, 1.8], which is far from 1.0. In this condition, it is difficult to form a single-direction seepage channel in the soil, and water can flow in multiple directions. The fractal dimension is close to 2.0, which means that the seepage channel can point in almost any direction in the plane, and the water can flow in any direction in the soil. The seepage path of water is not a straight line but is in a complex and changeable state.
In each section, the unit hydraulic conductivity is mostly distributed in the interval [2 × 10
−6, 4 × 10
−6], and only a few hydraulic conductivity units are distributed outside this interval. This phenomenon conforms to the objective law. In this research, the mean of hydraulic conductivity is 3.32 × 10
−6 cm/s, COV is 0.3, and the scale of fluctuations is 6 and 3 m, respectively. When the hydraulic conductivity random field is discretized, COV is within a certain range, and the value after discretization deviates little from the mean value. With increased COV, the value after discretization will be distributed in a larger range. In
Figure 5b,c,e, the discrete points show a slight downward bending phenomenon, which means that the unit permeability may decrease slowly with increased fractal dimension.
In order to study the relationship between the fractal dimension and hydraulic gradient of soil, four soil units were selected near the upstream slope angle of each section, which were in the same position. The random seepage field of the embankment was calculated by ABAQUS software, and the hydraulic gradient at each point was obtained. The variation in hydraulic gradient with fractal dimension in different sections is shown in
Figure 6. With increased fractal dimension, the hydraulic gradient increased accordingly, because the soil fractal dimension was inversely proportional to the hydraulic conductivity; when the fractal dimension increased the unit permeability decreased, which means that water flows the same distance in the soil, encounters more resistance, and needs more potential energy, resulting in increased hydraulic gradient.