On a Partial Fractional Hybrid Version of Generalized Sturm–Liouville–Langevin Equation
Abstract
1. Introduction and Preliminaries
2. Main Results
- There exist such that the following functional inequalities are satisfiedfor all .
- There exists such thatwhere
- There exist , such that for all and , we have the following functional inequalities hold true
- There exists such thatand
3. Examples
| w | u | ||||
|---|---|---|---|---|---|
| 0 | 0.5000 | 0 | 0 | 0.5000 | 0 |
| 0.1 | 0.5500 | 0.0309 | 0.2 | 0.6107 | 0.0911 |
| 0.2 | 0.7000 | 0.0587 | 0.4 | 0.7459 | 0.1682 |
| 0.3 | 0.8933 | 0.0809 | 0.6 | 0.9110 | 0.2350 |
| 0.4 | 0.9909 | 0.0951 | 0.8 | 1.1127 | 0.2938 |
| 0.5 | 1 | 0.1 | 1 | 1.3591 | 0.3465 |
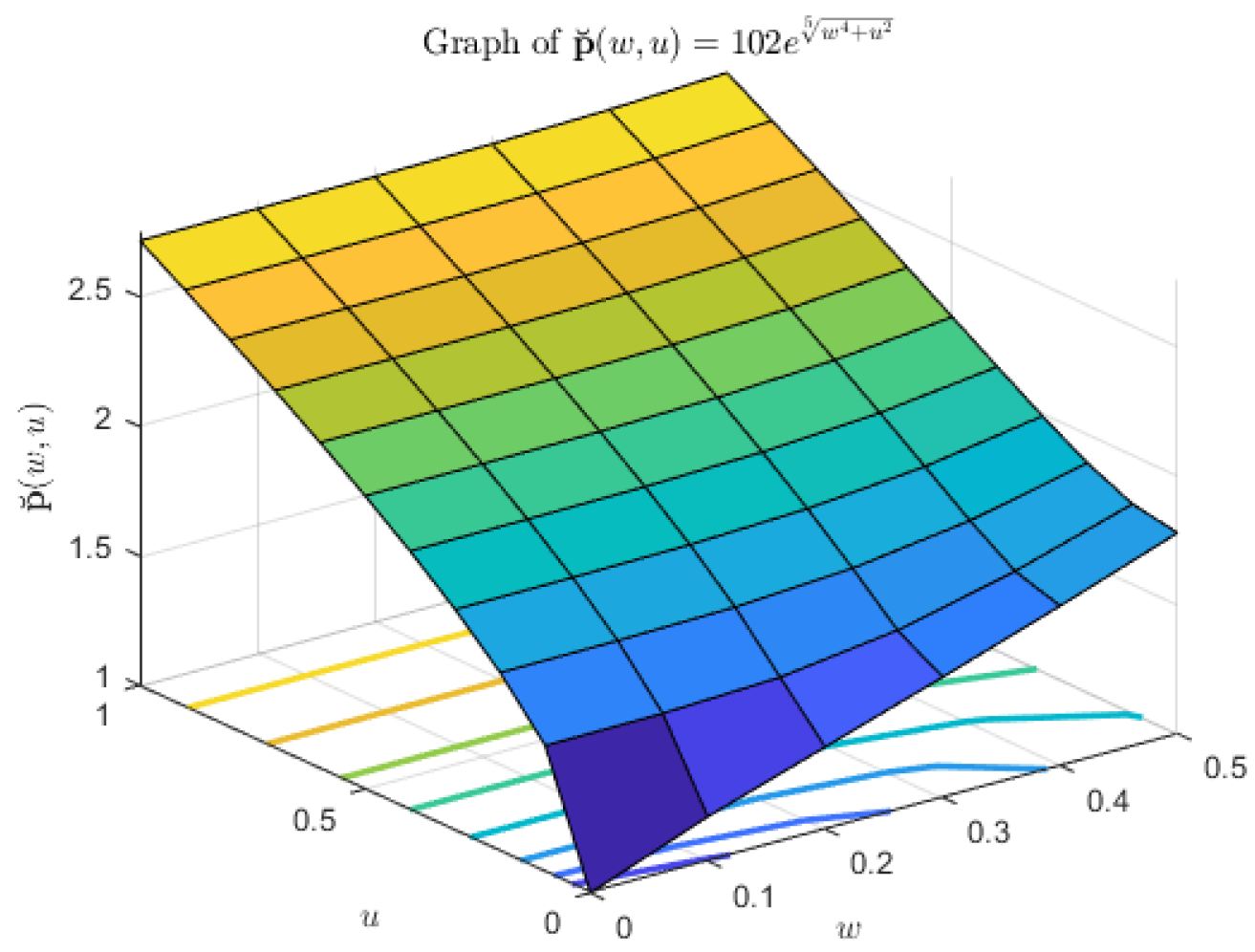

| w | u | ||||
|---|---|---|---|---|---|
| 0 | 0 | 1.6020 | 0 | 0 | 0.00166 |
| 0.3 | 9.8000 | 0.0014 | 0.1 | 0.0025 | 0.00150 |
| 0.5 | 1.3200 | 0.0012 | 0.15 | 0.0056 | 0.00142 |
| 0.7 | 49.8000 | 0.0011 | 0.2 | 0.01 | 0.00136 |
| 0.9 | 81.8000 | 0.0009 | 0.25 | 0.0156 | 0.00129 |
| 1 | 0.1250 | 0.0008 | 0.3 | 0.0225 | 0.00123 |
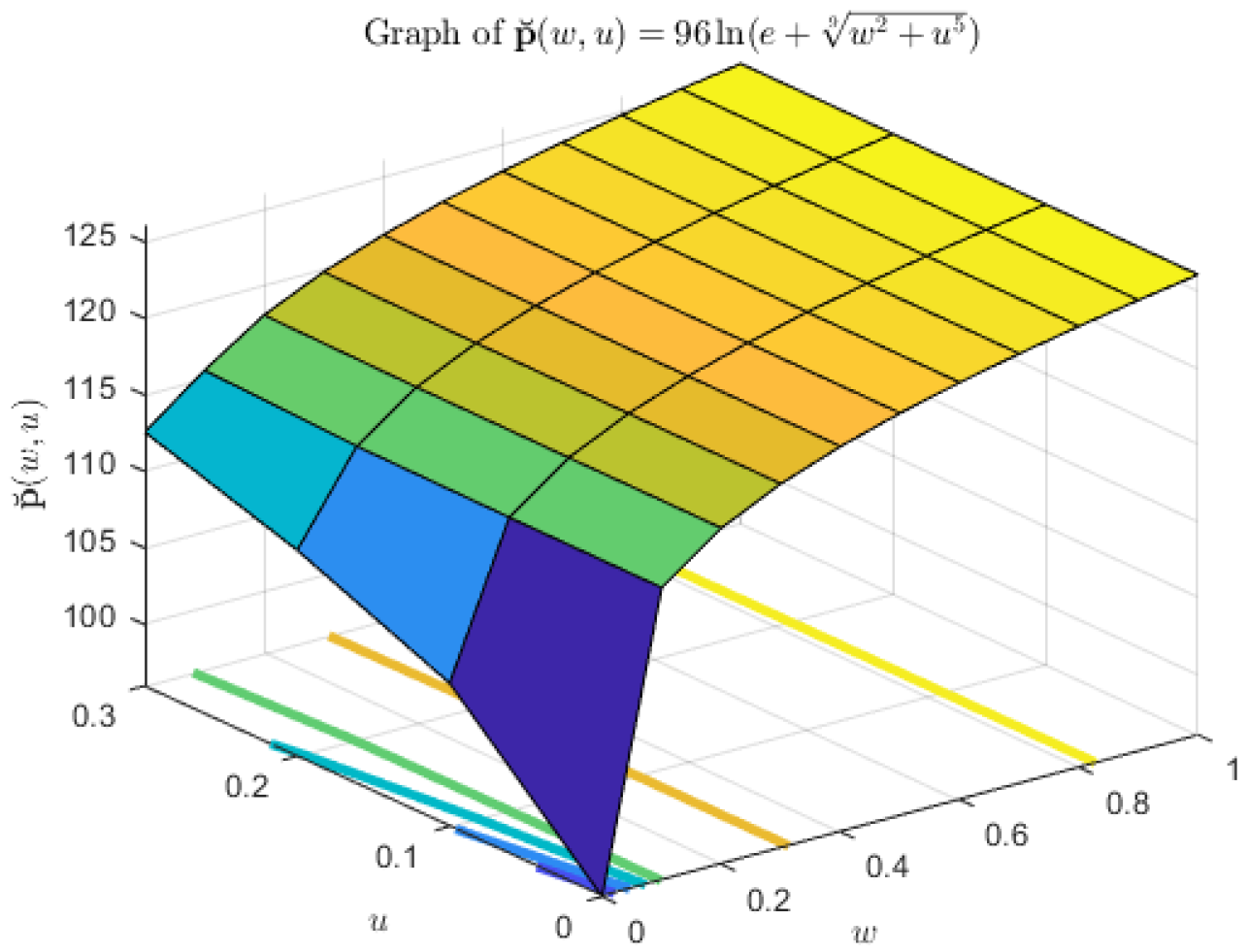

4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Mohammadi, H.; Kumar, S.; Rezapour, S.; Etemad, S. A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solitons Fractals 2021, 144, 110668. [Google Scholar] [CrossRef]
- Shabibi, M.; Samei, M.E.; Ghaderi, M.; Rezapour, S. Some analytical and numerical results for a fractional q-differential inclusion problem with double integral boundary conditions. Adv. Differ. Equs. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Sethi, A.K.; Ghaderi, M.; Rezapour, S.; Kaabar, M.K.A.; Inc, M.; Masiha, H.P. Sufficient conditions for the existence of oscillatory solutions to nonlinear second order differential equations. J. Appl. Math. Comput. 2021, 27, 105–113. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 2020, 71. [Google Scholar] [CrossRef]
- Ahmad, M.; Zada, A.; Ghaderi, M.; George, R.; Rezapour, S. On the existence and stability of a neutral stochastic fractional differential system. Fractal Fract. 2022, 6, 203. [Google Scholar] [CrossRef]
- Heymans, N. Dynamic Measurements in Long-memory Materials: Fractional Calculus Evaluation of Approach to Steady State. J. Vib. Control 2008, 14, 1587–1596. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. On a new fractional uncertainty relation and its implications in quantum mechanics and molecular physics. Proc. R. Soc. A 2008, 476, 20190729. [Google Scholar] [CrossRef]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 034101. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Path integral formulation of fractionally perturbed Lagrangian oscillators on fractal. J. Stat. Phys. 2018, 172, 1617–1640. [Google Scholar] [CrossRef]
- Jiang, D.; Yuan, C. The positive properties of the Green function for Dirichlet-type boundary value problems of nonlinear fractional differential equations and its application. Nonlinear Anal. Theory Methods Appl. 2010, 72, 710–719. [Google Scholar] [CrossRef]
- Abbas, S.; Baleanu, D.; Benchohra, M. Global attractivity for fractional order delay partial integro-differential equations. Adv. Differ. Equs. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M. Fractional order partial hyperbolic differential equations involving Caputo’s derivative. Stud. Univ. Babes-Bolyai Math. 2012, 57, 469–479. [Google Scholar]
- Matar, M.M.; Abbas, M.I.; Alzabut, J.; Kaabar, M.K.A.; Etemad, S.; Rezapour, S. Investigation of the p-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives. Adv. Differ. Equs. 2021, 2021, 68. [Google Scholar] [CrossRef]
- Benchohra, M.; Hellal, M. Perturbed partial functional fractional order differential equations with infnite delay. J. Adv. Res. Dyn. Control Syst. 2013, 5, 1–15. [Google Scholar]
- Baleanu, D.; Etemad, S.; Rezapour, S. A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020, 2020, 64. [Google Scholar] [CrossRef]
- Miandaragh, M.A.; Postolache, M.; Rezapour, S. Some Approximate Fixed Point Results for Generalized α-Contractive Mappings. Sci. Bull. Politeh. Univ. Buchar. Ser. A Appl. Math. Phys. 2013, 75, 3–10. [Google Scholar]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. On a nonlinear fractional differential equation on partially ordered metric spaces. Adv. Differ. Equs. 2013, 2013, 83. [Google Scholar] [CrossRef]
- Haghi, R.H.; Rezapour, S. Fixed points of multifunctions on regular cone metric spaces. Expo. Math. 2010, 28, 71–77. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Leela, S. Differential and Integral Inequalities: Theory and Applications: Volume I: Ordinary Differential Equations; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Wolfgang, W.; Leela, S. Differential and Integral Inequalities; Springer Science and Business Media: Berlin, Germany, 2012. [Google Scholar]
- Mohammed, P.O.; Abdeljawad, T. Modification of certain fractional integral inequalities for convex functions. Adv. Differ. Equs. 2020, 2020, 69. [Google Scholar] [CrossRef]
- Abdeljawad, T. Fractional operators with exponential kernels and a Lyapunov type inequality. Adv. Differ. Equs. 2017, 2017, 313. [Google Scholar] [CrossRef]
- Abdeljawad, T. A Lyapunov type inequality for fractional operators with nonsingular Mittag-Leffler kernel. J. Inequal. Appl. 2017, 2017, 130. [Google Scholar] [CrossRef] [PubMed]
- Al-Gwaiz, M.A. Sturm–Liouville Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Rivero, M.; Trujillo, J.; Velasco, M. A fractional approach to the Sturm–Liouville problem. Open Phys. 2013, 11, 1246–1254. [Google Scholar] [CrossRef]
- Klimek, M.; Agrawal, O.P. Fractional Sturm–Liouville problem. Comput. Math. Appl. 2013, 66, 795–812. [Google Scholar] [CrossRef]
- Mdallal, Q.M.A. An efficient method for solving fractional Sturm–Liouville problems. Chaos Solitons Fractals 2009, 40, 183–189. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winnn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Teschl, G. Mathematical Methods in Quantum Mechanics: With Applications to Schrödinger Operators. Grad. Stud. Math. 2009, 99, 106. [Google Scholar]
- Bairamov, E.; Erdal, I.; Yardimci, S. Spectral properties of an impulsive Sturm–Liouville operator. J. Inequal. Appl. 2018, 2018, 191. [Google Scholar] [CrossRef]
- Yokus, N.; Koprubasi, T. Spectrum of the Sturm–Liouville operators with boundary conditions polynomially dependent on the spectral parameter. J. Inequal. Appl. 2015, 2015, 42. [Google Scholar] [CrossRef][Green Version]
- Bensidhoum, F.Z.; Dib, H. On some regular fractional Sturm–Liouville problems with generalized Dirichlet conditions. J. Integral Equs. Appl. 2016, 28, 459–480. [Google Scholar] [CrossRef]
- Erturk, V.S. Computing eigenelements of Sturm–Liouville problems of fractional order via fractional differential transform method. Math. Comput. Appl. 2011, 16, 712–720. [Google Scholar] [CrossRef]
- Hassana, A.A. Green’s function solution of non-homogenous singular Sturm–Liouville problem. Int. J. Sci. Res. Eng. Dev. 2019, 2, 735–742. [Google Scholar]
- Kiataramkul, C.; Ntouyas, S.K.; Tariboon, J.; Kijjathanakorn, A. Generalized Sturm–Liouville and Langevin equations via Hadamard fractional derivatives with anti-periodic boundary conditions. Bound. Value Probl. 2016, 2016, 217. [Google Scholar] [CrossRef]
- Li, Y.; Sun, S.; Han, Z.; Lu, H. The existence of positive solutions for boundary value problem of the fractional Sturm–Liouville functional differential equation. Abstr. Appl. Anal. 2013, 2013, 301560. [Google Scholar] [CrossRef]
- Lian, H.; Ge, W. Existence of positive solutions for Sturm–Liouville boundary value problems on the half-line. J. Math. Anal. Appl. 2006, 321, 781–792. [Google Scholar] [CrossRef]
- Liu, Y.; He, T.; Shi, H. Three positive solutions of Sturm–Liouville boundary value problems for fractional differential equations. Differ. Equ. Appl. 2013, 5, 127–152. [Google Scholar] [CrossRef]
- Muensawat, T.; Ntouyas, S.K.; Tariboon, J. Systems of generalized Sturm–Liouville and Langevin fractional differential equations. Adv. Differ. Equs. 2017, 2017, 63. [Google Scholar] [CrossRef]
- Sun, F.; Li, K.; Qi, J.; Liao, B. Non-real eigenvalues of nonlocal indefinite Sturm–Liouville problems. Bound. Value Probl. 2019, 2019, 176. [Google Scholar] [CrossRef]
- Xu, J.; Abernathy, Z. On the solvability of nonlinear Sturm–Liouville problems. J. Math. Anal. Appl. 2012, 387, 310–319. [Google Scholar] [CrossRef][Green Version]
- Mainardi, F.; Pironi, P. The fractional Langevin equation: Brownian motion revisited. Extr. Math. 1996, 10, 140–154. [Google Scholar]
- Applebaum, D. Levy Processes and Stochastic Calculus; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Applebaum, D. On the Spectrum of Self–Adjoint Levy Generators. arXiv 2019, arXiv:1904.07548. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation, 2nd ed.; World Scientific: Singapore, 2004. [Google Scholar]
- Lim, S.C.; Li, M.; Teo, L.P. Langevin equation with two fractional orders. Phys. Lett. A 2008, 372, 6309–6320. [Google Scholar] [CrossRef]
- Uranagase, M.; Munakata, T. Generalized Langevin equation revisited: Mechanical random force and self-consistent structure. J. Phys. A Math. Theor. 2010, 43, 455003. [Google Scholar] [CrossRef]
- Denisov, S.I.; Kantz, H.; Hanggi, P. Langevin equation with super-heavy-tailed noise. J. Phys. A Math. Theor. 2010, 43, 285004. [Google Scholar] [CrossRef][Green Version]
- Lozinski, A.; Owens, R.G.; Phillips, T.N. The Langevin and Fokker–Planck equations in polymer rheology. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Ahmad, B.; Nieto, J.J.; Alsaedi, A.; El-Shahed, M. A study of nonlinear Langevin equation involving two fractional orders in different intervals. Nonlinear Anal. Real World Appl. 2012, 13, 599–606. [Google Scholar] [CrossRef]
- Lim, S.C.; Teo, L.P. The fractional oscillator process with two indices. J. Phys. A Math. Theor. 2009, 42, 065208. [Google Scholar] [CrossRef]
- Lizana, L.; Ambjornsson, T.; Taloni, A.; Barkai, E.; Lomholt, M.A. Foundation of fractional Langevin equation: Harmonization of a many-body problem. Phys. Rev. E 2010, 81, 051118. [Google Scholar] [CrossRef]
- Dhage, B.C.; Lakshmikantham, V. Basic results on hybrid differential equations. Nonlinear Anal. Hybrid Syst. 2010, 4, 414–424. [Google Scholar] [CrossRef]
- Dhage, B.C.; Lakshmikantham, V. Quadratic perturbations of periodic boundary value problems of second order ordinary differential equations. Differ. Equ. Appl. 2010, 2, 465–486. [Google Scholar] [CrossRef]
- Herzallah, M.A.E.; Baleanu, D. On fractional order hybrid differential equations. Nonlinear Anal. Hybrid Syst. 2014, 2014, 389386. [Google Scholar] [CrossRef]
- Ge, H.; Xin, J. On the existence of a mild solution for impulsive hybrid fractional differential equations. Adv. Differ. Equs. 2014, 2014, 211. [Google Scholar] [CrossRef][Green Version]
- Derbazi, C.; Hammouche, H.; Benchohra, M.; Zhou, Y. Fractional hybrid differential equations with three-point boundary hybrid conditions. Adv. Differ. Equs. 2019, 2019, 125. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, S.; Han, Z.; Li, Q. Theory of fractional hybrid differential equations. Comput. Math. Appl. 2011, 62, 1312–1324. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Gaafar, F.M. Existence and uniqueness of solution for Sturm–Liouville fractional differential equation with multi-point boundary condition via Caputo derivative. Adv. Differ. Equs. 2019, 2019, 46. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Singapore, 1999. [Google Scholar]
- Cousot, P.; Cousot, R. Constructive versions of Tarski’s fixed point theorems. Pac. J. Math. 1979, 82, 43–57. [Google Scholar] [CrossRef]
- Misra, J. Knaster-Tarski Theorem. 2014, pp. 1–3. Available online: https://www.cs.utexas.edu/users/misra/Notes.dir/KnasterTarski.pdf (accessed on 9 December 2014).
- Samet, B.; Vetro, C.; Vetro, P. Fixed point theorem for α-ψ contractive type mappings. Nonlinear Anal. Theory Methods Appl. 2012, 75, 2154–2165. [Google Scholar] [CrossRef]
- Aleomraninejad, S.M.A.; Rezapour, S.; Shahzad, N. Some fixed point results on a metric space with a graph. Topol. Its Appl. 2012, 159, 659–663. [Google Scholar] [CrossRef]
- Miandaragh, M.A.; Postolache, M.; Rezapour, S. Some approximate fixed point results for generalized α-contractive mappings. UPB Sci. Bull. Ser. A Appl. Math. Phys. 2012, 75, 3–10. [Google Scholar]
- Alfuraidan, M.R.; Ansari, Q.H. Fixed Point Theory and Graph Theory: Foundations and Integrative Approaches; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heydarpour, Z.; Izadi, J.; George, R.; Ghaderi, M.; Rezapour, S. On a Partial Fractional Hybrid Version of Generalized Sturm–Liouville–Langevin Equation. Fractal Fract. 2022, 6, 269. https://doi.org/10.3390/fractalfract6050269
Heydarpour Z, Izadi J, George R, Ghaderi M, Rezapour S. On a Partial Fractional Hybrid Version of Generalized Sturm–Liouville–Langevin Equation. Fractal and Fractional. 2022; 6(5):269. https://doi.org/10.3390/fractalfract6050269
Chicago/Turabian StyleHeydarpour, Zohreh, Javad Izadi, Reny George, Mehran Ghaderi, and Shahram Rezapour. 2022. "On a Partial Fractional Hybrid Version of Generalized Sturm–Liouville–Langevin Equation" Fractal and Fractional 6, no. 5: 269. https://doi.org/10.3390/fractalfract6050269
APA StyleHeydarpour, Z., Izadi, J., George, R., Ghaderi, M., & Rezapour, S. (2022). On a Partial Fractional Hybrid Version of Generalized Sturm–Liouville–Langevin Equation. Fractal and Fractional, 6(5), 269. https://doi.org/10.3390/fractalfract6050269







