Dynamic Response and Damage Regularity of Sandstone with Different Moisture States under Cyclic Loading
Abstract
:1. Introduction
2. Experimental Scheme and Sample Preparation
2.1. Rock Impact Test
2.2. NMR Test
2.3. Sample Preparation
3. SHPB Dynamic Pressure Test and Result Analysis
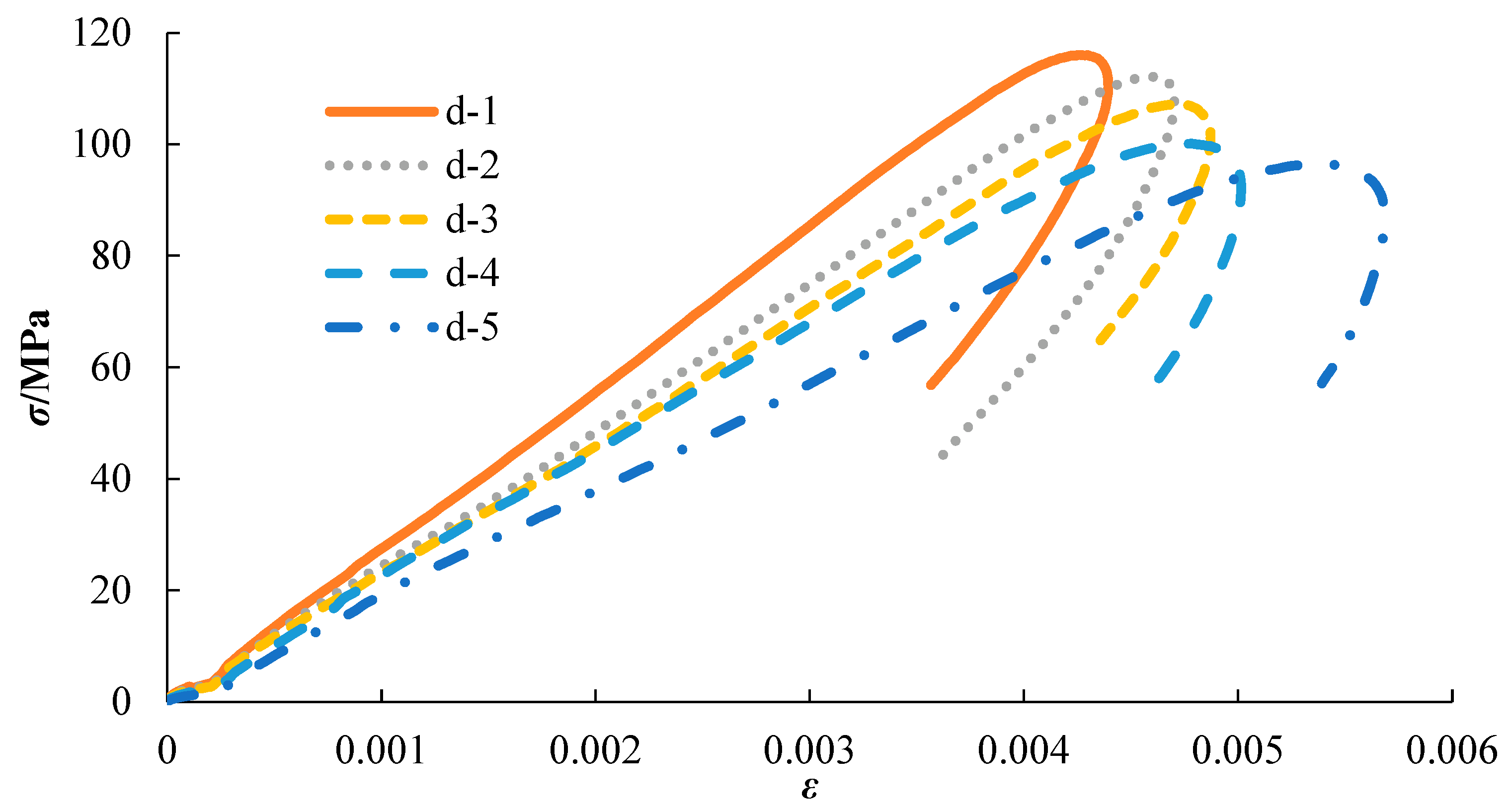
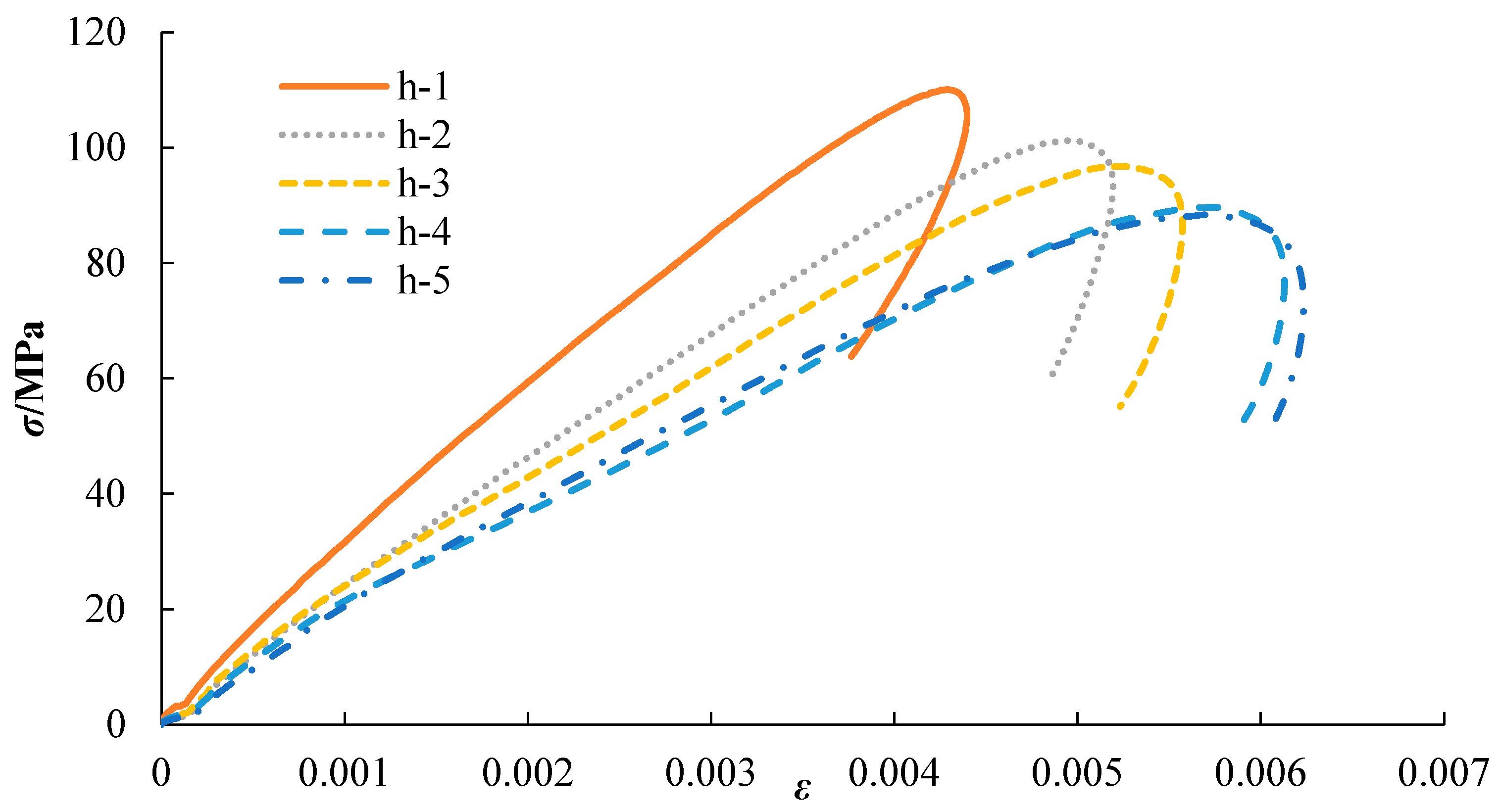
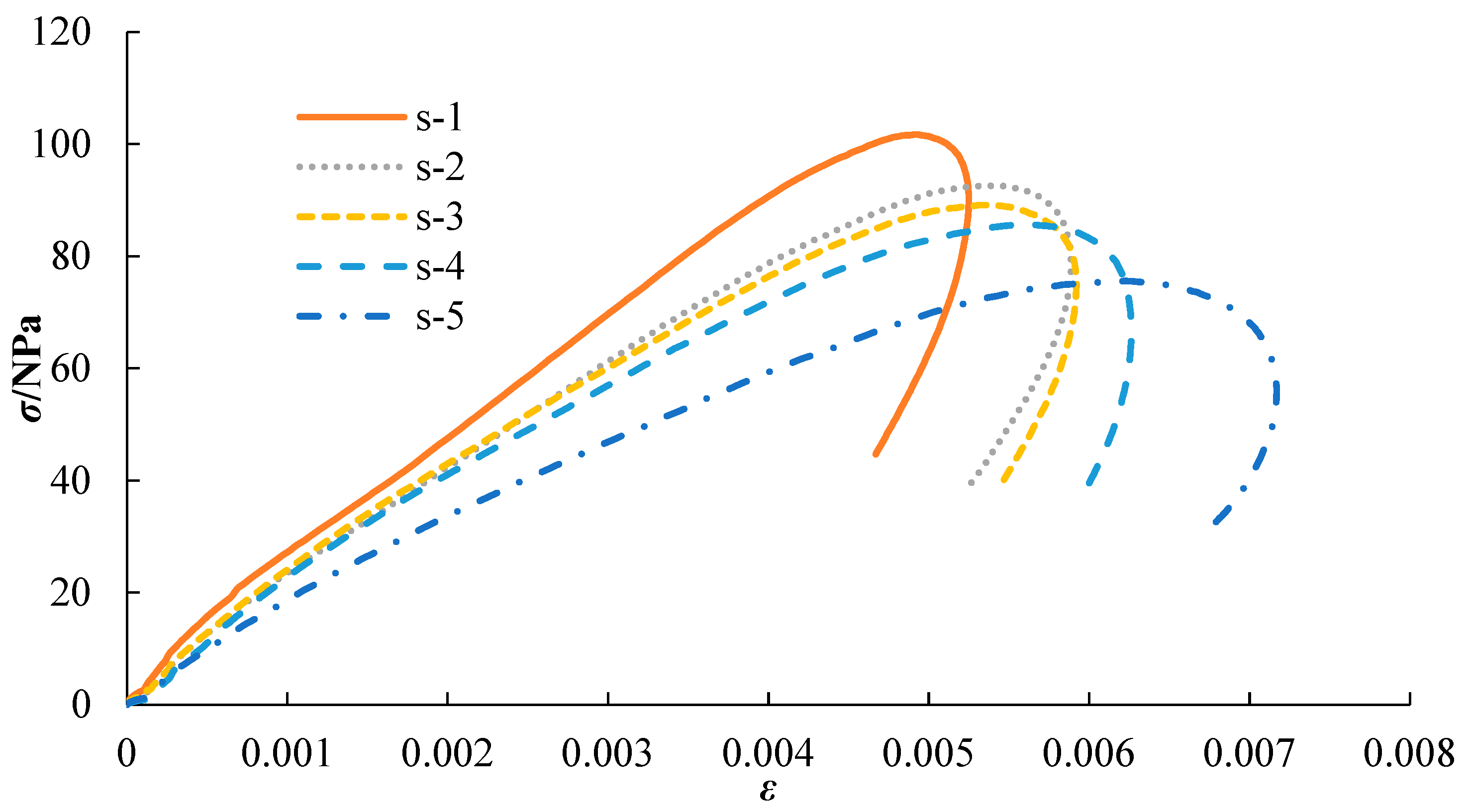
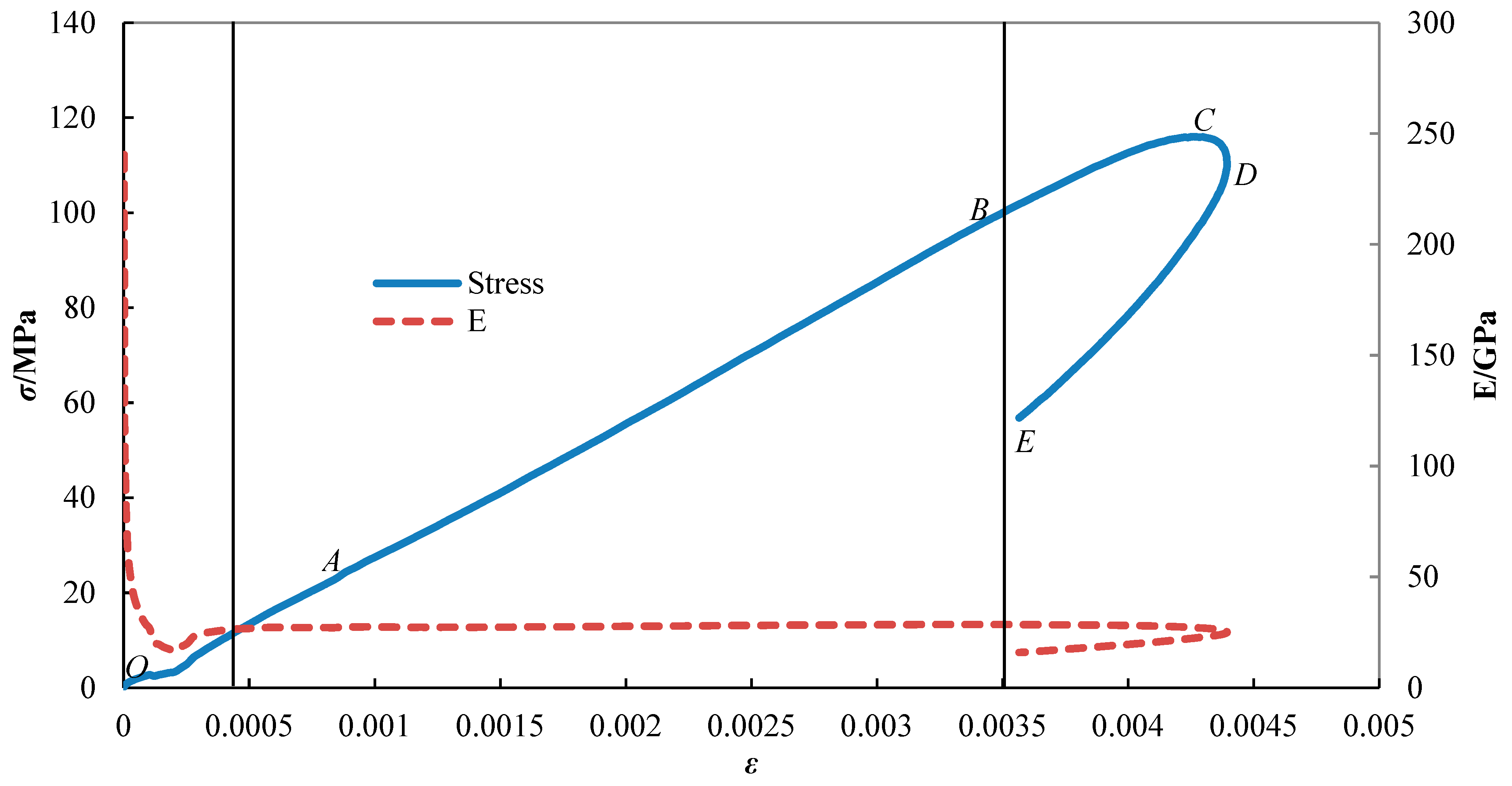
3.1. Stress-Strain Analysis
3.2. Destructive Morphology Analysis
4. Study on Rock Dynamic Damage Test
4.1. T2 Spectral Curve Analysis
4.2. Porosity Analysis
4.3. Magnetic Resonance Imaging Analysis
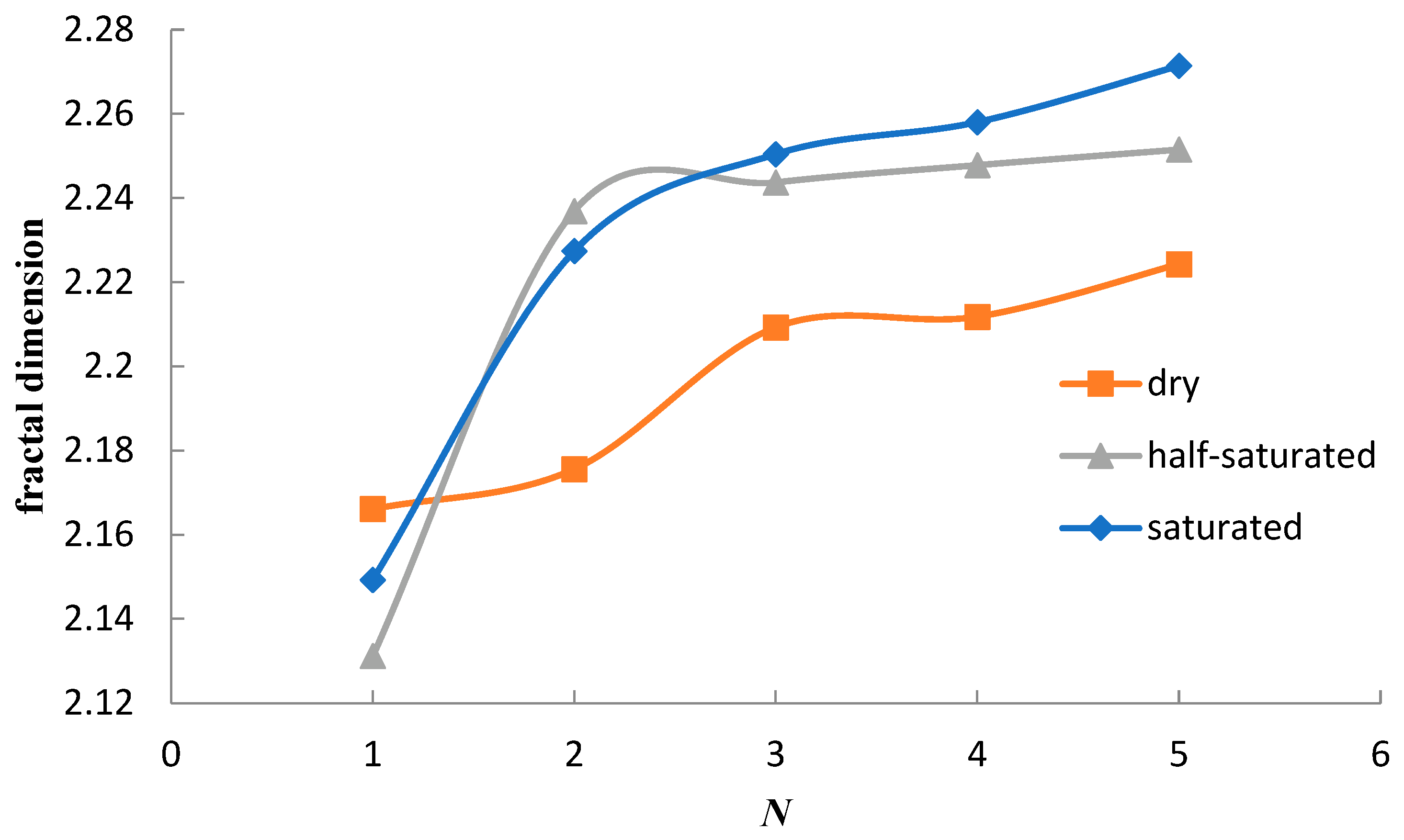
4.4. Fractal Analysis
5. Conclusions
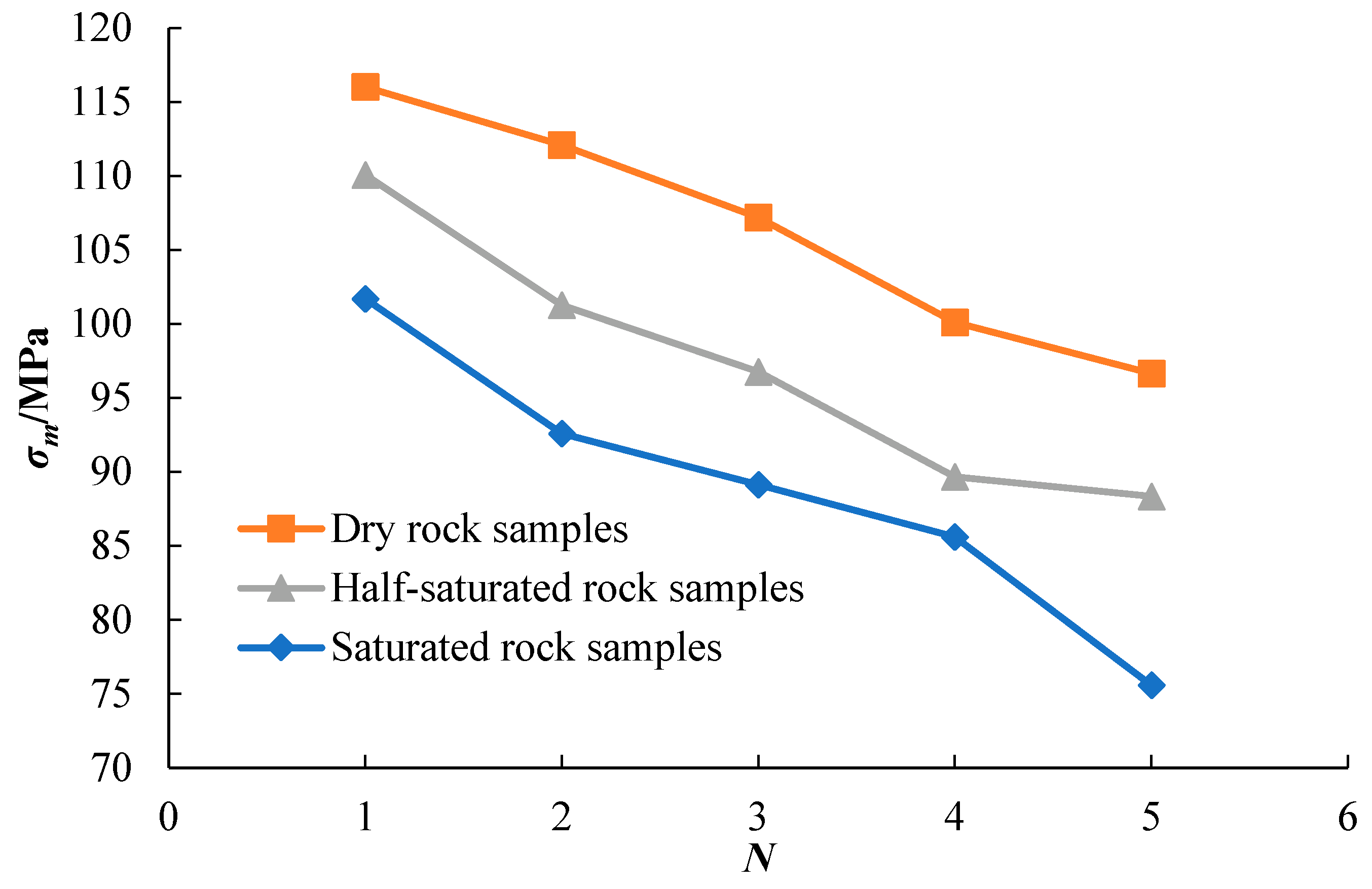
- Dynamic cyclic compression impact tests on rocks indicate that, as the impact time increased, the stress-strain curve of the rock moved to the lower right. The stress and strain curves of all the rock samples appeared during the loading and unloading stages. The peak stress of the rock was inversely proportional to the impact time, and the relationship between the peak strain and impact time was contrary to the above relationship. This phenomenon indicates that with the accumulation of rock damage, rock deformation became increasingly severe and its strength gradually decreased. At the same impact energy and frequency, few obvious damages occurred in the dry rock, and the damage to the saturated rock was the most severe. When the impact reached the third time, there was a very obvious crack on the surface of the rock sample, and the more the impact time, the more serious the damage. Therefore, the influence of water content in the rock on the mechanical properties, especially the dynamic properties, was evident.
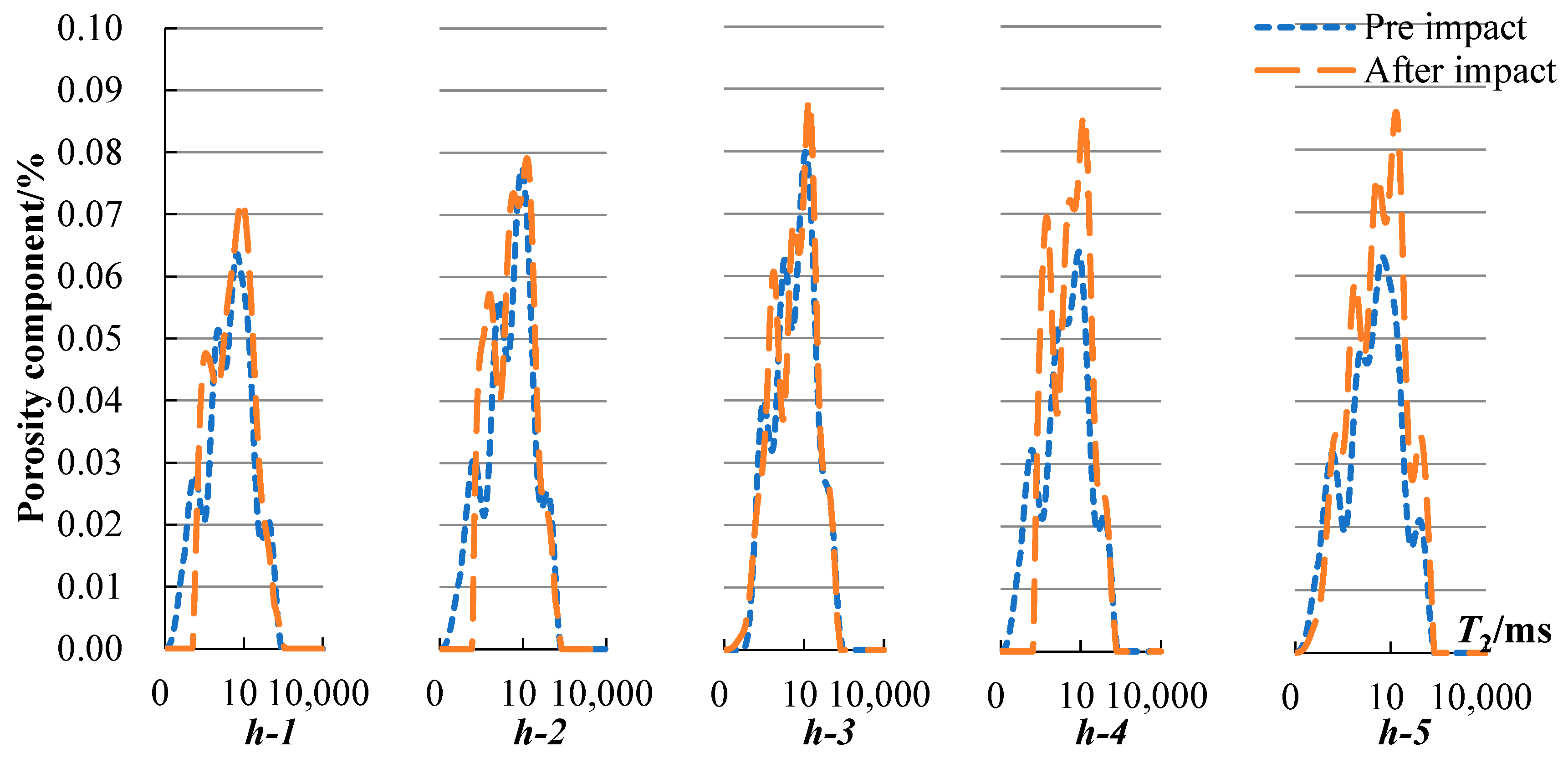
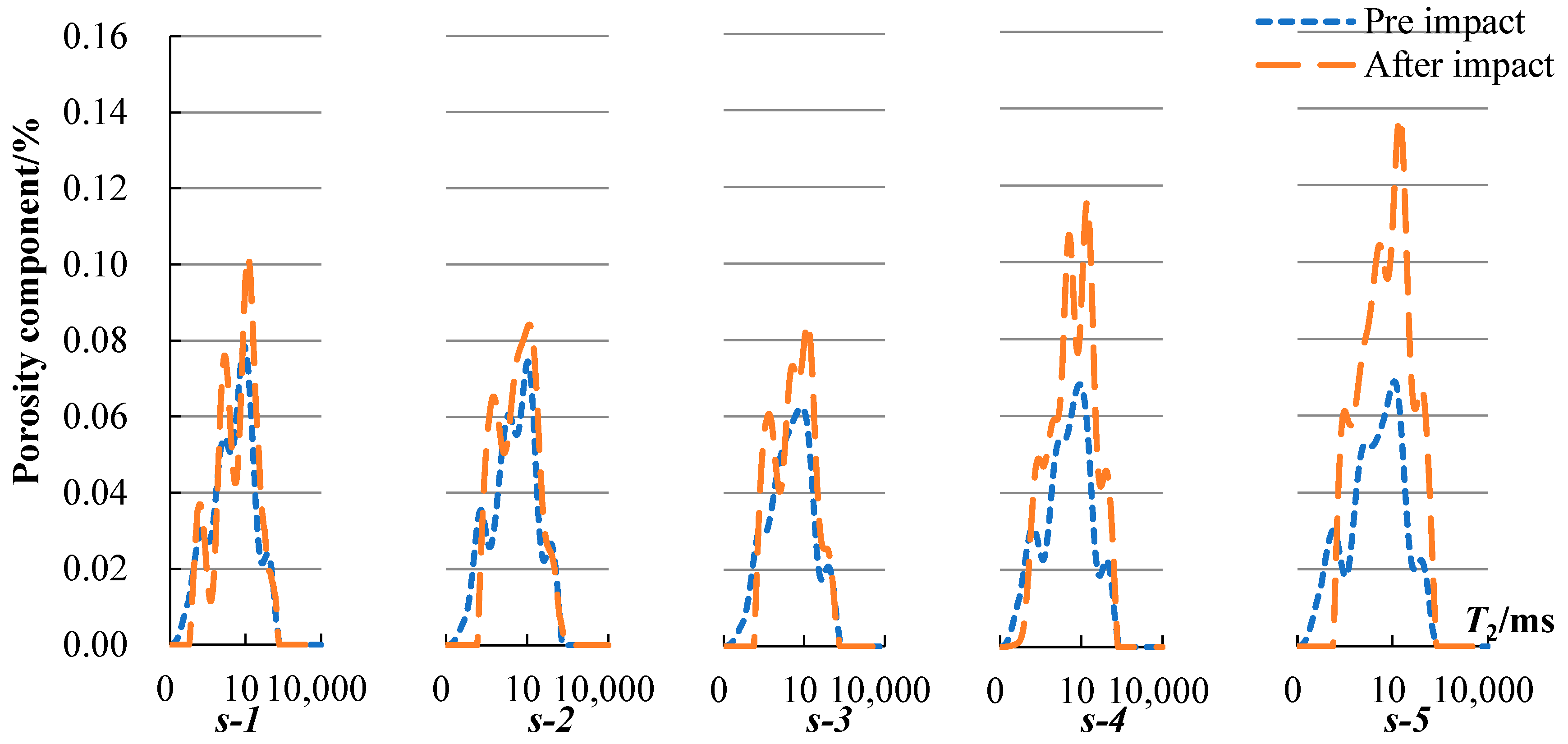
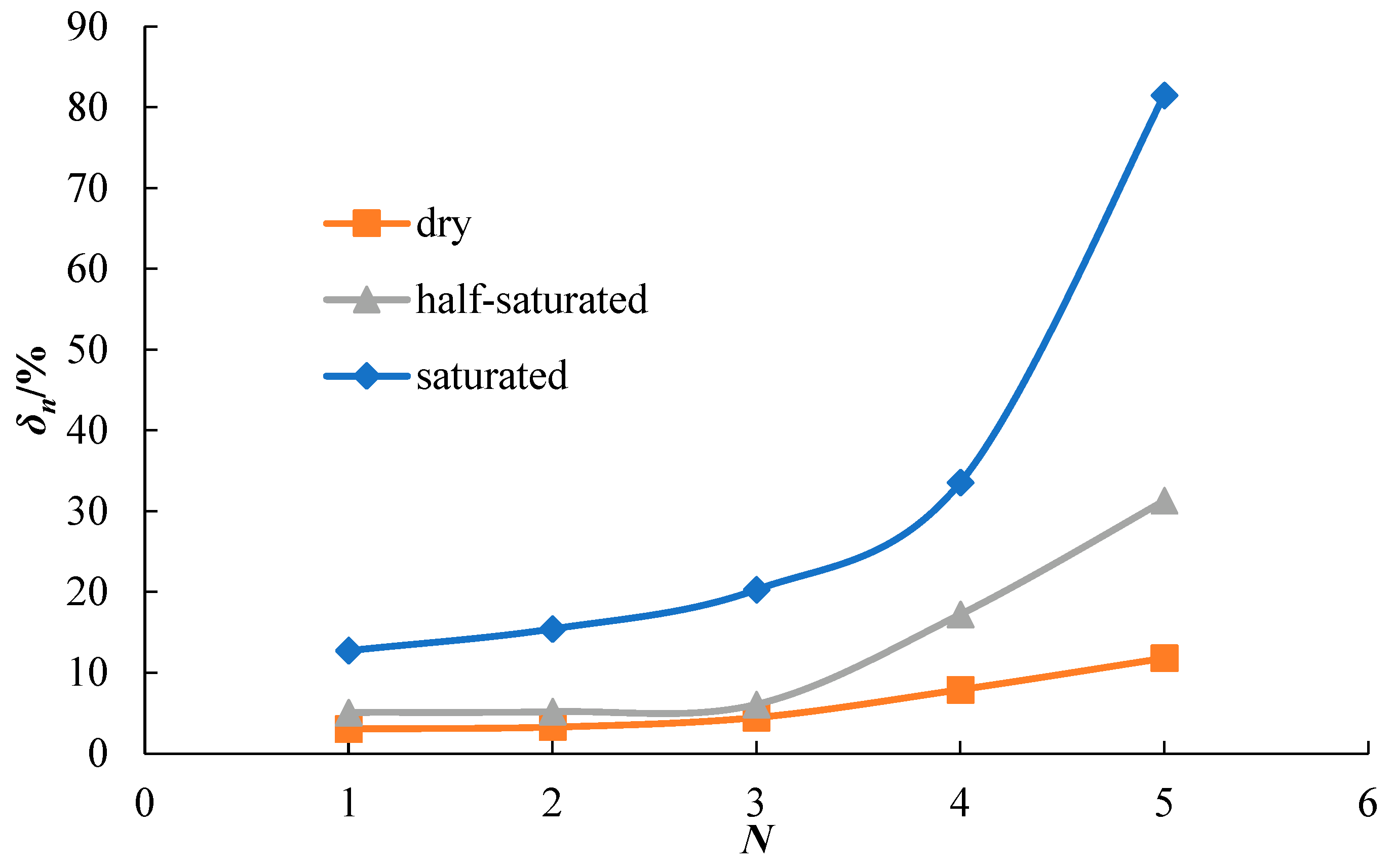
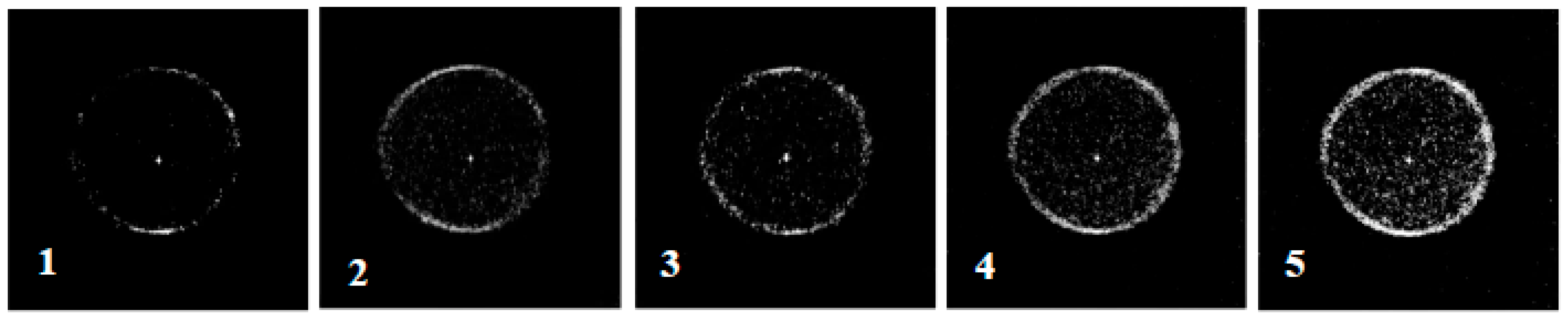
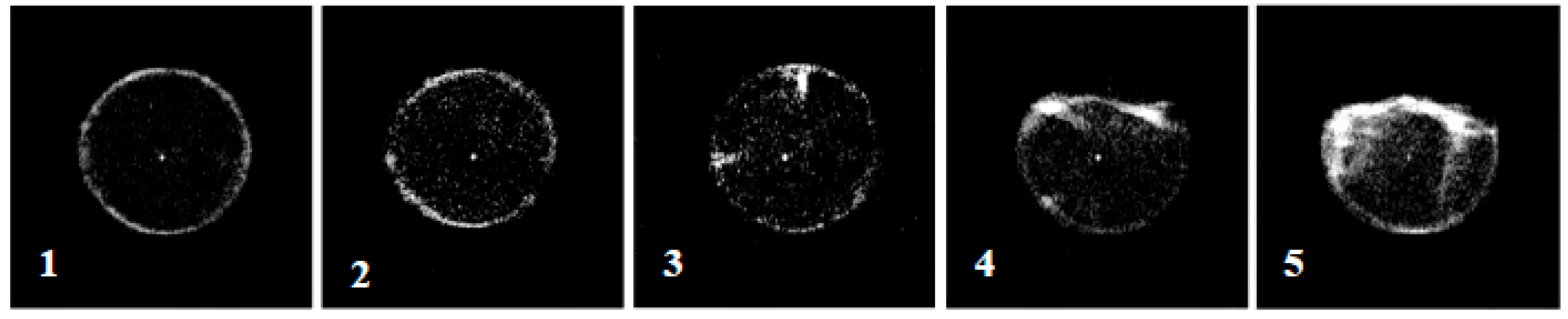
- According to the NMR scan of rock samples subjected to dynamic disturbance, the peak value of the T2 spectrum curve of the rock sample increased, especially for the water-containing samples and those with more frequent impacts. Small pores with a relaxation time < 0.1 ms were still reduced after impact compared to before impact. The peaks of the large pores increased or even exceeded the peaks before the impact in the case of more impacts. The analysis of porosity changes indicates that the porosity change rate and impact times exhibited a quadratic polynomial relationship, and the porosity change rate increased with the increase in moisture content under impact times. From the MRI images, it was observed that the internal pores of the dry rock sample were evenly distributed, and the porosity change rate was relatively stable after multiple impacts. The semi-saturated and saturated rock samples suffered damage and cracks on the fourth and third impacts, respectively. As the impact time increased, the rock was destroyed, and streaks with white and bright features appeared on the failure surface. In addition to streaks on the damaged surface of the saturated sample, several white markings also appeared inside the sample. This phenomenon indicates that there were obvious cracks inside the sample, and this was also confirmed by the fractal analysis. After 2–3 impacts on the sample, the internal pores reached equilibrium. If the impact continues, a pore will be formed internally. In the initial stage of penetration, a macrocrack was not formed. Continuous impact will form an obvious penetrating crack and lead to destruction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRI | Magnetic resonance imaging |
| NMR | Nuclear magnetic resonance |
| SHPB | Split Hopkinson pressure bar |
| T2 | Transverse relaxation time |
| mw | Weight of rock specimen (kg) |
| ms | Weight of dry rock (kg) |
| ωs | Rock moisture content |
| ωsa | Moisture content of rock under saturation conditions |
| Kω | Rock saturation coefficient |
| mp | Weight of sample before the test (kg) |
| Average saturation coefficient of rock | |
| Stress (MPa) | |
| Peak stress (MPa) | |
| Strain | |
| Peak strain | |
| N | Impact times |
| R2 | Goodness of fit |
| na | Porosity before sample is impacted |
| nb | Porosity after sample is impacted |
| δn | Porosity change rate |
References
- Yang, X.L. Discussion on damage effect on surrounding rock mass in tunneling blasting. Blasting 2003, 20, 19–23. [Google Scholar]
- Ramulu, M.; Chakraborty, A.K.; Sitharam, T.G. Damage assessment of basaltic rock mass due to repeated blasting in a railway tunnelling project—A case study. Tunn. Undergr. Space Technol. 2009, 24, 208–221. [Google Scholar] [CrossRef]
- Jong, H.S.; Hoon, G.M.; Sung, E.C. Effect of blast-induced vibration on existing tunnels in soft rocks. Tunn. Undergr. Space Technol. 2011, 26, 51–61. [Google Scholar]
- Wang, Z.L.; Li, Y.C.; Wang, J.G. Numerical analysis of blast-induced wave propagation and spalling damage in a rock plate. Int. J. Rock Mech. Min. Sci. 2008, 45, 600–608. [Google Scholar] [CrossRef]
- Kaushik, D.; Murthy, V.M.S.R. Prediction of blast-induced overbreak from uncontrolled bum-cut blasting in tunnels driven through medium rock class. Tunn. Undergr. Space Technol. 2012, 28, 49–56. [Google Scholar]
- Lv, X.C.; Xu, J.Y.; Ge, H.H.; Zhao, D.H.; Bai, E.L. Effects of confining pressure on mechanical behaviors of sandstone under dynamic impact loads. Chin. J. Rock Mech. Eng. 2010, 29, 193–201. [Google Scholar]
- Yuan, P.; Ma, R.Q. Analysis on energy absorption of rock under various water absorption contents in SHPB test. Acta Armamentarii 2013, 34 (Suppl. 1), 328–332. [Google Scholar]
- Yuan, P.; Ma, Q.Y. Split Hopkinson pressure bar tests on sandstone in coalmine under cyclic wetting and drying. Rock Soil Mech. 2013, 34, 2557. [Google Scholar]
- Yuan, P.; Ma, R.Q. Split Hopkinson pressure bar tests and analysis of coalmine sandstone with various moisture contents. Chin. J. Rock Mech. Eng. 2015, 34 (Suppl. 1), 2888. [Google Scholar]
- Rubin, A.M.; Ahrens, T.J. Dynamic tensile-failure-induced velocity deficits in rock. Geophys. Res. Lett. 1991, 18, 219. [Google Scholar] [CrossRef] [Green Version]
- Lou, W.T. Dynamic fracture behaviour of dry and waterlogged granites. Combust. Explos. Shock Waves 1994, 14, 249. [Google Scholar]
- Wang, B.; Li, X.B.; Yin, T.B.; Ma, C.D.; Yin, Z.Q.; Li, Z.G. Split Hopkinson pressure bar (SHPB) experiments on dynamic strength of water-saturated sandstone. Chin. J. Rock Mech. Eng. 2010, 29, 1003. [Google Scholar]
- Li, D.Y.; Sun, X.L.; Zhou, Z.L.; Cai, X.; Qiu, J.D. On the dynamic accumulated damage characteristics of granite subjected to repeated impact load action. J. Exp. Mech. 2016, 31, 827–835. [Google Scholar]
- Mei, N.F. Research on Fatigue Damage and Mechanical Characteristics of Brittle Rock under Cycle Dynamic Loading. Master’s Thesis, China University of Geosciences, Wuhan, China, 2014. [Google Scholar]
- Zhu, J.J. Experimental Study of Rock Mechanical Properties and Damage Model under Cyclical Dynamic Loads. Master’s Thesis, Central South University, Changsha, China, 2012. [Google Scholar]
- Jin, J.F. Study on Rock Mechanical Properties under Coupled Static-Cyclic Impact Loading. Ph.D. Thesis, Central South University, Changsha, China, 2012. [Google Scholar]
- Vsevolod, B.; Volodymyr, B. Fractional-Fractal Modeling of Filtration-Consolidation Processes in Saline Saturated Soils. Fractal Fract. 2020, 4, 59. [Google Scholar]
- Ullah, A.S.; D’Addona, D.M.; Seto, Y.; Yonehara, S.; Kubo, A. Utilizing Fractals for Modeling and 3D Printing of Porous Structures. Fractal Fract. 2021, 5, 40. [Google Scholar] [CrossRef]
- Malyk, I.V.; Gorbatenko, M.; Chaudhary, A.; Sharma, S.; Dubey, R.S. Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator. Fractal Fract. 2021, 5, 64. [Google Scholar] [CrossRef]
- He, S.H.; Ding, Z.; Hu, H.B.; Gao, M. Effect of Grain Size on Microscopic Pore Structure and Fractal Characteristics of Carbonate-Based Sand and Silicate-Based Sand. Fractal Fract. 2021, 5, 152. [Google Scholar] [CrossRef]
- Peroni, M.; Solomos, G.; Pizzinato, V. Impact behaviour testing of aluminium foam. Int. J. Impact Eng. 2013, 53, 74–83. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Y.; Li, F.; Lu, F.; Sun, H. Experimental study on dynamic properties and constitutive model of polypropylene fibre concrete under high-strain rates. Eur. J. Environ. Civ. Eng. 2013, 17, 294–303. [Google Scholar] [CrossRef]
- Corporation, H.P. Wave dispersion and attenuation in viscoelastic split hopkinson pressure bar. Shock Vib. 2013, 5, 307–315. [Google Scholar]
- Rougier, E.; Knight, E.E.; Broome, S.T.; Sussman, A.J.; Munjiza, A. Validation of a three-dimensional finite-discrete element method using experimental results of the split hopkinson pressure bar test. Int. J. Rock Mech. Min. Sci. 2014, 70, 101–108. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Cai, X.; Yang, X.; Zhou, Q. Dynamic response and fracture evolution of marble specimens containing rectangular cavities subjected to dynamic loading. Bull. Eng. Geol. Environ. 2021, 80, 7701–7716. [Google Scholar] [CrossRef]
- Chu, F.J.; Liu, D.W.; Tao, M.; Peng, H.D. Dynamic damage laws of sandstone under different water bearing conditions based on nuclear magnetic resonance. Chin. J. Eng. 2017, 40, 144–151. [Google Scholar]

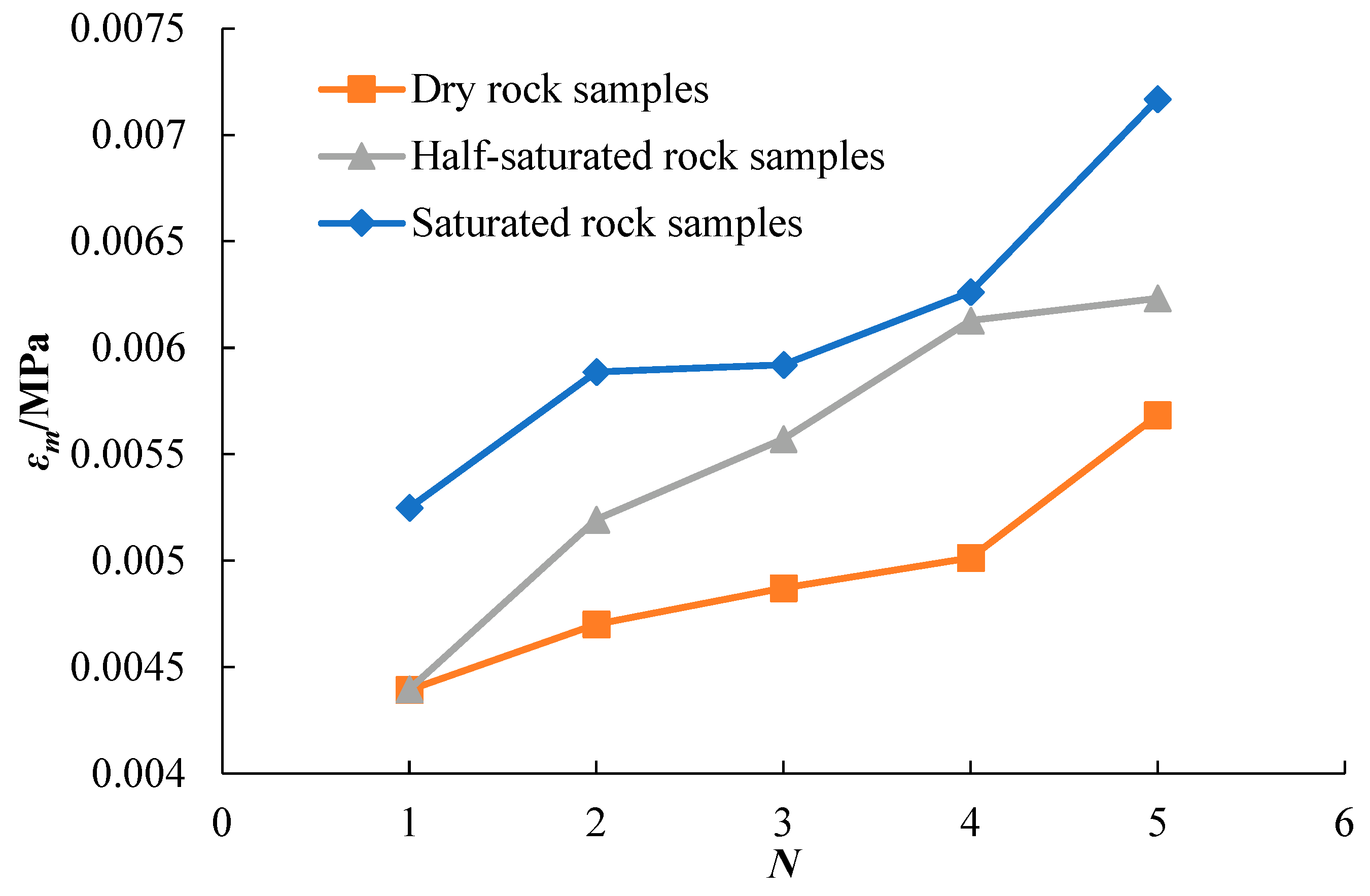




| Sample Name | ms/g | mp/g | Kω | |
|---|---|---|---|---|
| d-1 | 229.31 | 229.48 | 3.00% | 2.61% |
| d-2 | 227.37 | 227.5 | 2.45% | |
| d-3 | 231.6 | 231.75 | 2.96% | |
| d-4 | 227.06 | 227.17 | 2.11% | |
| d-5 | 230.46 | 230.59 | 2.54% | |
| h-1 | 227.36 | 230.22 | 55.86% | 54.04% |
| h-2 | 222.19 | 225.01 | 53.92% | |
| h-3 | 230.25 | 233.18 | 56.56% | |
| h-4 | 232.02 | 234.96 | 53.36% | |
| h-5 | 231.92 | 234.57 | 50.48% | |
| s-1 | 225.59 | 230.89 | 100.00% | 100.00% |
| s-2 | 229.51 | 234.67 | 100.00% | |
| s-3 | 227.41 | 232.69 | 100.00% | |
| s-4 | 229.96 | 235.31 | 100.00% | |
| s-5 | 229.63 | 235.11 | 100.00% |
| Rock Type | ||
|---|---|---|
| Dry | −5.0727 N + 121.63 (R2 = 0.9888) | = 0.0003 N + 0.0041 (R2 = 0.9107) |
| Half-saturated | −5.5056 N + 113.74 (R2 = 0.9544) | = 0.0005 N + 0.0041 (R2 = 0.9441) |
| Saturated | −5.9221 N + 106.69 (R2 = 0.9591) | = 0.0004 N + 0.0048 (R2 = 0.9016) |
| Sample Name | na/% | nb/% | δn/% |
|---|---|---|---|
| d-1 | 4.22 | 4.34 | 3.06 |
| d-2 | 4.56 | 4.71 | 3.29 |
| d-3 | 4.34 | 4.53 | 4.47 |
| d-4 | 4.45 | 4.80 | 7.92 |
| d-5 | 4.37 | 4.89 | 11.81 |
| h-1 | 4.34 | 4.56 | 5.09 |
| h-2 | 4.69 | 4.94 | 5.20 |
| h-3 | 4.84 | 5.13 | 6.10 |
| h-4 | 4.34 | 5.09 | 17.24 |
| h-5 | 4.30 | 5.65 | 31.31 |
| s-1 | 4.76 | 5.36 | 12.76 |
| s-2 | 4.65 | 5.37 | 15.44 |
| s-3 | 4.27 | 5.14 | 20.29 |
| s-4 | 4.58 | 6.12 | 33.56 |
| s-5 | 4.57 | 8.29 | 81.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, F.; Liu, D.; Zhang, X.; Yu, H.; Zhu, G. Dynamic Response and Damage Regularity of Sandstone with Different Moisture States under Cyclic Loading. Fractal Fract. 2022, 6, 226. https://doi.org/10.3390/fractalfract6040226
Chu F, Liu D, Zhang X, Yu H, Zhu G. Dynamic Response and Damage Regularity of Sandstone with Different Moisture States under Cyclic Loading. Fractal and Fractional. 2022; 6(4):226. https://doi.org/10.3390/fractalfract6040226
Chicago/Turabian StyleChu, Fujiao, Dunwen Liu, Xiaojun Zhang, Hui Yu, and Guangli Zhu. 2022. "Dynamic Response and Damage Regularity of Sandstone with Different Moisture States under Cyclic Loading" Fractal and Fractional 6, no. 4: 226. https://doi.org/10.3390/fractalfract6040226
APA StyleChu, F., Liu, D., Zhang, X., Yu, H., & Zhu, G. (2022). Dynamic Response and Damage Regularity of Sandstone with Different Moisture States under Cyclic Loading. Fractal and Fractional, 6(4), 226. https://doi.org/10.3390/fractalfract6040226






