Riemann–Liouville Fractional Newton’s Type Inequalities for Differentiable Convex Functions

Abstract

In this paper, we prove some new Newton’s type inequalities for differentiable convex functions through the well-known Riemann–Liouville fractional integrals. Moreover, we prove some inequalities of Riemann–Liouville fractional Newton’s type for functions of bounded variation. It is also shown that the newly established inequalities are the extension of comparable inequalities inside the literature. Finally, we give some examples with graphs and show the validity of newly established inequalities.

1. Introduction

Fractional calculus (that is, calculus of integrals and derivatives of any arbitrary real or complex order) has grown in popularity and relevance over the last three decades, owing to its demonstrated applications in a wide range of seemingly disparate domains of science and engineering. It does give some potentially valuable tools for solving differential and integral equations, a variety of other problems involving mathematical physics special functions, and their extensions and generalizations in one or more variables.

The concept of fractional calculus is widely thought to have originated with a question posed to Gottfried Wilhelm Leibniz (1646–1716) by Marquis de L’Hôpital (1661–1704) in 1695, in which he tried to understand the meaning of Leibniz’s notation $\frac{d^{n}y}{d{x}^n}$ for the derivative of order $n=\left\{0,1,2,\cdots \right\}$, when $n=\frac{1}{2}$ (What if $n=\frac{1}{2}$?). Leibniz replied to L’Hôpital on 30 September 1695, with the following message: “… This is an apparent paradox from which, one day, useful consequences will be drawn. …”.

The theories of differential, integral, and integro-differential equations, and special functions of mathematical physics, as well as their extensions and generalizations in one and more variables, some of the areas of present applications of fractional calculus include fluid flow, rheology, dynamical processes in self-similar and porous structures, diffusive transport akin to diffusion, electrical networks, probability and statistics, control theory of dynamical systems, viscoelasticity, electrochemistry of corrosion, chemical physics, optics, signal processing, etc.

Because of the importance of fractional calculus, researchers have utilized it to establish various fractional integral inequalities that are quite useful in approximation theory. Inequalities, such as Hermite–Hadamard, Simpson’s, midpoint, Ostrowski’s, and trapezoidal inequalities are examples, and by using these inequalities, we can obtain the bounds of formulas used in numerical integration. In [1], Sarikaya et al. proved some Hermite–Hadamard-type inequalities and trapezoidal-type inequalities for the first time using the Riemann–Liouville fractional integrals.

Set [2] proved a Riemann–Liouville fractional version of Ostrowski’s inequalities for differentiable functions. İşcan and Wu used harmonic convexity and proved Hermite–Hadamard-type inequalities in [3]. Sarikaya and Yildrim [4] used Riemann–Liouville fractional integrals to prove some new Hermite–Hadamard-type inequalities and midpoint-type inequalities for differentiable convex functions. Sarikaya et al. [5] proved the general version of Simpson’s type inequalities for differentiable s-convex functions.

In [6], the authors used Riemann–Liouville fractional integrals, and proved some of Simpson’s type inequalities for general convex functions. Chen and Huang provided another version of Simpson’s type inequalities for differentiable s-convex functions in [7]. Mubeen and Habibulla [8] introduced the notions of general Riemann–Liouville fractional integrals, called k-fractional integrals, and the authors used these integrals to prove some new Hermite–Hadamard-type inequalities in [9]. Using the k-fractional integrals, the authors proved Ostrowski’s type inequalities for differentiable functions in [10]. In [11], Zhang et al. used k-fractional integrals and proved different integral inequalities for general convex functions.

Recently, Sarikaya and Ertugral [12] defined a new class of fractional integrals, called generalized fractional, and they used these integrals to prove the general version of Hermite–Hadamard-type inequalities for convex functions. In [13], the authors used generalized fractional integrals and proved some trapezoidal-type inequalities for convex harmonic functions. Budak et al. [14] proved several variants of Ostrowski’s and Simpson’s type for differentiable convex functions via generalized fractional integrals. In [15], Awan et al. established some new Hermite–Hadamard-type inequalities involving Riemann–Liouville fractional integrals, and in [16], some new Hermite–Hadamard-type inequalities for k-fractional integrals were established. Khan et al. [17,18] proved some new estimates of Hermite–Hadamard-type inequalities for Riemann–Liouville fractional integrals and conformable fractional integrals. Set et al. [19] and Tunc [20] proved some new variants of Hermite–Hadamard-type inequalities for convex and h-convex functions, respectively using the fractional integrals. Zaho et al. [21] established generalized Hermite–Hadamard-type inequalities for interval-valued functions.

On the other hand, several papers focused on the functions of bounded vatiation to prove some important inequalities, such as Ostrowski-type [22], Simpson-type [23,24], trapezoid-type [25,26], and midpoint-type [27].

Motivated by the ongoing studies, we establish Newton’s formula-type inequalities for differentiable convex functions and bounded variations via Riemann–Liouville fractional integrals, and give some examples of their graphs to show the validity.

The following is a summary of the paper: The basics of fractional calculus and other relevant research in this discipline are briefly discussed in Section 2. We establish an integral identity in Section 3 that is critical in establishing the primary outcomes of the paper. Section 4 gives some new Newton’s type inequalities for differentiable convex functions using Riemann–Liouville fractional integrals. Section 5 contains some fractional Newton-type inequalities for functions of bounded variation. Section 6 finishes with some research ideas for the future.

2. Fractional Integrals and Related Inequalities

In this section, we review several fundamental, fractional, integral notations and concepts. Different fractional integrals are also used to recall various inequalities.

Definition 1.

([28,29]) Let $\mathsf{{\rm Y}}\in L_1\left[{\kappa }_1,{\kappa }_2\right].$ The Riemann–Liouville fractional integrals (RLFIs) $J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}$ and $J_{{\kappa }_2-}^{\alpha }\mathsf{{\rm Y}}$ of order $\alpha >0$ with ${\kappa }_1\ge 0$ are defined as follows:

$$J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(x\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{{\kappa }_1}^x{\left(x-\delta \right)}^{\alpha -1}\mathsf{{\rm Y}}\left(\delta \right)d\delta ,x>{\kappa }_1$$

and

$$J_{{\kappa }_2-}^{\alpha }\mathsf{{\rm Y}}\left(x\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_x^{{\kappa }_2}{\left(\delta -x\right)}^{\alpha -1}\mathsf{{\rm Y}}\left(\delta \right)d\delta ,x<{\kappa }_2,$$

respectively, where Γ is the well-known Gamma function.

For the first time in 2013, Sarikaya et al. proved the following fractional Hermite–Hadmard-type inequality:

Theorem 1.

([1]) For a positive convex function $\mathsf{{\rm Y}}:I\subset \mathbb{R}\to \mathbb{R}$ with $\mathsf{{\rm Y}}\in L_1\left[{\kappa }_1,{\kappa }_2\right]$ and $0\le {\kappa }_1<{\kappa }_2,$ the following inequality holds:

$$\begin{array}{cc}\hfill \mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)& \le \frac{\Gamma \left(\alpha +1\right)}{2{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)+J_{{\kappa }_2-}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_1\right)\right]\hfill \\ \hfill & \le \frac{\mathsf{{\rm Y}}\left({\kappa }_1\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)}{2}.\hfill \end{array}$$

(1)

Sarikaya and Yildrm then demonstrated the following new form of the fractional Hermite–Hadamard inequality:

Theorem 2.

([4]) For a positive convex function $\mathsf{{\rm Y}}:I\subset \mathbb{R}\to \mathbb{R}$ with $\mathsf{{\rm Y}}\in L_1\left[{\kappa }_1,{\kappa }_2\right],0\le {\kappa }_1<{\kappa }_2$ and ${\kappa }_1,{\kappa }_2\in I,$ the following inequality holds:

$$\begin{array}{cc}\hfill \mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)& \le \frac{\Gamma \left(\alpha +1\right)}{2^{1-\alpha }{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)+J_{\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)-}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_1\right)\right]\hfill \\ \hfill & \le \frac{\mathsf{{\rm Y}}\left({\kappa }_1\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)}{2}.\hfill \end{array}$$

(2)

Remark 1.

If we set $\alpha =1$ in inequalities (1) and (2), then we obtain the classical Hermite–Hadamard inequality (see, [30]):

$$\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)\le \frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(x\right)dx\le \frac{\mathsf{{\rm Y}}\left({\kappa }_1\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)}{2}.$$

(3)

Chen and Huang proposed the following fractional form of Simpson’s type inequality for differentiable s-convex functions:

Theorem 3.

([7]) Suppose that a differentiable function $\mathsf{{\rm Y}}:I\subset [0,\infty )\to \mathbb{R}$ with $\mathsf{{\rm Y}}\in L_1\left[{\kappa }_1,{\kappa }_2\right]$, $0\le {\kappa }_1<{\kappa }_2$ and ${\kappa }_1,{\kappa }_2\in I^{\circ }$ (interior of I). If $\left|{\mathsf{{\rm Y}}}^{\prime }\right|$ is a s-convex function, then following inequality holds:

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+4\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{\Gamma \left(\alpha +1\right)}{2^{1-\alpha }{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)+J_{{\kappa }_2-}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{s+1}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\right]\mathcal{I}\left(s,\alpha \right),\hfill \end{array}$$

(4)

where

$$\mathcal{I}\left(s,\alpha \right)={\int }_0^1\left|\frac{{\delta }^{\alpha }}{2}-\frac{1}{3}\right|\left[{\left(1+\delta \right)}^s+{\left(1-\delta \right)}^s\right]d\delta .$$

Remark 2.

From inequality (4), we have

(i) 

If we set $\alpha =1$, then we obtain the classical Simpson’s inequality for s-convex functions (see, [5] [Theorem 7]):

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+4\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]-\frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(x\right)dx\right|\hfill \\ \hfill & \le \frac{\left({\kappa }_2-{\kappa }_1\right)\left(s-4\right)6^{s+1}+2\times 5^{s+2}-2\times 3^{s+2}+2}{6^{s+2}\left(s+1\right)\left(s+2\right)}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\right].\hfill \end{array}$$

(5)

(ii) 

If we set $s=\alpha =1$, then we obtain the classical Simpson’s inequality for convex functions (see, [5] [Corollary 1]):

$$\begin{array}{cc}\hfill & \left|\frac{1}{6}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+4\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+{\kappa }_2}{2}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]-\frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(x\right)dx\right|\hfill \\ \hfill & \le \frac{5\left({\kappa }_2-{\kappa }_1\right)}{72}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\right].\hfill \end{array}$$

(6)

3. An Identity

We prove integral equality in this section to prove the main results of this paper.

Lemma 1.

For a mapping $\mathsf{{\rm Y}}:I\subset \mathbb{R}\to \mathbb{R}$, which is differentiable over $I^{\circ }$ with $\mathsf{{\rm Y}}\in L_1\left[{\kappa }_1,{\kappa }_2\right]$, we have the following RLFIs identity:

$$\begin{array}{cc}\hfill & \frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\hfill \\ \hfill & -\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\hfill \\ \hfill & =\frac{{\kappa }_2-{\kappa }_1}{9}\left[I_1+I_2+I_3\right],\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill I_1& ={\int }_0^1\left({\delta }^{\alpha }-\frac{5}{8}\right){\mathsf{{\rm Y}}}^{\prime }\left(\delta {\kappa }_1+\left(1-\delta \right)\frac{2{\kappa }_1+{\kappa }_2}{3}\right)d\delta ,\hfill \\ \hfill I_2& ={\int }_0^1\left({\delta }^{\alpha }-\frac{1}{2}\right){\mathsf{{\rm Y}}}^{\prime }\left(\delta \frac{2{\kappa }_1+{\kappa }_2}{3}+\left(1-\delta \right)\frac{{\kappa }_1+2{\kappa }_2}{3}\right)d\delta ,\hfill \\ \hfill I_3& ={\int }_0^1\left({\delta }^{\alpha }-\frac{3}{8}\right){\mathsf{{\rm Y}}}^{\prime }\left(\delta \frac{{\kappa }_1+2{\kappa }_2}{3}+\left(1-\delta \right){\kappa }_2\right)d\delta .\hfill \end{array}$$

Proof. 

From fundamental rules of integration by parts and change of variables, we have

$$\begin{array}{cc}\hfill I_1& ={\int }_0^1\left({\delta }^{\alpha }-\frac{5}{8}\right){\mathsf{{\rm Y}}}^{\prime }\left(\delta {\kappa }_1+\left(1-\delta \right)\frac{2{\kappa }_1+{\kappa }_2}{3}\right)d\delta \hfill \\ \hfill & =\frac{3\alpha }{\left({\kappa }_2-{\kappa }_1\right)}{\int }_0^1{\delta }^{\alpha -1}\mathsf{{\rm Y}}\left(\delta {\kappa }_1+\left(1-\delta \right)\frac{2{\kappa }_1+{\kappa }_2}{3}\right)d\delta \hfill \\ \hfill & -\left[\frac{15}{8\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+\frac{9}{8\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left({\kappa }_1\right)\right]\hfill \\ \hfill & =\frac{3^{\alpha +1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha +1}}{J}_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)\hfill \\ \hfill & -\left[\frac{15}{8\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+\frac{9}{8\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left({\kappa }_1\right)\right].\hfill \end{array}$$

(8)

Similarly, we have

$$\begin{array}{cc}\hfill I_2& ={\int }_0^1\left({\delta }^{\alpha }-\frac{1}{2}\right){\mathsf{{\rm Y}}}^{\prime }\left(\delta \frac{2{\kappa }_1+{\kappa }_2}{3}+\left(1-\delta \right)\frac{{\kappa }_1+2{\kappa }_2}{3}\right)d\delta \hfill \\ \hfill & =\frac{3^{\alpha +1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha +1}}{J}_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)\hfill \\ \hfill & -\left[\frac{3}{2\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\frac{3}{2\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)\right]\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill I_3& ={\int }_0^1\left({\delta }^{\alpha }-\frac{3}{8}\right){\mathsf{{\rm Y}}}^{\prime }\left(\delta \frac{{\kappa }_1+2{\kappa }_2}{3}+\left(1-\delta \right){\kappa }_2\right)d\delta \hfill \\ \hfill & =\frac{3^{\alpha +1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha +1}}{J}_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\hfill \\ \hfill & -\left[\frac{9}{8\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left({\kappa }_2\right)+\frac{15}{8\left({\kappa }_2-{\kappa }_1\right)}\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)\right].\hfill \end{array}$$

(10)

Hence, by adding (8)–(10) and multiplying the resultant one by $\frac{{\kappa }_2-{\kappa }_1}{9}$, we obtain the resultant equality. □

4. Fractional Newton’s Inequalities for Differentiable Convex Functions

In this section, we use RLFIs to show some new Newton’s inequalities for differentiable convex functions. We use the following notations for the sake of brevity:

$$\begin{array}{cc}\hfill A_1\left(\alpha \right)& ={\int }_0^1\delta \left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta =\frac{\alpha }{\alpha +2}{\left(\frac{3}{8}\right)}^{\frac{\alpha +2}{\alpha }}+\frac{1}{\alpha +2}-\frac{3}{16},\hfill \\ \hfill A_2\left(\alpha \right)& ={\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta =\frac{2\alpha }{\alpha +1}{\left(\frac{3}{8}\right)}^{\frac{\alpha +1}{\alpha }}+\frac{1}{\alpha +1}-\frac{3}{8},\hfill \\ \hfill A_3\left(\alpha \right)& ={\int }_0^1\delta \left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta =\frac{\alpha }{\alpha +2}{\left(\frac{1}{2}\right)}^{\frac{\alpha +2}{\alpha }}+\frac{1}{\alpha +2}-\frac{1}{4},\hfill \\ \hfill A_4\left(\alpha \right)& ={\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta =\frac{2\alpha }{\alpha +1}{\left(\frac{1}{2}\right)}^{\frac{\alpha +1}{\alpha }}+\frac{1}{\alpha +1}-\frac{1}{2},\hfill \\ \hfill A_5\left(\alpha \right)& ={\int }_0^1\delta \left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta =\frac{\alpha }{\alpha +2}{\left(\frac{5}{8}\right)}^{\frac{\alpha +2}{\alpha }}+\frac{1}{\alpha +2}-\frac{5}{16},\hfill \\ \hfill A_6\left(\alpha \right)& ={\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta =\frac{2\alpha }{\alpha +1}{\left(\frac{5}{8}\right)}^{\frac{\alpha +1}{\alpha }}+\frac{1}{\alpha +1}-\frac{5}{8}.\hfill \end{array}$$

Theorem 4.

Assume that the conditions of Lemma 1 hold. If $\left|{\mathsf{{\rm Y}}}^{\prime }\right|$ is convex function, then we have the following Newton’s type inequality:

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{27}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\left(3A_2\left(\alpha \right)-A_1\left(\alpha \right)+2A_4\left(\alpha \right)-A_3\left(\alpha \right)+A_6\left(\alpha \right)-A_5\left(\alpha \right)\right)\right.\hfill \\ \hfill & \left.+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|\left(A_1\left(\alpha \right)+A_4\left(\alpha \right)+A_3\left(\alpha \right)+2A_6\left(\alpha \right)+A_5\left(\alpha \right)\right)\right].\hfill \end{array}$$

(11)

Proof. 

Taking modulus in (7) and using convexity of $\left|{\mathsf{{\rm Y}}}^{\prime }\right|$, we have

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\delta \frac{{\kappa }_1+2{\kappa }_2}{3}+\left(1-\delta \right){\kappa }_2\right)\right|d\delta \right.\hfill \\ \hfill & +{\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\delta \frac{2{\kappa }_1+{\kappa }_2}{3}+\left(1-\delta \right)\frac{{\kappa }_1+2{\kappa }_2}{3}\right)\right|d\delta \hfill \\ \hfill & \left.+{\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\delta {\kappa }_1+\left(1-\delta \right)\frac{2{\kappa }_1+{\kappa }_2}{3}\right)\right|d\delta \right]\hfill \\ \hfill & =\frac{{\kappa }_2-{\kappa }_1}{9}\left[{\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{3-\delta }{3}{\kappa }_2+\frac{\delta }{3}{\kappa }_1\right)\right|d\delta \right.\hfill \\ \hfill & +{\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{2-\delta }{3}{\kappa }_2+\frac{1+\delta }{3}{\kappa }_1\right)\right|d\delta \hfill \\ \hfill & \left.+{\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{1-\delta }{3}{\kappa }_2+\frac{2+\delta }{3}{\kappa }_1\right)\right|d\delta \right]\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|{\int }_0^1\frac{3-\delta }{3}\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta +\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|{\int }_0^1\frac{\delta }{3}\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta \right.\hfill \\ \hfill & +\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|{\int }_0^1\frac{2-\delta }{3}\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta +\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|{\int }_0^1\frac{1+\delta }{3}\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta \hfill \\ \hfill & \left.+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|{\int }_0^1\frac{1-\delta }{3}\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta +\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|{\int }_0^1\frac{2+\delta }{3}\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta \right]\hfill \\ \hfill & =\frac{{\kappa }_2-{\kappa }_1}{27}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\left(3A_2\left(\alpha \right)-A_1\left(\alpha \right)+2A_4\left(\alpha \right)-A_3\left(\alpha \right)+A_6\left(\alpha \right)-A_5\left(\alpha \right)\right)\right.\hfill \\ \hfill & \left.+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|\left(A_1\left(\alpha \right)+A_4\left(\alpha \right)+A_3\left(\alpha \right)+2A_6\left(\alpha \right)+A_5\left(\alpha \right)\right)\right].\hfill \end{array}$$

This completes the proof. □

Example 1.

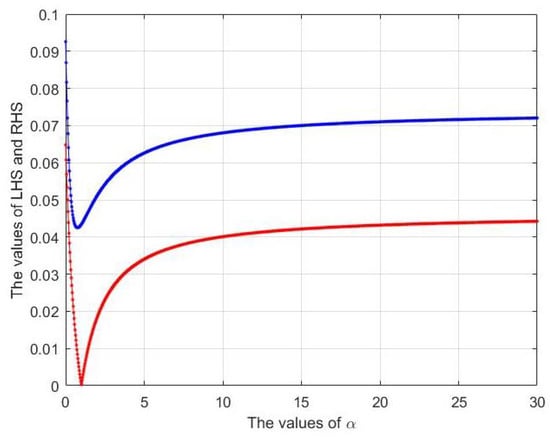
Let $\left[{\kappa }_1,{\kappa }_2\right]=\left[0,1\right]$ and define the function $\mathsf{{\rm Y}}:[0,1]\to \mathbb{R},\mathsf{{\rm Y}}\left(\delta \right)=\frac{{\delta }^3}{3}$ such that ${\mathsf{{\rm Y}}}^{\prime }\left(\delta \right)={\delta }^2$ and $\left|{\mathsf{{\rm Y}}}^{\prime }\right|$ is convex on $\left[0,1\right].$ Under these assumptions, we have

$$\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]=\frac{1}{12}.$$

By definition of Riemann-Liouville fractional integrals, we obtain

$$\begin{array}{cc}\hfill J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)& =J_{{}^{0+}}^{\alpha }\mathsf{{\rm Y}}\left(\frac{1}{3}\right)\hfill \\ \hfill & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^{\frac{1}{3}}{\left(\frac{1}{3}-x\right)}^{\alpha -1}\frac{x^3}{3}dx\hfill \\ \hfill & =\frac{2}{\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)3^{\alpha +4}},\hfill \\ \hfill J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)& =J_{{}^{\frac{1}{3}+}}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2}{3}\right)\hfill \\ \hfill & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_{\frac{1}{3}}^{\frac{2}{3}}{\left(\frac{2}{3}-x\right)}^{\alpha -1}\frac{x^3}{3}dx\hfill \\ \hfill & =\frac{{\alpha }^3+9{\alpha }^2+32\alpha +48}{\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)3^{\alpha +4}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)& =J_{{}^{\frac{2}{3}+}}^{\alpha }\mathsf{{\rm Y}}\left(1\right)\hfill \\ \hfill & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_{\frac{2}{3}}^1{\left(1-x\right)}^{\alpha -1}\frac{x^3}{3}dx\hfill \\ \hfill & =\frac{8{\alpha }^3+60{\alpha }^2+160\alpha +162}{\Gamma \left(\alpha \right)\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)3^{\alpha +4}}.\hfill \end{array}$$

By these equalities, we have

$$\begin{array}{cc}\hfill & \frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\hfill \\ \hfill & =\frac{9{\alpha }^3+69{\alpha }^2+192\alpha +216}{3^5\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}.\hfill \end{array}$$

The left hand side of the inequality (11) reduce to

$$\begin{array}{cc}\hfill & \left|\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{\frac{2{\kappa }_1+{\kappa }_2}{3}-}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_1\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}-}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{{\kappa }_2-}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)\right]\right|\hfill \\ \hfill & =\left|\frac{9{\alpha }^3+69{\alpha }^2+192\alpha +216}{3^5\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}-\frac{1}{12}\right|\hfill \\ \hfill & :=LHS.\hfill \end{array}$$

On the other hand, since $\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|=0$ and $\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|=1$, we have the right hand side of the inequality (11) as follows:

$$\begin{array}{cc}\hfill & \frac{{\kappa }_2-{\kappa }_1}{27}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\left(3A_2\left(\alpha \right)-A_1\left(\alpha \right)+2A_4\left(\alpha \right)-A_3\left(\alpha \right)+A_6\left(\alpha \right)-A_5\left(\alpha \right)\right)\right.\hfill \\ \hfill & \left.+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|\left(A_1\left(\alpha \right)+A_4\left(\alpha \right)+A_3\left(\alpha \right)+2A_6\left(\alpha \right)+A_5\left(\alpha \right)\right)\right]\hfill \\ \hfill & =\frac{1}{27}\left[3A_2\left(\alpha \right)-A_1\left(\alpha \right)+2A_4\left(\alpha \right)-A_3\left(\alpha \right)+A_6\left(\alpha \right)-A_5\left(\alpha \right)\right]\hfill \\ \hfill & :=RHS.\hfill \end{array}$$

It is clear from Figure 1 that $LHS\le RHS$ for all $\alpha >0.$

Figure 1. An example to Theorem 4.

Remark 3.

In Theorem 4, if we set $\alpha =1$, then we have the following inequality:

$$\begin{array}{cc}\hfill & \left|\frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(x\right)dx-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{75\left({\kappa }_2-{\kappa }_1\right)}{1728}\left[\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|+\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\right].\hfill \end{array}$$

Theorem 5.

Assume that the conditions of Lemma 1 hold. If ${\left|{\mathsf{{\rm Y}}}^{\prime }\right|}^q,$ $q\ge 1$ is convex function, then we have the following Newton’s type inequality:

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[A_2^{1-\frac{1}{q}}\left(\alpha \right){\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q\frac{3A_2\left(\alpha \right)-A_1\left(\alpha \right)}{3}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q\frac{A_1\left(\alpha \right)}{3}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +A_4^{1-\frac{1}{q}}\left(\alpha \right){\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q\frac{2A_4\left(\alpha \right)-A_3\left(\alpha \right)}{3}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q\frac{A_4\left(\alpha \right)+A_3\left(\alpha \right)}{3}\right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+A_6^{1-\frac{1}{q}}\left(\alpha \right){\left(\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\frac{A_6\left(\alpha \right)-A_5\left(\alpha \right)}{3}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q\frac{2A_6\left(\alpha \right)+A_5\left(\alpha \right)}{3}\right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

(12)

Proof. 

By taking modulus in (7) and applying power mean inequality, we have

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{3-\delta }{3}{\kappa }_2+\frac{\delta }{3}{\kappa }_1\right)\right|d\delta \right.\hfill \\ \hfill & +{\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{2-\delta }{3}{\kappa }_2+\frac{1+\delta }{3}{\kappa }_1\right)\right|d\delta \hfill \\ \hfill & \left.+{\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{1-\delta }{3}{\kappa }_2+\frac{2+\delta }{3}{\kappa }_1\right)\right|d\delta \right]\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta \right)}^{1-\frac{1}{q}}{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{3-\delta }{3}{\kappa }_2+\frac{\delta }{3}{\kappa }_1\right)\right|}^{q}d\delta \right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta \right)}^{1-\frac{1}{q}}{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{2-\delta }{3}{\kappa }_2+\frac{1+\delta }{3}{\kappa }_1\right)\right|}^{q}d\delta \right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta \right)}^{1-\frac{1}{q}}{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{1-\delta }{3}{\kappa }_2+\frac{2+\delta }{3}{\kappa }_1\right)\right|}^{q}d\delta \right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

Using convexity of ${\left|{\mathsf{{\rm Y}}}^{\prime }\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta \right)}^{1-\frac{1}{q}}\right.\hfill \\ \hfill & \times {\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q{\int }_0^1\frac{3-\delta }{3}\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta +{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q{\int }_0^1\frac{\delta }{3}\left|{\delta }^{\alpha }-\frac{3}{8}\right|d\delta \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta \right)}^{1-\frac{1}{q}}\hfill \\ \hfill & \times {\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q{\int }_0^1\frac{2-\delta }{3}\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta +{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q{\int }_0^1\frac{1+\delta }{3}\left|{\delta }^{\alpha }-\frac{1}{2}\right|d\delta \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta \right)}^{1-\frac{1}{q}}\hfill \\ \hfill & \left.\times {\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q{\int }_0^1\frac{1-\delta }{3}\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta +{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q{\int }_0^1\frac{2+\delta }{3}\left|{\delta }^{\alpha }-\frac{5}{8}\right|d\delta \right)}^{\frac{1}{q}}\right]\hfill \\ \hfill & =\frac{{\kappa }_2-{\kappa }_1}{9}\left[A_2^{1-\frac{1}{q}}\left(\alpha \right){\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q\frac{3A_2\left(\alpha \right)-A_1\left(\alpha \right)}{3}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q\frac{A_1\left(\alpha \right)}{3}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +A_4^{1-\frac{1}{q}}\left(\alpha \right){\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q\frac{2A_4\left(\alpha \right)-A_3\left(\alpha \right)}{3}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q\frac{A_4\left(\alpha \right)+A_3\left(\alpha \right)}{3}\right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+A_6^{1-\frac{1}{q}}\left(\alpha \right){\left(\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|\frac{A_6\left(\alpha \right)-A_5\left(\alpha \right)}{3}+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q\frac{2A_6\left(\alpha \right)+A_5\left(\alpha \right)}{3}\right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

Thus, the proof is completed. □

Remark 4.

In Theorem 5, if we set $\alpha =1$, then we have the following inequality:

$$\begin{array}{cc}\hfill & \left|\frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(x\right)dx-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{36}\left[{\left(\frac{17}{16}\right)}^{1-\frac{1}{q}}{\left(\frac{973{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+251{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{1152}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +\left(\frac{1}{4}\right){\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{2}\right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+{\left(\frac{17}{16}\right)}^{1-\frac{1}{q}}{\left(\frac{251\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|+973{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{1152}\right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

Theorem 6.

Assume that the conditions of Lemma 1 hold. If ${\left|{\mathsf{{\rm Y}}}^{\prime }\right|}^q,$ $q>1$ is convex function, then we have the following Newton’s type inequality:

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[A_7^{\frac{1}{p}}\left(\alpha ,p\right){\left(\frac{5{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{6}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & \left.+A_8^{\frac{1}{p}}\left(\alpha ,p\right){\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{2}\right)}^{\frac{1}{q}}+A_9^{\frac{1}{p}}\left(\alpha ,p\right)\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+5{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{6}\right){,}^{\frac{1}{q}}\right]\hfill \end{array}$$

(13)

where $q^{-1}+p^{-1}=1$ and

$$\begin{array}{cc}\hfill A_7\left(\alpha ,p\right)& ={\int }_0^1{\left|{\delta }^{\alpha }-\frac{3}{8}\right|}^{p}d\delta ,\hfill \\ \hfill A_8\left(\alpha ,p\right)& ={\int }_0^1{\left|{\delta }^{\alpha }-\frac{1}{2}\right|}^{p}d\delta ,\hfill \\ \hfill A_9\left(\alpha ,p\right)& ={\int }_0^1{\left|{\delta }^{\alpha }-\frac{5}{8}\right|}^{p}d\delta .\hfill \end{array}$$

Proof. 

Taking modulus in (7) and applyin Hölder inequality, we have

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & =\frac{{\kappa }_2-{\kappa }_1}{9}\left[{\int }_0^1\left|{\delta }^{\alpha }-\frac{3}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{3-\delta }{3}{\kappa }_2+\frac{\delta }{3}{\kappa }_1\right)\right|d\delta \right.\hfill \\ \hfill & +{\int }_0^1\left|{\delta }^{\alpha }-\frac{1}{2}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{2-\delta }{3}{\kappa }_2+\frac{1+\delta }{3}{\kappa }_1\right)\right|d\delta \hfill \\ \hfill & \left.+{\int }_0^1\left|{\delta }^{\alpha }-\frac{5}{8}\right|\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{1-\delta }{3}{\kappa }_2+\frac{2+\delta }{3}{\kappa }_1\right)\right|d\delta \right]\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\left({\int }_0^1{\left|{\delta }^{\alpha }-\frac{3}{8}\right|}^{p}d\delta \right)}^{\frac{1}{p}}{\left({\int }_0^1{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{3-\delta }{3}{\kappa }_2+\frac{\delta }{3}{\kappa }_1\right)\right|}^{q}d\delta \right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left({\int }_0^1{\left|{\delta }^{\alpha }-\frac{1}{2}\right|}^{p}d\delta \right)}^{\frac{1}{p}}{\left({\int }_0^1{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{2-\delta }{3}{\kappa }_2+\frac{1+\delta }{3}{\kappa }_1\right)\right|}^{q}d\delta \right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+{\left({\int }_0^1{\left|{\delta }^{\alpha }-\frac{5}{8}\right|}^{p}d\delta \right)}^{\frac{1}{p}}{\left({\int }_0^1{\left|{\mathsf{{\rm Y}}}^{\prime }\left(\frac{1-\delta }{3}{\kappa }_2+\frac{2+\delta }{3}{\kappa }_1\right)\right|}^{q}d\delta \right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

By using convexity of ${\left|{\mathsf{{\rm Y}}}^{\prime }\right|}^q$ with $q>1$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\left({\int }_0^1{\left|{\delta }^{\alpha }-\frac{3}{8}\right|}^{p}d\delta \right)}^{\frac{1}{p}}{\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q{\int }_0^1\frac{3-\delta }{3}d\delta +{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q{\int }_0^1\frac{\delta }{3}d\delta \right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left({\int }_0^1{\left|{\delta }^{\alpha }-\frac{1}{2}\right|}^{p}d\delta \right)}^{\frac{1}{p}}{\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q{\int }_0^1\frac{2-\delta }{3}d\delta +{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q{\int }_0^1\frac{1+\delta }{3}d\delta \right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+{\left({\int }_0^1{\left|{\delta }^{\alpha }-\frac{5}{8}\right|}^{p}d\delta \right)}^{\frac{1}{p}}{\left({\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q{\int }_0^1\frac{1-\delta }{3}d\delta +{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q{\int }_0^1\frac{2+\delta }{3}d\delta \right)}^{\frac{1}{q}}\right]\hfill \\ \hfill & =\frac{{\kappa }_2-{\kappa }_1}{9}\left[A_7^{\frac{1}{p}}\left(\alpha ,p\right){\left(\frac{5{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{6}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & \left.+A_8^{\frac{1}{p}}\left(\alpha ,p\right){\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{2}\right)}^{\frac{1}{q}}+A_9^{\frac{1}{p}}\left(\alpha ,p\right){\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+5{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{6}\right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

Thus, the proof is completed. □

Remark 5.

In Theorem 6, if we set $\alpha =1$, then we have the following inequality:

$$\begin{array}{cc}\hfill & \left|\frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(x\right)dx-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{{\kappa }_2-{\kappa }_1}{9}\left[{\left(\frac{5^{p+1}+3^{p+1}}{8^{p+1}\left(p+1\right)}\right)}^{\frac{1}{p}}{\left(\frac{5{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{6}\right)}^{\frac{1}{q}}\right.\hfill \\ \hfill & +{\left(\frac{1}{2^p\left(p+1\right)}\right)}^{\frac{1}{p}}{\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{2}\right)}^{\frac{1}{q}}\hfill \\ \hfill & \left.+{\left(\frac{5^{p+1}+3^{p+1}}{8^{p+1}\left(p+1\right)}\right)}^{\frac{1}{p}}{\left(\frac{{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_2\right)\right|}^q+5{\left|{\mathsf{{\rm Y}}}^{\prime }\left({\kappa }_1\right)\right|}^q}{6}\right)}^{\frac{1}{q}}\right].\hfill \end{array}$$

5. Fractional Newton Type Inequality for Functions of Bounded Variation

In this section, we prove a fractional Newton type inequality for the function of bounded variation.

Theorem 7.

Let $\mathsf{{\rm Y}}:\left[{\kappa }_1,{\kappa }_2\right]\to \mathbb{R}$ be a function of bounded variation on $\left[{\kappa }_1,{\kappa }_2\right].$ Then we have the following Newton type inequality for Riemann-Liouville fractional integrals

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{5}{24}\underset{{\kappa }_1}{\overset{{\kappa }_2}{\bigvee }}\left(\mathsf{{\rm Y}}\right),\hfill \end{array}$$

(14)

where ${\displaystyle \underset{c}{\overset{d}{\bigvee }}}\left(\mathsf{{\rm Y}}\right)$ denotes the total variation of Υ on $\left[c,d\right].$

Proof. 

Define the mapping $K_{\alpha }\left(x\right)$ by

$$K_{\alpha }\left(x\right)=\left\{\begin{array}{cc}{\displaystyle {\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }},}\hfill & {\displaystyle \mathrm{if}{\kappa }_1\le x\le \frac{2{\kappa }_1+{\kappa }_2}{3};}\hfill \\ {\displaystyle {\left(\frac{{\kappa }_1+2{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }},}\hfill & {\displaystyle \mathrm{if}\frac{2{\kappa }_1+{\kappa }_2}{3}<x\le \frac{{\kappa }_1+2{\kappa }_2}{3};}\hfill \\ {\displaystyle {\left({\kappa }_2-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}},}\hfill & {\displaystyle \mathrm{if}\frac{{\kappa }_1+2{\kappa }_2}{3}<x\le {\kappa }_2.}\hfill \end{array}\right.$$

It follows from that

$$\begin{array}{cc}\hfill {\int }_{{\kappa }_1}^{{\kappa }_2}{K}_{\alpha }\left(x\right)d\mathsf{{\rm Y}}\left(x\right)& ={\int }_{{\kappa }_1}^{\frac{2{\kappa }_1+{\kappa }_2}{3}}\left({\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\right)d\mathsf{{\rm Y}}\left(x\right)\hfill \\ \hfill & +{\int }_{\frac{2{\kappa }_1+{\kappa }_2}{3}}^{\frac{{\kappa }_1+2{\kappa }_2}{3}}\left({\left(\frac{{\kappa }_1+2{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\right)d\mathsf{{\rm Y}}\left(x\right)\hfill \\ \hfill & +{\int }_{\frac{{\kappa }_{1}2+{\kappa }_2}{3}}^{{\kappa }_2}\left({\left({\kappa }_2-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}}\right)d\mathsf{{\rm Y}}\left(x\right).\hfill \end{array}$$

(15)

Integrating by parts, we get

$$\begin{array}{cc}\hfill & {\int }_{{\kappa }_1}^{\frac{2{\kappa }_1+{\kappa }_2}{3}}\left({\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\right)d\mathsf{{\rm Y}}\left(x\right)\hfill \\ \hfill & ={\left.\left({\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\right)\mathsf{{\rm Y}}\left(x\right)\right|}_{{\kappa }_1}^{\frac{2{\kappa }_1+{\kappa }_2}{3}}+\alpha {\int }_{{\kappa }_1}^{\frac{2{\kappa }_1+{\kappa }_2}{3}}{\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha -1}\mathsf{{\rm Y}}\left(x\right)dx\hfill \\ \hfill & =-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{2}\right)-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}}\mathsf{{\rm Y}}\left({\kappa }_1\right)+\Gamma \left(\alpha +1\right)J_{{}^{\frac{2{\kappa }_1+{\kappa }_2}{3}-}}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_1\right).\hfill \end{array}$$

(16)

Similarly, we have

$$\begin{array}{cc}\hfill & {\int }_{\frac{2{\kappa }_1+{\kappa }_2}{3}}^{\frac{{\kappa }_1+2{\kappa }_2}{3}}\left({\left(\frac{{\kappa }_1+2{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\right)d\mathsf{{\rm Y}}\left(x\right)\hfill \\ \hfill & =-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{2}\right)-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{2}\right)+\Gamma \left(\alpha +1\right)J_{{}^{\frac{{\kappa }_1+2{\kappa }_2}{3}-}}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill & {\int }_{\frac{{\kappa }_1+2{\kappa }_2}{3}}^{{\kappa }_2}\left({\left({\kappa }_2-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}}\right)d\mathsf{{\rm Y}}\left(x\right)\hfill \\ \hfill & =-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}}\mathsf{{\rm Y}}\left({\kappa }_2\right)-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{2}\right)+\Gamma \left(\alpha +1\right)J_{{}^{{\kappa }_2-}}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right).\hfill \end{array}$$

(18)

By putting the Equalities (16)–(18) in (15), we have

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & =\frac{3^{\alpha -1}}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{\int }_{{\kappa }_1}^{{\kappa }_2}{K}_{\alpha }\left(x\right)d\mathsf{{\rm Y}}\left(x\right).\hfill \end{array}$$

It is well known that if $g,\mathsf{{\rm Y}}:\left[{\kappa }_1,{\kappa }_2\right]\to \mathbb{R}$ are such that g is continuous on $\left[{\kappa }_1,{\kappa }_2\right]$ and $\mathsf{{\rm Y}}$ is of bounded variation on $\left[{\kappa }_1,{\kappa }_2\right],$ then ${\int }_{{\kappa }_1}^{{\kappa }_2}g\left(\delta \right)d\mathsf{{\rm Y}}\left(\delta \right)$ exist and

$$\left|{\int }_{{\kappa }_1}^{{\kappa }_2}g\left(\delta \right)d\mathsf{{\rm Y}}\left(\delta \right)\right|\le \underset{\delta \in \left[{\kappa }_1,{\kappa }_2\right]}{sup}\left|g\left(\delta \right)\right|\underset{{\kappa }_1}{\overset{{\kappa }_2}{\bigvee }}\left(\mathsf{{\rm Y}}\right).$$

(19)

On the other hand, using (19), we get

$$\begin{array}{cc}\hfill & \left|\frac{3^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[J_{{\kappa }_1+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+J_{\frac{2{\kappa }_1+{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+J_{\frac{{\kappa }_1+2{\kappa }_2}{3}+}^{\alpha }\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right.\hfill \\ \hfill & \left.-\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]\right|\hfill \\ \hfill & \le \frac{2^{\alpha -1}}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left|{\int }_{{\kappa }_1}^{{\kappa }_2}{K}_{\alpha }\left(x\right)d\mathsf{{\rm Y}}\left(x\right)\right|\hfill \\ \hfill & \le \frac{3^{\alpha -1}}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[\left|{\int }_{{\kappa }_1}^{\frac{2{\kappa }_1+{\kappa }_2}{3}}\left({\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\right)d\mathsf{{\rm Y}}\left(x\right)\right|\right.\hfill \\ \hfill & +\left|{\int }_{\frac{2{\kappa }_1+{\kappa }_2}{3}}^{\frac{{\kappa }_1+2{\kappa }_2}{3}}\left({\left(\frac{{\kappa }_1+2{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\right)d\mathsf{{\rm Y}}\left(x\right)\right|\hfill \\ \hfill & \left.+\left|{\int }_{\frac{{\kappa }_1+2{\kappa }_2}{3}}^{{\kappa }_2}\left({\left({\kappa }_2-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}}\right)d\mathsf{{\rm Y}}\left(x\right)\right|\right]\hfill \\ \hfill & \le \frac{3^{\alpha -1}}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[\underset{x\in \left[{\kappa }_1,\frac{2{\kappa }_1+{\kappa }_2}{3}\right]}{sup}\left|{\left(\frac{2{\kappa }_1+{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\right|\underset{{\kappa }_1}{\overset{\frac{2{\kappa }_1+{\kappa }_2}{3}}{\bigvee }}\left(\mathsf{{\rm Y}}\right)\right.\hfill \\ \hfill & +\underset{x\in \left[\frac{2{\kappa }_1+{\kappa }_2}{3},\frac{{\kappa }_1+2{\kappa }_2}{3}\right]}{sup}\left|{\left(\frac{{\kappa }_1+2{\kappa }_2}{3}-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\right|\underset{\frac{2{\kappa }_1+{\kappa }_2}{3}}{\overset{\frac{{\kappa }_1+2{\kappa }_2}{3}}{\bigvee }}\left(\mathsf{{\rm Y}}\right)\hfill \\ \hfill & +\left.\underset{x\in \left[\frac{{\kappa }_1+2{\kappa }_2}{3},{\kappa }_2\right]}{sup}\left|{\left({\kappa }_2-x\right)}^{\alpha }-\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha -1}}\right|\underset{\frac{{\kappa }_1+2{\kappa }_2}{3}}{\overset{{\kappa }_2}{\bigvee }}\left(\mathsf{{\rm Y}}\right)\right]\hfill \\ \hfill & =\frac{3^{\alpha -1}}{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}\left[\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\underset{{\kappa }_1}{\overset{\frac{2{\kappa }_1+{\kappa }_2}{3}}{\bigvee }}\left(\mathsf{{\rm Y}}\right)+\frac{{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{2·3^{\alpha }}\underset{\frac{2{\kappa }_1+{\kappa }_2}{3}}{\overset{\frac{{\kappa }_1+2{\kappa }_2}{3}}{\bigvee }}\left(\mathsf{{\rm Y}}\right)+\frac{5{\left({\kappa }_2-{\kappa }_1\right)}^{\alpha }}{8·3^{\alpha }}\underset{\frac{{\kappa }_1+2{\kappa }_2}{3}}{\overset{{\kappa }_2}{\bigvee }}\left(\mathsf{{\rm Y}}\right)\right]\hfill \\ \hfill & \le \frac{5}{24}\underset{{\kappa }_1}{\overset{{\kappa }_2}{\bigvee }}\left(\mathsf{{\rm Y}}\right).\hfill \end{array}$$

This completes the proof. □

Remark 6.

If we take $\alpha =1$ in Theorem 7, then we get the inequality

$$\left|\frac{1}{8}\left[\mathsf{{\rm Y}}\left({\kappa }_1\right)+3\mathsf{{\rm Y}}\left(\frac{2{\kappa }_1+{\kappa }_2}{3}\right)+3\mathsf{{\rm Y}}\left(\frac{{\kappa }_1+2{\kappa }_2}{3}\right)+\mathsf{{\rm Y}}\left({\kappa }_2\right)\right]-\frac{1}{{\kappa }_2-{\kappa }_1}{\int }_{{\kappa }_1}^{{\kappa }_2}\mathsf{{\rm Y}}\left(\delta \right)d\delta \right|\le \frac{5}{24}\underset{{\kappa }_1}{\overset{{\kappa }_2}{\bigvee }}\left(\mathsf{{\rm Y}}\right),$$

which is given by Alomari in [31].

6. Conclusions

We demonstrated some new Newton’s type inequalities for differentiable convex functions using Riemann-Liouville fractional integrals. Furthermore, we established fractional Newton’s type inequalities for bounded variation functions via the Riemann-Liouville fractional integrals. We demonstrated the validity of newly obtained results with a mathematical example and graphs. We also proved that the newly established results are the extension of already existing results inside the literature. It is new problem that the upcoming researchers can obtain the similar inequalities for fractal sets and coordinated convex functions in their future work.