New Explicit Solutions of the Extended Double (2+1)-Dimensional Sine-Gorden Equation and Its Time Fractional Form

Abstract

In this paper, the extended double (2+1)-dimensional sine-Gorden equation is studied. First of all, using the symmetry method, the corresponding vector fields, Lie algebra and infinitesimal generators are derived. Then, from infinitesimal generators, the symmetry reductions are presented. In addition, these reduced equations are converted into the corresponding partial differential equations, which including classical double (1+1)-dimensional sine-Gorden equation. Moreover, based on the Lie symmetry method again, these reduced equations are investigated. Meanwhile, based on traveling wave transformation, some explicit solutions of the extended double (2+1)-dimensional sine-Gorden equation are obtained. Consequently, a conservation law is derived via conservation law multiplier method. Finally, especially with the help of the fractional complex transform, some solutions of double time fractional (2+1)-dimensional sine-Gorden equation are also derived. These results might explain complex nonlinear phenomenon.

1. Introduction

Recently, Wang, from extended Lax pairs, derived a (2+1)-dimensional sine-Gorden Equation [1],

$$\begin{array}{c}\hfill u_{xx}-u_{xy}-u_{xt}+u_{yt}=sinu,\end{array}$$

(1)

they studied the kink wave and anti-kink wave solutions, also derived conservation laws. Based on the results of ref. [1], this paper focuses on the following extended double (2+1)-dimensional sine-Gorden equation:

$$\begin{array}{c}\hfill u_{xx}-u_{xy}-u_{xt}+u_{yt}=sinu+asin2u,\end{array}$$

(2)

and time fractional form as follows:

$$\begin{array}{c}\hfill u_{xx}-u_{xy}-{\left(u_t^{\alpha }\right)}_x+{\left(u_t^{\alpha }\right)}_y=sinu+asin2u,\end{array}$$

(3)

where $D_t^{\alpha }\left(·\right)$ is the modified Riemann–Liouville derivative [2,3,4], $0<\alpha \le 1$, a is a constant. Some preliminaries of the modified Riemann–Liouville derivative refer to [2,3,4]. If $a=0$, Equation (2) reduced to Equation (1). Furthermore, it can be seen that if $\alpha =1$, Equation (3) becomes Equation (2). This paper extends our previous work in [1] to study the extended double (2+1)-dimensional sine-Gorden equation. The sine-Gorden-type equation appears in many science fields [5,6], such as nonlinear optics, quantum field theory, differential geometry, solid state physics and so on. The author [7] derived multiple optical kink wave solutions of sine-Gordon-type equations. In paper [8], they got some exact solitary wave solutions for sine-Gordon-type equations using an auxiliary ordinary differential equation method. In [9], they considered initial value problem for the sine-Gordon equation, this equation is solved by the inverse-scattering method. The author, in paper [10], using tanh method and a variable separated ODE method, solved double sine-Gordon equation, and some exact solutions are derived.

There are many methods to study the nonlinear evolution equations, such as the Lie symmetry method [11,12,13,14,15,16,17,18,19,20,21,22], Hamiltonian system [23,24,25,26], Hirota’s bilinear direct method [27], B$\ddot{a}$cklund transformation [28,29], inverse scattering transformation [6], Darboux transformations [30], Lax pairs [31,32] and so on. On the other hand, it is well known that fractional order differential equations are well suited to characterize materials and processes with memory and genetic properties, and their description of complex systems has the advantages of simple modeling, clear physical meaning of parameters, and accurate description, thus becoming one of the important tools for mathematical modeling of complex mechanics and physical processes [33,34,35,36]. With the development of science and technology, most of the problems in real-life natural phenomena such as optical and thermal systems, rheological and material and mechanical systems, signal processing and system identification, control and robotics, and other applications can be described by fractional order differential equations [37,38,39,40,41,42]. Therefore, the research on fractional order differential equations has also received extensive attention from more and more authors, especially the fractional order differential equations abstracted from practical problems have become a hot research topic for many mathematicians. As fractional order differential equations appear in more and more scientific fields, the study of both theoretical analysis and numerical computation of fractional order differential equations is particularly urgent [37,38,39,40,41,42]. This is because it can better explain the complex natural phenomena.

Lie symmetry method provides a powerful and fundamental framework to the investigation of differential equations, it can link between different differential equations, it also can construct conservation laws for differential equations. As this equation is obtained from the extended Lax pair and this equation can be reduced to the classical sine-Gorden equation, it is necessary to study this equation to provide stronger theoretical support for solving practical problems. The current paper is divided into the following main sections, in Section 2, the extended double (2+1)-dimensional sine-Gorden equation is studied using symmetry method. In Section 3, symmetry reductions and analytical solutions of the extended double (2+1)-dimensional sine-Gorden equation are presented. A conservation law is given by Section 4. Explicit solutions of the extended double time fractional (2+1)-dimensional sine-Gorden equation are obtained in Section 5. The last Section is the conclusion of this paper.

2. Symmetry Analysis of the Extended Double (2+1)-Dimensional Sine-Gorden Equation (2)

Given the following vector fields [11,12,13,14,15,16,17,18,19,20]

$$V={\xi }^3(x,y,t,u)\frac{\partial }{\partial t}+{\xi }^1(x,y,t,u)\frac{\partial }{\partial x}+{\xi }^2(x,y,t,u)\frac{\partial }{\partial y}+\eta (x,y,t,u)\frac{\partial }{\partial u},$$

(4)

where

$$\left\{\begin{array}{c}{t}^{*}=t+ϵ{\xi }^3(x,y,t,u)+O\left({ϵ}^2\right),x^{*}=x+ϵ{\xi }^1(x,y,t,u)+O\left({ϵ}^2\right),\hfill \\ y^{*}=y+ϵ{\xi }^2(x,y,t,u)+O\left({ϵ}^2\right),u^{*}=u+ϵ\eta (x,y,t,u)+O\left({ϵ}^2\right).\hfill \end{array}\right.$$

(5)

Consider the connection of vector field (4) and symmetry of the extended double (2+1)-dimensional sine-Gorden equation, V needs to satisfy Lie’s symmetry condition

$$p{r}^{\left(2\right)}V\left({\Delta }_1\right){|}_{{\Delta }_1=0}=0,$$

(6)

where ${\Delta }_1=u_{xx}-u_{xy}-u_{xt}+u_{yt}-sinu-asin2u.$

Given the second prolongation

$$p{r}^{\left(2\right)}V=\left\{\begin{array}{c}V+{\eta }^x(x,y,t,u)\frac{\partial }{\partial u_x}+{\eta }^y(x,y,t,u)\frac{\partial }{\partial u_y}+{\eta }^t(x,y,t,u)\frac{\partial }{\partial u_t}+{\eta }^{xt}(x,y,t,u)\frac{\partial }{\partial u_{xt}}\hfill \\ +{\eta }^{xy}(x,y,t,u)\frac{\partial }{\partial u_{xy}}+{\eta }^{xt}(x,y,t,u)\frac{\partial }{\partial u_{xt}}+{\eta }^{yt}(x,y,t,u)\frac{\partial }{\partial u_{yt}},\hfill \end{array}\right.$$

(7)

$p{r}^{\left(2\right)}V$ to the (2), the following infinitesimal criterion reads as

$$\begin{array}{c}\hfill {\eta }^{xx}-{\eta }^{xy}-{\eta }^{xt}+{\eta }^{yt}-\eta cosu-2acos2u\eta =0,\end{array}$$

(8)

where

$$\begin{array}{cc}\hfill & {\eta }^t=D_t\left(\eta \right)-u_x{D}_t\left({\xi }^1\right)-u_y{D}_t\left({\xi }^2\right)-u_t{D}_t\left({\xi }^3\right),\hfill \\ \hfill & {\eta }^x=D_x\left(\eta \right)-u_x{D}_x\left({\xi }^1\right)-u_y{D}_x\left({\xi }^2\right)-u_t{D}_x\left({\xi }^3\right),\hfill \\ \hfill & {\eta }^y=D_y\left(\eta \right)-u_x{D}_y\left({\xi }^1\right)-u_y{D}_y\left({\xi }^2\right)-u_t{D}_y\left({\xi }^3\right),\hfill \\ \hfill & {\eta }^{xx}=D_x\left({\eta }^x\right)-u_{xt}{D}_x\left({\xi }^3\right)-u_{xx}{D}_x\left({\xi }^1\right)-u_{xy}{D}_x\left({\xi }^2\right),\hfill \\ \hfill & {\eta }^{yy}=D_y\left({\eta }^y\right)-u_{yt}{D}_y\left({\xi }^3\right)-u_{xy}{D}_y\left({\xi }^1\right)-u_{yy}{D}_y\left({\xi }^2\right),\hfill \end{array}$$

(9)

and so on and here $D_i$ is the following total derivative operator

$$D_i=\frac{\partial }{\partial x^i}+u_i\frac{\partial }{\partial u}+u_{ij}\frac{\partial }{\partial u_j}+\cdots i=1,2,3,$$

(10)

and $(x^1,x^2,x^3)=(t,x,y)$.

After calculation, the following results are derived:

$$\begin{array}{cc}\hfill & \eta =0,{\xi }^3=(x+y)F_2(x+t+y)+F_3(x+t+y),\hfill \\ \hfill & {\xi }^1=(-x-2y)F_2(x+t+y)+F_4(x+t+y),\hfill \\ \hfill & {\xi }^2=F_1(x+t+y)+y{F}_2(x+t+y),\hfill \end{array}$$

(11)

where $F_i(i=1,2,3,4)$ are arbitrary functions of $x+t+y$. Therefore, from Equation (4), the following infinitesimal generators are obtained:

$$\begin{array}{c}\hfill V=V_1+V_2+V_3+V_4,\end{array}$$

(12)

where

$$\begin{array}{cc}\hfill & V_1=F_4(x+t+y)\frac{\partial }{\partial x},\hfill \\ \hfill & V_2=F_1(x+t+y)\frac{\partial }{\partial y},\hfill \\ \hfill & V_3=F_3(x+t+y)\frac{\partial }{\partial t},\hfill \\ \hfill & V_4=(x+y)F_2(x+t+y)\frac{\partial }{\partial t}+(-x-2y)F_2(x+t+y)\frac{\partial }{\partial x}+y{F}_2(x+t+y)\frac{\partial }{\partial y}.\hfill \end{array}$$

(13)

It is clear that if the appropriate functions for $F_1,F_2,F_3$, and $F_4$ are selected, an infinite number of symmetries are presented. Obviously, there are basic infinitesimal generators

$$\begin{array}{cc}\hfill & V_1=\frac{\partial }{\partial x},\hfill \\ \hfill & V_2=\frac{\partial }{\partial y},\hfill \\ \hfill & V_3=\frac{\partial }{\partial t},\hfill \\ \hfill & V_4=(x+y)\frac{\partial }{\partial t}+(-x-2y)\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}.\hfill \end{array}$$

(14)

Their Lie algebra and commutative relations are given by

$$\begin{array}{cc}\hfill & [V_1,V_1]=0,[V_2,V_2]=0,[V_3,V_3]=0,[V_4,V_4]=0,\hfill \\ \hfill & [V_1,V_2]=-[V_2,V_1]=0,[V_1,V_3]=-[V_3,V_1]=0,\hfill \\ \hfill & [V_2,V_3]=-[V_3,V_2]=0,[V_1,V_4]=-[V_4,V_1]=V_3-V_1,\hfill \\ \hfill & [V_2,V_4]=-[V_4,V_2]=V_3-2V_1+V_2,\hfill \\ \hfill & [V_3,V_4]=-[V_4,V_3]=0.\hfill \end{array}$$

(15)

Based on the Lie group method, if $u=f(x,y,t)$ is a solution of the extended double (2+1)-dimensional sine-Gorden equation, so are

$$\begin{array}{cc}\hfill & u^1=f(x-\epsilon ,y,t),\hfill \\ \hfill & u^2=f(x,y-\epsilon ,y),\hfill \\ \hfill & u^3=f(x,y,t-\epsilon ),\hfill \end{array}$$

(16)

and so on. In next section, some analytical solutions will be investigated.

3. Symmetry Reductions and Analytical Solutions of the Extended Double (2+1)-Dimensional Sine-Gorden Equation (2)

3.1. Symmetry Reductions

3.1.1. $V_1$

For generator $V_1$, the invariant function is $u=f(\tau ,\eta )$, where $\tau =t,\eta =y$ are invariants; therefore, the following partial differential equation (PDEs) are derived:

$$\begin{array}{c}\hfill u_{\tau \eta }=sinu+asin2u.\end{array}$$

(17)

It needs to be emphasized that this equation is just famous double (1+1)-dimensional sine-Gorden equation.

3.1.2. $V_2$

For vector $V_2$, the invariant function is $u=f(\xi ,\tau )$ and invariants are $\tau =t,\xi =x$. Thus, they generate following PDE

$$\begin{array}{c}\hfill -u_{\tau \xi }=sinu+asin2u.\end{array}$$

(18)

3.1.3. $V_3$

Considering $V_3$, the invariant function and invariants are $u=f(\xi ,\eta )$ and $\xi =x,\eta =y$, respectively. For this case, following PDE is presented

$$\begin{array}{c}\hfill u_{\xi \xi }-u_{\xi \eta }=sinu+asin2u.\end{array}$$

(19)

3.1.4. Traveling Wave Transformation

Given $u=f\left(\xi \right)$ and $\xi =x+ky-ct$, one can get the following PDE

$$\begin{array}{c}\hfill (1-kc-k+c)u_{\xi \xi }=sinu+asin2u.\end{array}$$

(20)

From the above analysis, it is found that (17)–(19) are PDEs and (20) is ordinary differential equation(ODE). Of course, (17)–(19) also can reduced to ODE via traveling wave transformation. Now, as (17)–(19) still are PDEs, these equations are studied again using again Lie symmetry method.

3.2. Symmetry Analysis of Reduced Equations

Base on the previous steps, we consider (17)–(19) using the Lie symmetry method again.

3.2.1. Lie Symmetry of Equations (17) and (18)

For these PDEs, one can obtain the infinitesimal generators as follows:

$$\begin{array}{cc}\hfill & V_1=\frac{\partial }{\partial x},\hfill \\ \hfill & V_2=\frac{\partial }{\partial t},\hfill \\ \hfill & V_3=x\frac{\partial }{\partial x}-t\frac{\partial }{\partial t}.\hfill \end{array}$$

(21)

3.2.2. Lie Symmetry of Equation  (19)

For this PDE, the following infinitesimal generators are derived

$$\begin{array}{cc}\hfill & V_1=\frac{\partial }{\partial x},\hfill \\ \hfill & V_2=\frac{\partial }{\partial t},\hfill \\ \hfill & V_3=(-2t-x)\frac{\partial }{\partial x}-t\frac{\partial }{\partial t}.\hfill \end{array}$$

(22)

Of course, these equations can continue to be handled in the same way and with the same steps as before. For the sake of simplicity, they are not listed in detail.

3.3. Analytical Solutions of the Extended Double (2+1)-Dimensional Sine-Gorden Equation (2)

In previous section, a ODE is derived via traveling wave transformation. Now, one can study this ODE (20).

For the extended double sine-Gordon equation, using the traveling wave transformation $\xi =x+ky-ct$

$$\begin{array}{c}\hfill u_{xx}-u_{xy}-u_{xt}+u_{yt}=sinu+asin2u,\end{array}$$

(23)

that can be converted to the following ODE

$$\begin{array}{c}\hfill (1-kc-k+c)u_{\xi \xi }=sinu+asin2u,\end{array}$$

(24)

or equivalently form

$$\begin{array}{c}\hfill u^{″}=\frac{1}{1-kc-k+c}sin\left(u\right)+\frac{a}{1-kc-k+c}sin\left(2u\right).\end{array}$$

(25)

From the above analysis, it can be seen that in order to guarantee the existence of solutions, it is required that k is not equal to 1. Assuming that $u\left(\xi \right)$ satisfies the following ODE:

$$\begin{array}{c}\hfill u^{\prime }=a_0+\sum _{j=1}^n\left(a_{j}cosu+b_{j}sinu\right),\end{array}$$

(26)

where $a_j(j=0,1,2,\cdots )$ and $b_j(j=1,2,\cdots )$ are constants need to be fixed, also the positive integer n can be fixed via the leading-order analysis method. In this way, one can get $n=1$, thus we have

$$\begin{array}{c}\hfill u^{\prime }=a_0+a_{1}cosu+b_{1}sinu,\end{array}$$

(27)

where $a_1$ and $b_1$ are constants that will be determined. Differentiating (27) with respect to $\xi$ gives

$$\begin{array}{cc}\hfill & u^{″}\left(\xi \right)=-a_{1}sinu{u}^{\prime }+b_{1}cosu{u}^{\prime }\hfill \\ \hfill & =-a_{1}sinu\left(a_0+a_{1}cosu+b_{1}sinu\right)+b_{1}cosu\left(a_0+a_{1}cosu+b_{1}sinu\right).\hfill \end{array}$$

(28)

Comparing (28) with (25) it can be found that $b_1$ has to equal to zero. Therefore, one can obtain

$$\begin{array}{c}\hfill -a_0{a}_1=\frac{1}{1-kc-k+c},-\frac{a_1^2}{2}=\frac{a}{1-kc-k+c},\end{array}$$

(29)

that is to say,

$$\begin{array}{c}\hfill a_0=\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}},a_1=\sqrt{\frac{2a}{kc+k-c-1}}.\end{array}$$

(30)

It can be seen that Equation (27) is separable, hence one can have

$$\begin{array}{c}\hfill \frac{1}{a_0+a_{1}cos\left(u\right)}du=d\xi ,\end{array}$$

(31)

where by integrating both sides, the following solutions [8] are derived

$$\begin{array}{c}\hfill u_{1,2}=\left\{\begin{array}{c}\hfill 2arctan\left[\pm \sqrt{\frac{a_1+a_0}{a_1-a_0}}tan\frac{\sqrt{a_1^2-a_0^2}}{2}\left(\xi +{\xi }_0\right)\right]\\ \hfill 2arctan\left[\pm \sqrt{\frac{a_1+a_0}{a_1-a_0}}cot\frac{\sqrt{a_1^2-a_0^2}}{2}\left(\xi +{\xi }_0\right)\right]\end{array}\mathrm{for}{a}_0^2>a_1^2\right.,\end{array}$$

(32)

$$u_{3,4}=\left\{\begin{array}{c}\hfill 2arctan\left[\pm \sqrt{\frac{a_1+a_0}{a_1-a_0}}tanh\frac{\sqrt{a_1^2-a_0^2}}{2}\left(\xi +{\xi }_0\right)\right]\\ \hfill 2arctan\left[\pm \sqrt{\frac{a_1+a_0}{a_1-a_0}}coth\frac{\sqrt{a_1^2-a_0^2}}{2}\left(\xi +{\xi }_0\right)\right]\end{array}\mathrm{for}{a}_0^2<a_1^2\right.,$$

(33)

$$\begin{array}{cc}\hfill u_5=2\arctan a_0\left(\xi +{\xi }_0\right)& \mathrm{for}{a}_1=a_0,\hfill \\ \hfill u_6=-2arccot{a}_0\left(\xi +{\xi }_0\right)& \mathrm{for}{a}_1=-a_0,\hfill \end{array}$$

(34)

where ${\xi }_0$ is the constant of integration. These solutions are solitary wave solutions, they have obvious physical implications, that is to say, the wave form does not change with time in the propagation process, and outside the zone of interaction (the collision zone), the solitary wave retains its shape and velocity. Therefore, in turn, it can be derived that the following analytical solutions

$$u_{1,2}=\left\{\begin{array}{cc}& 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}tan\right.\hfill \\ & \left.\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\left(x+ky-ct+{\xi }_0\right)\right]\hfill \\ & 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}cot\right.\hfill \\ & \left.\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\left(x+ky-ct+{\xi }_0\right)\right]\hfill \end{array}\right.$$

(35)

for $a_0^2>a_1^2$,

$$u_{3,4}=\left\{\begin{array}{cc}& 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}tanh\right.\hfill \\ & \left.\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\left(x+ky-ct+{\xi }_0\right)\right]\hfill \\ & 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}coth\right.\hfill \\ & \left.\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\left(x+ky-ct+{\xi }_0\right)\right]\hfill \end{array}\right.$$

(36)

for $a_0^2<a_1^2$,

$$\begin{array}{cc}\hfill u_5=2\arctan \sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}\left(x+ky-ct+{\xi }_0\right)& \mathrm{for}{a}_1=a_0,\hfill \\ \hfill u_6=-2arccot\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}\left(x+ky-ct+{\xi }_0\right)& \mathrm{for}{a}_1=-a_0.\hfill \end{array}$$

(37)

4. Conservation Laws of Equation (2)

A conservation law express the following form:

$$\begin{array}{c}\hfill D_{t}T+D_{x}X+D_{y}Y=0.\end{array}$$

(38)

By using conservation law multiplier method [13], let

$$\begin{array}{c}\hfill R\left[u\right]\triangleq u_{xx}-u_{xy}-u_{xt}+u_{yt}-sinu-asin2u=0.\end{array}$$

(39)

Therefore, one can get

$$\begin{array}{c}\hfill D_i{\Phi }^i\left[u\right]\triangleq D_1{\Phi }^1\left[u\right]+D_2{\Phi }^2\left[u\right]+D_3{\Phi }^3\left[u\right]=0,\end{array}$$

(40)

the total derivative operators satisfy solutions of Equation (39). Solving $\Lambda \left[u\right]R\left[u\right]\equiv D_i{\Phi }^i\left[u\right],$ for every u in Equation (39), one should get a multiplier $\Lambda \left[u\right]=\Lambda (x,y,t,u)$.

Theorem 1

([13]). Consider the divergence expression $D_i{\Phi }^i\left[u\right],$ one can have

$$\begin{array}{c}\hfill E_u\left(D_i{\Phi }^i\left[u\right]\right)\equiv 0,\end{array}$$

(41)

where $E_u$ is the Euler operator given by

$$\begin{array}{c}\hfill E_u=\frac{\partial }{\partial u}-D_i\frac{\partial }{\partial u}+\cdots +{(-1)}^s{D}_{i_1}\cdots D_{i_s}\frac{\theta }{\partial u_{i1}\cdots i_s}+\cdots \end{array}$$

(42)

Theorem 2

([13]). A divergence expression for Equation (39) can be derived by a conservation law multiplier $\Lambda (x,y,t,u)$ if and only if

$$\begin{array}{c}\hfill E_u(\Lambda (x,y,t,u)R\left[u\right])\equiv 0,\end{array}$$

(43)

holds for every u in Equation (39).

Theorem 3.

Consider second order multiplier $\left\{\Lambda \right\}=\{x,t,y,u_x,u_{xx}\}$, and arbitrary constant a, Equation (39) has a local conservation law

$$\begin{array}{cc}\hfill & T=\left(-\frac{1}{2}{u}_x^2+\frac{1}{2}{u}_x{u}_y\right),\hfill \\ \hfill & X=\left(\frac{1}{2}u{u}_{ty}-\frac{1}{2}u{u}_{xy}+\frac{1}{2}{u}_x^2-\frac{1}{2}{u}_x{u}_y+a{(cosu)}^2+cosu-a-1\right),\hfill \\ \hfill & Y=\left(-\frac{1}{2}u{u}_{tx}+\frac{1}{2}u{u}_{xx}\right),\hfill \end{array}$$

(44)

in other words,

$$\begin{array}{cc}\hfill & D_t\left(-\frac{1}{2}{u}_x^2+\frac{1}{2}{u}_x{u}_y\right)+D_y\left(-\frac{1}{2}u{u}_{tx}+\frac{1}{2}u{u}_{xx}\right)\hfill \\ \hfill & +D_x\left(\frac{1}{2}u{u}_{ty}-\frac{1}{2}u{u}_{xy}+\frac{1}{2}{u}_x^2-\frac{1}{2}{u}_x{u}_y+a{(cosu)}^2+cosu-a-1\right)=0.\hfill \end{array}$$

(45)

Proof. 

Consider Equation (43), one gets

$${\Lambda }_t={\Lambda }_x={\Lambda }_y={\Lambda }_u={\Lambda }_{u_{xx}}=0,u_x{\Lambda }_{u_x}=\Lambda .$$

Solving these equations, one can obtain

$$\Lambda =c_1{u}_x,$$

where $c_1$ is arbitrary constant. Thus, it shows that Theorem 3 holds. □

5. Analytical Solutions of the Extended Double Time Fractional (2+1)-Dimensional Sine-Gorden Equation (3)

For the extended double time fractional (2+1)-dimensional sine-Gorden Equation (3), using the fractional complex transform [3,4] $\xi =x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}$, and $u(x,y,t)=u\left(\xi \right)$, substitute them into Equation (3),

$$\begin{array}{c}\hfill u_{xx}-u_{xy}-{\left(u_t^{\alpha }\right)}_x+{\left(u_t^{\alpha }\right)}_y=sinu+asin2u,\end{array}$$

(46)

should be converted to the following ODE as follows

$$\begin{array}{c}\hfill (1-kc-k+c)u_{\xi \xi }=sinu+asin2u.\end{array}$$

(47)

If we assume $\xi =k_{1}x+k_{2}y-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}$, this requirement $k_1$ is not equal to $k_2$. Without loss in generality, we assume $k_1=1$. It can be found that k also cannot be equal to 1 in order to guarantee the existence of the solution. This means that after fractional complex transform, it also becomes the same ordinary differential equation as Equation (24). If $\alpha$ is equal to 1, it is the classical traveling wave transform. In this way, using the results obtained above, one can directly obtain solutions of the fractional order differential equation as described below

$$\begin{array}{c}\hfill u_{1,2}=\left\{\begin{array}{cc}& 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}tan\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\right.\hfill \\ & \left.\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)\right]\hfill \\ & 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}cot\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\right.\hfill \\ & \left.\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)\right]\hfill \end{array}\right.\\ \hfill \end{array}$$

(48)

for $a_0^2>a_1^2$,

$$\begin{array}{c}\hfill u_{3,4}=\left\{\begin{array}{cc}& 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}tanh\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\right.\hfill \\ & \left.\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)\right]\hfill \\ & 2arctan\left[\pm \sqrt{\frac{\sqrt{\frac{2a}{kc+k-c-1}}+\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}{\sqrt{\frac{2a}{kc+k-c-1}}-\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}}}coth\sqrt{\frac{4a^2-1}{8a(kc+k-c-1)}}\right.\hfill \\ & \left.\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)\right]\hfill \end{array}\right.\\ \hfill \end{array}$$

(49)

for $a_0^2<a_1^2$,

$$\begin{array}{cc}\hfill u_5=2\arctan \sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)& \mathrm{for}{a}_1=a_0,\hfill \\ \hfill u_6=-2arccot\sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)& \mathrm{for}{a}_1=-a_0.\hfill \end{array}$$

(50)

The above analysis shows that if $\alpha =1$, these solutions are transformed into Equations (35)–(37).

Take the following solution $u_5=2\arctan \sqrt{\frac{1}{2a\left(kc+k-c-1\right)}}\left(x+ky-c\frac{t^{\alpha }}{\Gamma (1+\alpha )}+{\xi }_0\right)$ as an example to describe how the solution changes with different $\alpha$. Let $k=c=2,a=\frac{1}{6},{\xi }_0=0$, one can get $u_5=2\arctan \left(x+2y-2\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right)$. Figure 1, Figure 2, Figure 3 and Figure 4 depict the solution $u_5$ for different $\alpha$ at $y=0$.

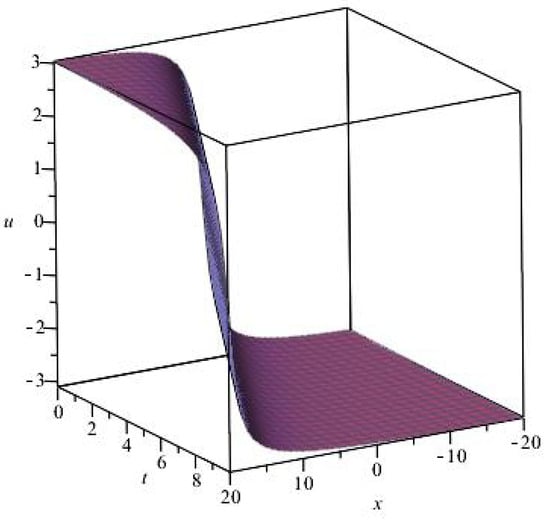
Figure 1. $\alpha =1$.

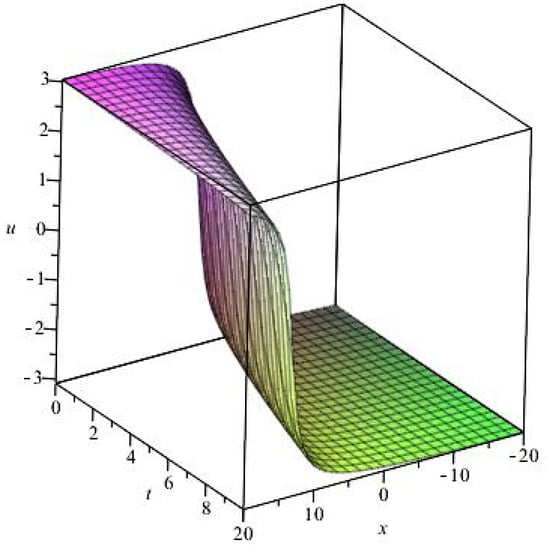
Figure 2. $\alpha =0.8$.

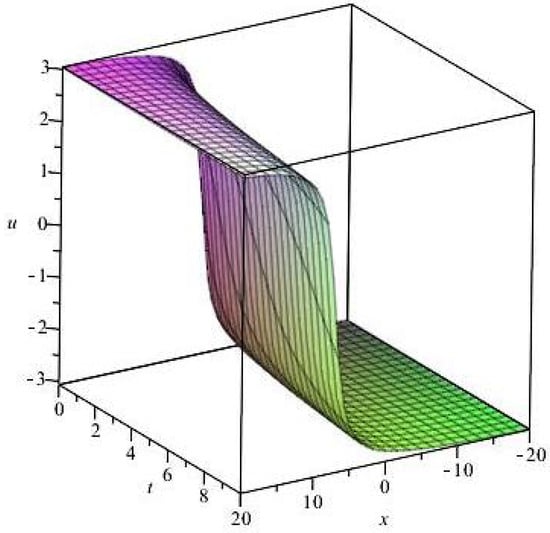
Figure 3. $\alpha =0.5$.

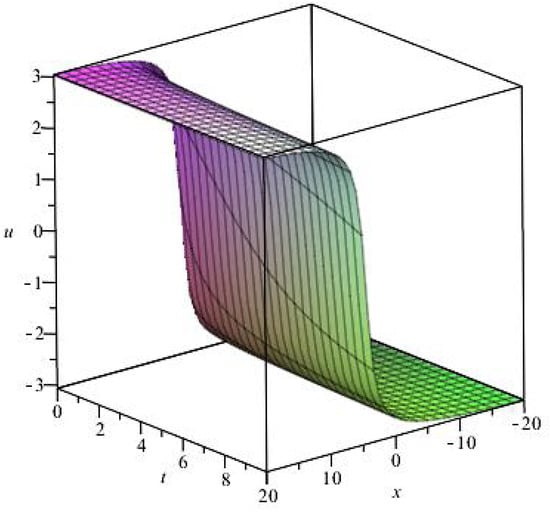
Figure 4. $\alpha =0.3$.

The following Figure 5 shown the solution with different $\alpha$ at $y=0,t=2$. As can be seen in Figure 5, the location of the solution changes as $\alpha$ changes. The larger the value of $\alpha$, the more forward the solution is located, and conversely, the smaller the value of $\alpha$, the more backward the solution is located.

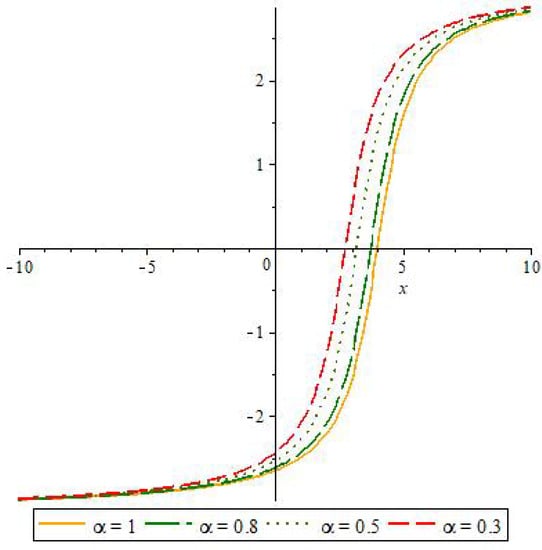
Figure 5. Plots of solutions with different $\alpha$ at $y=0,t=2$.

6. Conclusions

In this paper, the extended double (2+1)-dimensional sine-Gorden equation and its time fractional form are studied. It is clear that this paper generalizes the results in the literature [1]. This equation not only has extra terms $asin2u$, but also has the time fractional order form of this equation. More importantly, some explicit solutions are obtained.

The extended double (2+1)-dimensional sine-Gorden equation is reduced to a double (1+1)-dimensional sine-Gorden equation by the group method. In addition, it can be found that this equation has basic symmetries. By these basic symmetries, symmetry reductions are obtained. Furthermore, some exact solutions of the extended double (2+1)-dimensional sine-Gorden equation are obtained using traveling wave transform. After that, a conservation law of this equation is obtained based on the conservation law multiplier method. Meanwhile, using the fractional complex transform, some new explicit solutions of the extended double time fractional (2+1)-dimensional sine-Gorden equation also presented.

Consequently, the extended double (2+1)-dimensional sine-Gorden equation is an interesting new equation in nonlinear mathematical physics fields, it should be noted that there are still many issues worth investigating, such as non-local symmetry, non-local conservation laws and many more explicit solutions.