Fractal Characteristics of the Pore Structure of Coral Powder–Cement Slurry under Different Fractal Models
Abstract
:1. Introduction
2. Materials and Methods
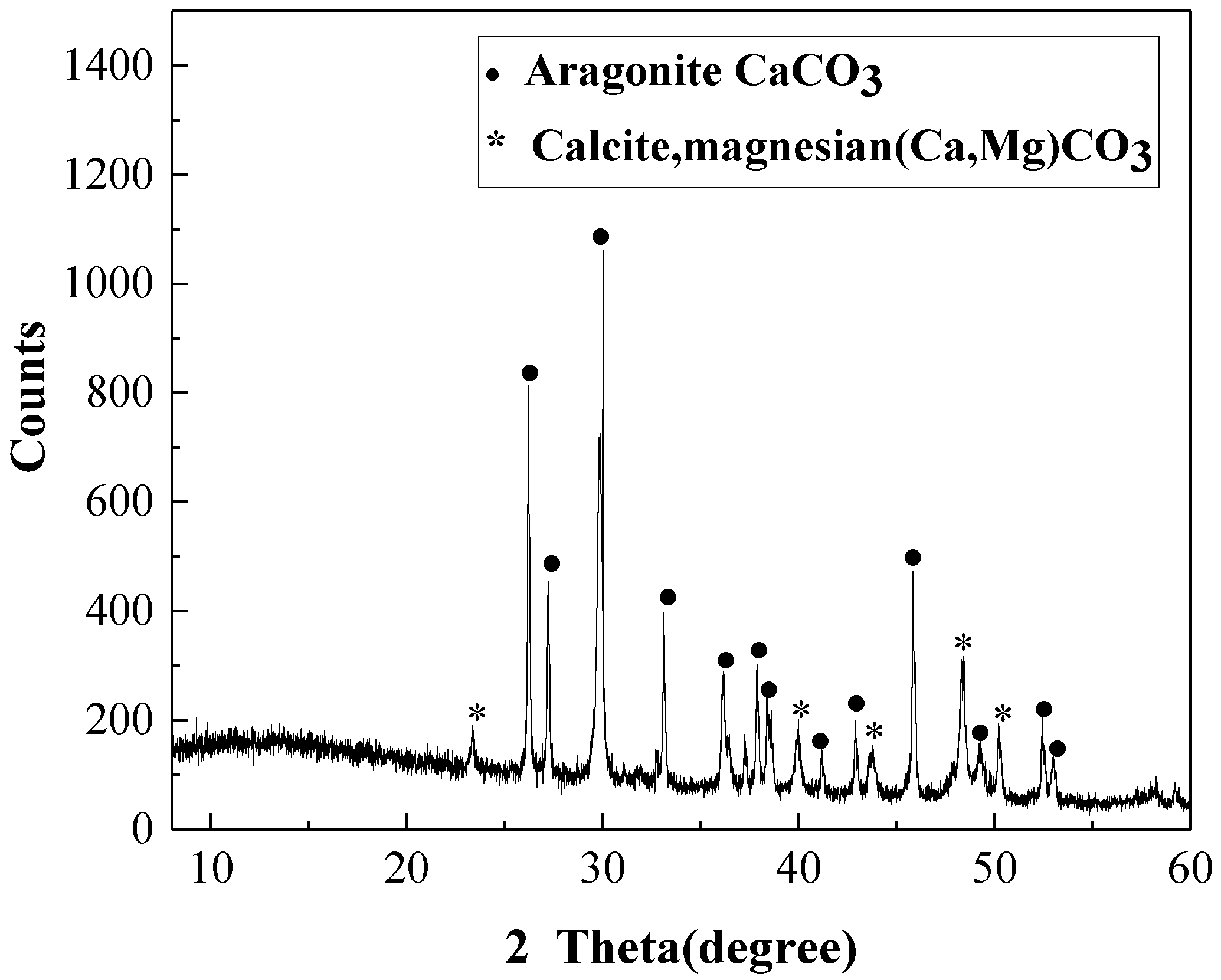
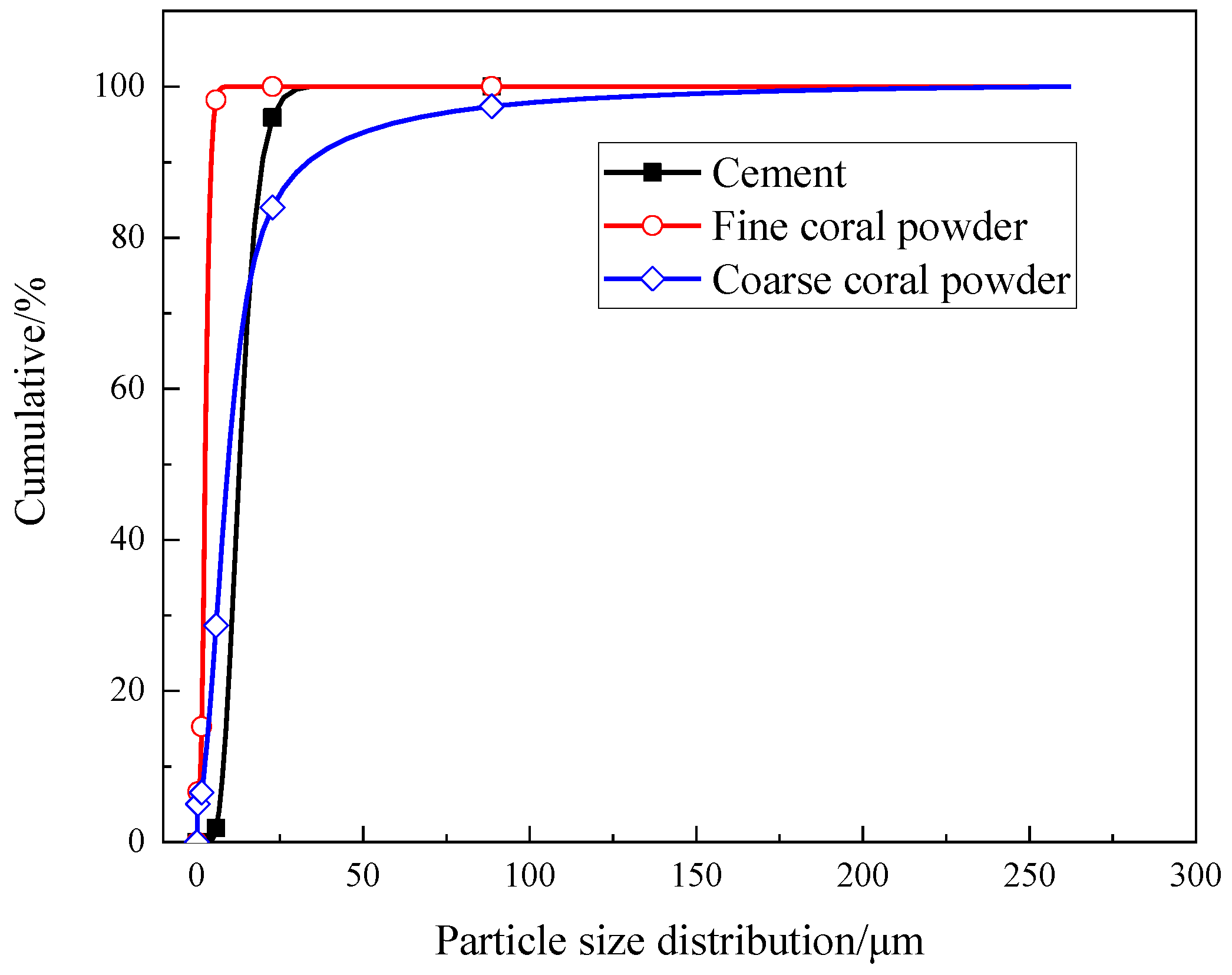
2.1. Raw Materials
2.2. Mixing Ratio Design
2.3. Test Methods
2.3.1. Mercury Intrusion Porosimetry Test (MIP)
2.3.2. Neimark’s Model
2.3.3. Ji’s Model
2.3.4. Pfeifer and Avnir’s Model
3. Results and Discussion
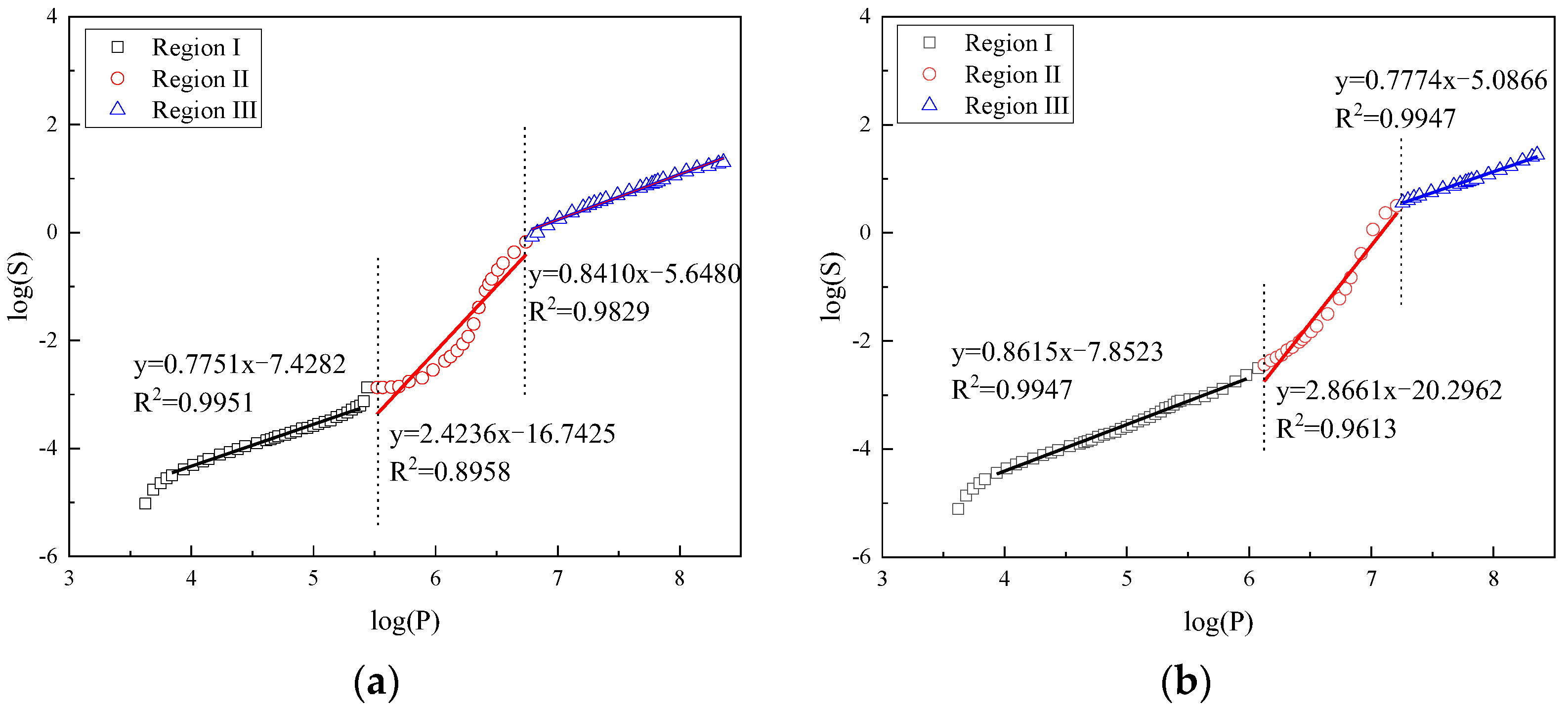
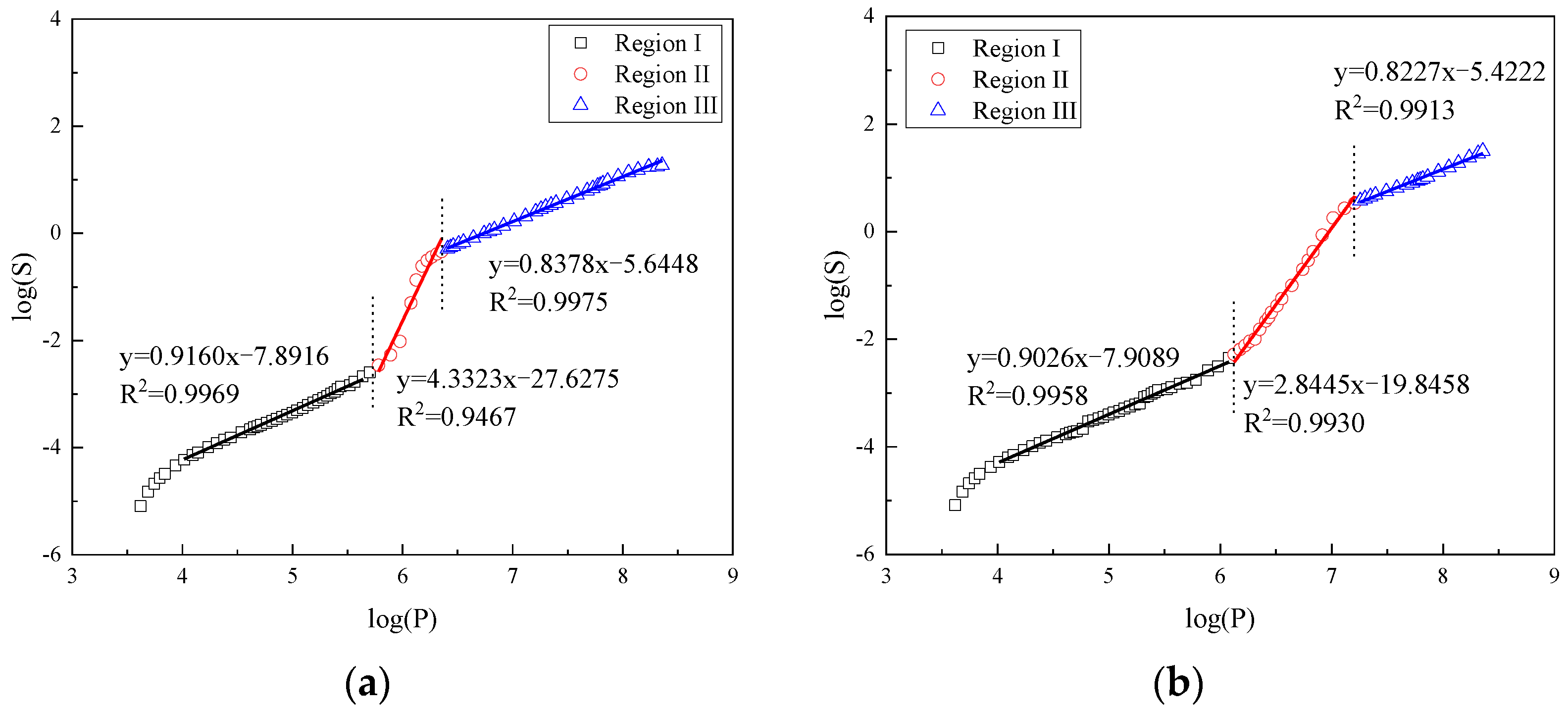
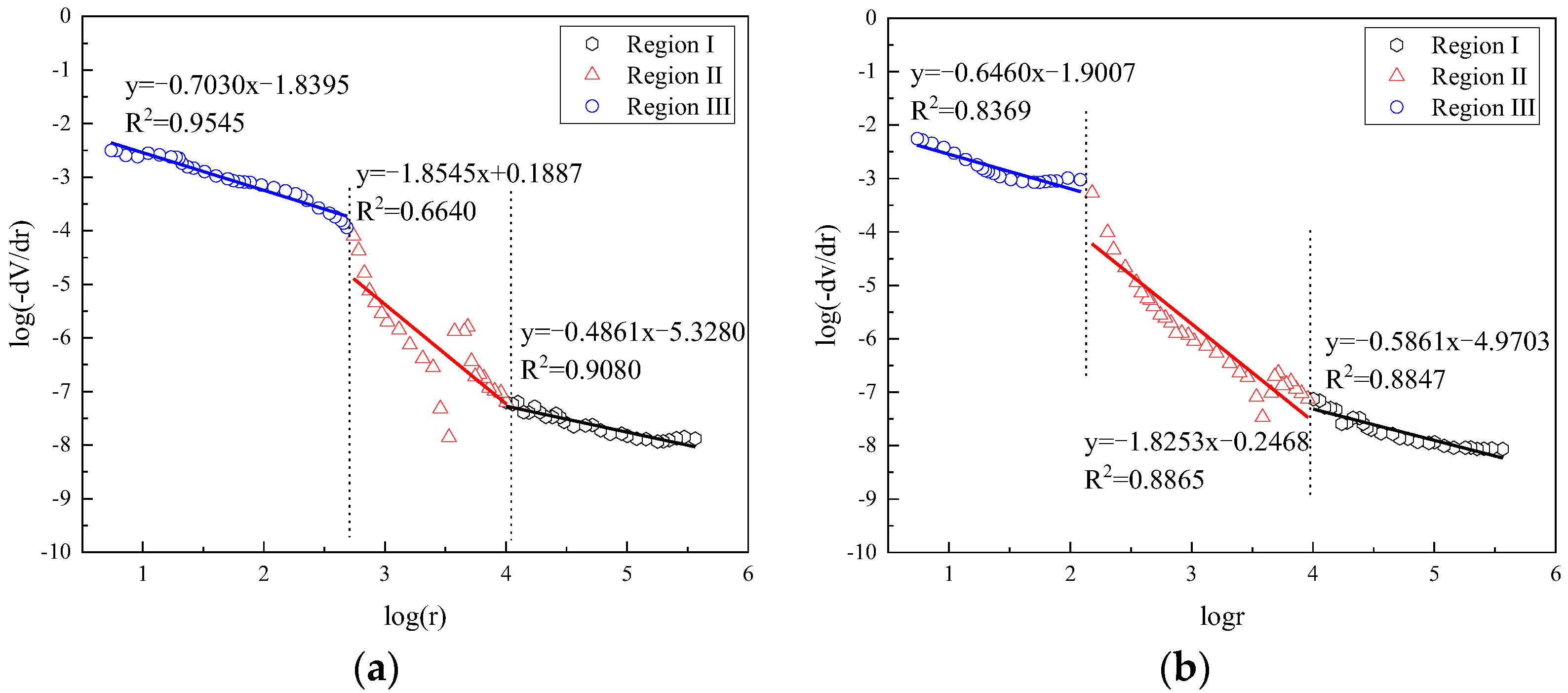
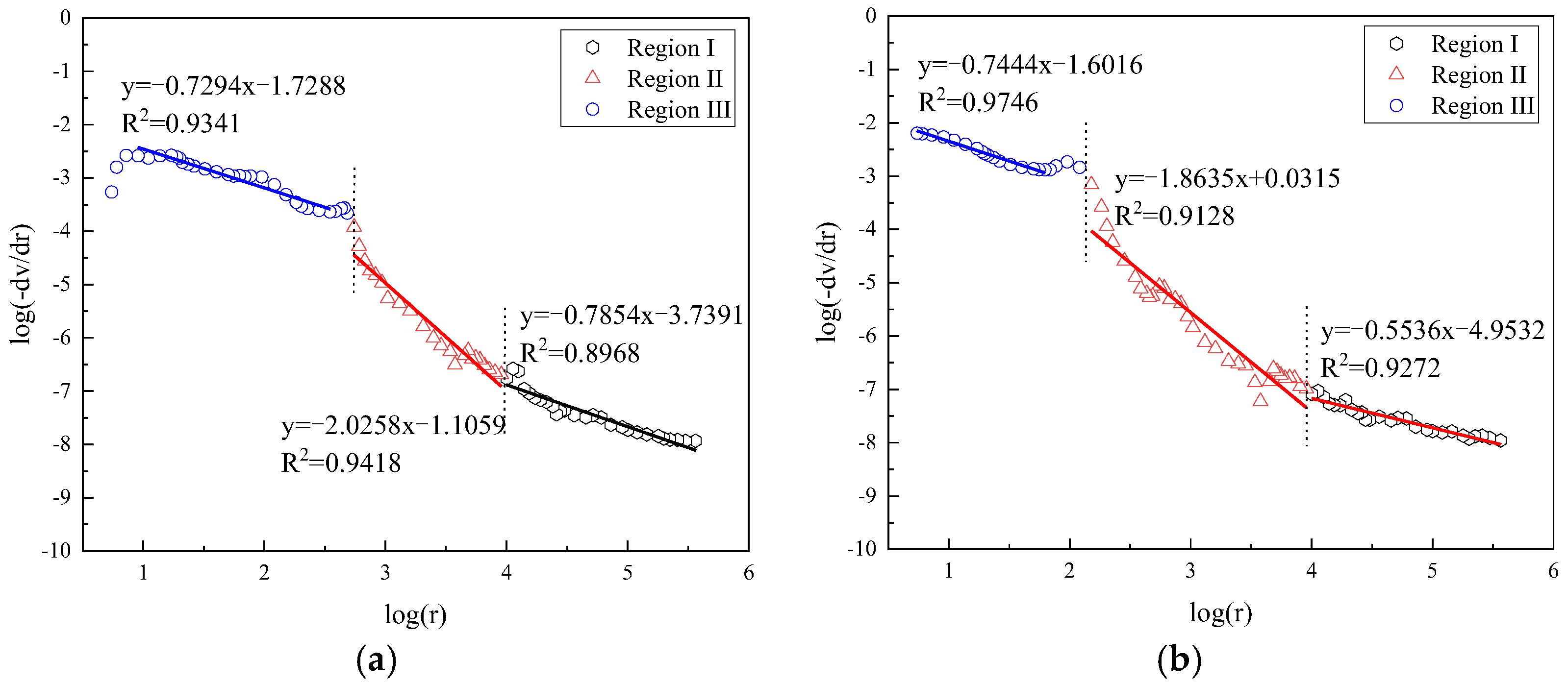
3.1. Analysis of Fractal Characteristics of Different Types of Cement Pastes Using Neimark’s Model
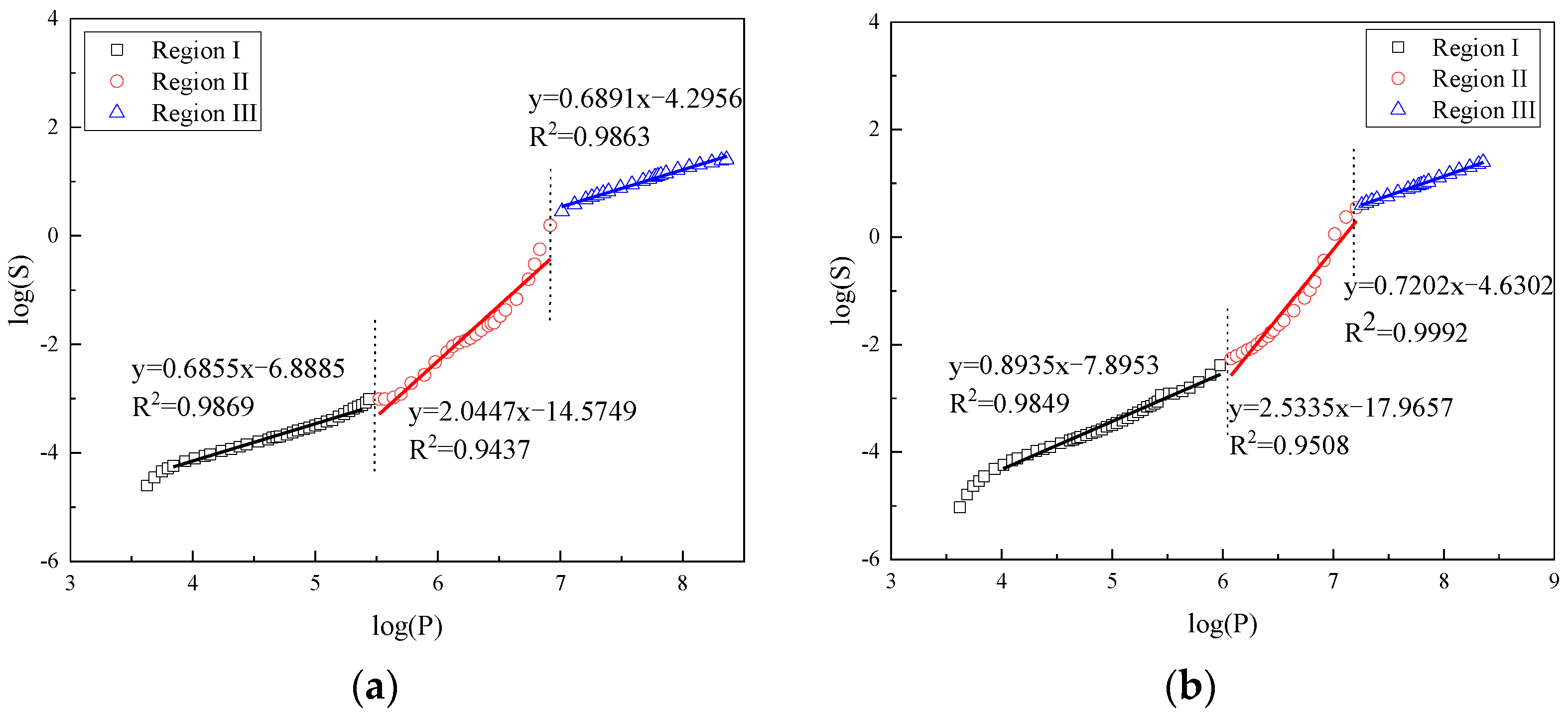
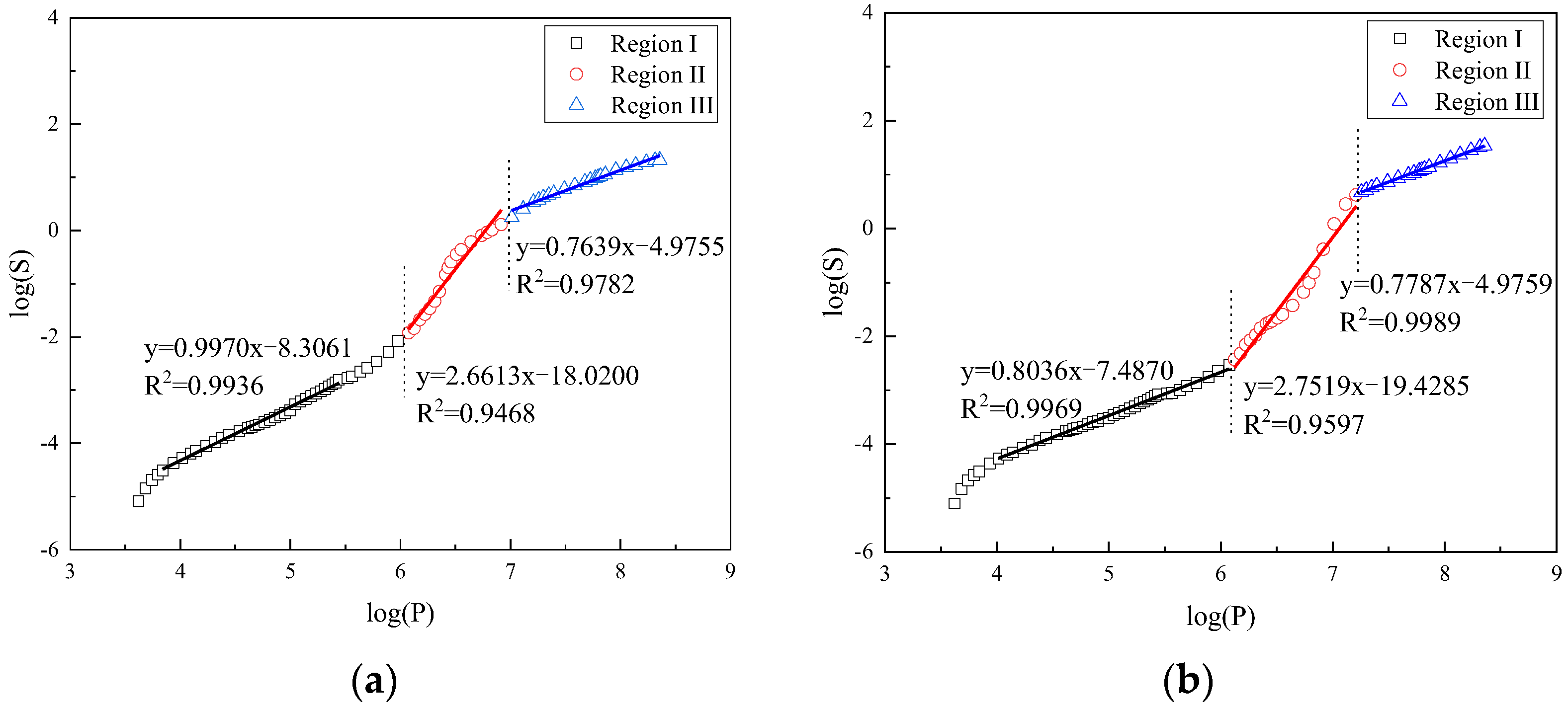
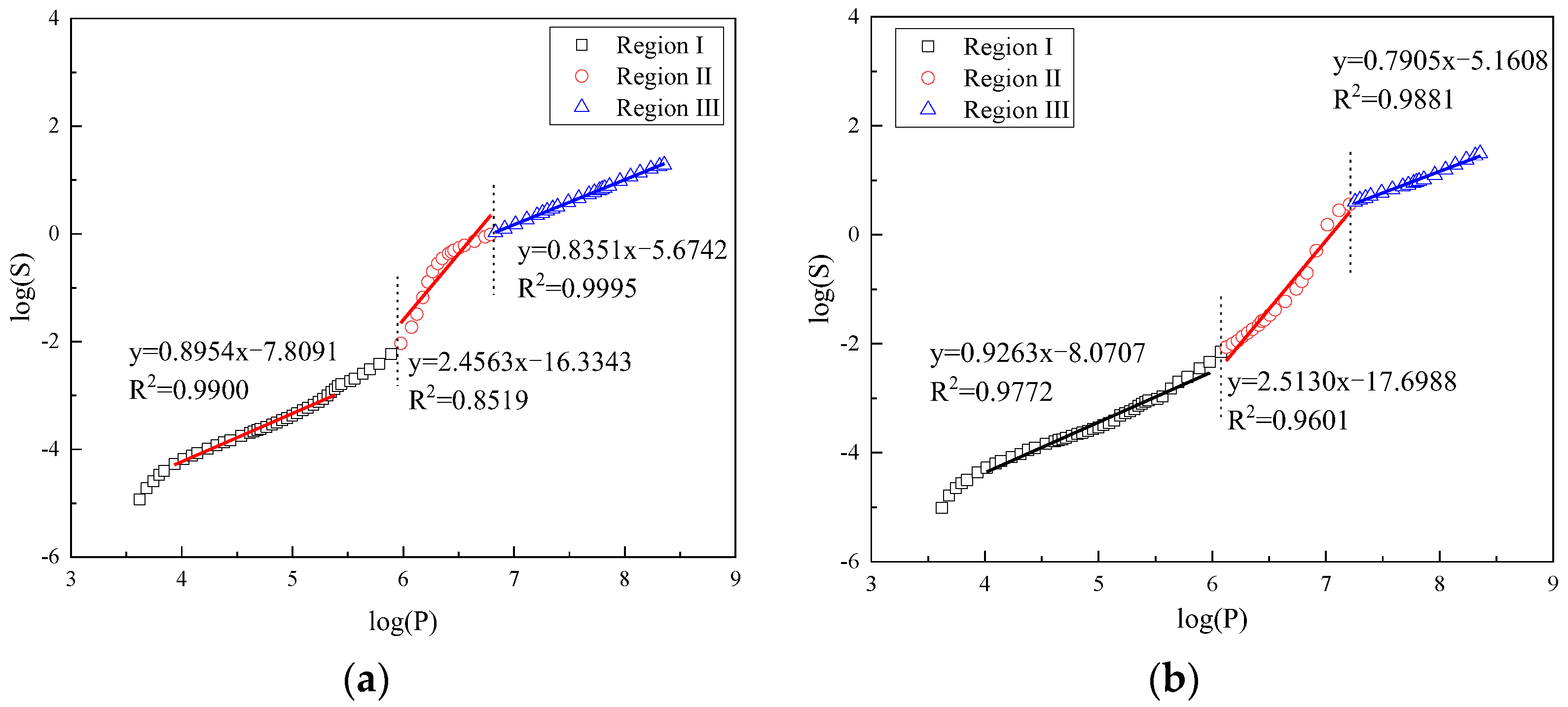
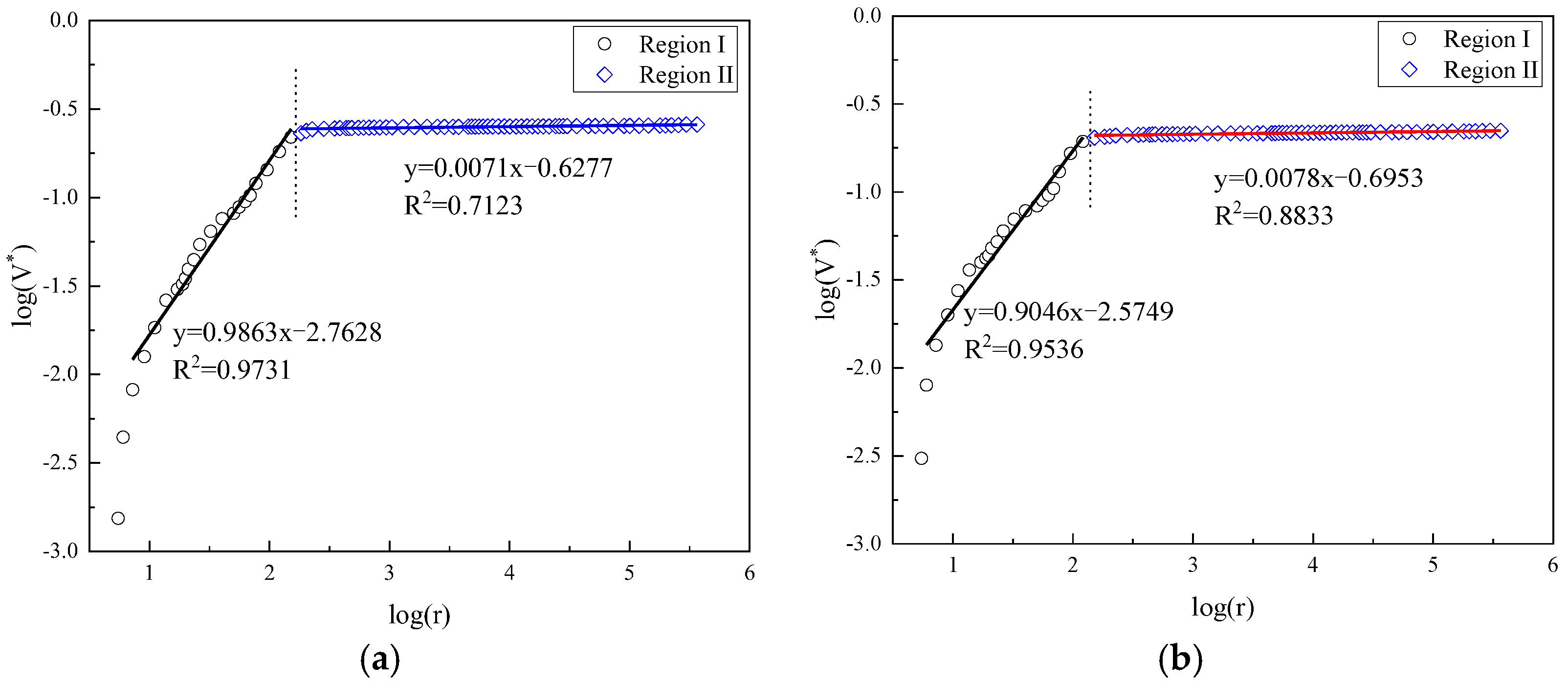
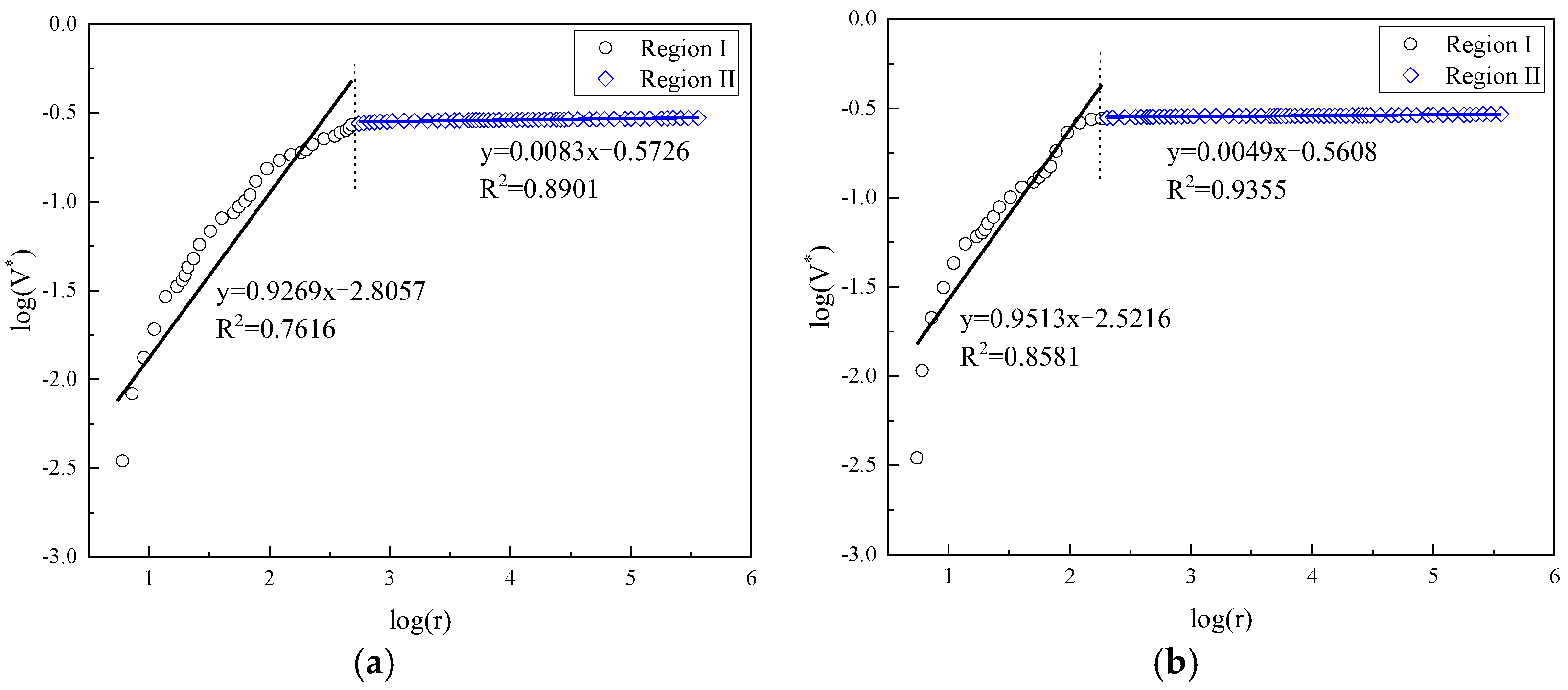
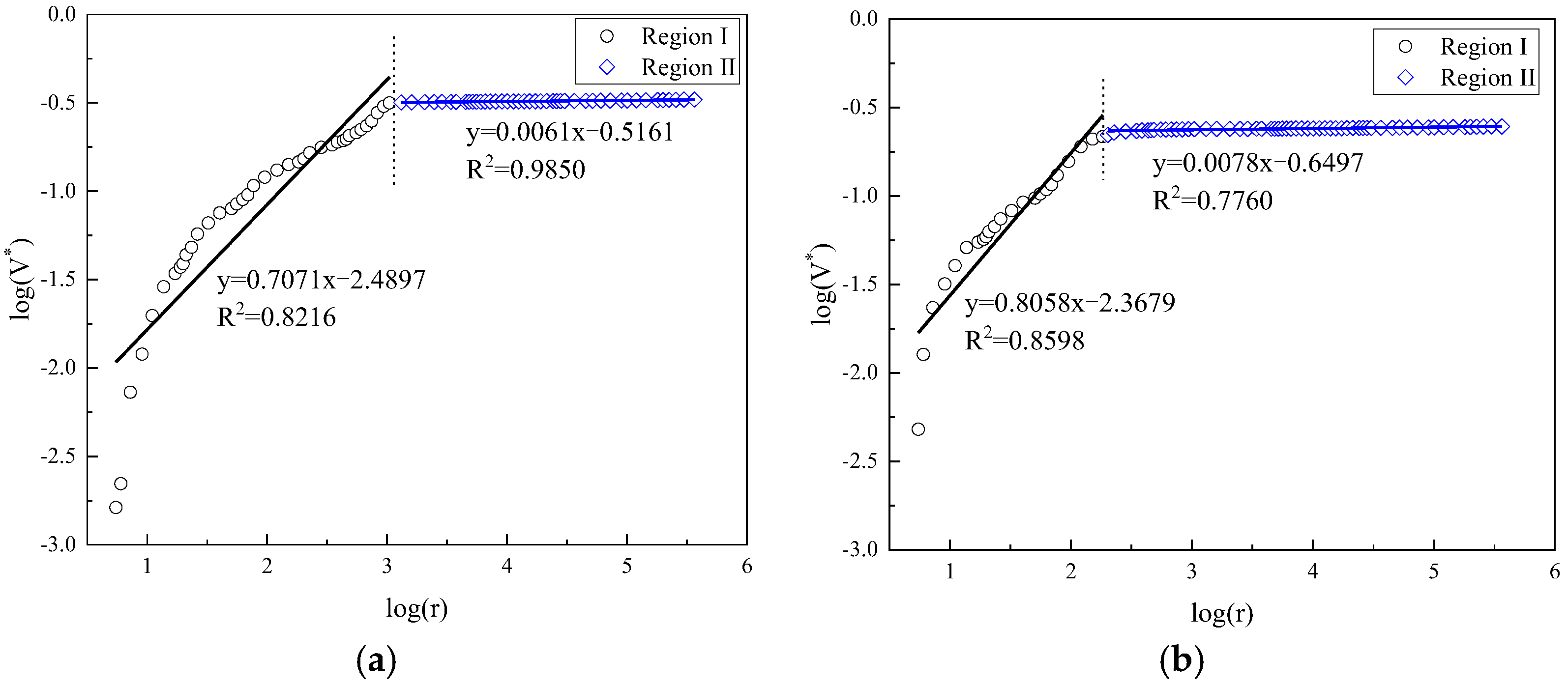
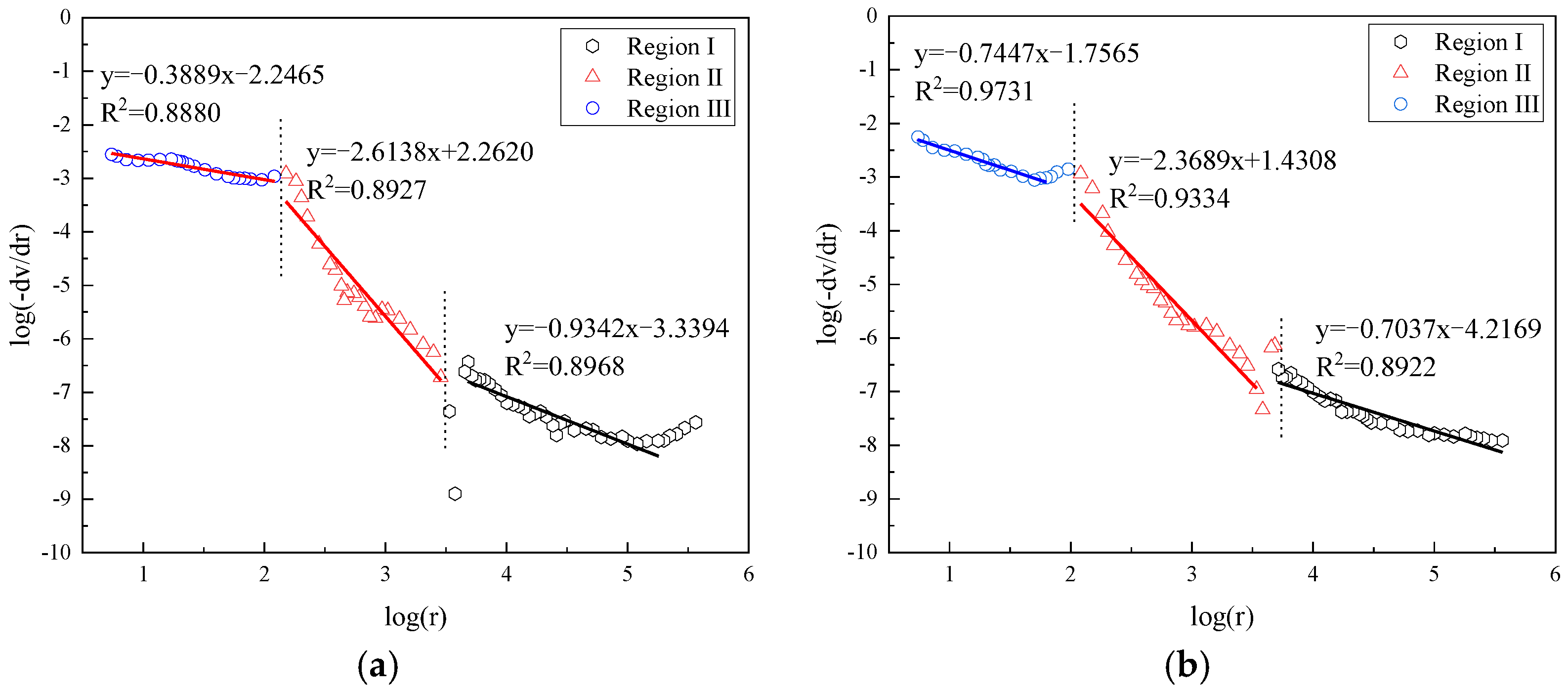
3.2. Analysis of Fractal Characteristics of Different Types of Cement Pastes Using Ji’s Model
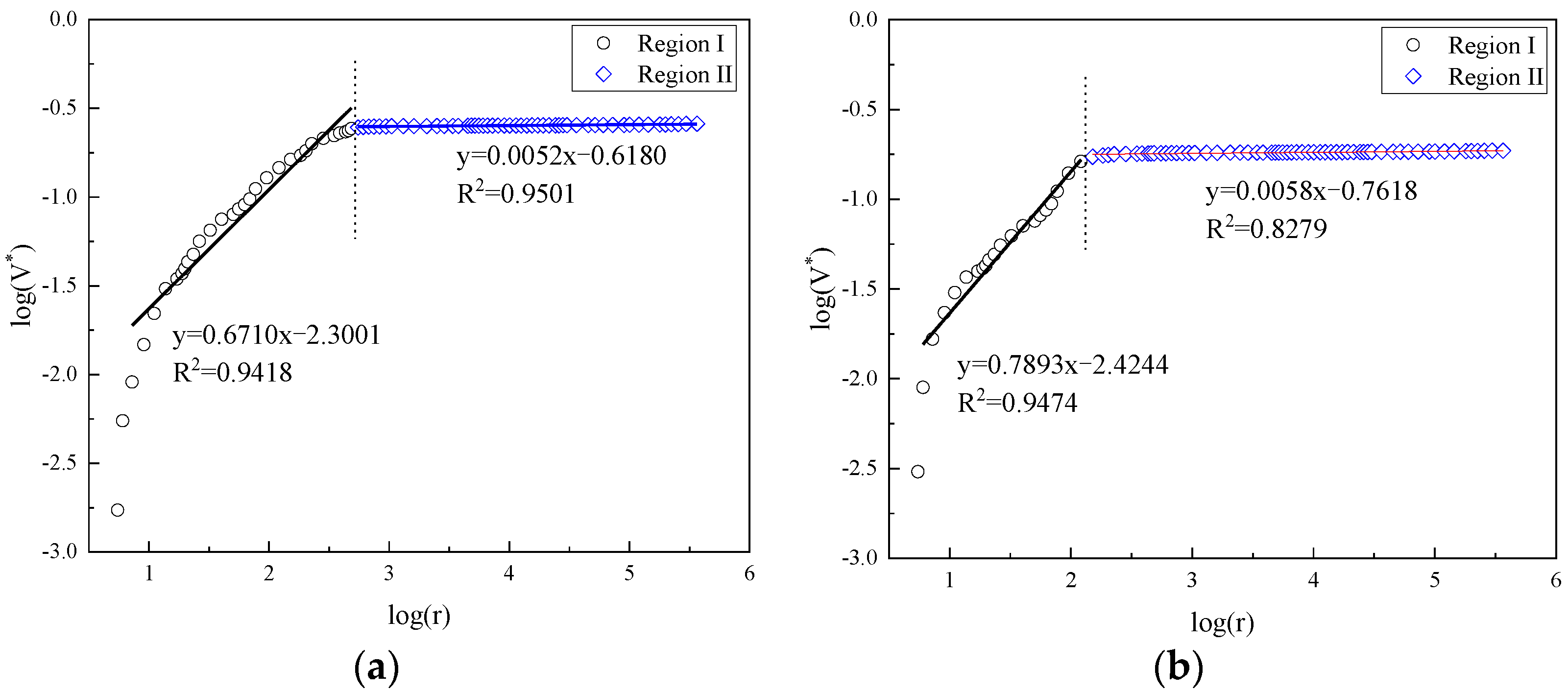
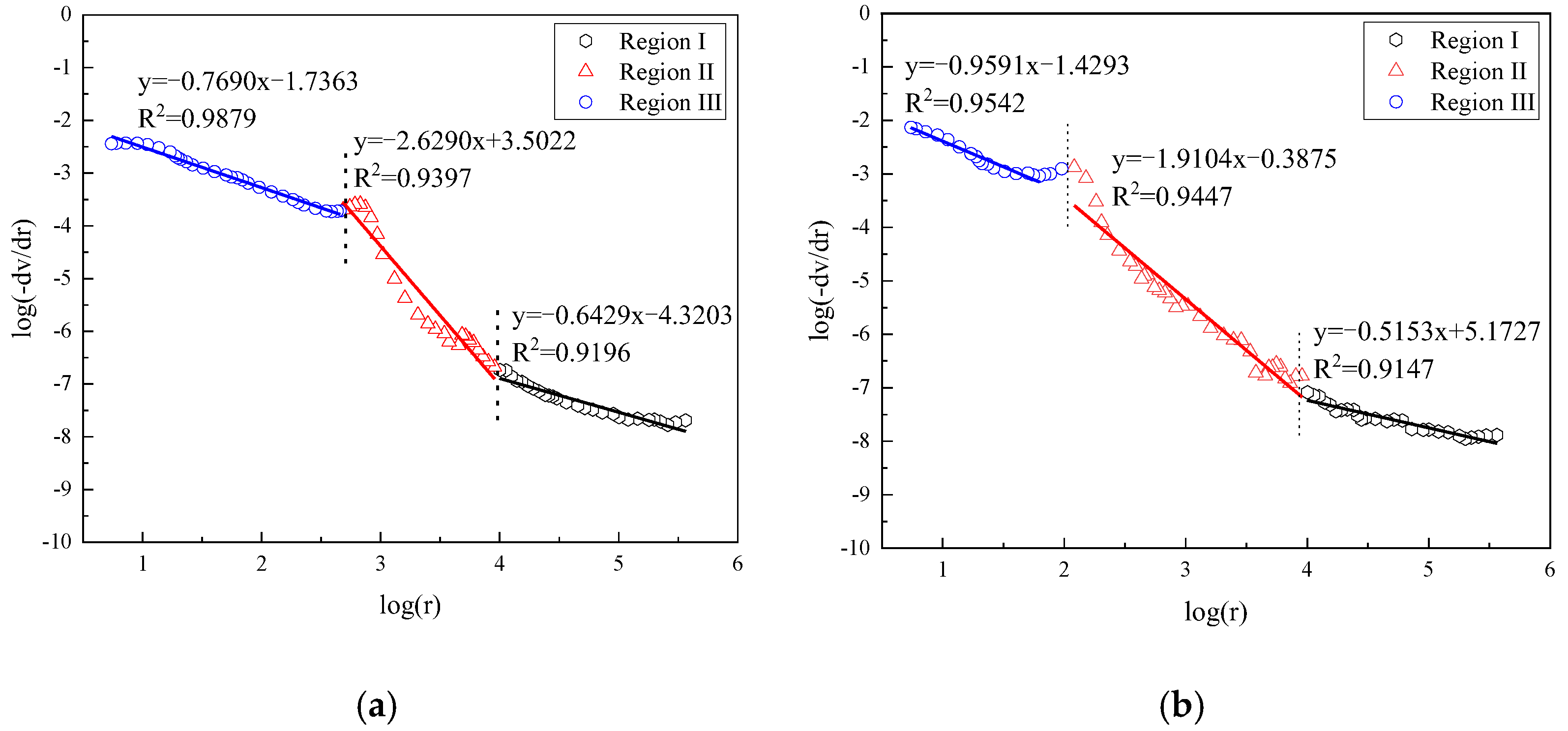
3.3. Analysis of Fractal Characteristics of Different Types of Cement Pastes Using Pfeifer and Avnir’s Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.J.; Cao, L. Chaos, Fractals and Their Applications; University of Science and Technology of China Press: Hefei, China, 1995; pp. 93–103. (In Chinese) [Google Scholar]
- Hou, D.; Li, D.; Hua, P.; Jiang, J.; Zhang, G. Statistical modelling of compressive strength controlled by porosity and pore size distribution for cementitious materials. Cem. Concr. Compos. 2019, 96, 11–20. [Google Scholar] [CrossRef]
- Li, D.; Li, Z.; Lv, C.; Zhang, G.; Yin, Y. A predictive model of the effective tensile and compressive strengths of concrete considering porosity and pore size. Constr. Build. Mater. 2018, 170, 520–526. [Google Scholar] [CrossRef]
- Panesar, D.K.; Francis, J. Influence of limestone and slag on the pore structure of cement paste based on mercury intrusion porosimetry and water vapour sorption measurements. Constr. Build. Mater. 2014, 52, 52–58. [Google Scholar] [CrossRef]
- Zeng, Q.; Luo, M.; Pang, X.; Li, L.; Li, K. Surface fractal dimension: An indicator to characterize the microstructure of cement-based porous materials. Appl. Surf. Sci. 2013, 282, 302–307. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, J. Fractal Characteristics of pore structure of hardened cement paste prepared by pressurized compact molding. Constr. Build. Mater. 2020, 259, 119856. [Google Scholar] [CrossRef]
- Tang, S.; Huang, J.; Duan, L.; Yu, P.; Chen, E. A review on fractal footprint of cement-based materials. Powder Technol. 2020, 370, 237–250. [Google Scholar] [CrossRef]
- Winslow, D.N. The fractal nature of the surface of cement paste. Cem. Concr. Res. 1985, 15, 817–824. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, J.; Han, S. Fractal analysis of relation between strength and pore structure of hardened mortar. Constr. Build. Mater. 2017, 135, 1–7. [Google Scholar] [CrossRef]
- Atzeni, C.; Pia, G.; Sanna, U. A geometrical fractal model for the porosity and permeability of hydraulic cement pastes. Constr. Build. Mater. 2010, 24, 1843–1847. [Google Scholar] [CrossRef]
- An, Q.; Chen, X.; Wang, H.; Yang, H.; Yang, Y. Segmentation of concrete cracks by using fractal dimension and UHK-net. Fractal Fract. 2022, 6, 95. [Google Scholar] [CrossRef]
- Guzmán-Castañeda, J.I.; García-Bórquez, A.; Arizabalo-Salas, R.D. Fractal dimension determined through optical and scanning elec tron microscopy on FeCrAl alloy after polishing, erosion, and oxidizing processes. Phys. Status Solidi B 2012, 249, 1224–1228. [Google Scholar] [CrossRef]
- Stanczak, G. Fractal Analysis of the Pore Space in Sandstones as Derived from Mercury Porosimetry and Image Analysis. In Proceedings of the International Multidisciplinary Microscopy Congress, Antalya, Turkey, 10–13 October 2014. [Google Scholar] [CrossRef]
- Bernardes, E.E.; Carrasco, E.V.M.; Vasconcelos, W.; de Magalhães, A.G. X-ray microtomography (μ-CT) to analyze the pore structure of a Portland cement composite based on the selection of different regions of interest. Constr. Build. Mater. 2015, 95, 703–709. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, R.; Ma, S.; Yang, X.; Wang, F. Fractal dimension of concrete meso-structure based on X-ray computed tomography. Powder Technol. 2019, 350, 91–99. [Google Scholar] [CrossRef]
- Tang, S.; Cai, X.; He, Z.; Shao, H.; Li, Z.; Chen, E. Hydration process of fly ash blended cement pastes by impedance measurement. Constr. Build. Mater. 2016, 113, 939–950. [Google Scholar] [CrossRef]
- Wang, F.; Li, S. Determination of the surface fractal dimension for porous media by capillary condensation. Ind. Eng. Chem. Res. 1997, 36, 1598–1602. [Google Scholar] [CrossRef]
- Ji, Y.; Sun, Z.; Jiang, X.; Liu, Y.; Shui, L.; Chen, C. Fractal characterization on pore structure and analysis of fluidity and bleeding of fresh ce ment paste based on 1H low-field NMR. Constr. Build. Mater. 2017, 140, 445–453. [Google Scholar] [CrossRef]
- Wang, L.; Song, X.; Yang, H.; Wang, L.; Tang, S.; Wu, B.; Mao, W. Pore structural and fractal analysis of the effects of MgO reactivity and dosage on permeability and F–T resistance of concrete. Fractal Fract. 2022, 6, 113. [Google Scholar] [CrossRef]
- Ma, H. Mercury intrusion porosimetry in concrete technology: Tips in measurement, pore structure parameter acquisition and application. J. Porous Mater. 2014, 21, 207–215. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Liu, W.; Liu, X.F. Scale-dependent nature of the surface fractal dimension for bi- and multi-disperse porous sol ids by mercury porosimetry. Appl. Surf. Sci. 2006, 253, 1349–1355. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three. I: Fractal theory of heterogeneous surfaces. J. Chem. Phys. 1983, 79, 3558–3565. [Google Scholar] [CrossRef]
- Friesen, W.I.; Mikula, R.J. Fractal dimensions of coal particles. J. Colloid Interface Sci. 1987, 120, 263–271. [Google Scholar] [CrossRef]
- Usteri, M.; Bonny, J.D.; Leuenberger, H. Fractal dimension of porous solid dosage forms. Pharm. Acta Helvetiae. 1990, 65, 55–61. [Google Scholar]
- Ji, X.; Chan, S.; Feng, N. Fractal model for simulating the space-filling process of cement hydrates nd fractal dimen sions of pore structure of cement-based materials. Cem. Concr. Res. 1997, 27, 1691–1699. [Google Scholar] [CrossRef]
- Neimark, A. A new approach to the determination of the surface fractal dimension of porous solids. Phys. A 1992, 191, 258–262. [Google Scholar] [CrossRef]
- Lange, D.; Jennings, H.M.; Shah, S.P. Image analysis techniques for characterization of pore structure of cement-based ma terials. Cem. Concr. Res. 1994, 24, 841–885. [Google Scholar] [CrossRef]
- Livingston, R.A. Fractal nucleation and growth model for the hydration of tricalcium silicate. Cem. Concr. Res. 2000, 30, 1853–1860. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; De Schutter, G.; Ye, G.; Sun, W. Fractal and multifractal analysis on pore structure in cement paste. Constr. Build. Mater. 2014, 69, 253–261. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-Chong, T.; Dangla, P. Surface fractal analysis of pore structure of high-volume fly-ash cement pastes. Appl. Surf. Sci. 2010, 257, 762–768. [Google Scholar] [CrossRef]
- Yu, L.H.; Ou, H.; Duan, Q.P. Fractal dimension of perlite doped cement stone pores and its relationship with pore structure and strength. J. Mater. Sci. Eng. 2007, 25, 201–205. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; He, X.; Wei, J.; Zhang, W.; Zhang, H.; Guo, S. Fractal dimension of pore volume of fly ash-cement slurry and its relationship with pore structure and strength. J. Chin. Ceram. Soc. 2003, 31, 774–779. (In Chinese) [Google Scholar] [CrossRef]
- Wei, J.X.; Yu, Q.J.; Zeng, X.X.; Bai, R.Y. Study of fractal dimension of pore structure in concrete. J. South China Univ. Technol. 2007, 35, 121–124. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.-Z.; Wang, X.; Jin, Z.-C.; Meng, Q.-S.; Zhu, C.-Q.; Wang, R. Shear characteristics of calcareous gravelly soil. Bull. Eng. Geol. Environ. 2017, 76, 561–573. [Google Scholar] [CrossRef]
- Wang, X.; Weng, Y.; Wei, H.; Meng, Q.; Hu, M. Particle obstruction and crushing of dredged calcareous soil in the Nansha Islands, South China Sea. Eng. Geol. 2019, 261, 105274. [Google Scholar] [CrossRef]
- Zhang, L.; Niu, D.; Wen, B.; Fu, Q.; Peng, G.; Su, L.; Blackwood, D.J. Initial-corrosion condition behavior of the Cr and Al alloy steel bars in coral concrete for marine construction. Cem. Concr. Compos. 2021, 120, 104051. [Google Scholar] [CrossRef]
- Da, B.; Chen, Y.; Yu, H.; Ma, H.; Chen, D.; Wu, Z.; Liu, J.; Li, Y. Preparation technology, mechanical properties and durability of coral aggregate seawater concrete in the island-reef environment. J. Clean. Prod. 2022, 339, 130572. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Hu, M.; Zhu, C.; Meng, Q.; Wang, R. Study of permeability of calcareous silty layer of foundation at an artificial reclamation island. Rock Soil Mech. 2017, 38, 3127–3135. (In Chinese) [Google Scholar] [CrossRef]
- Guo, M.L.; Xiao, J.; Zuo, S.H. Multifractal Analysis on Pore Structure of Cement-Based Materials Blended with Ground. Limestone and Its Relationship with Permeability. J. Chin. Ceram. Soc. 2019, 47, 617–624. (In Chinese) [Google Scholar] [CrossRef]
- Chen, X.; Zhou, J.; Ding, N. Fractal characterization of pore system evolution in cementitious materials. KSCE J. Civ. Eng. 2015, 19, 719–724. [Google Scholar] [CrossRef]

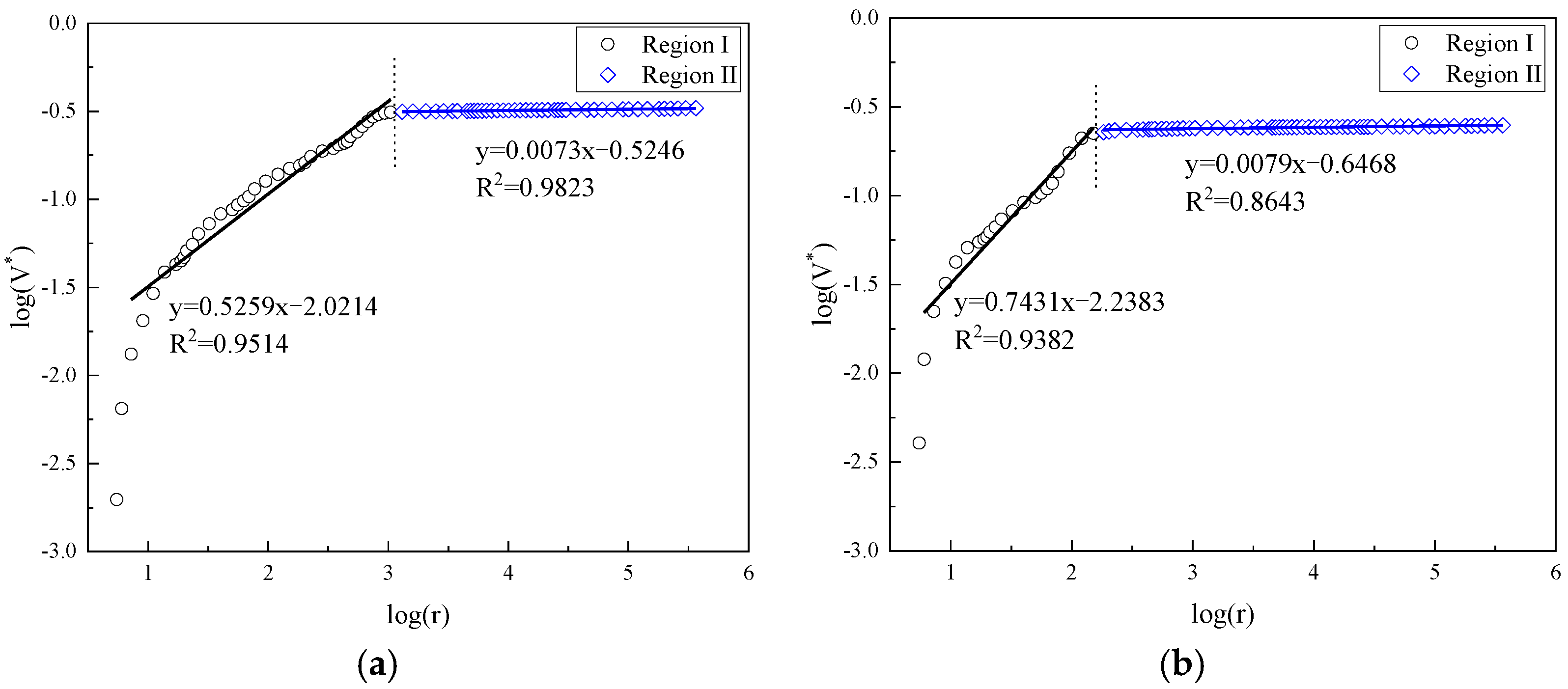
| Sample | SiO2 | CaO | Al2O3 | Fe2O3 | MgO | Na2O | SO3 | K2O | P2O5 | TiO2 | LOI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cement | 23.6 | 64.2 | 5.6 | 2.9 | 1.7 | 0.3 | 0.5 | - | - | - | 1.37 |
| Coral Powder | 2.5 | 53.3 | 0.2 | 0.8 | 1.7 | 0.1 | 0.2 | 0.1 | 0.1 | 0.04 | 39.8 |
| Sample NO. | W/C | Mass Fraction/% | ||
|---|---|---|---|---|
| Cement | Fine Coral Powder | Coarse Coral Powder | ||
| OPC0 | 0.5 | 100 | 0 | 0 |
| FCP10 | 90 | 10 | 0 | |
| FCP30 | 70 | 30 | 0 | |
| CCP10 | 90 | 0 | 10 | |
| CCP30 | 70 | 0 | 30 | |
| Sample NO. | Age | Region I | Region II | Region III |
|---|---|---|---|---|
| OPC0 | 3 days | 2.7751 | 4.4236 | 2.8410 |
| FCP10 | 2.6855 | 4.0447 | 2.6891 | |
| FCP30 | 2.9970 | 4.6613 | 2.7639 | |
| CCP10 | 2.8954 | 4.4563 | 2.8351 | |
| CCP30 | 2.9160 | 6.3323 | 2.8378 | |
| OPC0 | 28 days | 2.8615 | 4.8661 | 2.7774 |
| FCP10 | 2.8935 | 4.5335 | 2.7202 | |
| FCP30 | 2.8036 | 4.7519 | 2.7787 | |
| CCP10 | 2.9263 | 4.5130 | 2.7905 | |
| CCP30 | 2.9026 | 4.8445 | 2.8227 |
| Sample NO. | Age | Region I | Region II |
|---|---|---|---|
| OPC0 | 3 days | 2.3290 | 2.9948 |
| FCP10 | 2.0137 | 2.9929 | |
| FCP30 | 2.0731 | 2.9917 | |
| CCP10 | 2.4741 | 2.9927 | |
| CCP30 | 2.2929 | 2.9939 | |
| OPC0 | 28 days | 2.2107 | 2.9942 |
| FCP10 | 2.0954 | 2.9922 | |
| FCP30 | 2.0487 | 2.9951 | |
| CCP10 | 2.2569 | 2.9921 | |
| CCP30 | 2.1942 | 2.9922 |
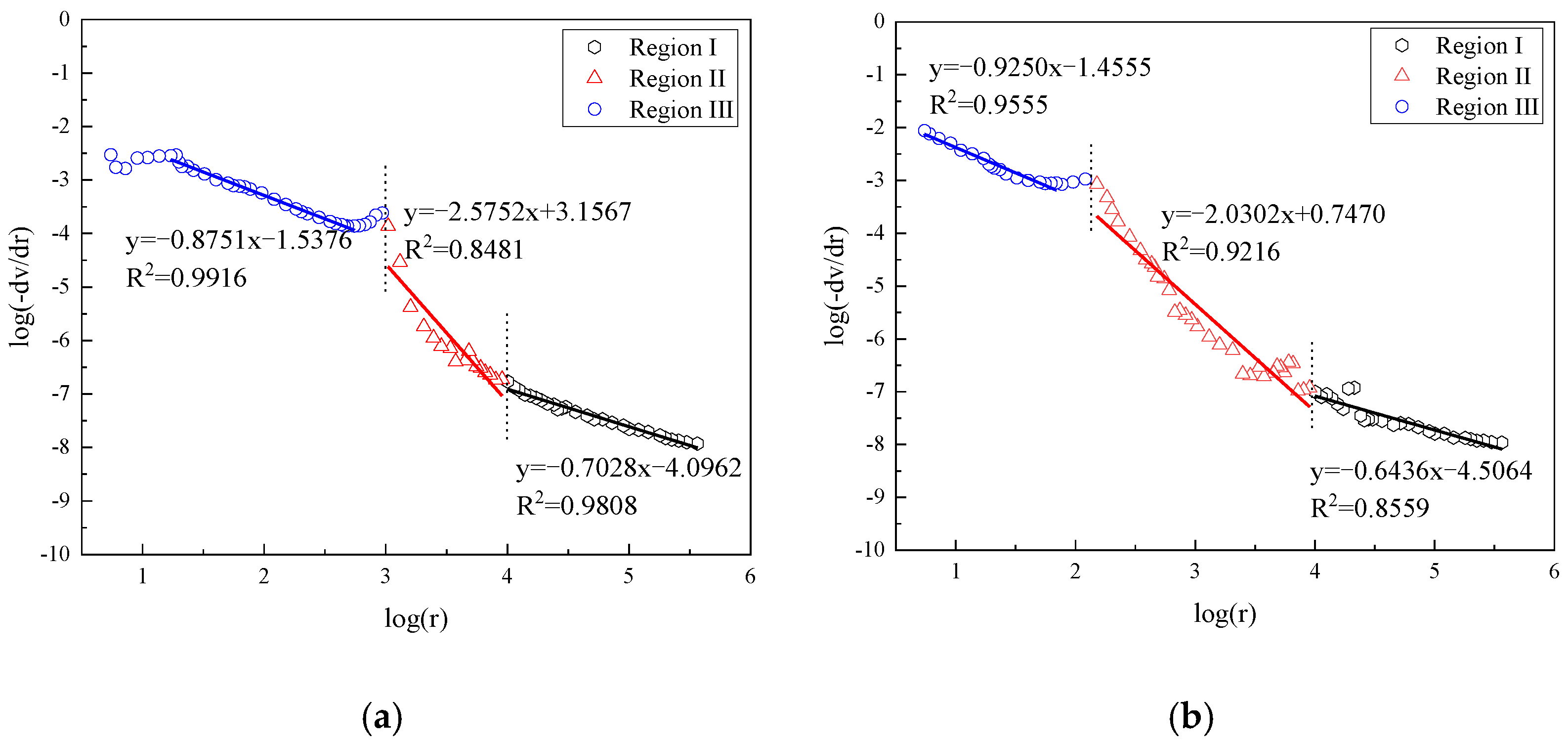
| Sample NO. | Age | Region I | Region II | Region III |
|---|---|---|---|---|
| OPC0 | 3 days | 2.7030 | 3.8545 | 2.4861 |
| FCP10 | 2.3889 | 4.6138 | 2.9342 | |
| FCP30 | 2.7294 | 4.0258 | 2.7854 | |
| CCP10 | 2.7690 | 4.6290 | 2.6429 | |
| CCP30 | 2.8751 | 4.5752 | 2.7028 | |
| OPC0 | 28 days | 2.6460 | 3.8253 | 2.5861 |
| FCP10 | 2.7447 | 4.3689 | 2.7037 | |
| FCP30 | 2.7444 | 3.8635 | 2.5536 | |
| CCP10 | 2.9591 | 3.9104 | 2.5153 | |
| CCP30 | 2.9250 | 4.0302 | 2.6436 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Qin, Q.; Yang, H.; Zhou, H.; Wu, K.; Wang, L. Fractal Characteristics of the Pore Structure of Coral Powder–Cement Slurry under Different Fractal Models. Fractal Fract. 2022, 6, 145. https://doi.org/10.3390/fractalfract6030145
Meng Q, Qin Q, Yang H, Zhou H, Wu K, Wang L. Fractal Characteristics of the Pore Structure of Coral Powder–Cement Slurry under Different Fractal Models. Fractal and Fractional. 2022; 6(3):145. https://doi.org/10.3390/fractalfract6030145
Chicago/Turabian StyleMeng, Qingshan, Qinglong Qin, Huamei Yang, Haoran Zhou, Kai Wu, and Lei Wang. 2022. "Fractal Characteristics of the Pore Structure of Coral Powder–Cement Slurry under Different Fractal Models" Fractal and Fractional 6, no. 3: 145. https://doi.org/10.3390/fractalfract6030145
APA StyleMeng, Q., Qin, Q., Yang, H., Zhou, H., Wu, K., & Wang, L. (2022). Fractal Characteristics of the Pore Structure of Coral Powder–Cement Slurry under Different Fractal Models. Fractal and Fractional, 6(3), 145. https://doi.org/10.3390/fractalfract6030145







