The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis
Abstract
1. Introduction
2. The SOV Method
2.1. Solution of
2.2. Solution of
3. The Exact Solution
4. The Cup-Mixing Average Concentration
4.1. (The Pipe Walls Act as a Perfect Sink)
4.2. (No Chlorine Consumption Takes Place at the Walls)
5. Results & Discussion
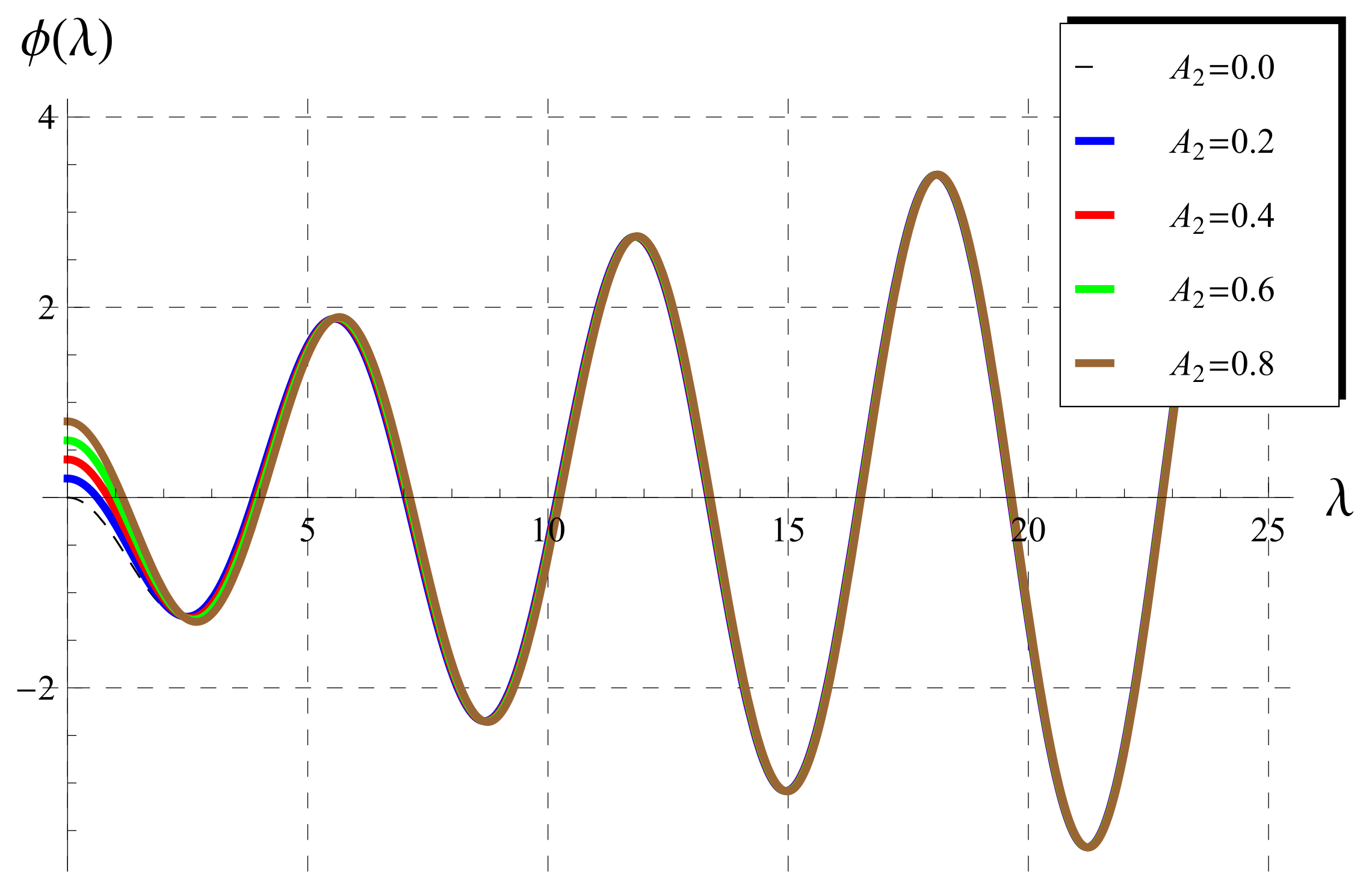
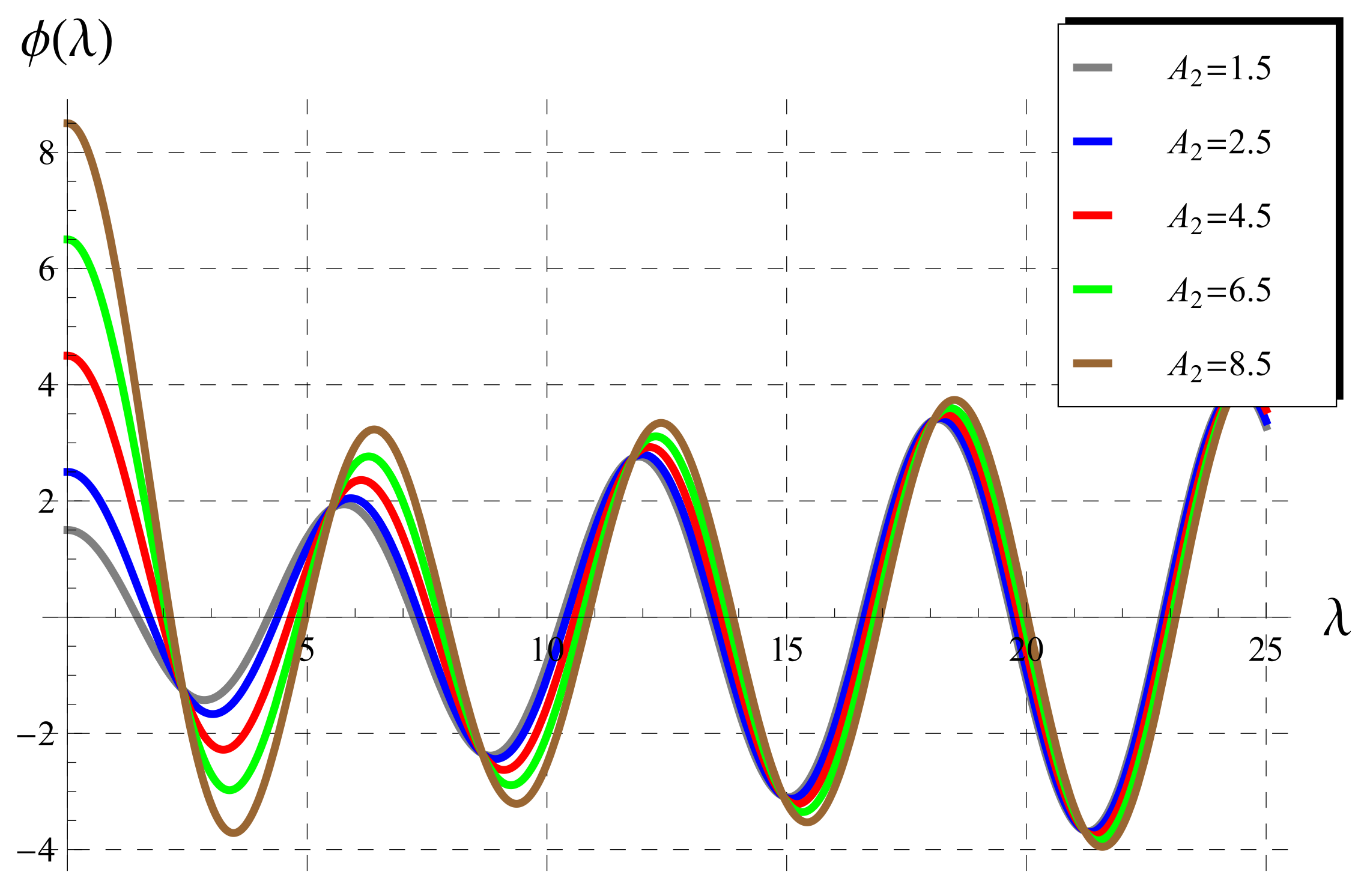
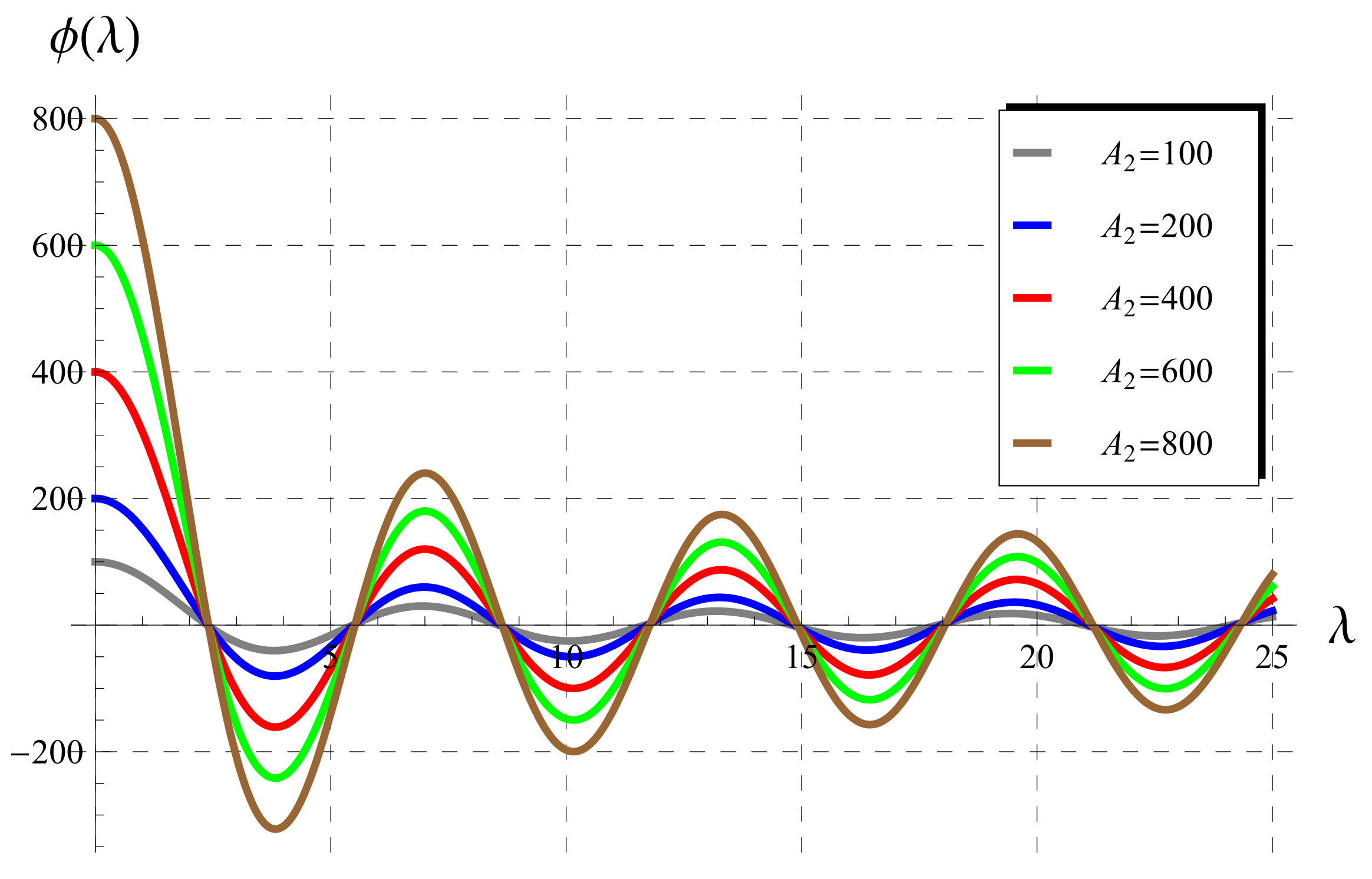
5.1. Behavior of
5.2. Experimental Values of (Wall Decay Rate)
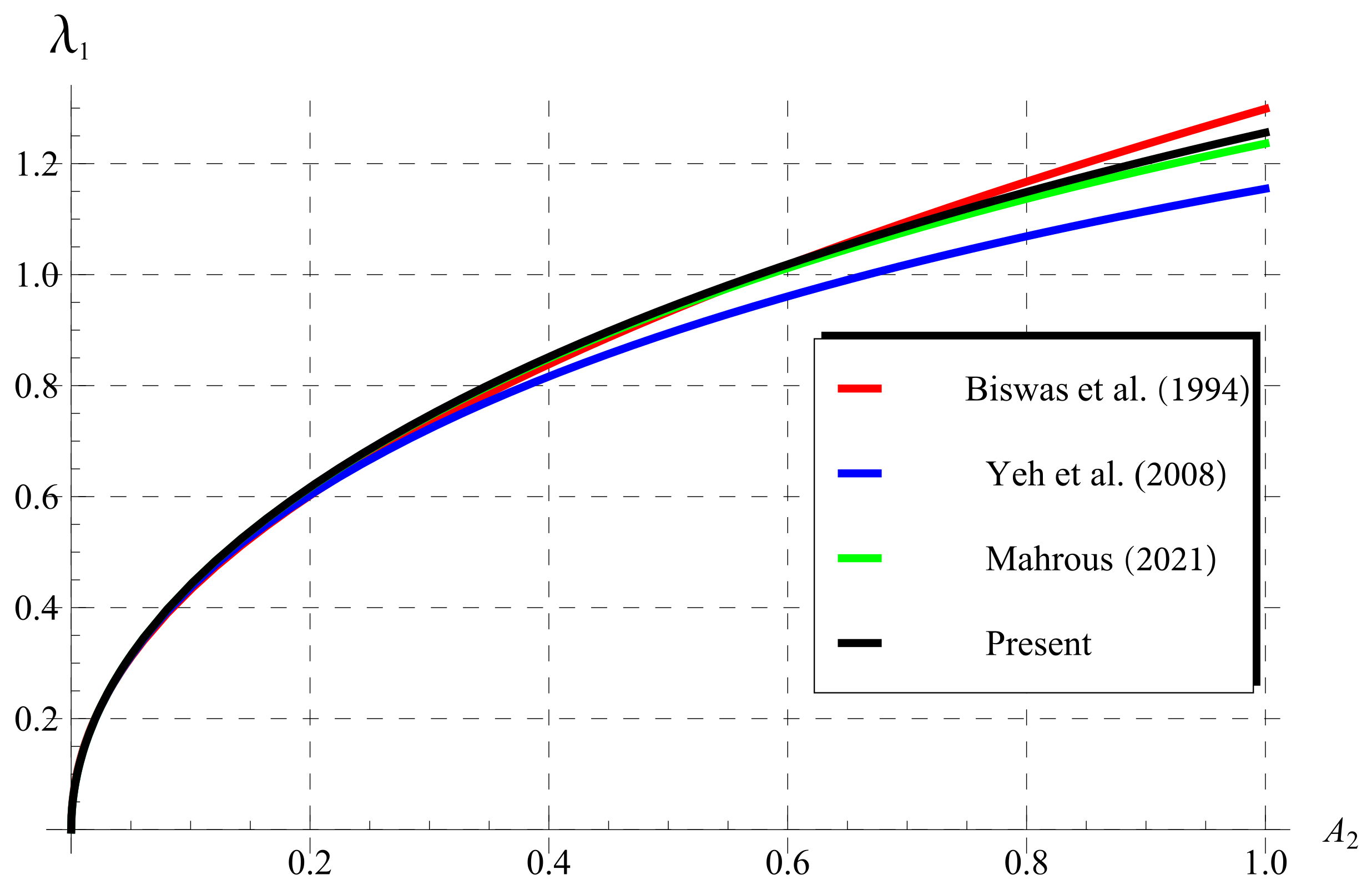
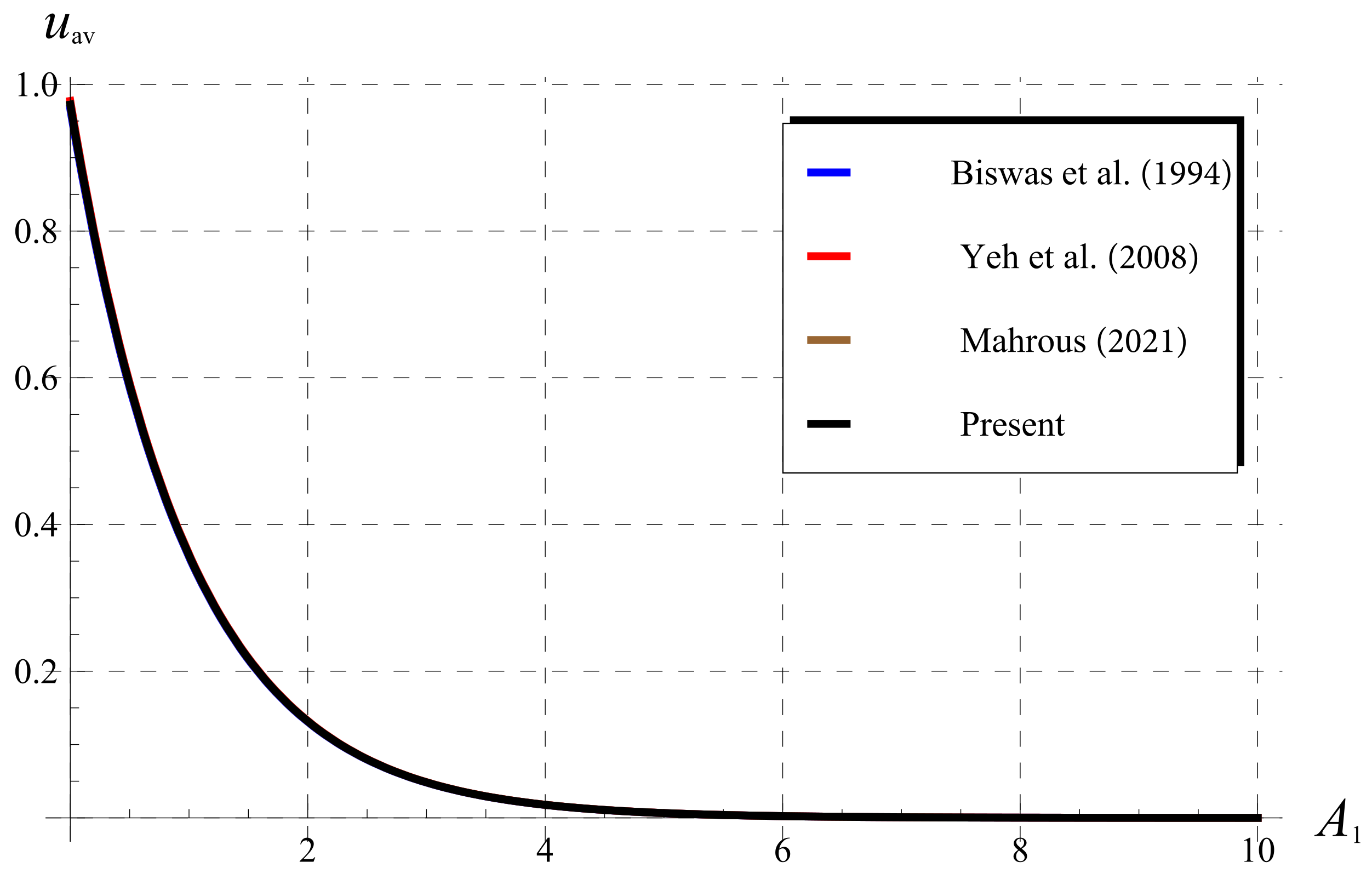
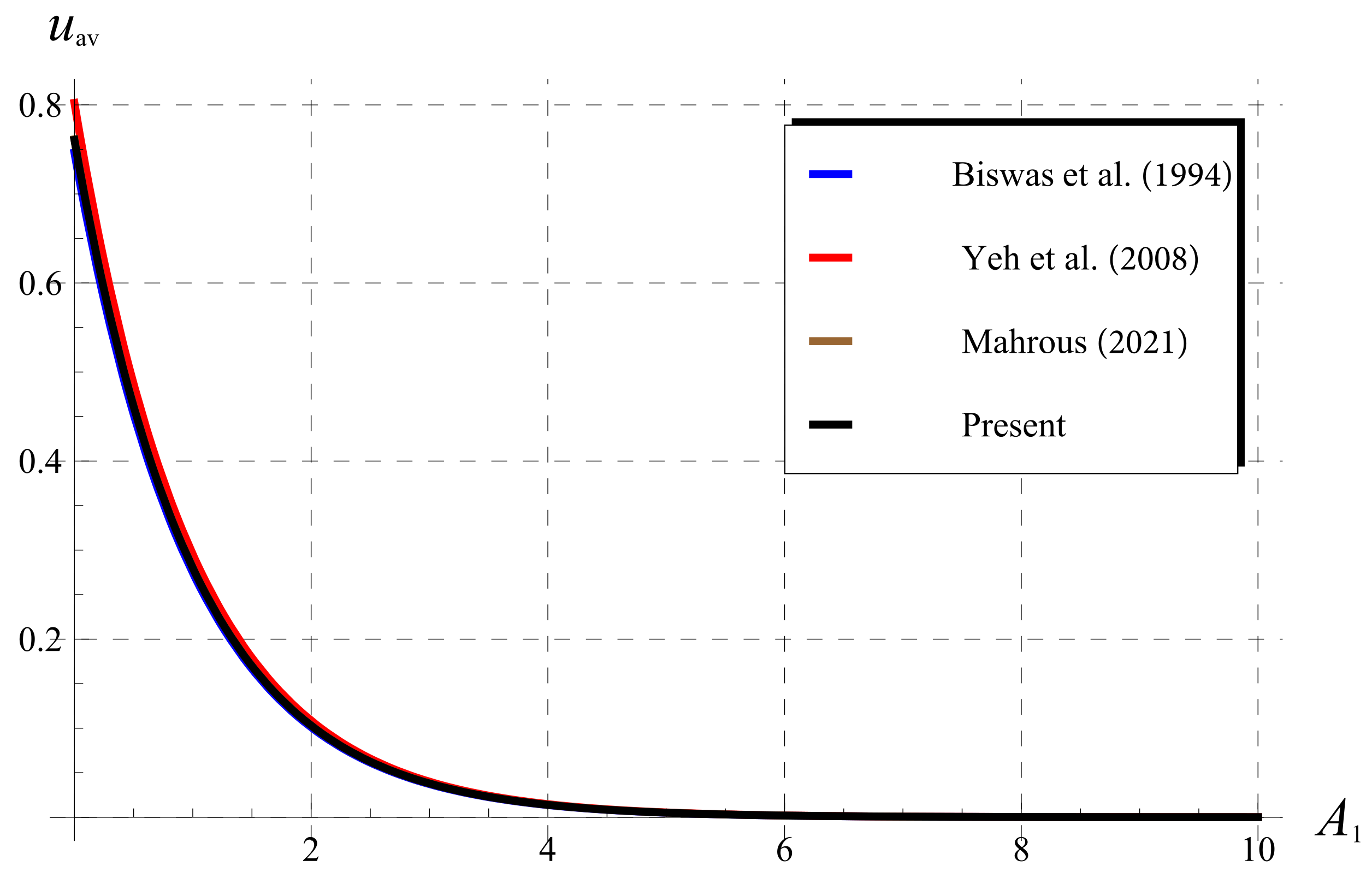
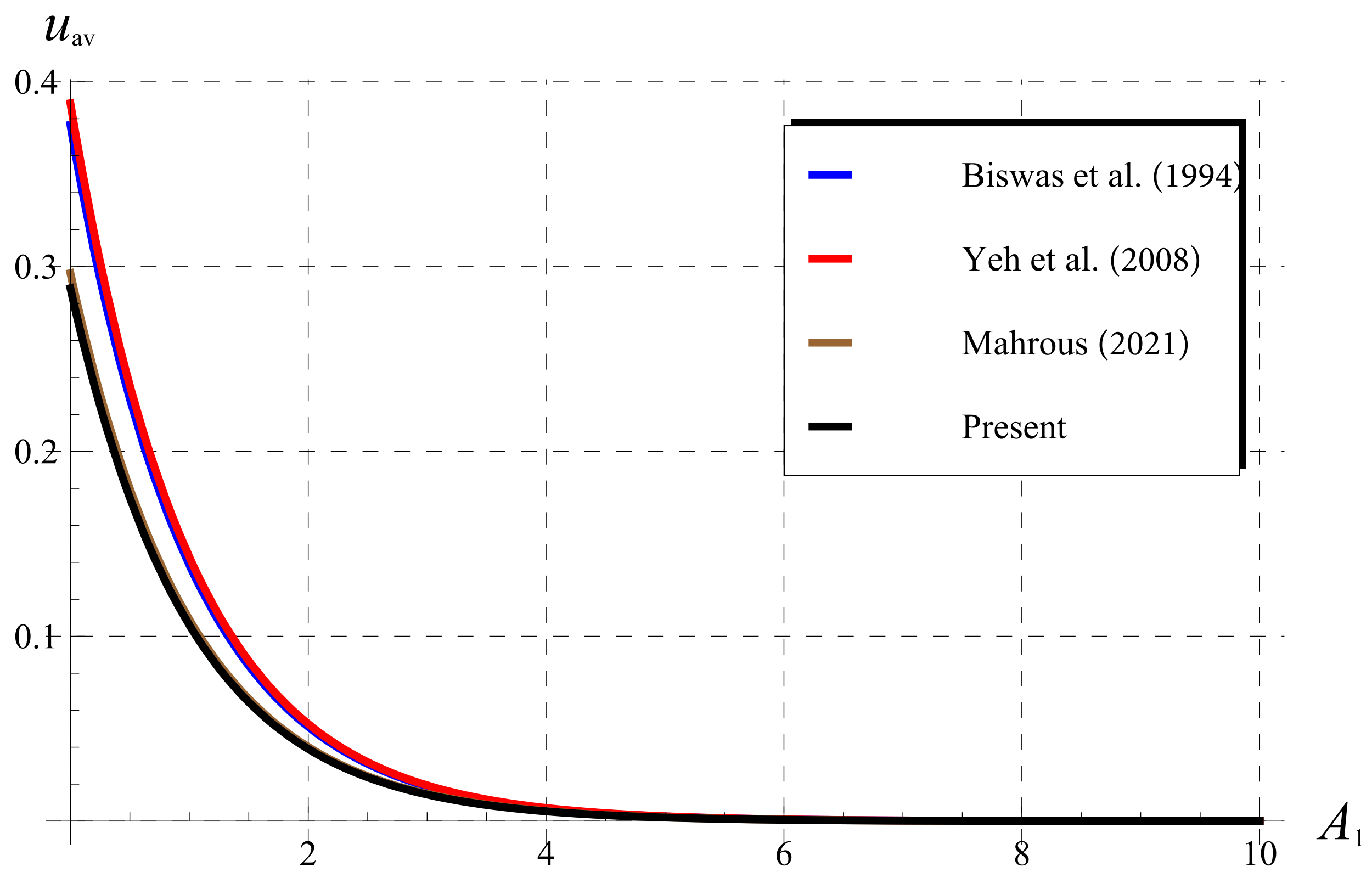
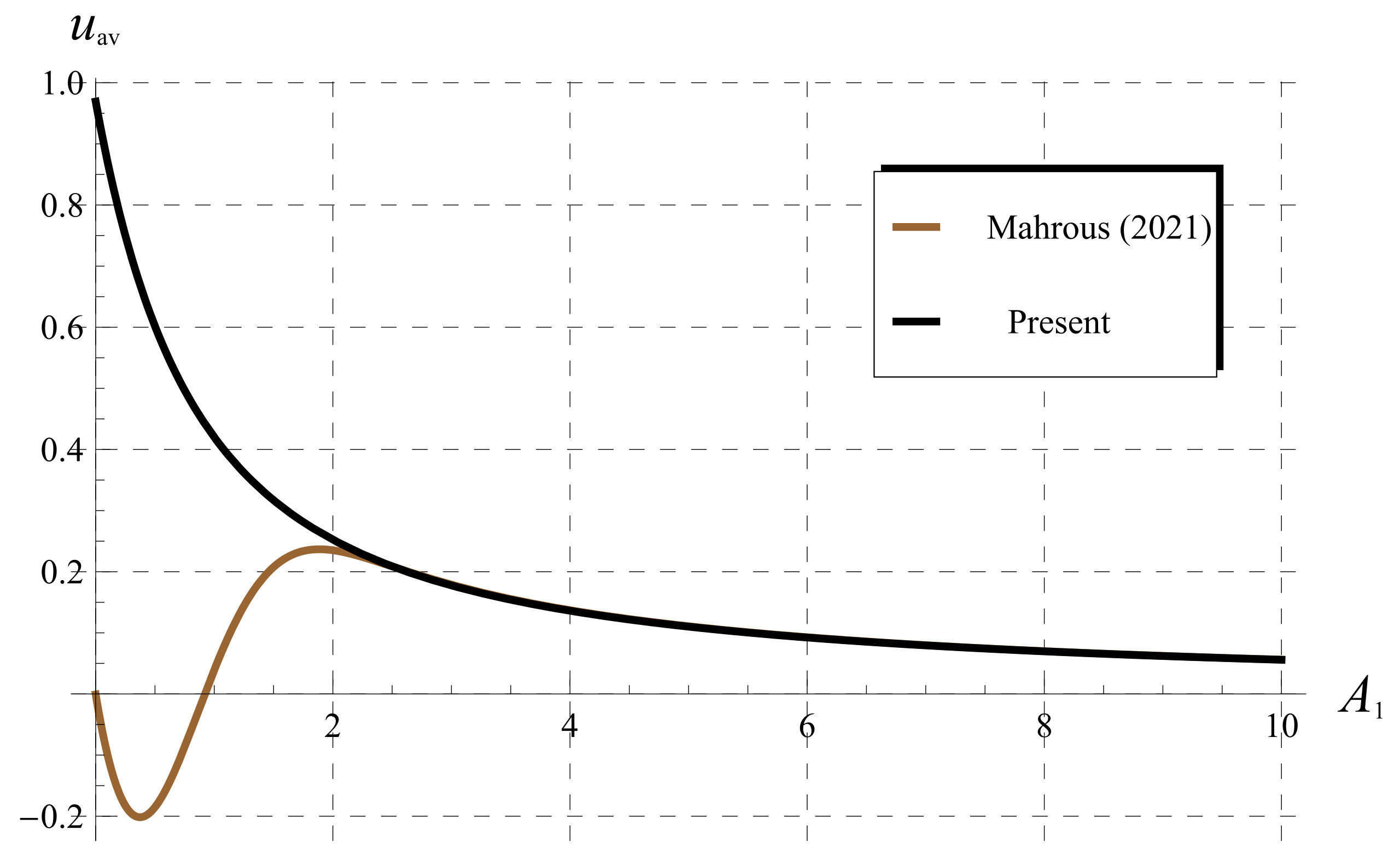
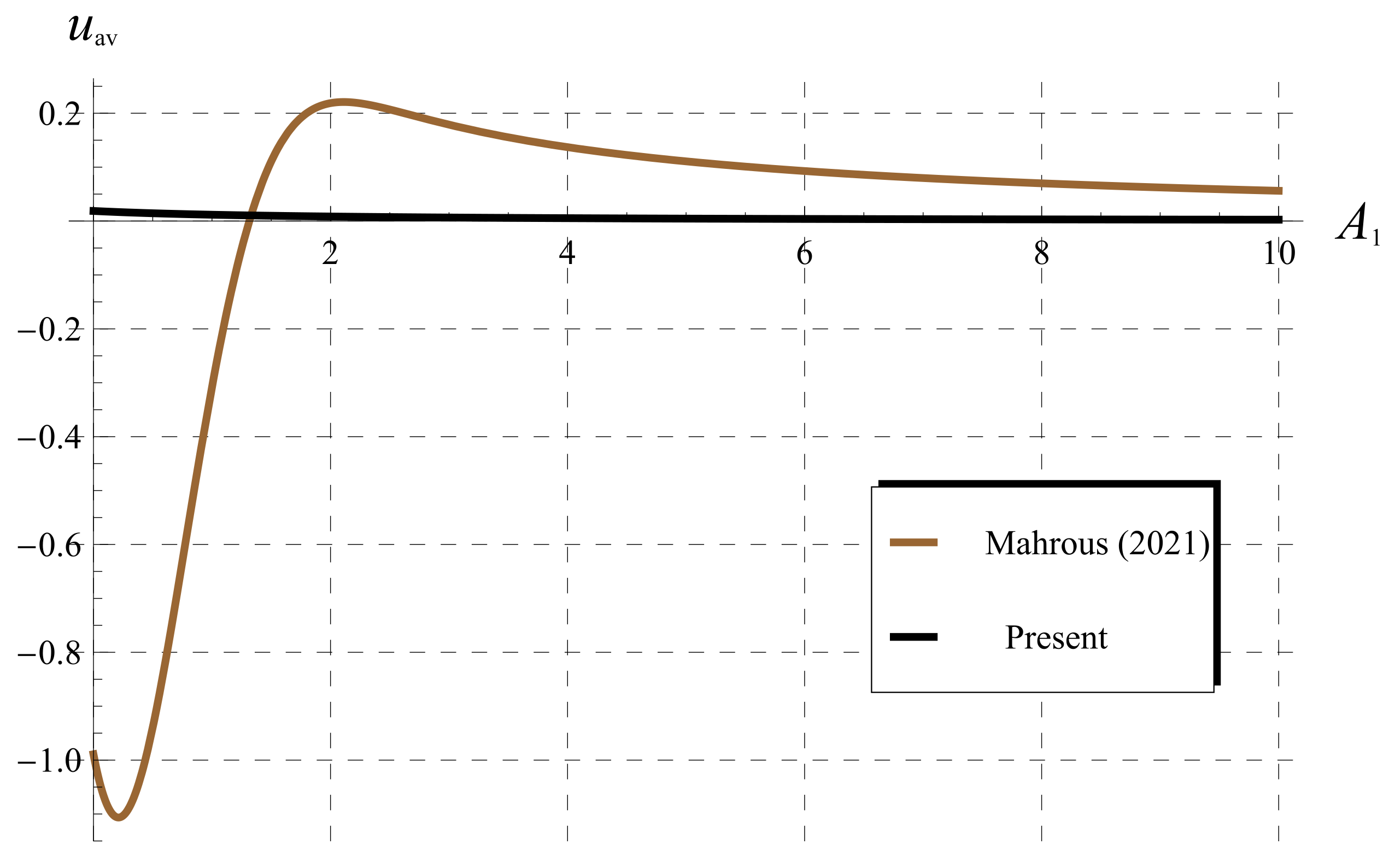
5.3. Comparisons as (Classical Chlorine Decay)
5.4. Comparisons for (Fractional Chlorine Decay)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clark, R.M.; Read, E.J.; Hoff, J.C. Analysis of Inactivation of Giardia Lamblia by Chlorine. J. Environ. Eng. 1989, 115, 80–90. [Google Scholar] [CrossRef]
- LeChevallier, M.W.; Cawthon, C.D.; Lee, R.G. Inactivation of biofilm bacteria. Appl. Environ. Microbiol. 1988, 54, 2492–2499. [Google Scholar] [CrossRef] [PubMed]
- Arnold, B.F.; Colford, J.M. Treating Water with Chlorine at Point-of-Use to Improve Water Quality and Reduce Child Diarrhea in Developing Countries: A Systematic Review and Meta-Analysis. Am. J. Trop. Med. Hyg. 2007, 76, 354–364. [Google Scholar] [CrossRef] [PubMed]
- Biswas, P.; Lu, C.; Clark, R.M. A model for chlorine concentration decay in pipes. Water Res. 1993, 27, 1715–1724. [Google Scholar] [CrossRef]
- Yeh, H.-D.; Wen, S.-B.; Chang, Y.-C.; Lu, C.-S. A new approximate solution for chlorine concentration decay in pipes. Water Res. 2008, 42, 2787–2795. [Google Scholar] [CrossRef]
- Mahrous, Y.M. Accurate approximation for the chlorine transport in pipe. Adv. Differ. Equ. Control Process. 2021, 25, 115–126. [Google Scholar] [CrossRef]
- Mahrous, Y.M. A possible generalized model of the chlorine concentration decay in pipes: Exact solution. Int. Anal. Appl. 2021, 19, 604–618. [Google Scholar] [CrossRef]
- Monteiro, L.; Viegas, R.; Covas, D.; Menaia, J. Assessment of Current Models Ability to Describe Chlorine Decay and Appraisal of Water Spectroscopic Data as Model Inputs. J. Environ. Eng. 2017, 143, 04016071. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y.J.; Shao, Y.; Neal, J.; Zhang, T. The dependence of chlorine decay and DBP formation kinetics on pipe flow properties in drinking water distribution. Water Res. 2018, 141, 32–45. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. New Model of Chlorine-Wall Reaction for Simulating Chlorine Concentration in Drinking Water Distribution Systems. Water Res. 2017, 125 (Suppl. C), 427–437. [Google Scholar] [CrossRef]
- Ozdemir, O.; Buyruk, T. Effect of travel time and temperature on chlorine bulk decay in water supply pipes. J. Environ. Eng. 2018, 144, 04018002. [Google Scholar] [CrossRef]
- Minaee, R.P.; Afsharnia, M.; Moghaddam, A.; Ebrahimi, A.A.; Askarishahi, M.; Mokhtari, M. Calibration of water quality model for distribution networks using genetic algorithm, particle swarm optimization, and hybrid methods. MethodsX 2019, 6, 540–548. [Google Scholar] [CrossRef] [PubMed]
- Minaee, R.P.; Afsharnia, M.; Moghaddam, A.; Ebrahimi, A.A.; Askarishahi, M.; Mokhtari, M. Wall decay coefficient estimation in a real-life drinking water distribution network. Water Resour. Manag. 2019, 33, 1557–1569. [Google Scholar] [CrossRef]
- Monteiro, L.; Carneiro, J.; Covas, D.I.C. Modelling chlorine wall decay in a full-scale water supply system. Urban Water J. 2020, 17, 754–762. [Google Scholar] [CrossRef]
- Moghaddam, A.; Mokhtari, M.; Afsharnia, M.; Minaee, R.P. Simultaneous Hydraulic and Quality Model Calibration of a Real-World Water Distribution Network. J. Water Resour. Plan. Manag. 2020, 146, 06020007. [Google Scholar] [CrossRef]
- Jakubowski, J.; Wisniewolski, M. On matching diffusions, Laplace transforms and partial differential equations. Stoch. Proc. Appl. 2015, 125, 3663–3690. [Google Scholar] [CrossRef][Green Version]
- Ebaid, A.; Sharif, M.A. Application of Laplace transform for the exact effect of a magnetic field on heat transfer of carbon-nanotubes suspended nanofluids. Z. Naturforsch. A 2015, 70, 471–475. [Google Scholar] [CrossRef]
- Ebaid, A.; Wazwaz, A.M.; Alali, E.; Masaedeh, B. Hypergeometric series solution to a class of second-order boundary value problems via Laplace transform with applications to nanofluids. Commun. Theor. Phys. 2017, 67, 231. [Google Scholar] [CrossRef]
- Ebaid, A.; Alali, E.; Saleh, H. The exact solution of a class of boundary value problems with polynomial coefficients and its applications on nanofluids. J. Assoc. Arab Univ. Basi Appl. Sci. 2017, 24, 156–159. [Google Scholar] [CrossRef]
- Khaled, S.M. The exact effects of radiation and joule heating on magnetohydrodynamic Marangoni convection over a flat surface. Therm. Sci. 2018, 22, 63–72. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Ebaid, A.; Cattani, C.; Juhani1, A.S.A.; El-Zahar, E.R. A novel exact solution for the fractional Ambartsumian equation. Adv. Differ. Equ. 2021, 2021, 88. [Google Scholar] [CrossRef]
- Handibag, S.; Karande, B.D. Laplace substitution method for solving partial differential equations involving mixed partial derivatives. Int. J. Comput. Eng. Res. 2012, 2, 1049–1052. [Google Scholar]
- Handibag, S.S.; Karande, B.D. Laplace substitution method for nth order linear and non-Linear PDE’s involving mixed partial derivatives. Int. Res. J. Eng. Technol. 2015, 2, 378–388. [Google Scholar]
- Pavani, P.V.; Priya, U.L.; Reddy, B.A. Solving differential equations by using Laplace transforms. Int. J. Res. Anal. Rev. 2018, 5, 1796–1799. [Google Scholar]
- Dhunde, R.R.; Waghmare, G.L. Double Laplace iterative method for solving nonlinear partial differential equations. New Trends Math. Sci. 2019, 7, 138–149. [Google Scholar] [CrossRef]
- Mousa, A.; Elzaki, T.M. Solution of volterra integro-differential equations by triple Laplace transform, Irish Interdiscip. J. Sci. Res. 2019, 3, 67–72. [Google Scholar]
- Zhang, H.; Nadeem, M.; Rauf, A.; Hui, Z.G. A novel approach for the analytical solution of nonlinear time-fractional differential equations. Int. J. Numer. Meth. Heat Fluid Flow 2021, 31, 1069–1084. [Google Scholar] [CrossRef]
- Ebaid, A.; Al-Jeaid, H.K. The Mittag–Leffler Functions for a Class of First-Order Fractional Initial Value Problems: Dual Solution via Riemann-Liouville Fractional Derivative. Fractal Fract. 2022, 6, 85. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Kumar, A.; Das, S.; Mehrez, K. Geometric Properties of a Certain Class of Mittag-Leffler-Type Functions. Fractal Fract. 2022, 6, 54. [Google Scholar] [CrossRef]
- Alharb, W.; Hristova, S. New Series Solution of the Caputo Fractional Ambartsumian Delay Differential Equationation by Mittag-Leffler Functions. Mathematics 2021, 9, 157. [Google Scholar] [CrossRef]



| 0.01 | 0.14125 | 3.83431 | 7.01701 |
| 0.1 | 0.44168 | 3.85771 | 7.02983 |
| 0.2 | 0.61698 | 3.88351 | 7.04403 |
| 0.5 | 0.94077 | 3.95937 | 7.08638 |
| 1 | 1.25578 | 4.07948 | 7.15580 |
| 2 | 1.59945 | 4.29096 | 7.28839 |
| 5 | 1.98981 | 4.71314 | 7.61771 |
| 10 | 2.17950 | 5.03321 | 7.95688 |
| 50 | 2.35724 | 5.41120 | 8.48399 |
| 100 | 2.38090 | 5.46521 | 8.56783 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljohani, A.F.; Ebaid, A.; Algehyne, E.A.; Mahrous, Y.M.; Cattani, C.; Al-Jeaid, H.K. The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis. Fractal Fract. 2022, 6, 125. https://doi.org/10.3390/fractalfract6030125
Aljohani AF, Ebaid A, Algehyne EA, Mahrous YM, Cattani C, Al-Jeaid HK. The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis. Fractal and Fractional. 2022; 6(3):125. https://doi.org/10.3390/fractalfract6030125
Chicago/Turabian StyleAljohani, Abdulrahman F., Abdelhalim Ebaid, Ebrahem A. Algehyne, Yussri M. Mahrous, Carlo Cattani, and Hind K. Al-Jeaid. 2022. "The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis" Fractal and Fractional 6, no. 3: 125. https://doi.org/10.3390/fractalfract6030125
APA StyleAljohani, A. F., Ebaid, A., Algehyne, E. A., Mahrous, Y. M., Cattani, C., & Al-Jeaid, H. K. (2022). The Mittag-Leffler Function for Re-Evaluating the Chlorine Transport Model: Comparative Analysis. Fractal and Fractional, 6(3), 125. https://doi.org/10.3390/fractalfract6030125









