Asset Pricing Model Based on Fractional Brownian Motion
Abstract
:1. Introduction
2. Decomposition of Real Data
3. Classical Model and Orthogonalization
3.1. Classical Model and Result
3.2. Orthogonalization of Stochastic Processes
4. Modelling of Fractional Brownian Motion
4.1. Solution of Single Risk Asset Model
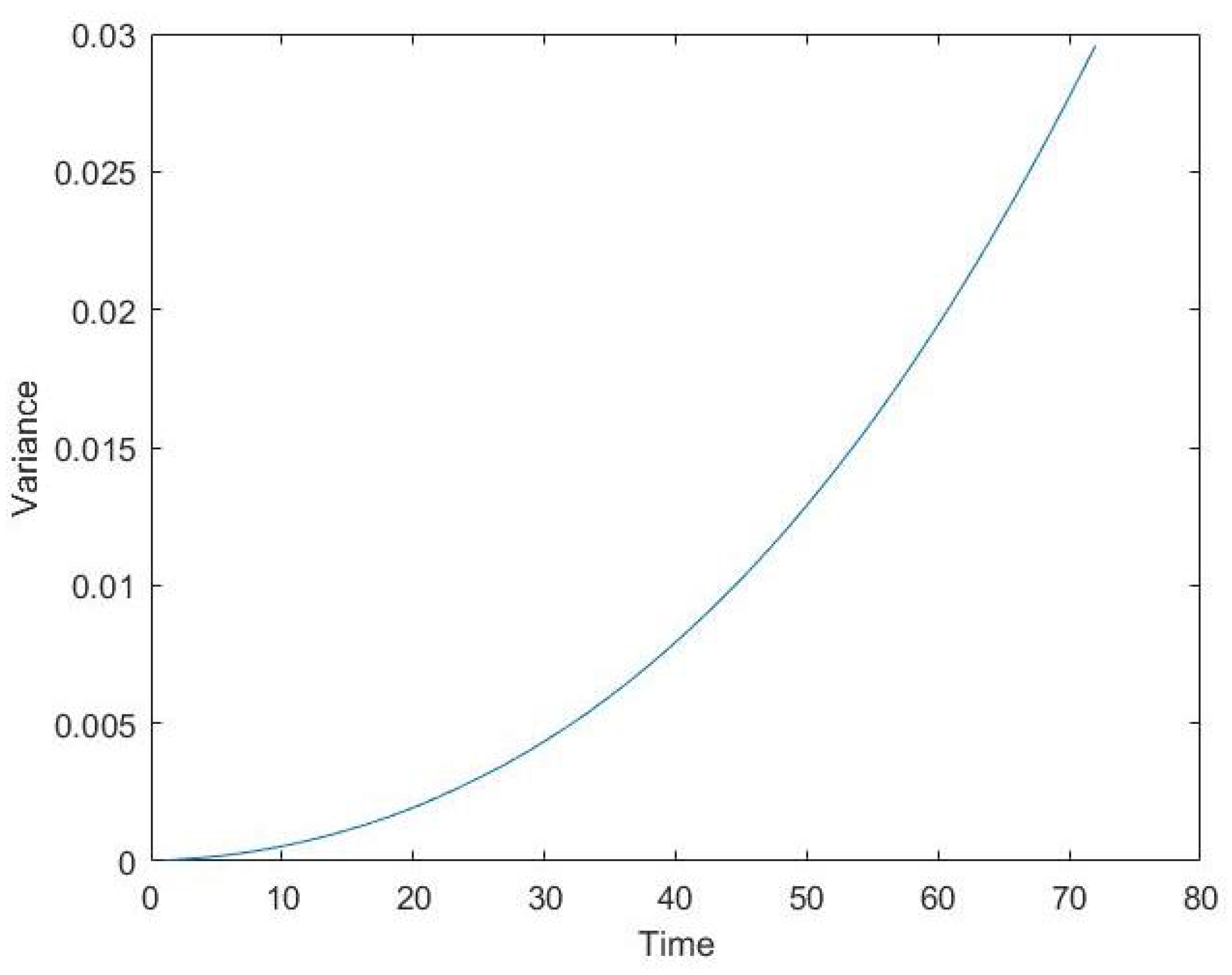
4.2. Comparison of Results and Numerical Simulations
4.3. Multidimensional Situation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Robustness Testing of Data Decomposition Results
| Variables | y1 | y2 | y3 | y4 | y5 | y6 |
|---|---|---|---|---|---|---|
| 3.95 × 10 | −1.12 × 10 | −3.79 × 10 | 1.35 × 10 *** | 1.89 × 10 *** | 1.53 × 10 *** | |
| 2.74 × 10 | 9.54 × 10 | 2.68 × 10 | 1.18 × 10 | 2.28 × 10 | 2.38 × 10 | |
| −0.00203 * | 0.00047 | 0.00146 | −0.000441 *** | −6.98 × 10 *** | −4.83 × 10 *** | |
| 0.00103 | 0.000361 | 0.00101 | 4.44 × 10 | 8.61 × 10 | 8.98 × 10 | |
| 0.0569 ** | −0.0118 | −0.0328 | 0.00952 *** | 0.00179 *** | 0.00117 *** | |
| 0.0242 | 0.00844 | 0.0237 | 0.00104 | 0.000201 | 0.00021 | |
| −0.184 ** | 0.0373 | 0.0972 | −0.0271 *** | −0.00490 *** | −0.00307 *** | |
| 0.0754 | 0.0263 | 0.0739 | 0.00324 | 0.000628 | 0.000655 | |
| 0.186 ** | −0.037 | −0.0893 | 0.0250 *** | 0.00470 *** | 0.00299 *** | |
| 0.0751 | 0.0262 | 0.0736 | 0.00323 | 0.000625 | 0.000652 | |
| Constant | −0.0540 ** | 0.0166 * | 0.0355 | −0.00711 *** | −0.00138 *** | −0.000865 *** |
| 0.0253 | 0.00881 | 0.0248 | 0.00109 | 0.000211 | 0.000219 | |
| Observations | 120 | 120 | 120 | 120 | 120 | 120 |
| R-squared | 0.964 | 0.058 | 0.089 | 1 | 1 | 1 |
Appendix B. Details of Numerical Simulation
Appendix C. Proof
References
- Merton, R.C. An intertemporal capital asset pricing model. Econom. J. Econom. Soc. 1973, 41, 867–887. [Google Scholar] [CrossRef]
- Merton, R.C. Optimum consumption and portfolio rules in a continuous-time model. In Stochastic Optimization Models in Finance; Elsevier: Amsterdam, The Netherlands, 1975; pp. 621–661. [Google Scholar]
- Davis, M.H.; Norman, A.R. Portfolio selection with transaction costs. Math. Oper. Res. 1990, 15, 676–713. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C. A Jump-Diffusion Approach to Modeling Credit Risk and Valuing Defaultable Securities. Available at SSRN 39800 1997. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=39800 (accessed on 10 January 2022).
- Liu, J. Portfolio selection in stochastic environments. Rev. Financ. Stud. 2007, 20, 1–39. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Wienersche spiralen und einige andere interessante kurven in hilbertscen raum, cr (doklady). Acad. Sci. URSS (NS) 1940, 26, 115–118. [Google Scholar]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994; Volume 24. [Google Scholar]
- Rogers, L.C.G. Arbitrage with fractional Brownian motion. Math. Financ. 1997, 7, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Cheridito, P. Regularizing Fractional Brownian Motion with a View Towards Stock Price Modelling. Ph.D. Thesis, ETH Zurich, Zurich, Germany, 2001. [Google Scholar]
- Sottinen, T. Fractional Brownian motion, random walks and binary market models. Financ. Stochastics 2001, 5, 343–355. [Google Scholar] [CrossRef]
- Guasoni, P. No arbitrage under transaction costs, with fractional Brownian motion and beyond. Math. Financ. 2006, 16, 569–582. [Google Scholar] [CrossRef]
- Hu, Y.; Øksendal, B. Fractional white noise calculus and applications to finance. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2003, 6, 1–32. [Google Scholar] [CrossRef]
- Elliott, R.J.; Van Der Hoek, J. A general fractional white noise theory and applications to finance. Math. Financ. 2003, 13, 301–330. [Google Scholar] [CrossRef]
- Xiao, W.L.; Zhang, W.G.; Zhang, X.L.; Wang, Y.L. Pricing currency options in a fractional Brownian motion with jumps. Econ. Model. 2010, 27, 935–942. [Google Scholar] [CrossRef]
- Xiao, W.; Yu, J. Asymptotic theory for estimating drift parameters in the fractional Vasicek model. Econom. Theory 2019, 35, 198. [Google Scholar] [CrossRef] [Green Version]
- Jumarie, G. Merton’s model of optimal portfolio in a Black-Scholes Market driven by a fractional Brownian motion with short-range dependence. Insur. Math. Econ. 2005, 37, 585–598. [Google Scholar] [CrossRef]
- Miao, J.; Yang, X. Pricing model for convertible bonds: A mixed fractional Brownian motion with jumps. East Asian J. Appl. Math. 2015, 5, 222–237. [Google Scholar] [CrossRef]
- Shokrollahi, F.; Kılıçman, A. Actuarial approach in a mixed fractional Brownian motion with jumps environment for pricing currency option. Adv. Differ. Equs. 2015, 2015, 275. [Google Scholar] [CrossRef]
- Rao, B.P. Pricing geometric Asian power options under mixed fractional Brownian motion environment. Phys. A Stat. Mech. Its Appl. 2016, 446, 92–99. [Google Scholar]
- Shokrollahi, F.; Kılıçman, A.; Magdziarz, M. Pricing European options and currency options by time changed mixed fractional Brownian motion with transaction costs. Int. J. Financ. Eng. 2016, 3, 1650003. [Google Scholar] [CrossRef]
- Zhang, W.G.; Li, Z.; Liu, Y.J.; Zhang, Y. Pricing European Option Under Fuzzy Mixed Fractional Brownian Motion Model with Jumps. Comput. Econ. 2020, 58, 483–515. [Google Scholar] [CrossRef]
- Eom, C.; Oh, G.; Jung, W.S. Relationship between degree of efficiency and prediction in stock price changes. arXiv 2007, arXiv:0708.4178. [Google Scholar]
- Brock, W.A.; Sayers, C.L. Is the business cycle characterized by deterministic chaos? J. Monet. Econ. 1988, 22, 71–90. [Google Scholar] [CrossRef]
- Ashley, R.A.; Patterson, D.M. Linear versus nonlinear macroeconomies: A statistical test. Int. Econ. Rev. 1989, 30, 685–704. [Google Scholar] [CrossRef]
- Karuppiah, J.; Los, C.A. Wavelet multiresolution analysis of high-frequency Asian FX rates, Summer 1997. Int. Rev. Financ. Anal. 2005, 14, 211–246. [Google Scholar] [CrossRef]
- Wang, F.; Yamasaki, K.; Havlin, S.; Stanley, H.E. Statistical regularities of equity market activity. arXiv 2009, arXiv:0911.4258. [Google Scholar]
- Hassani, H.; Thomakos, D. A review on singular spectrum analysis for economic and financial time series. Stat. Its Interface 2010, 3, 377–397. [Google Scholar] [CrossRef]
- Onali, E.; Goddard, J. Are European equity markets efficient? New evidence from fractal analysis. Int. Rev. Financ. Anal. 2011, 20, 59–67. [Google Scholar] [CrossRef] [Green Version]
- Garnier, J.; Sølna, K. Correction to Black—Scholes formula due to fractional stochastic volatility. SIAM J. Financ. Math. 2017, 8, 560–588. [Google Scholar] [CrossRef] [Green Version]
- Caraiani, P. Nonlinear dynamics in CEE stock markets indices. Econ. Lett. 2012, 114, 329–331. [Google Scholar] [CrossRef]
- Bal, D.P.; Rath, B.N. Nonlinear causality between crude oil price and exchange rate: A comparative study of China and India. Energy Econ. 2015, 51, 149–156. [Google Scholar]
- Jin, X. The impact of 2008 financial crisis on the efficiency and contagion of Asian stock markets: A Hurst exponent approach. Financ. Res. Lett. 2016, 17, 167–175. [Google Scholar] [CrossRef]
- Bariviera, A.F. The inefficiency of Bitcoin revisited: A dynamic approach. Econ. Lett. 2017, 161, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.C. Liquidity and market efficiency in cryptocurrencies. Econ. Lett. 2018, 168, 21–24. [Google Scholar] [CrossRef]
- Takaishi, T. Rough volatility of Bitcoin. Financ. Res. Lett. 2020, 32, 101379. [Google Scholar] [CrossRef]
- Shintani, M.; Linton, O. Is there chaos in the world economy? A nonparametric test using consistent standard errors. Int. Econ. Rev. 2003, 44, 331–357. [Google Scholar] [CrossRef] [Green Version]
- Brock, W.A.; Hommes, C.H. A rational route to randomness. Econom. J. Econom. Soc. 1997, 65, 1059–1095. [Google Scholar] [CrossRef]
- Hommes, C.; Huang, H.; Wang, D. A robust rational route to randomness in a simple asset pricing model. J. Econ. Dyn. Control 2005, 29, 1043–1072. [Google Scholar] [CrossRef] [Green Version]
- Chiarella, C.; Dieci, R.; Gardini, L. Asset price and wealth dynamics in a financial market with heterogeneous agents. J. Econ. Dyn. Control 2006, 30, 1755–1786. [Google Scholar] [CrossRef]
- Sommervoll, D.E.; Borgersen, T.A.; Wennemo, T. Endogenous housing market cycles. J. Bank. Financ. 2010, 34, 557–567. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.; Lifshitz, E. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 1981; Volume 3. [Google Scholar]
- Chung, K.L.; Williams, R.J. Introduction to Stochastic Integration; Springer: Boston, MA, USA, 1990; Volume 2. [Google Scholar]
- Gollier, C.; Pratt, J.W. Risk vulnerability and the tempering effect of background risk. Econom. J. Econom. Soc. 1996, 64, 1109–1123. [Google Scholar] [CrossRef]
- Peiro, A. Skewness in financial returns. J. Bank. Financ. 1999, 23, 847–862. [Google Scholar] [CrossRef]
- Patton, A.J. On the out-of-sample importance of skewness and asymmetric dependence for asset allocation. J. Financ. Econom. 2004, 2, 130–168. [Google Scholar] [CrossRef] [Green Version]
- Aït-sahali, Y.; Brandt, M.W. Variable selection for portfolio choice. J. Financ. 2001, 56, 1297–1351. [Google Scholar] [CrossRef] [Green Version]
- Kimball, M.S. Standard risk aversion. Econom. J. Econom. Soc. 1993, 61, 589–611. [Google Scholar] [CrossRef]
- Kyle, A.S.; Xiong, W. Contagion as a wealth effect. J. Financ. 2001, 56, 1401–1440. [Google Scholar] [CrossRef]
- Aït-Sahalia, Y.; Lo, A.W. Nonparametric estimation of state-price densities implicit in financial asset prices. J. Financ. 1998, 53, 499–547. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, W.M.; Al Mafrachi, M. Do higher-order realized moments matter for cryptocurrency returns? Int. Rev. Econ. Financ. 2021, 72, 483–499. [Google Scholar] [CrossRef]
- Bhandari, R.; Das, S.R. Options on portfolios with higher-order moments. Financ. Res. Lett. 2009, 6, 122–129. [Google Scholar] [CrossRef]
| Variables | Consumption | BP500 | Tick_Shanghai |
|---|---|---|---|
| Obs | 120 | 2000 | 1200 |
| Mean | 0.0299677 | 0.0873281 | 0.0000137 |
| Std. Dev. | 0.0291915 | 0.0492139 | 8.78 × 10 |
| Min | 0.0000297 | 0.0001219 | 2.43 × 10 |
| Max | 0.0988004 | 0.1808946 | 0.0000294 |
| Begin | Jan-59 | 1 January 1976 | 1 December 2018 |
| End | Jan-19 | 30 April 2020 | 31 December 2018 |
| Variables | U. S. Consumption | BP500 | Tick_Shanghai |
|---|---|---|---|
| 2.19 × 10 *** | 2.83 × 10 *** | −5.96 × 10 *** | |
| 7.11 × 10 | 1.26 × 10 | 0 | |
| −0.000357 *** | −3.83 × 10 *** | 5.99 × 10 *** | |
| 2.69 × 10 | 1.83 × 10 | 2.69 × 10 | |
| 0.00476 *** | 0.00310 *** | −2.91 × 10 *** | |
| 6.29 × 10 | 0.000162 | 1.85 × 10 | |
| −0.0114 *** | −0.0166 *** | 1.37 × 10 *** | |
| 0.000196 | 0.00097 | 9.79 × 10 | |
| 0.00887 *** | 0.0287 *** | −1.88 × 10 *** | |
| 0.000195 | 0.00184 | 1.64 × 10 | |
| Constant | −0.00188 *** | −0.0255 *** | 1.01 × 10 *** |
| 6.57 × 10 | 0.00219 | 1.53 × 10 | |
| Observations | 120 | 2000 | 1200 |
| R-squared | 1 | 0.997 | 1 |
| [2] | [18,19,20,21,22] | This Paper | |
|---|---|---|---|
| Research Issues | |||
| Subject of Study | Any Financial Asset | Options | Any Financial Asset |
| Consider Personal Decisions | YES | NO | YES |
| Number of Assets | Multi-Asset | Single Asset | Multi-Asset |
| Stochastic Process | Brownian Motion | FBM | FBM |
| Solution Method | |||
| Solving Methods | Stochastic Optimal Control | Arbitrage Free Pricing | Stochastic Optimal Control |
| Core Lemma | Ito Lemma | Ito Integral | New Lemma |
| Expandability | |||
| DSGE Model | YES | NO | YES |
| Heterogeneous Agents Model | YES | NO | YES |
| Study Results | |||
| Difference from Reality | No Consideration of FBM | No Microfoundations | Imaginary Numbers |
| FBM is Included | NO | YES | YES |
| Economic Variable Correlation is Given | YES | NO | YES |
| Agent Welfare | |||
| Utility Value | −2.9227 | - | −2.1076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Wang, Y. Asset Pricing Model Based on Fractional Brownian Motion. Fractal Fract. 2022, 6, 99. https://doi.org/10.3390/fractalfract6020099
Yan Y, Wang Y. Asset Pricing Model Based on Fractional Brownian Motion. Fractal and Fractional. 2022; 6(2):99. https://doi.org/10.3390/fractalfract6020099
Chicago/Turabian StyleYan, Yu, and Yiming Wang. 2022. "Asset Pricing Model Based on Fractional Brownian Motion" Fractal and Fractional 6, no. 2: 99. https://doi.org/10.3390/fractalfract6020099
APA StyleYan, Y., & Wang, Y. (2022). Asset Pricing Model Based on Fractional Brownian Motion. Fractal and Fractional, 6(2), 99. https://doi.org/10.3390/fractalfract6020099






