An Optimal Adaptive Grid Method Based on L1 Scheme for a Nonlinear Caputo Fractional Differential Equation
Abstract
1. Introduction
2. Preliminary Results
3. Truncation Error Estimation
4. Monitor Function and Convergence Analysis
5. Numerical Experiments
5.1. Mesh Generation Algorithm
5.2. A Test Example and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Magin, R. Fractional Calculus in Bioengineering; Begell House Publishers: Redding, CA, USA, 2006. [Google Scholar]
- Kaur, A.; Takhar, P.S.; Smith, D.M.; Mann, J.E.; Brashears, M.M. Fractional differential equations based modeling of microbial survival and growth curves: Model development and experimental validation. Food Eng. Phys. Prop. 2008, 73, E403–E414. [Google Scholar] [CrossRef]
- Lokenath, D. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 54, 3413–3442. [Google Scholar]
- Jin, B.; Lazarov, R.; Pasciak, J.; Rundell, W. Variational formulation of problems involving fractional order differential operators. Math. Comput. 2015, 84, 2665–2700. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations. An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theroy and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Chen, C.-M.; Liu, F.; Anh, V.; Turner, I. Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equation. SIAM J. Sci. Comput. 2010, 32, 1740–1760. [Google Scholar] [CrossRef]
- Gao, G.; Sun, Z. A compact finite difference scheme for the fractional sub-diffusion equations. J. Comput. Phys. 2011, 230, 586–595. [Google Scholar] [CrossRef]
- Liao, H.; Li, D.; Zhang, J. Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numer. Anal. 2018, 56, 1112–1133. [Google Scholar] [CrossRef]
- Liao, H.; Mclean, W.; Zhang, J. A discrete Grönwall inequality with applications to numerical scheme for sudiffusion problems. SIAM J. Numer. Anal. 2019, 57, 218–237. [Google Scholar] [CrossRef]
- Gracia, J.L.; O’Riordan, E.; Stynes, M. A fitted scheme for a Caputo initial-boundary value problem. J. Sci. Comput. 2018, 76, 583–609. [Google Scholar] [CrossRef]
- Kopteva, N.; Meng, X. Error analysis for a fractional-derivative parabolic problem on quasi-graded meshes using barrier function. SIAM J. Numer. Anal. 2020, 58, 1217–1238. [Google Scholar] [CrossRef]
- Kopteva, N. Error analysis of the L1 method on graded and uniform meshes for a fractional-derivative problem in two and three dimensions. Math. Comput. 2019, 88, 2135–2155. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. Numerical methods for time-fractional evolution equations with nonsmooth data: A concise overvies. Comput. Methods Appl. Mech. Eng. 2019, 346, 332–358. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of the space fractional Fokker-Planck equation. J. Comput. Appl. Math. 2004, 166, 209–219. [Google Scholar] [CrossRef]
- Lynch, V.; Carreras, B.; del Castillo-Negrete, D.; Ferreira-Mejias, K.; Hicks, H. Numerical methods for the solution of partial differential equations of fractional order. J. Comput. Phys. 2003, 192, 406–421. [Google Scholar] [CrossRef]
- Du, R.; Cao, W.R.; Sun, Z.-Z. A compact difference scheme for the fractional diffusion-wave equation. Appl. Math. Model. 2010, 34, 2998–3007. [Google Scholar] [CrossRef]
- Du, R.; Yan, Y.; Liang, Z. A high-order scheme to approximate the Caputo fractional derivative and its application to solve the fractional diffusion wave equation. J. Comput. Phys. 2019, 376, 1312–1330. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J. Numer. Anal. 2016, 36, 197–221. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. Two fully discrete schemes for fractional diffusion and diffusion-wave equations with nonsmooth data. SIAM J. Sci. Comput. 2016, 38, A146–A170. [Google Scholar] [CrossRef]
- Brunner, H. Collocation Methods for Volterra Integral and Related Functional Equations Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Cen, Z.; Le, A.; Xu, A. A posteriori error analysis for a fractional differential equation. Int. J. Comput. Math. 2017, 94, 1185–1195. [Google Scholar] [CrossRef]
- Liu, L.-B.; Chen, Y. A posteriori error estimation and adaptive strategy for a nonlinear fractional differential equation. Int. J. Comput. Math. 2022, 99, 240–246. [Google Scholar] [CrossRef]
- Kopteva, N. Pointwise-in-time a posteriori errror control for time-fractional parabolic equations. Appl. Math. Lett. 2022, 123, 107515. [Google Scholar] [CrossRef]
- Liu, L.-B.; Liang, Z.; Long, G.; Liang, Y. Convergence analysis of a finite difference scheme for a Riemann-Liouville fractional derivative two-point boundary value problem on an adaptive grid. J. Comput. Appl. Math. 2020, 375, 112809. [Google Scholar] [CrossRef]
- Cen, Z.; Liu, L.-B.; Huang, J. A posteriori error estimation in maximum norm for a two-point boundary value problem with a Riemann Liouville fractional derivative. Appl. Math. Lett. 2020, 102, 106086. [Google Scholar] [CrossRef]
- Huang, J.; Cen, Z.; Liu, L.B.; Zhao, J. An efficient numerical method for a Riemann-Liouville two-point boundary value problem. Appl. Math. Lett. 2020, 103, 106201. [Google Scholar] [CrossRef]
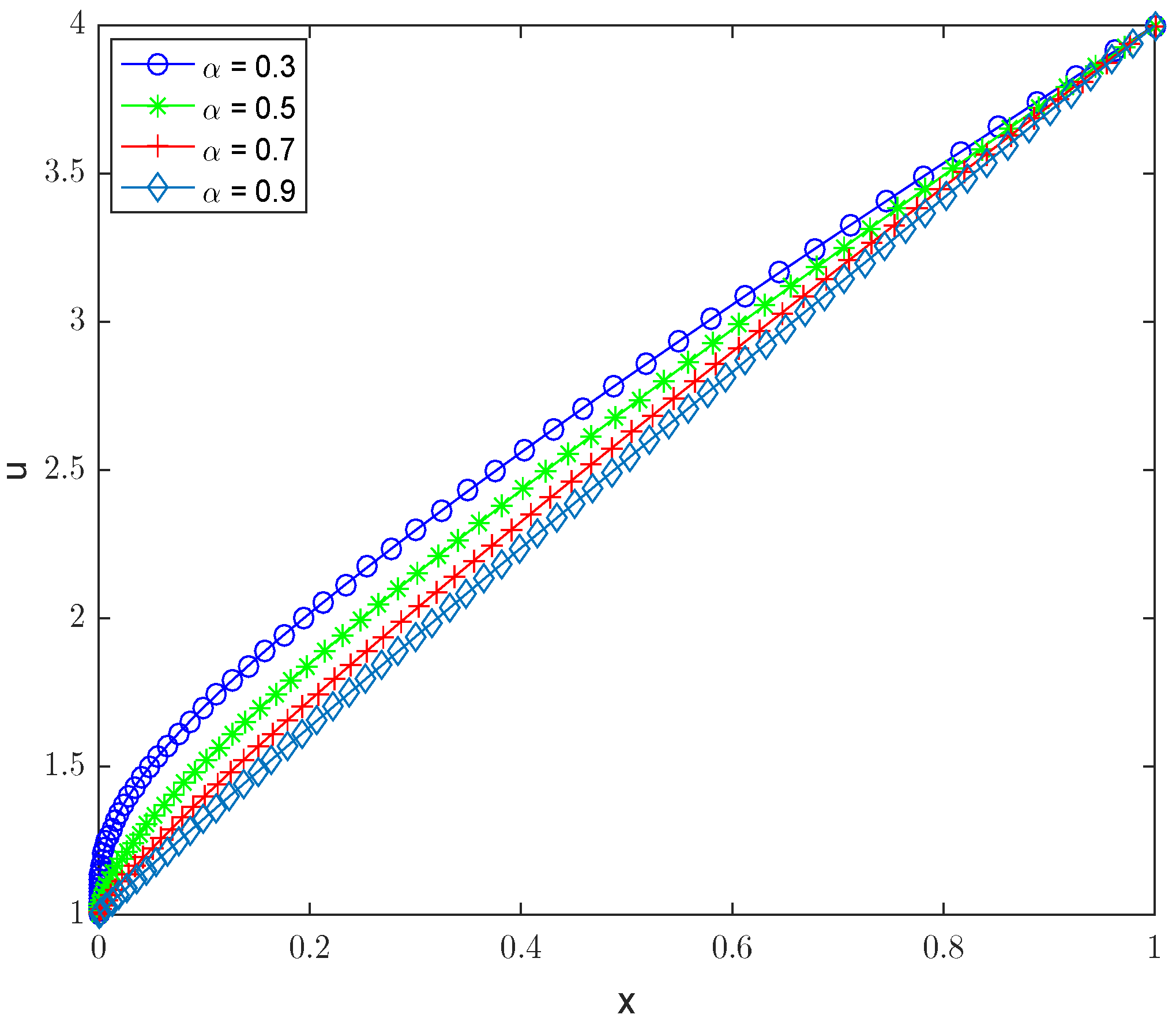
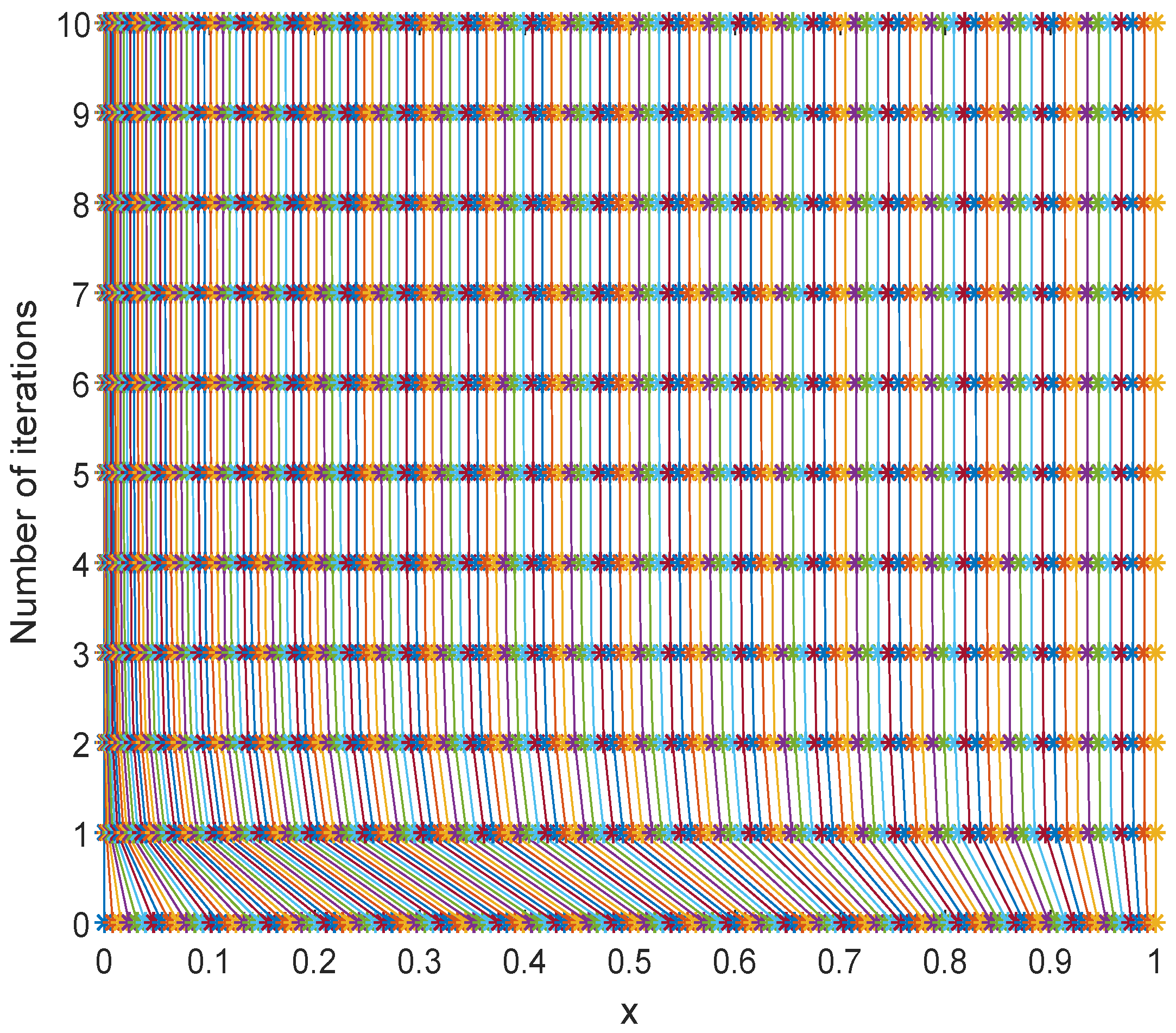
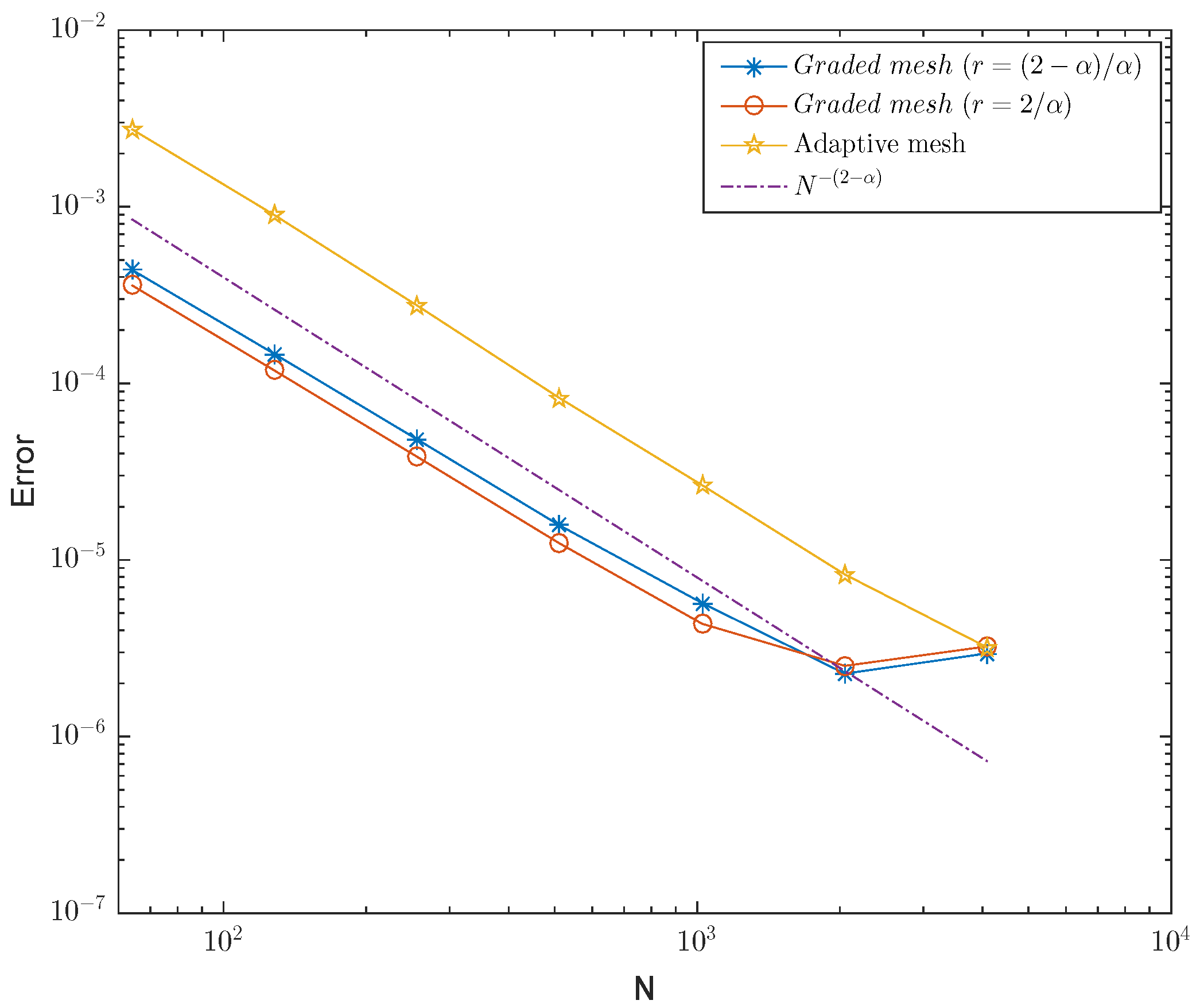
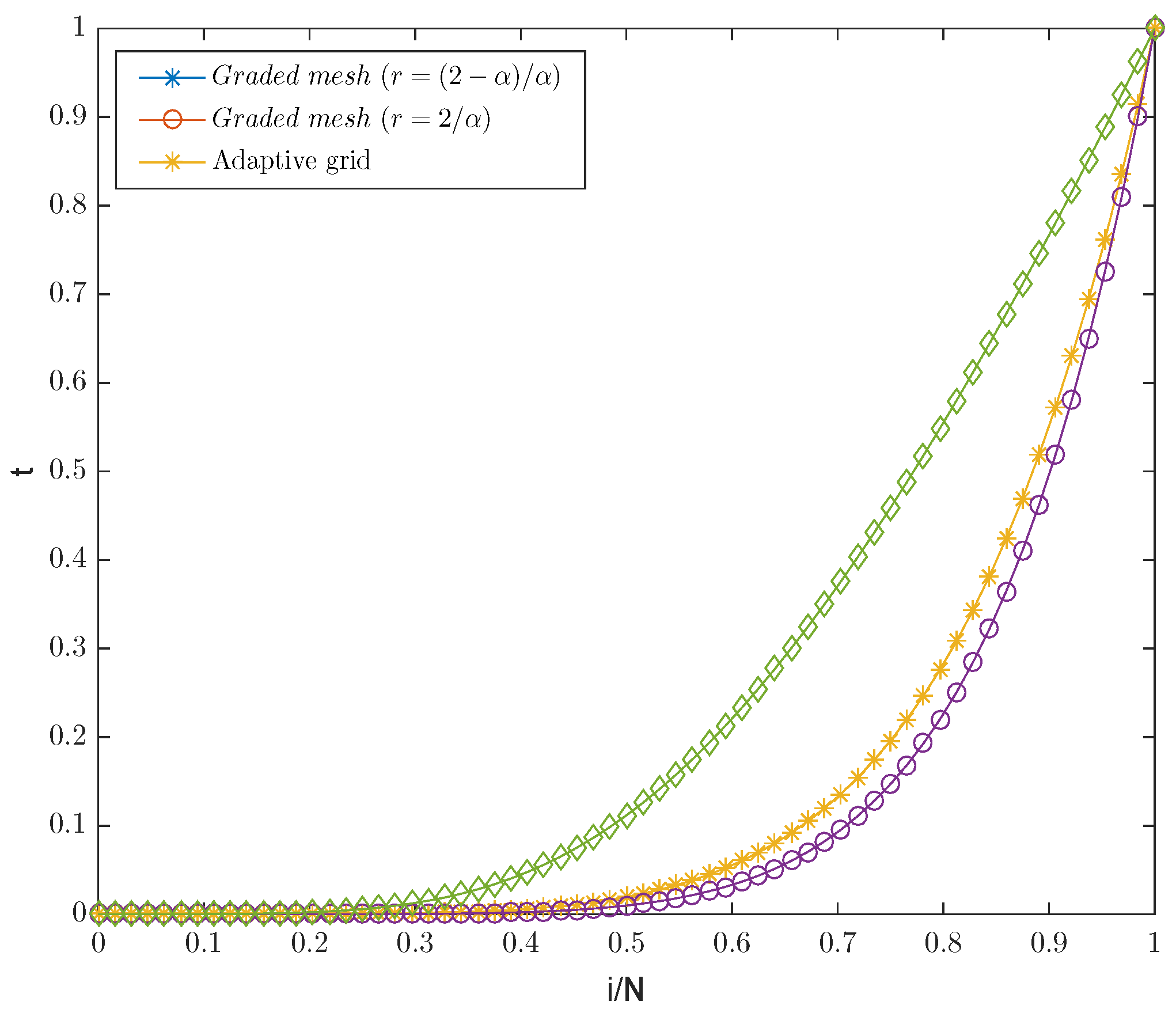
| 0.3 | |||||||
| 0.5565 | 0.5622 | 0.3578 | 0.7213 | −0.0834 | |||
| 0.5 | |||||||
| 0.8116 | 0.8627 | 0.8554 | 0.7570 | 0.9134 | |||
| 0.7 | |||||||
| 0.8057 | 0.8350 | 0.8558 | 0.8917 | 0.8709 | |||
| 0.9 | |||||||
| 0.7943 | 0.8233 | 0.8474 | 0.8635 | 0.8836 |
| 0.3 | |||||||
| 1.6689 | 1.7945 | 1.8599 | 1.8889 | 1.8539 | |||
| 0.5 | |||||||
| 1.7800 | 1.8738 | 1.5820 | 1.4982 | 1.4926 | |||
| 0.7 | |||||||
| 1.3796 | 1.3559 | 1.3306 | 1.3148 | 1.3066 | |||
| 0.9 | |||||||
| 1.0825 | 1.0997 | 1.1047 | 1.1046 | 1.1036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Liu, L.-B.; Bao, X.; Zhang, Y. An Optimal Adaptive Grid Method Based on L1 Scheme for a Nonlinear Caputo Fractional Differential Equation. Fractal Fract. 2022, 6, 647. https://doi.org/10.3390/fractalfract6110647
Yang T, Liu L-B, Bao X, Zhang Y. An Optimal Adaptive Grid Method Based on L1 Scheme for a Nonlinear Caputo Fractional Differential Equation. Fractal and Fractional. 2022; 6(11):647. https://doi.org/10.3390/fractalfract6110647
Chicago/Turabian StyleYang, Tao, Li-Bin Liu, Xiaobing Bao, and Yong Zhang. 2022. "An Optimal Adaptive Grid Method Based on L1 Scheme for a Nonlinear Caputo Fractional Differential Equation" Fractal and Fractional 6, no. 11: 647. https://doi.org/10.3390/fractalfract6110647
APA StyleYang, T., Liu, L.-B., Bao, X., & Zhang, Y. (2022). An Optimal Adaptive Grid Method Based on L1 Scheme for a Nonlinear Caputo Fractional Differential Equation. Fractal and Fractional, 6(11), 647. https://doi.org/10.3390/fractalfract6110647




