A Fractional Order Investigation of Smoking Model Using Caputo-Fabrizio Differential Operator
Abstract
1. Introduction
2. Analytical Preliminaries
3. General Solution for the Model (2)
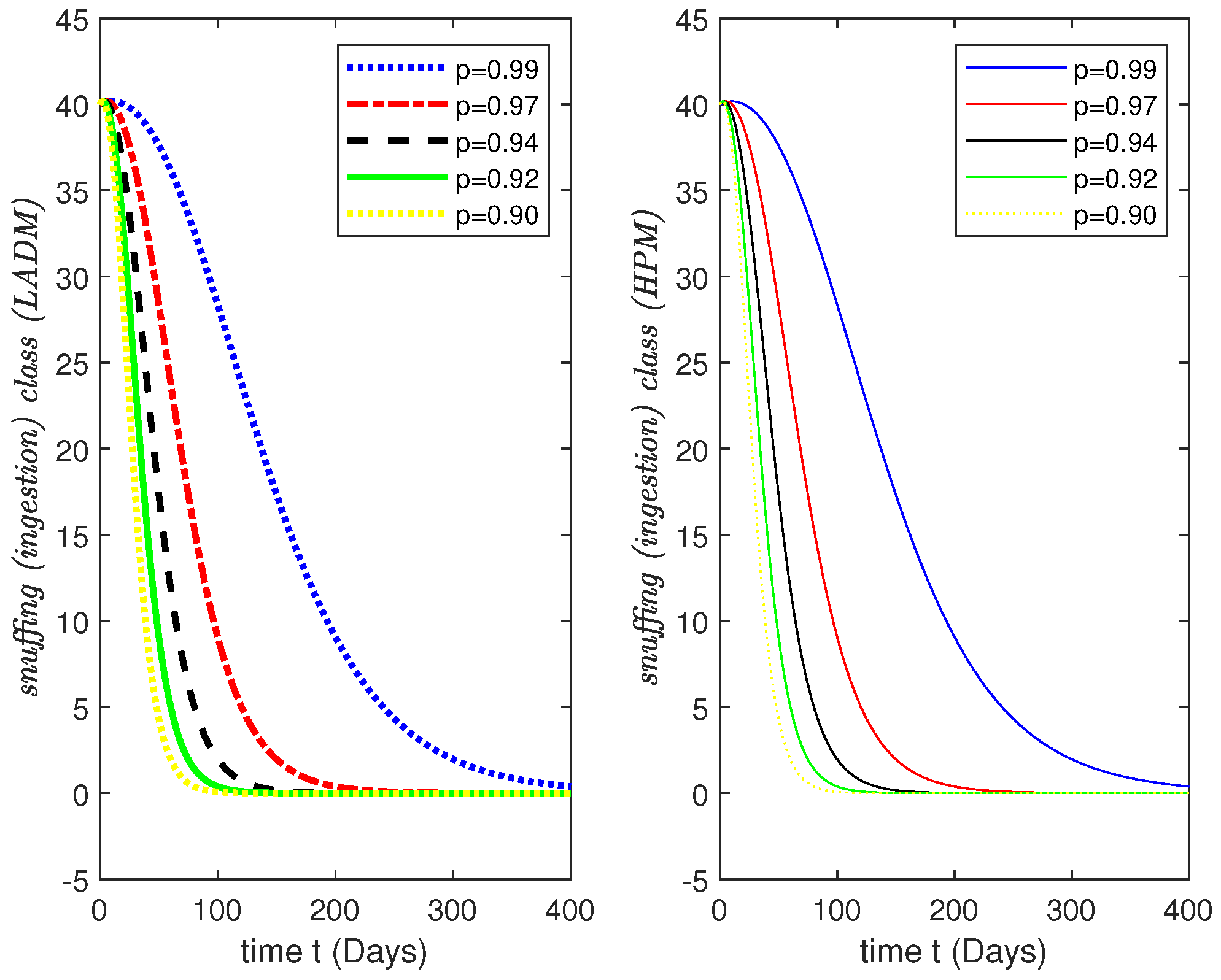
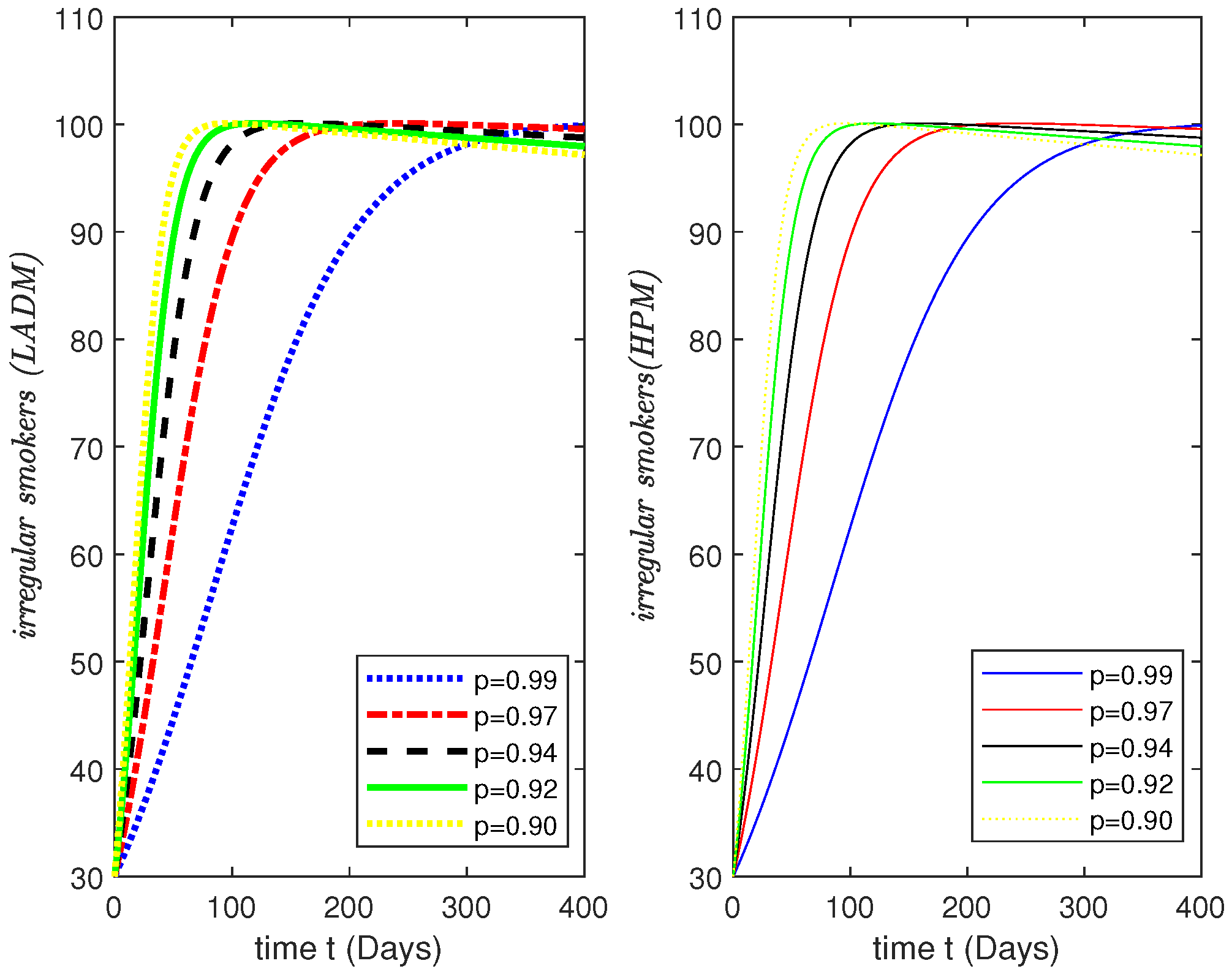
3.1. General Solution for Model (2) with (LADM)
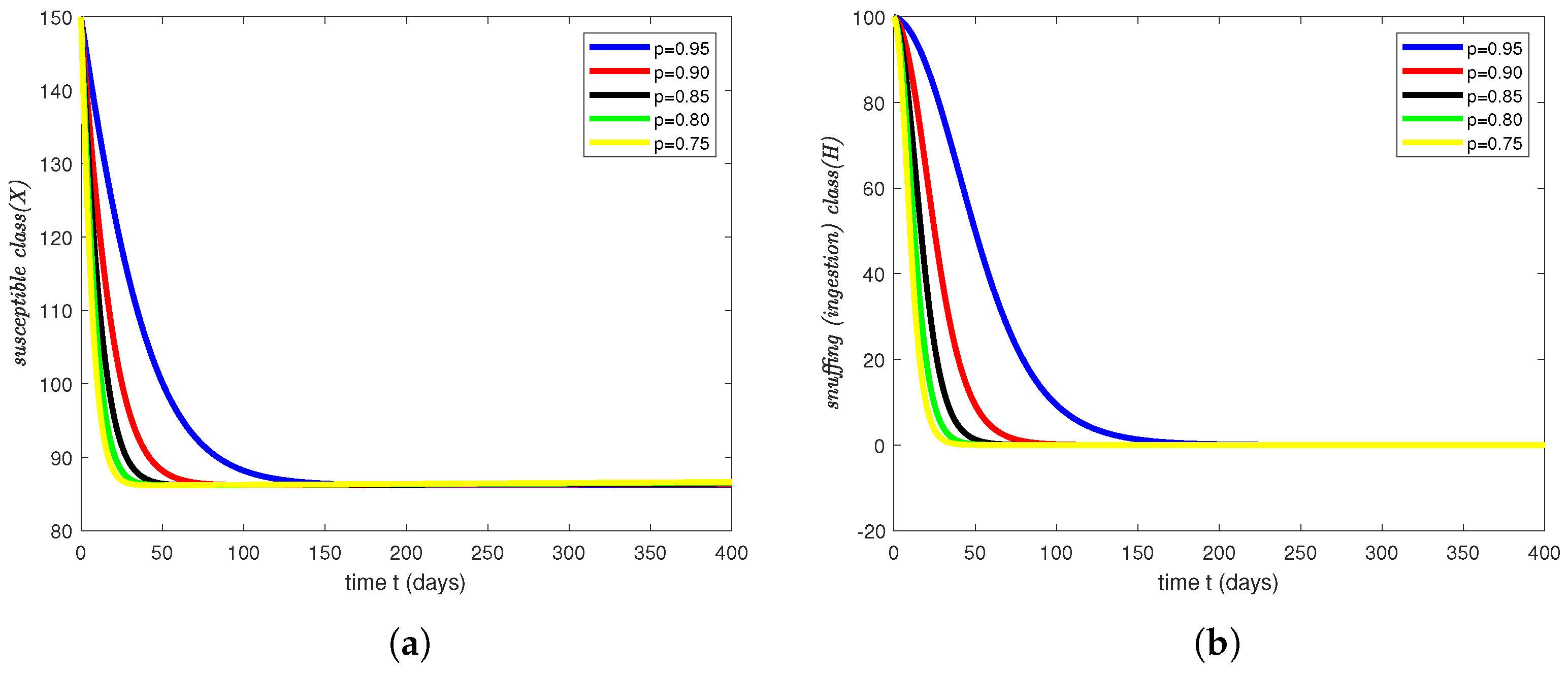
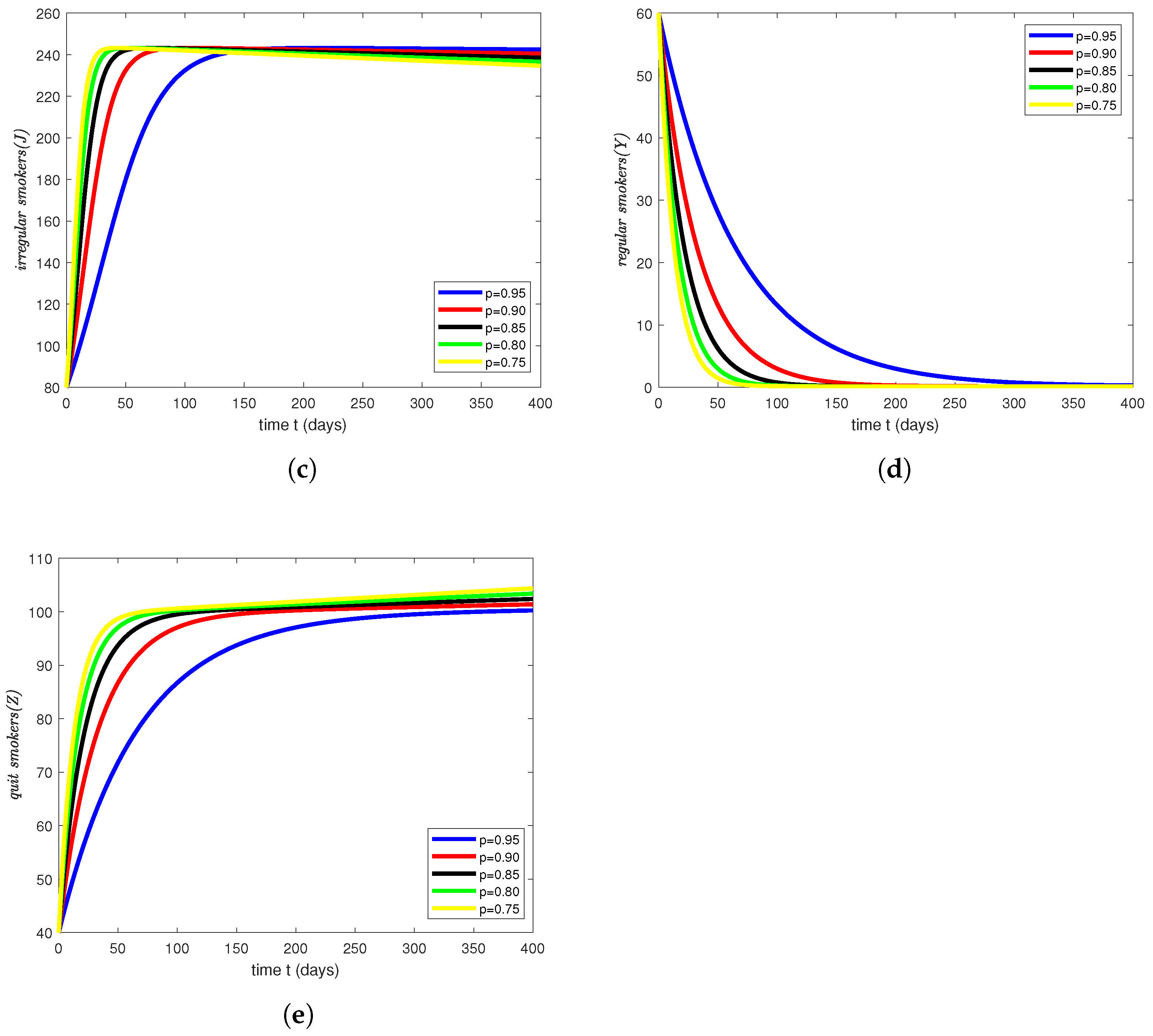
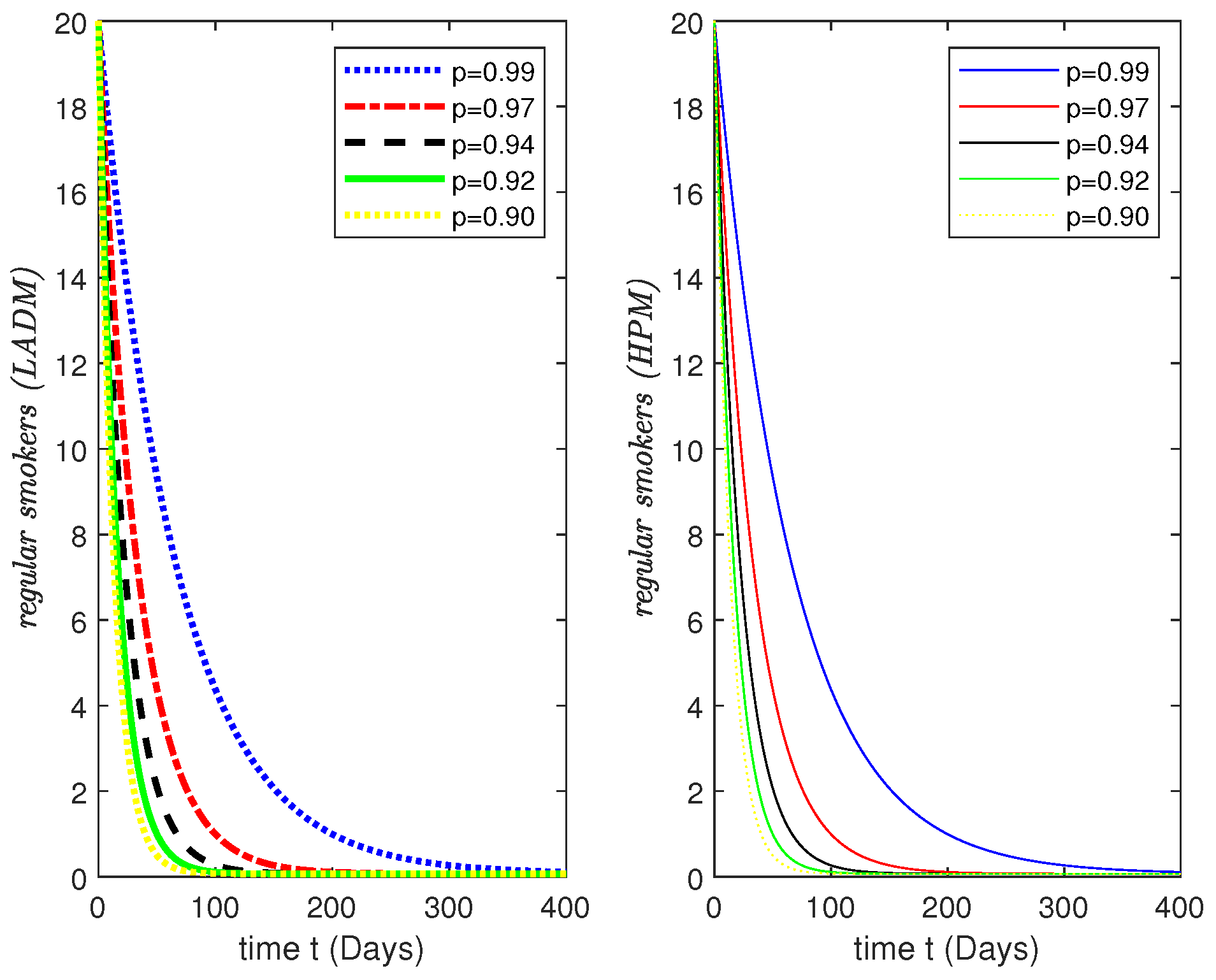
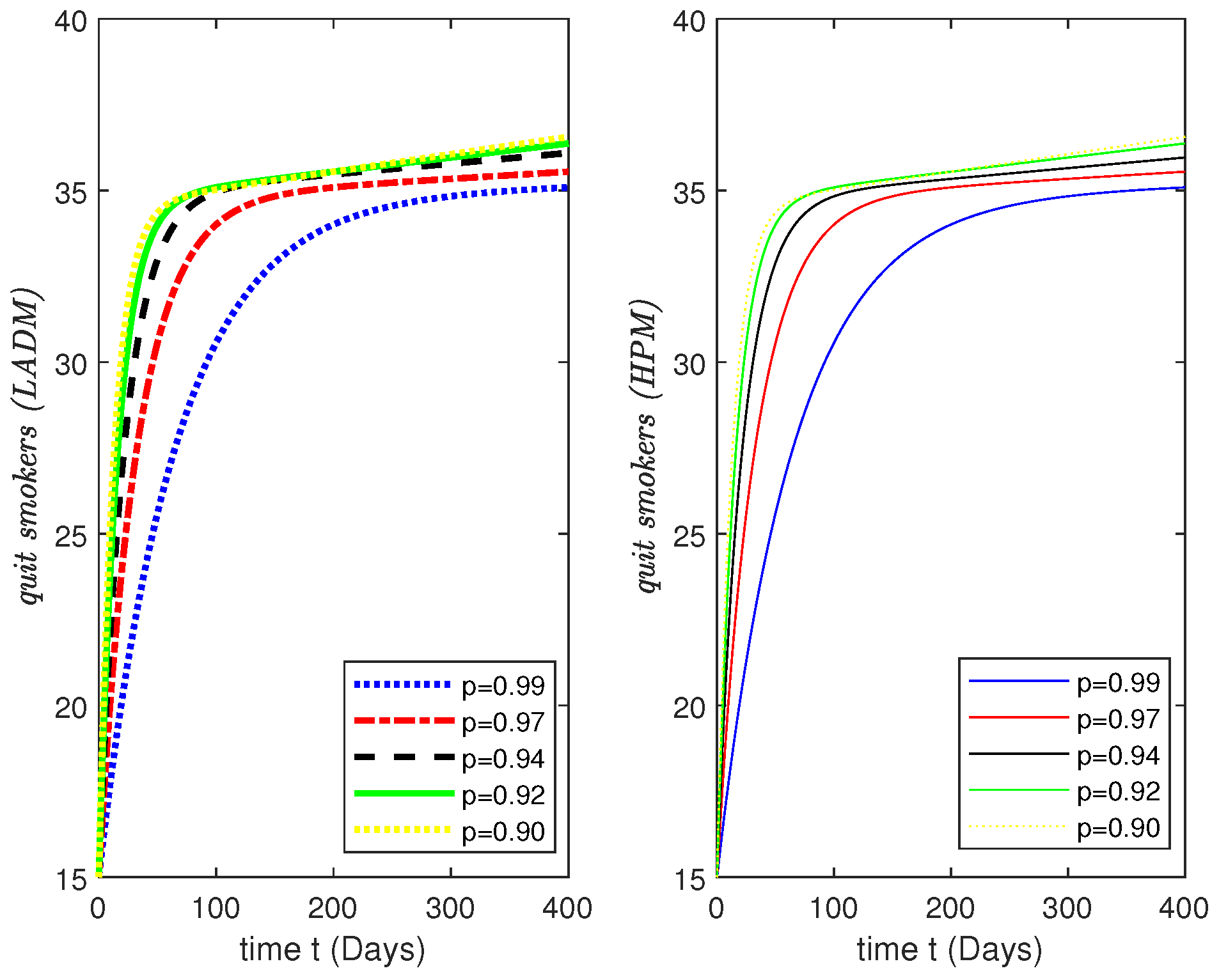
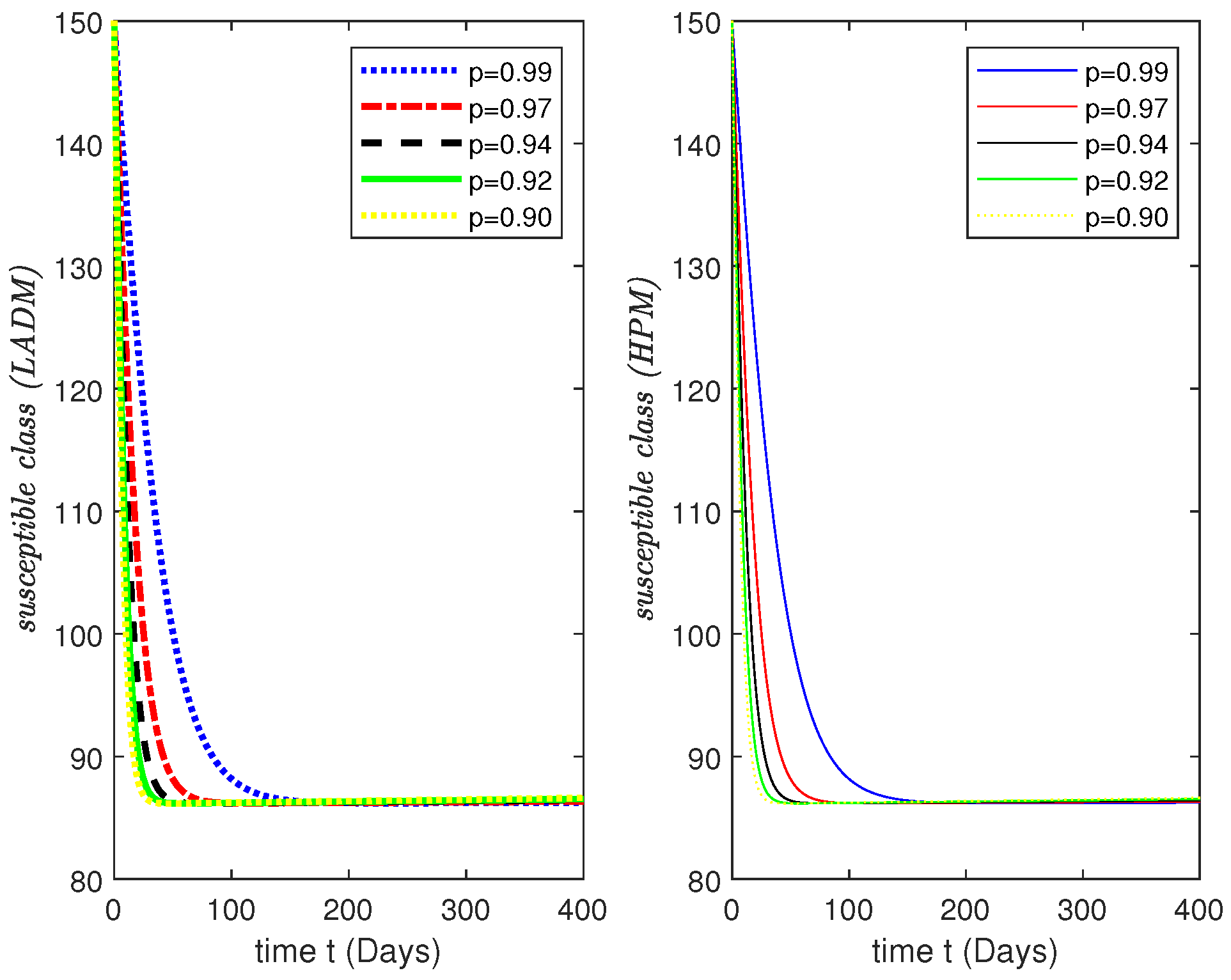
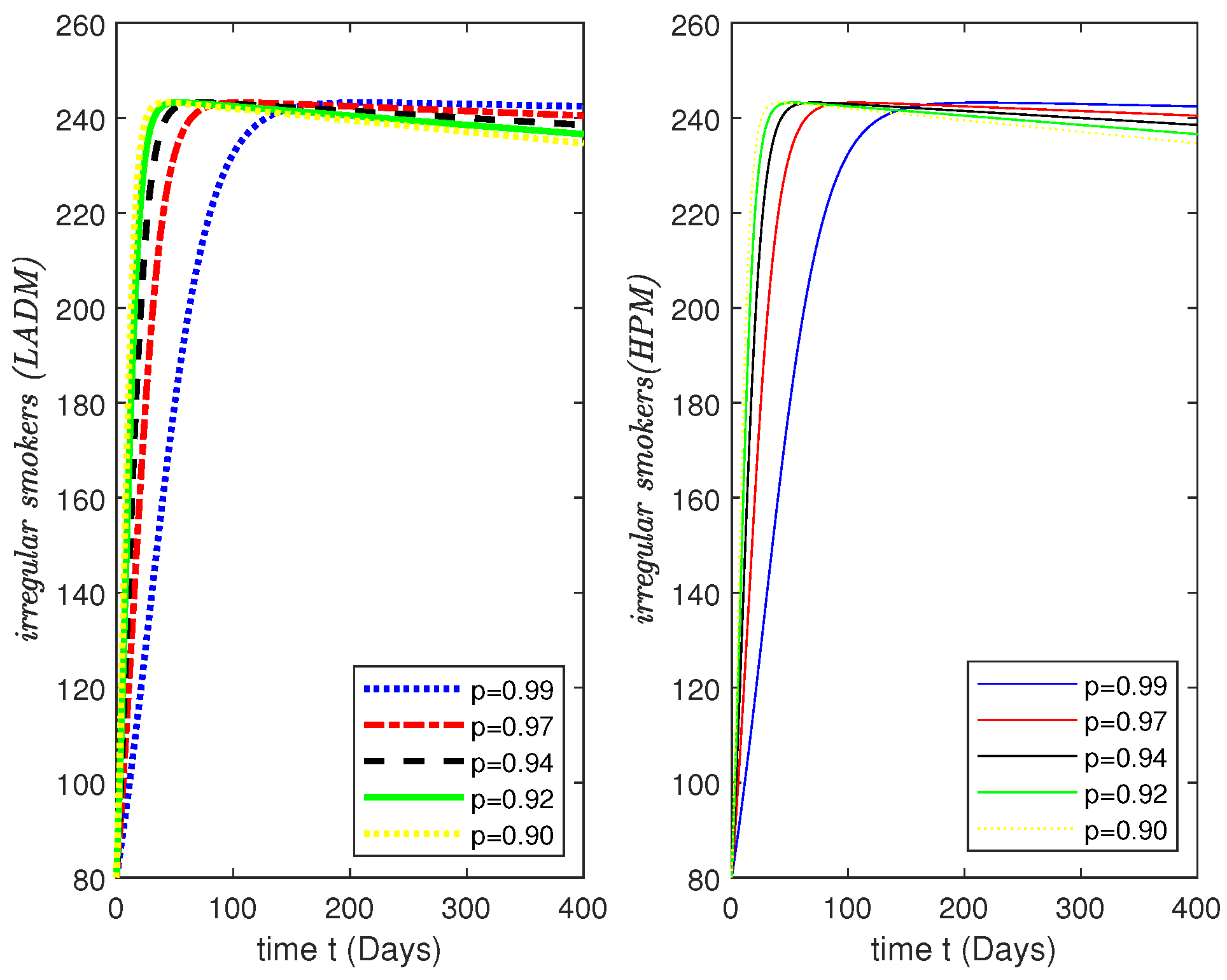
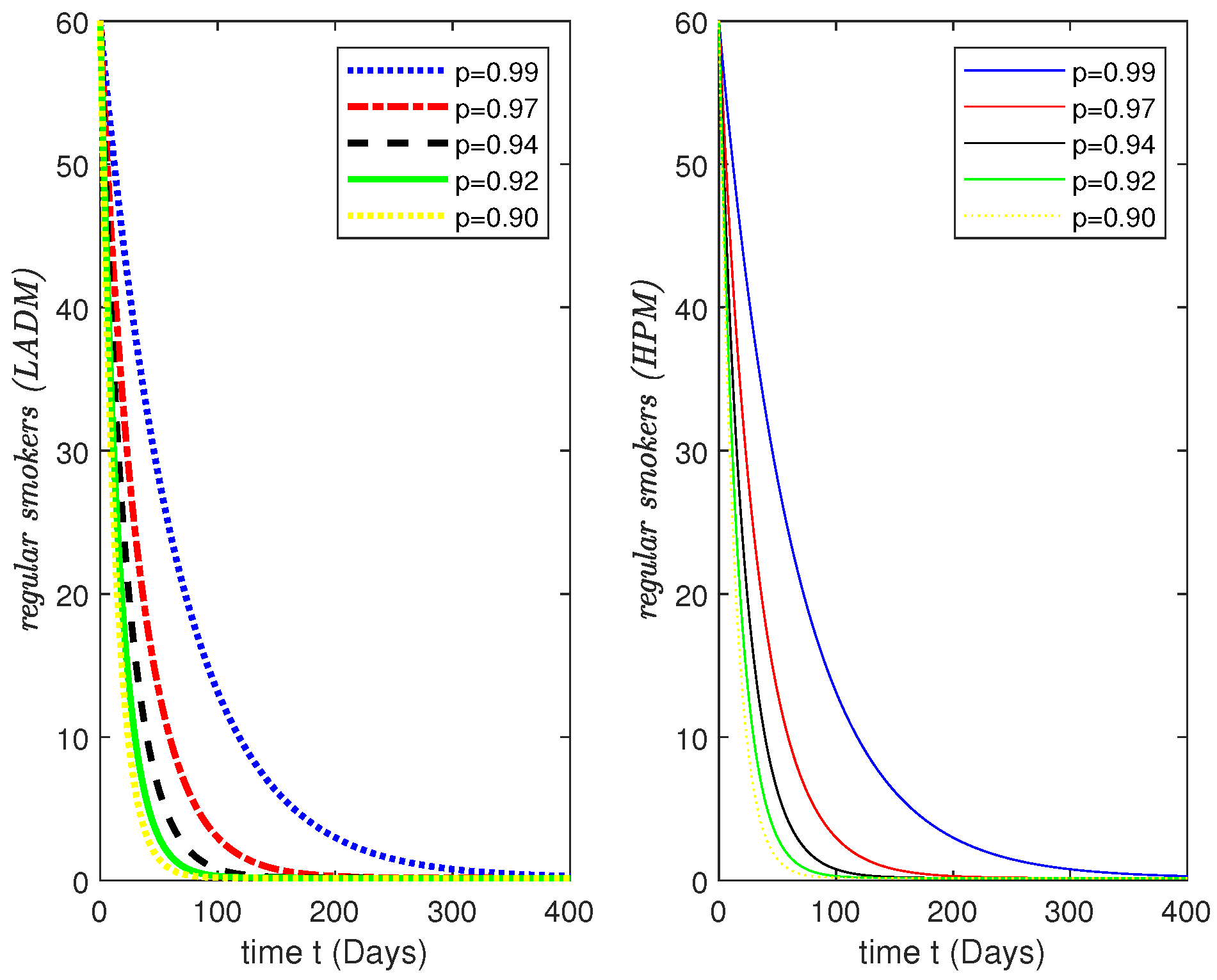
3.2. Numerical Results and Simulations
3.3. General Solution for Model (2) with (HPM)
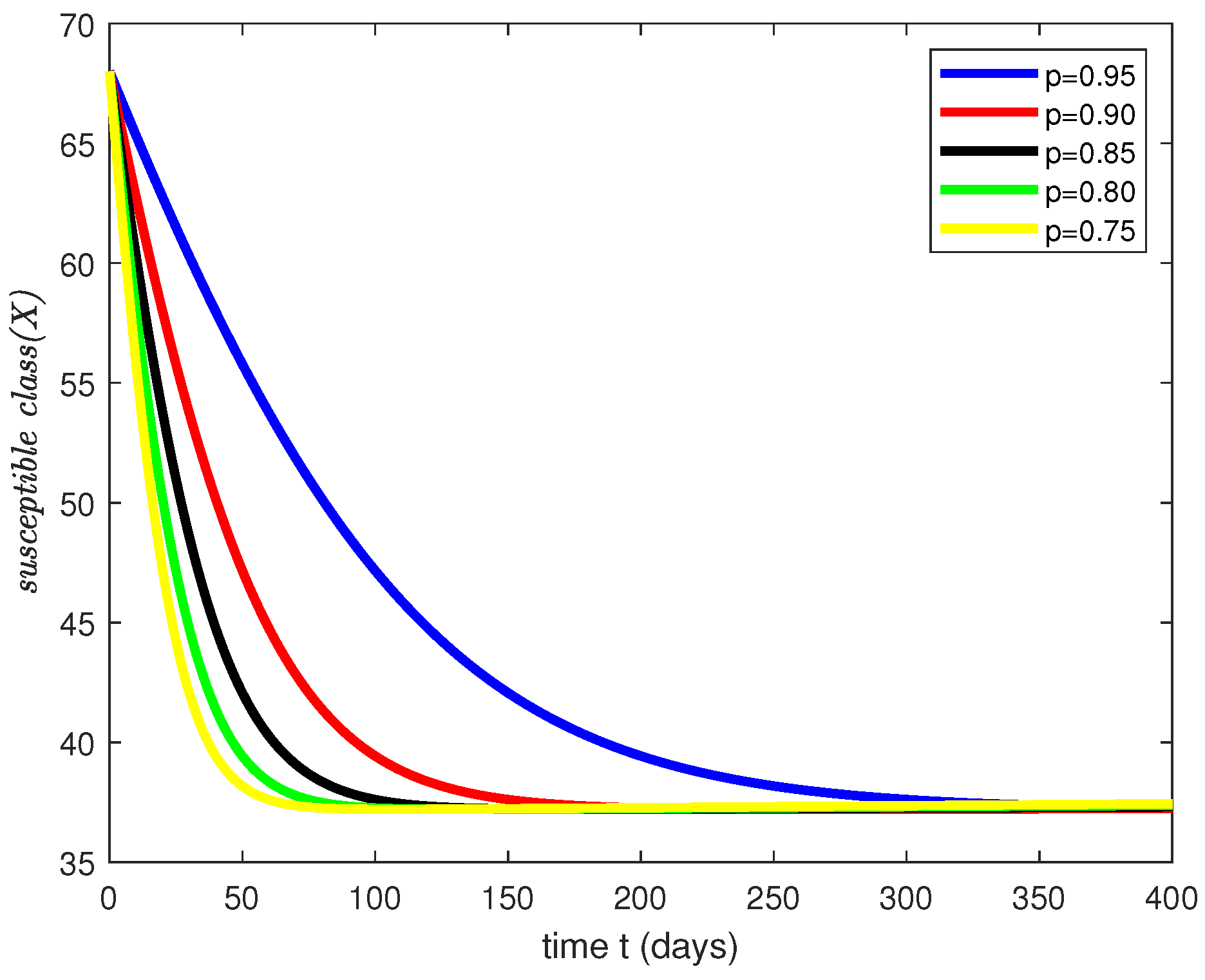
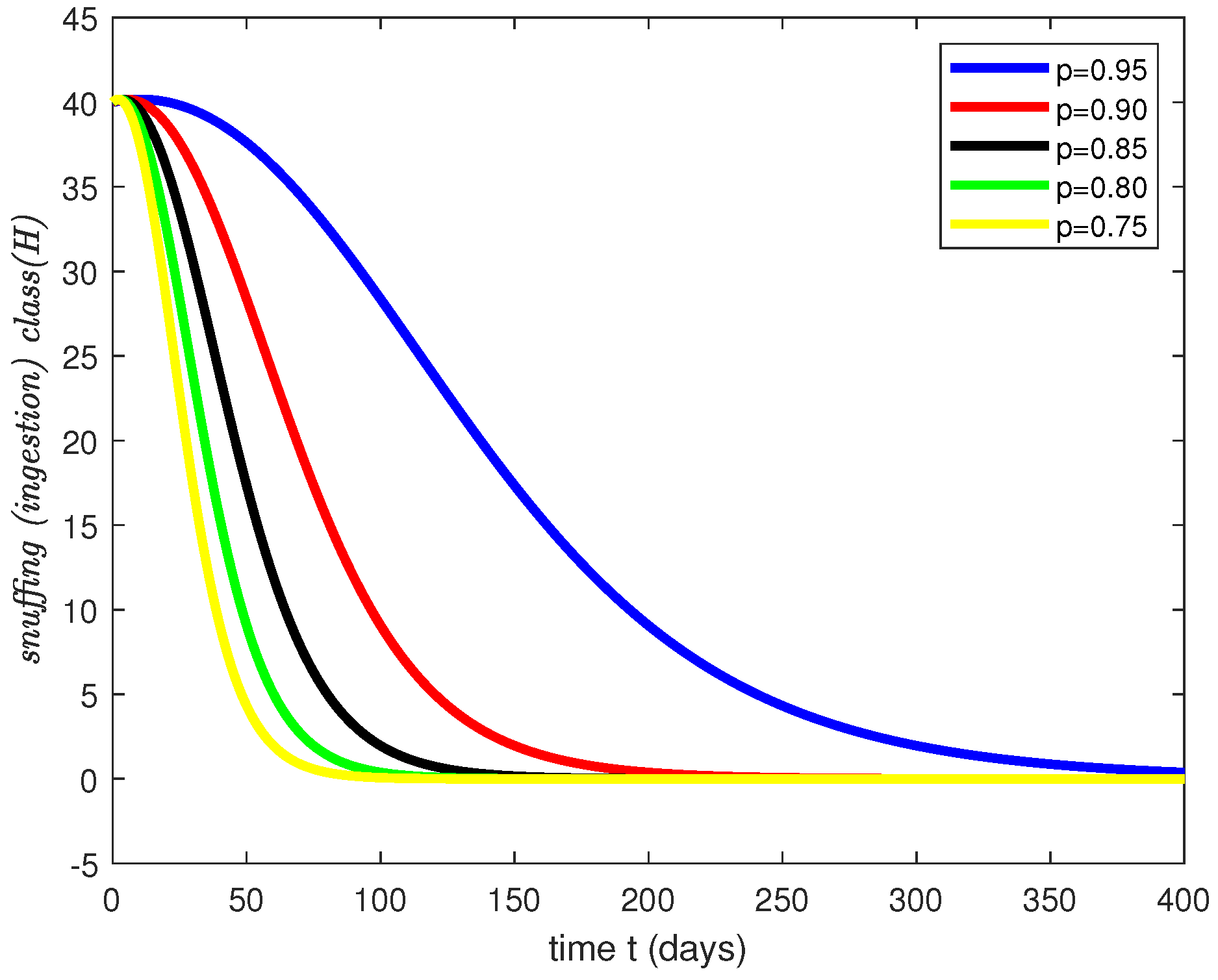
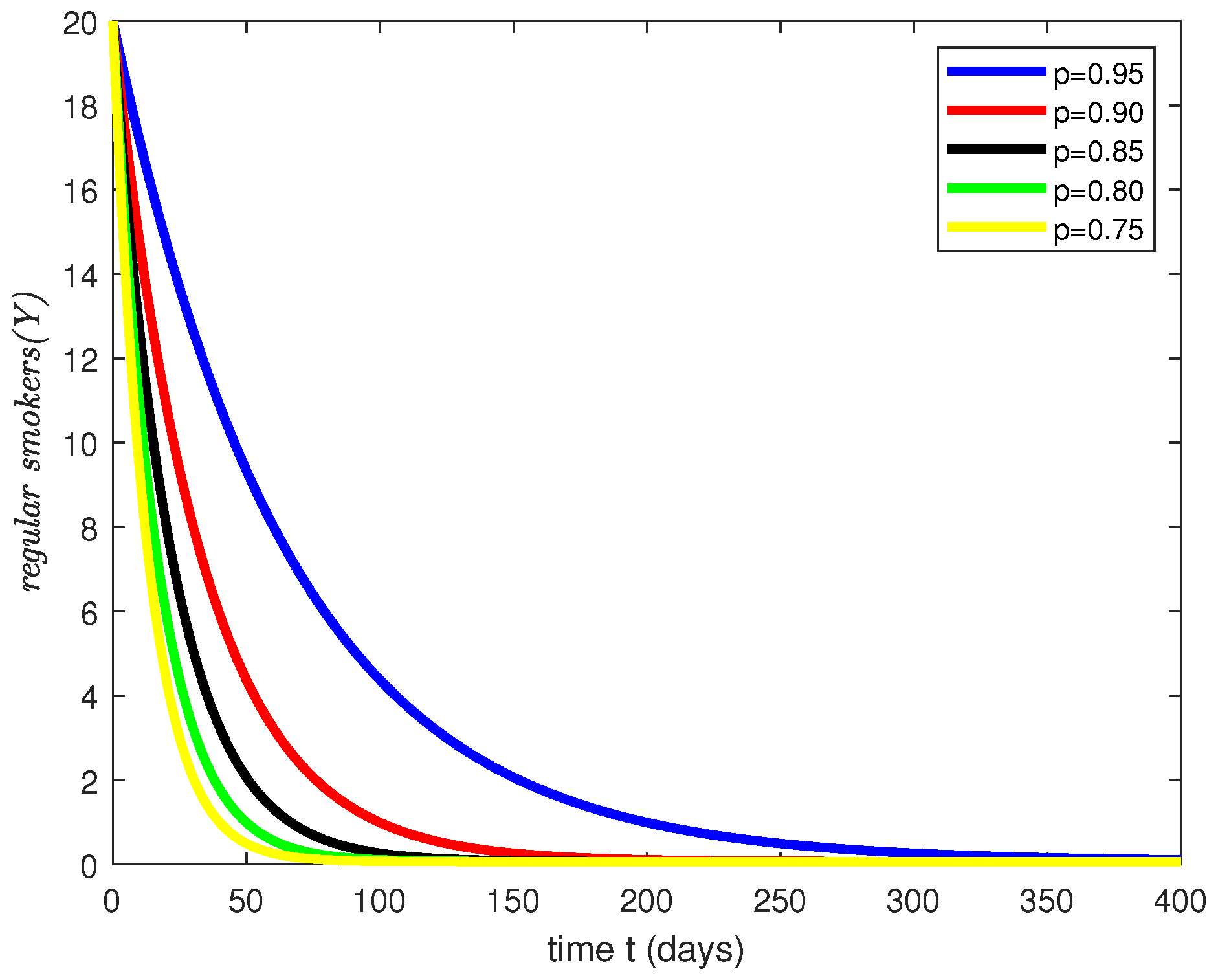
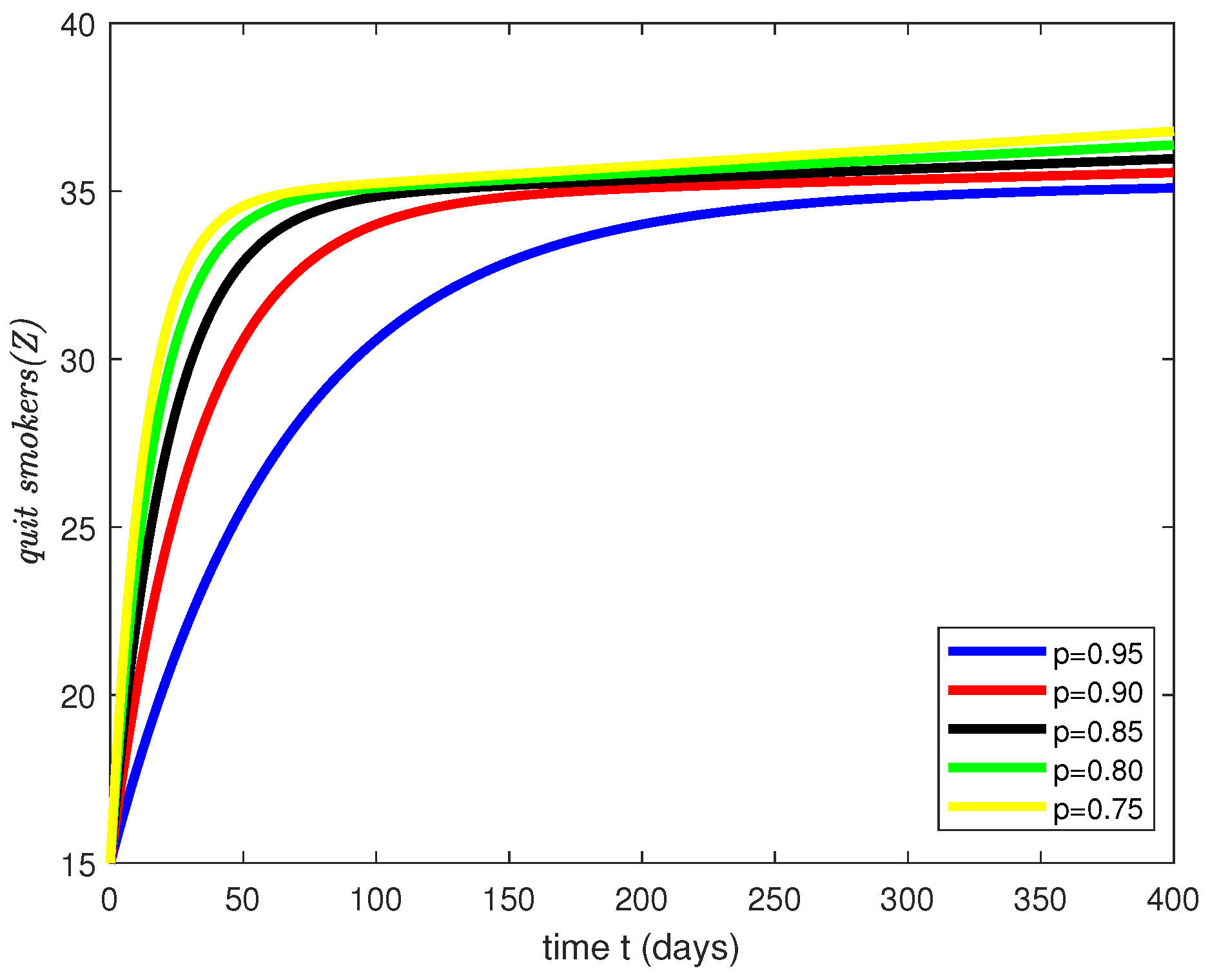
4. Simulations Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brownlee, J. Certain considerations on the causation and course of epidemics. Proc. R. Soc. Med. 1909, 2, 243–258. [Google Scholar] [CrossRef] [PubMed]
- Brownlee, J. The mathematical theory of random migration and epidemic distribution. Proc. R. Soc. Edinb. 1912, 31, 262–289. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. part 1. Proc. R. Soc. Edinb. Sect. A Math. 1927, 115, 700–721. [Google Scholar]
- Chong, J.R. Analysis clarifies route of AIDS. Los Angeles Times, 30 October 2000. [Google Scholar]
- Wang, K.; Wang, W.; Song, S. Dynamics of an HBV model with difusion and deley. J. Theor. Biol. 2008, 253, 36–44. [Google Scholar] [CrossRef] [PubMed]
- McCluskey, C.C. Complete global stability for an SIR epidemic model with delay distributed or discrete. Nonlinear Anal. Real World Appl. 2010, 11, 55–59. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z. Stability of a delayed SIRS epidemic model with a nonlinear incidence rate. Chaos Solitons Fractals 2009, 41, 2319–2325. [Google Scholar] [CrossRef]
- Leone, A.; Landini, L.; Leone, A. What is tobacco smoke? Sociocultural dimensions of the association with cardiovascular risk. Curr. Pharm. Des. 2010, 16, 2510–2517. [Google Scholar] [CrossRef]
- Saha, S.P.; Bhalla, D.K.; Whayne, T.F.; Gairola, C.G. Cigarette smoke and adverse health effects: An overview of research trends and future needs. Int. J. Angiol. 2007, 16, 77–83. [Google Scholar] [CrossRef]
- Smith, E.A.; Malone, R.E. Everywhere the soldier will be, wartime tobacco promotion in the US military. Am. J. Publ. Health 2009, 99, 1595–1602. [Google Scholar] [CrossRef]
- Costa, R.M.S.; Pavone, P. Diachronic biodiversity analysis of a metropolitan area in the Mediterranean region. Acta Hortic. 2018, 1215, 49–52. [Google Scholar] [CrossRef]
- Costa, R.M.S.; Avone, P. Invasive plants and natural habitats: The role of alien species in the urban vegetation. Acta Hortic. 2018, 1215, 57–60. [Google Scholar] [CrossRef]
- Sharomi, O.; Gumel, A.B. Curtailing smoking dynamics: A mathematical modeling approach. Appl. Math. Comput. 2008, 195, 475–499. [Google Scholar] [CrossRef]
- Liu, T.; Deiss, T.J.; Lippi, M.W.; Jauregui, A.; Vessel, K.; Ke, S.; Belzer, A.; Zhuo, H.; Kangelaris, K.N.; Gomez, A.D.; et al. Alternative Tobacco Product Use in Critically Ill Patients. Int. J. Environ. Res. Public Health 2020, 17, 8707. [Google Scholar] [CrossRef]
- Gerrits, N.; Elen, B.; Craenendonck, T.V.; Triantafyllidou, D.; Petropoulos, I.N.; Malik, R.A.; De Boever, P. Age and sex affect deep learning prediction of cardiometabolic risk factors from retinal images. Sci. Rep. 2020, 10, 9432. [Google Scholar]
- Yildirum, A.; Cherruault, Y. Analytical approximate solution of a SIR epidemic model with constant vaccination strategy by homotopy perturbation method. Emerald 2009, 38, 1566–1581. [Google Scholar]
- World Health Organisation. Monitoring Tobacco Use and Prevention Policies. Executive Summary; World Health Organisation: Geneva, Switzerland, 2017.
- Goldenberg, I.; Jonas, M.; Tenenbaum, A.; Boyko, V.; Matetzky, S.; Shotan, A.; Behar, S.; Reicher-Reiss, H.; Bezafibrate Infarction Prevention Study Group. Current smoking, smoking cessation, and the risk of sudden cardiac death in patients with coronary artery disease. Arch. Int. Med. 2003, 163, 2301–2305. [Google Scholar] [CrossRef]
- Castillo-Garsow, C.; Jordan-Salivia, G.; Rodriguez Herrera, A. Mathematical Models for Dynamics of Tobacco Use, Recovery and Relapse; Technical Report Series BU-1505-M; Cornell University: London, UK, 2000. [Google Scholar]
- Ham, O.K. Stages and processes of smoking cessation among adolescents. West. J. Nurs. Res. 2007, 29, 301–315. [Google Scholar]
- Zaman, G. Qualitative behavior of giving up smoking models. Bull. Malays. Math. Soc. 2011, 34, 403–415. [Google Scholar]
- Erturk, V.S.; Zaman, G.; Momani, S. A numeric analytic method for approximating a giving up smoking model containing fractional derivatives. Comput. Math. Appl. 2012, 64, 3068–3074. [Google Scholar] [CrossRef]
- Zeb, A.; Chohan, I.; Zaman, G. The homotopy analysis method for approximating of giving up smoking model in fractional order. Appl. Math. 2012, 3, 914–919. [Google Scholar] [CrossRef]
- Alkhudhari, Z.; Al-Sheikh, S.; Al-Tuwairqi, S. Global dynamics of a mathematical model on smoking. Appl. Math. 2014, 2014, 847075. [Google Scholar] [CrossRef]
- Khalid, M.; Khan, F.S.; Iqbal, A. Perturbation-iteration algorithm to solve fractional giving up smoking mathematical model. Int. J. Comput. Appl. 2016, 142, 1–6. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Diethelm, K.; Garrappa, R.; Stynes, M. Good (and not so good) practices in computational methods for fractional calculus. Mathematics 2020, 8, 324. [Google Scholar] [CrossRef]
- Salnikov, N.N.; Siryk, S.V.; Tereshchenko, I.A. On Construction of finite dimensional mathematical model of convection diffusion process with usage of the Petrov Galerkin method. J. Autom. Inf. Sci. 2010, 42, 67–83. [Google Scholar] [CrossRef]
- Roos, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 24. [Google Scholar]
- Stynes, M.; Stynes, D. Convection-Diffusion Problems; American Mathematical Society: Providence, RI, USA, 2018; Volume 196. [Google Scholar]
- Siryk, S.V. Accuracy and stability of the Petrov–Galerkin method for solving the stationary convection-diffusion equation. Cybern. Syst. Anal. 2014, 50, 278–287. [Google Scholar] [CrossRef]
- Siryk, S.V. Analysis of lumped approximations in the finite-element method for convection–diffusion problems. Cybern. Syst. Anal. 2013, 49, 774–784. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Frac. Diff. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- El-Saka, H.A.A. The fractional-order SIS epidemic model with variable population size. J. Egyp. Math. Soc. 2014, 22, 50–54. [Google Scholar] [CrossRef]
- Caponetto, R. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010; Volume 72. [Google Scholar]
- Ma, T.; Sun, N. Zhiliang Wang, Dongsheng Yang. Nonlinear Dyn. 2014, 75, 387–402. [Google Scholar]
- Kazem, S.; Abbasbandy, S.; Kumar, S. Fractional-order Legendre functions for solving fractional-order differential equations. Appl. Math. Model. 2013, 37, 5498–5510. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations. Math. Sci. Eng. 1999, 198, 41–119. [Google Scholar]
- Kilbas, A.A.; Trujillo, J.J. Differential equations of fractional order: Methods results and problem—I. Appl. Anal. 2001, 78, 153–192. [Google Scholar] [CrossRef]
- Liu, X.; ur Rahmamn, M.; Ahmad, S.; Baleanu, D.; Nadeem Anjam, Y. A new fractional infectious disease model under the non-singular Mittag–Leffler derivative. Waves Random Complex Media 2022, 1–27. [Google Scholar] [CrossRef]
- ur Rahman, M.; Arfan, M.; Shah, Z.; Alzahrani, E. Evolution of fractional mathematical model for drinking under Atangana-Baleanu Caputo derivatives. Phys. Scr. 2021, 96, 115203. [Google Scholar] [CrossRef]
- Xu, C.; ur Rahman, M.; Baleanu, D. On fractional-order symmetric oscillator with offset-boosting control. Nonlinear Anal. Model. Cont. 2022, 27, 994–1008. [Google Scholar] [CrossRef]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Caputo, M.; Fabrizio, M. On the singular kernels for fractional derivatives. Some applications to partial differential equations. Progr. Fract. Differ. Appl. 2021, 7, 1–4. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of the new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Bai, C.Z.; Fang, J.X. The existence of a positive solution for a singular coupled system of nonlinear fractional differential equations. Appl. Math. Comput. 2004, 150, 611–621. [Google Scholar] [CrossRef]
- Haq, F.; Shah, K.; Rahman, G.U.; Shahzad, M. Numerical analysis of fractional order model of HIV-1 infection of CD4+ T-cells. Comput. Meth. Diff. Equ. 2017, 5, 1–11. [Google Scholar]
- Biazar, J. Solution of the epidemic model by Adomian decomposition method. Appl. Math. Comput. 2006, 173, 1101–1106. [Google Scholar] [CrossRef]
- He, J.H. An elementary introduction to the homotopy perturbation method. Comput. Math. Appl. 2009, 57, 410–412. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; De la Sen, M. A novel homotopy perturbation method with applications to nonlinear fractional order KdV and Burger equation with exponential-decay kernel. J. Funct. Spaces 2021, 2021, 8770488. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Xu, Y. Similarity solution and heat transfer characteristics for a class of nonlinear convection-diffusion equation with initial value conditions. Math. Probl. Eng. 2019, 2019, 3467276. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Nchama, G.A.M.; Mecıas, A.L.; Richard, M.R. The Caputo–Fabrizio fractional integral to generate some new inequalities. Inf. Sci. Lett. 2019, 8, 73–80. [Google Scholar]
- He, J.H.; Jiao, M.L.; Gepreel, K.A.; Khan, Y. Homotopy perturbation method for strongly nonlinear oscillators. Math. Comput. Simul. 2023, 204, 243–258. [Google Scholar] [CrossRef]
- He, J.H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]




| Notation | Description of the Parameters |
|---|---|
| The frequency of recruitment (birth or migration) | |
| The rate of the vulnerable population transitions to the snuffing class | |
| The Rate of snuffing becomes an irregular smokers | |
| Rate of irregular smokers turning to a regular smoker | |
| Departing rate | |
| Rate of natural death | |
| Rate of recovery | |
| Rate of snuffing class deaths because of smoking | |
| Rate of death due to smoking |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anjam, Y.N.; Shafqat, R.; Sarris, I.E.; ur Rahman, M.; Touseef, S.; Arshad, M. A Fractional Order Investigation of Smoking Model Using Caputo-Fabrizio Differential Operator. Fractal Fract. 2022, 6, 623. https://doi.org/10.3390/fractalfract6110623
Anjam YN, Shafqat R, Sarris IE, ur Rahman M, Touseef S, Arshad M. A Fractional Order Investigation of Smoking Model Using Caputo-Fabrizio Differential Operator. Fractal and Fractional. 2022; 6(11):623. https://doi.org/10.3390/fractalfract6110623
Chicago/Turabian StyleAnjam, Yasir Nadeem, Ramsha Shafqat, Ioannis E. Sarris, Mati ur Rahman, Sajida Touseef, and Muhammad Arshad. 2022. "A Fractional Order Investigation of Smoking Model Using Caputo-Fabrizio Differential Operator" Fractal and Fractional 6, no. 11: 623. https://doi.org/10.3390/fractalfract6110623
APA StyleAnjam, Y. N., Shafqat, R., Sarris, I. E., ur Rahman, M., Touseef, S., & Arshad, M. (2022). A Fractional Order Investigation of Smoking Model Using Caputo-Fabrizio Differential Operator. Fractal and Fractional, 6(11), 623. https://doi.org/10.3390/fractalfract6110623







