Analysis of the Romanian Capital Market Using the Fractal Dimension

Abstract

The surrounding reality can be analyzed due to the interaction of complex nonlinear dynamic systems. The article’s main objective is to develop and analyze the models that best describe the efficient behavior of the Romanian capital market that generated the analyzed time series. The empirical analysis carried out in this paper does not aim to classify the Romanian market capital as efficient or ineffective but rather to identify the degree of deviation from efficiency relative to other markets, namely, an analysis of the dynamics of the degree of deviation over time. To describe the distribution of returns, we focused on the family of generalized hyperbolic distributions, which have statistical properties similar to financial returns. The presence of wide tails in the distributions (of extreme values) suggests using statistical tests and measures to detect dependencies, which take this behavior into account. Statistical methods and efficiency indicators are used, such as the Hurst exponent, Taken’s theorem, and the fractal dimension, which facilitate the detection of the main types of dependencies that could be present in the return series; measures that are robust to the heteroscedastic behavior of the returns. These statistical measures are applied to the entire period and sliding windows.

1. Introduction

The financial market represents one of the fascinating mechanisms of a functional market economy, constituting the framework for harmonizing the demand and supply of financial resources. This is a permanent movement and change market, freely regulated by supply and demand. As an integral part of the financial market, the capital market reflects, perhaps to the best extent, the property of harmonizing supply and demand, offering a continuously updated framework with existing information. In this context, there is interest in how new knowledge is integrated into the course of the titles, in this case, on the price formation mechanism. The statistical analysis of data specific to the capital market aims to identify and develop models that capture its behavior. In general, a model is a simplified presentation of reality. In economics, a model identifies and synthesizes behaviors suggested by economic theory or empirical data, explaining a process through a set of variables and the quantitative and qualitative relationships between them [1].

The concept that governs the theory of capital markets is that of an informationally efficient market, introduced by [2], in which prices immediately and wholly reflect the available information. A definition as simple as it is abstract and also comprehensive because it implies a perfect market governed by the rational behavior of investors, in which historical rates do not provide helpful information for predicting the future, and as such, sustained profits cannot be obtained. In the specialized literature, we find both studies that support the efficiency of markets and a series of authors that provide empirical evidence regarding the inefficiency of various markets worldwide. Technical analysis, which aims to anticipate future price movements based on historical evolution, becomes useless in an informationally efficient market because price variations are independent and identically distributed in a restrictive form [3]. Over time, the performance of technical analysis strategies has often been questioned. However, consistent empirical studies are conducted for important capital markets, where technical analysis strategies have proven to be effective, leading to sustained profit. Technical analysis is based on the statistical concept of predictability; studying historical behavior leads to observing specific patterns that are expected to be found in future courses [4].

The efficiency hypothesis is difficult to invalidate as long as no unanimously recognized statistical methodology disproves the efficiency of capital markets; tests are usually applied statistics targeting particular forms of deviations from efficiency. The approach through the prism of relative efficiency allows us, in addition, to observe the factors that lead to the change in the degree of efficiency over time. Until the foundation of chaos theory, a system’s complicated, inexplicable, and unpredictable evolution was considered random behavior [5]. With the emergence of chaos theory and its tools, a new world became visible, and things could be explained from a different perspective. The main advantage of chaos theory is that it allows short-term prediction of the evolution of chaotic systems and provides explanations for the respective type of dynamic behavior.

The particularities that ensure the originality of this study consist mainly in the use of appropriate research methodologies from the perspective of the statistical properties of the data recommended in recent specialized studies. To describe the distribution of returns, we focused on the family of generalized hyperbolic distributions, which have statistical properties similar to financial returns. The presence of wide tails in the distributions (of extreme values) suggests using statistical tests and measures to detect dependencies, which take this behavior into account [6]. Statistical methods and efficiency indicators are used (such as the Automatic Portmanteau Test, the Hurst exponent, and the fractal dimension) that facilitate the detection of the main types of dependencies that could be present in the return series; measures that are robust to the heteroscedastic behavior of the returns [7]. These statistical measures are applied to the entire period and sliding windows. The reconstruction of the phase space is based on Takens’ theorem. It allows the reconstruction of the dynamics of the initial system without knowing anything about the initial system, having only a univariate time series available. The purpose of the phase space reconstruction is to characterize the behavior of a dynamic system that manifests itself through an unknown process and to highlight the existence of an attractor with a fractal dimension.

The existing tests regarding informational efficiency address the issue of prices and the extent to which they reflect the available information but do not address the market investors’ preferences and behavior [8]. The following steps in the evolution of theories regarding the development of capital markets capture their evolutionary character, concretized by the introduction of the adaptive market hypothesis [9]. This theory is based on the hypothesis of limited rationality [10]. According to the new theory, investors act in their interest, make mistakes, learn, and adapt, and competition leads to adaptation and innovation, natural selection shapes market ecology, and evolution determines market dynamics over time [11]. To stay on the market, investors are forced to adapt and become more competitive; otherwise, they will be eliminated. The evolutionary process of the market is reflected in its efficiency, which varies over time. The expected return, namely, the prices, is affected by the changes in the market, so that, occasionally, there may be opportunities for profit for investors [12]. The fractal markets hypothesis emphasizes the impact of market liquidity and the investment period on balance in the market. Unlike the theory of efficient markets, where the focus is on market efficiency, the theory of fractal markets focuses on market stability [13]. In such a market, investors assume the same level of risk [14], which leads to similarities in distribution returns regardless of the time horizon allocated to the investment [15,16]. Due to these similarities, the association between the capital market and the notion of a fractal is made.

The paper is dedicated to studying the main statistical properties of stock returns from the perspective of the tracked statistical distribution; they usually have a more extensive distribution and wider tails than the normal distribution. The presentation of the statistical methodology emphasizes the predictability tests for detecting short- and long-term memory in the profitability series. The approach to the efficiency of the capital markets is carried out through the lens of moving away from the efficiency hypothesis and creating a hierarchy of the markets according to the deviations they present. Thus, using the efficiency context in relative form, the restrictive barrier of the “all or nothing” type, specific to the absolute efficiency hypothesis, is overcome. The Hurst exponent, fractal dimension, and Taken’s theorem are proposed here to be used as efficiency measures, and respectively, the efficiency index considers both short-term and long-term dependencies.

The work is organized into three sections, preceded by the introduction, and ends with a section dedicated to the conclusions and prospects for further research. In the first section, the mathematical methods of analysis using the Hurst exponent, fractal dimension, and Taken’s theorem are presented, in Section 2, the analysis of the case study for the capital market in Romania is given, and Section 3 is dedicated to the discussion of the obtained results.

2. Materials and Methods

2.1. Proposed Method

In this article, we will focus mainly on the first three features, which refer to the hypothesis of informational efficiency to the shape of the distribution of returns.

Regarding the time series typology, we identify the following applicable processes to model the financial data generation process:

• Stationary processes (zero-order integrated, d = 0), characterized by an exponentially decreasing autocorrelation function, corresponding to a short-memory time series. Observations at large intervals of time, one from the other, are independent.
• Integrated processes of the first order (d = 1), where the autocorrelation function decreases linearly, and the observations at large time intervals are not independent.
• Fractionally integrated processes [17], characterized by non-zero correlations between observations separated by large time distances, the autocorrelation function decreases slowly towards zero, according to a hyperbolic function. For d ∈ (0, 0.5), the process is stationary and has long persistent memory; autocorrelations are positive and decrease hyperbolically. If d ∈ (−0.5, 0), the process is stationary, generating a series with an anti-persistent behavior. When d ∈ (0.5, 1), the process is non-stationary, being strongly persistent in the long term. Long memory dependencies invalidate the random walk model of stock prices and provide arbitrage opportunities in the capital market [18]. Some of the stationary time series show small dependencies between the observations located at large time distances, which denotes a persistent character of the analyzed phenomenon, namely, long memory.

The statistical methods used to model this behavior fall into two approaches: the development of models for fractionally integrated processes, namely, methods for estimating the Hurst coefficient, which is related to the fractional differentiation ordinal d, through the relation H = d + 0.5. In the case of self-similar processes, long memory; although, it is a global characteristic of the return series, reflects the degree of local smoothing in the series, quantified by the fractal dimension. Between the fractal dimension and the Hurst exponent, there is the relation D + H = 2.

2.2. Nonlinear Time Series Analysis

Nonlinear behavior allows a better understanding of complex natural phenomena. Nonlinear dynamics introduces new concepts and tools that will enable the analysis and investigation of the dynamics generated by nonlinear processes. It can be stated that, now, there is a conceptual unification of the notions (attractors, doubling of the period, bifurcations, Lyapunov exponent, and sensitivity to initial conditions) [19]. Techniques that study the concepts introduced by nonlinear dynamics are grouped under the generic name of nonlinear signal processing or nonlinear analysis. The behavior of a nonlinear dynamic system is figured in the state space or the phase space, a conceptual space in which the dimensions correspond to the variables in the system. Changes in time of the system described by differential equations are reflected by the movements of a point in the state space; movements called trajectories. An image of the change in the state of a system over several time intervals is called a phase portrait. The phase portraits reveal the existence of some attractors, regions, or points of the phase space toward which all close trajectories converge. A strange attractor will occupy a part of the phase space in which all the courses will be captured, apparently randomly, covering its entire surface without repeating. A state space can be created starting from a time series by graphically representing the observations shifted by a specific time interval, a process called state space reconstruction. 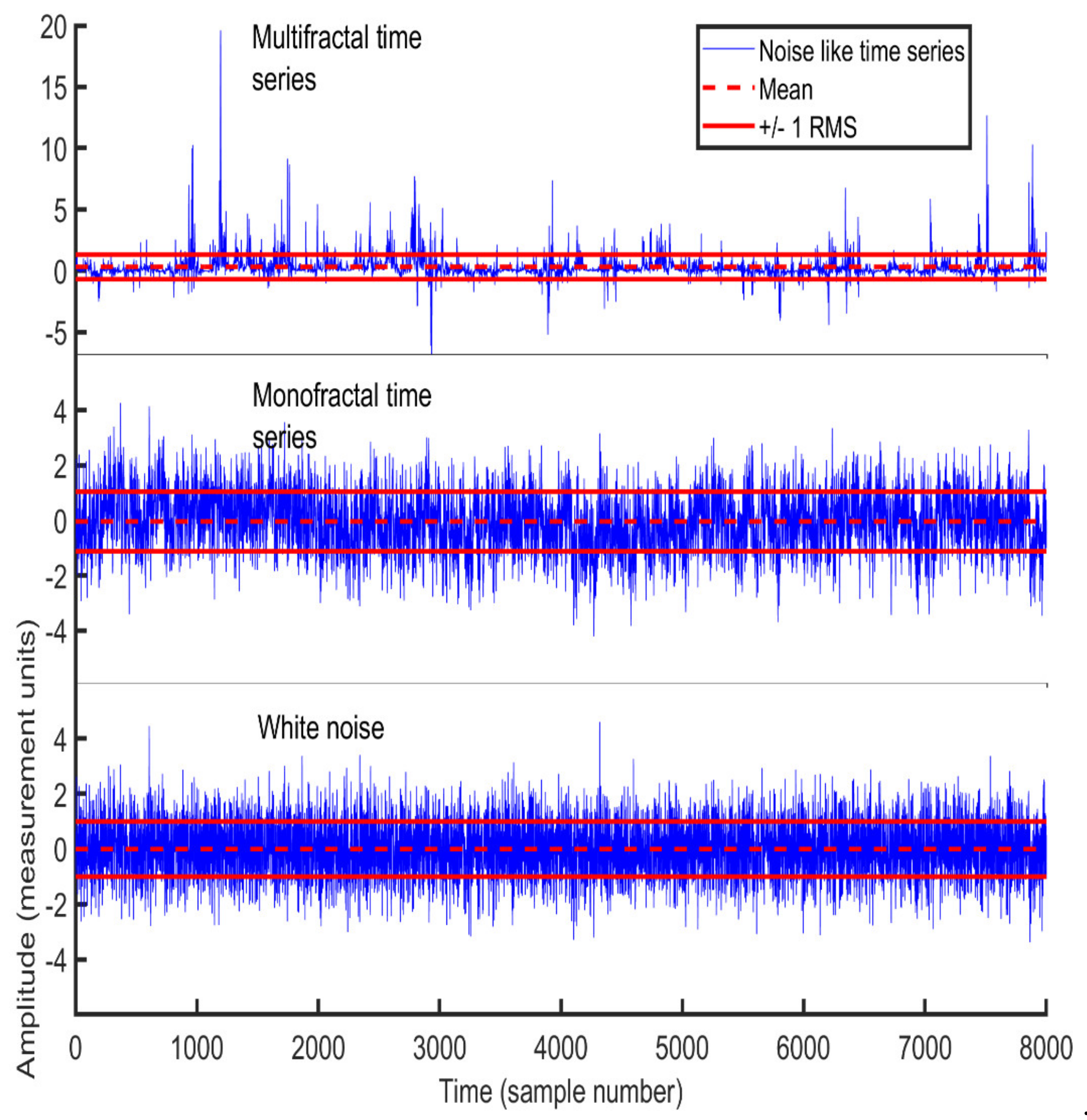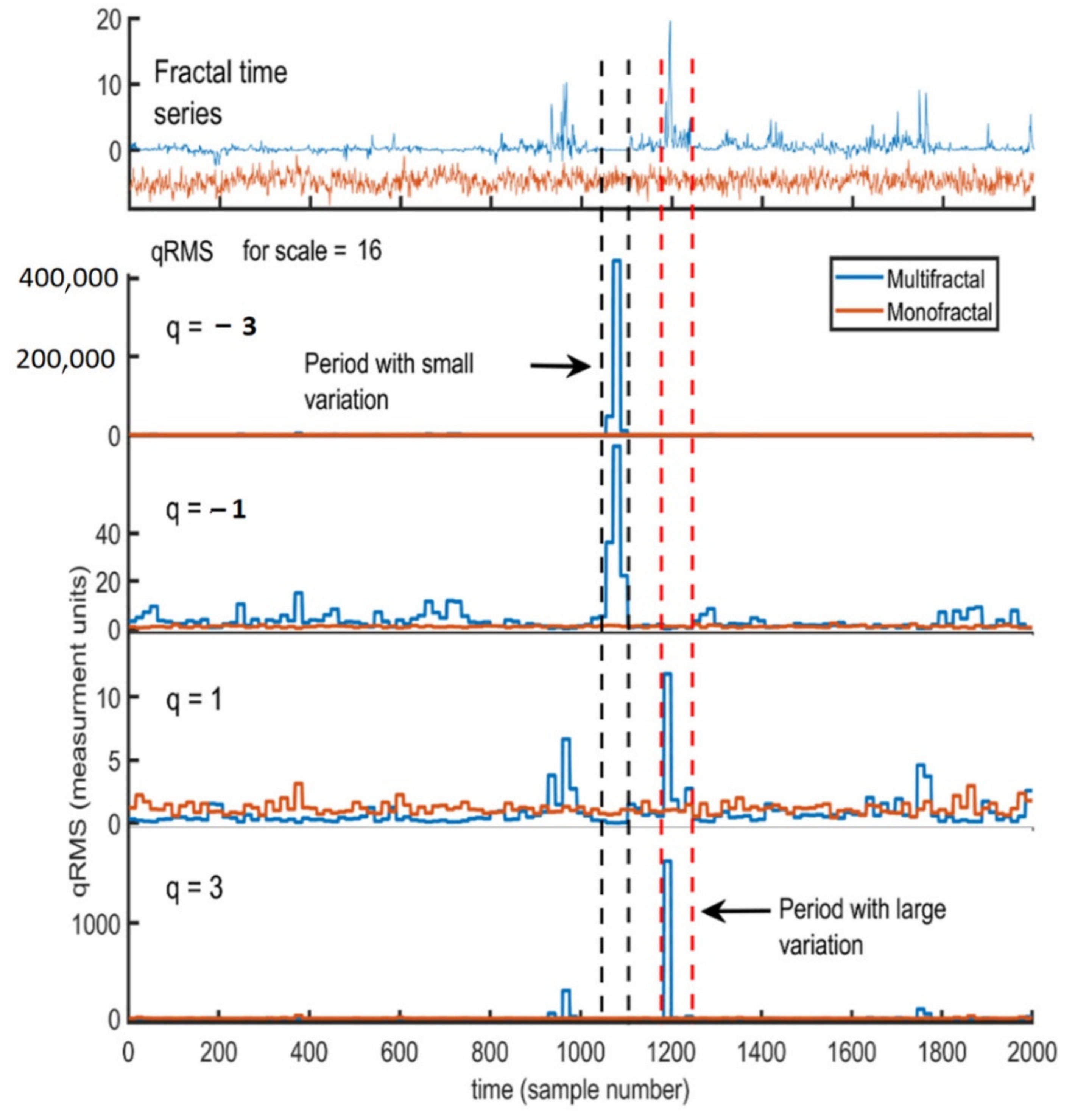Figure 1 presents the variation amplitude for different structures using signals such as white noise, monofractal, and multifractal.

2.3. Hurst Coefficient

The Hurst coefficient appears in several fields of applied mathematics, including chaos theory, memory processes, and spectral analysis [20]. The Hurst coefficient estimation, initially developed in hydrology, has been applied in fields ranging from biophysics to computer networks. However, the modern techniques used for estimation come from mathematics. The Hurst coefficient and the fractal size are, in turn, linked by the formula:

$$D=2-H$$

(1)

The fractal size indicates the roughness of a surface. A low-value Hurst exponent has a large fractal size and a rough surface, while a small Hurst value has a small fractal size and a smoother surface. The Higuchi method calculates the fractal size of the sample Hurst exponent. This consists of the formation of new waveforms by the interactive selection of different samples with the point starting m and delays factor k:

$$x_m^k=\left\{x\left(m\right), x\left(m+k\right),\dots ,x(m+\left[\frac{N-m}{k}\right]k)\right\}$$

(2)

In our case, the surface is represented by the signal distribution, and a high value of the Hurst exponent indicates desynchronization. Several methods can be used to estimate the Hurst coefficient: the differential dispersion method, the total dispersion method, the rescaled domain statistics method, the Higuchi method, the aggregate variance method, the absolute moment method, etc. The only techniques used to highlight the sensorimotor rhythms will be presented below. 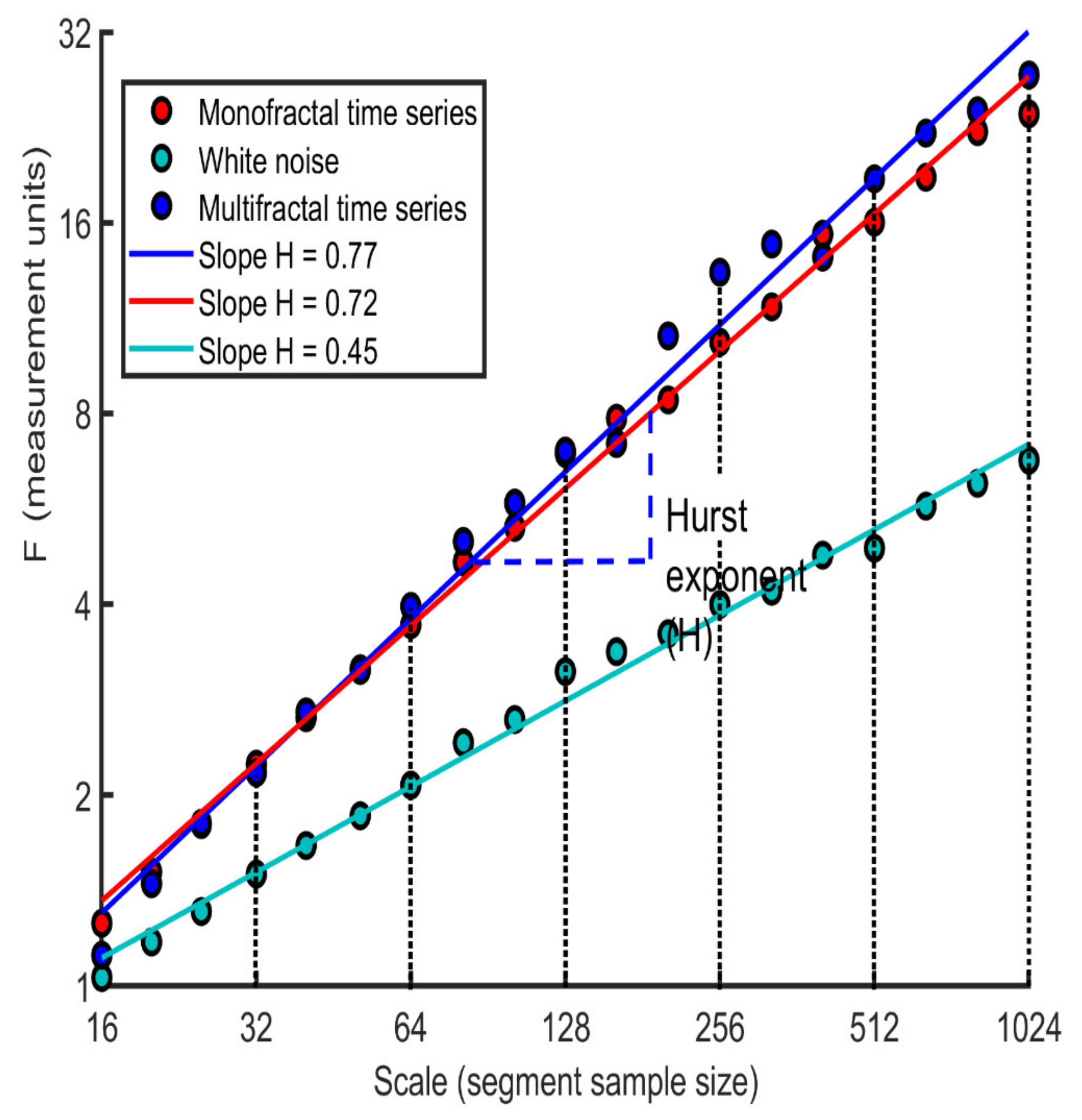Figure 2 shows the Hurst exponent (H) and its variation for the monofractal and multifractal time series compared with the white noise time series.

2.4. Fractal Dimension and Chaos Theory

The dimension concept has given rise to several variants, including box-counting, similarity, capacity, Hausdorff–Besicovich (or, simply, Hausdorff dimension), information, correlation, fractal, generalized, accumulation, and Lyapunov dimensions. A particular characteristic of fractal dimensions is that they do not necessarily have to be whole: they can take fractional values [21,22].

The slope of a straight line is represented on a logarithmic scale for which the x-axis determines the scale’s size, the y-axis determines the number of increments and the power or exponent in logarithmic proportionality. This power (or exponent) is called size. As we have noticed, the number of increments increases as the size of the measuring instrument decreases. This inverse dependence relationship shows that the exponent (dimension) in the power law is negative, which can be written as:

$$number of increments\propto {\left(scale size\right)}^{-dimension}$$

(3)

where the symbol $\propto$ means proportionality. Since the size is an exponent in this relationship, some authors call it an “exponential dimension”. Most of the time, the relation (3) is more useful in a form that gives us directly the value of the exponent (dimension). To obtain such a form, we logarithm both the members of Equation (3), and we will rearrange them:

$$\ln \left(number of increments\right)\propto -\left(dimension\right)\ln \left(scale size\right)$$

(4)

or

$$\left(-dimension\right)\propto \frac{\ln \left(number of increments\right)}{\ln \left(scale size\right)}$$

(5)

To remove the “−” sign, we will arbitrarily make the logarithm of the scale size negative and rewrite it as −ln (scale size) = ln (1 scale size). So, it will result:

$$\left(-dimension\right)\propto \frac{\ln \left(number of increments\right)}{\ln \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$scale size$}\right.\right)}$$

(6)

“Dimension” as a scaling exponent takes, in most cases, non-integer values.

An exponent dimension often remains constant over a wide range of scale dimensions and, thus, represents a quantitatively invariant quantity. It can indicate the degree of complexity of a system and represents a numerical quantitative way to evaluate or compare the geometric complexity of objects or systems of different sizes, shapes, and structures.

Dimensions as scaling exponents are of particular importance in chaos theory for two reasons:

• Measuring size (the exponent or slope of a line in a logarithmic coordinate system) allows for distinguishing between chaotic and random. The size of an object characterizes its geometry and represents a fundamental physical feature. For example, a chaotic attractor has a specific representation in phase space, and that representation has a particular finite and measurable dimension. By contrast, a randomly operating system can theoretically visit the entire phase space sooner or later; in this case, there will be no definite configuration (as is an attractor) in the phase space. Then the size becomes equal to the sink size and thus becomes infinite as we continue to increase the sink size.
• The size of an attractor reveals the number of variables or measurable quantities needed to describe or model the system. For example, dimension zero corresponds to a point in phase space (a constant value); to explain a line, we need a dimension; to describe a rectangle, we need two variables—length and width. Therefore, modeling a system or object requires several variables at least equal to its size.

There are many types of exponent dimensions, such as similarity dimension, capacity dimension, Hausdorff dimension, information dimension, correlation dimension, and fractal dimension [23]. These dimensions are interconnected, some having the same numerical value under certain conditions.

There are several reasons why the word “fractal” has become attached to the notion of “dimension”. The first of these would be that when the lengths of objects follow a power law when plotted against scale size, the objects are often fractals. In other words, the same geometric law or relationship applies to smaller and smaller scales. The second reason is that the value of the dimension in the case of analytical dimensions is usually incomplete, which leads to its association with the notion of the fractal. The term “fractal dimension” actually includes several types of dimensions, such as similarity, capacity, and Hausdorff. Grouping them in three implies that the linear dependence of the number of increments on the scale size (relation 6) can also be extrapolated to a zero-scale size. Suppose this assumption is correct (and there is no way to show that it is or is not), then, at a scale dimension equal to zero, the similarity, capacity, and Hausdorff dimensions take the same value since they derive from the same basic formula. With more recent discoveries, the term “fractal dimension” began to be applied to other types of dimensions. Therefore, when this notion is encountered in the literature, one of the two interpretation methods below must be chosen:

• The author refers to a group of exponent dimensions.
• The author refers only to a single exponent dimension (in which case it must be carefully studied which of them is being referred to) [24].

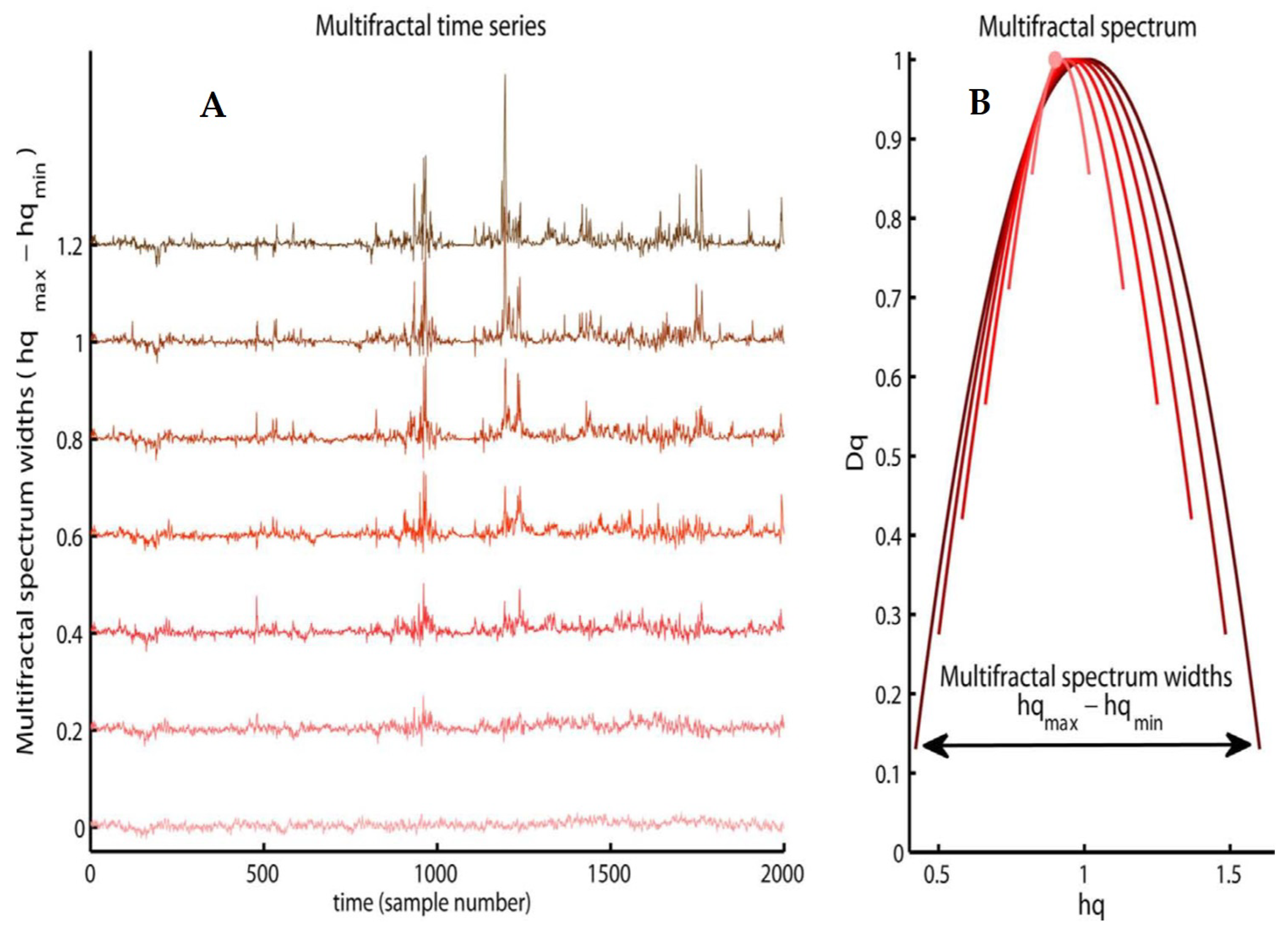
Figure 3 shows the multifractal and continuous time series analysis with the same order q-Hurst q = 2 but with different multifractal spectra. If we compare Figure 3A with Figure 3B, we notice the increase in the structural differences between periods with small and large fluctuations such as the multifractal spectrum, and the width becomes larger. Thus, each mean fractal structure for the Hurst exponent has deviations from the average fractal structure (see Figure 3). In addition, the shape of the multifractal spectrum in Figure 3 need not be symmetrical.

2.5. Phase Space Reconstruction from Taken’s Theorem

In the last 20 years, various techniques have been developed for analyzing and processing signals included in the category of chaotic nonlinear dynamics. These techniques are called “nonlinear signal processing techniques” and are especially based on the Takens theorem [25]. The theorem allows the reconstruction of a one-dimensional or multidimensional trajectory equivalent to the initial trajectory extracted from the phase space of the time series from which it started. However, the idea was used long before its publication. The authors in [26] used a graph with coordinates x(t), x(t + 1) − x(t − 1) for a sunspot time series analysis. Phase space embedding is a process by which a time series is transformed into a series of coordinates in the reconstructed phase space. The set of reconstructed coordinates defines a trajectory in the reconstructed phase space. If the reconstructed phase space has m dimensions, then each reconstructed spatial coordinate X_i is a vector of size m obtained from the initial time series, considering only some components of the original time series separated by a time interval called delay [27]. In practice, two important problems appear regarding the delay method as a phase space reconstruction method. The first problem, common to all reconstruction methods is establishing the minimum inclusion size. This minimum size is unknown and must be determined. When the system’s nonlinearity becomes more and more pronounced, more complicated attractors can appear. The final trajectory at which the system is established can have a very irregular shape without appearing periodic. However, the trajectory can still be called an attractor because neighboring trajectories are drawn into it, with no way out. An attractor with fractal dimensions (non-integer dimensions) is called a strange attractor [28]. Takens introduced the term to describe the attractor resulting from the series of bifurcations suffered by a system describing the flow of fluid [29]. Strange attractors are the basis of the concept of self-organization. Although, at first glance one, one could say that they are chaotic, they nevertheless manifest order at a subtle level, order that becomes evident over time if we look at it from the right perspective.

Strange attractors are unique in that they show a pronounced sensitivity to initial conditions, two very close trajectories at one point in time can diverge arbitrarily at the next point, their divergence increasing exponentially in time. This phenomenon is called the butterfly effect. Another method used in the dynamic analysis is that of the autocorrelation function. Following the theoretical studies carried out by Takens, Packard, and Ruelle [30], it was found that when building a set of coordinates in which the structure of the orbits traversed by the nonlinear system in its dynamics can be described, it is not necessary to use the time derivatives of the coordinates. Instead of them, you can directly use the physical quantity (s) whose evolution over time was recorded, in the form of $s\left(t+n\tau \right)$, where n = 1, 2, 3, …, d, $\tau =k{\tau }_s$ represents an appropriate delay time chosen, and τs is the sampling time of the recorded signal. The following relationship defines the vector of delayed coordinates:

$$y_n=\left\{s\left(t_0+{n\tau }_s\right), s\left(t_0+{n\tau }_s+{k\tau }_s\right),\dots ,s\left[t_0+{n\tau }_s+k\left(d-1\right){\tau }_s\right]\right\}$$

(7)

The space constructed with the help of these vectors $y_n$ is called reconstructed space. According to the theorems of Takens, the geometric structure of the dynamics of the nonlinear system for which the physical quantity s was measured can be observed in the Euclidean space reconstructed d-dimensionally if the condition is met:

$$d\ge 2d_a+1$$

(8)

where $d_a$ is the size of the attractor of interest, the integer d represents the sink size, and the method described above is called the delay method. In the case of a finite amount of noiseless data, the delay time can be chosen arbitrarily according to the theorems of Mané and Takens. In addition, the delay time must be a multiple of the time of sampling ${\tau }_s$, because the data are recorded exclusively at these times, and any interpolation may introduce errors. For a data set, $s_i=s\left(t_0+i{\tau }_s\right)$ where i = 1, 2, …, $N_0$, the autocorrelation function is given by the expression:

$$C\left(\tau \right)=\frac{{{\displaystyle \sum }}_{k=1}^{N_0}\left[s\left(t_0+k{\tau }_s+\tau \right)-s_{a\nu }\right]\left[s\left(t_0+k{\tau }_s\right)-s_{a\nu }\right]}{{{\displaystyle \sum }}_{k=1}^{N_0}{\left[s\left(t_0+k{\tau }_s\right)-s_{a\nu }\right]}^2}$$

(9)

where

$$s_{a\nu }=\frac{1}{N_0}{\displaystyle \sum }_{k=1}^{N_0}s\left(t_0+k{\tau }_s\right)$$

(10)

The method of determining the delay time using the autocorrelation function consists in choosing the value of τ at the time corresponding to the zero crossing of the $C\left(\tau \right)$ function. If the autocorrelation function does not pass through the zero value, the value corresponding to the first local minimum is chosen as the delay time. The values of the delay times calculated at the zero crossing of the autocorrelation function, or their integer multiples, are suitable for calculating the dip size. The autocorrelation of a periodic signal will give rise to a periodic function $C\left(\tau \right)$, while, in the case of a chaotic signal, the envelope of the autocorrelation function will exponentially tend to zero [31]. 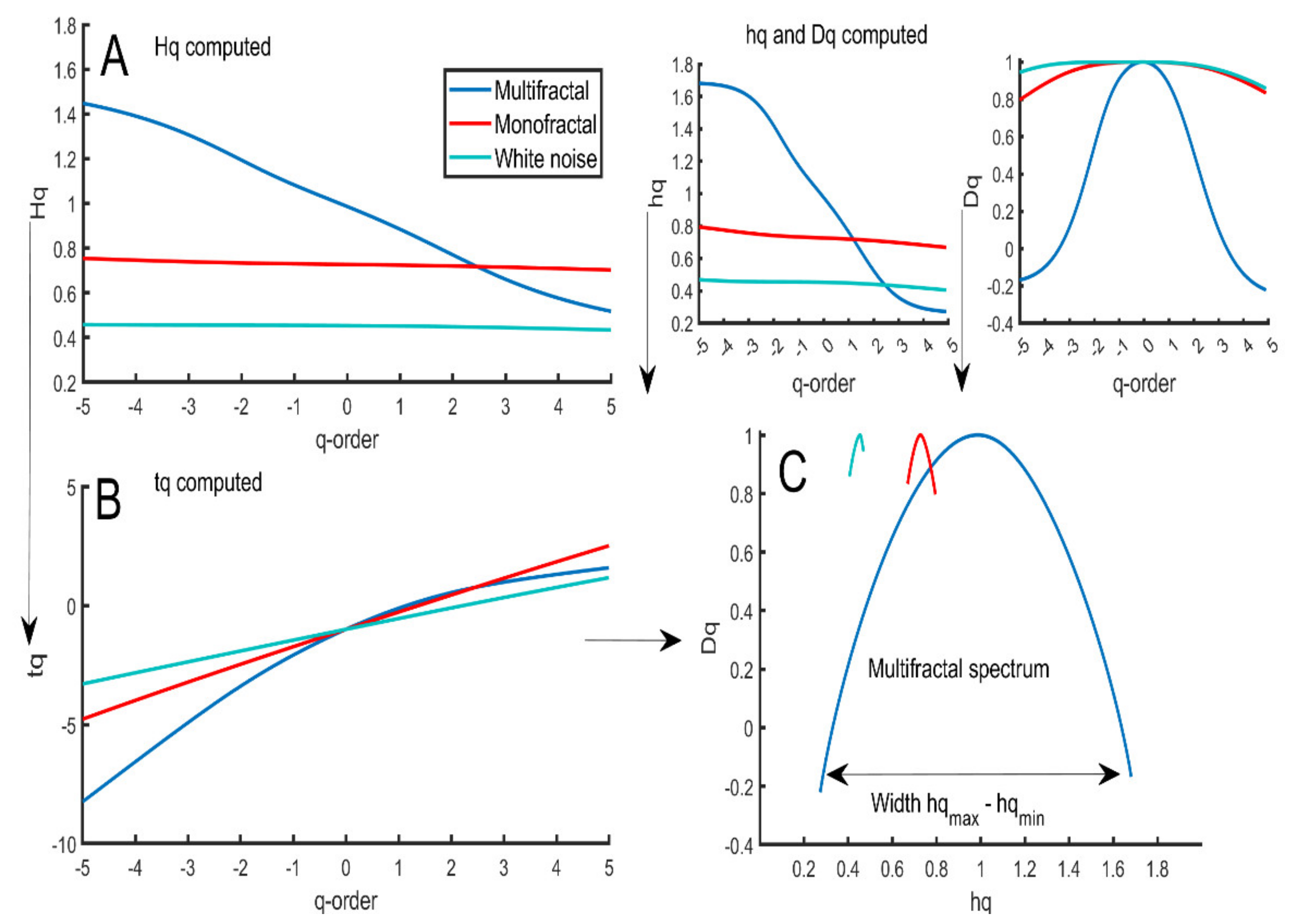Figure 4 shows the multiple representations of a multifractal spectrum.

Figure 5 shows the variation in the q parameter that influences small and large fluctuations for a monofractal and multifractal time series.

3. Results

In [32], empirical studies only establish how much the capital market approaches this ideal, and efficiency in absolute form remains an ideal, difficult to achieve in practice. Starting from the empirical analyses that support the previous statement, an essential step in analyzing the efficiency of the capital markets is the evolutionary approach to informational efficiency, by interpreting the predictions determined by the dynamics over time. This article’s main contribution consists in analyzing the efficiency of the European capital market, both from the perspective of dynamics over time and by using several elements to quantify the deviations related to an efficiency hypothesis. The elements used for predicting the degree of efficiency were calculated for a period using sliding analysis windows to ensure the highest possible accuracy for the estimated values for the short- and long-term dependencies. The determinations were based on three analyses, the Hurst exponent, the fractal dimension, and Taken’s theorem. The Hurst exponent identifies the presence of long memory, the fractal dimension is an indicator of local memory, and Taken’s theorem introduces the first-order autocorrelation coefficient (it measures short-term memory). We analyze the predictability of stock market returns based on deviations from the random walk model, determined by short-term dependence (linear or non-linear), respectively, of long-term dependence. We also use the tests developed in the theory of fractal markets [33] because this theory highlights a new way of approaching deviations from the reference model. In general, long memory can be described using the self-similarity properties determined by the fractal dimension as a local characteristic of the time series.

Multifractality has become a suitable scientific framework for studying efficiency [34]. Thus, the tests can be classified into heuristic, parametric, and non-parametric. The category of heuristic methods includes R/S analysis introduced in Hurst, KPSS statistics (Kwiatkowski), V/S analysis (Giraitis), DFA analysis (Peng), or the estimation method based on temporal aggregation [35]. This article used the rescaled domain method, R/S, to estimate the Hurst exponent. The R/S statistic is calculated as the difference between the maximum deviation from the mean and the minimum deviation, related to the standard deviation, which can be described by a relationship in the form of a power function ${\left(\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right)}_{\tau }=C{\tau }^H$.

For the analysis of capital markets, the fractal dimension quantifies the degree of smoothing in the financial series graph, being an estimator for the local memory, which can be found, based on the self-similarity property, in the global memory. The estimation methods used in this study are the Hall–Wood [36] and Genton [37] estimators. The Hall–Wood method divides the profitability series over time into petite sizes series to determine the existence of a repetitive pattern in the series graph. The graph of the series is covered with smaller and smaller squares. The Genton method uses the estimator:

$$\widehat{D_G}=2-\frac{log\widehat{V}\left(\frac{2}{n}\right)-log\widehat{V}\left(\frac{l}{n}\right)}{2log2}$$

(11)

which is based on the average square of the differences in returns found at $\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$ moments away. Long-term dependencies are estimated based on the Hurst exponent, calculated on the whole time period and overlapping windows. The overlapping window estimation methodology involves using, at each iteration, a fixed number of observations, namely, 200, and the estimation of the Hurst exponent for that window. At each iteration, a new analysis window is formed by introducing the subsequent profitability into the time series and removing the oldest observation. This way, several values of the Hurst exponent are obtained, namely, the total number of returns from which we subtract the window length. The fractal dimension is calculated as the average of the value estimated by the Hall–Wood method and that estimated by the Genton method. The generalized measure, introduced by Taken, is based on the magnitudes of long-term dependencies, short-term, and fractality dimensions, respectively, the Hurst exponent, the first-order autocorrelation coefficient, and the fractal dimension. The generalized measure of efficiency is determined by:

$$EI=\sqrt{{\displaystyle \sum }_{i=1}^N{\left(\frac{\widehat{M_i}-M_i^{*}}{R_i}\right)}^2}$$

(12)

where $\widehat{M_i}$ is the estimated value of the order efficiency measure i, $M_i^{*}$ is the expected value of measure i in the case of an efficient market, and $R_i$ is the interval in which measure i can take values. These values are between 0 and $\frac{\sqrt{n}}{2}$, for which n represents the number of measures taken into account. When the market is efficient, we have $EI=0$, and the value is $EI=\frac{\sqrt{n}}{2}$, related to the highest degree of inefficiency. To classify the results, indicators were used according to the degree of deviation from the efficiency model, using the results in the absolute value of the Hurst exponent and the fractal dimension (0.5 for the Hurst exponent, and 1.5 for the fractal dimension), compared to the results obtained by the generalized theorem of Taken’s.

The analysis was carried out for five stock market indices used in Romania’s capital markets, market indices from developed countries, and indices from countries with less mature capital markets. The data are daily and cover the period 2005–2019. The entire period was divided into three sub-periods, as follows: the period preceding the economic-financial crisis (2005–2006), the years 2007–2008, which mark the financial crisis, and the period 2009–2019 in which the markets entered a period of stability; although, the effects of the problem continue to be felt. The capital market in Romania analyzed based on the BET index, belongs to the group of markets with a low degree of informational efficiency, having an increased potential for predictability.

Table 1. Index values according to Hurst exponent, Fractal Dimension, and Generalized efficiency measure for the period 2005–2019.

Asset	Hurst Exponent	Long Memory (%)	Short Memory (%)	Excess Profitability
SIF 1	0.7724	0.7843	0.65	4.4614
SIF 2	0.7689	0.7284	0.46	4.8968
SIF 3	0.6578	0.6945	0.41	3.4272
SIF 4	0.5998	0.5891	0.19	2.3391
SIF 5	0.7685	0.7798	0.58	6.0728

shows the rankings according to the Hurst exponent, fractal dimension, and generalized efficiency measure over the entire period.

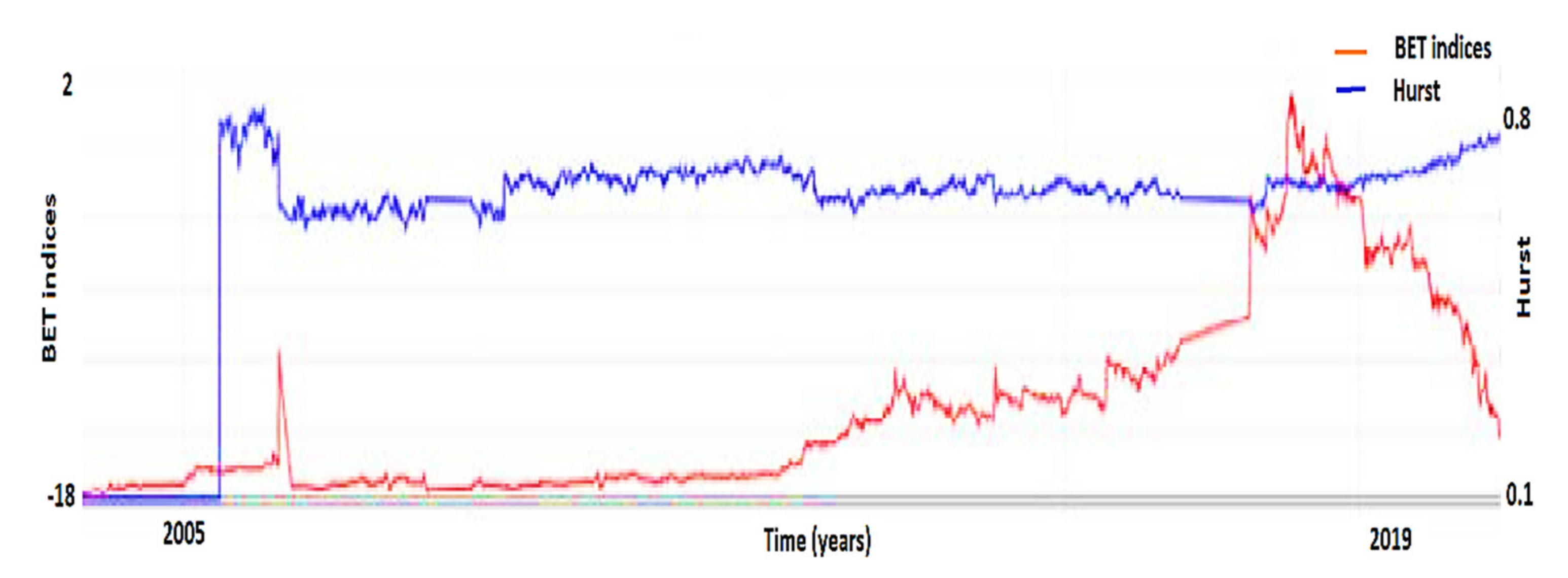
Figure 6 shows the evolution of calculating the fractal dimension for the BET indices performance for the period 2005–2019. The calculation parameters for the fractal dimension are: the dimension equal to 7 and the multiplication factor 2/3. Figure 7 shows the evolution of the Hurst exponent according to the BET index for the period 2005–2019.

4. Discussion

The presence of dependencies in the return series indicates that technical analysis strategies could be profitable. It is possible to ask to what extent the presence of long-term or short-term dependencies leads to obtaining financial benefits. The empirical results show that the presence of long memory is statistically positive and significantly influences excess profitability. The presence of short memory in the profitability series does not have a significant influence on excess profitability. The extra profitability is positively associated with the variables specific to the company, the risk being a statistically significant coefficient for both periods. At the same time, the return on equity significantly contributes to explaining the variance of the dependent variable only in the second period. Similar results are obtained when a transaction cost of 0.2% is considered. The empirical results confirm the prediction that the excess profitability of the moving average strategy is mainly due to long memory dependencies and not those with a short memory.

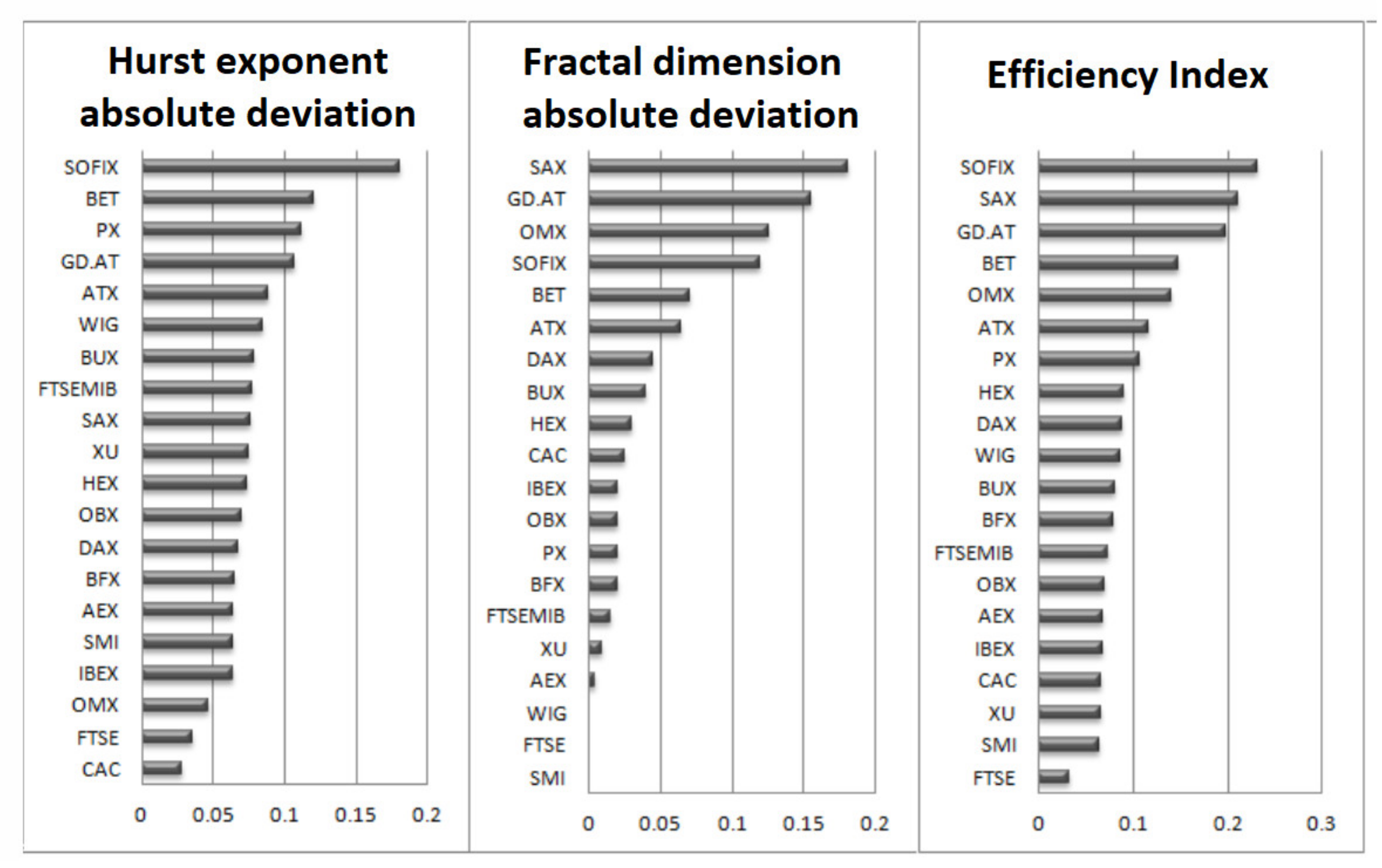
Figure 8 shows the index ranking according to the Hurst exponent, the Fractal Dimension, and the Generalized Measure of efficiency for 2005–2018 (source Bucharest Stock Exchange).

For the classification of indices according to the degree of deviation from efficiency, the values 0.5 for the Hurst exponent and 1.5 for the fractal dimension were used, thus determining the generalization condition.

For the entire period, 2005–2019, we draw the following conclusions:

Using the generalized measure, the most efficient markets are mature capital markets from developed countries, such as Great Britain, France, or Switzerland. A high degree of inefficiency appears in the capital markets of Bulgaria, Slovakia, Greece, and Romania;

• For most of the indices, significant deviations are found in the case of the Hurst exponent, indicating the presence of long memory in returns rather than local memory;
• Based on the determination of the generalization dimension and the degree of inefficiency, the Romanian capital market occupies the fourth position. The Hurst exponent indicates the presence of long memory in the series of high-intensity returns (second position in the BET index ranking).

As a whole, the markets of Bulgaria, Slovakia, Greece, and Romania show high deviations from efficiency. In contrast, mature markets such as Great Britain, France, Sweden, or Switzerland have a high-efficiency level. The results of the empirical study on the efficiency of the Romanian capital market identify a low level of efficiency, which is a positive evolution over time from the point of view of the degree of informational efficiency. Unlike the existing studies on the Romanian capital market, this study takes a more complex approach through the prism of the methodology used, as follows: (a) efficiency indicators recently recommended in the literature are used to identify the main types of dependencies (fractal dimension, generalized measure), (b) the dynamics over time were taken into account by applying the sliding window procedure (in the estimation the Hurst exponent), and (c) the degree of deviation from efficiency is investigated relative to the main mature European markets but also compared to similar markets. The capital market in Romania, analyzed using the BET index, can be included in the group of markets with a low degree of informational efficiency, presenting predictability potential. This aspect is the first clue that statistical forecasting methods or strategies from technical analysis could be used to obtain profit.

The fractal markets hypothesis emphasizes the impact of market liquidity and the investment period on market equilibrium. Unlike the theory of efficient markets where the focus is on market efficiency, the theory of fractal markets focuses on market stability. In such a market, investors assume the same level of risk, which leads to similarities in the distribution of returns regardless of the time horizon allocated to the investment. Due to these similarities, the association between the capital market and the notion of a fractal is made. Economic analysts admit that efficiency in absolute form remains an ideal that is difficult to achieve in practice, and empirical studies can only determine how closely a market approaches this ideal. Starting from the empirical evidence that supports this statement, a step forward in the theory of efficient markets is the evolutionary approach to informational efficiency by investigating the degree of efficiency of markets from the perspective of dynamics over time. This article’s main empirical contribution consists in analyzing the degree of the relative efficiency of five Romanian capital markets, both from the perspective of time dynamics and by using several measures to quantify the deviations from the efficiency hypothesis. Some measures used to quantify the degree of efficiency were calculated for the entire period and on sliding windows to ensure greater robustness of the estimated value. Among the measures used is a generalized measure, proposed relatively recently in the literature [38,39,40,41,42,43,44,45], which incorporates both the deviations that appear as a result of the existence, in the return series, of some short-term and some long-term dependencies. The rankings were based on three measures: the Hurst exponent, the fractal dimension, and the Takens generalized measure. The Hurst exponent identifies the presence of long memory, the fractal dimension is an indicator of local memory, and the generalized measure includes, in addition to the two indicators, the first-order autocorrelation coefficient (measures short-term memory). We analyze the predictability of stock market returns based on deviations from the walking pattern random generated by the existence of short-term, linear, or non-linear dependencies, and long-term dependencies. Mainly, long memory can be described by the fractal dimension based on the self-similarity property; this represents a local characteristic of the time series. Multifractality has become a suitable scientific framework for the study of efficiency.

To compare the results obtained with the proposed method, we referred to the following articles [46,47,48,49,50], which have as their theme the use of fractal theory for capital market analysis. The comparative results are presented in

Table 2. Comparative results.

Reference	Year	Method Used	Result
[46]	2022	Fractal-Random Walk	Price Prediction
[47]	2022	Fractal-Sliding windows	Stock indices
[48]	2022	Time Series-ARMA-GARCH	Stock indices
[49]	2021	Fractal–Lyapunov Exponent	Stock Exchange
[50]	2020	Time Series-Time varying parameter	Stock Market
Proposed Method	2022	Fractal Dimension, Hurst Exponent, Taken’s algorithm, sliding windows	Efficiency Market

.

By analyzing various studies on market efficiency and the fractal characteristic of stock markets, especially developed markets, it is concluded that developed markets are efficient, and long-term market efficiency and stability cannot be guaranteed. For the description of the distribution of national returns, attention was focused on generalized hyperbolic distributions, which have statistical properties similar to financial returns. The presence of wide tails in the distributions (of extreme values) suggests the use of statistical tests and measures, for detecting dependencies, and we have taken this behavior into account. For their modeling and analysis, we have combined several algorithms that allow the detection of the main types of dependencies that could be present in the profitability series, measures that are robust to the behavior of profitability variations. These statistical measures were applied both for the entire period and for sliding windows.

From a methodological point of view, to identify whether the considered Romanian markets present deviations from the weak form of efficiency, the Hurst exponent, the fractal dimension, and the generalized measure of the degree of efficiency are used as measures of efficiency. Long-term dependencies are estimated based on the Hurst exponent, and calculated on the whole period and overlapping windows. The overlapping window estimation methodology involves using, at each step, a fixed number of observations, namely, 300, and the estimation of the Hurst exponent for that window. A new window is formed at each stage by serially introducing the following return and discarding the oldest observation. In this way, several values of the Hurst exponent are obtained, namely, the total number of returns minus the length of the window. The average gives the Hurst exponent used in the comparisons between the exponent estimated over the entire period and the median value of the estimates obtained from the overlapping windows procedure. The fractal dimension is calculated as the average of the estimated value. The generalized measure introduced in the article is based on long-term, short-term dependency and fractality sizes, the Hurst exponent, the first-order autocorrelation coefficient, and the fractal dimension. In the calculation of the generalized measure, the following are considered: the average of the Hurst exponent estimators over the whole period and on overlapping windows, the average of the fractal dimension estimators, and the first-order autocorrelation coefficient. To determine the generalization method used for the classification of efficiency indices, we used the values 0.5 for the Hurst exponent, and 1.5 for the fractal dimension.

5. Conclusions

The empirical studies in this paper also aim to analyze the statistical characteristics and dynamics of returns/asset prices in the Romanian capital market. Although the results obtained during our scientific approach add more information to the existing literature, mainly to the empirical literature on the Romanian capital market, we can identify the limits of the present research, naturally suggesting some future research directions. The first future direction of the study regards the probability laws identified as appropriate for the daily returns relating to the five considered assets, namely, the generalized hyperbolic distribution, inverse Gaussian normal, and t-Student, and consists of extending the analysis to a more extensive set of assets, from the Romanian and foreign market respectively. In addition, the Anderson–Darling test can be an alternative to the KS test since it gives greater importance to the deviations in the empirical distribution function from the theoretical one for the distribution’s tails. The study regarding the estimation of the value at risk revealed the importance of the choice of the analysis period, namely, the test period, which, when testing the prediction ability of the estimation method, is an aspect that can be deepened in order to delimit some possible benchmarks in the choice of the two periods.

The work is dedicated to studying the main statistical properties of stock returns from the perspective of the followed statistical distribution; they usually have a higher distribution and wider tails than the normal distribution. The presentation of the statistical methodology emphasizes the predictability tests for the detection of short- and long-term memory in the profitability series. This article highlights an empirical study on the efficiency of the capital market in Romania in the context of 20 developed or developing markets in Europe. The approach to the efficiency of the capital markets is carried out through the prism of moving away from the efficiency hypothesis and ranking the markets according to the deviations they present. Thus, by using the efficiency context in relative form, the restrictive barrier of the "all or nothing" type, specific to the hypothesis of absolute efficiency, is overcome. The Hurst exponent, Fractal dimension, and Taken’s theorem are proposed here to be used as measures of efficiency, namely, an efficiency index that considers both short-term and long-term dependencies. Based on the three measures of efficiency, a ranking of the markets is carried out for 14 years but also on three sub-periods delimited according to the economic climate. The obtained results place the Romanian capital market among the markets with the most significant deviations from the weak-form efficiency concept and identify different degrees of efficiency throughout the investigated sub-periods. They make a synthesis in the very vast field of time series analysis and prediction. We particularly insisted on the non-linear analysis of the time series to identify the manifestation of chaos according to a methodology that involves going through successive stages. The identification of chaos in other time series corresponds to the manifestation of some processes in the real world and the establishment of possible correlations between the appearance of chaos and qualitative changes in the system’s evolution. The obtained results pave the way for a prediction algorithm that uses the combined capabilities of neural networks (MLP) and wavelet networks. We empirically demonstrated that, in the case of chaotic time series, the number of inputs of the MLP neural network for which optimal predictions are obtained must be approximately equal to the product of the inclusion size and the delay parameter used for the reconstruction of the state space. These results will be presented in a subsequent article.

To study the efficiency of the relative deviation of the capital markets, we used the deviations of the Hurst exponent of the fractal dimension from the characteristic value of an efficient market. From a statistical perspective, we ask to what extent these differences differ significantly from zero to be able to identify markets with statistically significant deviations from the efficiency hypothesis. The answer to this question can constitute a future direction of research.