Consensus of Julia Sets

Abstract

The Julia set is one of the most important sets in fractal theory. The previous studies on Julia sets mainly focused on the properties and graph of a single Julia set. In this paper, activated by the consensus of multi-agent systems, the consensus of Julia sets is introduced. Moreover, two types of the consensus of Julia sets are proposed: one is with a leader and the other is with no leaders. Then, controllers are designed to achieve the consensus of Julia sets. The consensus of Julia sets allows multiple different Julia sets to be coupled. In practical applications, the consensus of Julia sets provides a tool to study the consensus of group behaviors depicted by a Julia set. The simulations illustrate the efficacy of these methods.

1. Introduction

The consensus of a multi-agent system is that the status of the intelligences of the multi-agent system composed of multiple intelligences tends to be consistent through information exchange and coordinated cooperation among the intelligences [1,2]. There are many practical projects, such as formation tracking control, multi-mobile robot systems, autonomous underwater vehicles, and so on. The study of the consensus of the multi-agent system is one of the most important topics within the research about the multi-agent system, and there are many results available on the design of the control protocols [3,4,5].

In general, there are two types of control problems regarding the consensus control: one is with a leader and the other is with no leaders. The former has been studied extensively [6,7,8], where the goal is to guarantee that the multiple intelligences can track the state trajectory of a leader. For example, consensus problems with an active leader are discussed and a neighbor-based controller together with a neighbor-based state estimation rule is proposed for each autonomous agent in [9,10]. The latter requests that each agent converges to a certain state [11,12]. In [13], the consensus problems for a network of first-order agents are addressed.

Recently, an increasing number of works on the consensus of multi-agent systems have been presented. According to the structure of the system model, there are the first-order multi-agent systems, the second-order multi-agent systems, high-order multi-agent systems and the general linear and nonlinear multi-agent systems. Compared with the linear multi-agent systems, the nonlinear multi-agent systems can describe more accurately the actual system. However, the control of the nonlinear systems is more complicated and there are very few control methods that are suitable for all nonlinear systems. In recent years, many results regarding the consensus of nonlinear multi-agent systems have been obtained. Two different consensus agreements have been introduced to resolve the output consensus problem with a leader and with no leaders for the first-order nonlinear multi-agent systems in [14]. In [15], the leaderless consensus controller designed for nonlinear multi-agent systems subject to the input saturation nonlinearity by using an event-triggered mechanism is discussed. With the aid of dynamic encoding and decoding, the consensus problem with a limited communication rate is studied for nonlinear multi-agent systems in [16]. Moreover, the output feedback consensus of nonlinear multi-agent systems is researched in [17]. In [18], the distributed consensus problem for a class of nonlinear multi-agent systems is investigated and a distributed control protocol is proposed, which leads to a distributed asymptotic consensus of overall nonlinear systems with either a known or unknown Lipschitz constant through $\lceil {log}_2\left(2R\right)\rceil$-bit information exchange between each pair of agents. The fixed-time event-triggered leader-following consensus issue for the nonlinear multi-agent system with uncertain disturbances is discussed in [19]. Furthermore, two distributed fixed-time controllers based on event-triggered mechanisms are put forward, which can guarantee that the settling time does not depend on the initial conditions and continuous controller updates are not required. Moreover, the fixed-time event-triggered tracking problem for a multi-dimensional nonlinear multi-agent system with uncertain disturbances is considered.

The Julia set and Mandelbrot set are two important sets in fractal theory. The properties and graphs of these two sets have been discussed extensively [20,21,22]. Applications of these two sets have also been discussed in physics, biology, and so on. For example, based on the particle dynamic characteristics, the physical meaning of the generalized Mandelbrot set and Julia set has been discussed [23]. Moreover, the fractal structure characteristics of the generalized Mandelbrot set and Julia set could visually reflect the change rule of the particle’s velocity. For arbitrary c of the system

$$z_{n+1}=z_n^r+c,$$

where c is a complex and $r>1$, the generalized Julia set gives the closure of all the possible unstable orbits of the particle within the velocity space. According to the practical application of the particle’s movement, the control and synchronization of Julia sets and Mandelbrot sets have been researched [24,25,26,27,28] in recent years. However, the synchronization of Julia sets and Mandelbrot sets is one to one, i.e., both the numbers of the response system and the drive system are one. Based on the applications of Julia sets and the study of the consensus of multi-agent systems, a natural and interesting question is the following: does the consensus of the multiple particles’ behavior depicted by Julia sets happen with a leader or with no leaders? Then, the controlled behaviors will be the same as the desired behavior of the target particle in the first case and all the controlled behaviors will be identical to a certain behavior in the second case.

Motivated by the above discussion, two new types of synchronization of Julia sets are proposed in this paper: one has a drive system and N response systems, which is called the consensus of Julia sets with a leader, and the other has no drive systems, which is called the consensus of Julia sets with no leaders. Then, controllers are designed to achieve the consensus of Julia sets of the classical Julia sets of the complex quadratic polynomials.

In this paper, the following notations are used: let R, N and $R^{m\times n}$ be the sets of real numbers, positive integer numbers and $m\times n$ real matrices, respectively. Let J be the Julia set.

2. Preliminaries

Graphs provide a method to model the communication rules among the agents. Take a graph $G=\{v,\epsilon ,A\}$ with N nodes, i.e., $v=\{1,2,\cdots ,N\}$. The node i means the $ith$ agent. All edges or arcs are denoted as $\epsilon \subset v\times v$. The pair $(i,j)\in \epsilon$ means that there is an edge connecting the agents i and j. The structure of graph G can be depicted by the adjacency matrix $A=\left[a_{ij}\right]\in R^{N\times N}$, where $a_{ii}=0$ and $a_{ij}=1$ if $(i,j)\in \epsilon$; otherwise, $a_{ij}=0$, $i,j=1,2,\cdots ,N$.

Definition 1.

Agent j is called the neighbor of agent i if $(i,j)\in \epsilon$. The set of the neighbors of agent i is denoted as $N_i=\left\{j\right|(i,j)\in \epsilon \}$.

The Julia set is one of the most important notations in fractal theory. Let

$$z(n+1)=f\left(z\right(n\left)\right)$$

(1)

Definition 2.

In [29], Let ${\left\{z\left(n\right)\right\}}_{n=1}^{\infty }$ be the trajectory of system (1) in the complex plane. The set

$$D=\left\{z\left(1\right)\right|\{{z\left(n\right)\}}_{n=1}^{\infty }\mathrm{remains} \mathrm{bounded}\}.$$

is called the filled Julia set corresponding to the map $f\left(z\right)$. In addition, the boundary of D is called the Julia set of system (1), which is denoted by J, i.e, $J=\partial D$.

Once the parameters in the systems are given, their Julia sets are determined. In this paper, the Julia sets are taken to be the intelligences to consider the consensus of Julia sets with a leader and with no leaders.

3. The Scheme of Consensus of Julia Sets with a Leader

The leader Julia set denoted as J is generated from the system

$$w(n+1)=h\left(w\right(n\left)\right).$$

(2)

The m follower Julia sets denoted as $J_i$ are generated from the following systems

$$z_i(n+1)=f_i\left(z_i\left(n\right)\right),i=1,2,\cdots ,m,$$

(3)

where $z_i\left(n\right)$ is the status and $f_i$ is the nonlinear function of the $ith$ follower.

Definition 3.

The consensus of Julia sets with a leader is to design $u_i(w\left(n\right),z_1\left(n\right),z_2\left(n\right),$$\cdots ,$$z_m\left(n\right);k)$ added to the $ith$ follower system, which makes the Julia set $J_i\left(k\right)$ of the $ith$ controlled follower system

$$z_i\left(n+1\right)=f_i\left(z_i\left(n\right)\right)+u_i(w\left(n\right),z_1\left(n\right),z_2\left(n\right),\cdots ,z_m\left(n\right);k),i=1,2,\cdots m,$$

(4)

satisfy

$$\underset{k\to k_0}{lim}{J}_i\left(k\right)=J,i=1,2,\cdots m,$$

(5)

where k is the control parameter and $k_0$ is a certain number or possibly ∞.

Take

$$u_i(w_n,z_i;k)=k[{\displaystyle \sum _{j\in N_i}^m}(f_i\left(z_i\left(n\right)\right)-h\left(w\left(n\right)\right))+a_{j0}(f_j\left(z_j\left(n\right)\right)-h\left(w\left(n\right)\right))]+$$

$$\sum _{j\in N_i}^m{a}_{j0}(f_j\left(z_j\left(n\right)\right)-h\left(w\left(n\right)\right)),$$

(6)

where $a_{j0}=1$ when there is information communication between the leader system and the $ith$ follower system and $a_{j0}=0$ when there is no information communication between the leader system and the $ith$ follower system. Evidently, it is not possible that all $a_{j0}=0$ since the information needed to consider the consensus should be coupled. Then,

$$z_i\left(n+1\right)-w\left(n+1\right)=(1+k)(f_i\left(z_i\left(n\right)\right)-h\left(w\left(n\right)\right))+\sum _{j\in N_i}^m(1+k)a_{j0}(f_j\left(z_j\left(n\right)\right)-h\left(w\left(n\right)\right)).$$

(7)

From the definition of the Julia set, we simply need to consider the initial points where the trajectories are bounded. Therefore, suppose that there is an M satisfying $|f_i\left(z_i\left(n\right)\right)|\le M$ and $\left|h\right(w\left(n\right)\left)\right|\le M$. Thus,

$$\begin{array}{c}|z_i\left(n+1\right)-w\left(n+1\right)|\le |1+k|·|f_i\left(z_i\left(n\right)\right)-h\left(w\left(n\right)\right)|+(m-1)|1+\\ k\left|\right|f_j\left(z_j\left(n\right)\right)-h\left(w\left(n\right)\right)|\\ \le 2mM|1+k|.\end{array}$$

When $k\to -1$, we have $|z_i\left(n+1\right)-w\left(n+1\right)|\to 0,i=1,\cdots ,m$. The consensus of trajectories between the leader system and the follower systems is achieved. Thus, the consensus between the leader Julia set and the follower Julia sets is achieved.

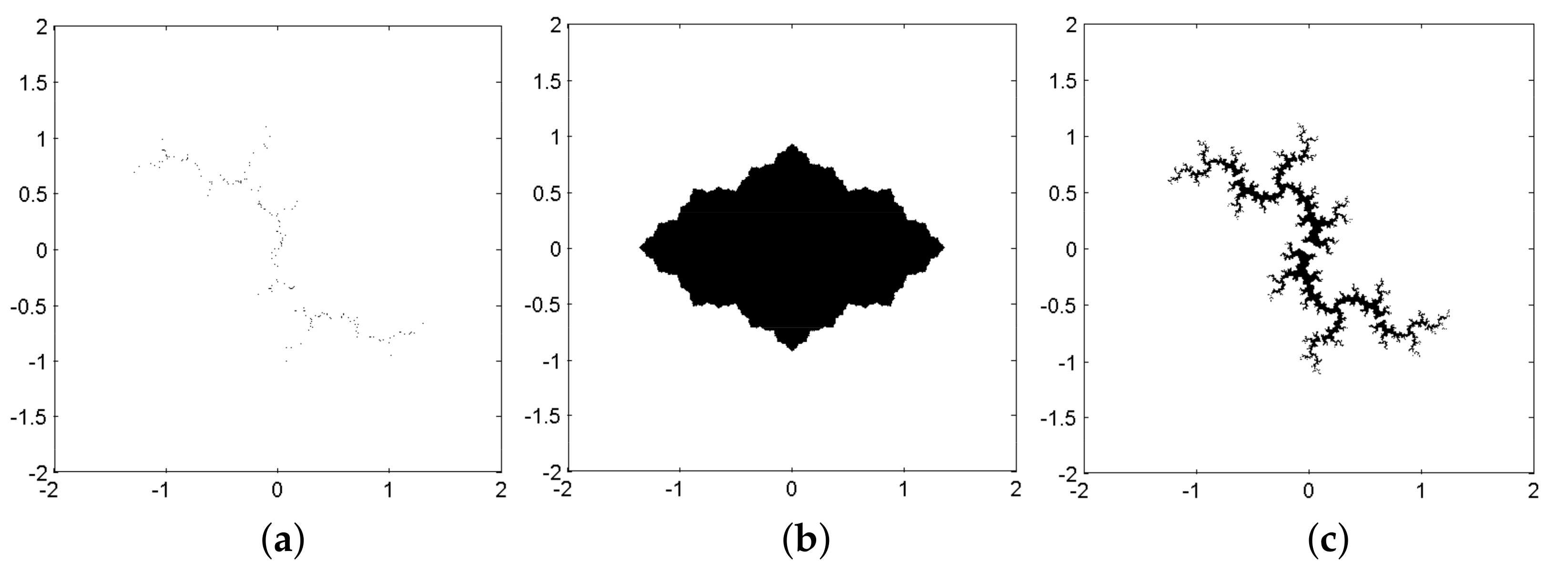
Now, the classical complex quadratic polynomial $z\left(n+1\right)=z^2\left(n\right)+c$ is taken to show the consensus of Julia sets with the leader, where one leader Julia set and three follower Julia sets are taken. Figure 1 shows the leader Julia set for $c=-1$. Figure 2a–c show the follower Julia sets for $c=i,-0.5,0.8i$, respectively.

In the general synchronization of Julia sets [30], two Julia sets are considered: one follower Julia set changes into the leader Julia set. In this case, when multiple Julia sets are controlled to change into one Julia set, respectively, the controlled Julia sets will not have a consensus in general, even though the controllers are taken to be the same, which is also the case $a_{j0}=0,j\ne i$ in (6). In other words, the controlled follower systems are

$$z_i\left(n+1\right)=f_i\left(z_i\left(n\right)\right)+k(f_i\left(z_i\left(n\right)\right)-h\left(w\left(n\right)\right)).$$

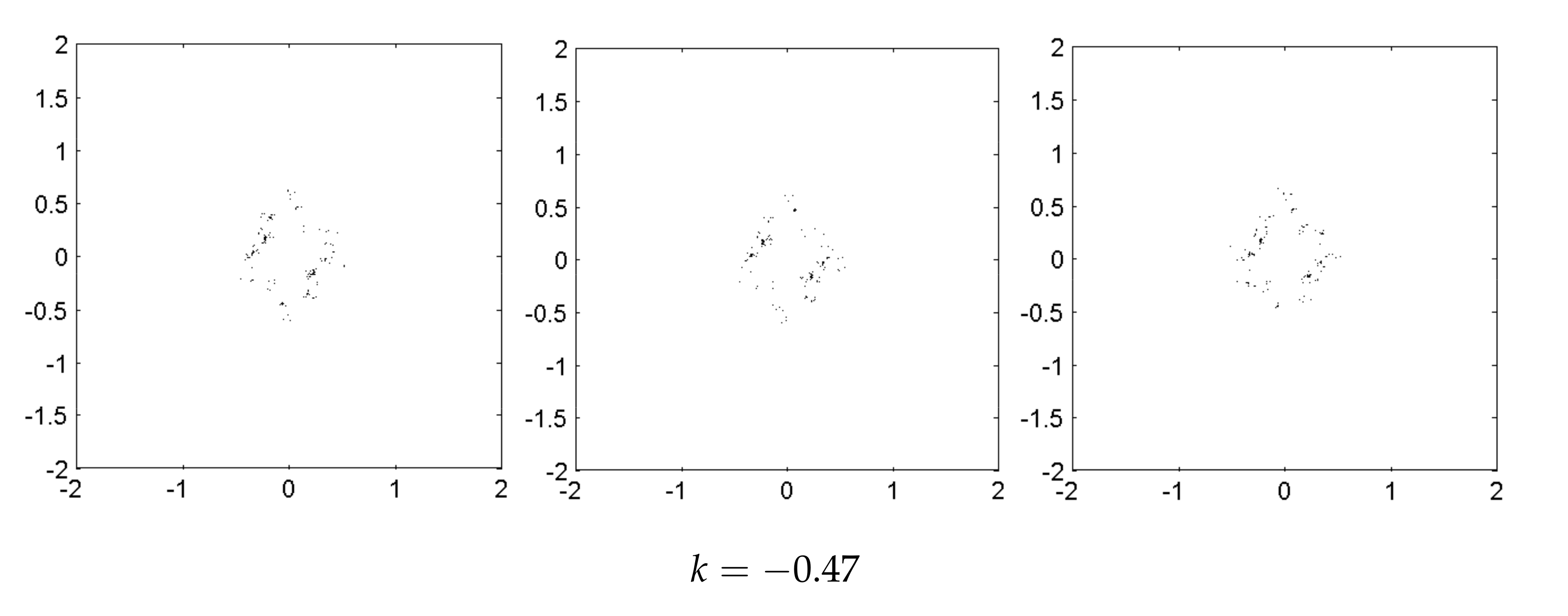
Each follower Julia set could be controlled to change into the leader Julia set. However, the synchronous processes are different for the same control parameter. The three figures in Figure 3 show the Julia sets when the control parameter takes the same values $k=-0.17$ for the follower Julia sets in Figure 2a–c, respectively. It is evident that the processes of changing do not have a consensus, although the follower Julia sets change into the leader Julia set, respectively.

In the consensus of Julia sets with the leader Julia set discussed in this section, not all $a_{j0},j\ne i$ in (6) are equal to 0. Moreover, items with $a_{j0}=1$ are sufficient to couple the information about the leader Julia set and the follower Julia sets. For example, the leader Julia set and the three follower Julia sets are taken to be the same as previously. For convenience, we rewrite the leader system and the three follower systems as

$$w\left(n+1\right)=w^2\left(n\right)-1$$

and

$$\begin{gathered} x\left(n+1\right)=x^2\left(n\right)+i, \\ y\left(n+1\right)=y^2\left(n\right)-0.5, \\ s\left(n+1\right)=s^2\left(n\right)+0.8i. \end{gathered}$$

Adding the control items to the follower systems, we have

$$\begin{array}{c}x\left(n+1\right)=x^2\left(n\right)+i+k[(x^2\left(n\right)+i)-(w^2\left(n\right)-1)+(y^2\left(n\right)-0.5)-(w^2\left(n\right)-1)+\\ (s^2\left(n\right)+0.8i)-(w^2\left(n\right)-1)]+[(y^2\left(n\right)-0.5)-(w^2\left(n\right)-1)+(s^2\left(n\right)+0.8i)-(w^2\left(n\right)-1)],\\ y\left(n+1\right)=y^2\left(n\right)-0.5+k[(x^2\left(n\right)+i)-(w^2\left(n\right)-1)+(y^2\left(n\right)-0.5)-(w^2\left(n\right)-1)]+\\ [(x^2\left(n\right)+i)-(w^2\left(n\right)-1)],\\ s\left(n+1\right)=s^2\left(n\right)+0.8i+k[(x^2\left(n\right)+i)-(w^2\left(n\right)-1)+(s^2\left(n\right)+0.8i)-(w^2\left(n\right)-1)]+\\ [(x^2\left(n\right)+i)-(w^2\left(n\right)-1)].\end{array}$$

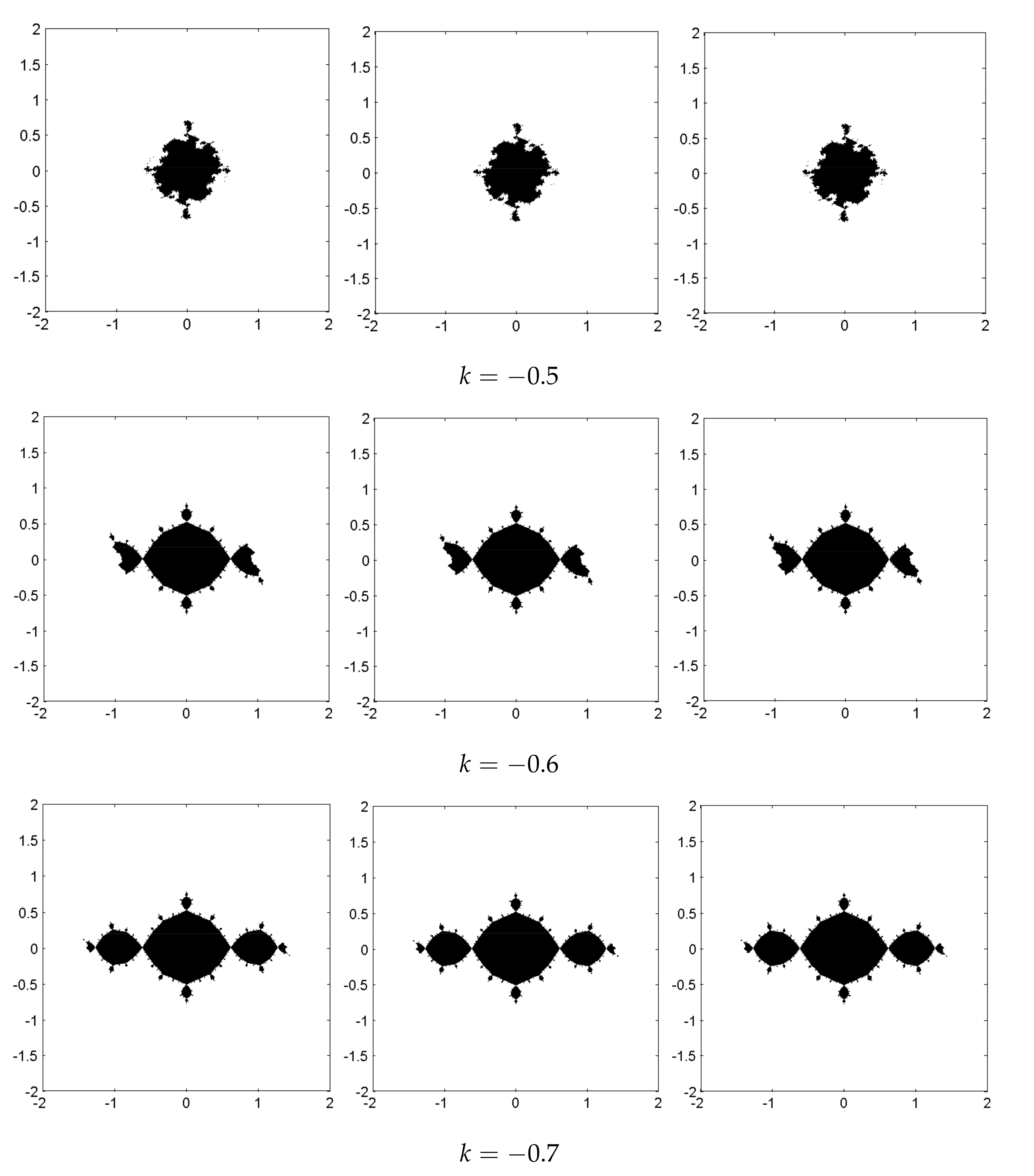
Figure 4 illustrates that the controlled follower Julia sets have a similar shape for the same control parameter k and change into the leader Julia set with $k\to -1$.

4. The Scheme of Consensus of Julia Sets with No Leaders

Let $J_i$ be the Julia set of the systems

$$x_i\left(n+1\right)=h_i\left(x_i\left(n\right)\right),i=1,2,\cdots ,m,$$

(8)

where $h_i\left(x_i\left(n\right)\right)$ is the nonlinear function of the $ith$ system.

Definition 4.

The consensus of Julia sets with no leaders is to design $u_i(x_1\left(n\right),x_2\left(n\right),\cdots$, $x_m\left(n\right);k)$ added to the $ith$ follower system, which makes the Julia sets $J_i\left(k\right)$ of the controlled systems

$$x_i\left(n+1\right)=h_i\left(x_i\left(n\right)\right)+u_i(x_1\left(n\right),x_2\left(n\right),\cdots ,x_m\left(n\right);k),i=1,2,\cdots ,m,$$

(9)

satisfy

$$\underset{k\to k_0}{lim}{J}_i\left(k\right)=J^{*},i=1,2,\cdots ,m,$$

(10)

where $J^{*}$ is a certain set, k is the control parameter and $k_0$ is a certain number or possibly ∞.

In this section, the control items are taken to be

$$u_i=v*h_i\left(x_i\left(n\right)\right)+t*\sum _{j\in N_i}{a}_{ij}(x_j\left(n\right)-x_i\left(n\right)),$$

(11)

where v and t are the control parameter. Then, the controlled systems are

$$x_i\left(n+1\right)=h_i\left(x_i\left(n\right)\right)+v*h_i\left(x_i\left(n\right)\right)+t*\sum _{j\in N_i}{a}_{ij}(x_j\left(n\right)-x_i\left(n\right)),i=1,2,\cdots ,m,$$

(12)

For any two systems in (12), we have

$$\begin{array}{c}{x}_p(n+1)-x_q(n+1)=\\ (1+v)[h_p\left(x_p\left(n\right)\right)-h_q\left(x_q\left(n\right)\right)]+t*[{\displaystyle \sum _{j\in N_i}}{a}_{pj}(x_j\left(n\right)-x_p\left(n\right))-{\displaystyle \sum _{j\in N_i}}{a}_{qj}(x_j\left(n\right)-x_q\left(n\right))].\end{array}$$

From the definition of the Julia set, we suppose that the trajectories are bounded. Additionally, there exists a $Tb0$ satisfying $|x_i|\le T$ and $|h_i\left(x_i\left(n\right)\right)|\le T$. Then,

$$|x_p(n+1)-x_q(n+1)|\le 2T|1+v|+4mT|t|.$$

Therefore, $|x_p(n+1)-x_q(n+1)|\to 0$ when $v\to -1$ and $t\to 0$.

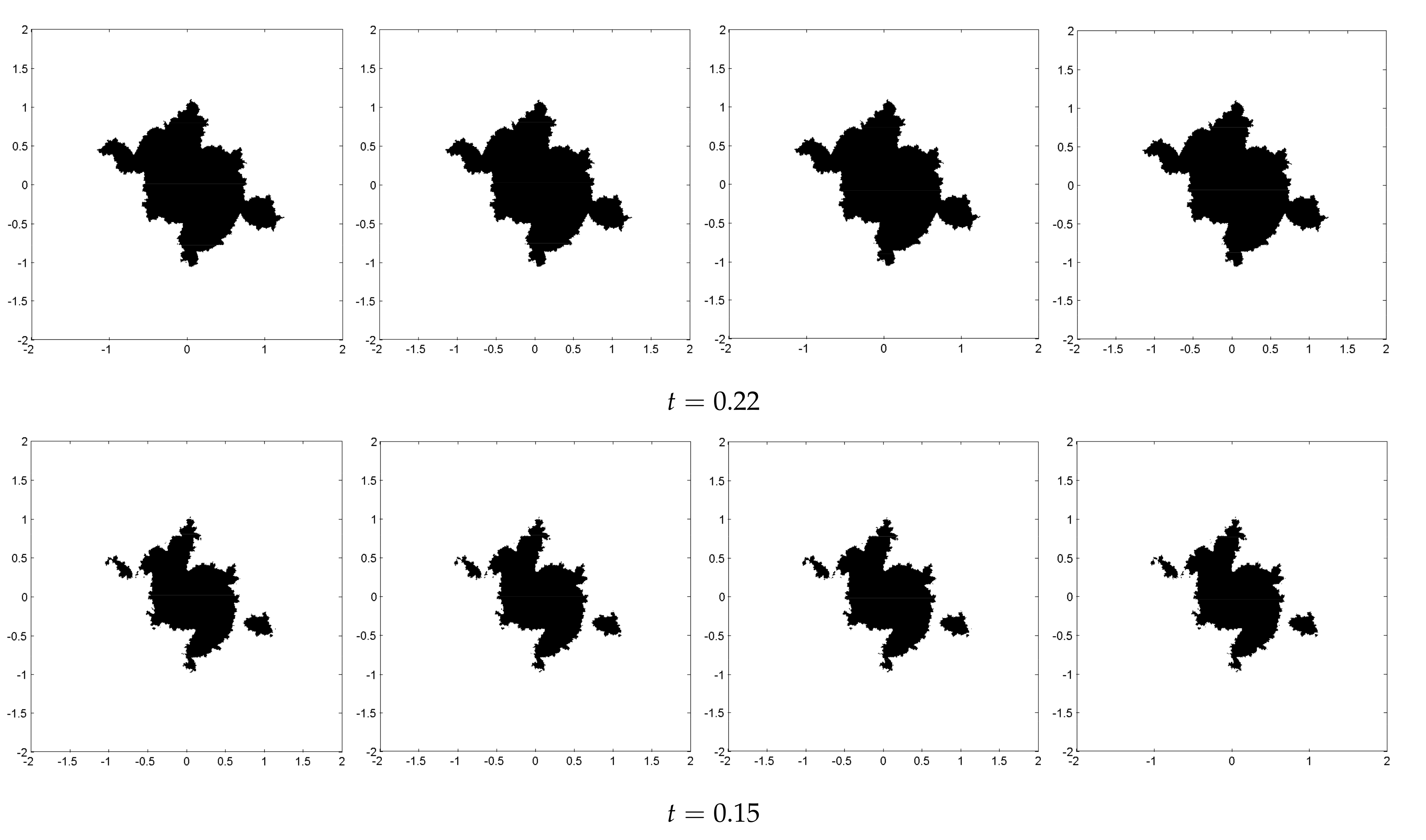
The classical complex quadratic polynomial $z\left(n+1\right)=z^2\left(n\right)+c$ is also taken as an example to show the consensus of Julia sets with no leaders. The system parameters c are $-1,i,-0.5,0.8i$ and the Julia sets are shown in Figure 1 and Figure 2, respectively. Consensus of Julia sets is achieved for different values of v and t; see Figure 5 and Figure 6. Different Julia sets with different system parameters become very similar to a certain set under the controller (11).

5. Discussion

The previous studies on the correlations of different Julia sets mainly focus on the synchronization and coupling of two different Julia sets. Can multiple Julia sets be associated, such as the synchronization or coupling of multiple Julia sets? In this paper, by use of cooperative control methods, consensuses of Julia sets with a leader and with no leaders are discussed in Section 3 and Section 4, respectively. Under control, each follower Julia set changes into the leader Julia set in the consensus of Julia sets with a leader, and each follower Julia set changes into a certain set in the consensus of Julia sets with no leaders, which are also the synchronization or coupling of multiple Julia sets. The changing progress of each follower Julia set is consistent according to Figure 4, Figure 5 and Figure 6 if the coupled information about the leader Julia set and the follower Julia sets is sufficient.

A Julia set is also the boundary of the attractive domain of the attractive fixed point, which is related to the stability of the system. Stability is the basic requirement for the research and application of the system. In particular, the research objects are multiple in the study of the group dynamical properties. In general, the multiple systems in group dynamics are required to have the same or similar stable behaviors. Moreover, the consensus of Julia sets can be used to describe the stability of the group dynamics.

For the application of the consensus of Julia sets, the application of a Julia set in the particle movement is considered. The study illustrates that the generalized Julia set gives the closure of all the possible unstable orbits of the particle within the velocity space. The consensus of Julia sets can be used to analyze the all particles required to have similar behaviors under control.

6. Conclusions

Many results provided by previous studies on the Julia set are focused on the properties, graph and control of a single Julia set. In this paper, the consensus of Julia sets is introduced, activated by the consensus of multi-agent systems, which are also the synchronization of multiple Julia sets. Furthermore, two types of consensus of Julia sets are discussed: one is with a leader and the other is with no leaders. Consensus of Julia sets with a leader causes multiple follower Julia sets to change, with one accordingly becoming the leader Julia set. Consensus of Julia sets with no leaders allows multiple Julia sets to change to become some set. It is important to analyze the group dynamical behavior depicted by the Julia set.

In this paper, the leader Julia set and the follower Julia sets are generated from systems with the same structure but different system parameters. In further research, we will consider the consensus of Julia sets generated from different system structures between the leader and the follower systems.