Analysis of Impulsive Boundary Value Pantograph Problems via Caputo Proportional Fractional Derivative under Mittag–Leffler Functions
Abstract
1. Introduction
- (i)
- We consider a new impulsive pantograph differential equations with Caputo proportional fractional derivative concerning a certain function.
- (ii)
- Under the Caputo proportional fractional derivative, we explore more broader proportional BVPs with constant coefficients.
2. Preliminaries
3. Existence Analysis
3.1. Uniqueness Property
3.2. Existence Property
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I.; Thimann, K.V. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, UK, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations In North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherland, 2006; Volume 204. [Google Scholar]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petráš, I. Fractional Order Systems: Modeling and Control Applications; World Scientific Series on Nonlinear Science Series A; World Scientific: Singapore, 2010; Volume 72. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Illustrated Edition; Imperial College Press: London, UK, 2010. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods, 2nd ed.; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Lakshmikantham, V.; Bainov, D.D.; Semeonov, P.S. Theory of Impulsive Differential Equations; Series in Modern Applied Mathematics; Worlds Scientific: Singapore, 1989; Volume 6. [Google Scholar]
- Samoilenko, A.M.; Perestyuk, N.A. Impulsive Differential Equations; World Scientific: Singapore, 1995. [Google Scholar]
- Benchohra, M.; Henderson, J.; Ntouyas, S.K. Impulsive Differential Equations and Inclusions; Contemporary Mathematics and Its Applications; Hindawi Publishing Corporation: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Wang, J.; Zhou, Y.; Feçkan, M. On Recent Developments in the Theory of Boundary Value Problems for Impulsive Fractional Differential Equations. Comput. Math. Appl. 2012, 64, 3008–3020. [Google Scholar] [CrossRef][Green Version]
- Ockendon, J.R.; Tayler, A.B. The Dynamics of Acurrent Collection System for an Electric Locomotive. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1971, 322, 447–468. [Google Scholar]
- Li, D.; Liu, M.Z. Runge-Kutta Methods for the Multi-Pantograph Delay Equation. Appl. Math. Comput. 2005, 163, 383–395. [Google Scholar] [CrossRef]
- Sezer, M.; Yalçinbaş, S.; Şahin, N. Approximate Solution of Multi-Pantograph Equation with Variable Coefficients. J. Comput. Appl. Math. 2008, 214, 406–416. [Google Scholar] [CrossRef]
- Yu, Z.H. Variational Iteration Method for Solving the Multi-Pantograph Delay Equation. Phys. Lett. A 2008, 372, 6475–6479. [Google Scholar] [CrossRef]
- Karimi Vanani, S.; Sedighi Hafshejani, J.; Soleymani, F.; Khan, M. On the Numerical Solution of Generalized Pantograph Equation. World Appl. Sci. J. 2011, 13, 2531–2535. [Google Scholar]
- Pappalardo, C.M.; De Simone, M.C.; Guida, D. Multibody Modeling and Nonlinear Control of the Pantograph/Catenary System. Arch. Appl. Mech. 2019, 89, 1589–1626. [Google Scholar] [CrossRef]
- Chamekh, M.; Elzaki, T.M.; Brik, N. Semi-Analytical Solution for Some Proportional Delay Differential Equations. SN Appl. Sci. 2019, 1, 148. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C. Long Time Numerical Behaviors of Fractional Pantograph Equations. Math. Comput. Simulat. MATCOM 2020, 172, 244–257. [Google Scholar] [CrossRef]
- Balachandran, K.; Kiruthika, S.; Trujillo, J.J. Existence of Solutions of Nonlinear Fractional Pantograph Equations. Acta Math. Sci. 2013, 33, 712–720. [Google Scholar] [CrossRef]
- Wang, J.R.; Lin, Z. On the Impulsive Fractional Anti-Periodic BVP Modelling with Constant Coefficients. J. Appl. Math. Comput. 2014, 46, 107–121. [Google Scholar] [CrossRef]
- Zuo, M.; Hao, X.; Liu, L.; Cui, Y. Existence Results for Impulsive Fractional Integro-Differential Equation of Mixed Type with Constant Coefficient and Antiperiodic Boundary Conditions. Bound. Value Probl. 2017, 2017, 161. [Google Scholar] [CrossRef]
- Ahmed, I.; Kumam, P.; Abubakar, J.; Borisut, P.; Sitthithakerngkiet, K. Solutions for Impulsive Fractional Pantograph Differential Equation via Generalized Anti-Periodic Boundary Value Condition. Adv. Differ. Equ. 2020, 2020, 477. [Google Scholar] [CrossRef]
- Shah, K.; Ali, A.; Bushnaq, S. Hyers-Ulam Stability Analysis to Implicit Cauchy Problem of Fractional Differential Equations with Impulsive Conditions. Math. Meth. Appl. Sci. 2018, 41, 8329–8343. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K.; Sutthasin, B. Impulsive Fractional Quantum Hahn Difference Boundary Value Problems. Adv. Differ. Equ. 2019, 2019, 220. [Google Scholar] [CrossRef]
- Malti, A.I.N.; Benchohra, M.; Graef, J.R.; Lazreg, J.E. Impulsive Boundary Value Problems for Nonlinear Implicit Caputo-Exponential Type Fractional Differential Equations. Electron. J. Qual. Theory Differ. Equ. 2020, 78, 1–17. [Google Scholar] [CrossRef]
- Abdo, M.S.; Abdeljawad, T.; Shah, K.; Jarad, F. Study of Impulsive Problems under Mittag-Leffler Power Law. Heliyon 2020, 6, e05109. [Google Scholar] [CrossRef]
- Abbas, M.I. On the Initial Value Problems for the Caputo-Fabrizio Impulsive Fractional Differential Equations. Asian-Eur. J. Math. 2020, 2150073. [Google Scholar] [CrossRef]
- Salim, A.; Benchohra, M.; Karapinar, E.; Lazreg, J.E. Existence and Ulam Stability for Impulsive Generalized Hilfer-Type Fractional Differential Equations. Adv. Differ. Equ. 2020, 2020, 601. [Google Scholar] [CrossRef]
- Salim, A.; Benchohra, M.; Lazreg, J.E.; Guérékata, G.N. Boundary Value Problem for Nonlinear Implicit Generalized Hilfer-Type Fractional Differential Equations with Impulses. Abst. Appl. Anal. 2021, 2021, 5592010. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Alzabut, J. Generalized Fractional Derivatives Generated by a Class of Local Proportional Derivatives. Eur. Phys. J. Spec. Top. 2017, 226, 3457–3471. [Google Scholar] [CrossRef]
- Jarad, F.; Alqudah, M.A.; Abdeljawad, T. On More Generalized Form of Proportional Fractional Operators. Open Math. 2020, 18, 167–176. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Rashid, S.; Hammouch, Z. More Properties of the Proportional Fractional Integrals and Derivatives of a Function with Respect to Another Function. Adv. Differ. Equ. 2020, 2020, 303. [Google Scholar] [CrossRef]
- Abbas, M.I.; Ragusa, M.A. On the Hybrid Fractional Differential Equations with Fractional Proportional Derivatives of a Function with Respect to a Certain Function. Symmetry 2021, 13, 264. [Google Scholar] [CrossRef]
- Tearnbucha, C.; Sudsutad, W. Stability Analysis of Boundary Value Problems for Caputo Proportional Fractional Derivative of a Function with Respect to Another Function via Impulsive Langevin Equation. AIMS Math. 2021, 6, 6647–6686. [Google Scholar] [CrossRef]
- Abbas, M.I. Non-Instantaneous Impulsive Fractional Integro-Differential Equations with Proportional Fractional Derivatives with Respect to Another Function. Math. Meth. Appl. Sci. 2021, 44, 10432–10447. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Hristova, S.; O’Regan, D.; Almeida, R. Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Dufferetial Equations with Generalized Proportional Fractional Derivatives. Mathematics 2021, 9, 1979. [Google Scholar] [CrossRef]
- Akgül, A.; Baleanu, B. Analysis and Applications of the Proportional Caputo Derivative. Adv. Differ. Equ. 2021, 2021, 136. [Google Scholar] [CrossRef]
- Alzahrani, A.K.; Razzaq, O.A.; Khan, N.A.; Alshomrani, A.S.; Ullah, M.Z. Transmissibility of Epidemic Diseases Caused by Delay with Local Proportional Fractional Derivative. Adv. Differ. Equ. 2021, 2021, 292. [Google Scholar] [CrossRef]
- Laadjal, Z.; Jarad, F. On a Langevin Equation Involving Caputo Fractional Proportional Derivatives with Respect to Another Function. AIMS Math. 2021, 7, 1273–1292. [Google Scholar] [CrossRef]
- Keten, A.; Yavuz, M.; Baleanu, D. Nonlocal Cauchy Problem via a Fractional Operator Involving Power Kernel in Banach Spaces. Fractal Fract. 2019, 3, 27. [Google Scholar] [CrossRef]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical Solutions and Synchronization of a Variable-Order Fractional Chaotic System. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Fundamental Calculus of the Fractional Derivative Defined with Rabotnov Exponential Kernel and Application to Nonlinear Dispersive Wave Model. J. Ocean Eng. Sci. 2021, 6, 196–205. [Google Scholar] [CrossRef]
- Akgül, E.K.; Akgül, A.; Yavuz, M. New Illustrative Applications of Integral Transforms to Financial Models with Different Fractional Derivatives. Chaos Solitons Fractals 2021, 146, 110877. [Google Scholar] [CrossRef]
- Das, P.; Rana, S.; Ramos, H. Homotopy Perturbation Method for Solving Caputo Type Fractional Order Volterra-Fredholm Integro-Differential Equations. Comput. Math. Meth. 2019, 1, e1047. [Google Scholar] [CrossRef]
- Das, P.; Rana, S.; Ramos, H. A Perturbation-Based Approach for Solving Fractional-Order Volterra-Fredholm Integro Differential Equations and Its Convergence Analysis. Int. J. Comput. Math. 2020, 97, 1994–2014. [Google Scholar] [CrossRef]
- Das, P.; Rana, S.; Ramos, H. On the Approximate Solutions of a Class of Fractional Order Nonlinear Volterra Integro-Differential Initial Value Problems and Boundary Value Problems of First Kind and Their Convergence Analysis. J. Comput. Appl. Math. 2020, 113116, In press. [Google Scholar] [CrossRef]
- Das, P.; Rana, S. Theoretical Prospects of Fractional Order Weakly Singular Volterra Integro Differential Equations and Their Approximations with Convergence Analysis. Math. Meth. Appl. Sci. 2021, 44, 9419–9440. [Google Scholar] [CrossRef]
- Katugampola, U.N. New Fractional Integral Unifying Six Existing Fractional Integrals. arXiv 2016, arXiv:1612.08596. Available online: https://arxiv.org/pdf/1612.08596.pdf (accessed on 1 October 2021).
- Jarad, F.; Ugurlu, E.; Abdeljawad, T.; Baleanu, D. On a New Class of Fractional Operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Khan, T.U.; Adil Khan, M. Generalized Conformable Fractional Operators. J. Comput. Appl. Math. 2019, 346, 378–389. [Google Scholar] [CrossRef]
- Wang, J.; Feçkan, M.; Zhou, Y. Presentation of Solutions of Impulsive Fractional Langevin Equations and Existence Results. Eur. Phys. J. Spec. Top. 2013, 222, 1857–1874. [Google Scholar] [CrossRef]
- Almalahi, M.A.; Panchal, S.K. Some Existence and Stability Results for ψ-Hilfer Fractional Implicit Diferential Equation with Periodic Conditions. J. Math. Anal. Model. 2020, 1, 1–19. [Google Scholar] [CrossRef]
- Wei, W.; Xiang, X.; Peng, Y. Nonlinear Impulsive Integro-Differential Equations of Mixed Type and Optimal Controls. Optimization 2006, 55, 141–156. [Google Scholar] [CrossRef]
- Krasnoselskii, M. Two Remarks About the Method of Successive Approximations. Usp. Mat. Nauk 1955, 10, 123–127. [Google Scholar]
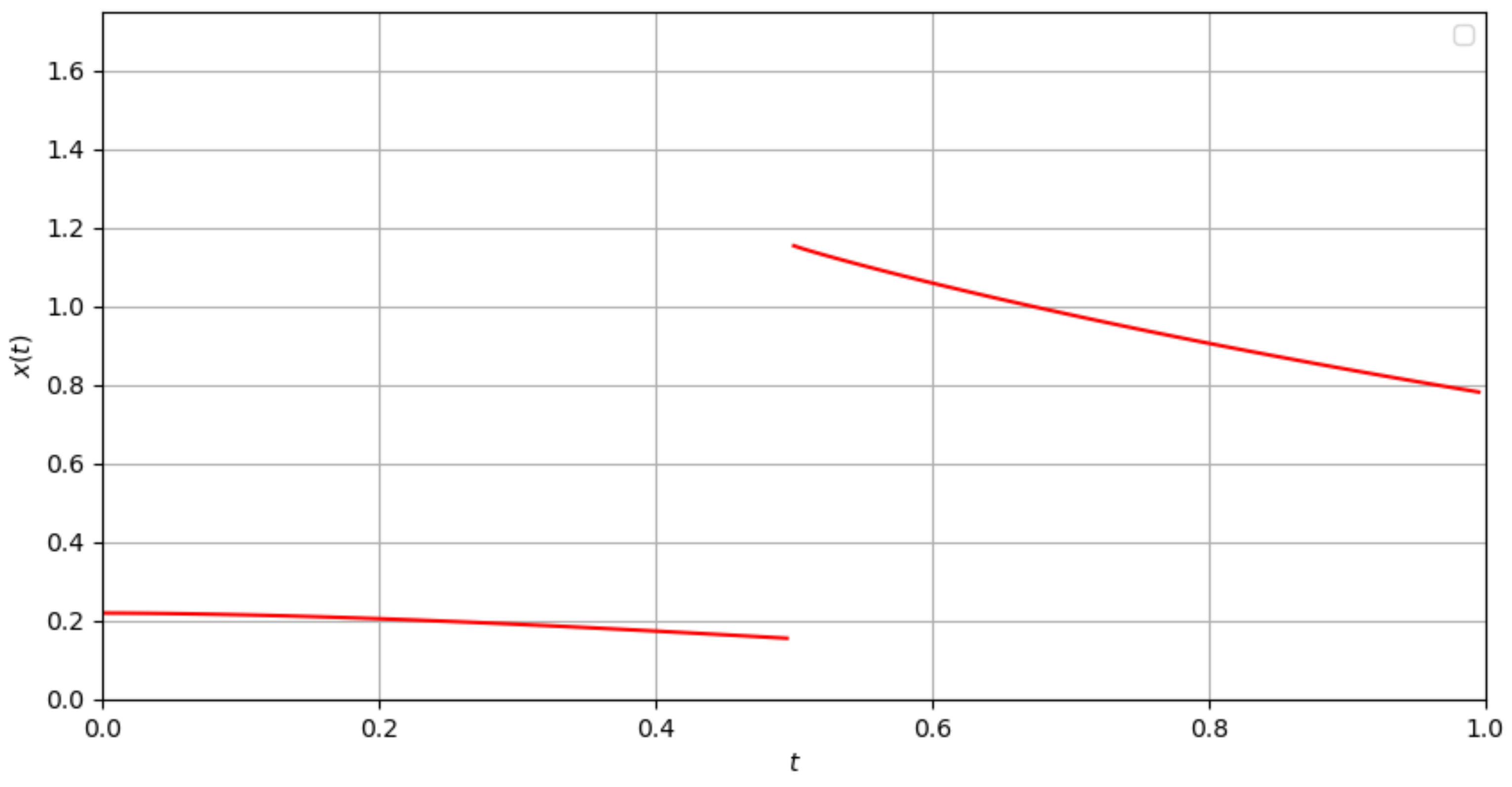
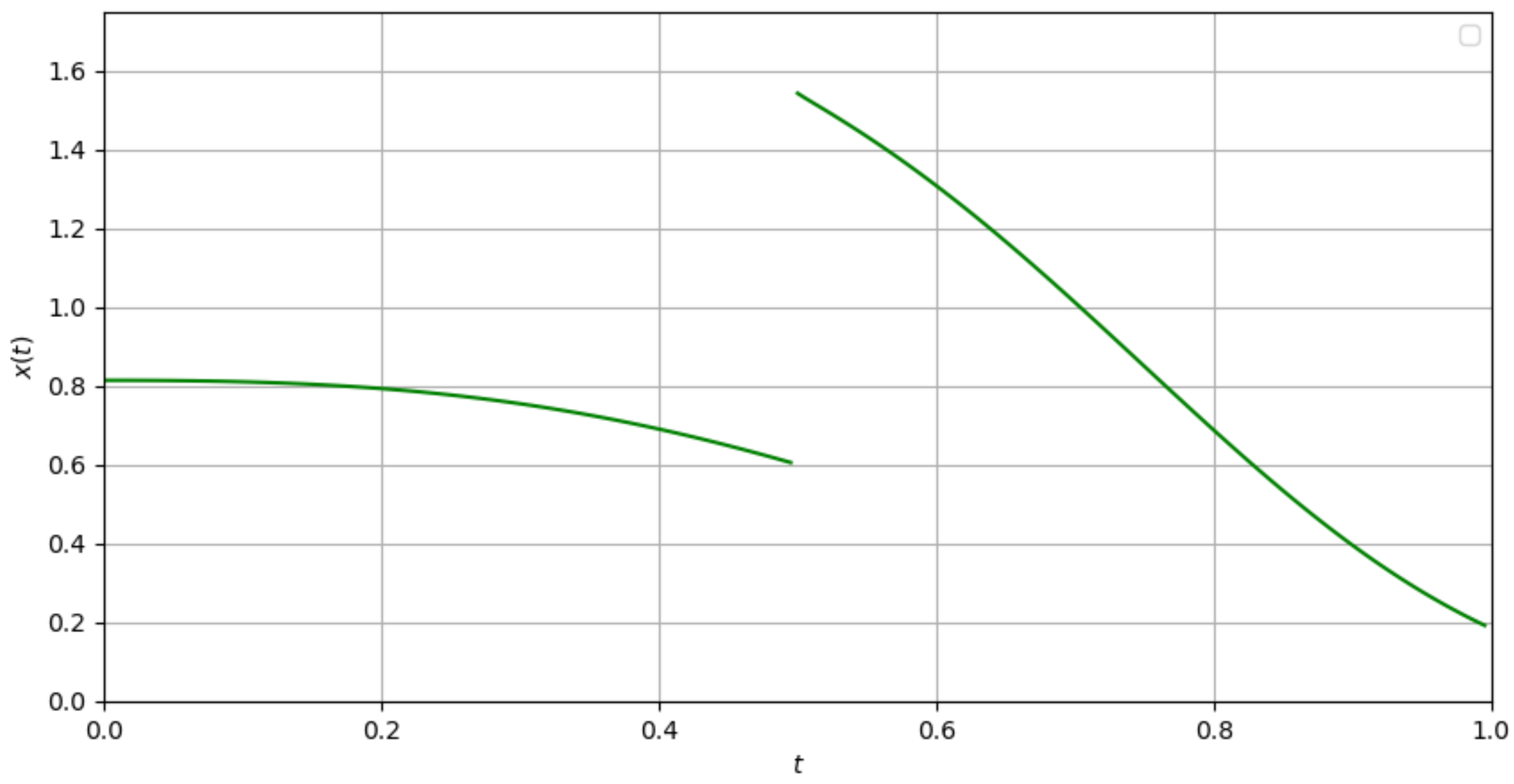
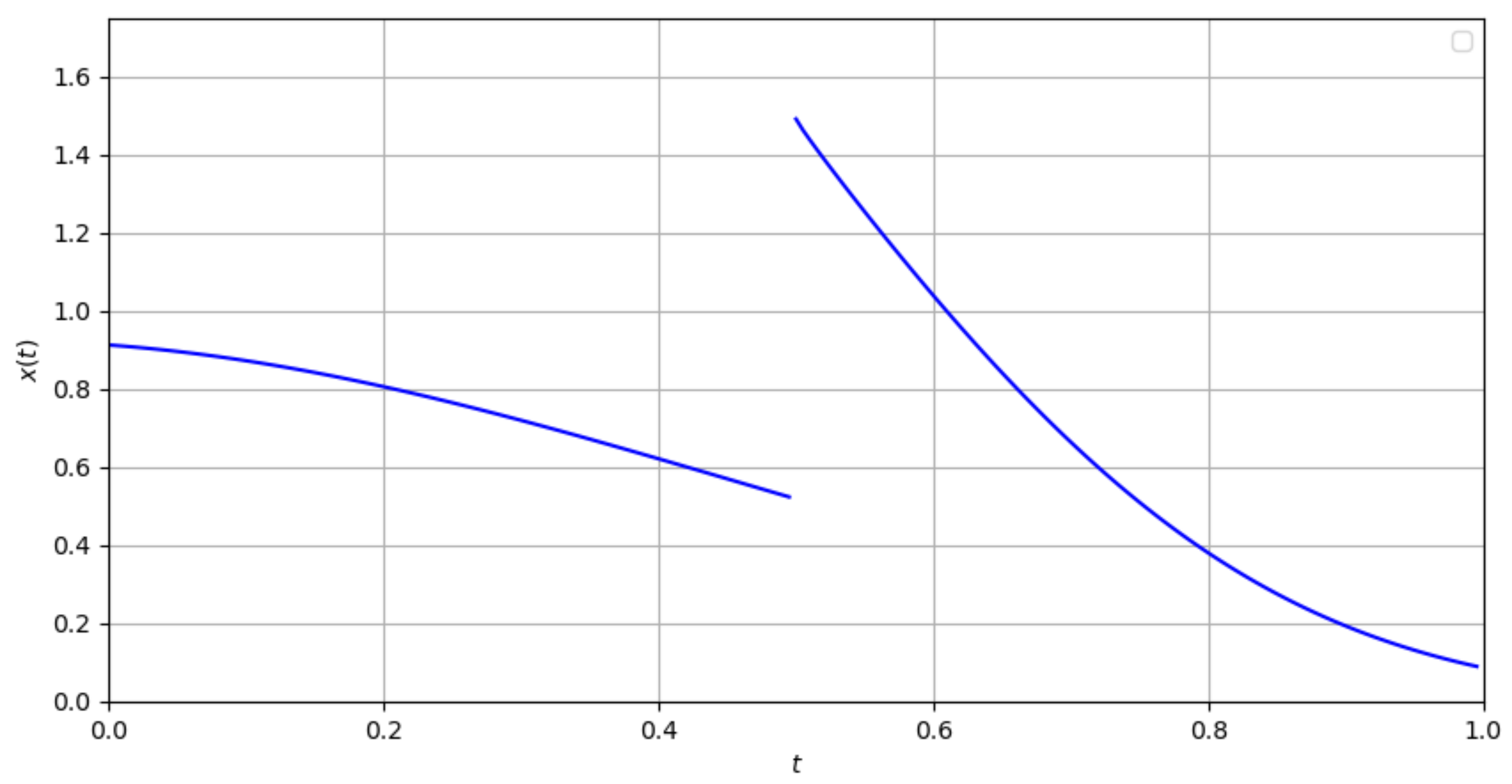
| Ω | ||||
|---|---|---|---|---|
| I | 1.44637 | |||
| II | 1.30799 | |||
| III | 1.032894 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaminsou, B.; Sudsutad, W.; Thaiprayoon, C.; Alzabut, J.; Pleumpreedaporn, S. Analysis of Impulsive Boundary Value Pantograph Problems via Caputo Proportional Fractional Derivative under Mittag–Leffler Functions. Fractal Fract. 2021, 5, 251. https://doi.org/10.3390/fractalfract5040251
Khaminsou B, Sudsutad W, Thaiprayoon C, Alzabut J, Pleumpreedaporn S. Analysis of Impulsive Boundary Value Pantograph Problems via Caputo Proportional Fractional Derivative under Mittag–Leffler Functions. Fractal and Fractional. 2021; 5(4):251. https://doi.org/10.3390/fractalfract5040251
Chicago/Turabian StyleKhaminsou, Bounmy, Weerawat Sudsutad, Chatthai Thaiprayoon, Jehad Alzabut, and Songkran Pleumpreedaporn. 2021. "Analysis of Impulsive Boundary Value Pantograph Problems via Caputo Proportional Fractional Derivative under Mittag–Leffler Functions" Fractal and Fractional 5, no. 4: 251. https://doi.org/10.3390/fractalfract5040251
APA StyleKhaminsou, B., Sudsutad, W., Thaiprayoon, C., Alzabut, J., & Pleumpreedaporn, S. (2021). Analysis of Impulsive Boundary Value Pantograph Problems via Caputo Proportional Fractional Derivative under Mittag–Leffler Functions. Fractal and Fractional, 5(4), 251. https://doi.org/10.3390/fractalfract5040251







