Analysis of a Nonlinear ψ-Hilfer Fractional Integro-Differential Equation Describing Cantilever Beam Model with Nonlinear Boundary Conditions

Abstract

In this paper, we establish sufficient conditions to approve the existence and uniqueness of solutions of a nonlinear implicit $\psi$-Hilfer fractional boundary value problem of the cantilever beam model with nonlinear boundary conditions. By using Banach’s fixed point theorem, the uniqueness result is proved. Meanwhile, the existence result is obtained by applying the fixed point theorem of Schaefer. Apart from this, we utilize the arguments related to the nonlinear functional analysis technique to analyze a variety of Ulam’s stability of the proposed problem. Finally, three numerical examples are presented to indicate the effectiveness of our results.

1. Introduction

During the last few decades, elastic beams ($\mathbb{EB}$) have been prominent in the realm of physical science and engineering problems. In particular, the construction of buildings and bridges requires careful computations of the elastic beam equations ($\mathbb{EBE}$s) to assure the safety of the structure. The equations of the $\mathbb{EB}$ problem have been created to represent real situations and their solutions have been provided by different mathematical techniques. $\mathbb{EBE}$s have attracted the interest of many researchers who formulate $\mathbb{EBE}$s in the form of fourth-order ordinary differential equations in various methods. For instance, in 1988, Gupta [1] discussed a fourth-order $\mathbb{EBE}$ with two-point boundary conditions as follows:

$$\left\{\begin{array}{c}{\displaystyle x^{\left(4\right)}\left(t\right)+f(t,x\left(t\right))=0,t\in (0,1),}\\ {\displaystyle x\left(0\right)=0,x^{″}\left(0\right)=0,x^{\prime }\left(1\right)=0,x^{″\prime }\left(1\right)=0.}\end{array}\right.$$

(1)

The problem (1) represents an elastic beam model of length 1 that is restrained at the left end with zero displacement and bending moment, and is free to travel at the right end with a diminishing angular attitude and shear force. Using the Leray–Schauder continuation theorem and Wirtinger-type inequalities, the existence properties of the problem (1) were established. In 2017, Cianciaruso and co-workers [2] studied the fourth-order differential equation of the cantilever beam ($\mathbb{CB}$) model with three-point boundary conditions as follows:

$$\left\{\begin{array}{c}{\displaystyle x^{\left(4\right)}\left(t\right)+f(t,x\left(t\right))=0,t\in (0,1),}\\ {\displaystyle x\left(0\right)=0,x^{\prime }\left(0\right)=0,x^{″}\left(1\right)=0,x^{″\prime }\left(1\right)=g(\xi ,x\left(\xi \right)),}\end{array}\right.$$

(2)

where $\xi \in (0,1)$ is a real constant. They proved the existence, non-existence, localization, and multiplicity of nontrivial solutions for problem (2) with their results by using topological methods. Further, the development of $\mathbb{EBE}$s with linear or nonlinear functions under a variety of boundary conditions is more varied and comprehensive. Many works in the literature deal with linear or nonlinear boundary value problems which consist of two or more points; for example, Zhong and co-workers [3] examined fourth-order nonlinear differential equations with the four-point boundary conditions:

$$\left\{\begin{array}{c}{\displaystyle x^{\left(4\right)}\left(t\right)+f(t,x\left(t\right),x^{″}\left(t\right))=0,t\in (0,1),}\\ {\displaystyle x\left(0\right)=x\left(1\right)=0,c_1{x}^{″}\left({\omega }_1\right)-c_2{x}^{″\prime }\left({\omega }_1\right)=0,c_3{x}^{″}\left({\omega }_2\right)+c_4{x}^{″\prime }\left({\omega }_1\right)=0,}\end{array}\right.$$

(3)

where $c_i$ represents non-negative constants, $i=1,2,3,4$, the points ${\omega }_1$, ${\omega }_2\in [0,1]$ with ${\omega }_1<{\omega }_2$, and $f\in \mathcal{C}\left(\right[0,1]\times [0,\infty )\times (-\infty ,0],[0,\infty \left)\right)$. By using Krasnoselskii’s fixed point theorem, the existence result is obtained. $\mathbb{EBE}$s with a variety of boundary conditions have been studied in recent years; see [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] and references cited therein.

Fractional calculus generalizes the ordinary differentiation and integration of arbitrary order, which may be non-integer order. It is widely utilized in several areas, including engineering and applied science. Different definitions of fractional derivative and integral operators, such as Riemann–Liouville, Caputo, Hilfer, Katugampola, and others, have been discovered. We refer to the thorough investigations in [26,27,28,29,30,31] for a detailed analysis of applications on fractional calculus. In recent years, several research papers have investigated fractional differential equations, the existence results of solutions, and analyzed system stability. One of the most fascinating aspects of differential equations is existence theory. In the previous several decades, a lot of research has been conducted in this field. Various techniques have been used in the current literature to demonstrate the existence and uniqueness of solutions to differential and integral equations. In addition, one of the most powerful techniques for stability analysis is Ulam’s stability, which includes Ulam–Hyers ($\mathcal{UH}$) stability, generalized Ulam–Hyers ($\mathcal{GUH}$) stability, Ulam–Hyers–Rassias ($\mathcal{UHR}$) stability, and generalized Ulam–Hyers–Rassias ($\mathcal{GUHR}$) stability. It is useful because the properties of Ulam’s stability guarantee the existence of solutions, and when the problem under consideration is Ulam’s stability, it ensures that a close exact solution exists; see [32,33,34,35,36,37,38,39,40,41,42] and references cited therein.

In response to the foregoing discussions, we study a class of nonlinear implicit $\psi$-Hilfer fractional integro-differential equations with nonlinear boundary conditions describing the $\mathbb{CB}$ model of the form:

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)=f(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)),t\in (a,b),}\\ {\displaystyle x\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(a\right)=0,}\\ {\displaystyle \sum _{i=1}^n{\mu }_i{}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }x\left({\kappa }_i\right)=\mathcal{H}(\eta ,x\left(\eta \right)),\sum _{j=1}^n{\phi }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }x\left({\varsigma }_j\right)=\mathcal{G}(\xi ,x\left(\xi \right)),}\end{array}\right.$$

(4)

where ${}^H{\mathfrak{D}}_{a^{+}}^{v,\rho ;\psi }$ denotes the $\psi$-Hilfer fractional derivative operators of order $v=\{\alpha ,\delta ,{\theta }_i,{\varphi }_j\}$, $\alpha \in (3,4]$, ${\theta }_i\in (0,1]$, $\delta \in (1,2]$, ${\varphi }_j\in (2,3]$, ${\kappa }_i,{\varsigma }_j,\eta ,\xi \in (a,b]$, ${\mu }_i,{\phi }_j\in \mathbb{R}$, for $i=1,2,\dots ,m$, $j=1,2,\dots ,n$, and $\rho \in [0,1]$. ${\mathcal{I}}_{a^{+}}^{\beta ;\psi }$ denotes the $\psi$-Riemann–Liouville fractional integral of order $\beta >0$, $f\in \mathcal{C}(\mathcal{J}\times {\mathbb{R}}^3,\mathbb{R})$, $\mathcal{H}$, $\mathcal{G}\in \mathcal{C}(\mathcal{J},\mathbb{R})$ and $\mathcal{J}:=[a,b]$, $b>a>0$.

The major goal of this paper is to use well-known fixed point theorems such as Banach’s and Schaefer’s to show the existence and uniqueness of the solution for the problem of (4). The different types of Ulam’s stability, such as $\mathcal{UH}$ stability, $\mathcal{GUH}$ stability, $\mathcal{UHR}$ stability, and $\mathcal{GUHR}$ stability, are used to investigate the stability of the solution for problem (4). Finally, we illustrate examples of various functions that are investigated to verify the theoretical results.

The rest of this paper is assembled as follows: In Section 2, we introduce some notations, definitions, lemmas, and essential results. The existence and uniqueness results are obtained by helping the fixed point theorems in Section 3. By using the nonlinear functional analysis technique, we analyzed a variety of Ulam’s stabilities for the proposed problem in Section 4. In Section 5, we present examples to guarantee the validity of the obtained results. The conclusion of this paper is presented at the end.

2. Preliminaries

We present a brief overview of the fundamental concepts of $\psi$-Hilfer fractional calculus as well as essential key results that will be employed in this paper.

Let $\mathcal{E}=\mathcal{C}(\mathcal{J},\mathbb{R})$ be the Banach space of continuous functions on $\mathcal{J}$ equipped with the supnorm $\parallel x\parallel ={sup}_{t\in \mathcal{J}}\left\{\right|x\left(t\right)\left|\right\}$. Let ${\mathcal{AC}}^n(\mathcal{J},\mathbb{R})$ be the space of n-times absolutely continuous functions where ${\mathcal{AC}}^n(\mathcal{J},\mathbb{R})=\{f:\mathcal{J}\to \mathbb{R};f^{(n-1)}\in \mathcal{AC}(\mathcal{J},\mathbb{R})\}$.

Definition 1

(The $\psi$-Riemann–Liouville fractional integral operator [43]). Let $(a,b)$ be a finite or infinite interval of the half-axis ${\mathbb{R}}^{+}$. Let $\psi \left(x\right)\in {\mathcal{C}}^1(\mathcal{J},\mathbb{R})$ be an increasing function with ${\psi }^{\prime }\left(x\right)\ne 0$ for each $t\in \mathcal{J}$. The ψ-Riemann–Liouville fractional integral of order α of a function f depending on the function ψ on $\mathcal{J}$ is defined by

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }f\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\alpha -1}f\left(s\right)ds,t>a>0,\alpha >0,$$

where $\mathsf{\Gamma }(·)$ represents the (Euler) Gamma function.

Definition 2

(The $\psi$-Riemann–Liouville fractional derivative operator [43]). Let $\psi \left(t\right)$ be define as in Definition 1 with ${\psi }^{\prime }\left(t\right)\ne 0$. The ψ-Riemann–Liouville fractional derivative of a function f depending on the function ψ is defined as ${\mathfrak{D}}_{a^{+}}^{\alpha ;\psi }f\left(t\right)={\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n{\mathcal{I}}_{a^{+}}^{n-\alpha ;\psi }f\left(t\right)$ or

$${\mathfrak{D}}_{a^{+}}^{\alpha ;\psi }f\left(t\right)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n{\int }_a^t{\psi }^{\prime }\left(s\right){\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{n-\alpha -1}f\left(s\right)ds,\alpha >0,$$

where $n=\left[\alpha \right]+1$ and $\left[\alpha \right]$ represents the integer part of $Re\left(\alpha \right)$.

Definition 3

(The $\psi$-Hilfer fractional derivative operator [44]). Let $\gamma =\alpha +\rho (n-\alpha )$, $\alpha \in (n-1,n)$ with $n\in \mathbb{N}$, $f\in {\mathcal{C}}^n(\mathcal{J},\mathbb{R})$ and $\psi \left(t\right)\in {\mathcal{C}}^1(\mathcal{J},\mathbb{R})$ be increasing with ${\psi }^{\prime }\left(t\right)\ne 0$ for each $t\in \mathcal{J}$. Then, the ψ-Hilfer fractional derivative of type $\rho \in [0,1]$ of a function f, depending on the function ψ, is defined as

$${}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }f\left(t\right)={\mathcal{I}}_{a^{+}}^{\rho (n-\alpha );\psi }{\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n{\mathcal{I}}_{a^{+}}^{(1-\rho )(n-\alpha );\psi }f\left(t\right)={\mathcal{I}}_{a^{+}}^{\gamma -\alpha ;\psi }{}^{}{\mathfrak{D}}_{a^{+}}^{\gamma ;\psi }f\left(t\right),$$

where ${}^{}{\mathfrak{D}}_{a^{+}}^{\gamma ;\psi }f\left(t\right)={}^{}{\mathfrak{D}}_{a^{+}}^{n;\psi }{\mathcal{I}}_{a^{+}}^{(1-\rho )(n-\alpha );\psi }f\left(t\right)$.

Lemma 1

(The semigroup property [43]). Let $\alpha ,\beta >0$. Then ${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{I}}_{a^{+}}^{\beta ;\psi }f\left(t\right)={\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }f\left(t\right)$, $t>a$.

Proposition 1

([43,44]). Let $t>a$ and consider $G^{\upsilon }\left(t\right)={\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\upsilon }$. Then, for $\upsilon >0$ and $\alpha \ge 0$, the following properties:

(i) 

${\displaystyle {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{G}^{\upsilon -1}\left(t\right)=\frac{\mathsf{\Gamma }\left(\upsilon \right)}{\mathsf{\Gamma }(\upsilon +\alpha )}{G}^{\upsilon +\alpha -1}\left(t\right)}$;

(ii) 

${\displaystyle {\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }{G}^{\upsilon -1}\left(t\right)=\frac{\mathsf{\Gamma }\left(\upsilon \right)}{\mathsf{\Gamma }(\upsilon -\alpha )}{G}^{\upsilon -\alpha -1}\left(t\right)}$;

(iii) 

${\displaystyle {{}^H\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }{G}^{\upsilon -1}\left(t\right)=\frac{\mathsf{\Gamma }\left(\upsilon \right)}{\mathsf{\Gamma }(\upsilon -\alpha )}{G}^{\upsilon -\alpha -1}\left(t\right),\upsilon >\gamma =\alpha +\rho (4-\alpha )}$.

Lemma 2

([44]). Let $f\in {\mathcal{C}}^n(\mathcal{J},\mathbb{R})$, $\alpha \in (n-1,n)$, $\rho \in [0,1]$, and $\gamma =\alpha +\rho (n-\alpha )$. Then,

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }f\left(t\right)=f\left(t\right)-\sum _{k=1}^n\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{q-k}}{\mathsf{\Gamma }(q-k+1)}{f}_{\psi }^{[n-k]}{\mathcal{I}}_{a^{+}}^{(1-\rho )(n-\alpha );\psi }f\left(a\right),$$

for all $t\in \mathcal{J}$, where $f_{\psi }^{\left[n\right]}f\left(t\right):={\left(\frac{1}{{\psi }^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n}f\left(t\right)$.

Lemma 3

([36]). Let $\alpha \in (m-1,m)$, $\beta \in (n-1,n)$, n, $m\in \mathbb{N}$, $n\le m$, $\rho \in [0,1]$ and $\alpha >\beta +\rho (n-\beta )$. If $h\in {\mathcal{C}}_{1-\gamma ,\psi }(\mathcal{J},\mathbb{R})$, then ${{}^H\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(\varsigma \right)={\mathcal{I}}_{0^{+}}^{\alpha -\beta ;\psi }h\left(\varsigma \right)$.

Lemma 4.

Let $\alpha \in (3,4]$, $\delta \in (0,1]$, ${\theta }_i\in (1,2]$, ${\varphi }_j\in (2,3]$, ($i=1,2,\dots ,m$, $j=1,2,\dots ,n$) with $\rho \in [0,1]$, $\gamma =\alpha +\rho (4-\alpha )$ and $\mathsf{\Lambda }={\mathsf{\Lambda }}_{11}{\mathsf{\Lambda }}_{22}-{\mathsf{\Lambda }}_{12}{\mathsf{\Lambda }}_{21}\ne 0$. Assume that $h\in \mathcal{E}$. Then, $x\in {\mathcal{C}}^4(\mathcal{J},\mathbb{R})$ is a solution of

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)=h\left(t\right),t\in (a,b),}\\ {\displaystyle x\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(a\right)=0,}\\ {\displaystyle \sum _{i=1}^m{\mu }_i{}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }x\left({\kappa }_i\right)=\mathcal{H}(\eta ,x\left(\eta \right)),\sum _{j=1}^n{\phi }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }x\left({\varsigma }_j\right)=\mathcal{G}(\xi ,x\left(\xi \right)),}\end{array}\right.$$

(5)

if and only if x satisfies the integral equation

$$\begin{array}{ccc}\hfill x\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -1}}{\mathsf{\Lambda }\mathsf{\Gamma }\left(\gamma \right)}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }h\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }h\left({\varsigma }_j\right)\right)]\hfill \\ & & +\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -2}}{\mathsf{\Lambda }\mathsf{\Gamma }(\gamma -1)}[{\mathsf{\Lambda }}_{11}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }h\left({\varsigma }_j\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }h\left({\kappa }_i\right)\right)],\hfill \end{array}$$

(6)

where

$$\begin{array}{ccc}\hfill {\mathsf{\Lambda }}_{11}& =& \sum _{i=1}^m\frac{{\mu }_i{\left(\psi \left({\kappa }_i\right)-\psi \left(a\right)\right)}^{\gamma -{\theta }_i-1}}{\mathsf{\Gamma }(\gamma -{\theta }_i)},{\mathsf{\Lambda }}_{12}=\sum _{i=1}^m\frac{{\mu }_i{\left(\psi \left({\kappa }_i\right)-\psi \left(a\right)\right)}^{\gamma -{\theta }_i-2}}{\mathsf{\Gamma }(\gamma -{\theta }_i-1)},\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathsf{\Lambda }}_{21}& =& \sum _{j=1}^n\frac{{\phi }_j{\left(\psi \left({\varsigma }_j\right)-\psi \left(a\right)\right)}^{\gamma -{\varphi }_j-1}}{\mathsf{\Gamma }(\gamma -{\varphi }_j)},{\mathsf{\Lambda }}_{22}=\sum _{j=1}^n\frac{{\phi }_j{\left(\psi \left({\varsigma }_j\right)-\psi \left(a\right)\right)}^{\gamma -{\varphi }_j-2}}{\mathsf{\Gamma }(\gamma -{\varphi }_j-1)}.\hfill \end{array}$$

(8)

Proof. 

Let $x\in \mathcal{E}$ be a solution of (5). Applying ${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }$ on both sides of (5) with Lemma 2 $(n=4)$, we have

$$\begin{array}{ccc}\hfill x\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -1}}{\mathsf{\Gamma }\left(\gamma \right)}{c}_1+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -2}}{\mathsf{\Gamma }(\gamma -1)}{c}_2\hfill \\ & & +\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -3}}{\mathsf{\Gamma }(\gamma -2)}{c}_3+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -4}}{\mathsf{\Gamma }(\gamma -3)}{c}_4,\hfill \end{array}$$

(9)

where $c_i\in \mathbb{R}$ for $i=1,2,3,4$. Taking the operator ${}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }$ into (9), we obtain

$$\begin{array}{ccc}\hfill {}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha -\delta ;\psi }h\left(t\right)+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -\delta -1}}{\mathsf{\Gamma }(\gamma -\delta )}{c}_1+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -\delta -2}}{\mathsf{\Gamma }(\gamma -\delta -1)}{c}_2\hfill \\ & & +\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -\delta -3}}{\mathsf{\Gamma }(\gamma -\delta -2)}{c}_3+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -\delta -4}}{\mathsf{\Gamma }(\gamma -\delta -3)}{c}_4.\hfill \end{array}$$

$x\left(a\right)={}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(a\right)=0$, which implies that $c_3=c_4=0$. Then,

$$x\left(t\right)={\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(t\right)+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -1}}{\mathsf{\Gamma }\left(\gamma \right)}{c}_1+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -2}}{\mathsf{\Gamma }(\gamma -1)}{c}_2.$$

(10)

Taking ${}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }$ and ${}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }$ into (10) with Proposition 1 (iii), we obtain

$$\begin{array}{ccc}\hfill {}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }x\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }h\left(t\right)+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -{\theta }_i-1}}{\mathsf{\Gamma }(\gamma -{\theta }_i)}{c}_1+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -{\theta }_i-2}}{\mathsf{\Gamma }(\gamma -{\theta }_i-1)}{c}_2,\hfill \\ \hfill {}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }x\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }h\left(t\right)+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -{\varphi }_j-1}}{\mathsf{\Gamma }(\gamma -{\varphi }_j)}{c}_1+\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -{\varphi }_j-2}}{\mathsf{\Gamma }(\gamma -{\varphi }_j-1)}{c}_2.\hfill \end{array}$$

By using the nonlinear boundary conditions in (5), we obtain the system of two unknowns variables $c_1$ and $c_2$,

$$\left(\begin{array}{cc}{\mathsf{\Lambda }}_{11}& {\mathsf{\Lambda }}_{12}\\ {\mathsf{\Lambda }}_{21}& {\mathsf{\Lambda }}_{22}\end{array}\right)\left(\begin{array}{c}{c}_1\\ c_2\end{array}\right)=\left(\begin{array}{c}\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }h\left({\kappa }_i\right)\\ \mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }h\left({\varsigma }_j\right)\end{array}\right),$$

(11)

where ${\mathsf{\Lambda }}_{11}$, ${\mathsf{\Lambda }}_{12}$, ${\mathsf{\Lambda }}_{21}$ and ${\mathsf{\Lambda }}_{22}$ are given by (7) and (8), respectively. Finding the solution of (11), we obtain the constants

$$\begin{array}{ccc}\hfill c_1& =& \frac{1}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }h\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }h\left({\varsigma }_j\right)\right)],\hfill \\ \hfill c_2& =& \frac{1}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }h\left({\varsigma }_j\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }h\left({\kappa }_i\right)\right)].\hfill \end{array}$$

Hence, the solution $x\left(t\right)$ follows by applying $c_1$ and $c_2$ in (9). This implies that $x\left(t\right)$ satisfies (6).

On the other hand, it is easy to show by a direct calculation that $x\left(t\right)$, which is given by (6), verifies the linear $\psi$-Hilfer $\mathbb{FCB}$ model (5) under the nonlinear boundary conditions. □

3. Existence and Uniqueness Results

For the sake of this paper, we set the notations ${\mathcal{F}}_x\left(t\right)=f(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right))$ and ${\mathcal{I}}_{a^{+}}^{u;\psi }{\mathcal{F}}_x\left(c\right)$, where

$${\mathcal{I}}_{a^{+}}^{u;\psi }{\mathcal{F}}_x\left(c\right)=\frac{1}{\mathsf{\Gamma }\left(u\right)}{\int }_a^c{\psi }^{\prime }\left(s\right){\left(\psi \left(c\right)-\psi \left(s\right)\right)}^{u-1}{\mathcal{F}}_x\left(s\right)ds,$$

with $u=\{\alpha ,\alpha -{\theta }_i,\alpha -{\varphi }_j\}$, $c=\{t,a,\xi ,{\kappa }_i,{\varsigma }_j\}$ for $i=1,2,\dots ,m$, $j=1,2,\dots ,n$. According to Lemma 4, we define $\mathcal{T}:\mathcal{E}\to \mathcal{E}$ and ${\mathsf{\Psi }}^{\gamma }(·)$

$$\begin{array}{ccc}\hfill \left(\mathcal{T}x\right)\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_x\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_x\left({\varsigma }_j\right)\right)]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_x\left({\varsigma }_j\right)\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & -{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_x\left({\kappa }_i\right)\right)],\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\mathsf{\Psi }}^{\gamma }\left(u\right)& =& \frac{{\left(\psi \left(u\right)-\psi \left(a\right)\right)}^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}.\hfill \end{array}$$

(13)

Clearly, the $\psi$-Hilfer fractional boundary value problem ($\mathbb{FBVP}$) describing the $\mathbb{CB}$ model (4) has solutions if and only if $\mathcal{T}$ has fixed points. For the tightness of calculation in this manuscript, we set the constants

$$\begin{array}{ccc}\hfill \mathsf{\Phi }(A,B)& =& \frac{1}{\left|\mathsf{\Lambda }\right|}\left(\left|A\right|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|B\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right),\hfill \\ \hfill \mathsf{\Omega }\left(u\right)& =& {\mathsf{\Psi }}^u\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{u-{\theta }_i}\left({\kappa }_i\right)\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & +\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{u-{\varphi }_j}\left({\varsigma }_j\right).\hfill \end{array}$$

(15)

3.1. Uniqueness Result

In the first our criteria, we will analyze the uniqueness result of the solution for the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) by applying Banach’s fixed point theorem (Lemma 5).

Lemma 5

(Banach’s fixed point theorem [45]). Let S be a non-empty closed subset of a Banach space $\mathcal{E}$. Then, any contraction mapping $\mathcal{Q}$ from $\mathcal{E}$ into itself has a unique fixed point.

Theorem 1.

Let $f:\mathcal{J}\times {\mathbb{R}}^3\to \mathbb{R}$ be continuous and

$\left({\mathcal{A}}_1\right)$

There exist positive constants ${\mathbb{L}}_1$, ${\mathbb{L}}_2$, ${\mathbb{L}}_3>0$ with ${\mathbb{L}}_2<1$, such that

$$\left|f(t,u_1,v_1,w_1)-f(t,u_2,v_2,w_2)\right|\le {\mathbb{L}}_1|u_1-u_2|+{\mathbb{L}}_2|v_1-v_2|+{\mathbb{L}}_3|w_1-w_2|,$$

for any $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2$ and $t\in \mathcal{J}$.

$\left({\mathcal{A}}_2\right)$

There exist positive constants ${\mathbb{H}}_1$, ${\mathbb{G}}_1>0$ such that

$$\left|\mathcal{H}(t,u_1)-\mathcal{H}(t,u_2)\right|\le {\mathbb{H}}_1|u_1-u_2|\mathrm{and}\left|\mathcal{G}(t,u_1)-\mathcal{G}(t,u_2)\right|\le {\mathbb{G}}_1|u_1-u_2|,$$

for any $u_i\in \mathbb{R}$, $i=1,2$ and $t\in \mathcal{J}$.

If

$$\left(\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1\mathsf{\Omega }\left(\alpha \right)+{\mathbb{L}}_3\mathsf{\Omega }(\beta +\alpha )\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\right)<1,$$

(16)

where${\mathsf{\Lambda }}_{ij}$, $i,j\in \{1,2\}$, $\mathsf{\Phi }(·,·)$and$\mathsf{\Omega }(·)$are defined by (7), (8), (14) and (15), respectively, and the ψ-Hilfer $\mathbb{FBVP}$ describing $\mathbb{CB}$ model (4) has a unique solution x in $\mathcal{E}$.

Proof. 

We transform the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) into $x=\mathcal{T}x$, where $\mathcal{T}$ is defined by (12). Clearly, the fixed points of $\mathcal{T}$ are the possible solutions of the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4). From Lemma 5, we will verify that $\mathcal{T}$ has a unique fixed point, which means that the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) has a unique solution.

Firstly, define a bounded, closed, convex and nonempty subset ${\mathcal{B}}_{r_1}:=\{x\in \mathcal{E}:\parallel x\parallel \le r_1\}$ with

$$r_1\ge \frac{\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}\mathsf{\Omega }\left(\alpha \right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{M}}_2+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{M}}_3}{1-\left(\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1\mathsf{\Omega }\left(\alpha \right)+{\mathbb{L}}_3\mathsf{\Omega }(\beta +\alpha )\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\right)},$$

(17)

where ${\mathsf{\Lambda }}_{ij}$ for i, $j\in \{1,2\}$, $\mathsf{\Phi }(·,·)$ and $\mathsf{\Omega }(·)$ are given by (7), (8), (14) and (15), respectively.

Let ${sup}_{t\in \mathcal{J}}\left|f(t,0,0,0)\right|:={\mathbb{M}}_1<\infty$, ${sup}_{t\in \mathcal{J}}\left|\mathcal{H}(t,0)\right|:={\mathbb{M}}_2<\infty$, ${sup}_{t\in \mathcal{J}}\left|\mathcal{G}(t,0)\right|:={\mathbb{M}}_3<\infty$. The process of proof will be divided in two steps:

Step I.$\mathcal{T}{\mathcal{B}}_{r_1}\subset {\mathcal{B}}_{r_1}$.

Let $x\in {\mathcal{B}}_{r_1}$ and $t\in \mathcal{J}$. Then,

$$\begin{array}{ccc}\hfill \left|\right(\mathcal{T}x\left)\right(t\left)\right|& \le & {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }|{\mathcal{F}}_x\left(b\right)|+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{22}\right|\left(\left|\mathcal{H}(\eta ,x\left(\eta \right))\right|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left({\kappa }_i\right)\right|\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{12}|\left(\left|\mathcal{G}(\xi ,x\left(\xi \right))\right|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left({\varsigma }_j\right)\right|\right)]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{11}\right|\left(\left|\mathcal{G}(\xi ,x\left(\xi \right))\right|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left({\varsigma }_j\right)\right|\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +|{\mathsf{\Lambda }}_{21}|\left(\left|\mathcal{H}(\eta ,x\left(\eta \right))\right|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left({\kappa }_i\right)\right|\right)].\hfill \end{array}$$

(18)

By applying Proposition 1 (i), we have

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{\beta ;\psi }\left|x\left(t\right)\right|& =& \frac{1}{\mathsf{\Gamma }\left(\beta \right)}{\int }_a^t{\psi }^{\prime }\left(s\right){\left(\psi \left(t\right)-\psi \left(s\right)\right)}^{\beta -1}\left|x\left(s\right)\right|ds\hfill \end{array}$$

$$\begin{array}{ccc}& \le & \frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\beta }}{\mathsf{\Gamma }(\beta +1)}∥x∥={\mathsf{\Psi }}^{\beta }\left(t\right)∥x∥.\hfill \end{array}$$

(19)

By applying $\left({\mathcal{A}}_1\right)$, $\left({\mathcal{A}}_2\right)$, and (19), we have

$$\begin{array}{ccc}\hfill \left|{\mathcal{F}}_x\left(t\right)\right|& \le & \left|f\right(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right))-f(t,0,0,0)|+\left|f(t,0,0,0)\right|\hfill \\ & \le & {\mathbb{L}}_1\left|x\left(t\right)\right|+{\mathbb{L}}_2|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)|+{\mathbb{L}}_3\left|{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)\right|+{\mathbb{M}}_1\hfill \\ & \le & \frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1+{\mathbb{L}}_3\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\beta }}{\mathsf{\Gamma }(\beta +1)}\right)+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}\hfill \end{array}$$

$$\begin{array}{ccc}& =& \frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta }\left(t\right)\right)+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill \left|\mathcal{H}(t,x(t\left)\right)\right|& \le & |\mathcal{H}(t,x\left(t\right))-\mathcal{H}(t,0)|+\left|\mathcal{H}(t,0)\right|\le {\mathbb{H}}_1\parallel x\parallel +{\mathbb{M}}_2,\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill \left|\mathcal{G}(t,x(t\left)\right)\right|& \le & |\mathcal{G}(t,x\left(t\right))-\mathcal{G}(t,0)|+\left|\mathcal{G}(t,0)\right|\le {\mathbb{G}}_1\parallel x\parallel +{\mathbb{M}}_3.\hfill \end{array}$$

(22)

From (20) with Proposition 1 (i), we can compute that

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\left|{\mathcal{F}}_x\left(b\right)\right|& \le & \frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)+\frac{{\mathbb{M}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)}{1-{\mathbb{L}}_2},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left({\kappa }_i\right)\right|& \le & \frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\right)+\frac{{\mathbb{M}}_1{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)}{1-{\mathbb{L}}_2},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left({\varsigma }_j\right)\right|& \le & \frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right)+\frac{{\mathbb{M}}_1{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)}{1-{\mathbb{L}}_2}.\hfill \end{array}$$

(25)

Substituting (20)–(25) into (18), we have

$$\begin{array}{ccc}& & \left|\right(\mathcal{T}x\left)\right(t\left)\right|\hfill \\ & \le & \frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}{\mathsf{\Psi }}^{\alpha }\left(b\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{22}\left|\right({\mathbb{H}}_1\parallel x\parallel +{\mathbb{M}}_2\hfill \\ & & +\sum _{i=1}^m\left|{\mu }_i\right|\left\{\frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\right)+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\right\})\hfill \\ & & +|{\mathsf{\Lambda }}_{12}\left|\right({\mathbb{G}}_1\parallel x\parallel +{\mathbb{M}}_3+\sum _{j=1}^n\left|{\phi }_j\right|\{\frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right)\hfill \\ & & +\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\left\}\right)]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{11}\left|\right(\sum _{j=1}^n\left|{\phi }_j\right|\{\frac{\parallel x\parallel }{1-{\mathbb{L}}_2}({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\hfill \\ & & +{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right))+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\}+{\mathbb{G}}_1\parallel x\parallel +{\mathbb{M}}_3)+|{\mathsf{\Lambda }}_{21}\left|\right({\mathbb{H}}_1\parallel x\parallel +{\mathbb{M}}_2\hfill \\ & & +\sum _{i=1}^m\left|{\mu }_i\right|\left\{\frac{\parallel x\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\right)+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\right\}\left)\right]\hfill \\ & \le & \left\{\frac{1}{1-{\mathbb{L}}_2}\right({\mathbb{L}}_1[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)]+{\mathbb{L}}_3[{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}(\left|{\mathsf{\Lambda }}_{12}\right|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{11}|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\left)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right])+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right){\mathbb{H}}_1\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right){\mathbb{G}}_1\}{r}_1+\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}[{\mathsf{\Psi }}^{\alpha }\left(b\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}(\left|{\mathsf{\Lambda }}_{12}\right|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{11}|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\left)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right]+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right){\mathbb{M}}_2\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right){\mathbb{M}}_3\hfill \end{array}$$

$$\begin{array}{ccc}& =& \left\{\frac{1}{1-{\mathbb{L}}_2}\right({\mathbb{L}}_1[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)]+{\mathbb{L}}_3[{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\left]\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\}{r}_1\hfill \\ & & +\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}\left[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right]\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{M}}_2+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{M}}_3.\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill \left|\right(\mathcal{T}x\left)\right(t\left)\right|& \le & \left\{\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1\mathsf{\Omega }\left(\alpha \right)+{\mathbb{L}}_3\mathsf{\Omega }(\beta +\alpha )\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\right\}{r}_1\hfill \\ & & +\frac{{\mathbb{M}}_1}{1-{\mathbb{L}}_2}\mathsf{\Omega }\left(\alpha \right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{M}}_2+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{M}}_3,\hfill \end{array}$$

which implies that $\parallel \mathcal{T}x\parallel \le r_1$. Then, $\mathcal{T}{\mathcal{B}}_{r_1}\subset {\mathcal{B}}_{r_1}$.

Step II.$\mathcal{T}:\mathcal{E}\to \mathcal{E}$ is a contraction.

Let x, $y\in \mathcal{E}$ and for any $t\in \mathcal{J}$. Then, we have

$$\begin{array}{ccc}& & \left|\left(\left(\mathcal{T}x\right)\left(t\right)-\left(\mathcal{T}y\right)\left(t\right)\right)\right|\hfill \\ & \le & {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }|{\mathcal{F}}_x\left(s\right)-{\mathcal{F}}_y\left(s\right)|\left(b\right)\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{22}\right|\left(|\mathcal{H}(\eta ,x\left(\eta \right))-\mathcal{H}(\eta ,y\left(\eta \right))|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }|{\mathcal{F}}_x\left(s\right)-{\mathcal{F}}_y\left(s\right)|\left({\kappa }_i\right)\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{12}|\left(|\mathcal{G}(\xi ,x\left(\xi \right))-\mathcal{G}(\xi ,y\left(\xi \right))|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }|{\mathcal{F}}_x\left(s\right)-{\mathcal{F}}_y\left(s\right)|\left({\varsigma }_j\right)\right)]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{11}\right|\left(|\mathcal{G}(\xi ,x\left(\xi \right))-\mathcal{G}(\xi ,y\left(\xi \right))|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }|{\mathcal{F}}_x\left(s\right)-{\mathcal{F}}_y\left(s\right)|\left({\varsigma }_j\right)\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +|{\mathsf{\Lambda }}_{21}|\left(|\mathcal{H}(\eta ,x\left(\eta \right))-\mathcal{H}(\eta ,y\left(\eta \right))|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }|{\mathcal{F}}_x\left(s\right)-{\mathcal{F}}_y\left(s\right)|\left({\kappa }_i\right)\right)].\hfill \end{array}$$

(26)

By applying $\left({\mathcal{A}}_1\right)$ and (19), we have

$$\begin{array}{ccc}& & \left|{\mathcal{F}}_x\left(t\right)-{\mathcal{F}}_y\left(t\right)\right|\hfill \\ & =& \left|f(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right))-f(t,y\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }y\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }y\left(t\right))\right|\hfill \\ & \le & {\mathbb{L}}_1|x\left(t\right)-y\left(t\right)|+{\mathbb{L}}_2\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)-{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }y\left(t\right)\right|+{\mathbb{L}}_3\left|{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)-{\mathcal{I}}_{a^{+}}^{\beta ;\psi }y\left(t\right)\right|\hfill \end{array}$$

$$\begin{array}{ccc}& \le & \left({\mathbb{L}}_1+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta }\left(t\right)\right)\frac{∥x-y∥}{1-{\mathbb{L}}_2}.\hfill \end{array}$$

(27)

Hence, by inserting (27) in (26) and using Proposition (i) with $\left({\mathcal{A}}_2\right)$, we obtain

$$\begin{array}{ccc}& & \left|\left(\mathcal{T}x\right)\left(t\right)-\left(\mathcal{T}y\right)\left(t\right)\right|\hfill \\ & \le & \frac{\parallel x-y\parallel }{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{22}\left|\right({\mathbb{H}}_1\parallel x-y\parallel \hfill \\ & & +\frac{\parallel x-y\parallel }{1-{\mathbb{L}}_2}\sum _{i=1}^m|{\mu }_i|\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\right))+|{\mathsf{\Lambda }}_{12}\left|\right({\mathbb{G}}_1\parallel x-y\parallel \hfill \\ & & +\frac{\parallel x-y\parallel }{1-{\mathbb{L}}_2}\sum _{j=1}^n\left|{\phi }_j\right|\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right)\left)\right]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\hfill \\ & & \times \left[\right|{\mathsf{\Lambda }}_{11}|\left({\mathbb{G}}_1\parallel x-y\parallel +\frac{\parallel x-y\parallel }{1-{\mathbb{L}}_2}\sum _{j=1}^n\left|{\phi }_j\right|\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right)\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{21}|\left({\mathbb{H}}_1\parallel x-y\parallel +\frac{\parallel x-y\parallel }{1-{\mathbb{L}}_2}\sum _{i=1}^m\left|{\mu }_i\right|\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\right)\right)]\hfill \\ & =& \left\{\frac{1}{1-{\mathbb{L}}_2}\right({\mathbb{L}}_1[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)]+{\mathbb{L}}_3[{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\left]\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\}∥x-y∥,\hfill \end{array}$$

which implies that

$$\begin{array}{ccc}& & ∥\mathcal{T}x-\mathcal{T}y∥\hfill \\ & \le & \left\{\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1\mathsf{\Omega }\left(\alpha \right)+{\mathbb{L}}_3\mathsf{\Omega }(\beta +\alpha )\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\right\}∥x-y∥.\hfill \end{array}$$

In view of (16), we find that $\mathcal{T}$ is a contraction. Therefore, in accordance with Lemma 5, the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) has a unique solution $x\in \mathcal{E}$. □

3.2. Existence Result

The second result is proved by applying Schaefer’s fixed point theorem (Lemma 6).

Lemma 6.

(Schaefer’s fixed point theorem [45].) Let $\mathcal{E}$ be a Banach space and $\mathcal{T}:\mathcal{E}\to \mathcal{E}$ is a completely continuous operator and the set $\mathbb{B}=\{x\in \mathcal{E}:x=\zeta \mathcal{T}x,0<\zeta \le 1\}$ is bounded. Then, $\mathcal{T}$ has a fixed point in $\mathcal{E}$.

Theorem 2.

Let $f:\mathcal{J}\times {\mathbb{R}}^3\to \mathbb{R}$ be continuous. Assume that:

$\left({\mathcal{A}}_3\right)$

There exist non-negative continuous functions $p_i\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+}\cup \left\{0\right\})$$(i=1,2,3,4)$ such that

$$\left|f(t,u,v,w)\right|\le p_1\left(t\right)+p_2\left(t\right)\left|u\right|+p_3\left(t\right)\left|v\right|+p_4\left(t\right)\left|w\right|,\forall (t,u,v,w)\in (\mathcal{J},{\mathbb{R}}^3),$$

with $p_i^{*}={sup}_{t\in \mathcal{J}}\left\{p_i\left(t\right)\right\}$, $i=1,2,3,4$, and $p_3^{*}<1$.

$\left({\mathcal{A}}_4\right)$

There exist non-negative continuous functions $h_i$, $g_i\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+}\cup \left\{0\right\})$$(i=1,2)$ such that

$$\begin{array}{ccc}\hfill \left|\mathcal{H}\right(t,u\left)\right|& \le & h_1\left(t\right)+h_2\left(t\right)\left|u\right|,(t,u)\in (\mathcal{J},\mathbb{R}),\hfill \\ \hfill \left|\mathcal{G}\right(t,u\left)\right|& \le & g_1\left(t\right)+g_2\left(t\right)\left|u\right|,(t,u)\in (\mathcal{J},\mathbb{R}),\hfill \end{array}$$

with $h_i^{*}={sup}_{t\in \mathcal{J}}\left\{h_i\left(t\right)\right\}$ and $g_i^{*}={sup}_{t\in \mathcal{J}}\left\{g_i\left(t\right)\right\}$, $i=1,2$.

Then, the ψ-Hilfer $\mathbb{FBVP}$ describing $\mathbb{CB}$ model (4) has at least one solution on $\mathcal{J}$.

Proof. 

The process will be analyzed in four steps as follows.

Step I.$\mathcal{T}$ is continuous.

Let $x_n$ be a sequence such that $x_n\to x\in \mathcal{E}$. Then, for any $t\in \mathcal{J}$, we have

$$\begin{array}{ccc}& & \left|\left(\mathcal{T}{x}_n\right)\left(t\right)-\left(\mathcal{T}x\right)\left(t\right)\right|\hfill \\ & \le & {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }|{\mathcal{F}}_{x_n}\left(s\right)-{\mathcal{F}}_x\left(s\right)|\left(b\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{22}\left|\right(|\mathcal{H}(\eta ,x_n\left(\eta \right))-\mathcal{H}(\eta ,x\left(\eta \right))|\hfill \\ & & +\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }|{\mathcal{F}}_{x_n}\left(s\right)-{\mathcal{F}}_x\left(s\right)|\left({\kappa }_i\right))+|{\mathsf{\Lambda }}_{12}\left|\right(|\mathcal{G}(\xi ,x_n\left(\xi \right))-\mathcal{G}(\xi ,x\left(\xi \right))|\hfill \\ & & +\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }|{\mathcal{F}}_{x_n}\left(s\right)-{\mathcal{F}}_x\left(s\right)|\left({\varsigma }_j\right)\left)\right]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{11}\left|\right(|\mathcal{G}(\xi ,x_n\left(\xi \right))\hfill \\ & & -\mathcal{G}(\xi ,x\left(\xi \right))|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }|{\mathcal{F}}_{x_n}\left(s\right)-{\mathcal{F}}_x\left(s\right)|\left({\varsigma }_j\right))+|{\mathsf{\Lambda }}_{21}\left|\right(|\mathcal{H}(\eta ,x_n\left(\eta \right))\hfill \\ & & -\mathcal{H}(\eta ,x\left(\eta \right))|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }|{\mathcal{F}}_{x_n}\left(s\right)-{\mathcal{F}}_x\left(s\right)|\left({\kappa }_i\right)\left)\right]\hfill \\ & \le & {\mathsf{\Psi }}^{\alpha }\left(b\right)\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{22}\right|\left({\mathbb{H}}_1\parallel x_n-x\parallel +\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \right)\hfill \\ & & +|{\mathsf{\Lambda }}_{12}|\left({\mathbb{G}}_1\parallel x_n-x\parallel +\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \right)]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{11}\right|\left({\mathbb{G}}_1\parallel x_n-x\parallel +\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \right)\hfill \\ & & +|{\mathsf{\Lambda }}_{21}|\left({\mathbb{H}}_1\parallel x_n-x\parallel +\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \right)]\hfill \\ & =& \{{\mathsf{\Psi }}^{\alpha }\left(b\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\}\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \hfill \\ & & +\{\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right){\mathbb{H}}_1\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right){\mathbb{G}}_1\}\parallel x_n-x\parallel \hfill \\ & =& \parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \left\{{\mathsf{\Psi }}^{\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right\}\hfill \\ & & +\left\{\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\right\}\parallel x_n-x\parallel \hfill \\ & =& \mathsf{\Omega }\left(\alpha \right)\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel +\left\{\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1\right\}\parallel x_n-x\parallel .\hfill \end{array}$$

The continuity of f implies the continuity of ${\mathcal{F}}_x$. Then, $\parallel {\mathcal{F}}_{x_n}-{\mathcal{F}}_x\parallel \to 0$, $\parallel x_n-x\parallel \to 0$, as $n\to \infty$, Hence, $\mathcal{T}$ is continuous.

Step II.$\mathcal{T}$ maps bounded set into bounded set in $\mathcal{E}$.

For $r_2>0$, there is $\mathcal{N}$ such that, for each $x\in {\mathcal{B}}_{r_2}$ where ${\mathcal{B}}_{r_2}=\{x\in \mathcal{E}:\parallel x\parallel \le r_2\}$, then $\parallel \mathcal{T}x\parallel \le \mathcal{N}$.

For any $t\in \mathcal{J}$ and $x\in {\mathcal{B}}_{r_2}$, we obtain

$$\begin{array}{ccc}\hfill \left|\left(\mathcal{T}x\right)\left(t\right)\right|& \le & {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }|{\mathcal{F}}_x\left(b\right)|+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{22}\right|\left(\left|\mathcal{H}(\eta ,x\left(\eta \right))\right|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left({\kappa }_i\right)\right|\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{12}|\left(\left|\mathcal{G}(\xi ,x\left(\xi \right))\right|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left({\varsigma }_j\right)\right|\right)]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{11}\right|\left(\left|\mathcal{G}(\xi ,x\left(\xi \right))\right|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left({\varsigma }_j\right)\right|\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{21}|\left(\left|\mathcal{H}(\eta ,x\left(\eta \right))\right|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left({\kappa }_i\right)\right|\right)].\hfill \end{array}$$

(28)

From $\left({\mathcal{A}}_3\right)$–$\left({\mathcal{A}}_4\right)$, it follows that

$$\begin{array}{ccc}\hfill \left|{\mathcal{F}}_x\left(t\right)\right|& \le & p_1\left(t\right)+p_2\left(t\right)\left|x\left(t\right)\right|+p_3\left(t\right)|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)|+p_4\left(t\right)\left|{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)\right|\hfill \\ & \le & \frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\beta }}{\mathsf{\Gamma }(\beta +1)}\right)\hfill \end{array}$$

$$\begin{array}{ccc}& =& \frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}{\mathsf{\Psi }}^{\beta }\left(t\right)\right),\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill \left|\mathcal{H}(t,x(t\left)\right)\right|& \le & h_1\left(t\right)+h_2\left|x\left(t\right)\right|\le h_1^{*}+h_2^{*}\parallel x\parallel ,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill \left|\mathcal{G}(t,x(t\left)\right)\right|& \le & g_1\left(t\right)+g_2\left(t\right)\left|x\left(t\right)\right|\le g_1^{*}+g_2^{*}\parallel x\parallel .\hfill \end{array}$$

(31)

Inserting (29)–(31) in (28), we can compute that

$$\begin{array}{ccc}& & \left|\left(\mathcal{T}x\right)\left(t\right)\right|\hfill \\ & \le & {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\left(\frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}{\mathsf{\Psi }}^{\beta }\left(s\right)\right)\right)\left(b\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{22}\left|\right(h_1^{*}+h_2^{*}\parallel x\parallel \hfill \\ & & +\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left(\frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}{\mathsf{\Psi }}^{\beta }\left(s\right)\right)\right)\left({\kappa }_i\right))+|{\mathsf{\Lambda }}_{12}\left|\right(g_1^{*}+g_2^{*}\parallel x\parallel \hfill \\ & & +\sum _{j=1}^n\left|{\phi }_j\right|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left(\frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}{\mathsf{\Psi }}^{\beta }\left(s\right)\right)\right)\left({\varsigma }_j\right)\left)\right]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(b\right)}{\left|\mathsf{\Lambda }\right|}\hfill \\ & & \times \left[\right|{\mathsf{\Lambda }}_{11}|\left(g_1^{*}+g_2^{*}\parallel x\parallel +\sum _{j=1}^n\left|{\phi }_j\right|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left(\frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}{\mathsf{\Psi }}^{\beta }\left(s\right)\right)\right)\left({\varsigma }_j\right)\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{21}|\left(h_1^{*}+h_2^{*}\parallel x\parallel +\sum _{i=1}^m\left|{\mu }_i\right|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left(\frac{p_1^{*}}{1-p_3^{*}}+\frac{\parallel x\parallel }{1-p_3^{*}}\left(p_2^{*}+p_4^{*}{\mathsf{\Psi }}^{\beta }\left(s\right)\right)\right)\left({\kappa }_i\right)\right)]\hfill \\ & \le & \left\{\right[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)]\frac{p_2^{*}}{1-p_3^{*}}\hfill \end{array}$$

$$\begin{array}{ccc}& & +[{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)]\frac{p_4^{*}}{1-p_3^{*}}\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)h_2^{*}\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)g_2^{*}\}\parallel x\parallel \hfill \\ & & +[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)]\frac{p_1^{*}}{1-p_3^{*}}\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)h_1^{*}+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)g_1^{*}\hfill \\ & =& \{\left[{\mathsf{\Psi }}^{\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right]\frac{p_2^{*}}{1-p_3^{*}}\hfill \\ & & +\left[{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\beta +\alpha -{\theta }_i}\left({\kappa }_i\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\beta +\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right]\hfill \\ & & \times \left[\frac{p_4^{*}}{1-p_3^{*}}\right]+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})h_2^{*}+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})g_2^{*}\}\parallel x\parallel +\frac{p_1^{*}}{1-p_3^{*}}[{\mathsf{\Psi }}^{\alpha }\left(b\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m|{\mu }_i|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)]\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})h_1^{*}+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})g_1^{*}.\hfill \end{array}$$

which implies that

$$\begin{array}{ccc}\hfill ∥\mathcal{T}x∥& \le & \left\{\mathsf{\Omega }\left(\alpha \right)\frac{p_2^{*}}{1-p_3^{*}}+\mathsf{\Omega }(\beta +\alpha )\frac{p_4^{*}}{1-p_3^{*}}+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})h_2^{*}+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})g_2^{*}\right\}{r}_2\hfill \\ & & +\mathsf{\Omega }\left(\alpha \right)\frac{p_1^{*}}{1-p_3^{*}}+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})h_1^{*}+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})g_1^{*}:=\mathcal{N}.\hfill \end{array}$$

Then, $\mathcal{T}$ maps bounded set into bounded set in $\mathcal{E}$.

Step III.$\mathcal{T}$ maps bounded sets into equicontinuous sets of $\mathcal{E}$.

For $a\le t_1<t_2\le b$ and $x\in {\mathcal{B}}_{r_2}$ where ${\mathcal{B}}_{r_2}$ as defined in Step II, by using the property that f is a bounded on the compact set $\mathcal{J}\times {\mathcal{B}}_{r_2}$, we estimate

$$\begin{array}{ccc}& & \left|\left(\mathcal{T}x\right)\left(t_2\right)-\left(\mathcal{T}x\right)\left(t_1\right)\right|\hfill \\ & \le & \frac{\left|{\mathsf{\Psi }}^{\gamma -1}\left(t_2\right)-{\mathsf{\Psi }}^{\gamma -1}\left(t_1\right)\right|}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{22}\right|\left(\left|\mathcal{H}(\eta ,x\left(\eta \right))\right|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left(s\right)\right|\left({\kappa }_i\right)\right)\hfill \\ & & +|{\mathsf{\Lambda }}_{12}|\left(\left|\mathcal{G}(\xi ,x\left(\xi \right))\right|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left(s\right)\right|\left({\varsigma }_j\right)\right)]\hfill \\ & & +\frac{\left|{\mathsf{\Psi }}^{\gamma -2}\left(t_2\right)-{\mathsf{\Psi }}^{\gamma -2}\left(t_1\right)\right|}{\left|\mathsf{\Lambda }\right|}[\left|{\mathsf{\Lambda }}_{11}\right|\left(\left|\mathcal{G}(\xi ,x\left(\xi \right))\right|+\sum _{j=1}^n|{\phi }_j|{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }\left|{\mathcal{F}}_x\left(s\right)\right|\left({\varsigma }_j\right)\right)\hfill \end{array}$$

$$+|{\mathsf{\Lambda }}_{21}|\left(\left|\mathcal{H}(\eta ,x\left(\eta \right))\right|+\sum _{i=1}^m|{\mu }_i|{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }\left|{\mathcal{F}}_x\left(s\right)\right|\left({\kappa }_i\right)\right)]+\left|{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t_2\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t_1\right)\right|.$$

By setting ${sup}_{(t,u,v,w)\in \mathcal{J}\times {\mathcal{B}}_{r_2}^3}\left|f(t,u,v,w)\right|=\widehat{f}<\infty$, ${sup}_{(t,u)\in \mathcal{J}\times {\mathcal{B}}_{r_2}}\left|\mathcal{H}(t,u)\right|=\widehat{\mathcal{H}}<\infty$, and ${sup}_{(t,u)\in \mathcal{J}\times {\mathcal{B}}_{r_2}}\left|\mathcal{G}(t,u)\right|=\widehat{\mathcal{G}}<\infty$, then

$$\begin{array}{ccc}& & \left|\left(\mathcal{T}x\right)\left(t_2\right)-\left(\mathcal{T}x\right)\left(t_1\right)\right|\hfill \\ & \le & \frac{\left|{\mathsf{\Psi }}^{\gamma -1}\left(t_2\right)-{\mathsf{\Psi }}^{\gamma -1}\left(t_1\right)\right|}{\left|\mathsf{\Lambda }\right|}\left[\right|{\mathsf{\Lambda }}_{22}|\left(\widehat{\mathcal{H}}+\widehat{f}\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\right)+\left|{\mathsf{\Lambda }}_{12}\right|(\widehat{\mathcal{G}}\hfill \\ & & +\widehat{f}\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\left)\right]+\frac{\left|{\mathsf{\Psi }}^{\gamma -1}\left(t_2\right)-{\mathsf{\Psi }}^{\gamma -2}\left(t_1\right)\right|}{\left|\mathsf{\Lambda }\right|}\left[\left|{\mathsf{\Lambda }}_{11}\right|\right(\widehat{\mathcal{G}}\hfill \\ & & +\widehat{f}\sum _{j=1}^n|{\phi }_j|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right))+\left|{\mathsf{\Lambda }}_{21}\right|\left(\widehat{\mathcal{H}}+\widehat{f}\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\right)]\hfill \\ & & +\frac{\widehat{f}}{\mathsf{\Gamma }(\alpha +1)}\left[\right|{\left(\psi \left(t_2\right)-\psi \left(a\right)\right)}^{\alpha }-{\left(\psi \left(t_2\right)-\psi \left(t_1\right)\right)}^{\alpha }-{\left(\psi \left(t_1\right)-\psi \left(a\right)\right)}^{\alpha }|\hfill \\ & & +{\left(\psi \left(t_2\right)-\psi \left(t_1\right)\right)}^{\alpha }].\hfill \end{array}$$

Note that the right hand-side of the above inequality is independent of the unknown variable x and tends to zero as $t_2\to t_1$. Hence, $\mathcal{T}$ is equicontinuous. Then, $\mathcal{T}$ is relatively compact on ${\mathcal{B}}_{r_2}$. We apply the Arzelá–Ascoli theorem, which implies that $\mathcal{T}$ is completely continuous.

Step IV. The set $\mathbb{B}=\{x\in \mathcal{E}:x=\zeta \mathcal{T}x,\zeta \in (0,1\left]\right\}$ is a bounded (a priori bounds).

Let $x\in \mathbb{B}$, then $x=\zeta \mathcal{T}x$ for some $\zeta \in (0,1]$. From $\left({\mathcal{A}}_3\right)$–$\left({\mathcal{A}}_4\right)$, for any $t\in \mathcal{J}$, then

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \zeta \{{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_x\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_x\left({\varsigma }_j\right)\right)]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}(\mathcal{G}(\xi ,x\left(\xi \right))\hfill \\ & & -\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_x\left({\varsigma }_j\right))-{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_x\left({\kappa }_i\right)\right)]\}.\hfill \end{array}$$

It follows from Step II, and for any $t\in \mathcal{J}$, that $\parallel \mathcal{T}x\parallel \le \mathcal{N}<\infty$. Then, $\mathbb{B}$ is a bounded set.

Using Theorem 2, we find that there exists $\mathcal{N}>0$ such that $\parallel x\parallel \le \mathcal{N}<\infty$. Thanks to Lemma 6, $\mathcal{T}$ has at least one fixed point, which is the corresponding solution of the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4). □

4. Ulam’s Stability Results

In this section, we analyze the $\mathcal{UH}$ stability, $\mathcal{GUH}$ stability, $\mathcal{UHR}$ stability, and $\mathcal{GUHR}$ stability of the solution to the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4).

Definition 4.

The ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (4) is said to be $\mathcal{UH}$-stable if there exists a positive real number ${\mathfrak{C}}_f>0$ such that for each $ϵ>0$ and for each solution $z\in \mathcal{E}$ of

$$\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)-{\mathcal{F}}_z\left(t\right)\right|\le ϵ,$$

(32)

there exists a solution $x\in \mathcal{E}$ of the ψ-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) such that

$$\left|z\left(t\right)-x\left(t\right)\right|\le {\mathfrak{C}}_fϵ,t\in \mathcal{J}.$$

(33)

Definition 5.

The ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (4) is said to be $\mathcal{GUH}$-stable if there exists a function $\mathcal{K}\in \mathcal{C}({\mathbb{R}}^{+},{\mathbb{R}}^{+})$ with $\mathcal{K}\left(0\right)=0$ such that, for each solution $z\in \mathcal{E}$ of

$$\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)-{\mathcal{F}}_z\left(t\right)\right|\le ϵ\mathcal{K}\left(t\right),$$

(34)

there exists a solution $x\in \mathcal{E}$ of the ψ-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) such that

$$\left|z\left(t\right)-x\left(t\right)\right|\le \mathcal{K}\left(ϵ\right),t\in \mathcal{J}.$$

(35)

Definition 6.

The ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (4) is said to be $\mathcal{UHR}$-stable with respect to $\mathcal{K}\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$ if there exists a positive real number ${\mathfrak{C}}_{f,\mathcal{K}}>0$ such that for each $ϵ>0$ and for each a solution $z\in \mathcal{E}$ of (34) there exists a solution $x\in \mathcal{E}$ of the ψ-Hilfer $\mathbb{FBCP}$ describing the $\mathbb{CB}$ model (4) such that

$$\left|z\left(t\right)-x\left(t\right)\right|\le {\mathfrak{C}}_{f,\mathcal{K}}ϵ\mathcal{K}\left(t\right),t\in \mathcal{J}.$$

(36)

Definition 7.

The ψ-Hilfer$\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) is said to be $\mathcal{GUHR}$-stable with respect to $\mathcal{K}\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$ if there exists a positive real number ${\mathfrak{C}}_{f,\mathcal{K}}>0$ such that for each a solution $z\in \mathcal{E}$ of

$$\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)-{\mathcal{F}}_z\left(t\right)\right|\le \mathcal{K}\left(t\right),$$

(37)

there exists a solution $x\in \mathcal{E}$ of the ψ-Hilfer $\mathbb{FBVP}$ describing $\mathbb{CB}$ model (4) such that

$$\left|z\left(t\right)-x\left(t\right)\right|\le {\mathfrak{C}}_{f,\mathcal{K}}\mathcal{K}\left(t\right),t\in \mathcal{J}.$$

(38)

Remark 1.

It is easy to see that $\left(a_1\right)$ Definition 4 ⇒ Definition 5; $\left(a_2\right)$ Definition 6 ⇒ Definition 7; $\left(a_3\right)$ Definition 6 for $\mathcal{K}\left(t\right)=1$⇒ Definition 4.

Remark 2.

A function$z\in \mathcal{E}$is a solution of (32) if and only if there exists a function $v\in \mathcal{E}$ (where v depends on solution z) such that: $\left(i\right)$$\left|v\right(t\left)\right|\le ϵ$, $\forall t\in \mathcal{J}$; $\left(ii\right)$${}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)={\mathcal{F}}_z\left(t\right)+v\left(t\right)$, $t\in \mathcal{J}$.

Remark 3.

A function$z\in \mathcal{E}$is a solution of (34) if and only if there exists a function $w\in \mathcal{E}$ (where w depends on solution z) such that: $\left(i\right)$$\left|w\right(t\left)\right|\le ϵ\mathcal{K}\left(t\right)$, $\forall t\in \mathcal{J}$; $\left(ii\right)$${}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)={\mathcal{F}}_z\left(t\right)+w\left(t\right)$, $t\in \mathcal{J}$.

Remark 4.

There exists an increasing function $\mathcal{K}\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$ and there exists a positive constant ${\lambda }_{\mathcal{K}}>0$, such that, for each $t\in \mathcal{J}$, we have the integral inequality

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\mathcal{K}\left(t\right)\le {\lambda }_{\mathcal{K}}\mathcal{K}\left(t\right).$$

(39)

4.1. The $\mathcal{UH}$ and $\mathcal{GUH}$ Stability Results

Firstly, we present an important lemma that will be used in the analyses of $\mathcal{UH}$ and $\mathcal{GUH}$ stability of the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4).

Lemma 7.

Let$\alpha \in (3,4]$, $\rho \in [0,1]$and let$z\in \mathcal{E}$be the solution of (32). Then, $z\in \mathcal{E}$ satisfies

$$\left|z\left(t\right)-{\chi }_z\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)\right|\le \mathsf{\Omega }\left(\alpha \right)ϵ,$$

(40)

where

$$\begin{array}{ccc}\hfill {\chi }_z\left(t\right)& =& \frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,z\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_z\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,z\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\varsigma }_j\right)\right)]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}(\mathcal{G}(\xi ,z\left(\xi \right))\hfill \\ & & -\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\varsigma }_j\right))-{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,z\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_z\left({\kappa }_i\right)\right)],\hfill \end{array}$$

(41)

with Λ, ${\mathsf{\Lambda }}_{ij}$, i, $j\in \{1,2\}$, and $\mathsf{\Omega }\left(\alpha \right)$ as in Lemma 4 and (15), respectively.

Proof. 

Let z be the solution of (32). Thanks to Remark 2 $\left(ii\right)$ and Lemma 4, we obtain

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)={\mathcal{F}}_z\left(t\right)+v\left(t\right)t\in (a,b),}\\ {\displaystyle z\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }z\left(a\right)=0,}\\ {\displaystyle \sum _{i=1}^m{\mu }_i{}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }z\left({\kappa }_i\right)=\mathcal{H}(\eta ,z\left(\eta \right)),\sum _{j=1}^n{\phi }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\varsigma }_j\right)=\mathcal{G}(\xi ,z\left(\xi \right)).}\end{array}\right.$$

(42)

Then, the solution of (42) can be written as

$$\begin{array}{ccc}\hfill z\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)+\frac{{\mathsf{\Psi }}^{q-1}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,z\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_z\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,z\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\varsigma }_j\right)\right)]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{q-2}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}\left(\mathcal{G}(\xi ,z\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\varsigma }_j\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,z\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_z\left({\kappa }_i\right)\right)]+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }v\left(t\right)\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{22}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }v\left({\kappa }_i\right)+{\mathsf{\Lambda }}_{12}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }v\left({\varsigma }_j\right)\right]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{11}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }v\left({\varsigma }_j\right)+{\mathsf{\Lambda }}_{21}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }v\left({\kappa }_i\right)\right].\hfill \end{array}$$

Remark 2 $\left(i\right)$ implies that

$$\begin{array}{ccc}& & \left|z\left(t\right)-{\chi }_z\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)\right|\hfill \\ & =& |{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }v\left(t\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{22}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }v\left({\kappa }_i\right)+{\mathsf{\Lambda }}_{12}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }v\left({\varsigma }_j\right)\right]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{11}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }v\left({\varsigma }_j\right)+{\mathsf{\Lambda }}_{21}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }v\left({\kappa }_i\right)\right]|\hfill \\ & \le & \{{\mathsf{\Psi }}^{\alpha }\left(b\right)+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{11}|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)+\left|{\mathsf{\Lambda }}_{12}\right|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)\right)\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\}ϵ\hfill \end{array}$$

$$\begin{array}{ccc}& =& \left\{{\mathsf{\Psi }}^{\alpha }\left(b\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|{\mathsf{\Psi }}^{\alpha -{\theta }_i}\left({\kappa }_i\right)+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|{\mathsf{\Psi }}^{\alpha -{\varphi }_j}\left({\varsigma }_j\right)\right\}ϵ\hfill \\ & =& \mathsf{\Omega }\left(\alpha \right)ϵ.\hfill \end{array}$$

Lemma 7 is obtained. □

Now, we prove the $\mathcal{UH}$ and $\mathcal{GUH}$ stability of solution to the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4).

Theorem 3.

Let $f:\mathcal{J}\times {\mathbb{R}}^3\to \mathbb{R}$ be continuous, and let $\left({\mathcal{A}}_1\right)$–$\left({\mathcal{A}}_2\right)$ be verified with

$$\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)<1.$$

Then, the ψ-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) is $\mathcal{UH}$ and $\mathcal{GUH}$-stable in $\mathcal{E}$.

Proof. 

Let $z\in \mathcal{E}$ be the solution of (32) and $x\in \mathcal{E}$ be a unique solution of the $\psi$-Hilfer fractional differential equation describing $\mathbb{CB}$ model (4) with the nonlinear boundary conditions of the form $x\left(a\right)=0$, ${}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(a\right)=0$, ${\sum }_{i=1}^m{\mu }_i{}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }x\left({\kappa }_i\right)=\mathcal{H}(\eta ,x\left(\eta \right))$, ${\sum }_{j=1}^n{\phi }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }x\left({\varsigma }_j\right)=\mathcal{G}(\xi ,x\left(\xi \right))$.

From Lemma 4, we obtain $x\left(t\right)={\chi }_x\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t\right)$, where

$$\begin{array}{ccc}\hfill {\chi }_x\left(t\right)& =& \frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,x(\eta \left)\right)-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_x\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,x\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_x\left({\varsigma }_j\right)\right)]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}(\mathcal{G}(\xi ,x\left(\xi \right))\hfill \\ & & -\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_x\left({\varsigma }_j\right))-{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,x\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_x\left({\kappa }_i\right)\right)].\hfill \end{array}$$

(43)

Moreover, if $x\left(a\right)=z\left(a\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(a\right)={}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }z\left(a\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }x\left({\kappa }_i\right)={}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }z\left({\kappa }_i\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }x\left({\varsigma }_j\right)={}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\varsigma }_j\right)$, $\mathcal{H}(\eta ,x(\eta \left)\right)=\mathcal{H}(\eta ,z(\eta \left)\right)$, and $\mathcal{G}(\xi ,x(\xi \left)\right)=\mathcal{G}(\xi ,z(\xi \left)\right)$, then ${\chi }_x\left(t\right)={\chi }_z\left(t\right)$. By applying the inequality, $|x+y|\le \left|x\right|+\left|y\right|$, and Lemma 7, for $t\in \mathcal{J}$, we have

$$\begin{array}{ccc}\hfill \left|z\right(t)-x(t\left)\right|& =& |z\left(t\right)-{\chi }_x\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t\right)|\hfill \\ & \le & |z\left(t\right)-{\chi }_z\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)|+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }|{\mathcal{F}}_z\left(t\right)-{\mathcal{F}}_x\left(t\right)|+|{\chi }_z\left(t\right)-{\chi }_x\left(t\right)|\hfill \\ & \le & \mathsf{\Omega }\left(\alpha \right)ϵ+\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)|z\left(t\right)-x\left(t\right)|,\hfill \end{array}$$

which implies that $|z\left(t\right)-x\left(t\right)|\le {\mathfrak{C}}_fϵ$, where

$${\mathfrak{C}}_f:=\frac{\mathsf{\Omega }\left(\alpha \right)}{1-\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)}.$$

Then, the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) is $\mathcal{UH}$-stable. Furthermore, if we take $\mathcal{K}\left(ϵ\right)={\mathfrak{C}}_fϵ$ with $\mathcal{K}\left(0\right)=0$, then the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) is $\mathcal{GUH}$-stable. □

4.2. The $\mathcal{UHR}$ and $\mathcal{GUHR}$ Stability Results

This lemma will be used in the proofs of $\mathcal{UHR}$ and $\mathcal{GUHR}$ stability of our results.

Lemma 8.

Let$\alpha \in (3,4]$, $\rho \in [0,1]$, and let$z\in \mathcal{E}$be the solution of (34). Then, $z\in \mathcal{E}$ is verifies

$$\left|z\left(t\right)-{\chi }_z\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)\right|\le \mathsf{\Theta }ϵ{\lambda }_{\mathcal{K}}\mathcal{K}\left(t\right),$$

where

$$\mathsf{\Theta }=1+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m|{\mu }_i|+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|,$$

(44)

and ${\chi }_z\left(t\right)$ is defined by (41).

Proof. 

Let z be a solution of (34). Thanks to Remark 3 (ii) and Lemma 4, the solution of

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }z\left(t\right)={\mathcal{F}}_z\left(t\right)+w\left(t\right)t\in (a,b),}\\ {\displaystyle z\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }z\left(a\right)=0,}\\ {\displaystyle \sum _{i=1}^m{\mu }_i{}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }z\left({\kappa }_i\right)=\mathcal{H}(\eta ,z\left(\eta \right)),\sum _{j=1}^n{\phi }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\varsigma }_j\right)=\mathcal{G}(\xi ,z\left(\xi \right)),}\end{array}\right.$$

(45)

can be written in the form:

$$\begin{array}{ccc}\hfill z\left(t\right)& =& {\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{22}\left(\mathcal{H}(\eta ,z\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_z\left({\kappa }_i\right)\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(\mathcal{G}(\xi ,z\left(\xi \right))-\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\varsigma }_j\right)\right)]+\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}[{\mathsf{\Lambda }}_{11}(\mathcal{G}(\xi ,z\left(\xi \right))\hfill \\ & & -\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\varsigma }_j\right))-{\mathsf{\Lambda }}_{21}\left(\mathcal{H}(\eta ,z\left(\eta \right))-\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }{\mathcal{F}}_z\left({\kappa }_i\right)\right)]\hfill \\ & & +{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }w\left(t\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{22}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }w\left({\kappa }_i\right)+{\mathsf{\Lambda }}_{12}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }w\left({\varsigma }_j\right)\right]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{11}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }w\left({\varsigma }_j\right)+{\mathsf{\Lambda }}_{21}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }w\left({\kappa }_i\right)\right].\hfill \end{array}$$

By using Remark 3 $\left(i\right)$ with Remark 4, we obtain the following estimation:

$$\begin{array}{ccc}& & \left|z\left(t\right)-{\chi }_z\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)\right|\hfill \\ & =& |{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }w\left(t\right)+\frac{{\mathsf{\Psi }}^{\gamma -1}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{22}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }w\left({\kappa }_i\right)+{\mathsf{\Lambda }}_{12}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }w\left({\varsigma }_j\right)\right]\hfill \\ & & +\frac{{\mathsf{\Psi }}^{\gamma -2}\left(t\right)}{\mathsf{\Lambda }}\left[-{\mathsf{\Lambda }}_{11}\sum _{j=1}^n{\phi }_j{\mathcal{I}}_{a^{+}}^{\alpha -{\varphi }_j;\psi }w\left({\varsigma }_j\right)+{\mathsf{\Lambda }}_{21}\sum _{i=1}^m{\mu }_i{\mathcal{I}}_{a^{+}}^{\alpha -{\theta }_i;\psi }w\left({\kappa }_i\right)\right]|\hfill \\ & \le & \{1+\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{22}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{21}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{i=1}^m\left|{\mu }_i\right|\hfill \\ & & +\frac{1}{\left|\mathsf{\Lambda }\right|}\left(|{\mathsf{\Lambda }}_{12}|{\mathsf{\Psi }}^{\gamma -1}\left(b\right)+\left|{\mathsf{\Lambda }}_{11}\right|{\mathsf{\Psi }}^{\gamma -2}\left(b\right)\right)\sum _{j=1}^n\left|{\phi }_j\right|\}ϵ{\lambda }_{\mathcal{K}}\mathcal{K}\left(t\right)\hfill \\ & =& \left\{1+\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\sum _{i=1}^m\left|{\mu }_i\right|+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\sum _{j=1}^n\left|{\phi }_j\right|\right\}ϵ{\lambda }_{\mathcal{K}}\mathcal{K}\left(t\right)\hfill \\ & =& \mathsf{\Theta }ϵ{\lambda }_{\mathcal{K}}\mathcal{K}\left(t\right).\hfill \end{array}$$

Lemma 8 is obtained. □

Next, we establish the $\mathcal{UHR}$ and $\mathcal{GUHR}$ stability of the solution to the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4).

Theorem 4.

Let$f:\mathcal{J}\times {\mathbb{R}}^3\to \mathbb{R}$be a continuous under$\left({\mathcal{A}}_1\right)$–$\left({\mathcal{A}}_2\right)$and let (39) be fulfilled. If

$$\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)<1,$$

then the ψ-Hilfer $\mathbb{FBVP}$ describing $\mathbb{CB}$ model (4) is $\mathcal{UHR}$ and $\mathcal{GUHR}$-stable in $\mathcal{E}$.

Proof. 

Let $z\in \mathcal{E}$ be the solution of (34) and x be a unique solution of (4). Thanks to Lemma 8, we obtain

$$x\left(t\right)={\chi }_x\left(t\right)+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t\right),$$

where ${\chi }_x\left(t\right)$ is given by (43). Similarly, if ${}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }x\left(a\right)={}^H{\mathfrak{D}}_{a^{+}}^{\delta ,\rho ;\psi }z\left(a\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }x\left({\kappa }_i\right)={}^H{\mathfrak{D}}_{a^{+}}^{{\theta }_i,\rho ;\psi }z\left({\kappa }_i\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }x\left({\varsigma }_j\right)={}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\varsigma }_j\right)$, $x\left(a\right)=z\left(a\right)$, $\mathcal{H}(\eta ,x(\eta \left)\right)=\mathcal{H}(\eta ,z(\eta \left)\right)$, and $\mathcal{G}(\xi ,x(\xi \left)\right)=\mathcal{G}(\xi ,z(\xi \left)\right)$, then ${\chi }_x\left(t\right)={\chi }_z\left(t\right)$. Applying the triangle inequality with Lemma 8, for $t\in \mathcal{J}$, we estimate

$$\begin{array}{ccc}\hfill \left|z\right(t)-x(t\left)\right|& =& |z\left(t\right)-{\chi }_x\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_x\left(t\right)|\hfill \\ & \le & |z\left(t\right)-{\chi }_z\left(t\right)-{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{F}}_z\left(t\right)|+{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }|{\mathcal{F}}_z\left(s\right)-{\mathcal{F}}_x\left(s\right)|\left(t\right)+|{\chi }_z\left(t\right)-{\chi }_x\left(t\right)|\hfill \\ & \le & \mathsf{\Theta }ϵ{\lambda }_{\mathcal{K}}\mathcal{K}\left(t\right)+\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)|z\left(t\right)-x\left(t\right)|,\hfill \end{array}$$

where $\mathsf{\Theta }$ is defined by (44). Then, $|z\left(t\right)-x\left(t\right)|\le {\mathfrak{C}}_{f,\mathcal{K}}\mathcal{K}\left(t\right)ϵ$ with

$${\mathfrak{C}}_{f,\mathcal{K}}=\frac{\mathsf{\Theta }{\lambda }_{\mathcal{K}}}{1-\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1{\mathsf{\Psi }}^{\alpha }\left(b\right)+{\mathbb{L}}_3{\mathsf{\Psi }}^{\beta +\alpha }\left(b\right)\right)}.$$

Hence, this proves that the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) is $\mathcal{UHR}$-stable. Moreover, if we set $ϵ=1$ with $\mathcal{K}\left(0\right)=0$, then the $\psi$-Hilfer $\mathbb{FBVP}$ describing $\mathbb{CB}$ model (4) is $\mathcal{GUHR}$-stable. □

5. Examples

This section contains several illustrated cases to highlight the relevance of our findings in this study.

Example 1.

Consider the following ψ-Hilfer fractional differential equation describing the $\mathbb{CB}$ model with nonlinear boundary conditions

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{0^{+}}^{\frac{7}{2},\frac{7}{10};sin\left(\frac{\pi t}{2t+2}\right)}x\left(t\right)=f(t,x\left(t\right),{}^H{\mathfrak{D}}_{0^{+}}^{\frac{7}{2},\frac{7}{10};sin\left(\frac{\pi t}{2t+2}\right)}x\left(t\right),{\mathcal{I}}_{0^{+}}^{\frac{5}{2};sin\left(\frac{\pi t}{2t+2}\right)}x\left(t\right)),}\\ {\displaystyle x\left(0\right)=0,{}^H{\mathfrak{D}}_{0^{+}}^{\frac{17}{10},\frac{7}{10};sin\left(\frac{\pi t}{2t+2}\right)}x\left(0\right)=0,}\\ {\displaystyle \sum _{i=1}^2\left(\frac{i}{i+1}\right){}^H{\mathfrak{D}}_{a^{+}}^{\frac{2i+1}{10},\frac{7}{10};sin\left(\frac{\pi t}{2t+2}\right)}x\left(\frac{4i-2}{2i+5}\right)=\mathcal{H}\left(\frac{4}{5},x\left(\frac{4}{5}\right)\right),}\\ {\displaystyle \sum _{j=1}^3\left(\frac{7-2j}{9-j}\right){}^H{\mathfrak{D}}_{a^{+}}^{\frac{30-2j}{10},\frac{7}{10};sin\left(\frac{\pi t}{2t+2}\right)}x\left(\frac{3i-1}{10}\right)=\mathcal{G}\left(\frac{11}{10},x\left(\frac{11}{10}\right)\right).}\end{array}\right.$$

(46)

Here,$\alpha =7/2$, $\rho =7/10$, $\psi \left(t\right)=sin(\pi t/(2t+2\left)\right)$, $\beta =5/2$, $a=0$, $b=6/5$, $\delta =17/10$, ${\mu }_i=i/(i+1)$, ${\theta }_i=(2i+1)/10$, ${\kappa }_i=(4i-2)/(2i+5)$, $\eta =4/5$, ${\phi }_j=(7-2j)/(9-j)$, ${\varphi }_j=(30-2j)/10$, ${\varsigma }_j=(3j-1)/10$, $\xi =11/10$, $i=1,2$, and $j=1,2,3$. From the given information, we can approximate that${\mathsf{\Lambda }}_{11}\approx 0.0768702$, ${\mathsf{\Lambda }}_{12}\approx 0.3392374$, ${\mathsf{\Lambda }}_{21}\approx 1.1518998$, ${\mathsf{\Lambda }}_{22}\approx 0.4227044$, and$\mathsf{\Lambda }\approx -0.3582742\ne 0$.

(i) 

Consider the nonlinear function

$$\begin{array}{ccc}& & f(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right))\hfill \\ & & =\frac{sin(t^4+2)}{3t^2+5t+1}+\frac{e^{-t+5}}{6-{cos}^2\pi t}·\frac{\left|x\right(t\left)\right|}{4+\left|x\right(t\left)\right|}\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{{(5t-4)}^2}{4}\left[\frac{|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)|}{21+|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)|}+\frac{|{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)|}{22+|{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)|}\right],\hfill \end{array}$$

(47)

and the nonlinear conditions

$$\mathcal{H}\left(\frac{4}{5},x\left(\frac{4}{5}\right)\right)=\frac{\left|x\left(\frac{4}{5}\right)\right|}{20+3\left|x\left(\frac{4}{5}\right)\right|},\mathcal{G}\left(\frac{11}{10},x\left(\frac{11}{10}\right)\right)=\frac{\left|x\left(\frac{11}{10}\right)+2\right|}{30}.$$

(48)

For $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2$, and $t\in [0,6/5]$, we can find that

$$\left|f(t,u_1,v_1,w_1)-f(t,u_2,v_2,w_2)\right|\le \frac{1}{20}|u_1-u_2|+\frac{1}{21}|v_1-v_2|+\frac{1}{22}|w_1-w_2|,$$

and

$$\left|\mathcal{H}(t,u_1)-\mathcal{H}(t,u_2)\right|\le \frac{1}{20}|u_1-u_2|,\left|\mathcal{G}(t,u_1)-\mathcal{G}(t,u_2)\right|\le \frac{1}{30}|u_1-u_2|.$$

The assumption$\left({\mathcal{A}}_1\right)$–$\left({\mathcal{A}}_2\right)$is satisfied with${\mathcal{L}}_1=1/20$, ${\mathcal{L}}_2=1/21$, ${\mathcal{L}}_3=1/22$, ${\mathbb{H}}_1=1/20$ and ${\mathbb{G}}_1=1/30$. For the given information, we have $\mathsf{\Omega }\left(\alpha \right)\approx 0.1575972$, $\mathsf{\Omega }(\beta +\alpha )\approx 0.0016180$, $\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\approx 0.1585503$, $\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21})\approx 0.1585503$, and $\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11})\approx 1.2012770$. Hence,

$$\begin{array}{ccc}& & (\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1\mathsf{\Omega }\left(\alpha \right)+{\mathbb{L}}_3\mathsf{\Omega }(\beta +\alpha )\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1)\approx 0.0736999<1.\hfill \end{array}$$

Since all the assumptions of Theorem 1 are fulfilled, the ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (46) has a unique solution on $\left[0,6/5\right]$ with (47) and (48). Furthermore, we can also compute the positive constant ${\mathfrak{C}}_f\approx 0.1578672>0$. By the conclusions of Theorem 3, the ψ-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (46) is both $\mathcal{UH}$- and also $\mathcal{GUH}$-stable on $[0,6/5]$ with (47) and (48). By setting $\mathcal{K}\left(t\right)={(\psi \left(t\right)-\psi \left(a\right))}^{1/2}$ and Proposition 1 (i), we have

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\mathcal{K}\left(t\right)=\frac{\mathsf{\Gamma }(3/2)}{\mathsf{\Gamma }\left(3/2+\alpha \right)}{(\psi \left(t\right)-\psi \left(a\right))}^{\frac{1}{2}+\alpha }\le \frac{\sqrt{\pi }{\left(\psi (6/5)-\psi \left(0\right)\right)}^{\alpha }}{2\mathsf{\Gamma }\left(3/2+\alpha \right)}\mathcal{K}\left(t\right).$$

Then, the inequality (39) is satisfied with ${\lambda }_{\mathcal{K}}=\frac{\sqrt{\pi }{\left(sin\left(\frac{3\pi }{11}\right)-sin\left(0\right)\right)}^{7/2}}{48}\approx 0.0138566>0$ and $\mathsf{\Theta }\approx 2.5949589$. We obtain ${\mathfrak{C}}_{f,\mathcal{K}}\approx 0.0360189>0$. Therefore, by all assumptions of Theorem 4, the ψ-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (46) is both $\mathcal{UHR}$- and $\mathcal{GUHR}$-stable on $[0,6/5]$ with (47) and (48).

(ii) 

Consider the nonlinear function

$$\begin{array}{ccc}& & f(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right))\hfill \\ & & =\frac{|t^2-3t|}{2t+1}+\frac{ln|-t+5|}{e^{cosh\pi t}}sin\left(x\left(t\right)\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{2+{cos}^2\pi t}{4t+3}\left[|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right)+{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right)|\right].\hfill \end{array}$$

(49)

For u, v, $w\in \mathbb{R}$, and $t\in [0,6/5]$, we can estimate

$$\left|f(t,u,v,w)\right|\le \frac{|t^2-3t|}{2t+1}+\frac{ln|5-t|}{e^{cosh\pi t}}\left|u\right|+\frac{2+{cos}^2\pi t}{4t+3}\left|v\right|+\frac{2+{cos}^2\pi t}{4t+3}\left|w\right|$$

and

$$\left|\mathcal{H}(t,u)\right|\le \frac{\left|u\right|}{20},\left|\mathcal{G}(t,u)\right|\le \frac{2}{30}+\frac{\left|u\right|}{30}.$$

The assumptions$\left({\mathcal{A}}_3\right)$–$\left({\mathcal{A}}_4\right)$is true with$p_1\left(t\right)=|t^2-3t|/(2t+1)$, $p_2\left(t\right)=(ln|5-t|)$$/e^{cosh\pi t}$, $p_3\left(t\right)=p_4\left(t\right)=(2+{cos}^2\pi t)/(4t+3)$, $h_1\left(t\right)=0$, $h_2\left(t\right)=1/20$, $g_1\left(t\right)=2/30$and$g_2\left(t\right)=1/30$. Therefore, all the assumptions of Theorem 2 are satisfied, which leads to the conclusion that the ψ-Hilfer$\mathbb{FBVP}$describing$\mathbb{CB}$model (46) has at least one solution on $[0,6/5]$ with (48) and (49). For $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2$, and $t\in [0,6/5]$, we can find that

$$\left|f(t,u_1,v_1,w_1)-f(t,u_2,v_2,w_2)\right|\le \frac{ln\left(5\right)}{8e}|u_1-u_2|+\frac{1}{2}|v_1-v_2|+\frac{1}{2}|w_1-w_2|.$$

The assumption$\left({\mathcal{A}}_1\right)$–$\left({\mathcal{A}}_2\right)$is satisfied with${\mathcal{L}}_1=ln\left(5\right)/8e$, ${\mathcal{L}}_2={\mathcal{L}}_3=1/2$, ${\mathbb{H}}_1=1/20$and${\mathbb{G}}_1=1/30$. Hence,

$$\begin{array}{ccc}& & (\frac{1}{1-{\mathbb{L}}_2}\left({\mathbb{L}}_1\mathsf{\Omega }\left(\alpha \right)+{\mathbb{L}}_3\mathsf{\Omega }(\beta +\alpha )\right)\hfill \\ & & +\mathsf{\Phi }({\mathsf{\Lambda }}_{22},{\mathsf{\Lambda }}_{21}){\mathbb{H}}_1+\mathsf{\Phi }({\mathsf{\Lambda }}_{12},{\mathsf{\Lambda }}_{11}){\mathbb{G}}_1)\approx 0.0902944<1.\hfill \end{array}$$

Since all the assumptions of Theorem 1 are fulfilled, the ψ-Hilfer$\mathbb{FBVP}$describing$\mathbb{CB}$model (46) has a unique solution on $[0,6/5]$ with (48) and (49). Further, we can also compute that ${\mathfrak{C}}_f\approx 0.1580267>0$. By the conclusions of Theorem 3, the ψ-Hilfer $\mathbb{FCB}$ model (46) is both $\mathcal{UH}$- and also $\mathcal{GUH}$-stable on $[0,6/5]$ with (48) and (49). By setting $\mathcal{K}\left(t\right)={\left(\psi \left(t\right)-\psi \left(0\right)\right)}^{3/2}$ and Proposition 1 (i), one has

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\mathcal{K}\left(t\right)=\frac{3\sqrt{\pi }}{4\mathsf{\Gamma }\left(\frac{5}{2}+\alpha \right)}{(\psi \left(t\right)-\psi \left(a\right))}^{\frac{3}{2}+\alpha }\le \frac{3\sqrt{\pi }{\left(\psi (6/5)-\psi \left(0\right)\right)}^{\alpha }}{4\mathsf{\Gamma }\left(\frac{5}{2}+\alpha \right)}\mathcal{K}\left(t\right).$$

Then, the inequality (39) is satisfied with ${\lambda }_{\mathcal{K}}=\frac{\sqrt{\pi }{\left(sin\left(\frac{3\pi }{11}\right)-sin\left(0\right)\right)}^{7/2}}{160}\approx 0.0041570>0$ and $\mathsf{\Theta }\approx 2.5949589$. One has ${\mathfrak{C}}_{f,\mathcal{K}}\approx 0.0108166>0$. Therefore, by all assumptions of Theorem 4, the ψ-Hilfer $\mathbb{FBVP}$ describing $\mathbb{CB}$ model (46), is both $\mathcal{UHR}$- and also $\mathcal{GUHR}$-stable on $[0,6/5]$ with (48) and (49).

(iii) 

Consider the function${\mathcal{F}}_x\left(t\right)=f(t,x\left(t\right),{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }x\left(t\right),{\mathcal{I}}_{a^{+}}^{\beta ;\psi }x\left(t\right))=1$, and the nonlinear conditions$\mathcal{H}(\eta ,x(\eta \left)\right)=\mathcal{G}(\xi ,x(\xi \left)\right)=1$. By Lemma 4, the implicit solution of the ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (46) is given by

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \frac{{\left(\psi \left(t\right)-\psi \left(0\right)\right)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}+\frac{{\left(\psi \left(t\right)-\psi \left(0\right)\right)}^{\gamma -1}}{\mathsf{\Lambda }\mathsf{\Gamma }\left(\gamma \right)}[{\mathsf{\Lambda }}_{22}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\left(\psi \left({\kappa }_i\right)-\psi \left(0\right)\right)}^{\alpha -{\theta }_i}}{\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\left(\psi \left({\varsigma }_j\right)-\psi \left(0\right)\right)}^{\alpha -{\varphi }_j}}{\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)]\hfill \\ & & +\frac{{\left(\psi \left(t\right)-\psi \left(a\right)\right)}^{\gamma -2}}{\mathsf{\Lambda }\mathsf{\Gamma }(\gamma -1)}[{\mathsf{\Lambda }}_{11}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\left(\psi \left({\varsigma }_j\right)-\psi \left(0\right)\right)}^{\alpha -{\varphi }_j}}{\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\left(\psi \left({\kappa }_i\right)-\psi \left(0\right)\right)}^{\alpha -{\theta }_i}}{\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)].\hfill \end{array}$$

(1)

If${\psi }_1\left(t\right)=\frac{1}{\alpha }{t}^{3/2}$, then the solution of the ψ-Hilfer$\mathbb{FBVP}$describing$\mathbb{CB}$model (46) is defined by

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \frac{t^{3\alpha /2}}{{\alpha }^{\alpha }\mathsf{\Gamma }(\alpha +1)}+\frac{t^{3(\gamma -1)/2}}{{\alpha }^{\gamma -1}\mathsf{\Lambda }\mathsf{\Gamma }\left(\gamma \right)}[{\mathsf{\Lambda }}_{22}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\kappa }_i^{3(\alpha -{\theta }_i)/2}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\varsigma }_j^{3(\alpha -{\varphi }_j)/2}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)]\hfill \\ & & +\frac{t^{3(\gamma -2)/2}}{{\alpha }^{\gamma -2}\mathsf{\Lambda }\mathsf{\Gamma }(\gamma -1)}[{\mathsf{\Lambda }}_{11}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\varsigma }_j^{3(\alpha -{\varphi }_j)/2}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\kappa }_i^{3(\alpha -{\theta }_i)/2}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)],t\in (0,6/5].\hfill \end{array}$$

(2)

If${\psi }_2\left(t\right)=\frac{\sqrt{log(t+1)}}{\alpha }$, then the solution of the ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (46) is defined by

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \frac{{\left(\sqrt{log(t+1)}\right)}^{\alpha }}{{\alpha }^{\alpha }\mathsf{\Gamma }(\alpha +1)}\hfill \\ & & +\frac{{\left(\sqrt{log(t+1)}\right)}^{\gamma -1}}{{\alpha }^{\gamma -1}\mathsf{\Lambda }\mathsf{\Gamma }\left(\gamma \right)}[{\mathsf{\Lambda }}_{22}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\left(\sqrt{log({\kappa }_i+1)}\right)}^{\alpha -{\theta }_i}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\left(\sqrt{log({\varsigma }_j+1)}\right)}^{\alpha -{\varphi }_j}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)]\hfill \\ & & +\frac{{\left(\sqrt{log(t+1)}\right)}^{\gamma -2}}{{\alpha }^{\gamma -2}\mathsf{\Lambda }\mathsf{\Gamma }(\gamma -1)}[{\mathsf{\Lambda }}_{11}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\left(\sqrt{log({\varsigma }_j+1)}\right)}^{\alpha -{\varphi }_j}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\left(\sqrt{log({\kappa }_i+1)}\right)}^{\alpha -{\theta }_i}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)],t\in (0,6/5].\hfill \end{array}$$

(3)

If${\psi }_3\left(t\right)=\frac{1}{\alpha }{e}^{2t}$then the solution of the ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (46) is defined by

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \frac{{(e^{2t}-1)}^{\alpha }}{{\alpha }^{\alpha }\mathsf{\Gamma }(\alpha +1)}+\frac{{(e^{2t}-1)}^{\gamma -1}}{{\alpha }^{\gamma -1}\mathsf{\Lambda }\mathsf{\Gamma }\left(\gamma \right)}[{\mathsf{\Lambda }}_{22}\left(1-\sum _{i=1}^m\frac{{\mu }_i{(e^{2{\kappa }_i}-1)}^{\alpha -{\theta }_i}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(1-\sum _{j=1}^n\frac{{\phi }_j(e^{2{\varsigma }_j}-1){)}^{\alpha -{\varphi }_j}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)]\hfill \\ & & +\frac{{(e^{2t}-1)}^{\gamma -2}}{{\alpha }^{\gamma -2}\mathsf{\Lambda }\mathsf{\Gamma }(\gamma -1)}[{\mathsf{\Lambda }}_{11}\left(1-\sum _{j=1}^n\frac{{\phi }_j(e^{2{\varsigma }_j}-1){)}^{\alpha -{\varphi }_j}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(1-\sum _{i=1}^m\frac{{\mu }_i(e^{2{\kappa }_i}-1){)}^{\alpha -{\theta }_i}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)],t\in (0,6/5].\hfill \end{array}$$

(4)

If${\psi }_4\left(t\right)=\frac{{sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)}{\alpha }$, then the solution of the ψ-Hilfer$\mathbb{FBVP}$describing the$\mathbb{CB}$model (46) is defined by

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \frac{{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)\right)}^{\alpha }}{{\alpha }^{\alpha }\mathsf{\Gamma }(\alpha +1)}+\frac{{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)\right)}^{\gamma -1}}{{\alpha }^{\gamma -1}\mathsf{\Lambda }\mathsf{\Gamma }\left(\gamma \right)}[{\mathsf{\Lambda }}_{22}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi {\kappa }_i}{4}\right)\right)}^{\alpha -{\theta }_i}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{12}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi {\varsigma }_j}{4}\right)\right)}^{\alpha -{\varphi }_j}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)]\hfill \\ & & +\frac{{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)\right)}^{\gamma -2}}{{\alpha }^{\gamma -2}\mathsf{\Lambda }\mathsf{\Gamma }(\gamma -1)}[{\mathsf{\Lambda }}_{11}\left(1-\sum _{j=1}^n\frac{{\phi }_j{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi {\varsigma }_j}{4}\right)\right)}^{\alpha -{\varphi }_j}}{{\alpha }^{\alpha -{\varphi }_j}\mathsf{\Gamma }(\alpha -{\varphi }_j+1)}\right)\hfill \\ & & -{\mathsf{\Lambda }}_{21}\left(1-\sum _{i=1}^m\frac{{\mu }_i{\left({sin}^{\sqrt{\alpha }}\left(\frac{\pi {\kappa }_i}{4}\right)\right)}^{\alpha -{\theta }_i}}{{\alpha }^{\alpha -{\theta }_i}\mathsf{\Gamma }(\alpha -{\theta }_i+1)}\right)],t\in (0,6/5].\hfill \end{array}$$

A graph representing the solution of the ψ-Hilfer$\mathbb{FBVP}$describing$\mathbb{CB}$model (46) with various values of $\alpha =\frac{31}{10}$, $\frac{33}{10}$, $\frac{35}{10}$, $\frac{37}{10}$, $\frac{39}{10}$, and $\frac{40}{10}$ involving a variety of functions ${\psi }_1\left(t\right)=\frac{1}{\alpha }{t}^{3/2}$, ${\psi }_2\left(t\right)=\frac{1}{\alpha }\sqrt{log(t+1)}$, ${\psi }_3\left(t\right)=\frac{1}{\alpha }{e}^{2t}$, and ${\psi }_4\left(t\right)=\frac{1}{\alpha }{sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)$, is shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

Figure 1. The graph of the solution $x\left(t\right)$ with ${\psi }_1\left(t\right)=\frac{1}{\alpha }{t}^{3/2}$ and $c=1.5$.

Figure 2. The graph of the function ${\psi }_1\left(t\right)=\frac{1}{\alpha }{t}^{3/2}$ with $c=1.5$.

Figure 3. The graph of the solution $x\left(t\right)$ with ${\psi }_2\left(t\right)=\frac{1}{\alpha }\sqrt{log(t+1)}$ and $c=0.5$.

Figure 4. The graph of the function ${\psi }_2\left(t\right)=\frac{1}{\alpha }\sqrt{log(t+1)}$ with $c=0.5$.

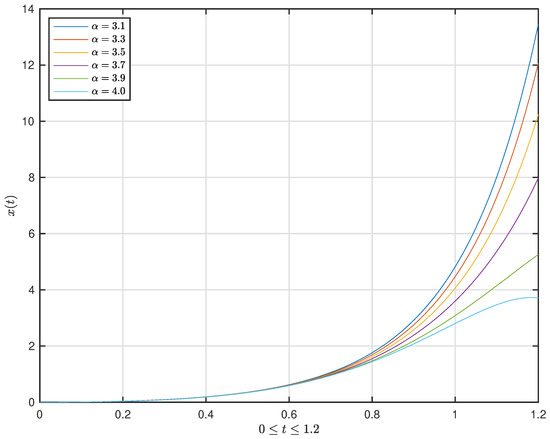Figure 5. The graph of the solution $x\left(t\right)$ with ${\psi }_3\left(t\right)=\frac{1}{\alpha }{e}^{2t}$ and $c=2$.

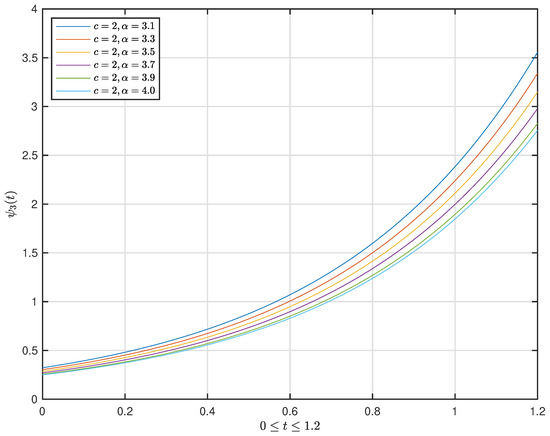Figure 6. The graph of the function ${\psi }_3\left(t\right)=\frac{1}{\alpha }{e}^{2t}$ with $c=2$.

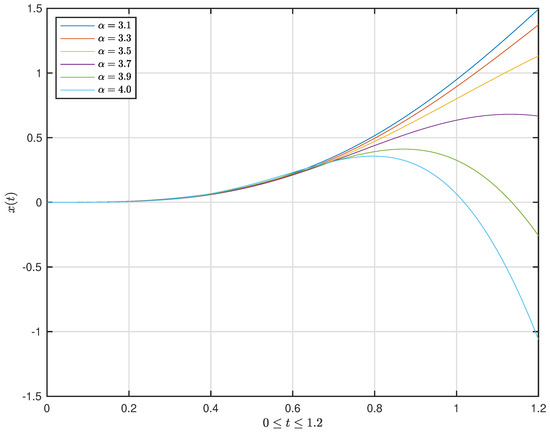Figure 7. The graph of the solution $x\left(t\right)$ with ${\psi }_4\left(t\right)=\frac{1}{\alpha }{sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)$ and $c=\frac{\pi }{4}$.

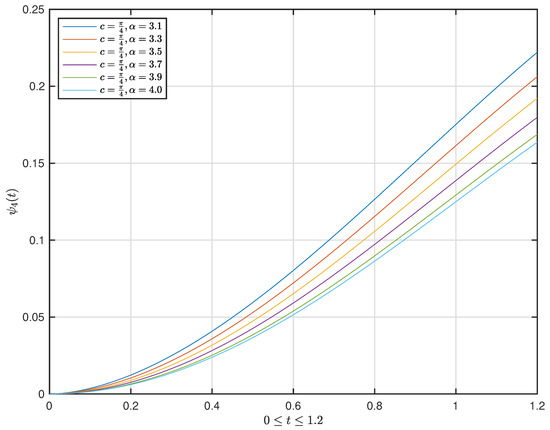Figure 8. The graph of the function ${\psi }_4\left(t\right)=\frac{1}{\alpha }{sin}^{\sqrt{\alpha }}\left(\frac{\pi t}{4}\right)$ with $c=\frac{\pi }{4}$.

6. Conclusions

We analyzed the existence and uniqueness of solutions for a class of a nonlinear implicit $\psi$-Hilfer fractional integro-differential equation subjected to nonlinear boundary conditions describing the $\mathbb{CB}$ model. The uniqueness result is established using Banach’s fixed point theorem, while the existence result is established using Schaefer’s fixed point theorem, both of which are well-known fixed point theorems. Ulam’s stability is also demonstrated in several ways, including $\mathcal{UH}$ stability, $\mathcal{GUH}$ stability, $\mathcal{UHR}$ stability, and $\mathcal{GUHR}$ stability. Finally, the numerical examples have been carefully selected to demonstrate how the results can be used. Moreover, the $\psi$-Hilfer $\mathbb{FBVP}$ describing the $\mathbb{CB}$ model (4) not only includes the identified previously works about a variety of boundary value problems. As special cases for various values $\rho$ and $\psi$, the considered problem does cover a large range of many problems as: the Riemann–Liouville-type problem for $\rho =0$ and $\psi \left(t\right)=t$, the Caputo-type problem for $\rho =1$ and $\psi \left(t\right)=t$, the $\psi$-Riemann–Liouville-type problem for $\rho =0$, the $\psi$-Caputo-type problem for $\rho =1$, the Hilfer-type problem for $\psi \left(t\right)=t$, the Hilfer–Hadamard-type problem for $\psi \left(t\right)=log\left(t\right)$, and the Katugampola-type problem for $\psi \left(t\right)=t^q$.

As a result, the fixed point technique is a powerful tool to investigate different nonlinear problems, which is very important in various qualitative theories. The present work is innovative and attractive and significantly contributes to the body of knowledge on $\psi$-Hilfer fractional differential equations and inclusions for researchers. In addition, our results are novel and intriguing for the elastic beam problem emerging from mathematical models of engineering and applied science.