An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models
Abstract
:1. Introduction
- The effective results of the HO-NSDM have been obtained based on the designed computing GNNs-GA-ASA.
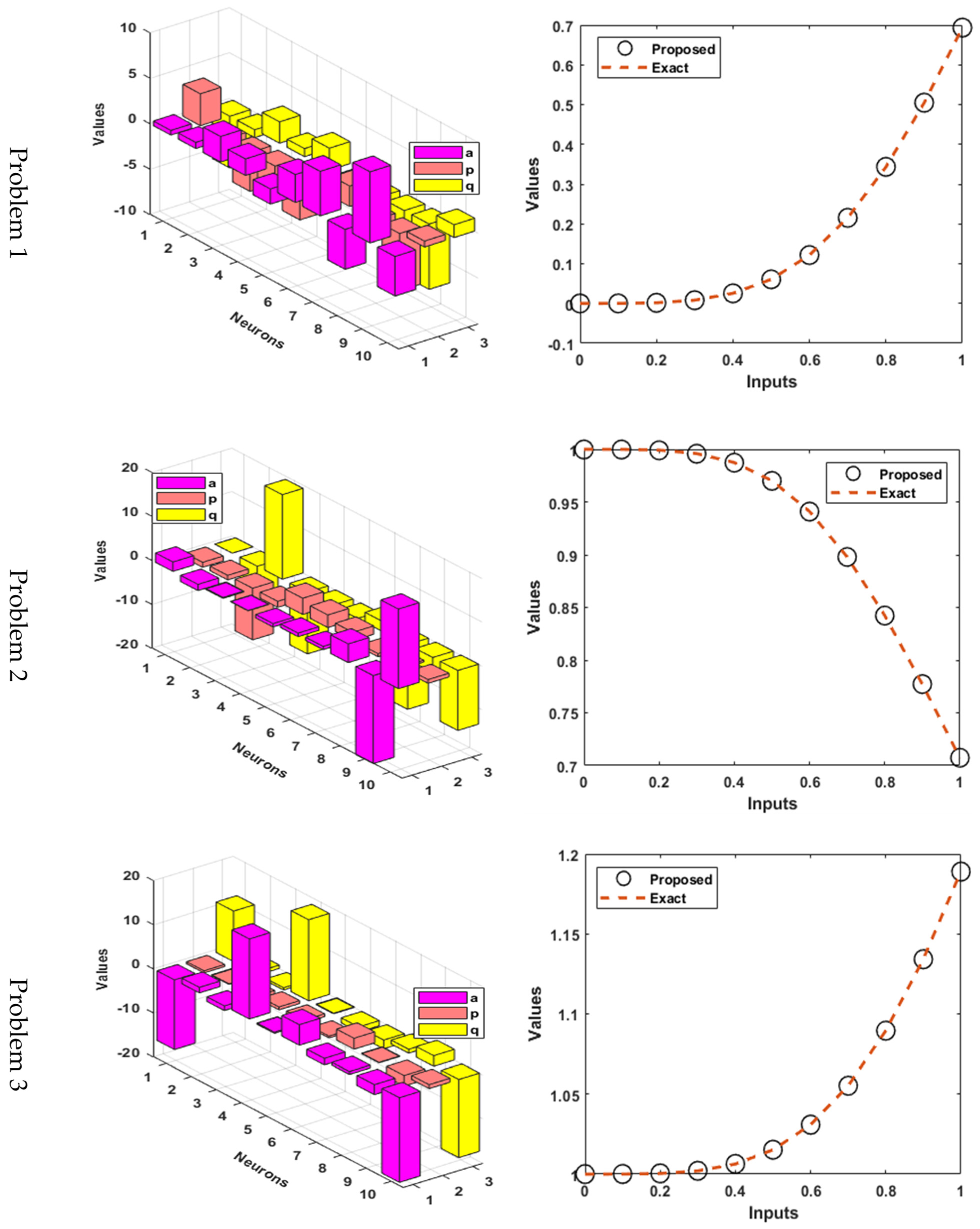
- It is clear to see that the overlapping of the attained results through GNNs-GA-ASA is noticed with exact or reference solutions, which demonstrate the viability and reliability of the computational GNNs-GA-ASA.
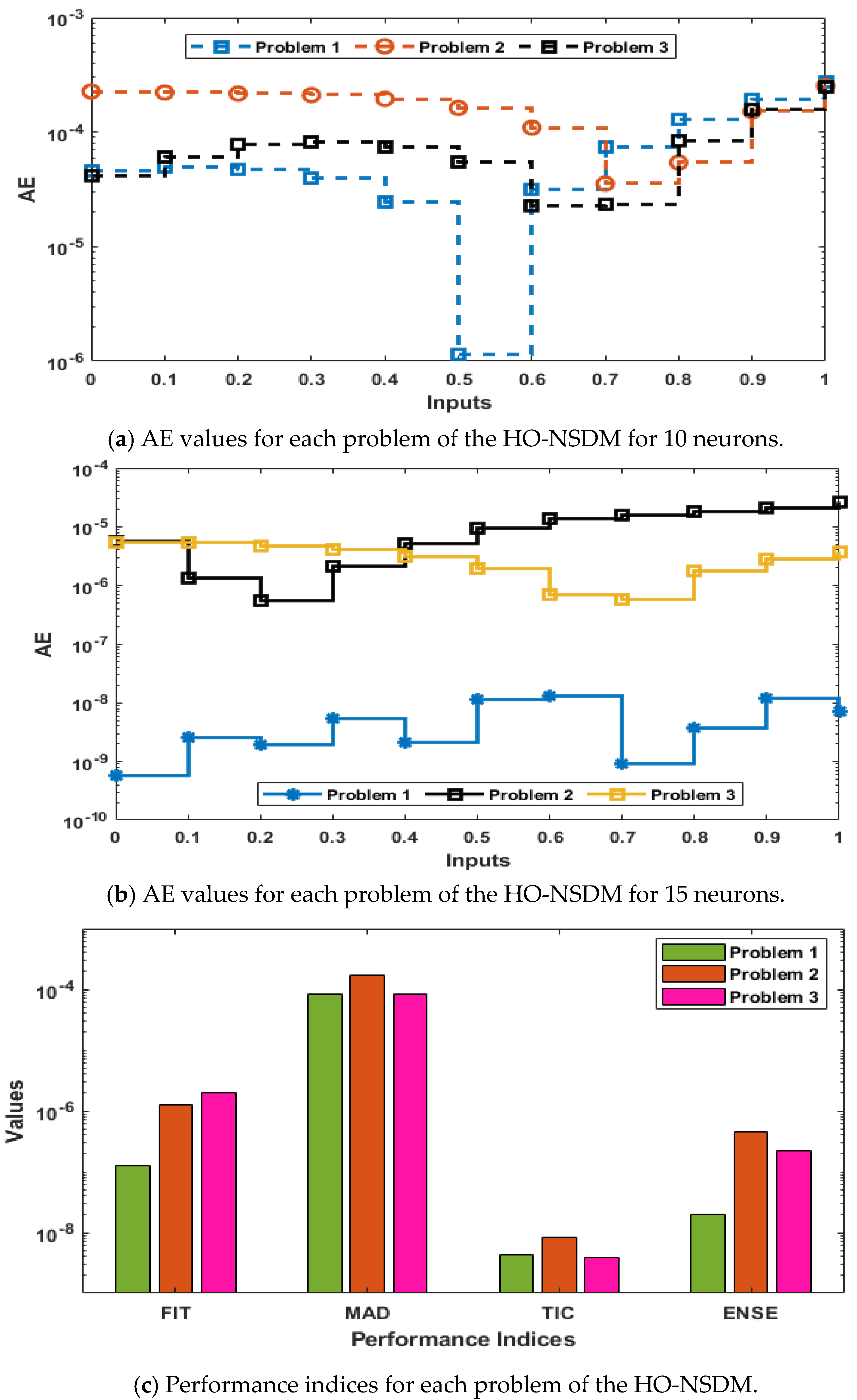
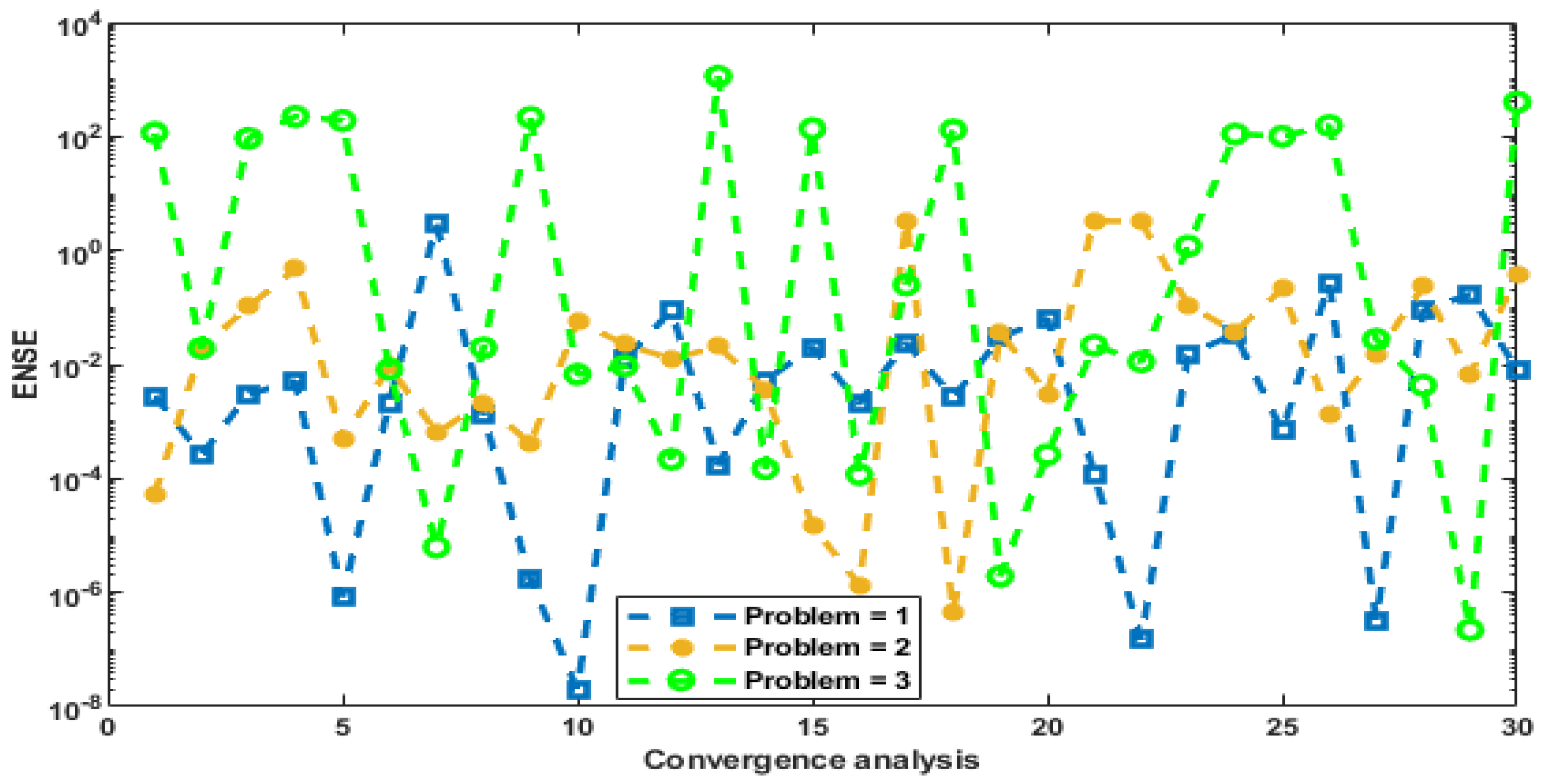
- The practically accurate performances of the GNNs-GA-ASA are authenticated through the statistical valuations in different tables and figures of merit.
2. Methodology
- The descriptions of an objective fitness function that is constructed on the basis of a differential model and its initial conditions; and
- The hybridization of GA-ASA is described to enhance the formulation of the fitness for HO-NSDM given in Equation (3).
2.1. ANNs Modeling by Using Gudermannian Function
2.2. Optimization Procedures: GA-SQP
3. Performance Measures
4. Results and Discussions
5. Conclusions
- A neuro-evolution was designed based on computing the GNNs-GA-ASA approach efficiently for the nonlinear higher order multi-singular differential systems.
- The designed GNNs-GA-ASA is a suitable procedure to solve the stiff singular problems effectively.
- The precision and accuracy of the GNN-GA-ASA was authenticated by comparing the obtained measures with the obtainable exact results to solve each variant of the HO-NSDM.
- The performance achieved through the AE values for solving the HO-NSDM authenticated good measures at around 10−4 to 10−6 for Problem 1, 10−3 to 10−5 for Problem 2 and 10−4 to 10−5 for Problem 3.
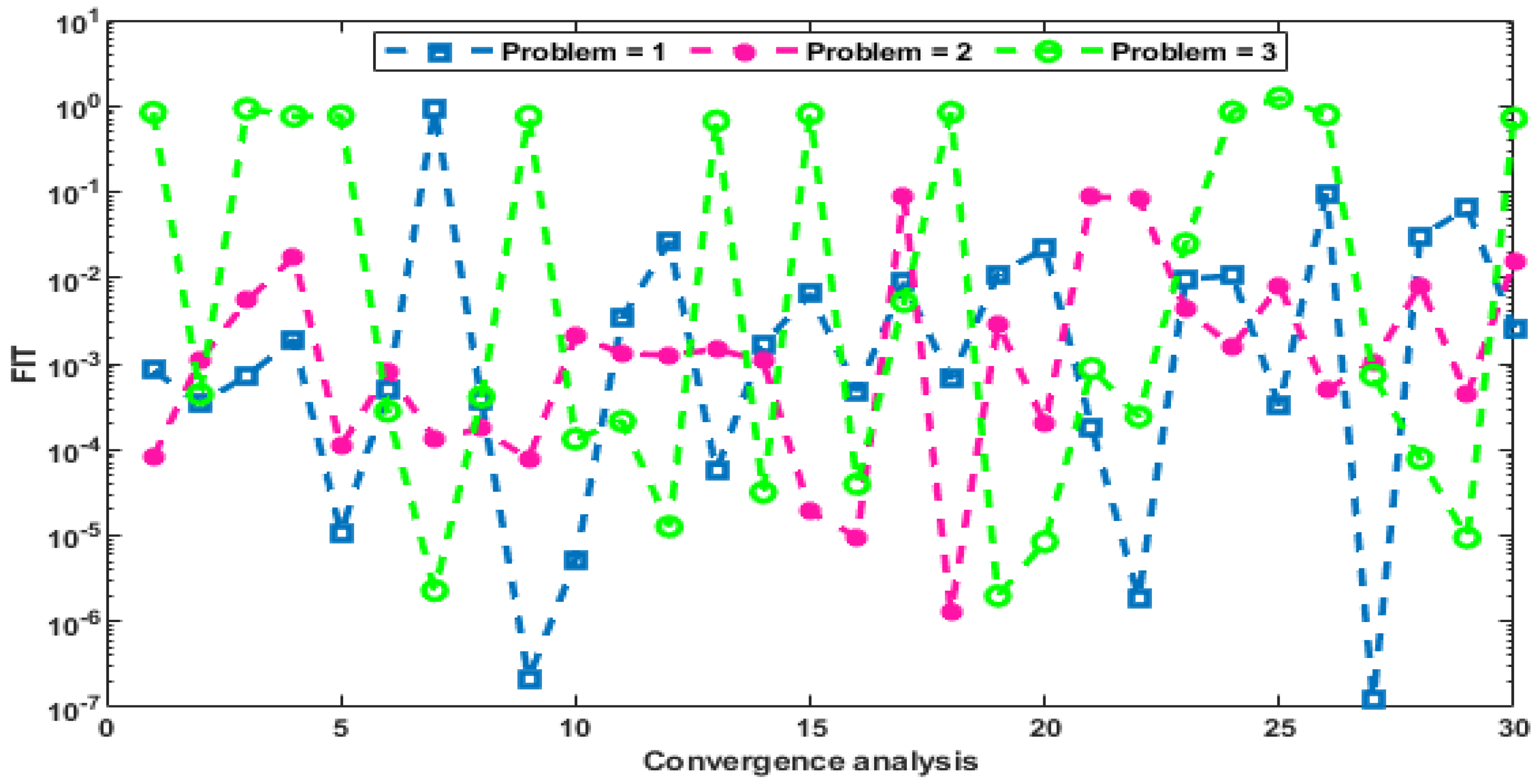
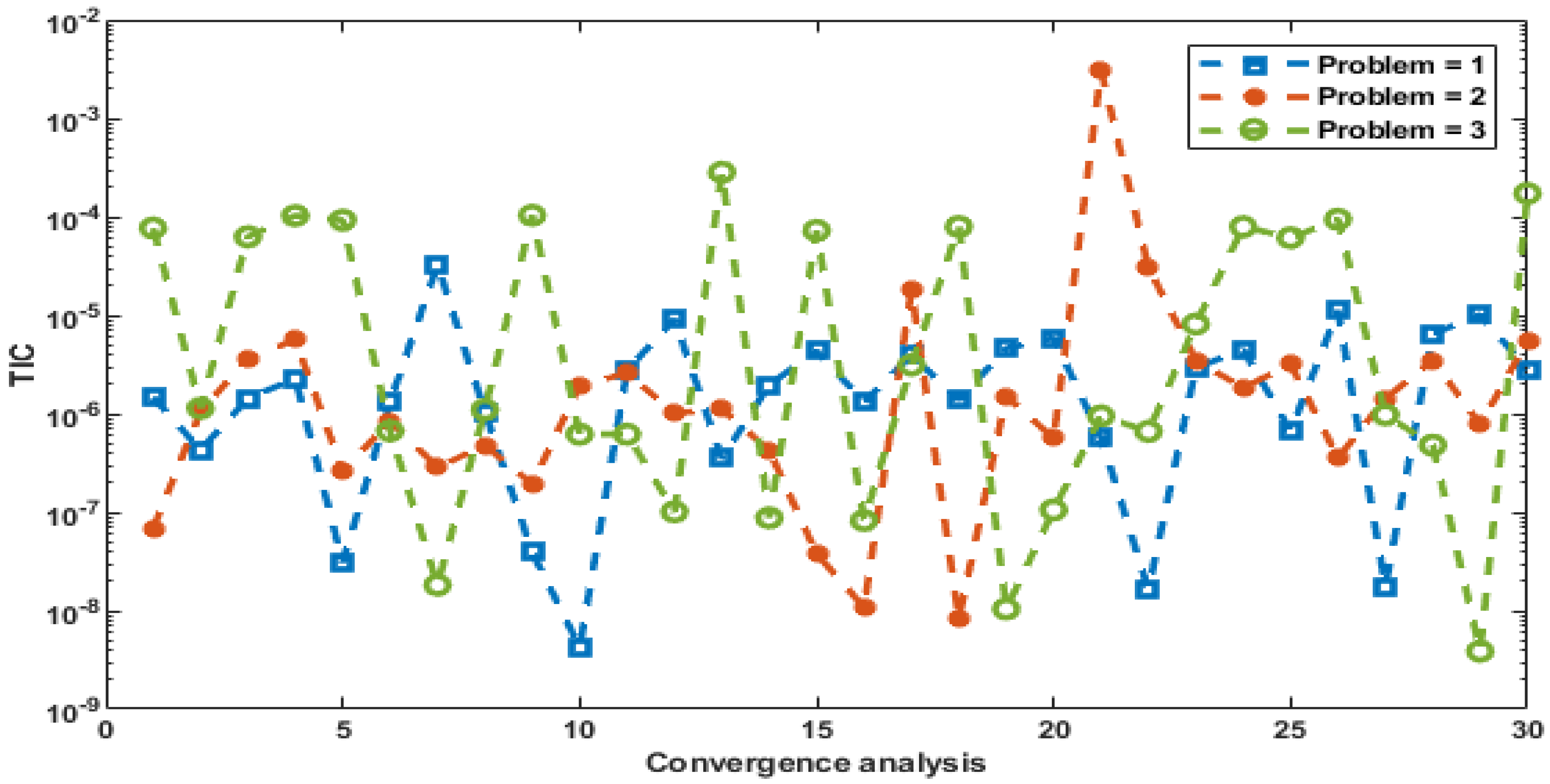
- The statistical assessments and analysis of 30 independent trials based on the GNNs-GA-ASA were implemented to establish the convergence and accuracy of the designed approach to solve three different variants of the HO-NSDM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, R. A modified homotopy perturbation method for nonlinear singular Lane–Emden equations arising in various physical models. Int. J. Appl. Comput. Math. 2019, 5, 64. [Google Scholar] [CrossRef]
- Abdullah Alderremy, A.; Elzaki, T.M.; Chamekh, M. Modified Adomian decomposition method to solve generalized Emden–Fowler systems for singular IVP. Math. Probl. Eng. 2019, 2019, 6097095. [Google Scholar] [CrossRef]
- Adel, W.; Sabir, Z. Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method. Eur. Phys. J. Plus 2020, 135, 427. [Google Scholar] [CrossRef]
- Sabir, Z.; Sakar, M.G.; Yeskindirova, M.; Saldir, O. Numerical investigations to design a novel model based on the fifth order system of Emden–Fowler equations. Theor. Appl. Mech. Lett. 2020, 10, 333–342. [Google Scholar] [CrossRef]
- Bender, C.M.; Milton, K.A.; Pinsky, S.S.; Simmons, L.M., Jr. A new perturbative approach to nonlinear problems. J. Math. Phys. 1989, 30, 1447–1455. [Google Scholar] [CrossRef]
- Shawagfeh, N.T. Non-perturbative approximate solution for Lane–Emden equation. J. Math. Phys. 1993, 34, 4364–4369. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A new algorithm for solving differential equations of Lane–Emden type. Appl. Math. Comput. 2001, 118, 287–310. [Google Scholar] [CrossRef]
- Liao, S. A new analytic algorithm of Lane–Emden type equations. Appl. Math. Comput. 2003, 142, 1–16. [Google Scholar] [CrossRef]
- Parand, K.; Razzaghi, M. Rational Legendre approximation for solving some physical problems on semi-infinite intervals. Phys. Scr. 2004, 69, 353. [Google Scholar] [CrossRef]
- Nouh, M.I. Accelerated power series solution of polytropic and isothermal gas spheres. New Astron. 2004, 9, 467–473. [Google Scholar] [CrossRef]
- Guirao, J.L.; Sabir, Z.; Saeed, T. Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model. Math. Probl. Eng. 2020, 2020, 7359242. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Wahab, H.A.; Altamirano, G.C.; Zhang, Y.D.; Le, D.N. Integrated intelligence of neuro-evolution with sequential quadratic programming for second-order Lane–Emden pantograph models. Math. Comput. Simul. 2021, 188, 87–101. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Saeed, T. Solution of novel multi-fractional multi-singular Lane–Emden model using the designed FMNEICS. Neural Comput. Appl. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Lane, J.H. ART. IX.--On the Theoretical Temperature of the Sun; under the Hypothesis of a Gaseous Mass maintaining its Volume by its Internal Heat, and depending on the Laws of Gases as known to Terrestrial Experiment. Am. J. Sci. Arts 1870, 50, 57. [Google Scholar] [CrossRef]
- Wong, J.S. On the generalized Emden–Fowler equation. Siam Rev. 1975, 17, 339–360. [Google Scholar] [CrossRef]
- Yu, J.; Guo, Z. Boundary value problems of discrete generalized Emden-Fowler equation. Sci. China Ser. A Math. 2006, 49, 1303–1314. [Google Scholar] [CrossRef]
- Ghergu, M.; Rădulescu, V.D. Bifurcation and asymptotics for the Lane–Emden–Fowler equation. Comptes Rendus Math. 2003, 337, 259–264. [Google Scholar] [CrossRef]
- Rach, R.; Duan, J.S.; Wazwaz, A.M. Solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions by the Adomian decomposition method. J. Math. Chem. 2014, 52, 255–267. [Google Scholar] [CrossRef]
- Boubaker, K.; Van Gorder, R.A. Application of the BPES to Lane–Emden equations governing polytropic and isothermal gas spheres. New Astron. 2012, 17, 565–569. [Google Scholar] [CrossRef]
- Luo, T.; Xin, Z.; Zeng, H. Nonlinear asymptotic stability of the Lane-Emden solutions for the viscous gaseous star problem with degenerate density dependent viscosities. Commun. Math. Phys. 2016, 347, 657–702. [Google Scholar] [CrossRef]
- Taghavi, A.; Pearce, S. A solution to the Lane–Emden equation in the theory of stellar structure utilizing the Tau method. Math. Methods Appl. Sci. 2013, 36, 1240–1247. [Google Scholar] [CrossRef]
- Khan, J.A.; Raja, M.A.Z.; Rashidi, M.M.; Syam, M.I.; Wazwaz, A.M. Nature-inspired computing approach for solving non-linear singular Emden–Fowler problem arising in electromagnetic theory. Connect. Sci. 2015, 27, 377–396. [Google Scholar] [CrossRef]
- Ramos, J.I. Linearization methods in classical and quantum mechanics. Comput. Phys. Commun. 2003, 153, 199–208. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Alofi, A.S.; Van Gorder, R.A. An Efficient Collocation Method for a Class of Boundary Value Problems Arising in Mathematical Physics and Geometry. In Abstract and Applied Analysis; Hindawi Publishing Corporation: New York, NY, USA, 2014; Volume 2014. [Google Scholar]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. Integrated intelligent computing with neuro-swarming solver for multi-singular fourth-order nonlinear Emden–Fowler equation. Comput. Appl. Math. 2020, 39, 307. [Google Scholar] [CrossRef]
- Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Wahab, H.A.; Arbi, A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation. Math. Comput. Simul. 2020, 178, 534–548. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Erdoğan, F. Stochastic numerical approach for solving second order nonlinear singular functional differential equation. Appl. Math. Comput. 2019, 363, 124605. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M. Neuro-swarm intelligent computing to solve the second-order singular functional differential model. Eur. Phys. J. Plus 2020, 135, 474. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Mehmood, J.; Sabir, Z.; Nasab, A.K.; Manzar, M.A. Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing. Neural Comput. Appl. 2019, 31, 793–812. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z. Intelligent computing for numerical treatment of nonlinear prey–predator models. Appl. Soft Comput. 2019, 80, 506–524. [Google Scholar] [CrossRef]
- Sabir, Z.; Manzar, M.A.; Raja, M.A.Z.; Sheraz, M.; Wazwaz, A.M. Neuro-heuristics for nonlinear singular Thomas-Fermi systems. Appl. Soft Comput. 2018, 65, 152–169. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Amin, F.; Guirao, J.L.; Raja, M.A.Z. Stochastic numerical technique for solving HIV infection model of CD4+ T cells. Eur. Phys. J. Plus 2020, 135, 403. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Aguilar, J.G.; Amin, F.; Shoaib, M. Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4+ T-cells. Math. Comput. Simul. 2021, 188, 241–253. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Baskonus, H.M.; Yao, S.W.; Ilhan, E. A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells. Results Phys. 2021, 25, 104235. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems. Front. Phys. 2020, 8, 224. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems. Alex. Eng. J. 2021, 60, 2641–2659. [Google Scholar] [CrossRef]
- Sridhar, R.; Chandrasekaran, M.; Sriramya, C.; Page, T. Optimization of Heterogeneous Bin Packing Using Adaptive Genetic Algorithm. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Chennai, India, 2017; Volume 183, p. 012026. [Google Scholar]
- Chang, F.S. Greedy-Search-based Multi-Objective Genetic Algorithm for Emergency Humanitarian Logistics Scheduling. Expert Syst. Appl. 2014, 41, 2947–2956. [Google Scholar]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Sakar, M.G.; Raja, M.A.Z. Novel design of Morlet wavelet neural network for solving second order Lane–Emden equation. Math. Comput. Simul. 2020, 172, 1–14. [Google Scholar] [CrossRef]
- Sabir, Z.; Amin, F.; Pohl, D.; Guirao, J.L. Intelligence computing approach for solving second order system of Emden–Fowler model. J. Intell. Fuzzy Syst. 2020, 1–16, Preprint. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Zuo, K.; Khan, M.J. An improved genetic algorithm optimization fuzzy controller applied to the wellhead back pressure control system. Mech. Syst. Signal Process. 2020, 142, 106708. [Google Scholar] [CrossRef]
- Elias, I.; Rubio, J.D.J.; Martinez, D.I.; Vargas, T.M.; Garcia, V.; Mujica-Vargas, D.; Meda-Campaña, J.A.; Pacheco, J.; Gutierrez, G.J.; Zacarias, A. Genetic algorithm with radial basis mapping network for the electricity consumption modeling. Appl. Sci. 2020, 10, 4239. [Google Scholar] [CrossRef]
- Pramanik, S.; Singh, R.P.; Ghosh, R. Application of bi-orthogonal wavelet transform and genetic algorithm in image steganography. Multimed. Tools Appl. 2020, 79, 17463–17482. [Google Scholar] [CrossRef]
- Alhijawi, B.; Kilani, Y. A collaborative filtering recommender system using genetic algorithm. Inf. Process. Manag. 2020, 57, 102310. [Google Scholar] [CrossRef]
- Zan, X.; Wu, Z.; Guo, C.; Yu, Z. A Pareto-based genetic algorithm for multi-objective scheduling of automated manufacturing systems. Adv. Mech. Eng. 2020, 12, 1687814019885294. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Q. An Active Set Smoothing Method for Solving Unconstrained Minimax Problems. Math. Probl. Eng. 2020, 2020, 9108150. [Google Scholar] [CrossRef]
- Arnström, D. On Complexity Certification of Active-Set QP Methods with Applications to Linear MPC. Ph.D. Thesis, Linköping University, LiU-Tryck, Linköping, Sweden, 2021. [Google Scholar]
- Piller, O.; Elhay, S.; Deuerlein, J.W.; Simpson, A.R. A content-based active-set method for pressure-dependent models of water distribution systems with flow controls. J. Water Resour. Plan. Manag. 2020, 146, 04020009. [Google Scholar] [CrossRef] [Green Version]
- Azizi, M.; Amir Fakhrian, M.; Araghi, M.A.F. A fuzzy system based active set algorithm for the numerical solution of the optimal control problem governed by partial differential equation. Eur. J. Control 2020, 54, 99–110. [Google Scholar] [CrossRef]
- Abide, S.; Barboteu, M.; Cherkaoui, S.; Danan, D.; Dumont, S. Inexact primal–dual active set method for solving elastodynamic frictional contact problems. Comput. Math. Appl. 2021, 82, 36–59. [Google Scholar] [CrossRef]
- Antonau, I.; Hojjat, M.; Bletzinger, K.U. Relaxed gradient projection algorithm for constrained node-based shape optimization. Struct. Multidiscip. Optim. 2021, 63, 1633–1651. [Google Scholar] [CrossRef]
- Chen, P.; Li, Y.; Zhang, X. Cauchy problem for stochastic non-autonomous evolution equations governed by noncompact evolution families. Discret. Contin. Dyn. Syst.-B 2021, 26, 1531. [Google Scholar]
- Chen, P. Periodic solutions to non-autonomous evolution equations with multi-delays. Discret. Contin. Dyn. Syst.-B 2021, 26, 2921. [Google Scholar]
- Chen, P.; Zhang, X. Non-autonomous stochastic evolution equations of parabolic type with nonlocal initial conditions. Discret. Contin. Dyn. Syst.-B 2021, 26, 4681. [Google Scholar] [CrossRef]


| start of GAs Inputs: The applicant solutions with real entries are equal to the unidentified parameters in GNNs as: W = [,,], where and Population: A Chromosomes set is designated as: , = [,,]t Output: The ANNs based decision variables are optimized with GA as WBest-GA Initialization: Form W with real entries. Adjust W vector to set an initial population “P”. Adjust the “gaoptimset” and “GA” functions. Evaluation of Fitness: Evaluate the fitness () of P for W with by using Equations (8) to (10) Termination: The procedure stops, if any below criteria are obtained.
Then [store], when the following standards meet Ranking: Adjust W in P to observe the excellence of the fitness Reproduction:
Use the ‘ evaluation’ Storage: Save WBest-GA, , time, function counts and generation. End of GA ASA process Start Inputs: WBest-GA is the starting point Output: The GA-ASA best weights are indicated as WGA-ASA Initialize: Iterations, Bounded constraints and assignments. Terminate: Terminate the scheme, when ≤ 10−20, TolX ≤ 10−20, MaxFunEvals ≤ 260,000 TolFun ≤ 10−19 & Iterations = 1200 obtains While (Terminate) Formulation of fitness For of W, the Equations (8) to (10) are used Modifications For ASA, invoke fmincon. Adjust W for each ASA generation. Compute , W again for Equations (8) to (10) Store Accumulate the WGA-ASA, function counts, , time and iterations for ASA trials. Procedure of ASA End Data Generations Repeat the data 30 times for the GA-ASA to achieve a larger data-set using the optimization variables of GNNs to solve the HO-NSDM |
| Problem 1 | Problem 2 | Problem 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Mean | Med | S.I.R | Min | Mean | Med | S.I.R | Min | Mean | Med | S.I.R | |
| 0 | 4.57 × 10−5 | 1.54 × 10−1 | 5.70 × 10−2 | 7.93 × 10−2 | 2.26 × 10−4 | 1.10 × 10−1 | 4.50 × 10−2 | 5.24 × 10−2 | 4.14 × 10−5 | 7.37 × 10−1 | 4.10 × 10−2 | 8.66 × 10−2 |
| 0.1 | 4.91 × 10−5 | 1.55 × 10−1 | 5.76 × 10−2 | 7.94 × 10−2 | 2.22 × 10−4 | 1.10 × 10−1 | 4.50 × 10−2 | 5.23 × 10−2 | 6.05 × 10−5 | 7.50 × 10−1 | 4.17 × 10−2 | 8.74 × 10−2 |
| 0.2 | 4.75 × 10−5 | 1.57 × 10−1 | 5.76 × 10−2 | 7.92 × 10−2 | 2.17 × 10−4 | 1.10 × 10−1 | 4.48 × 10−2 | 5.20 × 10−2 | 7.74 × 10−5 | 7.79 × 10−1 | 4.27 × 10−2 | 9.06 × 10−2 |
| 0.3 | 3.45 × 10−5 | 1.57 × 10−1 | 5.61 × 10−2 | 7.78 × 10−2 | 2.11 × 10−4 | 1.09 × 10−1 | 4.38 × 10−2 | 5.11 × 10−2 | 8.20 × 10−5 | 8.38 × 10−1 | 4.32 × 10−2 | 9.62 × 10−2 |
| 0.4 | 1.27 × 10−5 | 1.53 × 10−1 | 5.24 × 10−2 | 7.39 × 10−2 | 1.95 × 10−4 | 1.05 × 10−1 | 4.10 × 10−2 | 4.87 × 10−2 | 7.46 × 10−5 | 9.31 × 10−1 | 4.25 × 10−2 | 1.03 × 10−2 |
| 0.5 | 1.14× 10−6 | 1.44 × 10−1 | 4.51 × 10−2 | 6.59 × 10−2 | 1.63 × 10−4 | 9.81 × 10−2 | 3.53 × 10−2 | 4.38 × 10−2 | 5.55 × 10−5 | 1.06 × 10−1 | 3.95 × 10−2 | 1.10 × 10−2 |
| 0.6 | 3.17 × 10−5 | 1.28 × 10−1 | 3.26 × 10−2 | 5.31 × 10−2 | 1.09 × 10−4 | 8.65 × 10−2 | 2.58 × 10−2 | 3.57 × 10−2 | 2.31 × 10−5 | 1.21 × 10−1 | 3.34 × 10−2 | 1.23 × 10−2 |
| 0.7 | 7.46 × 10−5 | 1.02 × 10−1 | 1.35 × 10−2 | 3.33 × 10−2 | 3.55 × 10−5 | 6.98 × 10−2 | 1.25 × 10−2 | 2.39 × 10−2 | 2.34 × 10−5 | 1.40 × 10−1 | 2.33 × 10−2 | 1.36 × 10−2 |
| 0.8 | 1.04 × 10−4 | 7.77 × 10−2 | 1.38 × 10−2 | 9.44 × 10−3 | 5.43 × 10−5 | 5.18 × 10−2 | 3.65 × 10−3 | 6.85 × 10−3 | 5.21 × 10−5 | 1.61 × 10−1 | 8.77 × 10−3 | 1.52 × 10−2 |
| 0.9 | 1.94 × 10−4 | 7.87 × 10−2 | 4.21 × 10−2 | 2.72 × 10−2 | 1.52 × 10−4 | 4.77 × 10−2 | 1.92 × 10−2 | 9.68 × 10−3 | 1.59 × 10−4 | 1.86 × 10−1 | 1.45 × 10−2 | 1.69 × 10−2 |
| 1 | 2.75 × 10−4 | 1.04 × 10−1 | 7.48 × 10−2 | 5.06 × 10−2 | 2.53 × 10−4 | 5.55 × 10−2 | 3.77 × 10−2 | 2.24 × 10−2 | 2.48 × 10−4 | 2.13 × 10−1 | 3.48 × 10−2 | 1.87 × 10−2 |
| Problem | Iterations | Executed Time | Function Counts | |||
|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | |
| 1 | 113.2927 | 21.46765 | 1505 | 0 | 174,384.2 | 31,050.41 |
| 2 | 105.2282 | 30.46636 | 1455.467 | 271.3052 | 162,386.4 | 45,633.09 |
| 3 | 119.7212 | 14.01331 | 1505 | 0 | 185,438.2 | 18,692.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabir, Z.; Wahab, H.A.; Javeed, S.; Baskonus, H.M. An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models. Fractal Fract. 2021, 5, 176. https://doi.org/10.3390/fractalfract5040176
Sabir Z, Wahab HA, Javeed S, Baskonus HM. An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models. Fractal and Fractional. 2021; 5(4):176. https://doi.org/10.3390/fractalfract5040176
Chicago/Turabian StyleSabir, Zulqurnain, Hafiz Abdul Wahab, Shumaila Javeed, and Haci Mehmet Baskonus. 2021. "An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models" Fractal and Fractional 5, no. 4: 176. https://doi.org/10.3390/fractalfract5040176
APA StyleSabir, Z., Wahab, H. A., Javeed, S., & Baskonus, H. M. (2021). An Efficient Stochastic Numerical Computing Framework for the Nonlinear Higher Order Singular Models. Fractal and Fractional, 5(4), 176. https://doi.org/10.3390/fractalfract5040176







