A Variety of New Traveling Wave Packets and Conservation Laws to the Nonlinear Low-Pass Electrical Transmission Lines via Lie Analysis
Abstract
1. Introduction
2. Preliminaries
2.1. Modified Khater Method
2.2. Multiplier Approach
3. Lie Symmetry Analysis
4. Optimal System
4.1. Similarity Reduction of Equation (1)
4.2.
4.3.
4.4. Travelling Wave Solutions of Equation (1)
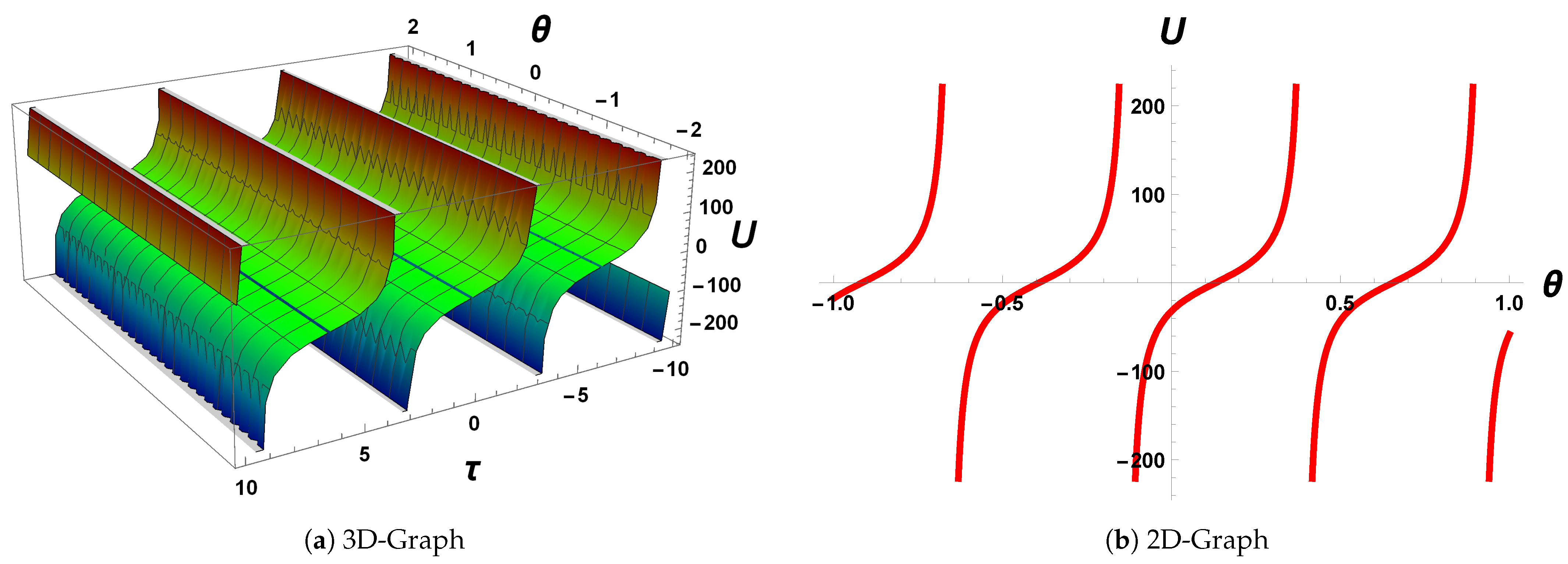
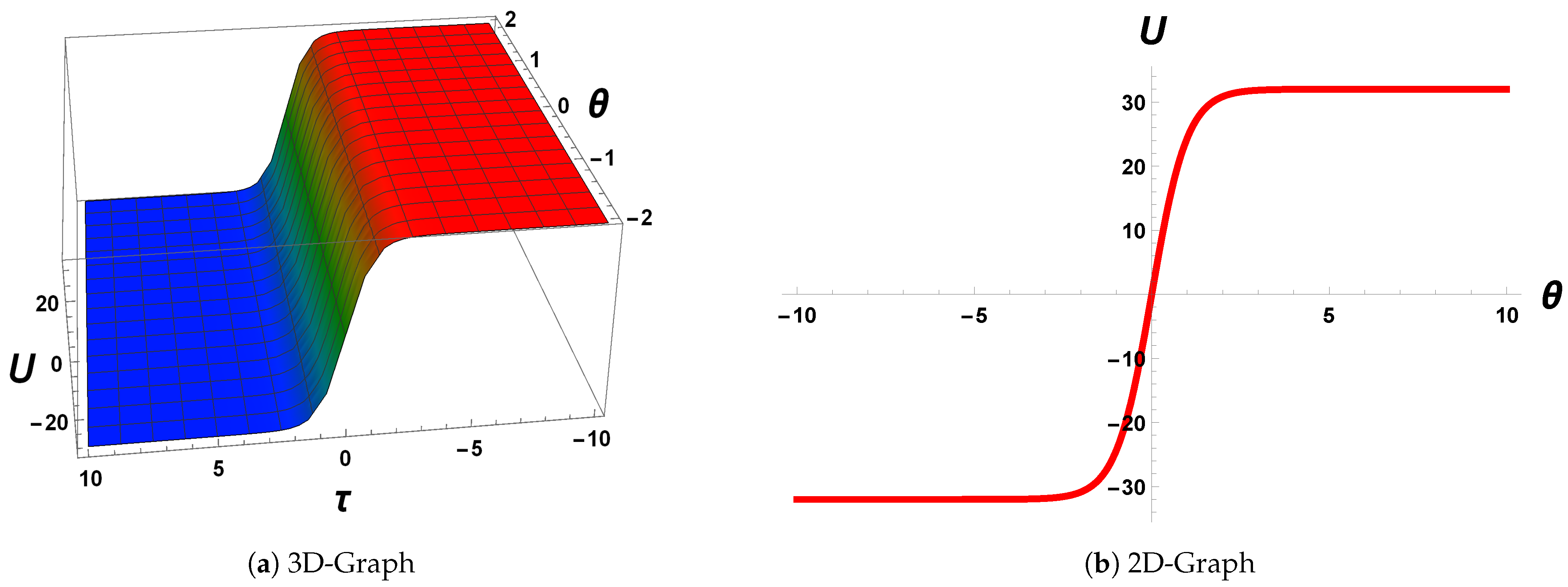
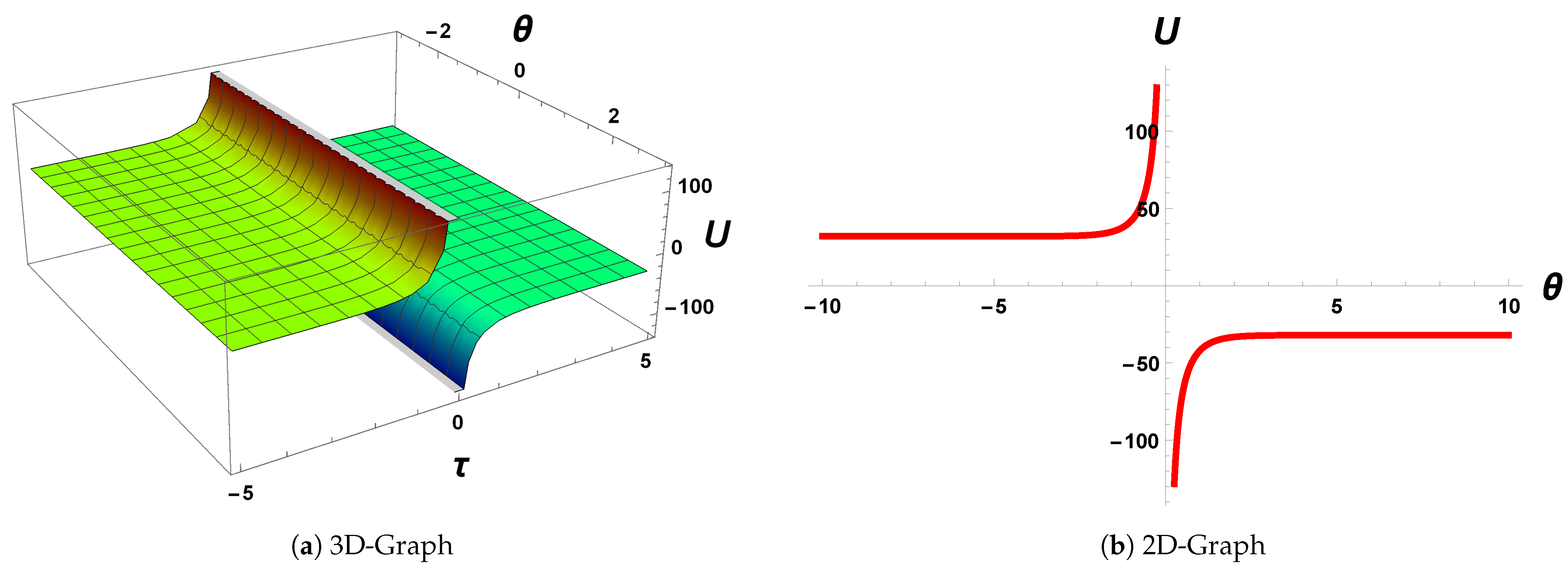
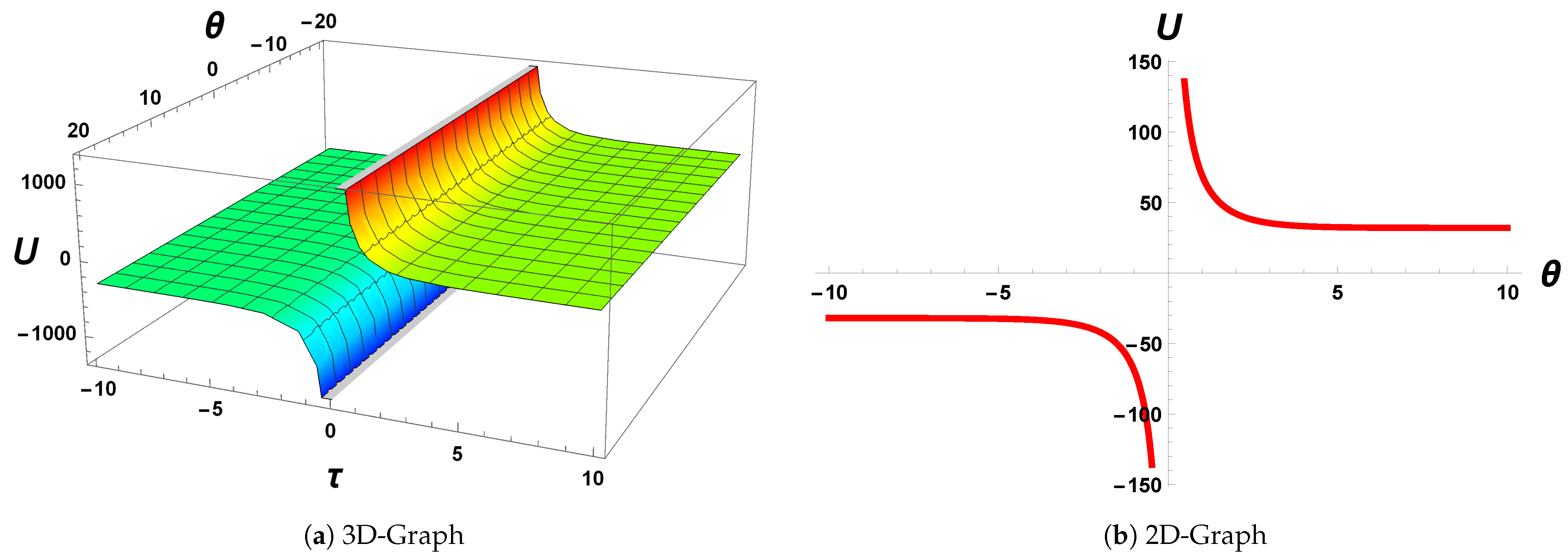
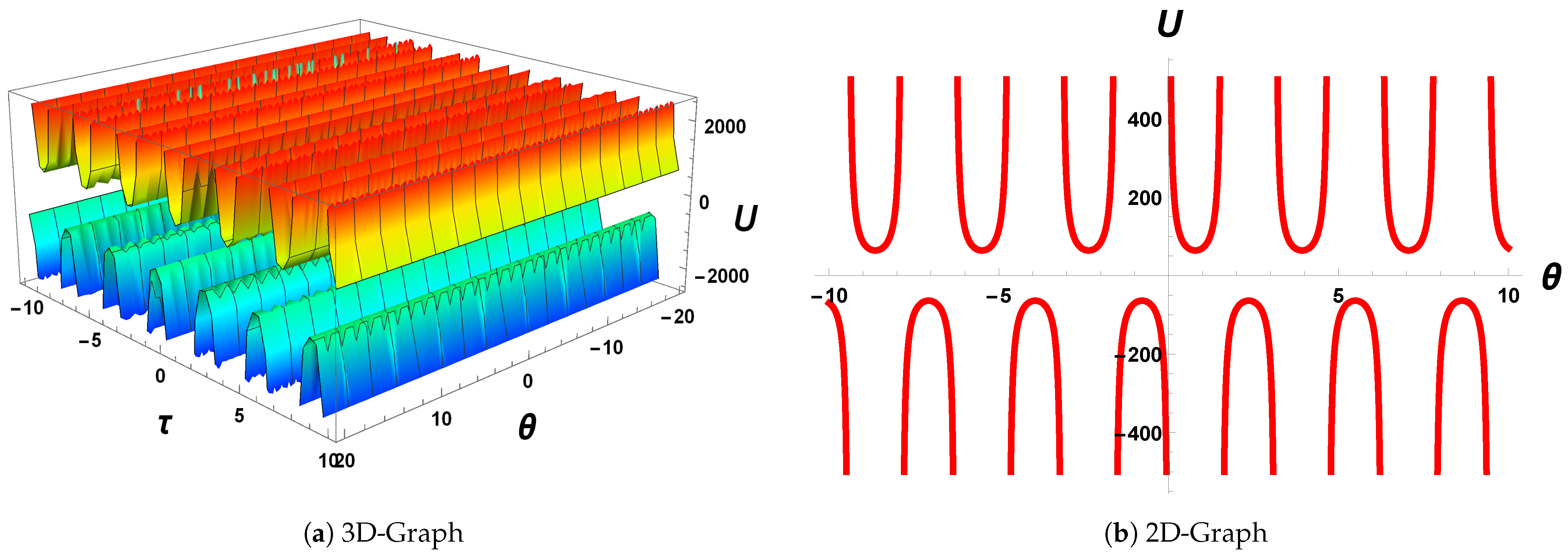
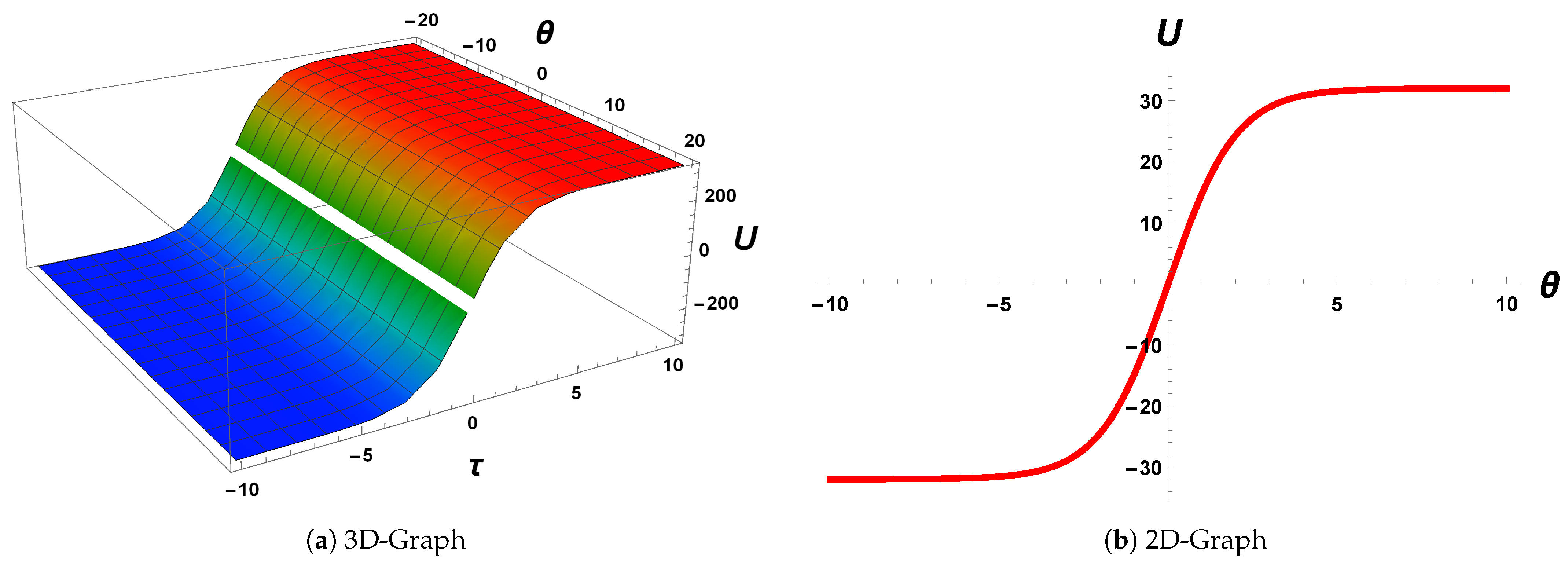
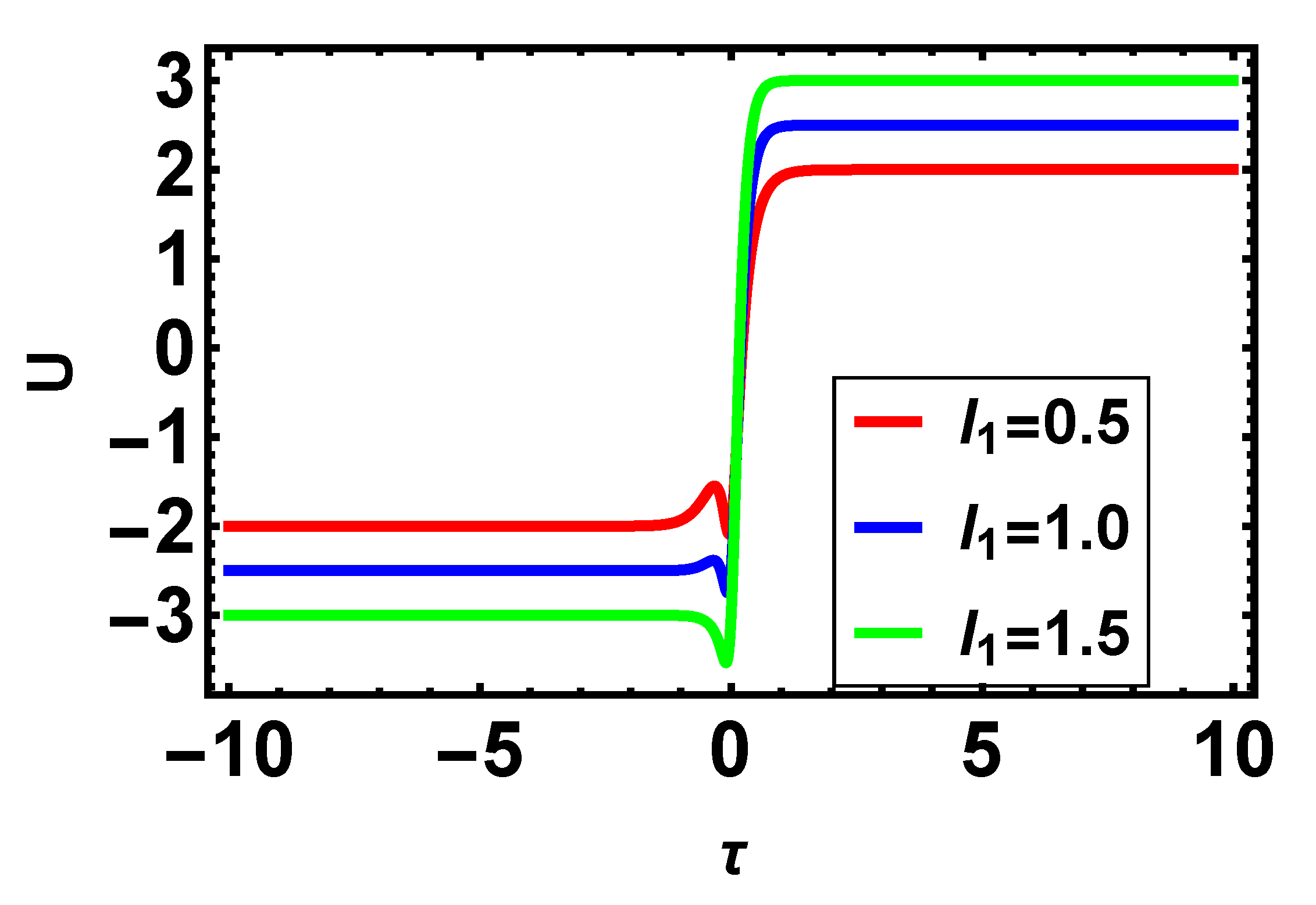
4.5. Graphical Behaviour of Wave Patterns
5. Conservation Laws
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.G.; Osman, M.S.; Zhu, W.H.; Zhou, L.; Ai, G.P. Different complex wave structures described by the Hirota equation with variable coefficients in inhomogeneous optical fibers. Appl. Phys. B 2019, 125, 175. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Partial Differential Equations and Solitary Wave’s Theory; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Yang, X.J.; Tenreiro, M.J.A.; Srivastava, H.M. A new numerical technique for solving the local fractional diffusion equation: Two-dimensional extended differential transform approach. Appl. Math. Comput. 2016, 274, 143–151. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Zahran, E.H.M.; Khater, M.M.A. The exp(-ϕ(ξ))-expansion method and its application for solving nonlinear evolution equations. Int. J. Mod. Nonlinear Theory Appl. 2015, 4, 37–47. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Roy, R. Closed form solutions of two time fractional nonlinear wave equations. Results Phys. 2018, 9, 1031–1039. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, J. Solving (3 + 1)-dimensional generalized BKP equations by the improved (G′/G)-expansion method. Indian J. Pure Appl. Phys. 2015, 53, 713–717. [Google Scholar]
- Islam, M.T.; Akbar, M.A.; Azad, A.K. Traveling wave solutions to some nonlinear fractional partial differential equations through the rational (G′/G)expansion method. J. Ocean Eng. Sci. 2018, 3, 76–81. [Google Scholar] [CrossRef]
- Abdou, M.A.; Soliman, A.A. New exact travelling wave solutions for space-time fractional nonlinear equations describing nonlinear transmission lines. Results Phys. 2018, 9, 1497–1501. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Abbasb, Y.S.; Hashim, I. Heat flux performance in a porous medium embedded Maxwell fluid flow over a vertically stretched plate due to heat absorption. J. Nonlinear Sci. Appl. 2016, 9, 2986–3001. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Ibrahim, A.I.N.; Siri, Z.; Noor, N.F.M. Mean Monte-Carlo finite difference method for random sampling of a nonlinear epidemic system. Sociol. Methods Res. 2016, 48, 34–61. [Google Scholar] [CrossRef]
- Manafian, J.; Ilhan, O.A.; Alizadeh, A. Periodic wave solutions and stability analysis for the KP-BBM equation with abundant novel interaction solutions. Phys. Scr. 2020, 95, 065203. [Google Scholar] [CrossRef]
- Islam, R.; Khan, K.; Akbar, M.A.; Islam, M.E.; Ahmed, M.T. Traveling wave solutions of some nonlinear evolution equations. Alex. Eng. J. 2015, 54, 263–269. [Google Scholar] [CrossRef][Green Version]
- Akbar, M.A.; Ali, N.H.M. The improved F-expansion method with Riccati equation and its applications in mathematical physics. Cogent Math. 2017, 4, 1282577. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Zhang, L. A direct algorithm of exp-function method for non-linear evolution equations in fluids. Therm. Sci. 2016, 20, 881–884. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New complex hyperbolic structures to the Lonngren wave equation by using sine-Gordon expansion method. Appl. Math. Nonlinear Sci. 2019, 4, 129–138. [Google Scholar] [CrossRef]
- El-Sayed, M.F.; Moatimid, G.M.; Moussa, M.H.M.; El-Shiekh, R.M.; Khawlani, M.A. New exact solutions for coupled equal width wave equation and (2+1)-dimensional Nizhnik-Novikov-Veselov system using modified Kudryashov method. Int. J. Adv. Appl. Math. Mech. 2014, 2, 19–25. [Google Scholar]
- Mohyud-Din, S.T.; Irshad, A. Solitary wave solutions of some nonlinear PDEs arising in electronics. Opt. Quantum Electron. 2017, 49, 130. [Google Scholar] [CrossRef]
- Manafian, J.; Heidari, S. Periodic and singular kink solutions of the Hamiltonian amplitude equation. Adv. Math. Models Appl. 2019, 4, 134–149. [Google Scholar]
- Akbar, M.A.; Ali, N.H.M.; Hussain, J. Optical soliton solutions to the (2 + 1)- dimensional Chaffee-Infante equation and the dimensionless form of the Zakharov equation. Adv. Differ. Equ. 2019, 2019, 446. [Google Scholar] [CrossRef]
- Qasim, A.F.; Al-Rawi, E.S. Adomian decomposition method with modified Bernstein polynomials for solving ordinary and partial differential equations. J. Appl. Math. 2018, 2018, 1803107. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Osman, M.S.; Eslami, M.; Mirzazadeh, M.; Zhou, Q.; Badri, S.A.; Korkmaz, A. Hyperbolic rational solutions to a variety of conformable fractional Boussinesqlike equations. Nonlinear Eng. 2019, 8, 224–230. [Google Scholar] [CrossRef]
- Ghanbari, B.; Osman, M.S.; Baleanu, D. Generalized exponential rational function method for extended Zakharov Kuznetsov equation with conformable derivative. Mod. Phys. Lett. A 2019, 34, 1950155. [Google Scholar] [CrossRef]
- Osman, M.S.; Rezazadeh, H.; Eslami, M. Traveling wave solutions for (3 + 1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity. Nonlinear Eng. 2019, 8, 559–567. [Google Scholar] [CrossRef]
- Shahoot, A.M.; Alurrfi, K.A.E.; Hassan, I.M.; Almsri, A.M. Solitons and other exact solutions for two nonlinear PDEs in mathematical physics using the generalized projective Riccati equations method. Adv. Math. Phys. 2018, 2018, 6870310. [Google Scholar] [CrossRef]
- Hu, W.P.; Deng, Z.C.; Han, S.M.; Fa, W. Multi-symplectic Runge-Kutta methods for Landau Ginzburg-Higgs equation. Appl. Math. Mech. 2009, 30, 1027–1034. [Google Scholar] [CrossRef]
- Raslan, K.R.; Ali, K.K.; Shallal, M.A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations. Chaos Solitons Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]
- Osman, M.S. One-soliton shaping and inelastic collision between double solitons in the fifth-order variable-coefficient Sawada-Kotera equation. Nonlinear Dyn. 2019, 96, 1491–1496. [Google Scholar] [CrossRef]
- Lu, D.; Osman, M.S.; Khater, M.M.A.; Attia, R.A.M.; Baleanu, D. Analytical and numerical simulations for the kinetics of phase separation in iron (Fe-Cr-X (X = Mo, Cu)) based on ternary alloys. Phys. A 2020, 537, 122634. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Mohamed, M.S.; Attia, R.A.M. On semi analytical and numerical simulations for a mathematical biological model; the time-fractional nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation. Chaos Solitons Fractals 2021, 144, 110676. [Google Scholar] [CrossRef]
- Chu, Y.; Khater, M.M.A.; Hamed, Y.S. Diverse novel analytical and semi-analytical wave solutions of the generalized (2 + 1)-dimensional shallow water waves model. AIP Adv. 2021, 11, 015223. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Ahmed, A.E.; El-Shorbagy, M.A. Abundant stable computational solutions of Atangana—Baleanu fractional nonlinear HIV-1 infection of CD4+T-cells of immunodeficiency syndrome. Result Phys. 2021, 22, 103890. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Ahmed, A.E.; Alfalqi, S.H.; Alzaidi, J.F.; Elbendary, J.; Alabdali, A.M. Computational and approximate solutions of complex nonlinearFokas-Lenells equation arising in optical fiber. Result Phys. 2021, 25, 104322. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Mousa, A.A.; El-Shorbagy, M.A.; Attia, R.A.M. Analytical and semi-analytical solutions for Phi-four equation through three recent schemes. Result Phys. 2021, 22, 103954. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Nisar, K.S.; Mohamed, M.S. Numerical investigation for the fractional nonlinearspace-time telegraph equation via the trigonometricQuintic B-spline scheme. Math. Meth. Appl. Sci. 2021, 44, 4598–4606. [Google Scholar] [CrossRef]
- Tashlykov, O.L.; Vlasova, S.G.; Kovyazina, I.S.; Mahmoud, K.A. Repercussions of yttrium oxides on radiation shielding capacity of sodium-silicate glass system: Experimental and Monte Carlo simulation study. Eur. Phys. J. Plus. 2021, 136, 428. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Nofal, T.A.; Abu-Zinadah, H.; Lotayif, M.S.M.; Lu, D. Novel computational and accurate numericalsolutions of the modified Benjamin-Bona-Mahony(BBM) equation arising in the optical illusions field. Alex. Eng. J. 2021, 1, 1797–1806. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Mohamed, M.S.; Elagan, S.K. Diverse accurate computational solutions of the nonlinear Klein-Fock-Gordon equation. Result Phys. 2021, 23, 104003. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Anwar, S.; Tariq, K.U.; Mohamed, M.S. Some optical soliton solutions to the perturbed nonlinear Schrödinger equation by modified Khater method. AIP Adv. 2021, 11, 025130. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Bekir, A.; Lu, D.; Attia, R.A.M. Analytical and semi-analytical solutions for time-fractional Cahn-Allen equation. Math. Meth. Appl. Sci. 2021, 44, 2682–2691. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Testing the nature of Gauss–Bonnet gravity by four-dimensional rotating black hole shadow. Eur. Phys. J. Plus. 2021, 136, 436. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Elagan, S.K.; Mousa, A.A.; El-Shorbagy, M.A.; Alfalqi, S.H.; Alzaidi, J.F.; Lu, D. Sub-10-fs-pulse propagation between analytical and numerical investigation. Result Phys. 2021, 25, 104133. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, J.; Yan, C.; Qin, R.; Lu, Z.; Geng, H.; Xu, T.; Ju, L. A review on optoelectronic device applications of 2D transition metalcarbides and nitrides. AIP Adv. 2021, 11, 055105. [Google Scholar]
- Khater, M.M.A. Abundant breather and semi-analytical investigation: On high-frequency waves’ dynamics in the relaxation medium. Mod. Phys. Lett. B 2021, 35, 2150372. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Lu, D. Analytical versus numerical solutions of the nonlinear fractional time–space telegraph equation. Mod. Phys. Lett. B 2021, 35, 2150324. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Ahmed, A.E. Strong Langmuir turbulence dynamics through the trigonometric quintic and exponential B-spline schemes. AIMS Math. 2021, 6, 5896–5908. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, M. Passive synchronization in optomechanical resonators coupled through an optical field. Chaos Solitons Fractals 2021, 144, 110717. [Google Scholar] [CrossRef]
- Abdoulkary, S.; Beda, T.; Dafounamssou, O.; Tafo, E.W.; Mohamadou, A. Dynamics of solitary pulses in the nonlinear low-pass electrical transmission lines through the auxiliary equation method. J. Mod. Phys. Appl. 2013, 2, 69–87. [Google Scholar]
- Malwe, B.H.; Betchewe, G.; Doka, S.Y.; Kofane, T.C. Travelling wave solutions and soliton solutions for the nonlinear transmission line using the generalized Ric- cati equation mapping method. Nonlinear Dyn. 2016, 84, 171–177. [Google Scholar] [CrossRef]
- Kae, A.; Mom, E.; Almsiri, A.M.; Amh, A. The expansion method for describing the nonlinear low-pass electrical lines. J Taibah Uni Sci 2019, 13, 63–70. [Google Scholar]
- Eme, Z.; Kae, A. The generalized projective Riccati equations method and its applications to nonlinear PDEs describing nonlinear transmission lines. Commun. Appl. Electron 2015, 3, 2394–4714. [Google Scholar]
- Lie, S. Theories der Tranformationgruppen, Dritter and Letzter Abschnitt; Teubner: Leipzig, Germany; Berlin, Germany, 1888. [Google Scholar]
- Li, C.; Zhang, J. Lie symmetry analysis and exact solutions of generalized fractional Zakharov-Kuznetsov equations. Symmetry 2019, 11, 601. [Google Scholar] [CrossRef]
- Jhangeer, A.; Hussain, A.; Junaid-U-Rehman, M.; Baleanu, D.; Riaz, M.B. Quasi-periodic, chaotic and travelling wave structures of modified Gardner equation. Chaos Solitons Fractals 2021, 143, 110578. [Google Scholar] [CrossRef]
- Liu, H.; Bai, C.-L.; Xin, X.; Zhang, L. A novel Lie group classification method for generalized cylindrical KdV type of equation: Exact solutions and conservation laws. J. Math. Fluid Mech. 2019, 21, 21–55. [Google Scholar] [CrossRef]
- Hussain, A.; Jhangeer, A.; Abbas, N. Symmetries, conservation laws and dust acoustic solitons of two-temperature ion in inhomogeneous plasma. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150071. [Google Scholar] [CrossRef]
- Hussain, A.; Jhangeer, A.; Abbas, N.; Khan, I.; Nisar, K.S. Solitary wave patterns and conservation laws of fourth-order nonlinear symmetric regularized long-wave equation arising in plasma. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Riaz, M.B.; Baleanu, D.; Jhangeer, A.; Abbas, N. Nonlinear self-adjointness, conserved vectors, and traveling wave structures for the kinetics of phase separation dependent on ternary alloys in iron (Fe-Cr-Y (Y = Mo, Cu)). Results Phys. 2021, 25, 104151. [Google Scholar] [CrossRef]
- Jhangeer, A.; Hussain, A.; Junaid-U-Rehman, M.; Khan, I.; Baleanu, D.; Nisar, K.S. Lie analysis, conservation laws and travelling wave structures of nonlinear Bogoyavlenskii–Kadomtsev–Petviashvili equation. Results Phys. 2020, 19, 103492. [Google Scholar] [CrossRef]
- Jhangeer, A.; Seadawy, A.R.; Ali, F.; Ahmed, A. New complex waves of perturbed Shrödinger equation with Kerr law nonlinearity and Kundu-Mukherjee-Naskar equation. Results Phys. 2020, 16, 102816. [Google Scholar] [CrossRef]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Olver, P.J. Application of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic: New York, NY, USA, 1982. [Google Scholar]
- El-Ganaini, S.; Kumar, H. A variety of new traveling and localized solitary wave solutions of a nonlinear model describing the nonlinear low- pass electrical transmission lines. Chaos Solitons Fractals 2020, 140, 110218. [Google Scholar] [CrossRef]
- Eme, Z.; Kae, A. A new Jacobi elliptic function expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines. Chaos Solitons Fractals 2015, 78, 148–155. [Google Scholar]
- Jhangeer, A.; Rezazadeh, H.; Abazari, R.; Yildirim, K.; Sharif, S.; Ibraheem, F. Lie analysis, conserved quantities and solitonic structures of Calogero-Degasperis-Fokas equation. Alex. Eng. J. 2021, 60, 2513–2523. [Google Scholar] [CrossRef]
- Naz, R.; Mahomed, F.M.; Mason, D.P. Comparison of different approaches to conservation laws for some partial differential equations in fluid mechanics. Appl. Math. Comp. 2008, 205, 212–230. [Google Scholar] [CrossRef]
- Hereman, W. Symbolic computation of conservation laws of nonlinear partial differential equations in multi-dimensions. Int. J. Quantum Chem. 2006, 106, 278–299. [Google Scholar] [CrossRef]
- Cheviakov, A.F. GeM software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Comm. 2007, 176, 48–61. [Google Scholar] [CrossRef]
- Cheviakov, A.F. Computation of fluxes of conservation laws. J. Eng. Math. 2010, 66, 153–173. [Google Scholar] [CrossRef]
- Hussain, A.; Jhangeer, A.; Abbas, N.; Khan, I.; Sherif, E.S.M. Optical solitons of fractional complex Ginzburg-Landau equation with conformable, beta, and M-truncated derivatives: A comparative study. Adv. Differ. Equ. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Anco, S.C.; Bluman, G. Direct construction method for conservation laws of partial differential equations Part II: General treatment. Eur. J. Appl. Math. 2002, 41, 567–585. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.B.; Awrejcewicz, J.; Jhangeer, A.; Junaid-U-Rehman, M. A Variety of New Traveling Wave Packets and Conservation Laws to the Nonlinear Low-Pass Electrical Transmission Lines via Lie Analysis. Fractal Fract. 2021, 5, 170. https://doi.org/10.3390/fractalfract5040170
Riaz MB, Awrejcewicz J, Jhangeer A, Junaid-U-Rehman M. A Variety of New Traveling Wave Packets and Conservation Laws to the Nonlinear Low-Pass Electrical Transmission Lines via Lie Analysis. Fractal and Fractional. 2021; 5(4):170. https://doi.org/10.3390/fractalfract5040170
Chicago/Turabian StyleRiaz, Muhammad Bilal, Jan Awrejcewicz, Adil Jhangeer, and Muhammad Junaid-U-Rehman. 2021. "A Variety of New Traveling Wave Packets and Conservation Laws to the Nonlinear Low-Pass Electrical Transmission Lines via Lie Analysis" Fractal and Fractional 5, no. 4: 170. https://doi.org/10.3390/fractalfract5040170
APA StyleRiaz, M. B., Awrejcewicz, J., Jhangeer, A., & Junaid-U-Rehman, M. (2021). A Variety of New Traveling Wave Packets and Conservation Laws to the Nonlinear Low-Pass Electrical Transmission Lines via Lie Analysis. Fractal and Fractional, 5(4), 170. https://doi.org/10.3390/fractalfract5040170







