A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel

Abstract

Fractional differential equations can present the physical pathways with the storage and inherited properties due to the memory factor of fractional order. The purpose of this work is to interpret the collocation approach for tackling the fractional partial integro-differential equation (FPIDE) by employing the extended cubic B-spline (ECBS). To determine the time approximation, we utilize the Caputo approach. The stability and convergence analysis have also been analyzed. The efficiency and reliability of the suggested technique are demonstrated by two numerical applications, which support the theoretical results and the effectiveness of the implemented algorithm.

1. Introduction

Fractional calculus (FC) has explored the concept of differentiation and integration to non-integer order. FC is a more generalized version of classical calculus. FC is as old as classical calculus, but it is gaining popularity these days because of the implementations in many domains like science and engineering. Fractional partial differential equations (FPDEs) have gained much popularity because of their exceptional simulation properties in various scientific areas. It has been used to represent physical and technical phenomena that are described tremendously by fractional differential equations. The fractional derivative models are used to recognize better those systems, which required accurate modeling of damping, non-Fourier heat conduction, acoustic dissipation, geophysics, relaxation, creep, viscoelasticity, rheology, and fluid dynamics, Malaria and COVID-19 [1,2,3,4].

Integro-differential equations of fractional order are the type of models that include both integro-differential equations and fractional derivatives. The analysis of partial integro-differential equations with fractional specifications is an important element of the theory and implementations of FC, which have considered crucial mathematical methods for describing and analysing a broad variety of actual challenges in natural science, technology, and engineering [5,6,7,8]. The mathematical models of physical phenomena and their implementations in heat conduction [9], reactor dynamics [10], flow in fractured bio-materials [11], electricity swaption [12], visco-elasticity [13], population dynamics, convection diffusion [14] and grain growth [15]. In this study, we will look at the nonlinear FPIDE [16]:

$${}_0^C{D}_t^{\gamma }V(y,t)+V{V}_y={\int }_0^t{(t-s)}^{\alpha -1}{V}_{yy}(y,s)ds+G(y,t),0<y<L,0<t<T,$$

(1)

with initial condition

$$V(y,0)=f\left(y\right),0\le y\le L,$$

(2)

and boundary conditions

$$V(0,t)=V(L,T)=0,0\le t\le T,$$

(3)

where $\gamma ,\alpha \in (0,1)$, $T,$ L are positive constants, and $G(y,t)$, $f\left(y\right)$ are given functions. ${}_0^C{D}_t^{\gamma }$ denotes the Caputo fractional derivative (CFD) and is interpreted as

$${}_0^C{D}_t^{\gamma }F\left(y\right)=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }(n-\gamma )}{\int }_0^y{(y-\xi )}^{n-1-\gamma }{F}^{\left(n\right)}\left(\xi \right)d\xi ,\hfill & n-1<\gamma \le n,n\in \mathbb{N},\hfill \\ F^{\left(n\right)}\left(y\right),\hfill & \gamma =n.\hfill \end{array}\right.$$

(4)

where $\mathsf{\Gamma }$ is the Euler’s Gamma function.

At various stages of real systems, fractional derivatives and integral operators are more suitable than standard derivatives and integration, which provide a more precise explanation of structural and genetic features of several dynamical and physical procedures. As a result, accurate computational methods are used to approximately cope with the complexities of fractional derivatives contained in such equations. These complexities are due to the possibility of the singularities of the kernels causing drastic fluctuations in the solution. Consequently, it isn’t easy to acquire a closed-form solution in several implementations, particularly in nonlinear scenarios, so an approximation of physical description is needed. Alternatively, many studies have been conducted to investigate the presence of a unique solution to fractional order integro-differential equations, such as Hu et al. [17], Li et al. [18], Karthikeyan and Trujillo [19], Chuong et al. [20].

The majority of FPIDE cannot be addressed exact analytically, finding more effective approximate approaches using computational methods would be extremely beneficial. Several authors have focused their attention on searching and exploring solutions of the Fractional partial intego-differential equations (FPIDEs) using various analytical and numerical strategies. Awawdeh et al. [21] utilized the homotopy analysis approximation to solve the linear FPIDE analytically. Hussain et al. [22] solved the FPIDE analytically by the variation iteration method. Mittal and Nigam [23] implemented the Adomian decomposition method to handle the FPIDE. Rawashdeh [24] suggested a collocation approach for solving the FPIDE numerically by the polynomial spline. Eslahchi et al. [25] developed the jacobi technique to solve nonlinear FPIDE, also analyzed stability and convergence. Zhao et al. [26] employed piecewise polynomial collocation approaches to tackle FPIDEs containing weakly singular kernels. Arshed [27] demonstrated the B-spline technique for solving linear FPIDE. Unhale and Kendre [28] presented collocation technique to solve the nonlinear FPIDE utilizing the Chebyshev polynomials and the shifted Legendre polynomials. Avazzadeh et al. [29] established a hybrid technique by blending the Legendre wavelets, and operational matrix of fractional integration. A numerical technique based on Legendre-Laguerre and the collocation method has been considered by Dehestani et al. [30].

The B-spline was proposed by many authors to solve fractional partial differential models [31,32,33,34,35,36,37,38]. These functions can adjust every point in the domain and approximate the solution with maximum frequency accuracy. For solving FPDEs, a variety of numerical approaches have already been developed. However, so far as we know, no such research on the utilization of B-splines exists in solving the nonlinear FPIDE. Therefore, we intend to fill this gap. We aim to extend the ECBS technique for the solution of the nonlinear FPIDE model with a weakly singular kernel. The article is partitioned as follows: In Section 2, the basis functions and the time approximation are presented. In Section 3, a derivation of the method is described. The stability and convergence of recommended technique are analyzed in Section 4. Two applications and discussions are shown in Section 5. Finally, the results of the recommended technique are displayed in Section 6.

2. Preliminaries

Definition 1.

Let $\left\{y_i\right\}$ be an evenly distributed splitting of a finite domain for $i\in \mathbb{Z}$. As a result, the proposed interval is segregated into M equivalent subparts at the connections as $y_i=y_0+ih$, where h is the moving scale. The ECBS functions at the $y_i$ over the proposed interval are shown below [39]:

$$B_i(y,\rho )=\frac{1}{24h^4}\left\{\begin{array}{cc}4h(1-\rho ){(y-y_{i-2})}^3+3\rho {(y-y_{i-2})}^4,\hfill & y\in [y_{i-2},y_{i-1}),\hfill \\ (4-\rho )h^4+12h^3(y-y_{i-1})+6h^2(2+\rho ){(y-y_{i-1})}^2\hfill \\ -12h{(y-y_{i-1})}^3-3\rho {(y-y_{i-1})}^4,\hfill & y\in [y_{i-1},y_i),\hfill \\ (4-\rho )h^4+12h^3(y_{i+1}-y)+6h^2(2+\rho ){(y_{i+1}-y)}^2\hfill \\ -12h{(y_{i+1}-y)}^3-3\rho {(y_{i+1}-y)}^4,\hfill & y\in [y_i,y_{i+1}),\hfill \\ 4h(1-\rho ){(y_{i+2}-y)}^3+3\rho {(y_{i+2}-y)}^4,\hfill & y\in [y_{i+1},y_{i+2}),\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

(5)

where $i=-1\left(1\right)M+1$, $\rho \in \mathbb{R}$ is a free parameter in the interval $[-8,1]$ and $y\in \mathbb{R}$ is a variable. The cubic B-spline and ECBS basis have identical characteristics for $\rho \in [-8,1]$. For $\rho =0$, the ECBS converts to cubic B-spline. There is a unique $\widehat{V}(y,t)$, that preserves the specified conditions, so that

$$v(y,t)=\sum _{i=-1}^{M+1}{\eta }_i\left(t\right)E_i(y,\rho ).$$

(6)

The following are the $\widehat{V}(y,t)$, ${\widehat{V}}^{\prime }(y,t)$ and ${\widehat{V}}^{″}(y,t)$ at the edges:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\widehat{V}(y_i,t)={\sigma }_1{\eta }_{i-1}\left(t\right)+{\sigma }_2{\eta }_i\left(t\right)+{\sigma }_1{\eta }_{i+1}\left(t\right),\hfill \\ {\widehat{V}}^{\prime }(y_i,t)=-{\sigma }_3{\eta }_{i-1}\left(t\right)+{\sigma }_3{\eta }_{i+1}\left(t\right),\hfill \\ {\widehat{V}}^{″}(y_i,t)={\sigma }_4{\eta }_{i-1}\left(t\right)+{\sigma }_5{\eta }_i\left(t\right)+{\sigma }_4{\eta }_{i+1}\left(t\right),\hfill \end{array}\right.\end{array}$$

(7)

where ${\sigma }_1=\frac{4-\rho }{24}$, ${\sigma }_2=\frac{8+\rho }{12}$, ${\sigma }_3=\frac{1}{2h}$, ${\sigma }_4=\frac{2+\rho }{2h^2}$, ${\sigma }_5=-\frac{2+\rho }{h^2}$.

Temporal Approximation

Let $t^q=q\tau$, $q=0,1,\cdots ,Q$, while $\tau =\frac{T}{Q}$ is a time moving scale. The CFD approximation in the form of difference technique can be interpreted as

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\gamma }V(y,t^{p+1})=\frac{1}{\mathsf{\Gamma }(2-\gamma )}\sum _{p=0}^q{b}_p^{\gamma }\frac{V(y,t^{q-p+1})-V(y,t^{q-p})}{{\tau }^{\gamma }}+D^{q+1},\end{array}$$

(8)

$$\begin{array}{c}\hfill |D^{q+1}|\le D_1{\tau }^{2-\gamma },\end{array}$$

(9)

where $D_1$ is a constant and $b_p={(p+1)}^{1-\gamma }-p^{1-\gamma }$. The integral expression of Equation (1) can be explained as:

$$\begin{array}{ccc}\hfill {\int }_0^t{(t^{q+1},s)}^{\alpha -1}{V}_{yy}(y,s)ds& =& {\int }_0^{t^{q+1}}{s}^{\alpha -1}{V}_{yy}(y,t^{q+1}-s)ds,\hfill \\ & =& \sum _{p=0}^q{\int }_{t^p}^{t^{p+1}}{s}^{\alpha -1}{V}_{yy}(y,t^{q+1}-s)ds,\hfill \\ & =& \sum _{p=0}^q{V}_{yy}(y,t^{q-p+1}){\int }_{t^p}^{t^{p+1}}{s}^{\alpha -1}ds,\hfill \end{array}$$

$$\begin{array}{c}\hfill {\int }_0^t{(t^{q+1},s)}^{\alpha -1}{V}_{yy}(y,s)ds=\frac{{\tau }^{\alpha }}{\alpha }\sum _{p=0}^q{V}_{yy}(y,t^{q-p+1})[{(p+1)}^{\alpha }-p^{\alpha }]=\frac{{\tau }^{\alpha }}{\alpha }\sum _{p=0}^q{V}_{yy}(y,t^{q-p+1})b_p^{\alpha }.\end{array}$$

(10)

Lemma 1.

The $b_p^{\prime }s$ assure the following constrains [40]:

• $b_0^{\gamma }=1,b_0^{\alpha }=1.$
• $b_0^{\gamma }>b_1^{\gamma }>b_2^{\gamma }>\cdots >b_p^{\gamma },$ and $b_0^{\alpha }>b_1^{\alpha }>b_2^{\alpha }>\cdots >b_p^{\alpha },$$b_p^{\alpha },b_p^{\gamma }\to 0$ as $p\to \infty .$
• $b_p^{\gamma },b_p^{\alpha }>0$ for $p=0,1,\cdots ,q.$
• ${\sum }_{p=0}^q(b_p^{\gamma }-b_{p+1}^{\gamma })+b_{q+1}^{\gamma }=(1-b_1^{\gamma })+{\sum }_{p=1}^{q-1}(b_p^{\gamma }-b_{p+1}^{\gamma })+b_q^{\gamma }=1.$
• ${\sum }_{p=0}^q{b}_p^{\alpha }>1.$

Proof. All parts can be easily verified.

$$\begin{array}{ccc}\hfill \sum _{p=0}^q{b}_p^{\alpha }& =& \sum _{p=0}^q[{(p+1)}^{\alpha }-p^{\alpha }]\hfill \\ & =& (1^{\alpha }-0)+(2^{\alpha }-1^{\alpha })+(3^{\alpha }-2^{\alpha })+\cdots +({(q+1)}^{\alpha }-q^{\alpha })\hfill \\ & =& {(q+1)}^{\alpha }>1,forq\ge 1.\hfill \end{array}$$

□

3. Derivation of the Procedure

We employ the ECBS and the CFD to address the proposed model. By plugging Equations (8) and (10) in (1), we obtain

$$\begin{array}{c}\hfill \frac{{\tau }^{-\gamma }}{\mathsf{\Gamma }(2-\gamma )}\sum _{p=0}^q{b}_p^{\gamma }[V^{q-p+1}-V^{q-p}]+{\left(V{V}_y\right)}^{q+1}=\frac{{\tau }^{\alpha }}{\alpha }\sum _{p=0}^q{V}_{yy}^{q-p+1}{b}_p^{\alpha }+G^{q+1}.\end{array}$$

(11)

Linearize the non-linear term as [41]:

$${\left(V{V}_y\right)}^{q+1}=V^{q+1}{V}_y^q+V^q{V}_y^{q+1}-{\left(V{V}_y\right)}^q.$$

(12)

By plugging Equation $\left(12\right)$ into $\left(11\right)$, we have

$$\begin{array}{c}\hfill \frac{-{\tau }^{-\gamma }}{\mathsf{\Gamma }(2-\gamma )}\sum _{p=0}^q{b}_p^{\gamma }[V^{q-p+1}-V^{q-p}]+V^{q+1}{V}_y^q+V^q{V}_y^{q+1}-{\left(V{V}_y\right)}^q=\frac{{\tau }^{\alpha }}{\alpha }\sum _{p=0}^q{V}_{yy}^{q-p+1}{b}_p^{\alpha }+G^{q+1}.\end{array}$$

Using expression $\left(6\right)$ in the above equation, we obtain

$$\begin{array}{c}\frac{{\tau }^{-\gamma }}{\mathsf{\Gamma }(2-\gamma )}\sum _{p=0}^q{b}_p^{\gamma }\left[\sum _{i=-1}^{M+1}{\eta }_i^{q-p+1}{E}_i-\sum _{i=-1}^{M+1}{\eta }_i^{q-p}{E}_i\right]+\sum _{i=-1}^{M+1}{\eta }_i^{q+1}{E}_i\sum _{i=-1}^{M+1}{\eta }_i^q{E}_i^{\prime }+\sum _{i=-1}^{M+1}{\eta }_i^q{E}_i\sum _{i=-1}^{M+1}{\eta }_i^{q+1}{E}_i^{\prime }\hfill \\ \hfill -\sum _{i=-1}^{M+1}{\eta }_i^q{E}_i\sum _{i=-1}^{M+1}{\eta }_i^q{E}_i^{\prime }=\frac{{\tau }^{\alpha }}{\alpha }\sum _{p=0}^q{b}_p^{\alpha }\left[\sum _{i=-1}^{M+1}{\eta }_i^{q-p+1}{E}_i^{″}\right]+G^{q+1}.\end{array}$$

After some computation in the above expression, we get

$$\begin{array}{c}\hfill {\widehat{V}}^{q+1}+r{\widehat{V}}^q{\widehat{V}}_y^{q+1}+r{\widehat{V}}^{q+1}{\widehat{V}}_y^q-r{r}_1{\widehat{V}}_{yy}^{q+1}=b_q^{\gamma }{\widehat{V}}^0+r{\widehat{V}}^q{\widehat{V}}_y^q+\sum _{p=0}^{q-1}(b_q^{\gamma }-b_{q+1}^{\gamma }){\widehat{V}}^{q-p}+r{r}_1\sum _{p=1}^q{b}_q^{\alpha }{\widehat{V}}_{yy}^{q-p+1}+r{G}^{q+1},\end{array}$$

where $r={\tau }^{\gamma }\mathsf{\Gamma }(2-\gamma )$, $r_1=\frac{{\tau }^{\alpha }}{\alpha }.$ The above equation can be rewritten as:

$$\begin{array}{c}\left({\sigma }_1{\eta }_{i-1}^{q+1}+{\sigma }_2{\eta }_i^{q+1}+{\sigma }_1{\eta }_{i+1}^{q+1}\right)+r\left({\sigma }_1{\eta }_{i-1}^{q+1}+{\sigma }_2{\eta }_i^{q+1}+{\sigma }_1{\eta }_{i+1}^{q+1}\right)\left(-{\sigma }_3{\eta }_{i-1}^q+{\sigma }_3{\eta }_{i+1}^q\right)\hfill \\ +r\left({\sigma }_1{\eta }_{i-1}^q+{\sigma }_2{\eta }_i^q+{\sigma }_1{\eta }_{i+1}^q\right)\left(-{\sigma }_3{\eta }_{i-1}^{q+1}+{\sigma }_3{\eta }_{i+1}^{q+1}\right)-r{r}_1\left({\sigma }_4{\eta }_{i-1}^{q+1}+{\sigma }_5{\eta }_i^{q+1}+{\sigma }_4{\eta }_{i+1}^{q+1}\right)\\ =b_q^{\gamma }\left({\sigma }_1{\eta }_{i-1}^0+{\sigma }_2{\eta }_i^0+{\sigma }_1{\eta }_{i+1}^0\right)r\left({\sigma }_1{\eta }_{i-1}^q+{\sigma }_2{\eta }_i^q+{\sigma }_1{\eta }_{i+1}^q\right)\left(-{\sigma }_3{\eta }_{i-1}^q+{\sigma }_3{\eta }_{i+1}^q\right)+r{G}^{q+1}\\ \hfill +\sum _{p=0}^{q-1}(b_q^{\gamma }-b_{q+1}^{\gamma })\left({\sigma }_1{\eta }_{i-1}^{q-p}+{\sigma }_2{\eta }_i^{q-p}+{\sigma }_1{\eta }_{i+1}^{q-p}\right)+r{r}_1\sum _{p=0}^{q-1}{b}_{q+1}^{\alpha }\left({\sigma }_4{\eta }_{i-1}^{q-p}+{\sigma }_5{\eta }_i^{q-p}+{\sigma }_4{\eta }_{i+1}^{q-p}\right).\end{array}$$

(13)

The Equation $\left(13\right)$ can be converted into matrix form as:

$$A{\eta }^{q+1}=B\left(b_q^{\gamma }{\eta }^0+\sum _{p=0}^{q-1}(b_q^{\gamma }-b_{q+1}^{\gamma }){\eta }^{q-p}\right)+C\sum _{p=0}^{q-1}{b}_{q+1}^{\alpha }{\eta }^{q-p}+G.$$

(14)

The order of the system $\left(14\right)$ is $(M+1)\times (M+3)$. Two linear equations from the boundary conditions are required for a unique solution. To initiate the iteration on $\left(13\right)$, the corresponding initial conditions are applied:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\widehat{V}}_0^{\prime }=V^{\prime }\left(y_0\right),\hfill \\ {\widehat{V}}_i^0=V\left(y_i\right),i=0,1,2,\cdots ,M\hfill \\ {\widehat{V}}_M^{\prime }=V^{\prime }\left(y_M\right).\hfill \end{array}\right.\end{array}$$

(15)

As a result, $\left(15\right)$ transforms to a matrix system:

$$\begin{array}{c}\hfill G_1{\eta }^0=G_2,\end{array}$$

(16)

where

$$\begin{array}{c}\hfill G_1=\left[\begin{array}{ccccccc}-{\sigma }_3& 0& {\sigma }_3& 0& \dots & \dots & 0\\ {\sigma }_1& {\sigma }_2& {\sigma }_1& 0& \dots & \dots & 0\\ 0& {\sigma }_1& {\sigma }_2& {\sigma }_1& \dots & \dots & 0\\ ⋮& \dots & \ddots & \ddots & \ddots & \dots & ⋮\\ ⋮& \dots & \dots & \dots & {\sigma }_1& {\sigma }_2& {\sigma }_1\\ 0& \dots & \dots & \dots & -{\sigma }_3& 0& {\sigma }_3\end{array}\right]\end{array}$$

(17)

and $G_2={[V_0^{\prime }\left(y_0\right),V_0\left(y_0\right),\dots ,V_0\left(y_M\right),V_0^{\prime }\left(y_M\right)]}^T$.

4. Stability and Convergence Analysis

This section is devoted to analyzes the stability and convergence of the recommended technique.

Theorem 1.

The recommended technique of the problem FPIDE ((1)–(3)), is unconditionally stable.

Proof. The Neumann approach is employed to evaluate the stability of existing algorithm. Assume the difference expression in the form of Fourier series is

$${\mathsf{\Phi }}_k^q=V(y_k,t^q)-{\widehat{V}}_k^q={\psi }^q{e}^{ik\varphi h},$$

(18)

where $i=\sqrt{-1}$. ϕ and h are the mode number and moving scale in space direction respectively. The nonlinear expression $V{V}_y$ is linearized in this way by making V a constant $r_2$ in Equation (11), then we get the following equation by applying (18):

$$\begin{array}{c}\hfill {\psi }_k^{q+1}+r{r}_2{\left({\psi }_y\right)}_k^{q+1}-r{r}_1{\left({\psi }_{yy}\right)}_k^{q+1}=b_q^{\gamma }{\psi }_k^0+\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]{\psi }_k^{q-p}+r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }{\left({\psi }_{yy}\right)}_k^{q-p}.\end{array}$$

(19)

So, Equation (24) is explained as:

$$\begin{array}{c}{\psi }^{q+1}\left({\sigma }_1{e}^{i(k-1)\varphi h}+{\sigma }_2{e}^{ik\varphi h}+{\sigma }_1{e}^{i(k+1)\varphi h}\right)+r{r}_2{\psi }^{q+1}\left(-{\sigma }_3{e}^{i(k-1)\varphi h}+{\sigma }_3{e}^{i(k+1)\varphi h}\right)\hfill \\ -r{r}_1{\psi }^{q+1}\left({\sigma }_4{e}^{i(k-1)\varphi h}+{\sigma }_5{e}^{ik\varphi h}+{\sigma }_4{e}^{i(k+1)\varphi h}\right)=b_q^{\gamma }{\psi }^0\left({\sigma }_1{e}^{i(k-1)\varphi h}+{\sigma }_2{e}^{ik\varphi h}+{\sigma }_1{e}^{i(k+1)\varphi h}\right)\\ +\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]\left({\sigma }_1{e}^{i(k-1)\varphi h}+{\sigma }_2{e}^{ik\varphi h}+{\sigma }_1{e}^{i(k+1)\varphi h}\right){\psi }^{q-p}\\ \hfill +r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }{\psi }^{q+1}\left({\sigma }_4{e}^{i(k-1)\varphi h}+{\sigma }_5{e}^{ik\varphi h}+{\sigma }_4{e}^{i(k+1)\varphi h}\right).\end{array}$$

Rearranging the above equation, we obtain

$$\begin{array}{c}\left[({\sigma }_2+2{\sigma }_{1}cos\left(\varphi h\right))-2ir{r}_2{\sigma }_{3}sin\left(\varphi h\right)+r{r}_1({\sigma }_5+2{\sigma }_{4}cos\left(\varphi h\right))\right]{\psi }^{q+1}=b_q^{\gamma }({\sigma }_2+2{\sigma }_{1}cos\left(\varphi h\right)){\psi }^0\hfill \\ \hfill +\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]({\sigma }_2+2{\sigma }_{1}cos\left(\varphi h\right)){\psi }^{q-p}+r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }({\sigma }_5+2{\sigma }_{4}cos\left(\varphi h\right)).\end{array}$$

By applying the values of ${\sigma }_k^{\prime }s$, we achieve

$$\begin{array}{c}\left[\left(1+\frac{\rho -4}{6}{sin}^2\left(\varphi h\right)\right)+\frac{2r{r}_1}{h^2}(2+\rho ){sin}^2\left(\varphi h\right)-\frac{r{r}_{2}i}{h}sin\left(\varphi h\right)\right]{\psi }^{q+1}=b_q^{\gamma }\left(1+\frac{\rho -4}{6}{sin}^2\left(\varphi h\right)\right){\psi }^0\hfill \\ \hfill +\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]\left(1+\frac{\rho -4}{6}{sin}^2\left(\varphi h\right)\right){\psi }^{q-p}-\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }\left(\frac{2r{r}_1}{h^2}(2+\rho ){sin}^2\left(\varphi h\right)\right),\end{array}$$

Implies that

$$[{\beta }_1+{\beta }_2-i{\beta }_3]{\psi }^{q+1}={\beta }_1{b}_q^{\gamma }{\psi }^0+{\beta }_1\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]{\psi }^{q-p}-{\beta }_2\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }{\psi }^{q-p},$$

(20)

where ${\beta }_1={\sigma }_2+2{\sigma }_{1}cos\left(\varphi h\right),$ ${\beta }_2=\frac{2r{r}_1}{h^2}(2+\rho ){sin}^2\left(\varphi h\right),$ and ${\beta }_3=\frac{r{r}_2}{h}sin\left(\varphi h\right).$ □

From Equation (20), we acquire

$$|{\psi }^{q+1}{|}^2=\frac{{\left[|{\beta }_1\left(b_q^{\gamma }{\psi }^0+{\sum }_{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]{\psi }^{q-p}\right)-{\beta }_2{\sum }_{p=0}^{q-1}{b}_{p+1}^{\alpha }{\psi }^{q-p}|\right]}^2}{|{({\beta }_1+{\beta }_2)}^2+{\left({\beta }_3\right)}^2|}.$$

(21)

For $q=0$, Equation (20) becomes

$$\begin{array}{ccc}\hfill |{\psi }^1{|}^2& =& \frac{|{\beta }_1{b}_0^{\gamma }{\psi }^0{|}^2}{|{({\beta }_1+{\beta }_2)}^2+{\left({\beta }_3\right)}^2|}\le {\left|{\psi }^0\right|}^2,\hfill \\ \hfill |{\psi }^1|& \le & |{\psi }^0|.\hfill \end{array}$$

Suppose that it is true for $|{\psi }^q|\le |{\psi }^0|,$ it must be satisfied for $|{\psi }^{q+1}|$. From (20), we have

$$\begin{array}{ccc}\hfill [{\beta }_1+{\beta }_2-i{\beta }_3]{\psi }^{q+1}& =& {\beta }_1{b}_q^{\gamma }{\psi }^0+{\beta }_1\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]{\psi }^{q-p}-{\beta }_2\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }{\psi }^{q-p},\hfill \\ & \le & \frac{{\beta }_1{b}_q^{\gamma }{\psi }^0+{\beta }_1{\sum }_{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]{\psi }^{q-p}}{[{\beta }_1+{\beta }_2-i{\beta }_3]},\hfill \\ \hfill |{\psi }^{q+1}|& \le & \frac{|{\beta }_1|b_q^{\gamma }|{\psi }^0|+|{\beta }_1|{\sum }_{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]\left|{\psi }^{q-p}\right|}{\sqrt{{({\beta }_1+{\beta }_2)}^2+{\left({\beta }_3\right)}^2}},\hfill \\ & \le & \frac{1}{\sqrt{{({\beta }_1+{\beta }_2)}^2+{\left({\beta }_3\right)}^2}}\left[(b_0^{\gamma }-b_1^{\gamma })+(b_1^{\gamma }-b_2^{\gamma })+\cdots +(b_{q-1}^{\gamma }-b_q^{\gamma })+b_q^{\gamma }\right]\left|{\psi }^0\right|\hfill \\ & =& |{\psi }^0|.\hfill \end{array}$$

Therefore, for every $q\ge 0,$ we achieve

$$|{\psi }^{q+1}|\le |{\psi }^0|.$$

(22)

From Equations (18) and (22), we have

$${\mathsf{\Phi }}^{q+1}\le {\mathsf{\Phi }}^0,\forall q\ge 0.$$

(23)

Hence, the FPIDE with the suggested approximation is unconditionally stable.

Theorem 2.

Let $V(y_i,t^q)$ be the exact solution of the Equations ((1)–(3)) and ${\widehat{V}}^q$ be the time discrete solution of the assumed problem, then

$$\begin{array}{c}\hfill \parallel {\mathsf{\Psi }}^{k+1}\parallel \le D_1{\tau }^{2-\gamma },\end{array}$$

(24)

where ${\gamma }^{q+1}=V(y_i,t^{q+1})-{\widehat{V}}^{q+1}$.

Proof. Take V be a $r_2$ constant in Equation (11) by linearizing the nonlinear expression, we obtain the difference of exact and time discrete solution as shown below:

$$\begin{array}{c}\hfill {\mathsf{\Psi }}^{q+1}+r{r}_2{\left({\mathsf{\Psi }}_y\right)}^{q+1}-r{r}_1{\left({\mathsf{\Psi }}_{yy}\right)}^{q+1}=b_q^{\gamma }{\mathsf{\Psi }}^0+\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]{\mathsf{\Psi }}^{q-p}+r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }{\left({\mathsf{\Psi }}_{yy}\right)}^{q-p}+D^{q+1}.\end{array}$$

For $q=0$, we have

$$\begin{array}{c}\hfill {\mathsf{\Psi }}^1+r{r}_2{\left({\mathsf{\Psi }}_y\right)}^1-r{r}_1{\left({\mathsf{\Psi }}_{yy}\right)}^1=b_0^{\gamma }{\mathsf{\Psi }}^0+D^1.\end{array}$$

As ${\mathsf{\Psi }}^0=0,$ we get

$$\begin{array}{c}\hfill <{\mathsf{\Psi }}^1,{\mathsf{\Psi }}^1>+r{r}_2<{\mathsf{\Psi }}_y^1,{\mathsf{\Psi }}^1>-r{r}_1<{\mathsf{\Psi }}_{yy}^1,{\mathsf{\Psi }}^1>=b_0^{\gamma }<{\mathsf{\Psi }}^0,{\mathsf{\Psi }}^1>+<D^1,{\mathsf{\Psi }}^1>.\end{array}$$

Using $<z_{xx},z>=-<z_x,z_x>$, $<z,z>={\parallel z\parallel }^2$, $<z_x,z>=-<z,z_y>$, and $<z,z_1>\le \parallel z\parallel \parallel z_1\parallel$, we get

$$\begin{array}{c}\hfill <{\mathsf{\Psi }}^1,{\mathsf{\Psi }}^1>=-r{r}_2<{\mathsf{\Psi }}_y^1,{\mathsf{\Psi }}^1>-r{r}_1<{\mathsf{\Psi }}_y^1,{\mathsf{\Psi }}_y^1>+<D^1,{\mathsf{\Psi }}^1>.\end{array}$$

$$\begin{array}{ccc}\hfill \parallel {\mathsf{\Psi }}^1{\parallel }^2& \le & \parallel D^1\parallel \parallel {\mathsf{\Psi }}^1\parallel ,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \parallel {\mathsf{\Psi }}^1\parallel & \le & \parallel D^1\parallel \le D_1{\tau }^{2-\gamma }.\hfill \end{array}$$

(26)

Suppose that (25), is true for $q=0,1,\cdots ,Q.$ Take inner product of Equation (25) with ${\mathsf{\Psi }}^{q+1}$, we have

$$\begin{array}{c}<{\mathsf{\Psi }}^{q+1},{\mathsf{\Psi }}^{q+1}>+r{r}_2<{\mathsf{\Psi }}_y^{q+1},{\mathsf{\Psi }}^{q+1}>-r{r}_1<{\mathsf{\Psi }}_{yy}^{q+1},{\mathsf{\Psi }}^{q+1}>=b_q^{\gamma }<{\mathsf{\Psi }}^0,{\mathsf{\Psi }}^{q+1}>\hfill \\ \hfill +\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]<{\mathsf{\Psi }}^{q-p},{\mathsf{\Psi }}^{q+1}>+r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }<{\mathsf{\Psi }}_{yy}^{q-p},{\mathsf{\Psi }}^{q+1}>+<D^{q+1},{\mathsf{\Psi }}^{q+1}>.\end{array}$$

Using $<z_{xx},z>=-<z_x,z_x>$, $<z_x,z>=-<z,z_x>$, we have

$$\begin{array}{c}<{\mathsf{\Psi }}^{q+1},{\mathsf{\Psi }}^{q+1}>=-r{r}_2<{\mathsf{\Psi }}_y^{q+1},{\mathsf{\Psi }}^{q+1}>-r{r}_1<{\mathsf{\Psi }}_y^{q+1},{\mathsf{\Psi }}_y^{q+1}>+b_q^{\gamma }<{\mathsf{\Psi }}^0,{\mathsf{\Psi }}^{q+1}>\hfill \\ \hfill +\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]<{\mathsf{\Psi }}^{q-p},{\mathsf{\Psi }}^{q+1}>-r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }<{\mathsf{\Psi }}_y^{q-p},{\mathsf{\Psi }}_y^{q+1}>+<D^{q+1},{\mathsf{\Psi }}^{q+1}>,\end{array}$$

implies that

$$\begin{array}{c}<{\mathsf{\Psi }}^{q+1},{\mathsf{\Psi }}^{q+1}>=-r{r}_2<{\mathsf{\Psi }}_y^{q+1},{\mathsf{\Psi }}^{q+1}>-r{r}_1<{\mathsf{\Psi }}_y^{q+1},{\mathsf{\Psi }}_y^{q+1}>+b_q^{\gamma }<{\mathsf{\Psi }}^0,{\mathsf{\Psi }}^{q+1}>\hfill \\ \hfill +\sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]<{\mathsf{\Psi }}^{q-p},{\mathsf{\Psi }}^{q+1}>-r{r}_1\sum _{p=0}^{q-1}{b}_{p+1}^{\alpha }<{\mathsf{\Psi }}_y^{q-p},{\mathsf{\Psi }}_y^{q+1}>+<D^{q+1},{\mathsf{\Psi }}^{q+1}>,\end{array}$$

By applying $<z,z>={\parallel z\parallel }^2$, $<z,z_1>\le \parallel z\parallel \parallel z_1\parallel$, we obtain

$$\begin{array}{ccc}\hfill \parallel {\mathsf{\Psi }}^{q+1}{\parallel }^2& \le & \sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]\parallel {\mathsf{\Psi }}^{q-p}\parallel \parallel {\mathsf{\Psi }}^{q+1}\parallel +\parallel D^{q+1}\parallel \parallel {\mathsf{\Psi }}^{q+1}\parallel ,\hfill \\ \hfill \parallel {\mathsf{\Psi }}^{q+1}\parallel & \le & \sum _{p=0}^{q-1}[b_p^{\gamma }-b_{p+1}^{\gamma }]\parallel {\mathsf{\Psi }}^{q-p}\parallel +\parallel D^{q+1}\parallel .\hfill \end{array}$$

Utilizing the Gronwall’s inequality we get

$$\begin{array}{c}\hfill \parallel {\mathsf{\Psi }}^{q+1}\parallel \le (\parallel D^{q+1}\parallel +(1-b_1){\mathsf{\Psi }}^q)exp\left(\sum _{p=0}^{q-1}[b_p-b_{p+1}]\right)\le D_1{\tau }^{2-\gamma }.\end{array}$$

□

5. Numerical Implementation

Here, we include the simulation results of the problem (1)–(3) by employing the suggested algorithm. Maximum errors, $L_2$ errors and order of convergence between exact and computed solutions are employed to demonstrate the reliability of the applied model. The following formula can be utilized in order to calculate the convergence order numerically.

$$Order=\frac{log\left(L_{\infty }\left(Q_i\right)\right)-log\left(L_{\infty }\left(Q_{i+1}\right)\right)}{log\left(2\right)},$$

(27)

where $L_{\infty }\left(Q_i\right)$ and $L_{\infty }\left(Q_{i+1}\right)$ are the maximum errors at $Q_i$ and $Q_{i+1}$ respectively.

Example 1.

Consider the modeled problem (1)–(3) with the initial condition and source term are shown below:

$${}_0^C{D}_t^{\gamma }V(y,t)+V{V}_y={\int }_0^t{(t-s)}^{\alpha -1}{V}_{yy}(y,s)ds+G(y,t),$$

with

$$V(y,0)=y^2{(1-y)}^2,$$

where

$$G(y,t)=\frac{\mathsf{\Gamma }\left(\frac{7}{2}\right)}{\mathsf{\Gamma }(\frac{7}{2}-\gamma )}{t}^{\frac{5}{2}-\gamma }{y}^2{(1-y)}^2-2\left(\frac{1}{\alpha }{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(\frac{7}{2}\right)\mathsf{\Gamma }\left(\alpha \right)}{\mathsf{\Gamma }\left(\frac{7}{2}\right)+\alpha }{t}^{\frac{5}{2}+\alpha }\right)(1-6y+6y^2)+2{(1+t^{\frac{5}{2}})}^2(1-2y)y^3{(1-y)}^3,$$

and analytical solution is $V(y,t)=(1+t^{\frac{5}{2}})y^2{(1-y)}^2$.

Table 1 shows the $L_{\infty }$, $L_2$ errors and order of the recommended technique for $\gamma =0.25,0.5$, $\alpha =0.15$, $h=\frac{1}{1024}$ at various $\tau$. Table 2 presents the comparison of the $L_2$ errors with the results given by [16] and the order of convergence at different h. In Table 3, the absolute errors are demonstrated for the $\alpha =0.15$ and different $\gamma$ at $T=1$. Figure 1 illustrates the 3D error plot of (1) for $\gamma =0.5$, $\alpha =0.05$, when $M=16$ and $Q=16$ at $T=1$. Figure 2 shows the compatibility of exact and computed values for $\gamma =0.5$, $\alpha =0.05$. In Figure 3, we present the approximated and exact graph of Example 1, for $M=50$, $Q=100$, $\gamma =0.5$, and $\alpha =0.01$ at $T=1$. Graphs show that the close relationship between the exact and calculated values.

Table 1. The $L_{\infty }$, $L_2$ errors of Example 1 for $\alpha =0.15$, $h=\frac{1}{1024}$, at $T=1$.

$\mathit{\gamma }$	$\mathit{\tau }$			ECBS
		${\mathit{L}}_2$ [16]	${\mathit{L}}_2$	${\mathit{L}}_{\mathit{\infty }}$	Order
0.25	1/4	0.000338928	0.000102331	0.005061940	…
0.25	1/8	0.000095387	0.000031934	0.001507530	1.74750
0.25	1/16	0.000026007	0.000008542	0.000445685	1.75809
0.25	1/32	0.000006788	0.000001882	0.000133631	1.73777
0.5	1/4	0.000336809	0.000102183	0.00505510	…
0.5	1/8	0.000050628	0.000031976	0.00151014	1.74750
0.5	1/16	0.000025630	0.000008178	0.00045565	1.72618
0.5	1/32	0.000006784	0.000001955	0.00013491	1.75595

Table 2. The $L_{\infty }$, $L_2$ errors of Example 1 for $\alpha =0.15$, $\tau =\frac{1}{1000}$, at $T=1$.

$\mathit{\gamma }$	h			ECBS
		${\mathit{L}}_2$ [16]	${\mathit{L}}_2$	${\mathit{L}}_{\mathit{\infty }}$	Order
0.5	1/4	0.0223389	0.01822370	0.0549348	…
0.5	1/8	0.0055991	0.00345180	0.0136426	2.00960
0.5	1/16	0.0014002	0.00078340	0.0033125	2.04213
0.5	1/32	0.0003501	0.00002505	0.00080164	2.04690

Table 3. Absolute errors Example 1 for $\alpha =0.15$, at various knots.

y	$\mathit{\gamma }=0.25$	$\mathit{\gamma }=0.50$	$\mathit{\gamma }=0.75$	$\mathit{\gamma }=0.95$
0.1	0.0002278	0.0002393	0.0002611	0.0000426
0.2	0.0018783	0.0019005	0.0019430	0.0011812
0.3	0.0035717	0.0036034	0.0036639	0.0023206
0.4	0.0042866	0.0043257	0.0043997	0.0026410
0.5	0.0034757	0.0035196	0.0036008	0.0017125
0.6	0.0011975	0.0012421	0.0013230	0.0003752
0.7	0.0017931	0.0017525	0.0016805	0.0029206
0.8	0.0040788	0.0040474	0.0039930	0.0046428
0.9	0.0038964	0.0038792	0.0038497	0.0039922

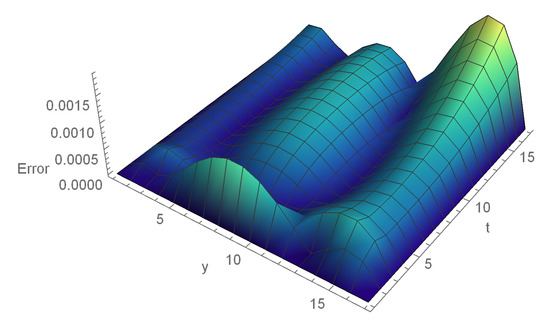
Figure 1. Error graph of Example 1 at $\gamma =0.5$ and $\alpha =0.05$.

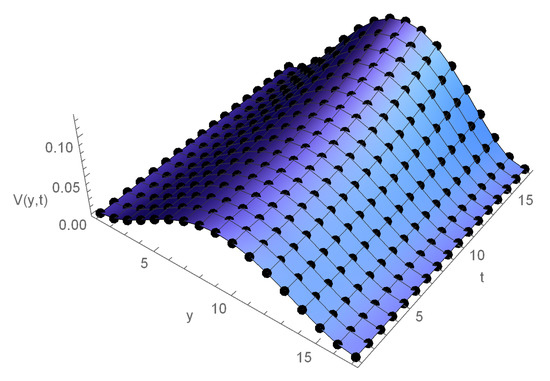
Figure 2. Comparison of the exact (dots) and the computed values (solid lines) of Example 1 at $\gamma =0.5$ and $\alpha =0.05$.

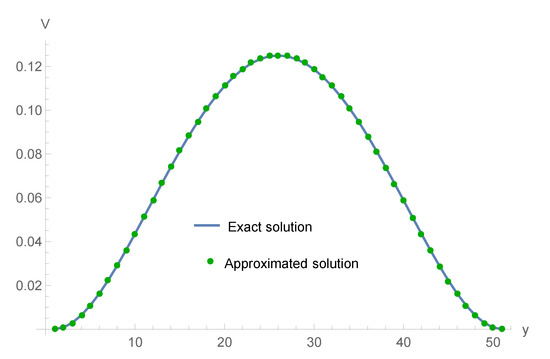
Figure 3. Comparison of the exact and the computed values at $\gamma =0.5$ and $\alpha =0.01$.

Example 2.

Take the FPIDE with

$$V(y,0)=sin\left(\pi y\right),$$

and

$$\begin{array}{ccc}\hfill G(y,t)& =& \pi \left(\frac{\pi }{\alpha }{t}^{\alpha }-4t^{3}cos\left(2\pi y\right)\right)sin\left(\pi y\right)+\left(\frac{\pi }{2}-\frac{12}{\mathsf{\Gamma }(4-\gamma )}{t}^{3-\gamma }-2\pi t^{3}cos\left(\pi y\right)-\frac{48{\pi }^2\gamma \left(\alpha \right)}{\mathsf{\Gamma }(\alpha +4)}{t}^{3+\alpha }\right)\hfill \\ & +& (8\pi t^{6}cos\left(2\pi y\right))sin\left(2\pi y\right).\hfill \end{array}$$

The analytic solution is

$$V(y,t)=sin\left(\pi y\right)-2t^{3}sin\left(2\pi y\right).$$

Table 4 demonstrates the $L_2$ and order in time side $\alpha =0.15$, $\gamma =0.5$ and various $\tau$ at $T=1$. In Table 5, the comparison of $L_2$ errors of 2 for $\alpha =0.15$, $\gamma =0.5$, $\tau =\frac{1}{1000}$ at different h. In Table 6, we present the absolute errors for $\alpha =0.05$ and several values of $\gamma$ at some knots, when $h=\frac{1}{100}$, $\tau =\frac{1}{100}$, and $T=1$. Therefore, we achieve the convergence order in time direction is ${\tau }^{2-\gamma }$, and space direction is 2. A comparison plot of computed and exact values has been displayed in Figure 4 for $\gamma =0.5$, $\alpha =0.15$ at $T=1$. Figure 5 depicts the errors of Example 2 for $\tau =\frac{1}{100}$, $\alpha =0.15$, $\gamma =0.5$ for $M=16$ and $Q=100$ at $T=1.$ The exact and calculated values are presented in Figure 6 for $N=70$, $Q=100$, $\gamma =0.5$, $\alpha =0.01$.

Table 4. The $L_2$ errors of Example 2 for $\alpha =0.15$, $h=\frac{1}{1024}$, at $T=1$.

$\mathit{\gamma }$	$\mathit{\tau }$	${\mathit{L}}_2$ [16]	${\mathit{L}}_2$	Order
0.5	1/4	0.0177409	0.0130166	…
0.5	1/8	0.0051229	0.0050567	1.489999
0.5	1/16	0.0014272	0.0011256	1.495493
0.5	1/32	0.0003866	0.0003048	1.497291

Table 5. The $L_2$ errors of Example 2 for $\alpha =0.15$, $\tau =\frac{1}{1000}$, at $T=1$.

$\mathit{\gamma }$	h	${\mathit{L}}_2$ [16]	${\mathit{L}}_2$	Order
0.5	1/4	0.3295713	0.2219332	…
0.5	1/8	0.0750875	0.0456438	1.489999
0.5	1/16	0.0183464	0.0058752	1.495493
0.5	1/32	0.0045605	0.0006886	1.497291

Table 6. Absolute errors of Example 2 for $\alpha =0.05$, at various connections.

y	$\mathit{\gamma }=0.25$	$\mathit{\gamma }=0.50$	$\mathit{\gamma }=0.75$	$\mathit{\gamma }=0.95$
0.1	0.0237447	0.0216525	0.0224432	0.0224217
0.2	0.0364358	0.0332549	0.0344475	0.0344188
0.3	0.0390615	0.0364304	0.0373676	0.0373676
0.4	0.0391821	0.0387213	0.0388031	0.0388078
0.5	0.0363214	0.0389181	0.0377829	0.0378141
0.6	0.0214206	0.0267798	0.0245592	0.0246163
0.7	0.0062788	0.0004300	0.0256691	0.0022242
0.8	0.0292914	0.0232263	0.0039930	0.0255941
0.9	0.0270044	0.0234284	0.0248600	0.0248123

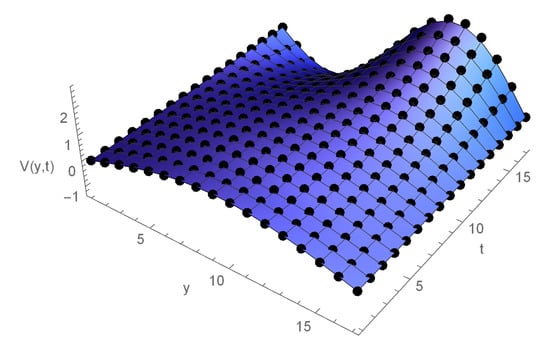
Figure 4. A Comparison plot (dots show the exact solution while the solid lines illustrate approximated solution) of Example 2 at $\gamma =0.5$ and $\alpha =0.15$.

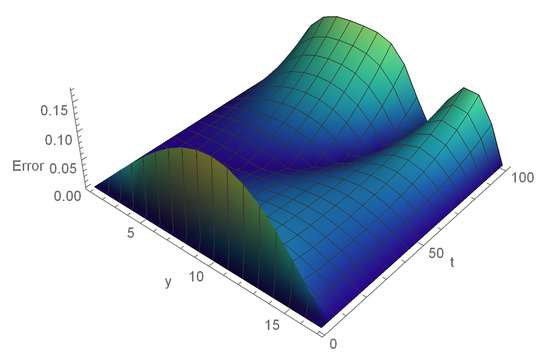
Figure 5. Error graph of Example 2 for $\alpha =0.15$, $N=16$ at $T=1$.

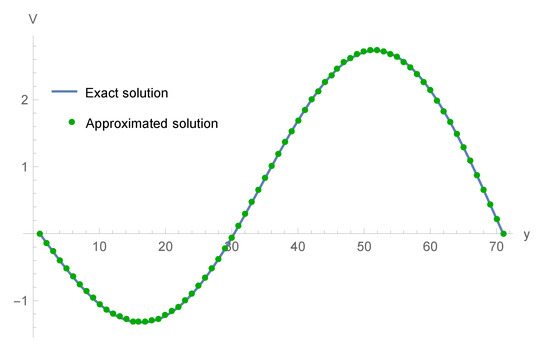
Figure 6. Comparison of the exact and the computed values of Example 2 at $\gamma =0.5$ and $\alpha =0.01$.

6. Conclusions

In this manuscript, the ECBS collocation strategy is successfully described for the computed solutions of the nonlinear FPIDE with a weakly singular kernel. The CFD is approximated in terms of the finite difference technique. The discretized form of the CFD is applied to the time direction while the ECBS is utilized in the space dimension. In addition, the stability analysis and convergence analysis of the implemented algorithm is also presented to check the method is stable and convergent. The convergence order is demonstrated as $({\tau }^{2-\gamma }+h^2)$, which is consistent with the theoretical results. Furthermore, The computational outcomes have been compared with the results given by [16] and some comparative findings demonstrate the effectiveness of the proposed collocation algorithm. The proposed technique can be implemented on the linear FPIDE model and the other linear and nonlinear second-order FPDEs. The suggested method can be extended for the higher-order hybrid and memory differential equations.