Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator
Abstract
:1. Introduction
2. Definitions
3. Existence of Solution of Fractional Diffusion Equation Using Yang–Abdel–Cattani Derivative Operator
4. -HATM Solution of Nonlinear Time-Fractional Diffusion Equation
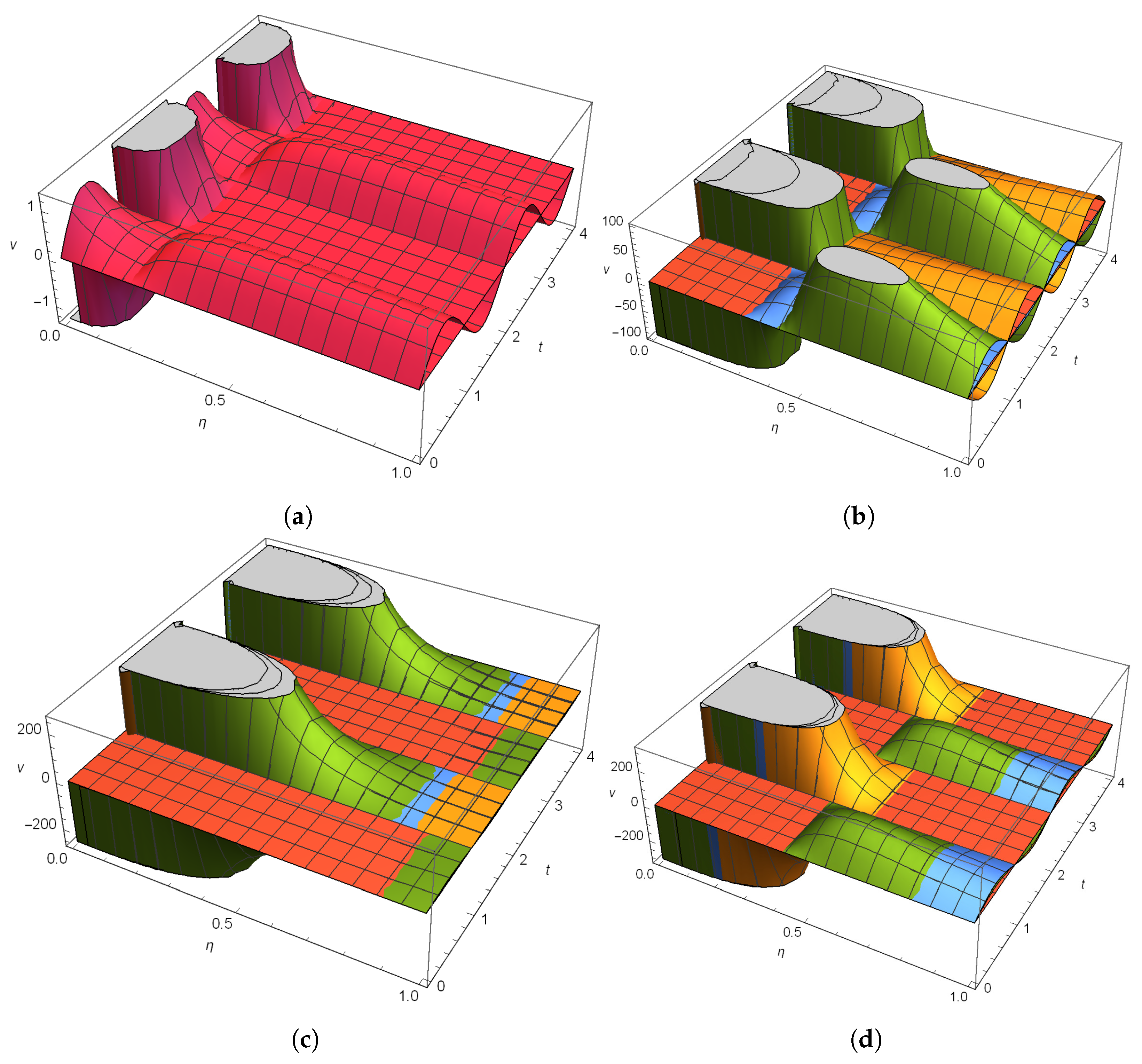
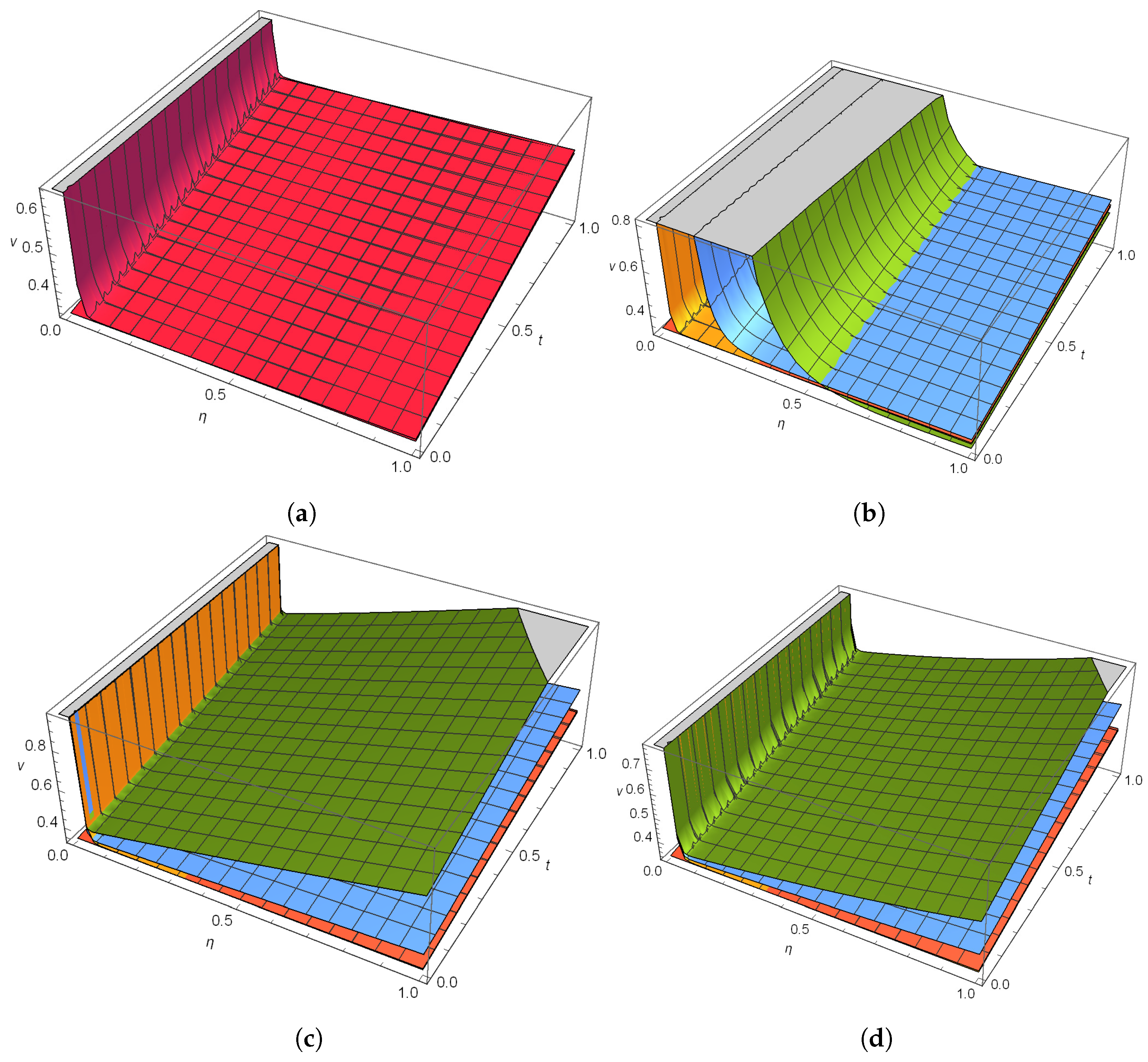
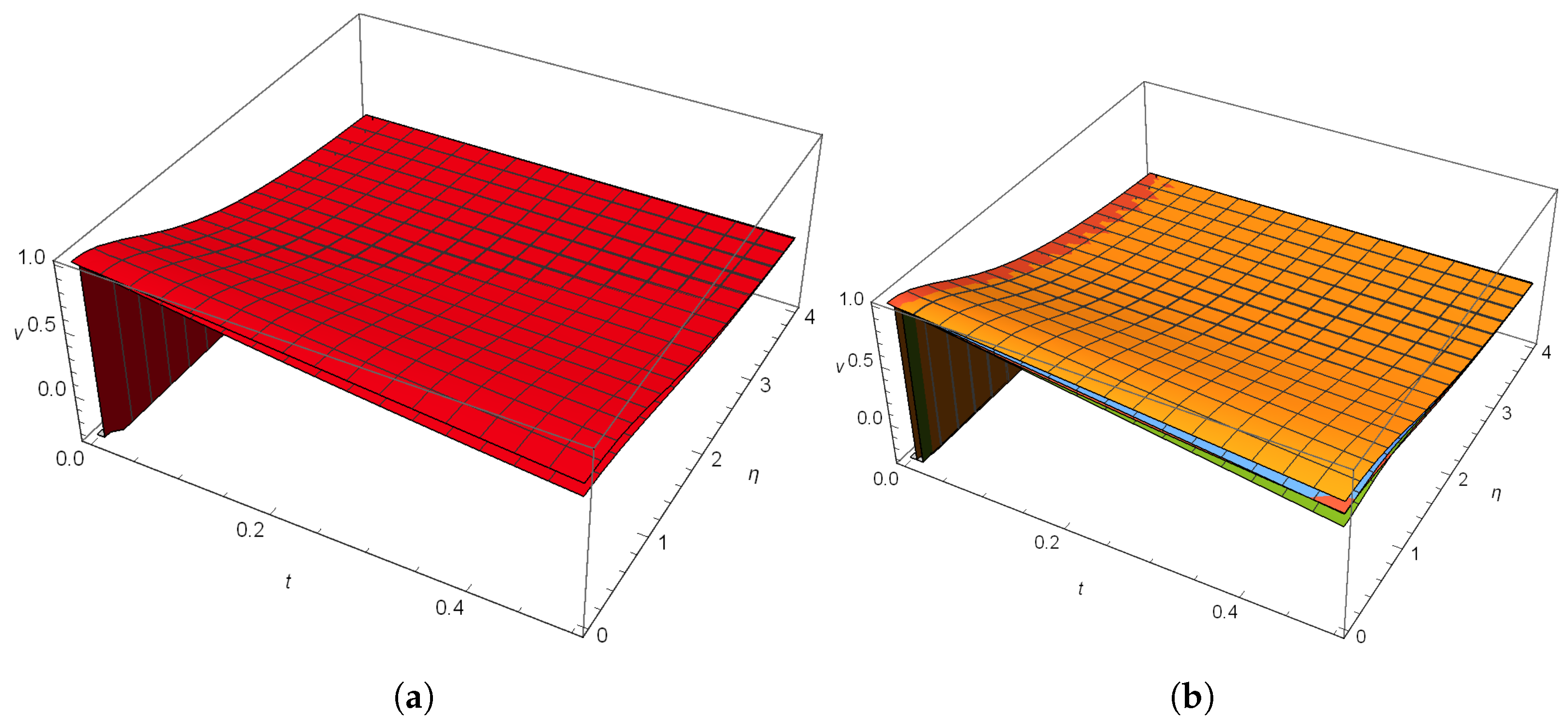
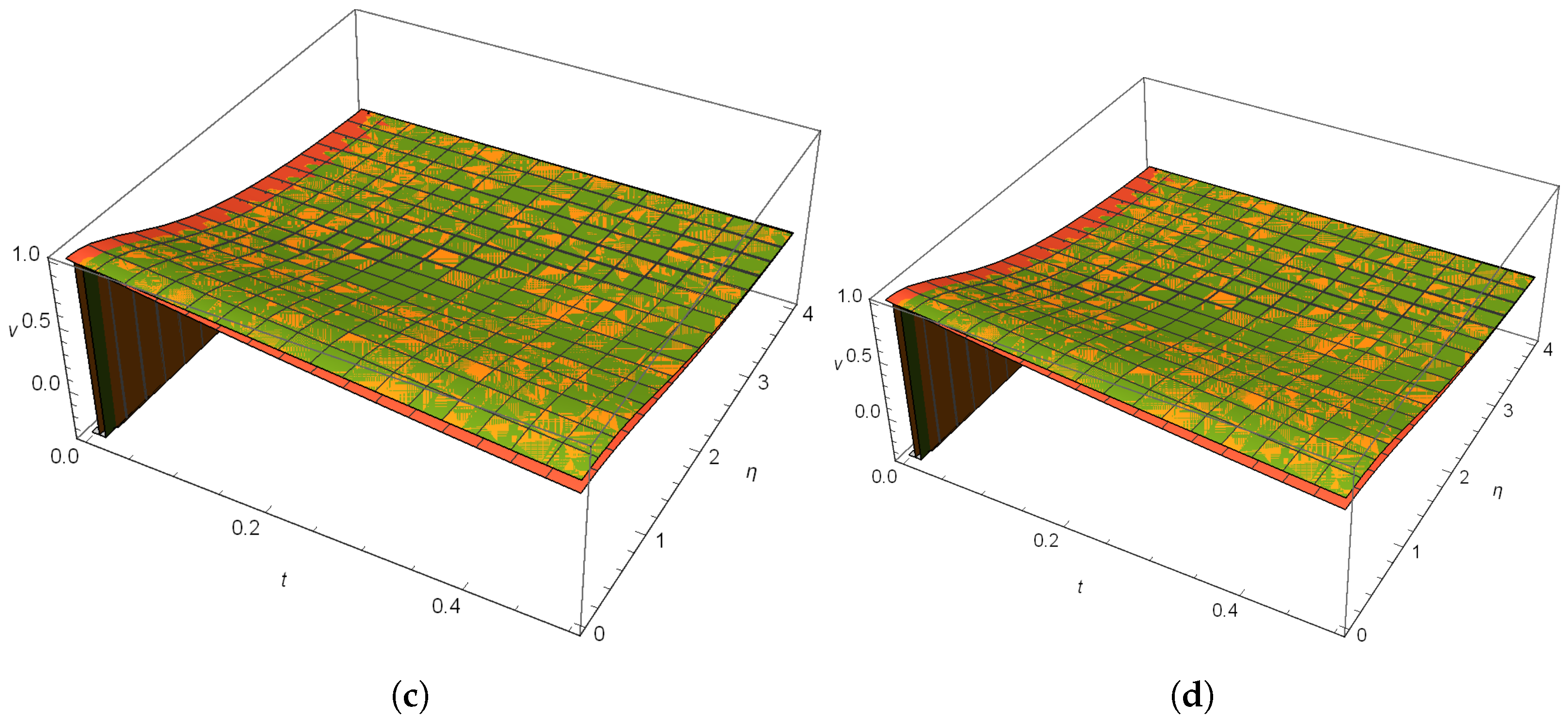
4.1. Case 1
4.2. Case 2
4.3. Case 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; A Wiley-Interscience Publication; John Wiley and Sons, Inc.: New York, NY, USA, 1993; p. xvi+366. ISBN 0-471-58884-9. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; With an Annotated Chronological Bibliography by Bertram Ross; Academic Press: New York, NY, USA; London, UK,, 1974; Volume 111, p. xiii+234. ISBN 9780125255509. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204, p. xvi+523. ISBN 978-0-444-51832-3. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press, Inc.: San Diego, CA, USA, 1999; Volume 198, p. xxiv+340. ISBN 0-12-558840-2. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2014; p. x+293. ISBN 978-981-4579-89-6. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012; ISBN 13 9781938576010. [Google Scholar]
- Caputo, M.; Fabrizio, M. A New Definition of Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and nonsingular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discret. Contin. Dyn. Syst.-S 2020, 13, 709–722. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J. General Fractional Derivatives: Theory, Methods and Applications; Chapman and Hall/ CRC: Boca Raton, FL, USA, 2019; ISBN 9781138336162. [Google Scholar]
- Yang, X.J.; Gao, F.; Ju, Y. General Fractional Derivatives with Applications in Viscoelasticity; Academic Press: Cambridge, MA, USA, 2020; ISBN 9780128172087. [Google Scholar]
- Yang, X.J.; Abdel-Aty, M.; Cattani, C. A new general fractional order derivative with Rabotnov fractional-exponential kernel applied to model the anomalous heat. Therm. Sci. 2019, 23, 1677–1681. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A. On the new fractional derivative and application to non-linear Fisher’s reaction-diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Aguilar, J.P.; Korbel, J.; Luchko, Y. Application of the Fractional Diffusion Equation to Option Pricing and Risk Calculations. Mathematics 2019, 7, 796. [Google Scholar] [CrossRef] [Green Version]
- Sontakke, B.R.; Shelke, A.S. Appropriate Scheme for Time fractional Diffusion Equation and Its Applications. Glob. J. Pure Appl. Math. 2019, 13, 4333–4345. [Google Scholar]
- Constantinescu, C.D.; Ramirez, J.M.; Zhu, W.B. An application of fractional differential equations to risk theory. Math. Stochastics 2019, 23, 1001–1024. [Google Scholar] [CrossRef] [Green Version]
- Ali, K.K.; Osman, M.S.; Baskonus, H.C.; Elazabb, N.S.; İlhan, E. Analytical and numerical study of the HIV-1 infection of CD4+ T-cells conformable fractional mathematical model that causes acquired immunodeficiency syndrome with the effect of antiviral drug therapy. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Gao, W.; Ghanbari, B.; Baskonus, H.C. New numerical simulations for some real world problems with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2019, 128, 34–43. [Google Scholar] [CrossRef]
- Ghanbari, B.; Gómez-Aguilar, J.F. Modelling the dynamics of nutrient-phytoplankton-zooplankton system with variable-order fractional derivatives. Chaos Solitons Fractals 2018, 116, 114–120. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, S.; Samet, B.; Goufo, E.F.D. An analysis for heat equations arises in diffusion process using new Yang-Abdel-Aty-Cattani fractional operator. Math. Methods Appl. Sci. 2020, 1–19. [Google Scholar] [CrossRef]
- Jleli, M.; Kumar, S.; Kumar, R.; Samet, B. Analytical approach for time fractional wave equations in the sense of Yang-Abdel-Aty-Cattani via the homotopy perturbation transform method. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [CrossRef] [PubMed]
- Belmor, S.; Ravichandran, C.; Jarad, F. Nonlinear generalized fractional differential equations with generalized fractional integral conditions. J. Taibah Univ. Sci. 2020. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Fractional nonlinear dynamics of learning with memory. Non-Linear Dyn. 2020, 100, 1231–1242. [Google Scholar] [CrossRef]
- Shone, T.T.; Patra, A. Solution for non-linear fractional partial differential equations using fractional complex transform. Int. J. Appl. Comput. Math. 2019, 5, 90. [Google Scholar] [CrossRef]
- Tarasov, V.E. Exact solutions of Bernoulli and Logistic fractional differential equations with power law coefficients. Mathematics 2020, 8, 2231. [Google Scholar] [CrossRef]
- Dubey, R.S.; Goswami, P. Analytical solution of the nonlinear diffusion equation. Eur. Phys. J. Plus 2018, 133. [Google Scholar] [CrossRef]
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.196571 | 0.263464 | 0.263544 | ||
| 0.2 | 0.902091 | 0.0981688 | 0.098225 | ||
| 0.3 | 0.0303086 | 0.0361351 | 0.0366092 | ||
| 0.4 | 0.0165324 | 0.0131774 | 0.0136445 | ||
| 0.5 | 0.00463999 | 0.00507924 | 0.00508543 | ||
| 0.6 | 0.00134119 | 0.00188248 | 0.00189538 | ||
| 0.7 | 0.000591754 | 0.000645395 | 0.000706423 | ||
| 0.8 | 0.000208632 | 0.000240379 | 0.000263289 | ||
| 0.9 | 0.0000935588 | 0.0000971667 | 0.00009813 | ||
| 1.0 | 0.0000300947 | 0.0000351593 | 0.0000365738 |
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.362916 | 0.377039 | 0.377101 | ||
| 0.2 | 0.375416 | 0.377759 | 0.379237 | ||
| 0.3 | 0.379474 | 0.381023 | 0.381411 | ||
| 0.4 | 0.380159 | 0.383075 | 0.383622 | ||
| 0.5 | 0.382443 | 0.384292 | 0.3858872 | ||
| 0.6 | 0.387566 | 0.388041 | 0.388162 | ||
| 0.7 | 0.388769 | 0.390407 | 0.390493 | ||
| 0.8 | 0.39034 | 0.392672 | 0.392867 | ||
| 0.9 | 0.390757 | 0.395034 | 0.395285 | ||
| 1.0 | 0.405465 | 0.397722 | 0.397748 |
| t | |||||
|---|---|---|---|---|---|
| 0.1 | 0.842589 | 0.861515 | 0.882539 | ||
| 0.2 | 0.780412 | 0.805378 | 0.802101 | ||
| 0.3 | 0.698454 | 0.723338 | 0.728431 | ||
| 0.4 | 0.640023 | 0.64123 | 0.661101 | ||
| 0.5 | 0.589874 | 0.559094 | 0.599676 | ||
| 0.6 | 0.521176 | 0.553665 | 0.543718 | ||
| 0.7 | 0.462397 | 0.484287 | 0.492802 | ||
| 0.8 | 0.460085 | 0.45875 | 0.446521 | ||
| 0.9 | 0.428753 | 0.394834 | 0.404486 | ||
| 1.0 | 0.387562 | 0.330926 | 0.366333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malyk, I.V.; Gorbatenko, M.; Chaudhary, A.; Sharma, S.; Dubey, R.S. Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator. Fractal Fract. 2021, 5, 64. https://doi.org/10.3390/fractalfract5030064
Malyk IV, Gorbatenko M, Chaudhary A, Sharma S, Dubey RS. Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator. Fractal and Fractional. 2021; 5(3):64. https://doi.org/10.3390/fractalfract5030064
Chicago/Turabian StyleMalyk, Igor V., Mykola Gorbatenko, Arun Chaudhary, Shivani Sharma, and Ravi Shanker Dubey. 2021. "Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator" Fractal and Fractional 5, no. 3: 64. https://doi.org/10.3390/fractalfract5030064
APA StyleMalyk, I. V., Gorbatenko, M., Chaudhary, A., Sharma, S., & Dubey, R. S. (2021). Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator. Fractal and Fractional, 5(3), 64. https://doi.org/10.3390/fractalfract5030064






