Alternating Inertial and Overrelaxed Algorithms for Distributed Generalized Nash Equilibrium Seeking in Multi-Player Games

Abstract

This paper investigates the distributed computation issue of generalized Nash equilibrium (GNE) in a multi-player game with shared coupling constraints. Two kinds of relatively fast distributed algorithms are constructed with alternating inertia and overrelaxation in the partial-decision information setting. We prove their convergence to GNE with fixed step-sizes by resorting to the operator splitting technique under the assumptions of Lipschitz continuity of the extended pseudo-gradient mappings. Finally, one numerical simulation is given to illustrate the efficiency and performance of the algorithm.

1. Introduction

Game theory is the study of mathematical models for describing competition and cooperation interaction among intelligent rational decision-makers [1]. In the past few years, networked games have received increasing attention due to their wide applications in different areas such as competitive economy [2], power allocation in interference channel models [3,4], environmental pollution control [5], cloud computing [6], wireless communication [7,8,9], and adversarial classification [10,11].

The Nash equilibrium (NE) is a set of strategies where each player’s choice is its best response to the choices of the other players of the game [12]. An NE in games with shared coupling constraints is referred to as generalized Nash equilibrium (GNE) [13]. In order to compute the GNE, a great number of algorithms have been proposed [14,15,16,17,18], most of which depend on full-decision information, i.e., each player is assumed to have full access to all of the other players’ actions. However, such an assumption could be impractical in large-scale distributed networks [19,20]. To overcome this shortcoming, fully distributed algorithms under the partial-decision information setting have recently become a research topic that attracts recurring interest.

Under the partial-decision information setting, each player can communicate only with its neighbors (instead of all its opponents) via a certain communication graph. In this case, the player has no direct access to some necessary decision information involving its cost function. In order to make up for the missing information, the player estimates other players’ actions and exchanges its estimates with neighbors. Such an estimate would tend to be the real actions of players by designing an appropriate consensus protocol [21]. So far, some efforts have been devoted to the GNE seeking problem with partial-decision information. For example, an adaption of a fictitious play algorithm for large-scale games is introduced in [22], and information exchange techniques for aggregative games are studied in [23]. An operator-theoretic approach has been introduced to analyze GNE problems [16,21], under which the problem is cast as finding a zero of a sum of monotone operators through primal-dual analysis and show its convergence by reformulating it as a forward–backward fixed-point iteration.

Compared with the existing distributed algorithms for diminishing steps [24], the algorithm for fixed steps has the potential to exhibit a faster convergence [16]. Very recently, some distributed proximal algorithms and project-gradient algorithms have been proposed for seeking the GNE with fixed steps [16,25,26,27,28]. It is worth noting that most of the existing algorithms, under the partial-decision information setting, require that the extended pseudo-gradient mapping in the augmented space of actions and estimates is strictly/strongly monotone. Such an assumption seems strong and how to relax it becomes a technical difficulty. In this paper, we would like to investigate the GNE seeking algorithm under a mild assumption of the extended pseudo-gradient mapping, like [21].

In addition, some refined GNE seeking algorithms with inertia and relaxation have been proposed in ([16], [Alg. 6.1]), ([29], [Alg. 2]) and ([25], [Alg. 3]) to accelerate the convergence to GNE. Although the fast convergence of the mentioned algorithms has been validated numerically, more computation resources are inevitably required at each iteration. Note that the computation resources could be limited and expensive in many situations. Inspired by the above discussion, in this paper, we combine a projection based algorithm via a doubly augmented operator splitting from the work [21] with the inertia/overrelaxation idea from the paper [25]. Specifically, we design distributed GNE seeking algorithms to balance the convergence rate and computation consumption in games with shared coupling constraints under a partial-decision information setting. Two kinds of fully distributed algorithms, i.e., alternating inertial algorithms and alternating overrelaxed algorithms, are proposed with fixed step-sizes. Their convergence to the GNE are guaranteed under a mild assumption on the extended pseudo-gradient mappings, compared to [26], by using the Karush–Kuhn–Tucker (KKT) conditions of an optimization problem and variational inequality. Finally, a numerical example is provided to show the effectiveness of our algorithms that are validated numerically to have a relatively fast convergence rate.

The remainder of the paper is organized as follows. In Section 2, we introduce some notations and backgroud theory. Section 3 describes the problem that we are interested in, formulates it into mathematical model, and rewrites the game into a problem of finding the solution of the stochastic variational inequality (SVI). In Section 4, we propose two alternating fully distributed GNE seeking algorithms under a partial-decision information setting and assumptions to guarantee convergence; the convergence analysis is also presented in this section. We present numerical results in Section 5 and finally conclude in Section 6.

Notations: Let ${\mathbf{R}}^m\left({\mathbf{R}}_{+}^m\right)$ represent an m-dimensional (non-negative) Euclidean space. ${\mathbf{0}}_n\in {\mathbf{R}}^n$ is an $n-$ dimensional vector with all elements equal to $0,$ and $I_m\in {\mathbf{R}}^{m\times m}$ is the identity matrix with $m\times m$ dimension. ${\mathbf{1}}_N$ denotes the N-dimension column vector with all elements equal to 1. We denote ${\mathsf{\Omega }}_1\times \cdots \times {\mathsf{\Omega }}_n$ or ${\prod }_{i=1}^n{\mathsf{\Omega }}_i$ as the Cartesian product of the sets ${\mathsf{\Omega }}_i,i=1,\cdots ,n$. For given n column vectors $x_1,\cdots ,x_n$, $\mathrm{col}(x_1,\cdots ,x_n)={[x_1^{\top },\cdots ,x_n^{\top }]}^{\top }$. Let ${\left[x\right]}_k$ denote the k-th element in column vector x, let $\langle x,y\rangle =x^{\top }y$ denote the inner product of $x,y$, and $\parallel x\parallel =\sqrt{x^{\top }x}$ denotes the norm induced by the inner product $\langle ·,·\rangle$. $\mathsf{\Phi }\succ 0$ stands for a symmetric positive definite matrix. Similarly, the $\mathsf{\Phi }$-induced product is ${\langle x,y\rangle }_{\mathsf{\Phi }}=\langle \mathsf{\Phi }x,y\rangle$, and the $\mathsf{\Phi }$-induced norm is ${\parallel x\parallel }_{\mathsf{\Phi }}=\sqrt{\langle \mathsf{\Phi }x,x\rangle }.$⊗ is the Kronecker product, and $diag(A_1,\cdots ,A_n)$ denotes the block diagonal matrix with $A_1,\cdots ,A_N$ on its diagonal. Suppose $A\in {\mathbf{R}}^{m\times n}$, then ${\parallel A\parallel }_{\infty }=max\{{\sum }_{k=1}^n|{\left[A_i\right]}_{1k}|,\cdots ,{\sum }_{k=1}^n|{\left[A_i\right]}_{mk}\left|\right\},$ where ${\left[A_i\right]}_{jk}$ denotes the element of $A_i$ in the j-th row and k-th column.

2. Preliminary

2.1. Operator Theory

The following concepts are reviewed from [30]. Let $\mathfrak{A}:{\mathbf{R}}^m\to 2^{{\mathbf{R}}^m}$ be a set-valued operator. Denote $Id$ as the identity operator, i.e., $Id\left(x\right)=x$. The graph of $\mathfrak{A}$ is $gra\mathfrak{A}=\{(x,u)\in {\mathbf{R}}^m\times {\mathbf{R}}^m|u\in \mathfrak{A}x\}$. The zero set of operator $\mathfrak{A}$ is $zer\mathfrak{A}=\{x\in {\mathbf{R}}^m|\mathbf{0}\in \mathfrak{A}x\}$. Define the resolvent of operator $\mathfrak{A}$ as $R_{\mathfrak{A}}={(Id+\mathfrak{A})}^{-1}$. An operator $\mathfrak{A}$ is called monotone if $\forall (x,u),\forall (y,v)\in gra\mathfrak{A}$, we have $\langle x-y,u-v\rangle \ge 0$. Moreover, it is maximally monotone if $gra\mathfrak{A}$ is not strictly contained in the graph of any other monotone operator, i.e., for every $(x,u)\in {\mathbf{R}}^m\times {\mathbf{R}}^m,(x,u)\in gra\mathfrak{A}\iff \forall (y,v)\in gra\mathfrak{A},\langle x-y,u-v\rangle \ge 0$. $\mathfrak{A}$ is nonexpansive if it is Lipschitz continuous with constant 1, i.e., $\forall x,y\in {\mathbf{R}}^m,\parallel \mathfrak{A}x-\mathfrak{A}y\parallel \le \parallel x-y\parallel ,$ and is firmly nonexpansive if ${\parallel \mathfrak{A}x-\mathfrak{A}y\parallel }^2{+\parallel (Id-\mathfrak{A})x-(Id-\mathfrak{A})y\parallel }^2\le {\parallel x-y\parallel }^2$. The operator $\mathfrak{A}$ is $\alpha$-averaged with the constant $\alpha \in [0,1]$, denoted by $\mathfrak{A}\in \mathcal{A}\left(\alpha \right)$, if $\forall x,y\in {\mathbf{R}}^m{,\parallel \mathfrak{A}x-\mathfrak{A}y\parallel }^2\le {\parallel x-y\parallel }^2-(1-\alpha )/\alpha {\parallel (Id-\mathfrak{A})x-(Id-\mathfrak{A})y\parallel }^2$. We can easily derive that if $\mathfrak{A}$ is averaged then it is nonexpansive, and $\mathfrak{A}$ is firmly nonexpansive if and only if it is 1/2-averaged. $\mathfrak{A}$ is $\beta$-cocoercive for $\beta >0$, if $\forall x,y\in {\mathbf{R}}^m,\beta {\parallel \mathfrak{A}x-\mathfrak{A}y\parallel }^2\le \langle x-y,\mathfrak{A}x-\mathfrak{A}y\rangle$. The normal cone operator of the set $\mathsf{\Omega }$ is defined as

$$N_{\mathsf{\Omega }}\left(x\right)=\left\{\begin{array}{cc}\varnothing \hfill & x\notin \mathsf{\Omega }\hfill \\ \left\{v\right|\langle v,y-x\rangle \le 0,\forall y\in \mathsf{\Omega }\}\hfill & x\in bd\left(\mathsf{\Omega }\right)\hfill \\ \mathbf{0}\hfill & x\in int\left(\mathsf{\Omega }\right).\hfill \end{array}\right.$$

(1)

Let the projection of x onto $\mathsf{\Omega }$ be $P_{\mathsf{\Omega }}\left(x\right)=arg{min}_{y\in \mathsf{\Omega }}\parallel x-y\parallel$, and $P_{\mathsf{\Omega }}\left(x\right)=R_{N_{\mathsf{\Omega }}}\left(x\right)={(Id+N_{\mathsf{\Omega }})}^{-1}\left(x\right)$.

2.2. Graph Theory

Let the graph $\mathcal{G}=(\mathcal{N},\mathcal{E})$ describe the information exchanged among agents, where $\mathcal{N}:=\{1,\cdots ,N\}$ is the set of players and $\mathcal{E}\subset \mathcal{N}\times \mathcal{N}$ is the edge set. If player i can obtain information from player j, then $(i,j)\in \mathcal{E}$ and j belong to player i’s neighbor set ${\mathcal{N}}_i:=\left\{j\right|(i,j)\in \mathcal{E}\}$. $\mathcal{G}$ is said to be undirected when $(i,j)\in \mathcal{E}$ if and only if $(j,i)\in \mathcal{E}$. Let $W:=\left[w_{ij}\right]\in {\mathbf{R}}^{N\times N}$ be the weighted adjacency matrix of $\mathcal{G}$ with $w_{ij}>0$ if $j\in {\mathcal{N}}_i$ and $w_{ij}=0$ otherwise. Assume that $W=W^{\top }.$ The degree matrix is defined as $Deg:=diag[d_1,\cdots ,d_N]=diag[{\sum }_{j=1}^N{w}_{1j},\cdots ,{\sum }_{j=1}^N{w}_{Nj}]$, and the weighted Laplacian of graph $\mathcal{G}$ is $L:=Deg-W$. If $\mathcal{G}$ is connected and undirected, then 0 is an eigenvalue of L, and the eigenvalues of L are $0<s_2\left(L\right)\le \cdots \le s_N\left(L\right)$ in ascending order.

3. Game Formulation

In this section, we build a mathematical setup about the problem considered.

Consider a set of players $\mathcal{N}=\{1,\cdots ,N\}$, where every player $i\in \mathcal{N}$ controls its local decision variable $x_i\in {\mathsf{\Omega }}_i\subseteq {\mathbf{R}}^{n_i}$ and ${\mathsf{\Omega }}_i$ is the private decision set of player i. Denote $n:={\sum }_{i=1}^N{n}_i$ and $\mathsf{\Omega }:={\mathsf{\Omega }}_1\times \cdots \times {\mathsf{\Omega }}_N\in {\mathbf{R}}^n$, then the stacked vector of all the players’ decisions $x:=\mathrm{col}{\left(x_i\right)}_{i\in \mathcal{N}}\in {\mathbf{R}}^n$ is called the decision profile. We also write $x=(x_i,x_{-i})$, where $x_{-i}:=\mathrm{col}{\left(x_j\right)}_{j\in \mathcal{N}/\left\{i\right\}}=\mathrm{col}(x_1,\cdots ,x_{i-1},x_{i+1},\cdots ,x_N)$ denotes all of the decisions except player i’s.

The local objective function of each player $i\in \mathcal{N}$ is denoted by $J_i(x_i,x_{-i})$, and the affine coupling constrained set is defined as

$$K:=\prod _{i=1}^N{\mathsf{\Omega }}_i\cap \{x\in {\mathbf{R}}^n|Ax\le b\}$$

(2)

where $A:=[A_1,\cdots ,A_N]\in {\mathbf{R}}^{m\times n},$$A_i\in {\mathbf{R}}^{m\times n_i}$ and $b:={\sum }_{i=1}^N{b}_i\in {\mathbf{R}}^m.$ Here, $A_i$ and $b_i$ are the local data only accessible to player $i.$ Define the feasible set of player i as $K_i\left(x_{-i}\right):=\{x_i\in {\mathbf{R}}^{n_i}|(x_i,x_{-i})\in K\}$, which implies that the feasible set of each player depends on the action of the other players. Every player aims to optimize its objective function, and the game can be represented by the inter-dependent optimization problems

$$\forall i\in \mathcal{N}:\underset{x_i\in {\mathbf{R}}^{n_i}}{min}{J}_i(x_i,x_{-i})\mathrm{s}.\mathrm{t}.x_i\in K_i\left(x_{-i}\right).$$

(3)

Definition 1.

A GNE of game (3) is a collective strategy $x^{*}=\mathrm{col}{\left(x_i^{*}\right)}_{i\in \mathcal{N}}$ such that for all $i\in \mathcal{N}$

$$x_i^{*}\in argmin{J}_i(x_i,x_{-i}^{*})\mathrm{s}.\mathrm{t}.x_i\in K_i\left(x_{-i}\right).$$

(4)

In order to deal with the coupling constraints and solve the problems, we define the Lagrange function of each player $i\in \mathcal{N}$:

$${\mathcal{L}}_i(x_i,{\mathsf{\lambda }}_i;x_{-i})=J_i(x_i,x_{-i})+{\mathsf{\lambda }}_i^{\top }(Ax-b)$$

(5)

where ${\mathsf{\lambda }}_i\in {\mathbf{R}}_{+}^m$ is a dual variable. According to optimization theory, if $x_i^{*}$ is an optimal solution to (3), then there exists ${\mathsf{\lambda }}_i^{*}\in {\mathbf{R}}^{n_i}$ such that the following KKT conditions are satisfied:

$$\left\{\begin{array}{c}{\nabla }_{x_i}{\mathcal{L}}_i(x_i^{*},{\mathsf{\lambda }}_i^{*};x_{-i}^{*})={\mathbf{0}}_{n_i}\hfill \\ \langle {\mathsf{\lambda }}_i^{*},A{x}^{*}-b\rangle =0\hfill \\ -(A{x}^{*}-b)\ge 0\hfill \\ {\mathsf{\lambda }}_i^{*}\ge \mathbf{0}.\hfill \end{array}\right.$$

(6)

By using the normal cone operator, the KKT conditions (6) are equivalent to

$$\left\{\begin{array}{c}{\mathbf{0}}_{n_i}\in {\nabla }_{x_i}{J}_i(x_i^{*},x_{-i}^{*})+A_i^{\top }{\mathsf{\lambda }}_i^{*}+N_{{\mathsf{\Omega }}_i}\left(x_i^{*}\right)\hfill \\ {\mathbf{0}}_m\in -(A{x}^{*}-b)+N_{{\mathbf{R}}_{+}^m}\left({\mathsf{\lambda }}_i^{*}\right).\hfill \end{array}\right.$$

(7)

Note that by the definition of a normal cone, one has $N_{{\mathbf{R}}_{+}^m}\left({\mathsf{\lambda }}_i^{*}\right)=\varnothing$ when ${\mathsf{\lambda }}_i^{*}\notin {\mathbf{R}}_{+}^m$, which implies ${\mathsf{\lambda }}_i^{*}\in {\mathbf{R}}_{+}^m$ (equivalently ${\left[{\mathsf{\lambda }}_i^{*}\right]}_k\ge 0$) when (7) holds. Furthermore, $N_{{\mathbf{R}}_{+}^m}={\prod }_{k=1}^m{N}_{{\mathbf{R}}_{+}}$, that is, if ${\left[{\mathsf{\lambda }}_i^{*}\right]}_k=0$, then $N_{{\mathbf{R}}_{+}}\left({\left[{\mathsf{\lambda }}_i^{*}\right]}_k\right)=-{\mathbf{R}}_{+}$, and thus ${[A{x}^{*}-b]}_k\le 0$; if ${\left[{\mathsf{\lambda }}_i^{*}\right]}_k>0$, then $N_{{\mathbf{R}}_{+}}\left({\left[{\mathsf{\lambda }}_i^{*}\right]}_k\right)=0$, and hence ${[A{x}^{*}-b]}_k=0$. This result implies that $A{x}^{*}-b\le 0$ and $\langle {\mathsf{\lambda }}_i^{*},A{x}^{*}-b\rangle =0$.

We consider the GNE with the same Lagrangian multipliers for every player, i.e., ${\mathsf{\lambda }}_1^{*}={\mathsf{\lambda }}_2^{*}=\cdots ={\mathsf{\lambda }}_N^{*}={\mathsf{\lambda }}^{*}$, which is called variational GNE (v-GNE). The v-GNE $x^{*}$ is a solution of the following inequality $VI(F,K):$

$$\langle F\left(x^{*}\right),x-x^{*}\rangle \ge 0,\forall x\in K$$

(8)

where F is the pseudo-gradient mapping of the game with the following form:

$$F\left(x\right):=\mathrm{col}{\left({\nabla }_{x_i}{J}_i(x_i,x_{-i})\right)}_{i\in \mathcal{N}}.$$

(9)

Assumption 1.

Given $x_{-i}$, $J_i(x_i,x_{-i})$ is continuously differentiable and convex in $x_i$, and ${\mathsf{\Omega }}_i$ is nonempty, compact and convex for each player i, then K is nonempty and satisfies Slater’s constraint qualification.

Assumption 2.

F is μ-monotone and ${\theta }_0$-Lipschitz continuous, i.e., for any point x and $x^{\prime }$, $\langle x-x^{\prime },F\left(x\right)-F\left(x^{\prime }\right)\rangle \ge \mu {\parallel x-x^{\prime }\parallel }^2$ and $\parallel F\left(x\right)-F\left(x^{\prime }\right)\parallel \le {\theta }_0\parallel x-x^{\prime }\parallel$.

It follows from ([15], [Theorem 4.8]) that $x^{*}$ solves $VI(F,K)$ (8) if and only if there exists a ${\mathsf{\lambda }}^{*}\in {\mathbf{R}}^m$ such that the KKT conditions are satisfied:

$$\left\{\begin{array}{c}{\mathbf{0}}_n\in F\left(x^{*}\right)+A^{\top }{\mathsf{\lambda }}^{*}+N_{\mathsf{\Omega }}\left(x^{*}\right)\hfill \\ {\mathbf{0}}_m\in -(A{x}^{*}-b)+N_{{\mathbf{R}}_{+}^m}\left({\mathsf{\lambda }}^{*}\right)\hfill \end{array}\right.$$

(10)

where $N_{\mathsf{\Omega }}\left(x^{*}\right)={\prod }_{i=1}^N{N}_{{\mathsf{\Omega }}_i}\left(x_i^{*}\right)$.

Assumption 1 guarantees the existence of the v-GNE for game (3) by ([31], [Corollary 2.2.5]). The goal of this paper is to design distributed algorithms for seeking the v-GNE under a partial-decision information setting, where both the computational cost and convergence rate are taken into consideration.

4. Alternating Distributed v-GNE Algorithms

In this section, we propose two kinds of distributed algorithms for seeking the v-GNE of game (3) with partial-decision information, where each player controls its own actions and exchanges information with its neighbors via the communication graph.

Remark 1.

Some GNE seeking algorithms with inertia and overrelaxation have been proposed [28,29]. Although the fast convergence of these algorithms has been validated numerically, more computation resources are inevitably required at each iteration. Note that the computation resources could be limited and expensive in many situations. Inspired by the above discussion, in this section we design distributed GNE seeking algorithms with alternated inertia and alternated overrelaxation, where both fast convergence rate and low computation consumption are taken into consideration.

Suppose that player $i\in \mathcal{N}$ controls its local decision $x_i\in {\mathbf{R}}^{n_i}$ and ${\mathsf{\lambda }}_i\in {\mathbf{R}}_{+}^m$ (i.e., the estimation of ${\mathsf{\lambda }}^{*}$ in (10)). In order to make up for the lack of non-neighbors’ information, we introduce an auxiliary variable ${\mathbf{x}}_i$ for each player i that provides the estimation of the other players’ decisions. To be specific, ${\mathbf{x}}_i=\mathrm{col}{\left({\mathbf{x}}_i^j\right)}_{j\in \mathcal{N}}$ where ${\mathbf{x}}_i^j$ denotes the player i’s estimation of player j’s decision and ${\mathbf{x}}_i^i=x_i$. We can also rewrite ${\mathbf{x}}_i=(x_i,{\mathbf{x}}_i^{-i})$, where ${\mathbf{x}}_i^{-i}$ represents player i’s estimation vector except its own decisions. In addition, an auxiliary variable $z_i\in {\mathbf{R}}_{+}^m$ is introduced for each player $i\in \mathcal{N}.$ We assume that each player exchanges its local variable $\{{\mathbf{x}}_i,{\mathsf{\lambda }}_i,z_i\}$ with its neighbor through the communication graph $\mathcal{G}.$

Assumption 3.

The communication graph $\mathcal{G}$ is undirected and connected.

4.1. Alternating Inertial Distributed v-GNE Seeking Algorithm

In this subsection, we propose an alternating inertial distributed algorithm for seeking the v-GNE, where the inertia is adopted intermittently (see Algorithm 1). Here, $x_{i,k},{\mathbf{x}}_{i,k}^{-i}$ and $z_{i,k},{\mathsf{\lambda }}_{i,k}$ denote $x_i,{\mathbf{x}}_i^{-i},z_i,{\mathsf{\lambda }}_i$ at iteration $k,$ respectively, and ${\tilde{x}}_{i,k},{\tilde{\mathbf{x}}}_{i,k}^{-i},{\tilde{z}}_{i,k},{\tilde{\mathsf{\lambda }}}_{i,k}$ denote ${\tilde{x}}_i,{\tilde{\mathbf{x}}}_i^{-i},{\tilde{z}}_i,{\tilde{\mathsf{\lambda }}}_i$ at iteration $k,$ respectively. $\rho$ is the inertial parameter, c is the coupling parameter, and ${\tau }_i,{\nu }_i,{\sigma }_i$ are the fixed step-sizes of player i in the update step. $P_{{\mathsf{\Omega }}_i}$ is the projection operator on to the set ${\mathsf{\Omega }}_i$.

Let $\mathbf{x}:=\mathrm{col}{\left({\mathbf{x}}_i\right)}_{i\in \mathcal{N}},$$\mathit{z}:=\mathrm{col}{\left(z_i\right)}_{i\in \mathcal{N}}$ and $\mathsf{\lambda }:=\mathrm{col}{\left({\mathsf{\lambda }}_i\right)}_{i\in \mathcal{N}}.$ Let $\tilde{\mathbf{x}}:=\mathrm{col}{\left({\tilde{\mathbf{x}}}_i\right)}_{i\in \mathcal{N}}$ with ${\tilde{\mathbf{x}}}_i:=({\tilde{x}}_i,{\tilde{\mathbf{x}}}_i^{-i}),$$\tilde{\mathbf{z}}:=\mathrm{col}{\left({\tilde{z}}_i\right)}_{i\in \mathcal{N}}$ and $\tilde{\mathsf{\lambda }}:=\mathrm{col}{\left({\tilde{\mathsf{\lambda }}}_i\right)}_{i\in \mathcal{N}}.$ In addition, $\mathit{A}:=diag\left({\left(A_i\right)}_{i\in \mathcal{N}}\right).$${\mathbf{L}}_{\mathsf{\lambda }}:=L\otimes I_m,$${\mathbf{L}}_x:=L\otimes I_n,$$\mathit{b}:=\mathrm{col}{\left(b_i\right)}_{i\in \mathcal{N}},$${\mathsf{\tau }}^{-1}:=diag\left({\left({\mathsf{\tau }}_i^{-1}{I}_n\right)}_{i\in \mathcal{N}}\right)$, ${\mathsf{\nu }}^{-1}:=diag\left({\left({\mathsf{\nu }}_i^{-1}{I}_n\right)}_{i\in \mathcal{N}}\right)$ and ${\mathbf{\sigma }}^{-1}:=diag\left({\left({\sigma }_i^{-1}{I}_n\right)}_{i\in \mathcal{N}}\right).$

The extended pseudo-gradient mapping $\mathbf{F}$ is defined as

$$\mathbf{F}\left(\mathbf{x}\right):=col{\left({\nabla }_{x_i}{J}_i(x_i,{\mathbf{x}}_i^{-i})\right)}_{i\in \mathcal{N}}.$$

(11)

Let $\varpi :=\mathrm{col}(\mathbf{x},\mathit{z},\mathsf{\lambda })\in \mathsf{\Omega }$, where $\mathsf{\Omega }:={\mathit{R}}^{Nn}\times {\mathit{R}}^{Nm}\times {\mathit{R}}_{+}^{Nm}$, and we define operators $\mathfrak{A},\mathfrak{B}$ and matrix $\mathsf{\Phi }$ as follows:

$$\begin{array}{cc}\hfill & \mathfrak{A}:\mathsf{\varpi }\mapsto \left. [\begin{array}{c}{\mathcal{R}}^{\top }{N}_{\mathsf{\Omega }}\left(\mathcal{R}\mathbf{x}\right)\\ \mathbf{0}\\ N_{{\mathit{R}}_{+}^{Nm}}\left(\mathsf{\lambda }\right)\end{array}\right]+\left. [\begin{array}{ccc}\mathbf{0}& \mathbf{0}& {\mathcal{R}}^{\top }{\mathit{A}}^{\top }\\ \mathbf{0}& \mathbf{0}& -{\mathbf{L}}_{\mathsf{\lambda }}\\ -\mathit{A}\mathcal{R}& {\mathbf{L}}_{\mathsf{\lambda }}& \mathbf{0}\end{array}\right]\varpi \hfill \\ \hfill & \mathfrak{B}:\mathsf{\varpi }\mapsto \left. [\begin{array}{c}{\mathcal{R}}^{\top }\mathbf{F}\left(\mathbf{x}\right)+c{\mathbf{L}}_x\mathbf{x}\\ \mathbf{0}\\ {\mathbf{L}}_{\mathsf{\lambda }}\mathsf{\lambda }+\mathbf{b}\end{array}\right]\hfill \end{array}$$

(12)

$$\mathsf{\Phi }:=\left. [\begin{array}{ccc}{\mathsf{\tau }}^{-1}& \mathbf{0}& -{\mathcal{R}}^{\top }{\mathit{A}}^{\top }\\ \mathbf{0}& {\mathsf{\nu }}^{-1}& {\mathbf{L}}_{\mathsf{\lambda }}\\ -\mathit{A}\mathcal{R}& {\mathbf{L}}_{\mathsf{\lambda }}& {\mathsf{\sigma }}^{-1}\end{array}\right]$$

(13)

where $\mathcal{R}:=diag\left({\left({\mathcal{R}}_i\right)}_{i\in \mathcal{N}}\right)$ with

$${\mathcal{R}}_i:=\left. [\begin{array}{ccc}{\mathbf{0}}_{n_i\times n_{<i}}& I_{n_i}& {\mathbf{0}}_{n_i\times n_{>i}}\end{array}\right],$$

(14)

$n_{<i}:={\sum }_{j<i}{n}_j$ and $n_{>i}:={\sum }_{j>i}{n}_j.$

Algorithm 1 Distributed alternating inertial v-GNE seeking.

Initialization: $x_{i,0}\in {\mathsf{\Omega }}_i,{\mathbf{x}}_{i,0}^{-i}\in {\mathbf{R}}^{n-n_i},{\mathsf{\lambda }}_{i,0}\in {\mathbf{R}}_{+}^m,z_{i,0}\in {\mathbf{R}}^m$ Acceleration: Set ${\rho }_k=0$ if k is even, ${\rho }_k=\rho$ if k is odd. $$\begin{array}{cc}\hfill {\tilde{x}}_{i,k}& =x_{i,k}+{\rho }_k(x_{i,k}-x_{i,k-1})\hfill \\ \hfill {\tilde{\mathbf{x}}}_{i,k}^{-i}& ={\mathbf{x}}_{i,k}^{-i}+{\rho }_k({\mathbf{x}}_{i,k}^{-i}-{\mathbf{x}}_{i,k-1}^{-i})\hfill \\ \hfill {\tilde{z}}_{i,k}& =z_{i,k}+{\rho }_k(z_{i,k}-z_{i,k-1})\hfill \\ \hfill {\tilde{\mathsf{\lambda }}}_{i,k}& ={\mathsf{\lambda }}_{i,k}+{\rho }_k({\mathsf{\lambda }}_{i,k}-{\mathsf{\lambda }}_{i,k-1})\hfill \end{array}$$ Update: $$\begin{array}{cc}\hfill x_{i,k+1}& =P_{{\mathsf{\Omega }}_i}({\tilde{x}}_{i,k}-{\tau }_i({\nabla }_{x_i}{J}_i({\tilde{x}}_{i,k},{\tilde{\mathbf{x}}}_{i,k}^{-i})+A_i^{\top }{\tilde{\mathsf{\lambda }}}_{i,k}\hfill \\ \hfill & +c\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\tilde{x}}_{i,k}-{\tilde{\mathbf{x}}}_{j,k}^i)\left)\right)\hfill \\ \hfill {\mathbf{x}}_{i,k+1}^{-i}& ={\tilde{\mathbf{x}}}_{i,k}^{-i}-{\tau }_{i}c\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\tilde{\mathbf{x}}}_{i,k}^{-i}-{\tilde{\mathbf{x}}}_{j,k}^{-i})\hfill \\ \hfill z_{i,k+1}& ={\tilde{z}}_{i,k}+{\nu }_i\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\tilde{\mathsf{\lambda }}}_{i,k}-{\tilde{\mathsf{\lambda }}}_{j,k})\hfill \\ \hfill {\mathsf{\lambda }}_{i,k+1}& =P_{{\mathbf{R}}_{+}^m}({\tilde{\mathsf{\lambda }}}_{i,k}+{\mathsf{\sigma }}_i(A_i(2x_{i,k+1}-{\tilde{x}}_{i,k})-b_i\hfill \\ \hfill & -\sum _{j\in {\mathcal{N}}_i}{w}_{ij}(2(z_{i,k+1}-z_{j,k+1})-({\tilde{z}}_{i,k}-{\tilde{z}}_{j,k}))\hfill \\ \hfill & -\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\tilde{\mathsf{\lambda }}}_{i,k}-{\tilde{\mathsf{\lambda }}}_{j,k})\left)\right)\hfill \end{array}$$

Let ${\varpi }_k:=\mathrm{col}({\mathbf{x}}_k,{\mathit{z}}_k,{\varpi }_k),{\tilde{\mathsf{\varpi }}}_k:=\mathrm{col}({\tilde{\mathbf{x}}}_k,{\tilde{\mathit{z}}}_k,{\tilde{\mathsf{\lambda }}}_k),$ where ${\mathbf{x}}_k,{\mathit{z}}_k,{\mathsf{\lambda }}_k,{\tilde{\mathbf{x}}}_k,{\tilde{\mathit{z}}}_k,{\tilde{\mathsf{\lambda }}}_k$ denote $\mathbf{x}$, $\mathit{z}$, $\mathsf{\lambda }$, $\tilde{\mathbf{x}}$, $\tilde{\mathit{z}}$, $\tilde{\mathsf{\lambda }}$ at iteration $k,$ respectively. Suppose that $\mathsf{\Phi }\succ 0$ and ${\mathsf{\Phi }}^{-1}\mathfrak{A}$ is maximally monotone, then Algorithm 1 is equivalent to

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\varpi }_{k+1}=T\left({\varpi }_k\right),\hfill & \mathrm{if}k\mathrm{is}\mathrm{even}\hfill \\ {\varpi }_{k+1}=T({\varpi }_k+\rho ({\varpi }_k-{\varpi }_{k-1})),\hfill & \mathrm{if}k\mathrm{is}\mathrm{odd}\hfill \end{array}\right.\end{array}$$

(15)

where $\mathsf{\Phi },$$\mathfrak{A},$$\mathfrak{B}$ in (12)–(13), $T:=T_2\circ T_1,$$T_1:=Id-{\mathsf{\Phi }}^{-1}\mathfrak{B},$ and $T_2:={(Id+{\mathsf{\Phi }}^{-1}\mathfrak{A})}^{-1}.$

Lemma 1.

Suppose $\mathsf{\Phi }\succ 0$ and ${\mathsf{\Phi }}^{-1}\mathfrak{A}$ is maximally monotone, then any limit point $\overline{\mathsf{\varpi }}=\mathrm{col}(\overline{\mathbf{x}},\overline{\mathit{z}},\overline{\mathsf{\lambda }})$ of Algorithm 1 is a zero of $\mathfrak{A}+\mathfrak{B}$ and a fixed point of $T_2\circ T_1$.

Proof. 

By the continuity of the right hand of (15), $\overline{\varpi }=T\left(\overline{\varpi }\right)$. Since $\mathsf{\Phi }$ is positive definite,

$$\begin{array}{cc}\hfill & \overline{\varpi }=T_2\circ T_1\left(\overline{\varpi }\right):={(Id+{\mathsf{\Phi }}^{-1}\mathfrak{A})}^{-1}\circ (Id-{\mathsf{\Phi }}^{-1}\mathfrak{B})\left(\overline{\varpi }\right)\hfill \\ \hfill & \iff (Id+{\mathsf{\Phi }}^{-1}\mathfrak{A})\left(\overline{\varpi }\right)\in (Id-{\mathsf{\Phi }}^{-1}\mathfrak{B})\left(\overline{\varpi }\right)\hfill \\ \hfill & \iff \mathbf{0}\in {\mathsf{\Phi }}^{-1}(\mathfrak{A}+\mathfrak{B})\left(\overline{\varpi }\right)\hfill \\ \hfill & \iff \mathbf{0}\in (\mathfrak{A}+\mathfrak{B})\left(\overline{\varpi }\right).\hfill \end{array}$$

   □

In order to show the convergence of the algorithm, the following assumptions are introduced.

Assumption 4.

The extended pseudo-gradient mapping $\mathbf{F}$ in (11) is θ-Lipschitz continuous, i.e., there exists $\theta >0$ such that for any $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$, $\parallel \mathbf{F}\left(\mathbf{x}\right)-\mathbf{F}\left({\mathbf{x}}^{\prime }\right)\parallel \le \theta \parallel \mathbf{x}-{\mathbf{x}}^{\prime }\parallel$.

Let $c_{\min }:=\frac{1}{s_2\left(L\right)}(\frac{{(\theta +{\theta }_0)}^2}{4\mu }+\theta )$ with $\mu$, ${\theta }_0$ in Assumption 2, and $\theta$ in Assumption 4. Let ${\mathit{E}}_x:=\{\mathbf{x}\in {\mathit{R}}^{Nn}|\mathbf{x}={\mathbf{1}}_N\otimes x,x\in {\mathit{R}}^n\}$. It follows from ([21], [Lemma 4]) that if c is selected such that $c>c_{\min }$, then $\mathfrak{A}$ is maximally monotone and $\mathfrak{B}$ is $\beta$-restricted cocoercive, i.e., for any $\varpi$ and any ${\varpi }^{\prime }\in {\mathsf{\Omega }}_E$, where ${\mathsf{\Omega }}_E:={\mathit{E}}_x\times {\mathit{R}}^{Nm}\times {\mathit{R}}_{+}^{Nm}$,

$$\begin{array}{c}\hfill \langle \varpi -{\varpi }^{\prime },\mathfrak{B}\varpi -\mathfrak{B}{\varpi }^{\prime }\rangle \ge \beta {\parallel \mathfrak{B}\varpi -\mathfrak{B}{\varpi }^{\prime }\parallel }^2,\end{array}$$

(16)

where $0<\beta \le min\{\frac{1}{2d^{*}},\frac{\mu }{{\theta }^2}\}$, and $d^{*}$ is the maximal weighted degree of $\mathcal{G}$, i.e., $d^{*}=max\{{\sum }_{j=1}^N{w}_{1j},\cdots ,{\sum }_{j=1}^N{w}_{Nj}\}$.

Similar to [21], a mild assumption (Assumption 4) on the pseudo-gradient mapping $\mathbf{F}$ is required only, while the requirement of strong monotonicity is relaxed for $\mathbf{F}$.

Theorem 1.

Suppose Assumptions $\mathit{1}$–$\mathit{4}$ hold. Choose $c>c_{\min },$$\delta >\frac{1}{2\beta }$, and the step sizes ${\tau }_i\le \frac{1}{\parallel A_i^{\top }{\parallel }_{\infty }+\delta },$${\nu }_i\le \frac{1}{2d_i+\delta }$, and ${\sigma }_i\le \frac{1}{\parallel A_i{\parallel }_{\infty }+2d_i+\delta }$. Then for any $\rho \in [0,\frac{1}{2})$, the sequence ${\{{\mathbf{x}}_k,{\mathbf{z}}_k,{\mathsf{\lambda }}_k\}}_{k\in \mathbb{N}}$ generated by Algorithm 1 converges to the equilibrium $({\mathbf{x}}^{*},{\mathbf{z}}^{*},{\mathsf{\lambda }}^{*})$, where ${\mathbf{x}}^{*}={\mathbf{1}}_N\otimes x^{*}$ and $x^{*}$ is a v-GNE of the game (3).

Proof. 

It follows from the Gershgorin’s circle theorem ([32], [§6.8 Theorem 1]) that, given any $\delta >0,$$\mathsf{\Phi }$ is positive definite and $\mathsf{\Phi }-\delta I_{n+2mN}$ is positive semi-definite if the step sizes ${\tau }_i\le \frac{1}{\parallel A_i^{\top }{\parallel }_{\infty }+\delta }$ and ${\nu }_i\le \frac{1}{2d_i+\delta }.$

Next, we first show the convergence of $\left\{{\varpi }_{2k}\right\}$ and then show the convergence of $\left\{{\varpi }_k\right\}$.

By ([21], [Lemma 6]), we have $T_2\in \mathcal{A}\left(\frac{1}{2}\right)$ and $T_1$ is $\frac{1}{2\beta \delta }$-restricted averaged, i.e., for any $\varpi$ and any ${\varpi }^{\prime }\in {\mathsf{\Omega }}_E$,

$$\begin{array}{cc}\hfill \parallel T_1\varpi -T_1{\varpi }^{\prime }{\parallel }_{\mathsf{\Phi }}^2\le & \parallel \varpi -{\varpi }^{\prime }{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill -& (2\beta \delta -1)\parallel \varpi -{\varpi }^{\prime }-(T_1\varpi -T_1{\varpi }^{\prime }){\parallel }_{\mathsf{\Phi }}^2.\hfill \end{array}$$

(17)

It follows from ([30], [Proposition 4.32]) that $T=T_2\circ T_1$ is $\mathsf{\alpha }$-restricted averaged, with $\alpha =\frac{2}{3}$ when $\delta >\frac{1}{\beta }.$ Let ${\varpi }^{*}$ be a fixed point of T, then ${\varpi }^{*}\in {\mathsf{\Omega }}_E$ according to ([21], [Theorem 1]).

(i) For the subsequence $\left\{{\varpi }_{2k}\right\},$ by (15), we have ${\varpi }_{2(k+1)}=T(T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})).$ Then, by T is $\alpha -restricted$ averaged, we obtain

$$\begin{array}{cc}\hfill & \parallel {\varpi }_{2k+2}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill =& \parallel T(T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k}))-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill \le & \parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & -\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }_{2k+2}\parallel }_{\mathsf{\Phi }}^2.\hfill \end{array}$$

(18)

By resorting to ${\parallel \alpha x+(1-\alpha )y\parallel }^2{+\alpha (1-\alpha )\parallel x-y\parallel }^2={\alpha \parallel x\parallel }^2+(1-\alpha ){\parallel y\parallel }^2,$

$$\begin{array}{cc}\hfill & \parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill =& (1+\rho )\parallel T\left({\varpi }_{2k}\right)-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\rho {\parallel {\varpi }_{2k}-{\varpi }^{*}\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & +(1+\rho )\rho \parallel T\left({\varpi }_{2k}\right)-{\varpi }_{2k}{\parallel }_{\mathsf{\Phi }}^2,\hfill \end{array}$$

(19)

and by using (17) again, (18) can be rewritten as

$$\begin{array}{cc}\hfill & \parallel {\varpi }_{2k+2}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill \le & (1+\rho )\parallel {\varpi }_{2k}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\rho {\parallel {\varpi }_{2k}-{\varpi }^{*}\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & -(1+\rho )\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_{2k}\right)-{\varpi }_{2k}\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & +(1+\rho )\rho \parallel T\left({\varpi }_{2k}\right)-{\varpi }_{2k}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & -\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }_{2k+2}\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill =& \parallel {\varpi }_{2k}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-(1+\rho )\left(\frac{1-\alpha }{\alpha }-\rho \right){\parallel T\left({\varpi }_{2k}\right)-{\varpi }_k\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & -\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }_{2k+2}\parallel }_{\mathsf{\Phi }}^2.\hfill \end{array}$$

(20)

Choose $\rho \le \frac{1-\alpha }{\alpha }=\frac{1}{2}$, then

$$\begin{array}{c}\hfill \parallel {\varpi }_{2k+2}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\le {\parallel {\varpi }_{2k}-{\varpi }^{*}\parallel }_{\mathsf{\Phi }}^2\\ \hfill -\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }_{2k+2}\parallel }_{\mathsf{\Phi }}^2.\end{array}$$

(21)

This result implies that the sequence $\{\parallel {\varpi }_{2k}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\}$ is decreasing and non-negative, and thus converges. Moreover, we have

$$\begin{array}{c}\hfill \sum _{k=0}^{\infty }{\parallel T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }_{2(k+1)}\parallel }_{\mathsf{\Phi }}^2<\infty \end{array}$$

and $T\left({\varpi }_{2k}\right)+\rho (T\left({\varpi }_{2k}\right)-{\varpi }_{2k})-{\varpi }_{2(k+1)}\to 0.$ Note that since $\left\{{\varpi }_{2k}\right\}$ is bounded, then there exists a convergent subsequence $\left\{{\varpi }_{2n_k}\right\}$ that converges to $\tilde{\varpi }.$ Obviously,

$$\begin{array}{c}\hfill {\varpi }_{2(n_k+1)}=T(T\left({\varpi }_{2n_k}\right)+\rho (T\left({\varpi }_{2n_k}\right)-{\varpi }_{2n_k})).\end{array}$$

Let $k\to \infty$, we have $\tilde{\varpi }=T\tilde{\varpi }$, which implies that $\tilde{\varpi }$ is a fixed point of T and thus $\{\parallel {\varpi }_{2k}-\tilde{\varpi }{\parallel }_{\mathsf{\Phi }}^2\}$ converges. Since $\{\parallel {\varpi }_{2n_k}-\tilde{\varpi }{\parallel }_{\mathsf{\Phi }}^2\}$ converges to 0, $\left\{{\varpi }_{2k}\right\}$ converges to $\tilde{\varpi }.$

(ii) T is restricted nonexpansive since it is $\frac{2}{3}$-restricted averaged, and then one obtains

$$\parallel {\varpi }_{2k+1}-\tilde{\varpi }\parallel =\parallel T{\varpi }_{2k}-T\tilde{\varpi }\parallel \le \parallel {\varpi }_{2k}-\tilde{\varpi }\parallel ,$$

(22)

which implies that the odd subsequence $\left\{{\varpi }_{2k+1}\right\}$ also converges to $\tilde{\varpi }$, and thus $\left\{{\varpi }_k\right\}$ converges to $\tilde{\varpi }.$ Note that $\mathsf{\Phi }\succ 0$ and ${\mathsf{\Phi }}^{-1}\mathfrak{A}$ is maximally monotone. $\tilde{\varpi }$ is a fixed point of $T,$ and hence is a zero of $\mathfrak{A}+\mathfrak{B}$ by Lemma 1. It follows from ([21], [Theorem 1]) that given any $\tilde{\varpi }:=\mathrm{col}({\mathbf{x}}^{*},{\mathbf{z}}^{*},{\mathsf{\lambda }}^{*})\in zer(\mathfrak{A}+\mathfrak{B})$, then ${\mathbf{x}}^{*}={\mathbf{1}}_N\otimes x^{*},$ and $x^{*}$ solves $VI(F,K)$ (8), that is, $x^{*}$ is a v-GNE of game (3).    □

4.2. Alternating Overrelaxed Distributed v-GNE Seeking Algorithm

In this subsection, an alternating overrelaxed distributed algorithm is constructed for seeking the v-GNE, presented in Algorithm 2, and also that $\eta$ is an overrelaxed parameter. Here the partial-decision information setting is considered.

Algorithm 2 Distributed alternating overrelaxed v-GNE seeking.

Initialization: $x_{i,0}\in {\mathsf{\Omega }}_i,{\mathbf{x}}_{i,0}^{-i}\in {\mathbf{R}}^{n-n_i},{\mathsf{\lambda }}_{i,0}\in {\mathbf{R}}_{+}^m,z_{i,0}\in {\mathbf{R}}^m$ Update: $$\begin{array}{cc}\hfill {\tilde{x}}_{i,k}& =P_{{\mathsf{\Omega }}_i}(x_{i,k}-{\mathsf{\tau }}_i({\nabla }_{x_i}{J}_i(x_{i,k},{\mathbf{x}}_{i,k}^{-i})+A_i^{\top }{\mathsf{\lambda }}_{i,k}\hfill \\ \hfill & +c\sum _{j\in {\mathcal{N}}_i}{w}_{ij}(x_{i,k}-{\mathbf{x}}_{j,k}^i)\left)\right)\hfill \\ \hfill {\tilde{\mathbf{x}}}_{i,k}^{-i}& ={\mathbf{x}}_{i,k}^{-i}-{\mathsf{\tau }}_{i}c\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\mathbf{x}}_{i,k}^{-i}-{\mathbf{x}}_{j,k}^{-i})\hfill \\ \hfill {\tilde{z}}_{i,k}& =z_{i,k}+{\mathsf{\nu }}_i\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\mathsf{\lambda }}_{i,k}-{\mathsf{\lambda }}_{j,k})\hfill \\ \hfill {\tilde{\mathsf{\lambda }}}_{i,k}& =P_{{\mathbf{R}}_{+}^m}({\mathsf{\lambda }}_{i,k}+{\mathsf{\sigma }}_i(A_i(2{\tilde{x}}_{i,k}-x_{i,k})-b_i\hfill \\ \hfill & -\sum _{j\in {\mathcal{N}}_i}{w}_{ij}(2({\tilde{z}}_{i,k}-{\tilde{z}}_{j,k})-(z_{i,k}-z_{j,k}))\hfill \\ \hfill & -\sum _{j\in {\mathcal{N}}_i}{w}_{ij}({\mathsf{\lambda }}_{i,k}-{\mathsf{\lambda }}_{j,k})\left)\right)\hfill \end{array}$$ Acceleration: Set ${\eta }_k=1$ if k is even, ${\eta }_k=\eta$ if k is odd. $$\begin{array}{cc}\hfill x_{i,k+1}& ={\tilde{x}}_{i,k}+({\eta }_k-1)({\tilde{x}}_{i,k}-x_{i,k})\hfill \\ \hfill {\mathbf{x}}_{i,k+1}^{-i}& ={\tilde{\mathbf{x}}}_{i,k}^{-i}+({\eta }_k-1)({\tilde{\mathbf{x}}}_{i,k}^{-i}-{\mathbf{x}}_{i,k}^{-i})\hfill \\ \hfill z_{i,k+1}& ={\tilde{z}}_{i,k}+({\mathsf{\eta }}_k-1)({\tilde{z}}_{i,k}-z_{i,k})\hfill \\ \hfill {\mathsf{\lambda }}_{i,k+1}& ={\tilde{\mathsf{\lambda }}}_{i,k}+({\mathsf{\eta }}_k-1)({\tilde{\mathsf{\lambda }}}_{i,k}-{\mathsf{\lambda }}_{i,k})\hfill \end{array}$$

Similar to (15), we suppose that $\mathsf{\Phi }\succ 0$ and ${\mathsf{\Phi }}^{-1}\mathfrak{A}$ is maximally monotone, then Algorithm 2 is equivalent to

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\varpi }_{k+1}=T\left({\varpi }_k\right)\hfill & \mathrm{if}k\mathrm{is}\mathrm{even}\hfill \\ {\varpi }_{k+1}=T\left({\varpi }_k\right)+(\eta -1)(T\left({\varpi }_k\right)-{\varpi }_k)\hfill & \mathrm{if}k\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.\end{array}$$

(23)

where ${\varpi }_k=\mathrm{col}({\mathbf{x}}_k,{\mathit{z}}_k,{\mathsf{\lambda }}_k)$ and T is given in (15).

Next, we prove the convergence of Algorithm 2 to a v-GNE.

Theorem 2.

Suppose Assumptions $\mathit{1}$–$\mathit{4}$ hold. Take any $c>c_{\min }$, $\delta >\frac{1}{2\beta }$, and the step sizes ${\tau }_i\le \frac{1}{\parallel A_i^{\top }{\parallel }_{\infty }+\delta },$${\nu }_i\le \frac{1}{2d_i+\delta }$, and ${\sigma }_i\le \frac{1}{\parallel A_i{\parallel }_{\infty }+2d_i+\delta }$. Then, for any $\eta \in [1,\frac{3}{2})$, the sequence ${\{{\mathbf{x}}_k,{\mathit{z}}_k,{\mathsf{\lambda }}_k\}}_{k\in \mathbb{N}}$ generated by Algorithm 2 converges to the equilibrium $({\mathbf{x}}^{*},{\mathit{z}}^{*},{\mathsf{\lambda }}^{*})$, where ${\mathbf{x}}^{*}={\mathbf{1}}_N\otimes x^{*}$ and $x^{*}$ is a v-GNE of the game (3).

Proof. 

Similar to Theorem 1, we first show the convergence of $\left\{{\varpi }_{2k}\right\},$ and then prove the convergence of $\left\{{\varpi }_k\right\}$. Note that $T=T_2\circ T_1$ is $\alpha$-restricted averaged with $\alpha =\frac{2}{3}$ when $\delta >\frac{1}{\beta }.$ Let ${\varpi }^{*}$ be any fixed point of $T.$

First, we consider the subsequence $\left\{{\varpi }_{2k}\right\},$ and according to (23) and (17), one has

$$\begin{array}{cc}\hfill & \parallel {\varpi }_{k+2}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill \le & \eta [\parallel T\left({\varpi }_k\right)-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\frac{1-\alpha }{\alpha }\parallel T\left({\varpi }_k\right)-T\left(T\left({\varpi }_k\right)\right){\parallel }_{\mathsf{\Phi }}^2]\hfill \\ \hfill & +(1-\eta )[\parallel {\varpi }_k-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\frac{1-\alpha }{\alpha }\parallel {\varpi }_k-T\left({\varpi }_k\right){\parallel }_{\mathsf{\Phi }}^2]\hfill \\ \hfill & -\eta (1-\eta )\parallel T\left(T\left({\varpi }_k\right)\right)-T\left({\varpi }_k\right){\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill =& (1-\eta )\parallel {\varpi }_k-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2+\eta {\parallel T\left({\varpi }_k\right)-{\varpi }^{*}\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & +[-\eta (\frac{1}{\alpha }-\eta )]{\parallel T\left({\varpi }_k\right)-T\left(T\left({\varpi }_k\right)\right)\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & -(1-\eta )\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_k\right)-{\varpi }_k\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill \le & \parallel {\varpi }_k-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_k\right)-{\varpi }_k\parallel }_{\mathsf{\Phi }}^2\hfill \\ \hfill & +[-\eta (\frac{1}{\alpha }-\eta )]{\parallel T\left({\varpi }_k\right)-T\left(T\left({\varpi }_k\right)\right)\parallel }_{\mathsf{\Phi }}^2\hfill \end{array}$$

where the first equality holds due to ${\parallel \alpha x+(1-\alpha )y\parallel }^2{+\alpha (1-\alpha )\parallel x-y\parallel }^2={\alpha \parallel x\parallel }^2+(1-\alpha ){\parallel y\parallel }^2.$ By choosing $\eta \le \frac{1}{\alpha }$, we have

$$\begin{array}{c}\hfill \parallel {\varpi }_{k+2}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\le \parallel {\varpi }_k-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\frac{1-\alpha }{\alpha }{\parallel T\left({\varpi }_k\right)-{\varpi }_k\parallel }_{\mathsf{\Phi }}^2\end{array}$$

(24)

which implies that $\{\parallel {\varpi }_{k+2}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2\}$ is monotonically decreasing and bounded, and is thus convergent. Furthermore,

$$\begin{array}{cc}\hfill & \sum _{k=0}^{\infty }(\parallel {\varpi }_{2(k+1)}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2-\parallel {\varpi }_{2k}-{\varpi }^{*}{\parallel }_{\mathsf{\Phi }}^2)\hfill \\ \hfill \le & -\frac{1-\alpha }{\alpha }\sum _{k=0}^{\infty }{\parallel T\left({\varpi }_{2k}\right)-{\varpi }_{2k}\parallel }_{\mathsf{\Phi }}^2,\hfill \end{array}$$

(25)

that is, ${\sum }_{k=0}^{\infty }\parallel T\left({\varpi }_{2k}\right)-{\varpi }_{2k}{\parallel }_{\mathsf{\Phi }}^2\le {\parallel {\varpi }_0-{\varpi }^{*}\parallel }_{\mathsf{\Phi }}^2<\infty$, and hence

$$\begin{array}{c}\hfill \parallel T\left({\varpi }_{2k}\right)-{\varpi }_{2k}\parallel \to 0.\end{array}$$

(26)

Note that if $\left\{{\varpi }_{2k}\right\}$ is bounded, there exists a convergent subsequence $\left\{{\varpi }_{2n_k}\right\}\to \tilde{\varpi }$ for some limit $\tilde{\varpi }$.

Let $k\to \infty$ in (26), we have $T\left(\tilde{\varpi }\right)\to \tilde{\varpi }$ which implies $\tilde{\varpi }$ is a fixed point of T, thus $\{\parallel {\varpi }_{2k}-\tilde{\varpi }{\parallel }_{\mathsf{\Phi }}^2\}$ converges. Since $\{\parallel {\varpi }_{2n_k}-\tilde{\varpi }{\parallel }_{\mathsf{\Phi }}^2\}\to 0$, $\left\{{\varpi }_{2k}\right\}$ converges to $\tilde{\varpi }$.

(ii) If T is restricted nonexpansive since it is $\frac{2}{3}$-restricted averaged, then one obtains

$$\begin{array}{c}\hfill \parallel {\varpi }_{2k+1}-\tilde{\varpi }\parallel =\parallel T\left({\varpi }_{2k}\right)-T\left(\tilde{\varpi }\right)\parallel \le \parallel {\varpi }_{2k}-\tilde{\varpi }\parallel ,\end{array}$$

(27)

which implies that the sequence $\left\{{\varpi }_{2k+1}\right\}$ converges to the same limit of $\left\{{\varpi }_{2k}\right\}$, and thus $\left\{{\varpi }_k\right\}$ converges to $\tilde{\varpi }$. □

5. Numerical Simulation

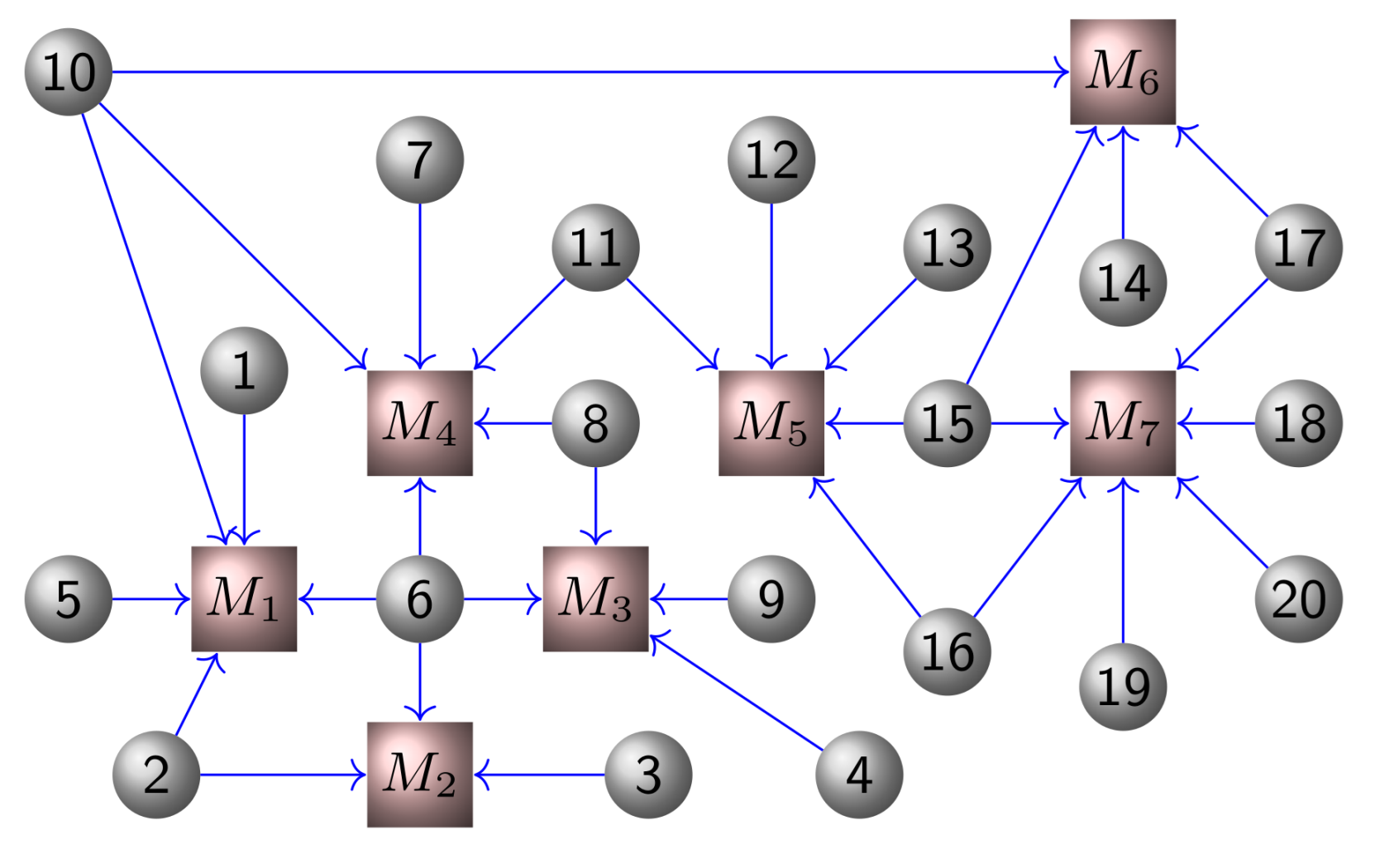
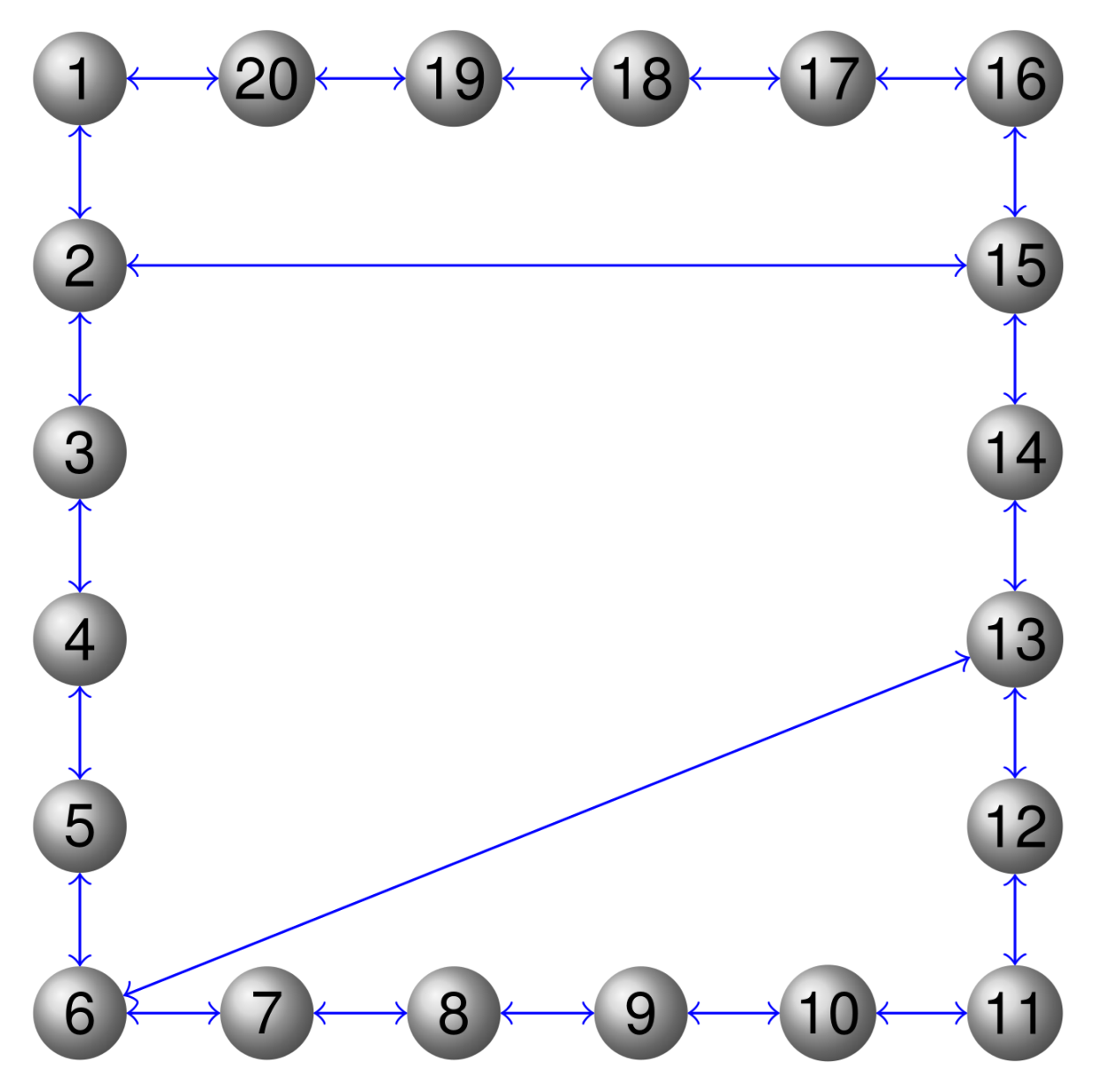
In this section, we consider a classic Nash–Cournot game over a network as [21], where there are N firms and each firm $i\in \{1,\cdots ,N\}$ produces commodities to participate in the competition over m markets (see Figure 1). Each market (denoted by $M_1,\cdots ,M_m$) has limited capacity. Here, the partial-decision information setting is considered where each firm has limited access to its neighboring firms’ information over the communication graph as in Figure 2.

We assume that firm i participates in $n_i$ markets by producing $x_i\in {\mathbf{R}}^{n_i}$ amount of commodities and its production is limited by the set ${\mathsf{\Omega }}_i\in {\mathbf{R}}^{n_i}$. The local matrix $A_i\in {\mathbf{R}}^{m\times n_i}$ for firm i represents which markets it participates in. Specifically, for the j-th column of $A_i,$ its k-th element is 1 if and only if firm i delivers ${\left[x_i\right]}_j$ amount of production to market $M_k;$ all other elements are $0.$ Each market $M_k$ has a maximal capacity of $r_k>0,$ that is, $Ax\le r$, where $A=[A_1,\cdots ,A_N],x=\mathrm{col}{\left(x_i\right)}_{i\in \mathcal{N}}\in {\mathbf{R}}^n,n={\sum }_{i=1}^N{n}_i$ and $r=\mathrm{col}{\left(r_k\right)}_{k=1,\cdots ,m}\in {\mathbf{R}}^m$. Suppose that each firm i has the production cost $c_i\left(x_i\right):{\mathsf{\Omega }}_i\to \mathbf{R},$ and the price function $P:{\mathbf{R}}^n\to {\mathbf{R}}^m$ maps the total supply of each market to the market’s price vector. The local objective function of firm i is $J_i(x_i,x_{-i})=c_i\left(x_i\right)-{\left(P\left(Ax\right)\right)}^{\top }{A}_i{x}_i$.

Suppose $N=20$ and $m=7.$ Let ${\mathsf{\Omega }}_i=\{x_i\in {\mathbf{R}}^{n_i}|\mathbf{0}\le x_i\le {\mathsf{\Theta }}_i\}$, where each component of ${\mathsf{\Theta }}_i$ is randomly drawn from $(5,10)$. $r_k$ is randomly drawn from $(1,2).$ The local cost function of firm i is $c_i\left(x_i\right)=x_i^{\top }{H}_i{x}_i+h_i^{\top }{x}_i$, where $H_i$ is a diagonal matrix with the elements randomly drawn from $(1,8)$ and $h_i$ is randomly drawn from $(1,2)$. The price function is taken as the linear function $P=\overline{P}-DAx$ with $\overline{P}=\mathrm{col}{\left({\overline{P}}_k\right)}_{k=1,\cdots ,m}\in {\mathbf{R}}^m$ and $D=diag{\left(d_k\right)}_{k=1,\cdots ,m}\in {\mathbf{R}}^{m\times m},$ where ${\overline{P}}_k$ and $d_k$ are randomly drawn from $(10,20)$ and $(1,3),$ respectively. Set the step-sizes as $c=100,$${\mathsf{\tau }}_i=0.003,$${\nu }_i=0.02,$ and ${\sigma }_i=0.003$.

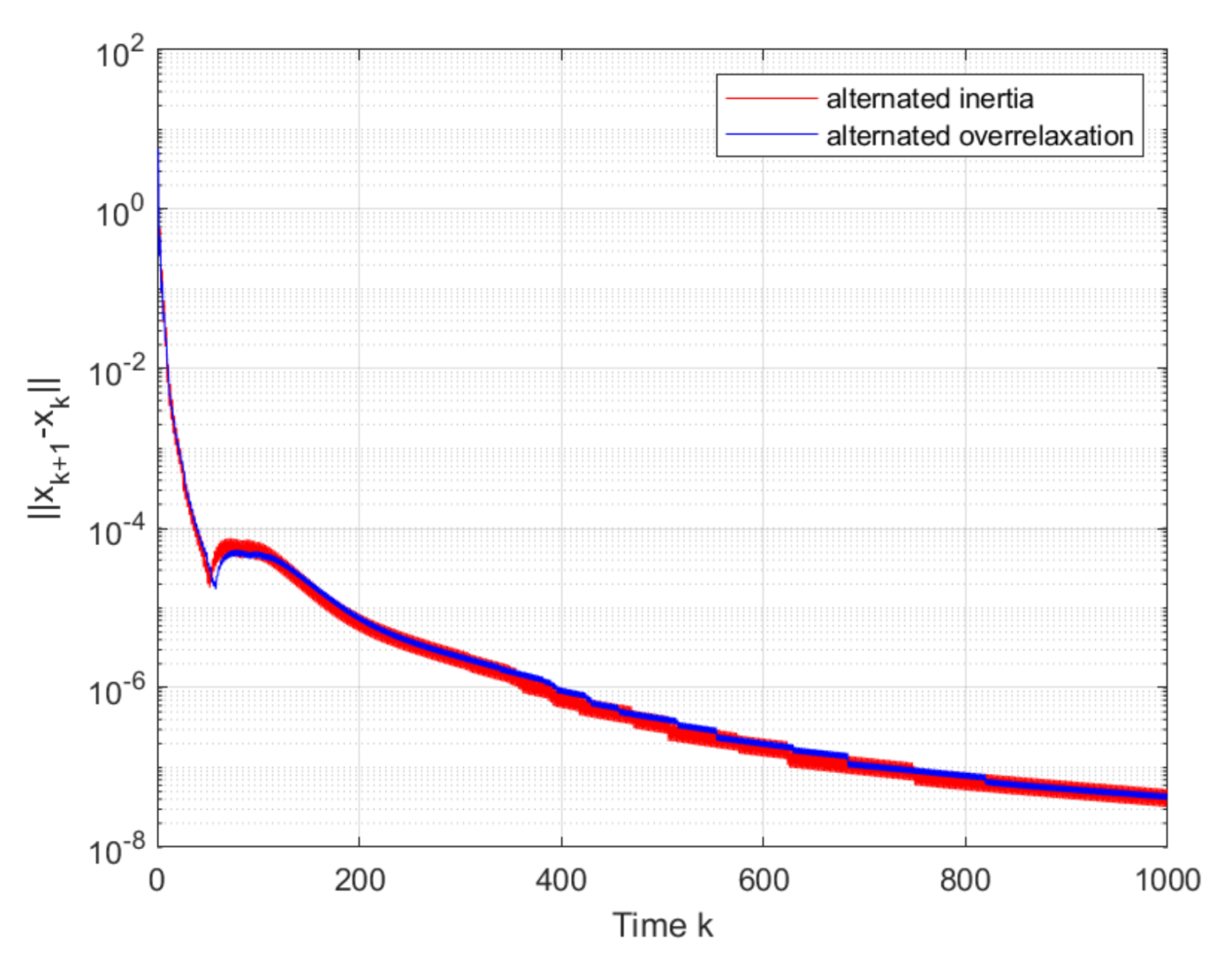
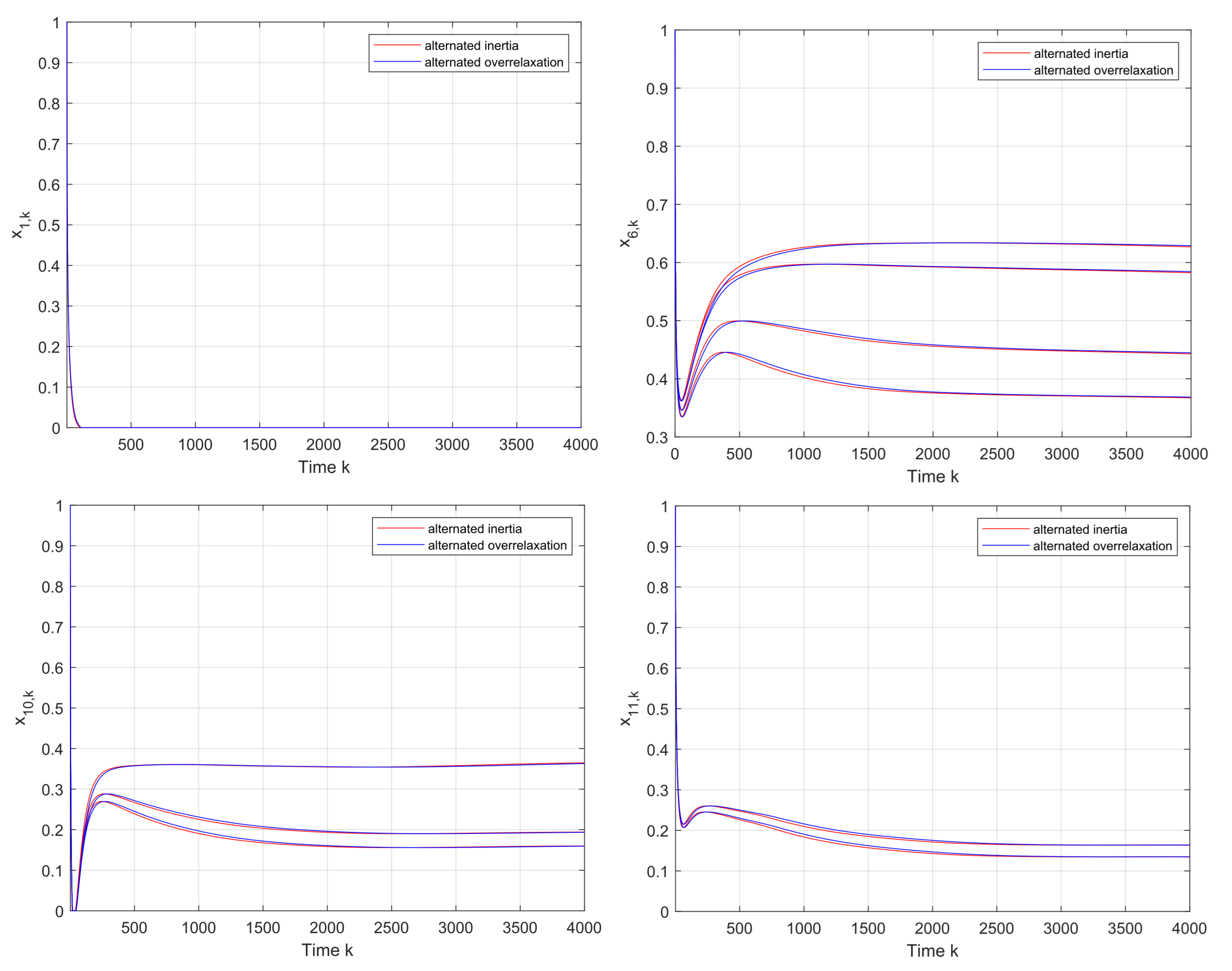
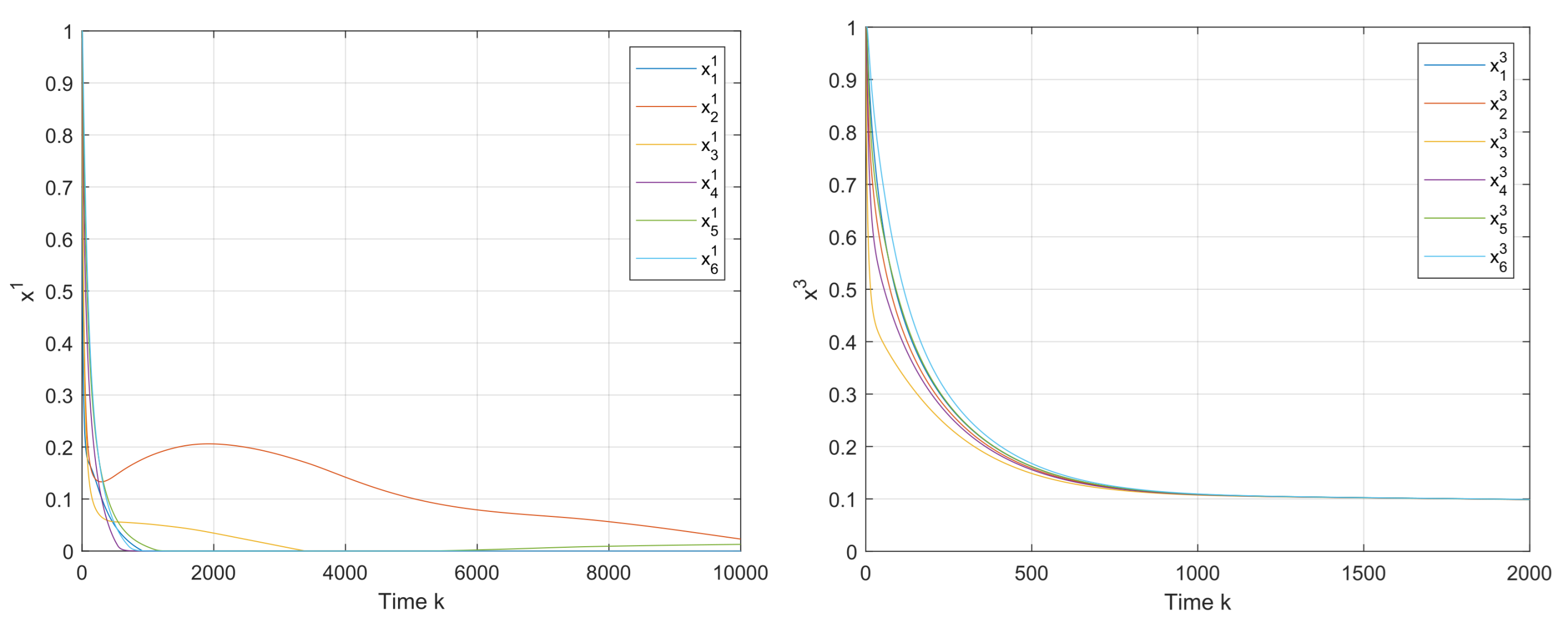
First, Figure 3 shows that the convergence to the v-GNE can be guaranteed under Algorithms 1 and 2, and the trajectories of the local decision $x_{i,k}$ of firms $1,6,10,11$ are displayed in Figure 4. It can be seen in Figure 5 that the estimates on the firms 1 and 3 asymptotically tend to their real actions by using the proposed algorithms.

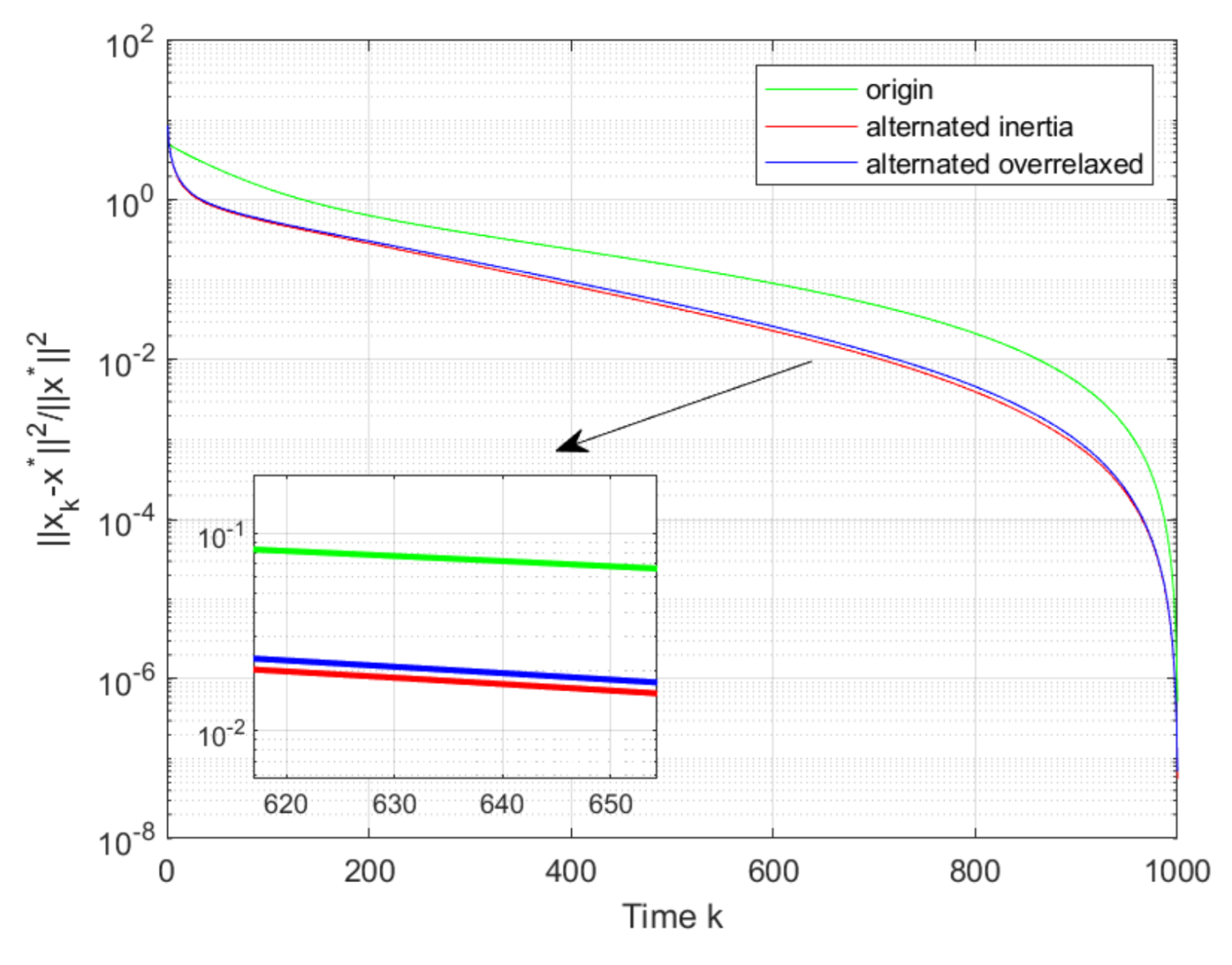
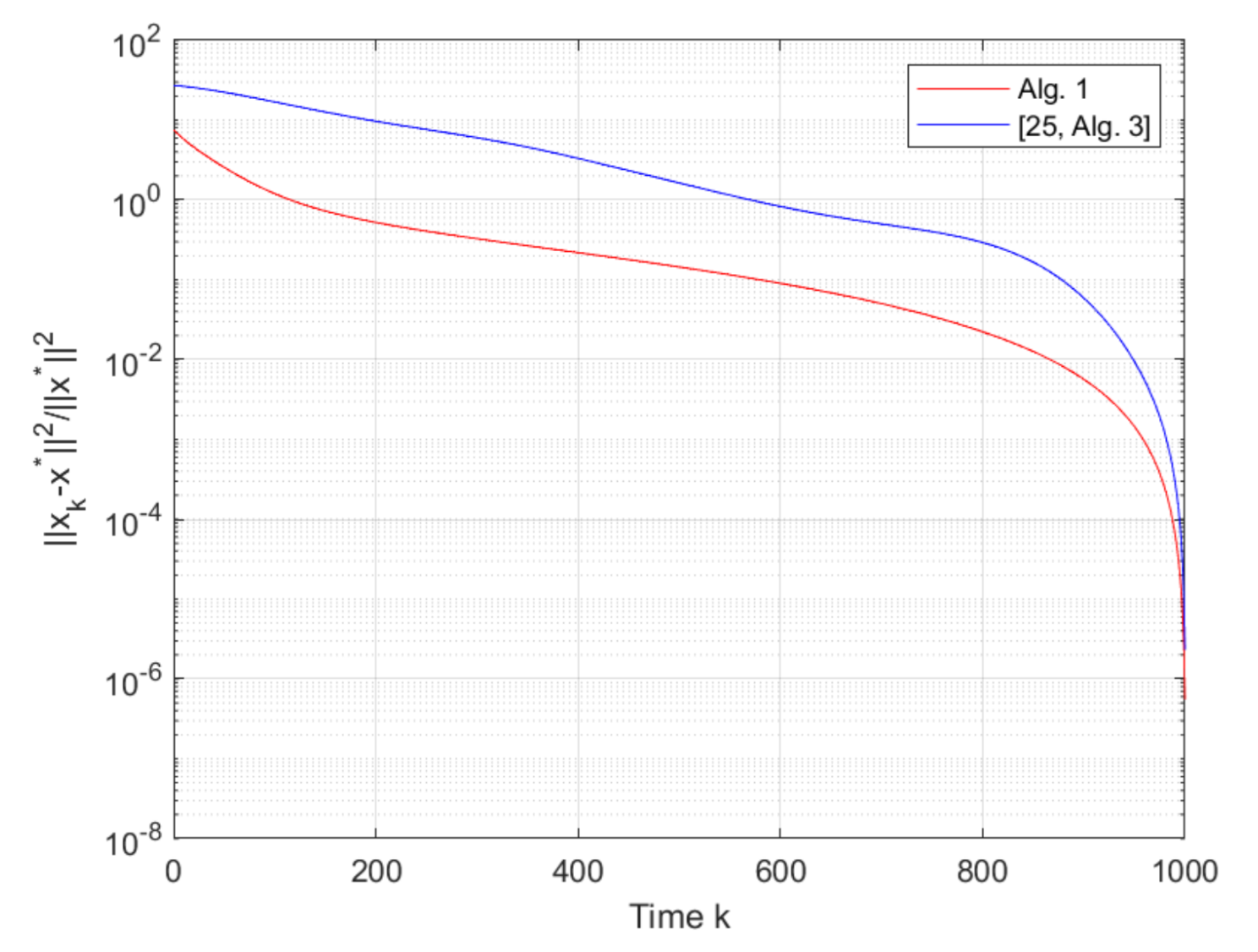
Then, it can be seen from Figure 6, that both of the proposed Algorithms 1 and 2 converge to the GNE $x^{*}$ with a faster convergence as compared with ([21], [Alg. 1]), where Algorithm 1 has the fastest convergent rate. From Figure 7 we can see that the proposed Algorithm 1 also has a faster convergence rate than ([25], [Alg. 3]). We set $\alpha =4.3\times {10}^{-3}$ in ([25], [Alg. 3]), the same step-sizes ${\mathsf{\tau }}_i,{\nu }_i$ and ${\sigma }_i$ and the same other parameters as Algorithms 1 and 2 in ([21], [Alg. 1]) and ([25], [Alg. 3]). On the other hand, as compared with the algorithm with inertia, Algorithm 1 with alternating inertia requires less computation resources. Thus, Algorithm 1 could be the best choice when both fast convergence rate and low computation cost are taken into consideration.

Remark 2.

It is worthwhile to note that the introduction of the inertia and overrelaxation steps has the potential of accelerating the convergence rate. As such, in this paper, the inertial and overrelaxed distributed algorithms are developed based on the pseudo-gradient method for seeking generalized Nash equilibrium in multi-player games. The similar inertia idea has been considered in the proximal-point algorithm (see ([25], [Alg. 3])). However, the proximal-point algorithm generally needs to solve the optimization problem at each step k, which may be time-consuming and possibly costs a great amount of computation resources in many situations. As such, pseudo-gradient algorithms with inertia and overrelaxation were constructed in this paper, which successfully guarantees the convergence to v-GNE with a fast convergence rate. Moreover, we note that the introduction of the inertia and overrelaxation steps increases the computation burden, and thus two alternating inertial and overrelaxed algorithms are established in Algorithms 1 and 2 to balance the convergence rate and computation burden. In order to better display the effectiveness of our algorithms, we have added the comparison with ([25], [Alg. 3]) in the simulation part (see Figure 7). From Figure 7, it can be seen that Algorithm 1 in this paper outperforms the ([25], [Alg. 3]) in terms of the convergence rate.

6. Conclusions

This paper has studied the GNE computation issue in multi-player games with shared coupling constraints under the partial-decision information setting. Two distributed algorithms with alternating inertia and alternating overrelaxation have been developed, respectively, with fixed step-sizes. Both algorithms have guaranteed the convergence to the GNE under a mild assumption, which have the potential of improving the convergence rate and saving computation cost. Finally, one simulation example has been provided to show the effectiveness of the proposed algorithms. Further research topics can be focused on stochastic NE seeking problems subject to time-varying topologies with and without event-triggered communication protocols.