On the Connectivity Measurement of the Fractal Julia Sets Generated from Polynomial Maps: A Novel Escape-Time Algorithm
Abstract
1. Introduction
- (1)
- This is the first attempt to solve the problem of measuring the connectivity of Julia sets generated from polynomial maps.
- (2)
- A criterion is designed to map the connectivity degree to the range of . In this way, the quantification of connectivity degree is effectively achieved.
- (3)
- The connectivity is visualized by coloring Julia sets with different brightnesses, which provides an intuitive way to identify the connectivity degree.
2. Definitions and Preliminaries
- (1)
- denotes the locations of ensuring the connectedness of .
- (2)
- denotes the locations of ensuring the disconnectedness of .
- (3)
- denotes the locations of ensuring the totally disconnectedness of .
3. Escape-Time Algorithm Design
- (I)
- First, similar to the classical : for polynomial maps f, denote R,N as the escape radius and escape-time, respectively. For each point in the lattice ℓ which contains , a serial number is assigned (, where . is the image’s resolution.
- (II)
- Travel all in the range to get a set K based on the following rule: if in which , the point is abandoned. Otherwise, . The number of points in K is defined as .
- (III)
- In the set K, and are iterated successively. Once a point is reached, we express it as and regard it as the initial point of a connected region , .
- (IV)
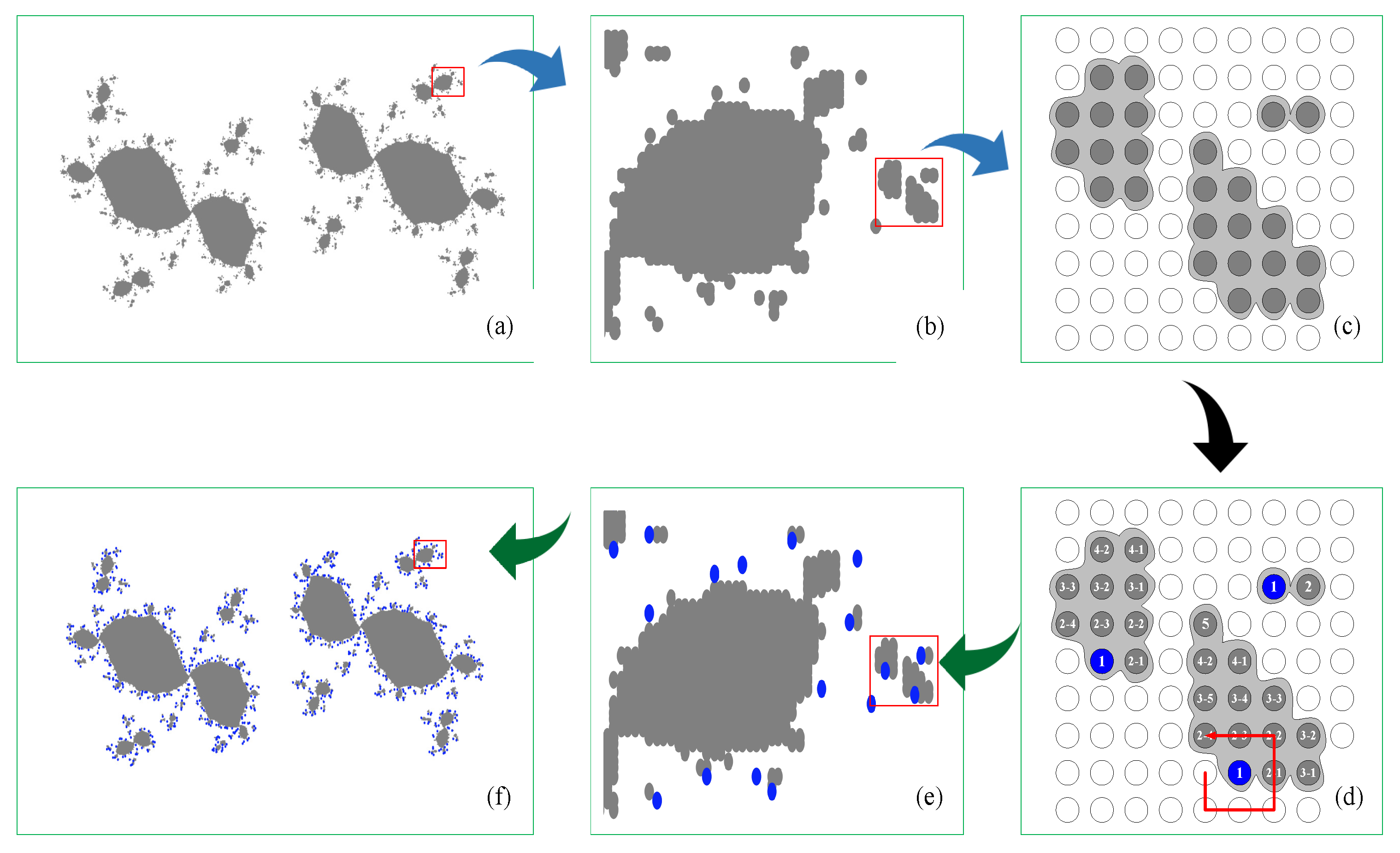
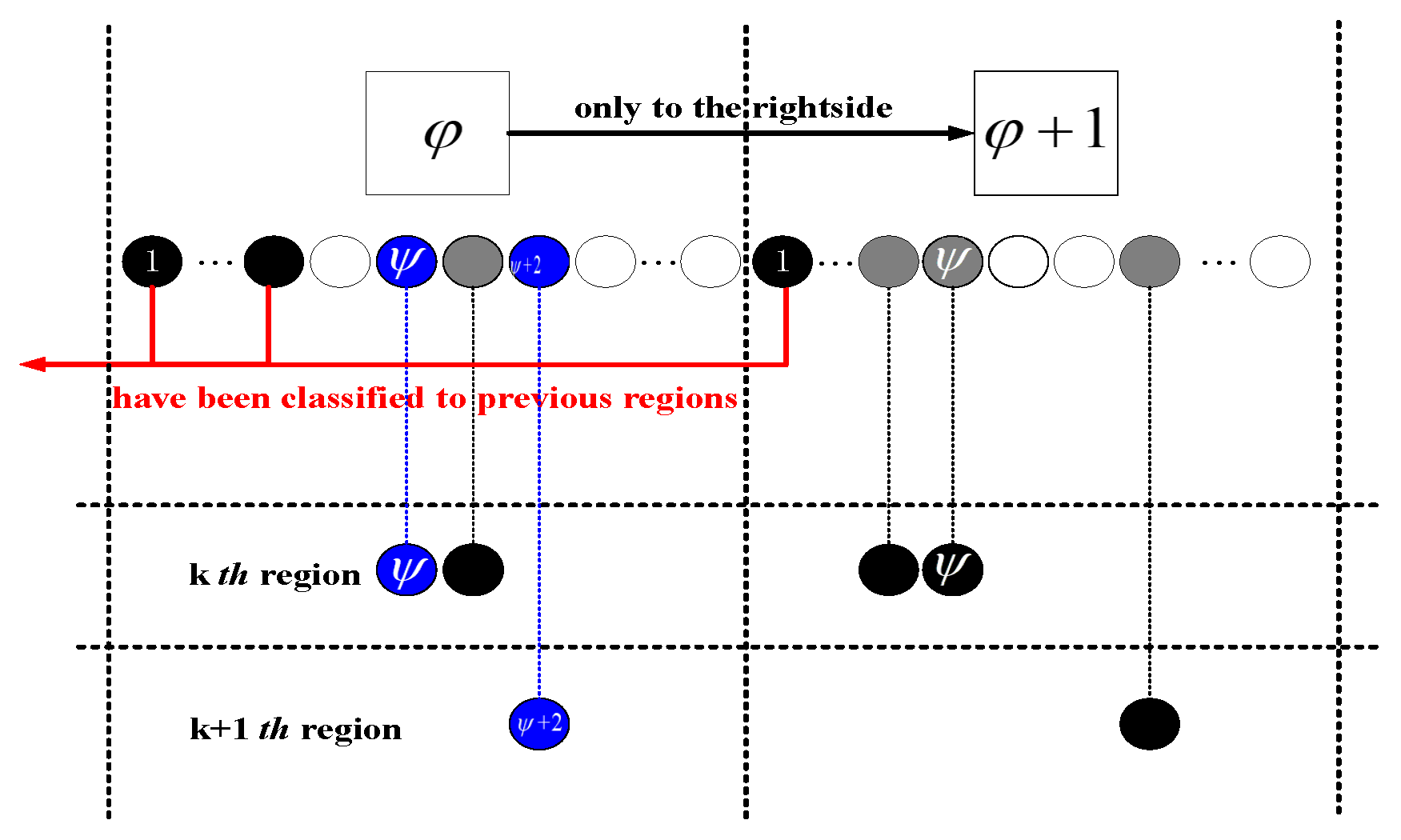
- Each has, at most, eight neighbors in K. In counter-clockwise order, the eight points ,,,, ,,, are denoted as , which means the second generation of . Suppose that connected regions have been classified; then, all the points before the iteration (always in counter-clockwise order) of are separated into a set , defined asThe iteration of yieldsAs shown in Figure 1, we illustrate a flowchart for a more intuitive explanation of the algorithm. The (a)–(c) parts of Figure 1 illustrate steps (I), (II), which are in accordance with the classical .The labelling process in steps (III), (IV) is shown in Figure 1d. Blue points in Figure 1d are the first points in regions . The grey points labeled with several generations are those connected with . It can be seen from step (IV) that there are some redundant computations in the labelling process. Specifically, 43-times redundant computations occur in Figure 1d. To handle this problem, the linked storage structure illustrated in Figure 2 is adopted. In Figure 2, the white points depict that do not belong to the set K, and the black points are those that have been classified in the previous regions. The grey and blue ones are those that will be classified only in the set
- (V)
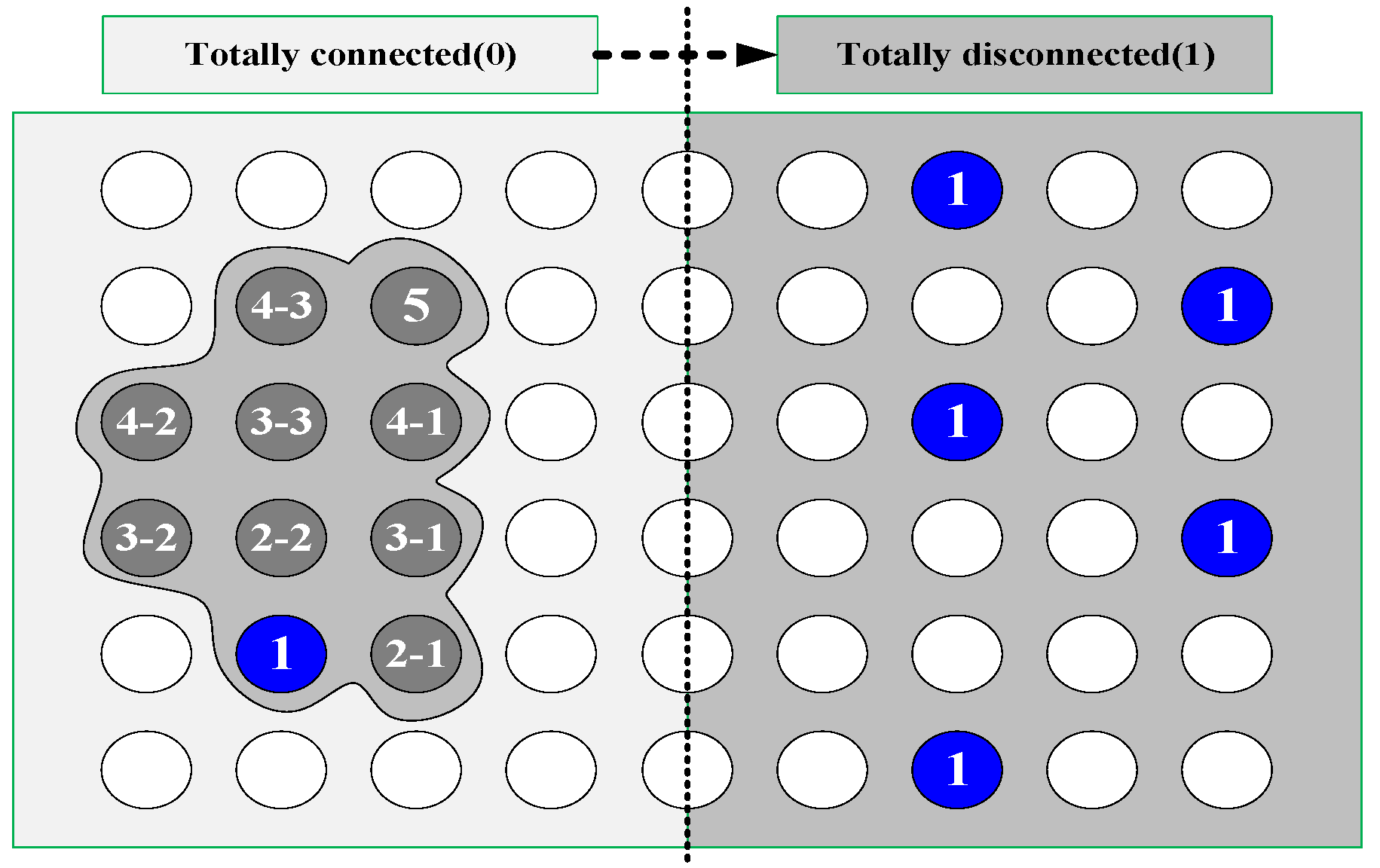
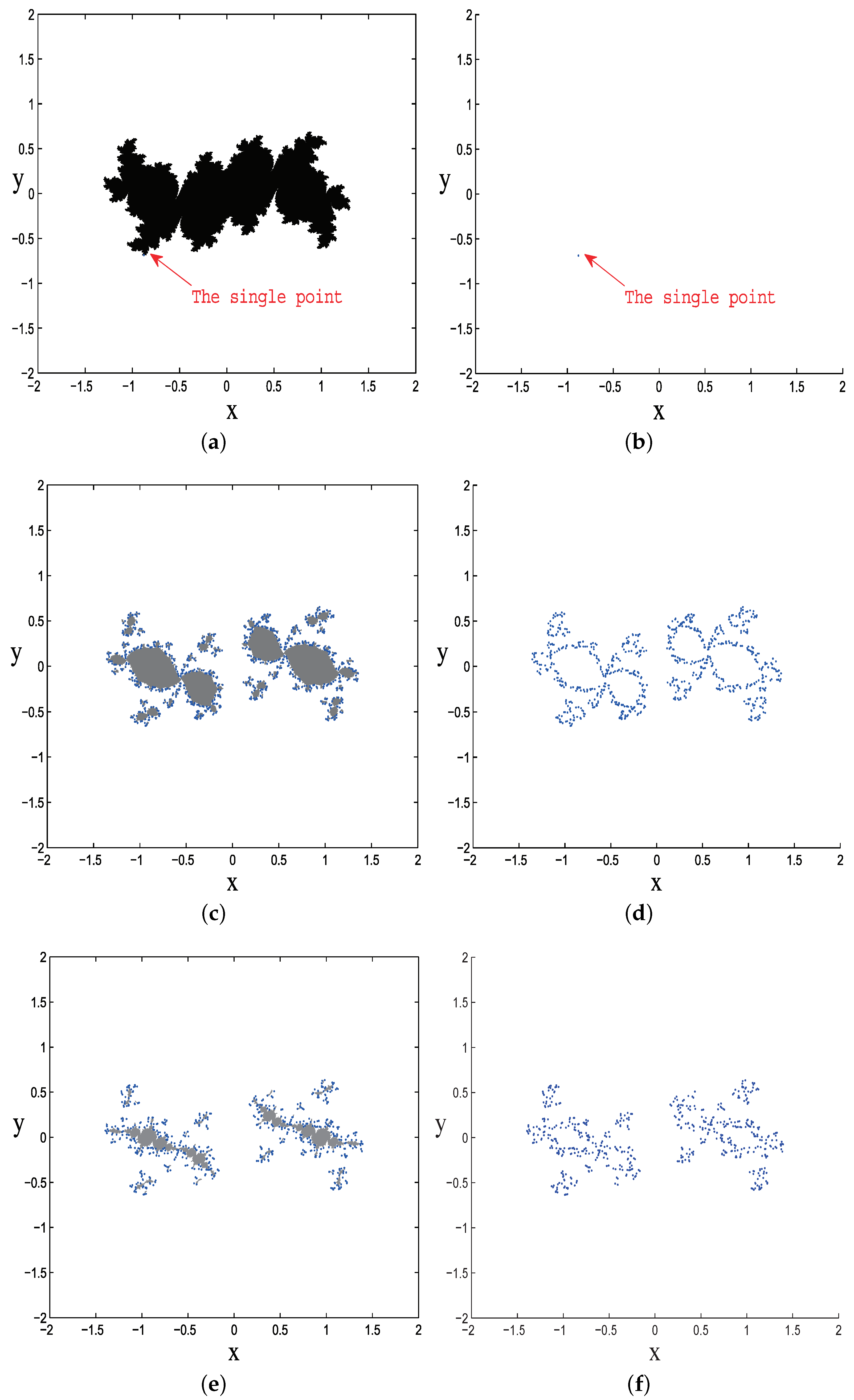
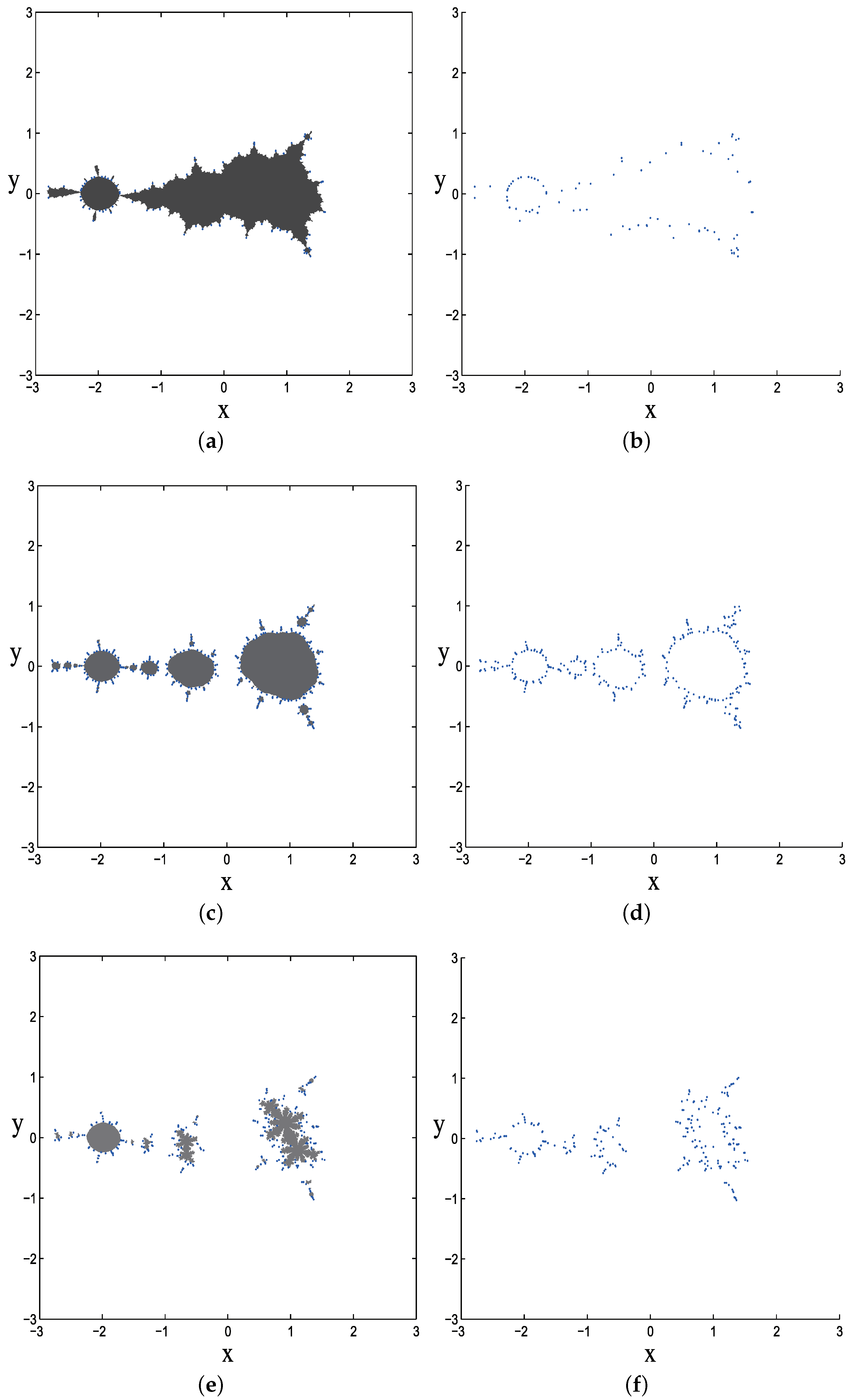
- Repeat steps (III) and (IV) until all points in K are classified. Count all the in each region and define the number as . It is clear that means the number of connected regions, that is, the degree of the fragmentation. Then, the connectivity criterion is defined asThe two extreme cases of connectivity are shown in Figure 3. For the right-side case, the Julia set is totally disconnected; herein, . For the left-side case, since there is a unique blue point and a unique , we define , which makes change in the closed interval [0, 1]. The smaller the value, the better the connectivity.
- (VI)
- According to the value of , the color ranges from dark gray to light gray. Highlight and separate all the with different colors.
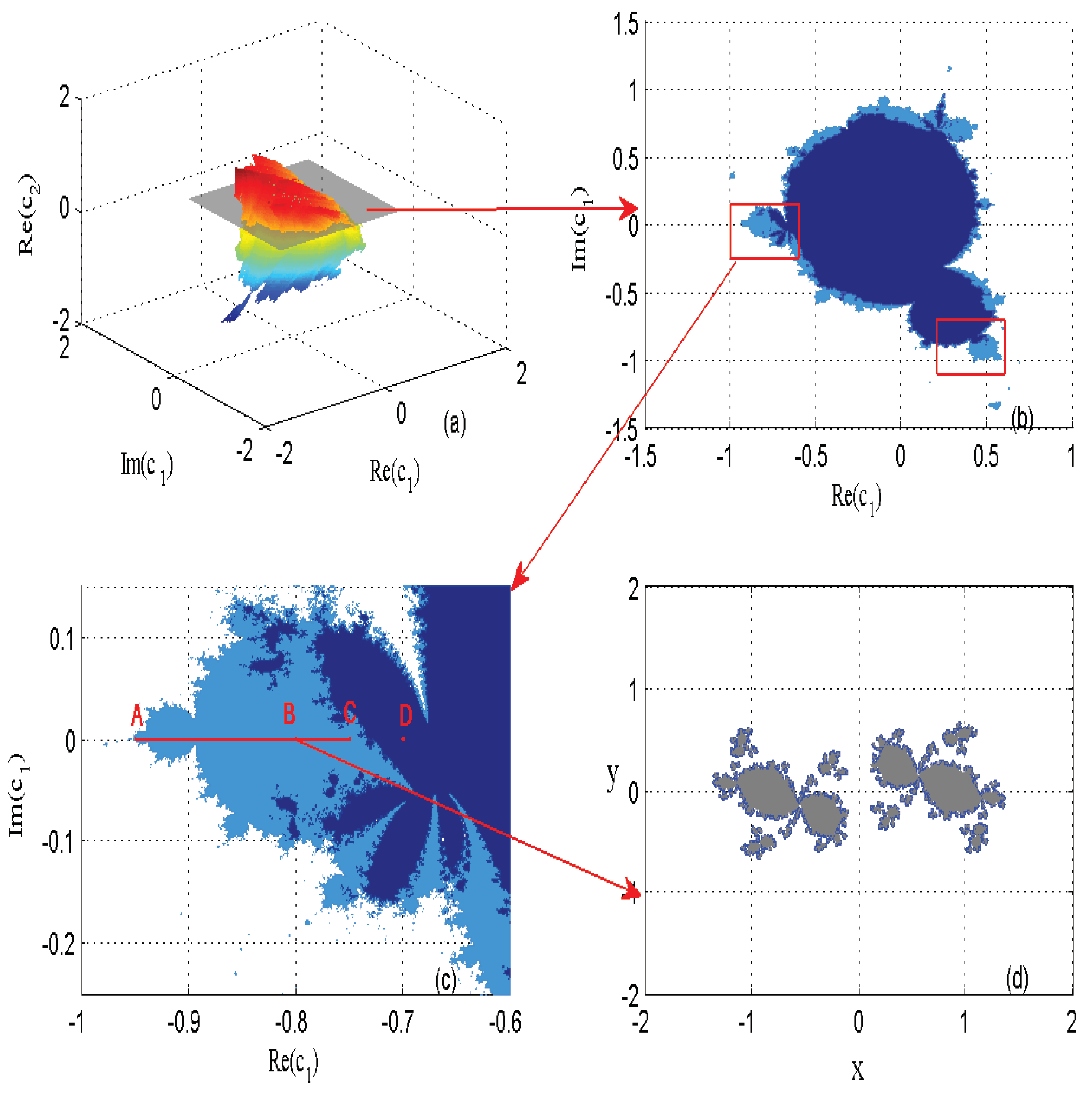
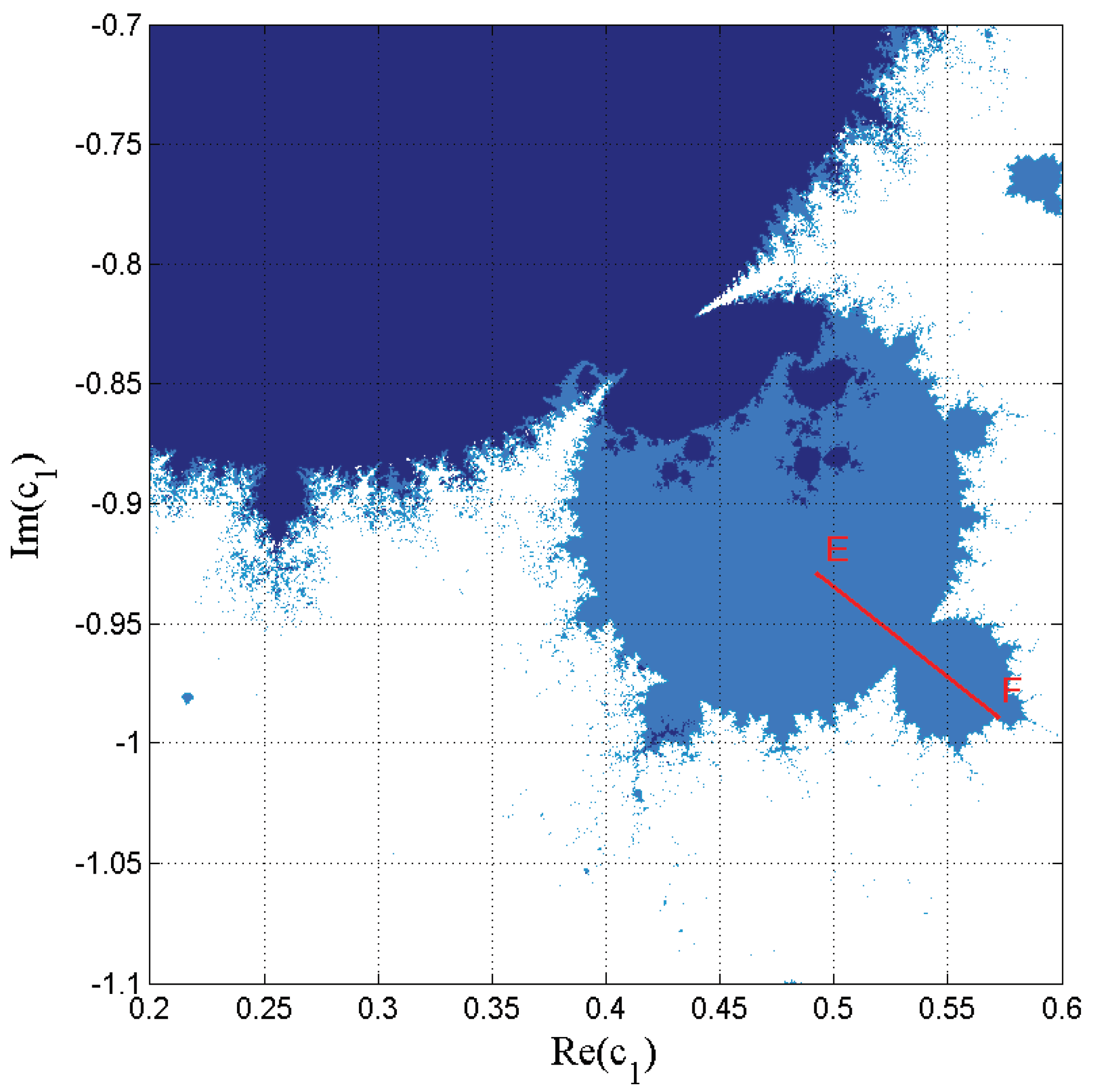
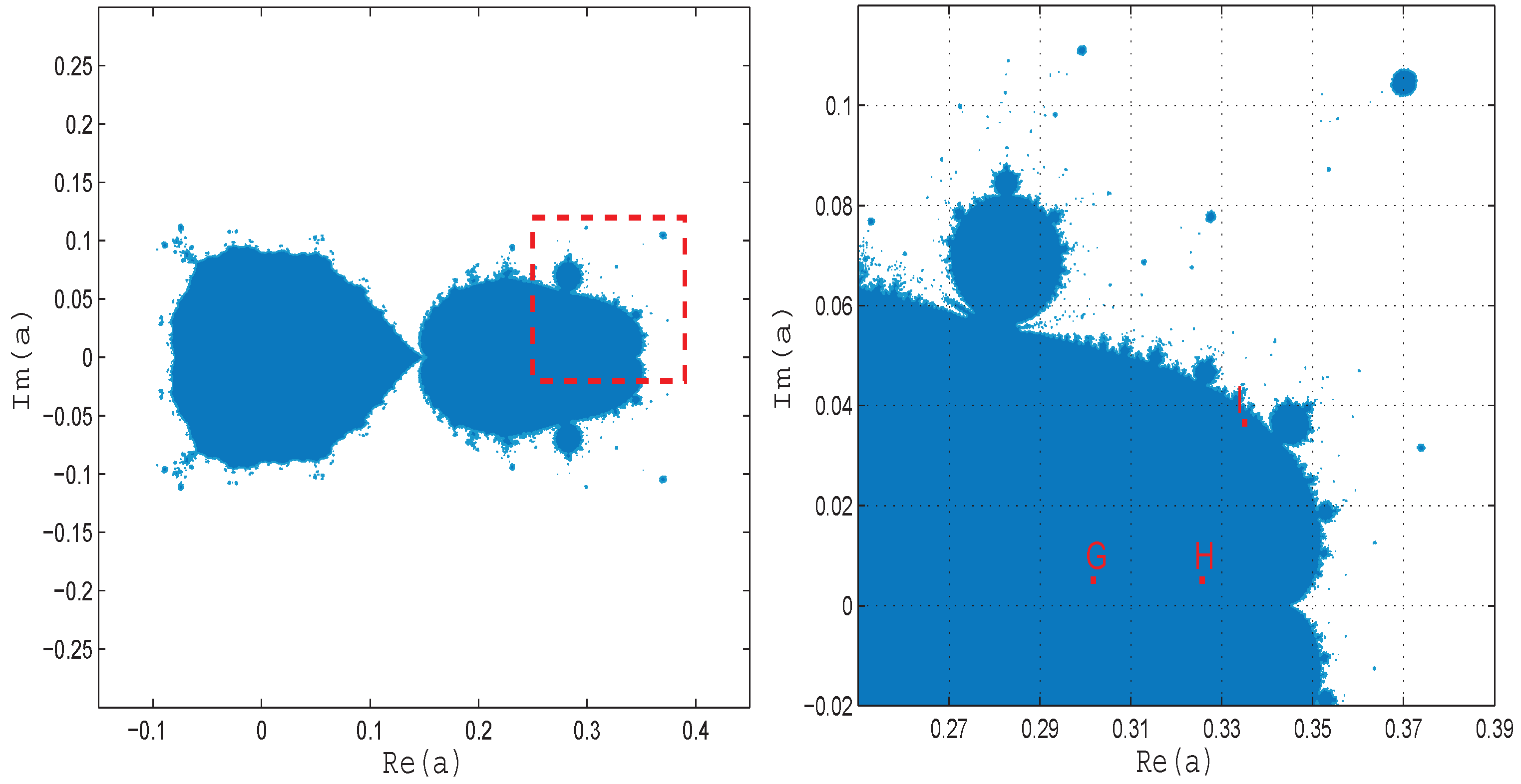
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peitgen, H.O.; Richter, P.H. The Beauty of Fractals; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Hutchinson, J.E. Fractals and self similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Boston, MA, USA, 1988. [Google Scholar]
- Blankers, V.; Rendfrey, T.; Shukert, A.; Shipman, P.D. Julia and Mandelbrot Sets for Dynamics over the Hyperbolic Numbers. Fractal Fract. 2019, 3, 6. [Google Scholar] [CrossRef]
- Losa, G.A. Fractals in biology and medicine. In Reviews in Cell Biology and Molecular Medicine; Birkhäuser: Locarno, Switzerland, 2006. [Google Scholar]
- Pickover, C.A. Biom orphs: Computer displays of biological forms generated from mathematical feedback loops. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 1986; Volume 5, pp. 313–316. [Google Scholar]
- Bercioux, D.; Iñiguez, A. Quantum fractals. Nat. Phys. 2019, 15, 111–112. [Google Scholar] [CrossRef]
- Wang, X.Y.; Liu, W.; Yu, X.J. Research on Brownian movement based on generalized Mandelbrot–Julia sets from a class complex mapping system. Mod. Phys. Lett. B 2007, 21, 1321–1341. [Google Scholar] [CrossRef]
- Ortiz, S.M.; Parra, O.; Miguel, J.; Espitia, R. Encryption through the Use of Fractals. Int. J. Math. Anal. 2017, 11, 1029–1040. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Xu, R.D.; Chen, L.N.; Hu, X.P. Image compression and encryption scheme using fractal dictionary and Julia set. IET Image Process. 2015, 9, 173–183. [Google Scholar] [CrossRef]
- Julia, G. Mémoire sur l’itération des fonctions rationnelles. J. Math. Pures Appl. 1918, 8, 47–245. [Google Scholar]
- Fatou, P. Sur les équations fonctionnelles. Bull. De La Société Mathématique De Fr. 1919, 47, 161–271. [Google Scholar]
- Smale, S. Differentiable dynamical systems. Bull. Am. Math. Soc. 1967, 73, 747–817. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B.; Peitgen, H.O.; Saupe, D. The Science of Fractal Images; Springer: New York, NY, USA, 1988. [Google Scholar]
- Welstead, S.T.; Cromer, T.L. Coloring periodicities of two-dimensional mappings. Comput. Graph. 1989, 13, 539–543. [Google Scholar] [CrossRef]
- Liu, X.D.; Zhu, Z.L.; Wang, G.X.; Zhu, W.Y. Composed accelerated escape-time algorithm to construct the general Mandelbrot sets. Fractals 2001, 9, 149–153. [Google Scholar] [CrossRef]
- Liu, S.; Cheng, X.C.; Fu, W.H.; Zhou, Y.P.; Li, Q.Z. Numeric characteristics of generalized M-set with its asymptote. Appl. Math. Comput. 2014, 243, 767–774. [Google Scholar] [CrossRef]
- Liu, M.; Liu, S.; Fu, W.; Zhou, J. Distributional escape-time algorithm based on generalized fractal sets in cloud environment. Chin. J. Electron. 2015, 24, 124–127. [Google Scholar] [CrossRef]
- Jovanovic, P.; Tuba, M.I.; Simian, D.A.; Romania, S.S. A new visualization algorithm for the Mandelbrot set. In Proceedings of the 10th WSEAS International Conference on Mathematics and Computers in Biology and Chemistry; World Scientific and Engineering Academy and Society (WSEAS): Stevens Point, WI, USA, 2009; pp. 162–166. [Google Scholar]
- Sun, Y.Y.; Hou, K.N.; Zhao, X.D.; Lu, Z.X. Research on characteristics of noise-perturbed M-J sets based on equipotential point algorithm. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 284–298. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Wang, X.Y. Quaternion M set with none zero critical points. Fractals 2009, 17, 427–439. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Wang, X.Y. Noise-perturbed quaternionic Mandelbrot sets. Int. J. Comput. Math. 2009, 86, 2008–2028. [Google Scholar] [CrossRef]
- Martineau, É.; Rochon, D. On a bicomplex distance estimation for the Tetrabrot. Int. J. Bifurc. Chaos 2005, 15, 3039–3050. [Google Scholar] [CrossRef]
- Mohammed, A.J. A comparison of fractal dimension estimations for filled Julia fractal sets based on the escape-time algorithm. In AIP Conference Proceedings; AIP Publishing LLC: Malang, Indonesia, 2019; Volume 2086, p. 030026. [Google Scholar]
- Wang, H.X.; Zhao, X.F.; Shi, Y.Q.; Kim, H.J.; Piva, A. Digital Forensics and Watermarking; Springer Nature: Chengdu, China, 2019. [Google Scholar]
- Rǎdulescu, A.; Pignatelli, A. Real and complex behavior for networks of coupled logistic maps. Nonlinear Dyn. 2017, 87, 1295–1313. [Google Scholar] [CrossRef]
- Danca, M.F.; Romera, M.; Pastor, G. Alternated Julia sets and connectivity properties. Int. J. Bifurc. Chaos 2009, 19, 2123–2129. [Google Scholar] [CrossRef]
- Danca, M.F.; Bourke, P.; Romera, M. Graphical exploration of the connectivity sets of alternated Julia sets. Nonlinear Dyn. 2013, 73, 1155–1163. [Google Scholar] [CrossRef]
- Zhang, Y.X. Switching-induced Wada basin boundaries in the Héon map. Nonlinear Dyn. 2013, 73, 2221–2229. [Google Scholar] [CrossRef]
- Wang, D.; Liu, S.T. On the boundedness and symmetry properties of the fractal sets generated from alternated complex map. Symmetry 2016, 8, 7. [Google Scholar] [CrossRef]
- Wang, D.; Liu, S.T.; Zhao, Y. A preliminary study on the fractal phenomenon: Disconnected+disconnected=connected. Fractals 2017, 25, 1750004. [Google Scholar] [CrossRef]
- Andreadis, I.; Karakasidis, T.E. On a numerical approximation of the boundary structure and of the area of the Mandelbrot set. Nonlinear Dyn. 2015, 80, 929–935. [Google Scholar] [CrossRef]
- Andreadis, I.; Karakasidis, T.E. On a topological closeness of perturbed Julia sets. Appl. Math. Comput. 2010, 217, 2883–2890. [Google Scholar] [CrossRef]
- Andreadis, I.; Karakasidis, T.E. On a closeness of the Julia sets of noise-perturbed complex quadratic maps. Int. J. Bifurc. Chaos 2012, 22, 1250221. [Google Scholar] [CrossRef]
- Jovanovic, R.; Tuba, M. A visual analysis of calculation-paths of the Mandelbrot set. WSEAS Trans. Comput. 2009, 8, 1205–1214. [Google Scholar]
- Katagata, K. Quartic Julia sets including any two copies of quadratic Julia sets. Discret. Contin. Dyn. Syst. 2016, 36, 2103. [Google Scholar] [CrossRef][Green Version]
- Sajid, M.; Kapoor, G.P. Chaos in dynamics of a family of transcendental meromorphic functions. J. Nonlinear Anal. Appl. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Sajid, M. Bifurcation and chaos in real dynamics of a two-parameter family arising from generating function of generalized Apostol-type polynomials. Math. Comput. Appl. 2018, 23, 7. [Google Scholar] [CrossRef]
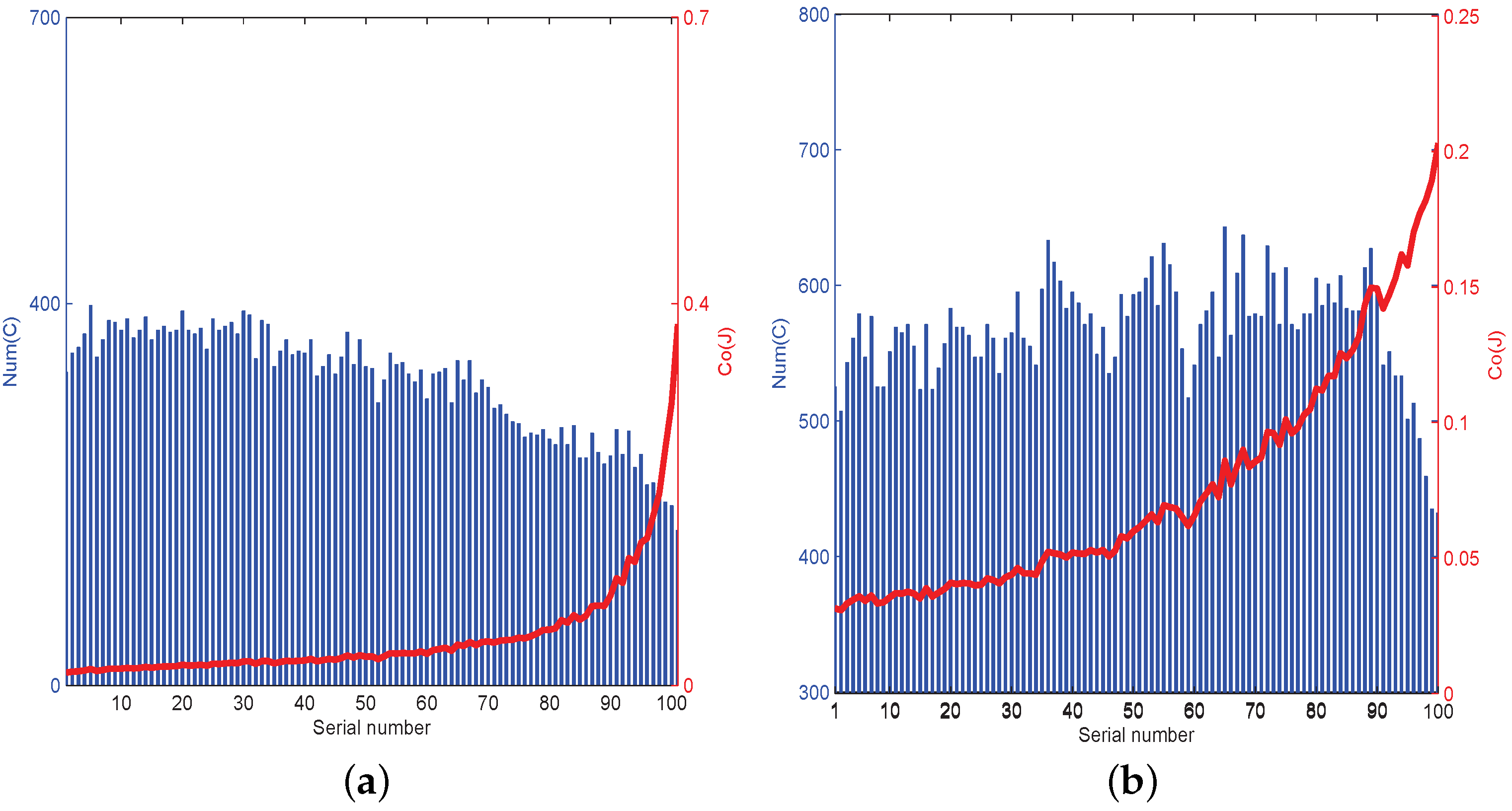
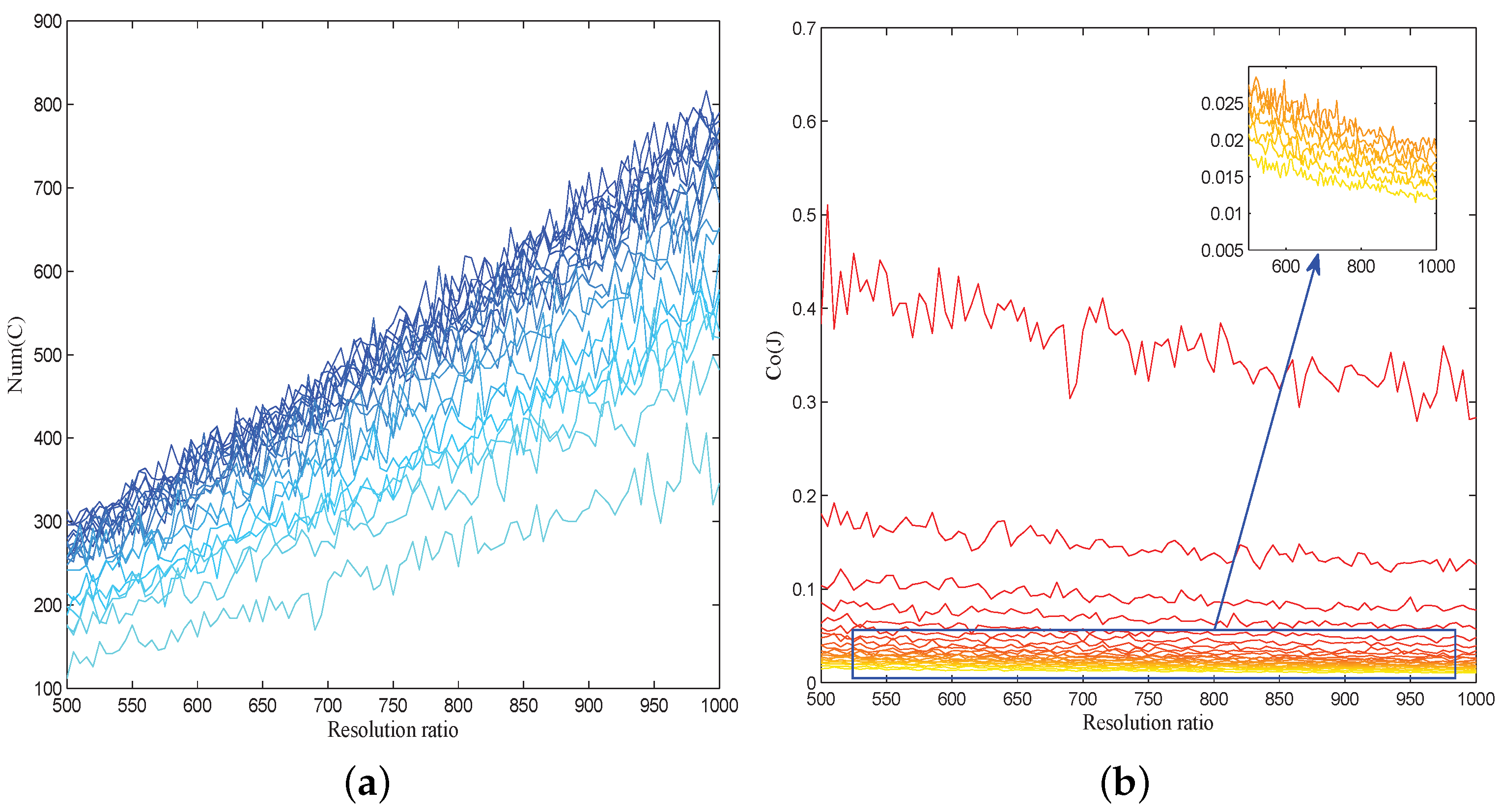
| No. | 1 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 348 | 344 | 384 | 372 | 372 | 372 | 388 | 350 | 362 | 344 | 332 | |
| 0.0143 | 0.0151 | 0.0183 | 0.0192 | 0.0207 | 0.0224 | 0.0252 | 0.0245 | 0.0276 | 0.0286 | 0.0303 | |
| No. | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | - |
| 338 | 326 | 320 | 290 | 260 | 252 | 238 | 268 | 210 | 162 | - | |
| 0.0339 | 0.0370 | 0.0412 | 0.0447 | 0.0492 | 0.0597 | 0.0729 | 0.1121 | 0.1542 | 0.3785 | - |
| No. | 1 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 311 | 299 | 317 | 319 | 311 | 349 | 395 | 397 | 363 | 411 | 439 | |
| 0.0194 | 0.0193 | 0.0213 | 0.0224 | 0.0229 | 0.0271 | 0.0322 | 0.0347 | 0.0338 | 0.0415 | 0.0484 | |
| No. | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | - |
| 371 | 445 | 371 | 423 | 429 | 391 | 417 | 381 | 349 | 321 | - | |
| 0.0450 | 0.0594 | 0.0548 | 0.0697 | 0.0797 | 0.0830 | 0.1040 | 0.1202 | 0.1707 | 0.2967 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhao, S.; Zhang, Y.; Wang, D. On the Connectivity Measurement of the Fractal Julia Sets Generated from Polynomial Maps: A Novel Escape-Time Algorithm. Fractal Fract. 2021, 5, 55. https://doi.org/10.3390/fractalfract5020055
Zhao Y, Zhao S, Zhang Y, Wang D. On the Connectivity Measurement of the Fractal Julia Sets Generated from Polynomial Maps: A Novel Escape-Time Algorithm. Fractal and Fractional. 2021; 5(2):55. https://doi.org/10.3390/fractalfract5020055
Chicago/Turabian StyleZhao, Yang, Shicun Zhao, Yi Zhang, and Da Wang. 2021. "On the Connectivity Measurement of the Fractal Julia Sets Generated from Polynomial Maps: A Novel Escape-Time Algorithm" Fractal and Fractional 5, no. 2: 55. https://doi.org/10.3390/fractalfract5020055
APA StyleZhao, Y., Zhao, S., Zhang, Y., & Wang, D. (2021). On the Connectivity Measurement of the Fractal Julia Sets Generated from Polynomial Maps: A Novel Escape-Time Algorithm. Fractal and Fractional, 5(2), 55. https://doi.org/10.3390/fractalfract5020055





